Semester 2 Block 2 (Advanced Topics for LM) Recap

The probability \(p\) ranges from 0 to 1.
The odds \(\frac{p}{1-p}\) ranges from 0 to \(\infty\).
The log-odds \(\log \left( \frac{p}{1-p} \right)\) ranges from \(-\infty\) to \(\infty\).

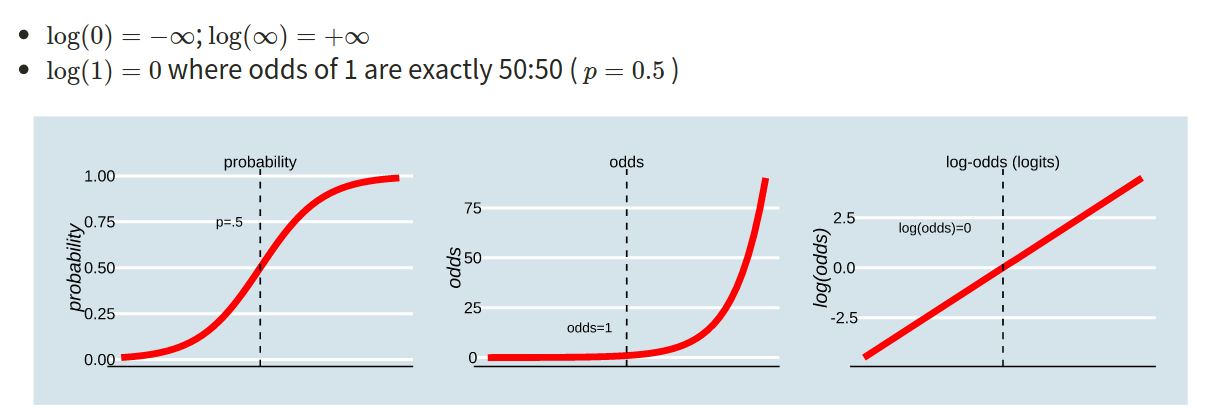
Figure 1: Probability, Odds and Log-odds

In order to understand the connections among these concepts, lets work with an example where the probability of an event occurring is 0.2:

Odds of event occurring:

\[ \text{odds} = (\frac{0.2}{0.8}) = 0.25 \]

Log-odds of the event occurring:

\[ log(\frac{0.2}{0.8}) = -1.3863 \\ \ \\ \text{OR} \\ \ \\ log(0.25) = -1.3863 \]

Probability can be reconstructed as:

\[ (\frac{odds}{1+odds}) = (\frac{0.25}{1+0.25}) = 0.2 \\ \ \\ \text{OR} \\ \ \\ (\frac{exp(log(odds))}{1+exp(log(odds))}) = (\frac{exp(-1.3863)}{1+exp(-1.3683)}) = (\frac{0.25}{1.25}) = 0.2 \]

In R:

obtain the odds

odds <- 0.2 / (1 - 0.2)
obtain the log-odds for a given probability

log_odds <- log(0.25)

OR

log_odds <- qlogis(0.2)
obtain the probability from the odds

prob_O <- odds / (1 + odds)
obtain the probability from the log-odds

prob_LO <- exp(log_odds) / (1 + exp(log_odds))

OR

prob_LO <- plogis(log_odds)

Generalized linear models can be fitted in R using the glm function, which is similar to the lm function for fitting linear models. However, we also need to specify the family (i.e., link) function. There are three key components to consider:

Random component / probability distribution - The distribution of the response/outcome variable. Can be from any family of distributions as listed below.
Systematic component / linear predictor - the explanatory/predictor variable(s) (can be continuous or discrete).
Link function - specifies the link between a random and systematic components.

Formula:

\(y_i = \beta_0 + \beta_1 x_i + + \beta_2 x_i + \epsilon_i\)

In R:

glm(y ~ x1 + x2, data = data, family = <INSERT_FAMILY>)

The family argument takes (the name of) a family function which specifies the link function and variance function (as well as a few other arguments not entirely relevant to the purpose of this course).

The exponential family functions available in R are:

binomial (link = “logit”)
gaussian (link = “identity”)
poisson (link = “log”)
Gamma (link = “inverse”)
inverse.gaussian (link = “1/mu2”)

See ?glm for other modeling options. See ?family for other allowable link functions for each family.

When a response (y) is binary coded (e.g., 0/1; failure/success; no/yes; fail/pass; unemployed/employed) we must use logistic regression. The predictors can either be continuous or categorical.

\[ {\log(\frac{p_i}{1-p_i})} = \beta_0 + \beta_1 \ x_{i1} \]

In R:

glm(y ~ x1 + x2, data = data, family = binomial)

To translate log-odds to odds in order to aid interpretation, you must exponentiate (i.e., by using exp()) the coefficients from your model.

In R:

exp(coef(modelname))

We can also use R to extract predicted probabilities for us from our models.

Calculate the predicted log-odds (probabilities on the logit scale): predict(model, type="link")
Calculate the predicted probabilities: predict(model, type="response")

Exploratory analyses are conducted when either (1) you have a hypothesis but no clear analysis plan/strategy; (2) you have lots of variables that might be associated with an outcome variable, but you’re not sure which or in what ways i.e., no clear predictions. It also provides tools for hypothesis generation - particularly via visualisation of data.

Confirmatory analyses are conducted when you have a specific research question to test. You can think of this type of analysis as putting your hypotheses to trial - does your data support or fail to support your argument?

There are a number of steps involved in exploratory analyses:

Step 1: Check coding of data and visualise variables of interest
Step 2: Compare models of interest to find if your variables of interest are good predictors of your outcome variable
Step 3: Compute the k-fold cross validation MSE for each of your models
Step 4: Identify best fitting model

Power for regression

In linear regression, the relevant function in R is

library(pwr)
pwr.f2.test(u = , v = , f2 = , sig.level = , power = )

where

u = numerator degrees of freedom
v = denominator degrees of freedom
f2 = effect size

The formula for the effect size \(f^2\) is different depending on your goal.

Goal 1. Test on all slopes

Here you have one model, \[ y = \beta_0 + \beta_1 x_1 + \dots + \beta_k x_k + \epsilon \]

and you wish to find the minimum sample size required to answer the following test of hypothesis with a given power: \[ \begin{aligned} H_0 &: \beta_1 = \beta_2 = \dots = \beta_k = 0 \\ H_1 &: \text{At least one } \beta_i \neq 0 \end{aligned} \]

The appropriate formula for the effect size is: \[ f^2 = \frac{R^2}{1 - R^2} \]

And the numerator degrees of freedom are \(\texttt u = k\), the number of predictors in the model.

The denominator degrees of freedom returned by the function will give you: \[ \texttt v = n - (k + 1) = n - k - 1 \]

From which you can infer the sample size as \[ n = \texttt v + k + 1 \]

Goal 2. Test on a subset of slopes

In this case you would have a smaller model \(m\) with \(k\) predictors and a larger model \(M\) with \(K\) predictors: \[ \begin{aligned} m &: \quad y = \beta_0 + \beta_1 x_1 + \dots + \beta_{k} x_k + \epsilon \\ M &: \quad y = \beta_0 + \beta_1 x_1 + \dots + \beta_{k} x_k + \underbrace{\beta_{k + 1} x_{k+1} + \dots + \beta_{K} x_K}_{\text{extra predictors}} + \epsilon \end{aligned} \]

This case is when you wish to find the minimum sample size required to answer the following test of hypothesis: \[ \begin{aligned} H_0 &: \beta_{k+1} = \beta_{k+2} = \dots = \beta_K = 0 \\ H_1 &: \text{At least one of the above } \beta \neq 0 \end{aligned} \]

You need to use the R-squared from the larger model \(R^2_M\) and the R-squared from the smaller model \(R^2_m\). The appropriate formula for the effect size is: \[ f^2 = \frac{R^2_{M} - R^2_{m}}{1 - R^2_M} \]

Here, the numerator degrees of freedom are the extra predictors: \(\texttt u = K - k\).

The denominator degrees of freedom returned by the function will give you (here you use \(K\) the number of all predictors in the larger model): \[ \texttt v = n - (K + 1) = n - K - 1 \]

From which you can infer the sample size as \[ n = \texttt v + K + 1 \]

3. Generic guidelines

But what can you do if you have no clue what effect size to expect in a given study? Cohen (1988)¹ provided guidelines for what a small, medium, or large effect typically is in the behavioural sciences.

Type of test	Small	Medium	Large
t-test	0.20	0.50	0.80
ANOVA	0.10	0.25	0.40
Linear regression	0.02	0.15	0.35

For more information, please refer to Cohen J. (1992).²