Multiple linear regression basics
Information about solutions
Solutions for these exercises are available immediately below each question.
We would like to emphasise that much evidence suggests that testing enhances learning, and we strongly encourage you to make a concerted attempt at answering each question before looking at the solutions. Immediately looking at the solutions and then copying the code into your work will lead to poorer learning.
We would also like to note that there are always many different ways to achieve the same thing in R, and the solutions provided are simply one approach.
Be sure to check the solutions to last week’s exercises.
You can still ask any questions about previous weeks’ materials if things aren’t clear!
LEARNING OBJECTIVES
- Extend the ideas of SLR to consider regression models with two or more predictors.
- Understand and interpret the coefficients in multiple linear regression models
- (Categorical pred.) Understand the meaning of a MLR model with categorical predictors (no interaction case). For example, two parallel regression lines, one for each of two groups.
In this block of exercises, we move from the simple linear regression model (one outcome variable, one explanatory variable) to the multiple regression model (one outcome variable, multiple explanatory variables). Everything we just learned about simple linear regression can be extended (with minor modification) to the multiple regresion model. The key conceptual difference is that for simple linear regression we think of the distribution of errors at some fixed value of the explanatory variable, and for multiple linear regression, we think about the distribution of errors at fixed set of values for all our explanatory variables.
~ Numeric + Numeric
Research question
Reseachers are interested in the relationship between psychological wellbeing and time spent outdoors.
The researchers know that other aspects of peoples’ lifestyles such as how much social interaction they have can influence their mental well-being. They would like to study whether there is a relationship between well-being and time spent outdoors after taking into account the relationship between well-being and social interactions.
Create a new RMarkdown, and in the first code-chunk, load the required libraries and import the wellbeing data into R. Assign them to a object called mwdata.
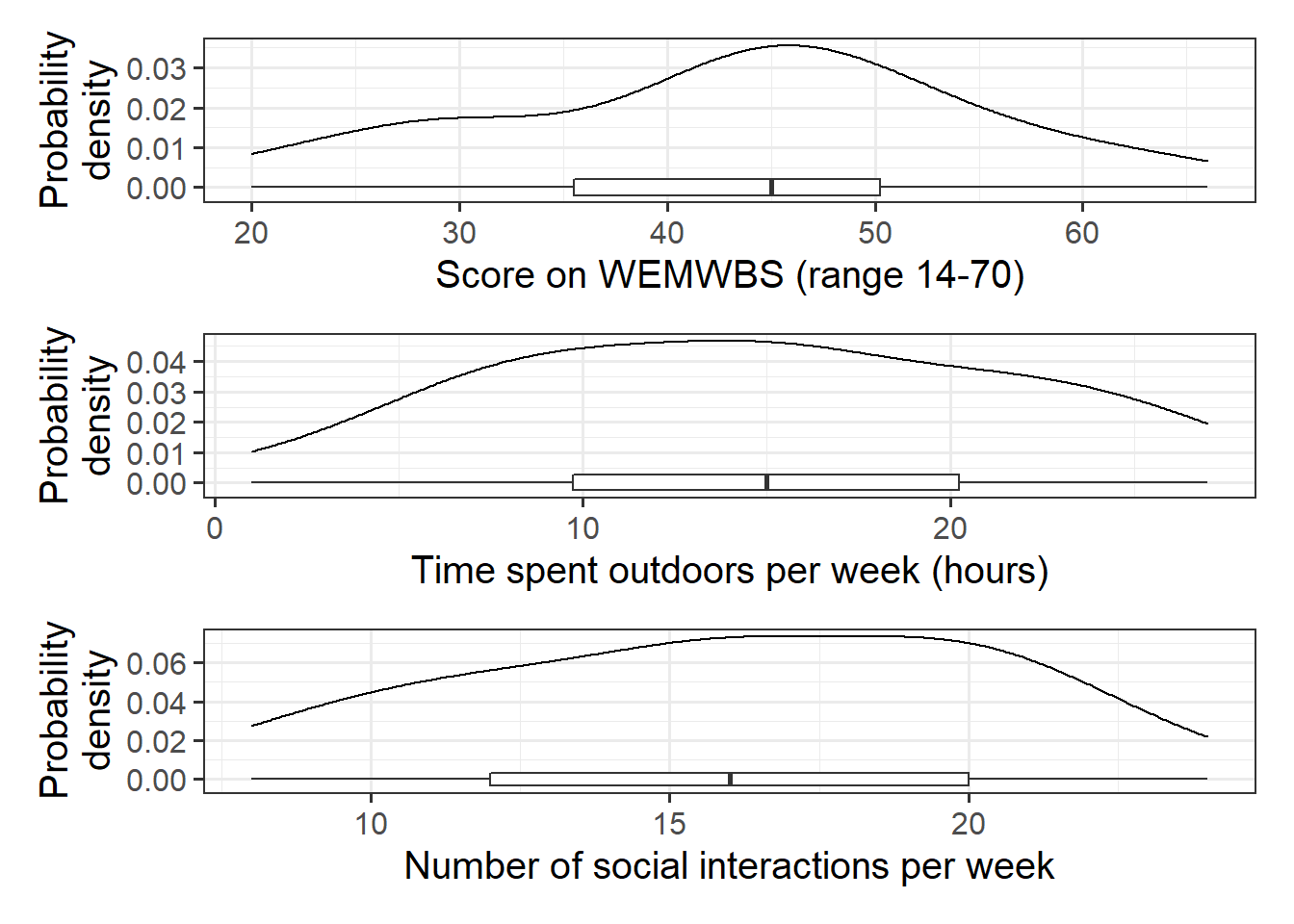
Produce plots of the marginal distributions (the distributions of each variable in the analysis without reference to the other variables) of the wellbeing, outdoor_time, and social_int variables.
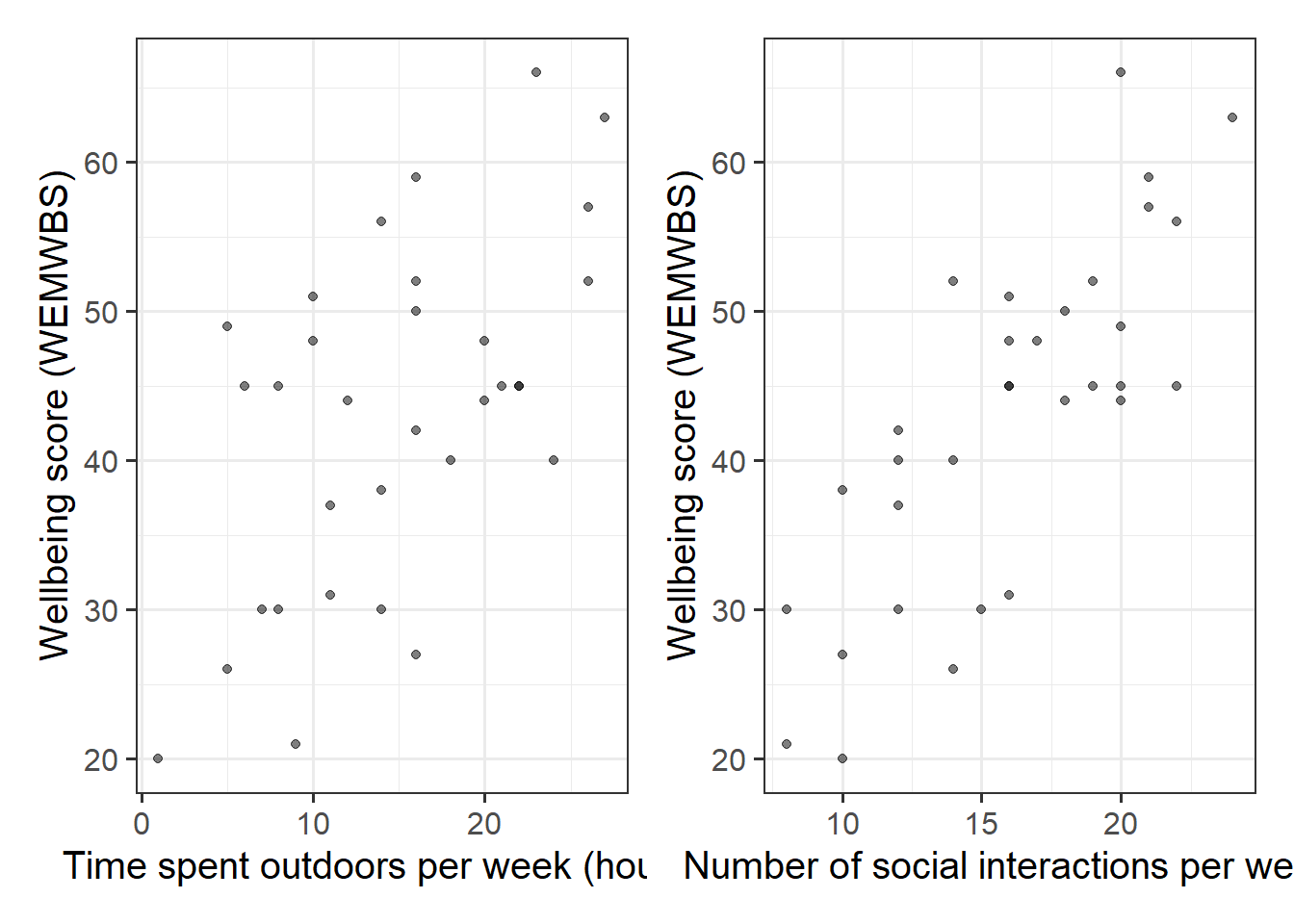
Produce plots of the marginal relationships between the outcome variable (wellbeing) and each of the explanatory variables.
Produce a correlation matrix of the variables which are to be used in the analysis, and write a short paragraph describing the relationships.
Correlation matrix
A table showing the correlation coefficients - \(r_{(x,y)}=\frac{\mathrm{cov}(x,y)}{s_xs_y}\) - between variables. Each cell in the table shows the relationship between two variables. The diagonals show the correlation of a variable with itself (and are therefore always equal to 1).
We can create a correlation matrix easily by giving the cor() function a dataframe. However, we only want to give it 3 columns here. Think about how we select specific columns, either using select(), or giving the column numbers inside [].
The scatterplots we created above show moderate, positive, and linear relationships both between outdoor time and wellbeing, and between numbers of social interactions and wellbeing.
Specify the form of your model, where \(x_1\) = weekly outdoor time, \(x_2\) = weekly numbers of social interactions and \(y\) = scores on the WEMWBS.
What are the parameters of the model. How do we denote parameter estimates?
Visual
Note that for simple linear regression we talked about our model as a line in 2 dimensions: the systematic part \(\beta_0 + \beta_1 x\) defined a line for \(\mu_y\) across the possible values of \(x\), with \(\epsilon\) as the random deviations from that line. But in multiple regression we have more than two variables making up our model.
In this particular case of three variables (one outcome + two explanatory), we can think of our model as a regression surface (See Figure 3). The systematic part of our model defines the surface across a range of possible values of both \(x_1\) and \(x_2\). Deviations from the surface are determined by the random error component, \(\hat \epsilon\).
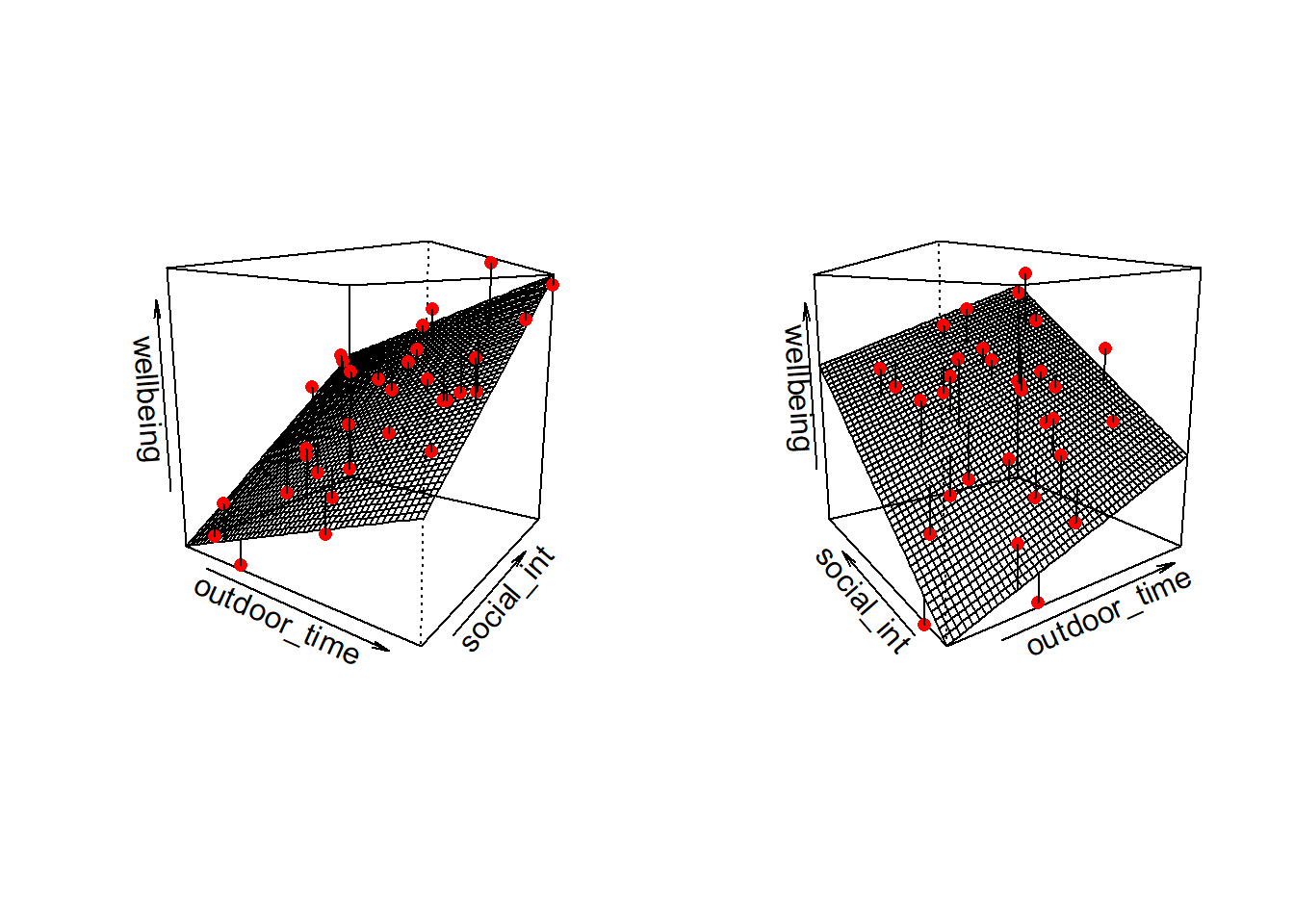
Figure 3: Regression surface for wellbeing ~ outdoor_time + social_int, from two different angles
Don’t worry about trying to figure out how to visualise it if we had any more explanatory variables! We can only concieve of 3 spatial dimensions. One could imagine this surface changing over time, which would bring in a 4th dimension, but beyond that, it’s not worth trying!.
Fit the linear model in R, assigning the output to an object called mdl1.
lm() function. We can add as many explanatory variables as we like, separating them with a +.lm( <response variable> ~ 1 + <explanatory variable 1> + <explanatory variable 2> + ... , data = <dataframe> )
IMPORTANT!
You can think of the sequence of steps involved in statistical modeling as:
\[
\text{Choose} \rightarrow \text{Fit} \rightarrow \text{Assess} \rightarrow \text{Use}
\]
So far for our multiple regression model we have completed the first two steps (Choose and Fit) in that we have:
- Explored/visualised our data and specified our model
- fitted the model in R.
We are going to skip straight to the Use step here, and move to interpreting our parameter estimates and construct confidence intervals around them. Please note that this when conducting real analyses, this would be an inappropriate thing to do. We will look at how to Assess whether a multiple regression model meets assumptions in a later lab.
Using any of:
mdl1mdl1$coefficientscoef(mdl1)coefficients(mdl1)summary(mdl1)
Write out the estimated parameter values of:
- \(\hat \beta_0\), the estimated average wellbeing score associated with zero hours of outdoor time and zero social interactions per week.
- \(\hat \beta_1\), the estimated increase in average wellbeing score associated with one hour increase in weekly outdoor time, holding the number of social interactions constant (i.e., when the remaining explanatory variables are held at the same value or are fixed).
- \(\hat \beta_2\), the estimated increase in average wellbeing score associated with an additional social interaction per week (an increase of one), holding weekly outdoor time constant.
Interpretation of Muliple Regression Coefficients
You’ll hear a lot of different ways that people explain multiple regression coefficients.
For the model \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon\), the estimate \(\hat \beta_1\) will often be reported as:
the increase in \(y\) for a one unit increase in \(x_1\) when…
- holding the effect of \(x_2\) constant.
- controlling for differences in \(x_2\).
- partialling out the effects of \(x_2\).
- holding \(x_2\) equal.
- accounting for effects of \(x_2\).
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.3703775 4.3205141 1.242995 2.238259e-01
## outdoor_time 0.5923673 0.1689445 3.506284 1.499467e-03
## social_int 1.8034489 0.2690982 6.701825 2.369845e-07The coefficient 0.59 of weekly outdoor time for predicting wellbeing score says that among those with the same number of social interactions per week, those who have one additional hour of outdoor time tend to, on average, score 0.59 higher on the WEMWBS wellbeing scale. The multiple regression coefficient measures that average conditional relationship.
Within what distance from the model predicted values (the regression surface) would we expect 95% of wEMWBS wellbeing scores to be?
Hint: either sigma(mdl1) or part of the output from summary(mdl1) will help you here.
Obtain 95% confidence intervals for the regression coefficients, and write a sentence about each one.
~ Numeric + Categorical
Let’s do that again, but paying careful attention to where and how the process differs when we have a categorical (or “qualitative”) predictor.
Suppose that the group of researchers were instead wanting to study the relationship between well-being and time spent outdoors after taking into account the relationship between well-being and having a routine.
We have already visualised the marginal distribution of weekly outdoor time in an earlier question, as well as its relationship with wellbeing scores.
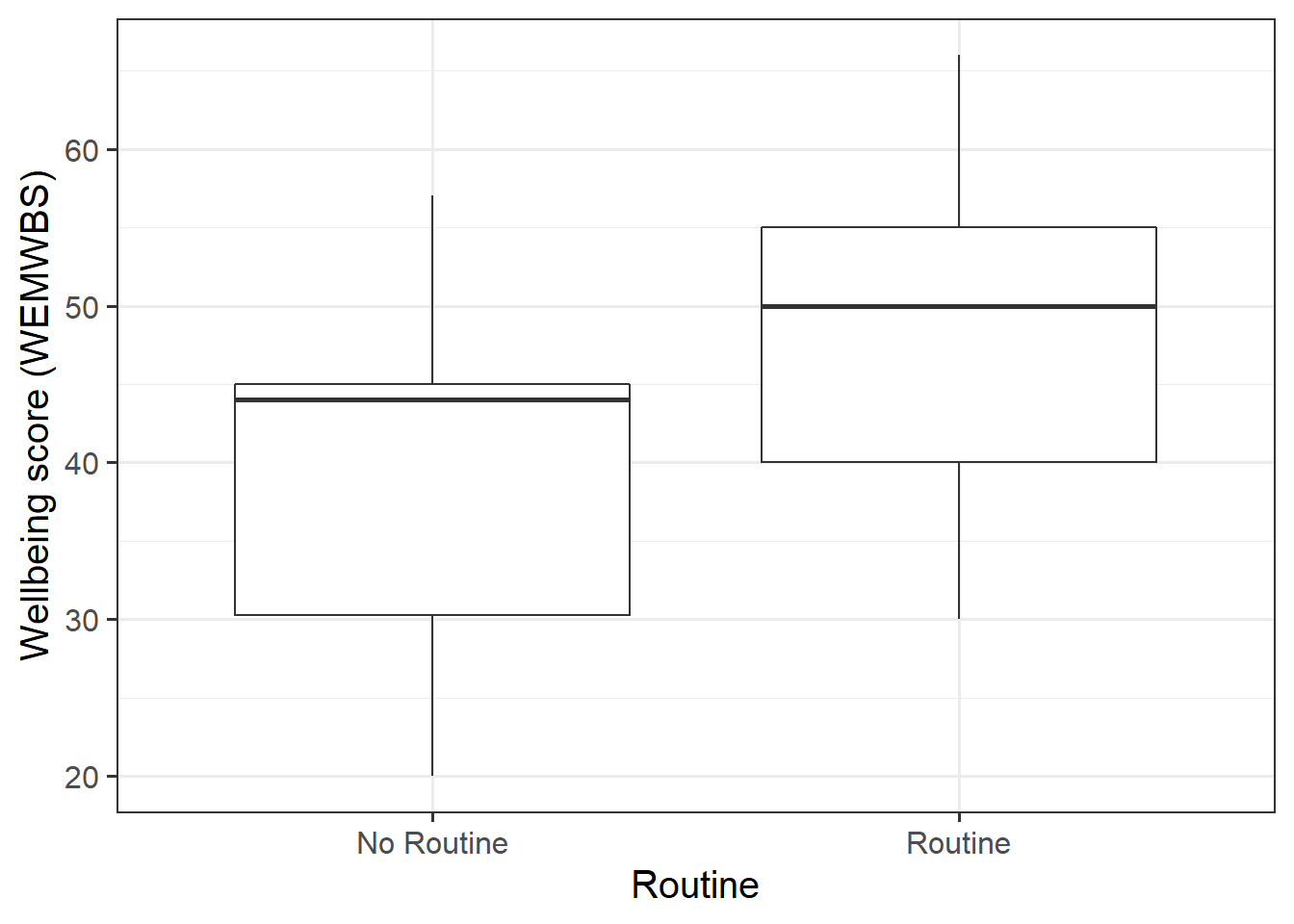
Produce visualisations of:
- the distribution of the
routinevariable - the relationship between
routineandwellbeing.
Note: We cannot visualise the distribution of routine as a density curve or boxplot, because it is a categorical variable (observations can only take one of a set of discrete response values).
Fit the multiple regression model below using lm(), and assign it to an object named mdl2. Examine the summary output of the model.
\[ Wellbeing = \beta_0 + \beta_1 \cdot OutdoorTime + \beta_2 \cdot Routine + \epsilon \]
\(\hat \beta_0\) (the intercept) is the estimated average wellbeing score associated with zero hours of weekly outdoor time and zero in the routine variable.
What group is the intercept the estimated wellbeing score for when they have zero hours of outdoor time? Why (think about what zero in the routine variable means)?
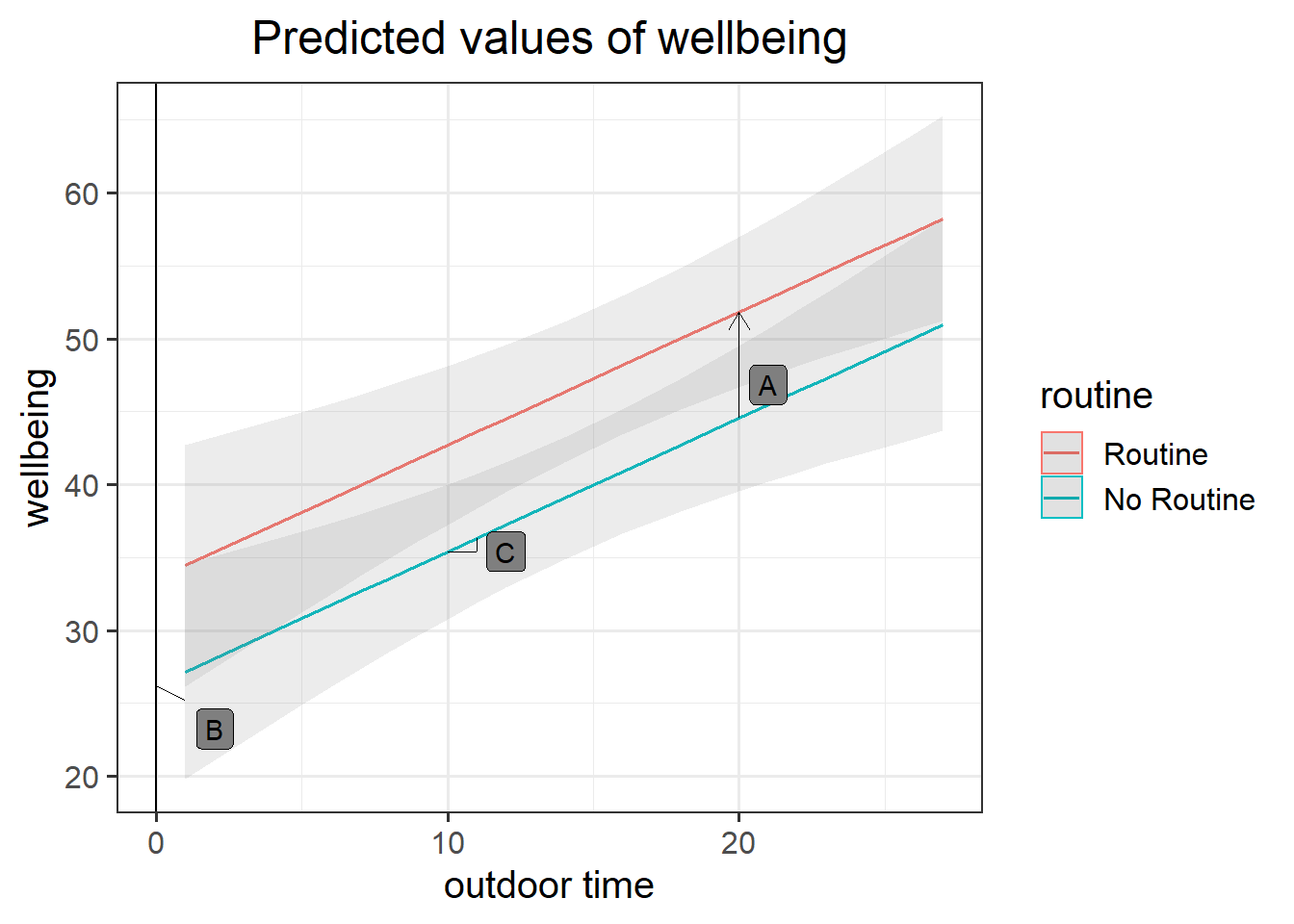
In the previous example, we had a visualisation of our model as a regression surface (Figure 3).
Here, one of our explanatory variables has only two possible responses. How might we visualise the model?
- one line
- one surface
- two lines
- two surfaces
- a curved (not flat) surface
Get a pen and paper, and sketch out the plot shown in Figure 6.
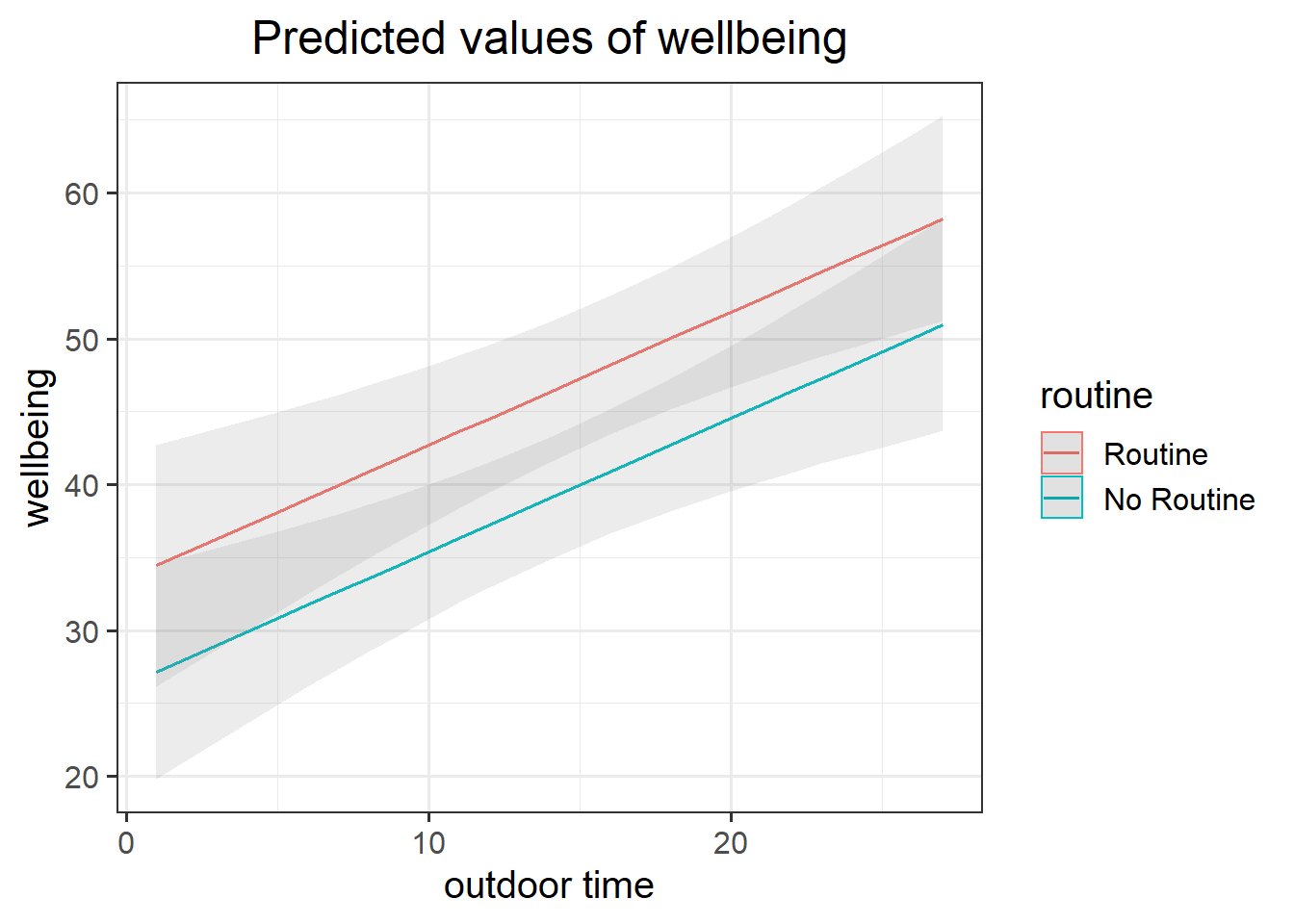
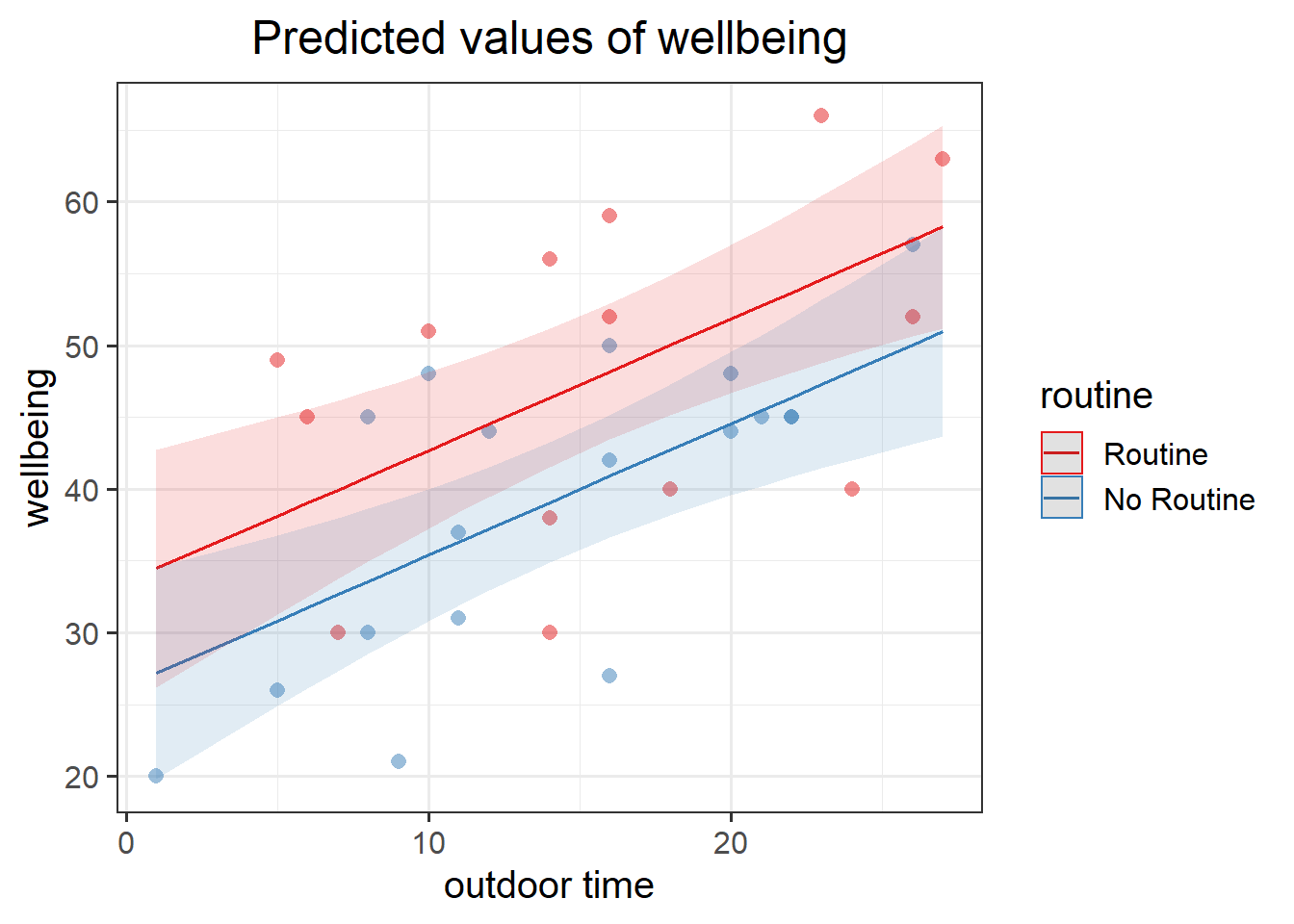
Figure 6: Multiple regression model: Wellbeing ~ Outdoor Time + Routine
Annotate your plot with labels for each of parameter estimates from your model:
| Parameter Estimate | Model Coefficient | Estimate |
|---|---|---|
| \(\hat \beta_0\) | (Intercept) |
26.25 |
| \(\hat \beta_1\) | outdoor_time |
0.92 |
| \(\hat \beta_2\) | routineRoutine |
7.29 |
Load the sjPlot package using library(sjPlot) and try running the code below. (You may already have the sjPlot package installed from previous exercises on simple linear regression, if not, you will need to install it first).
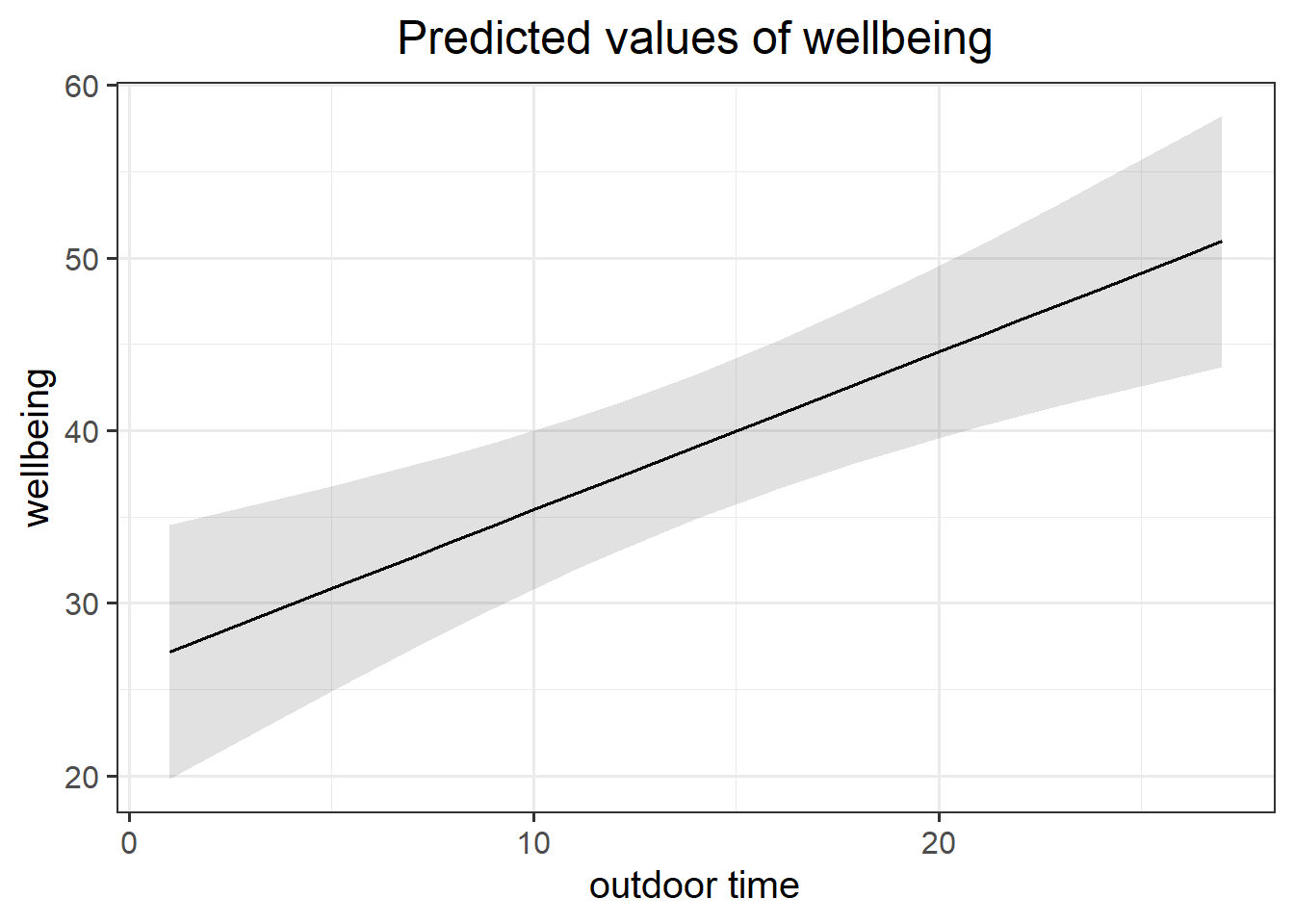
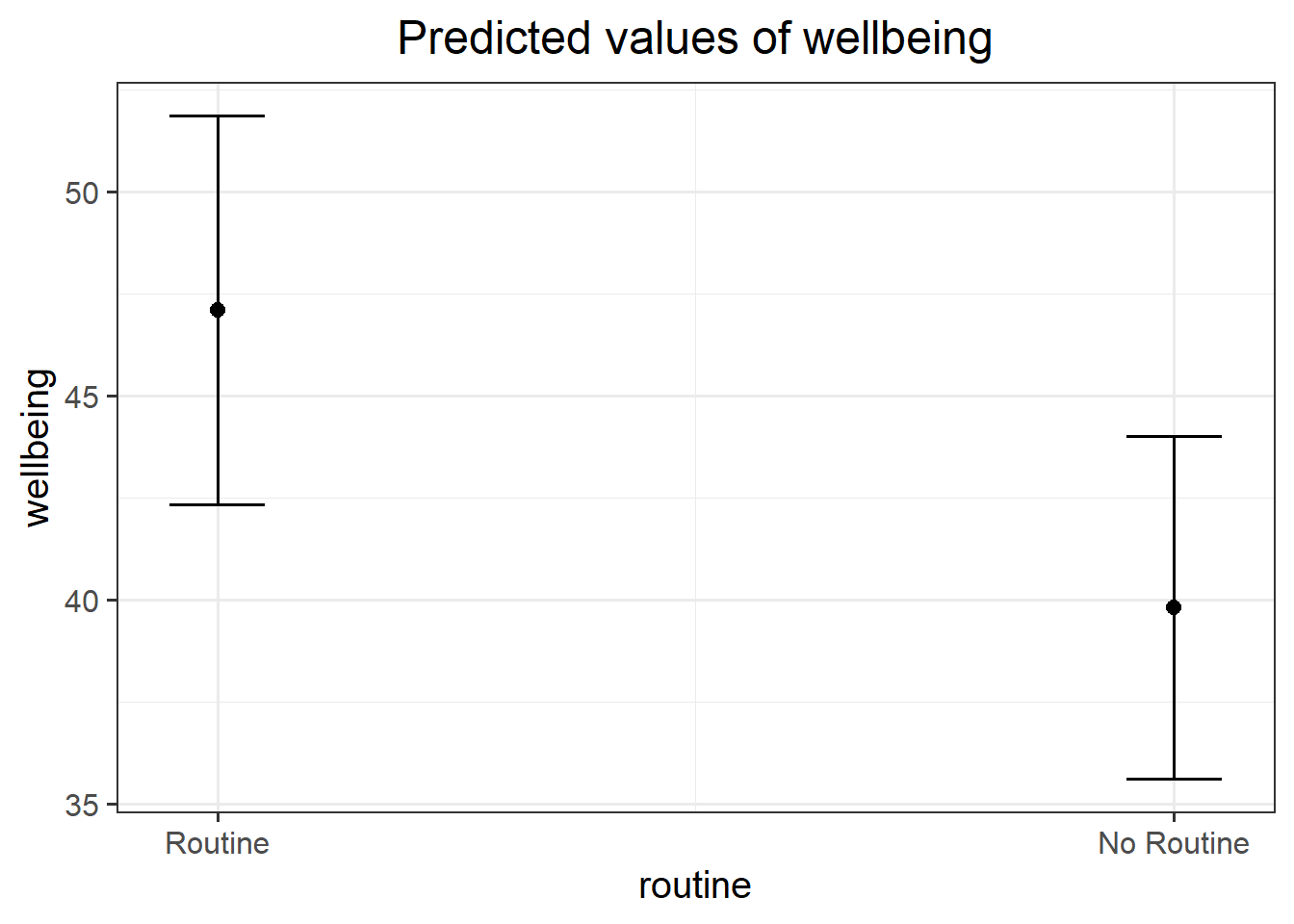
plot_model(mdl2)
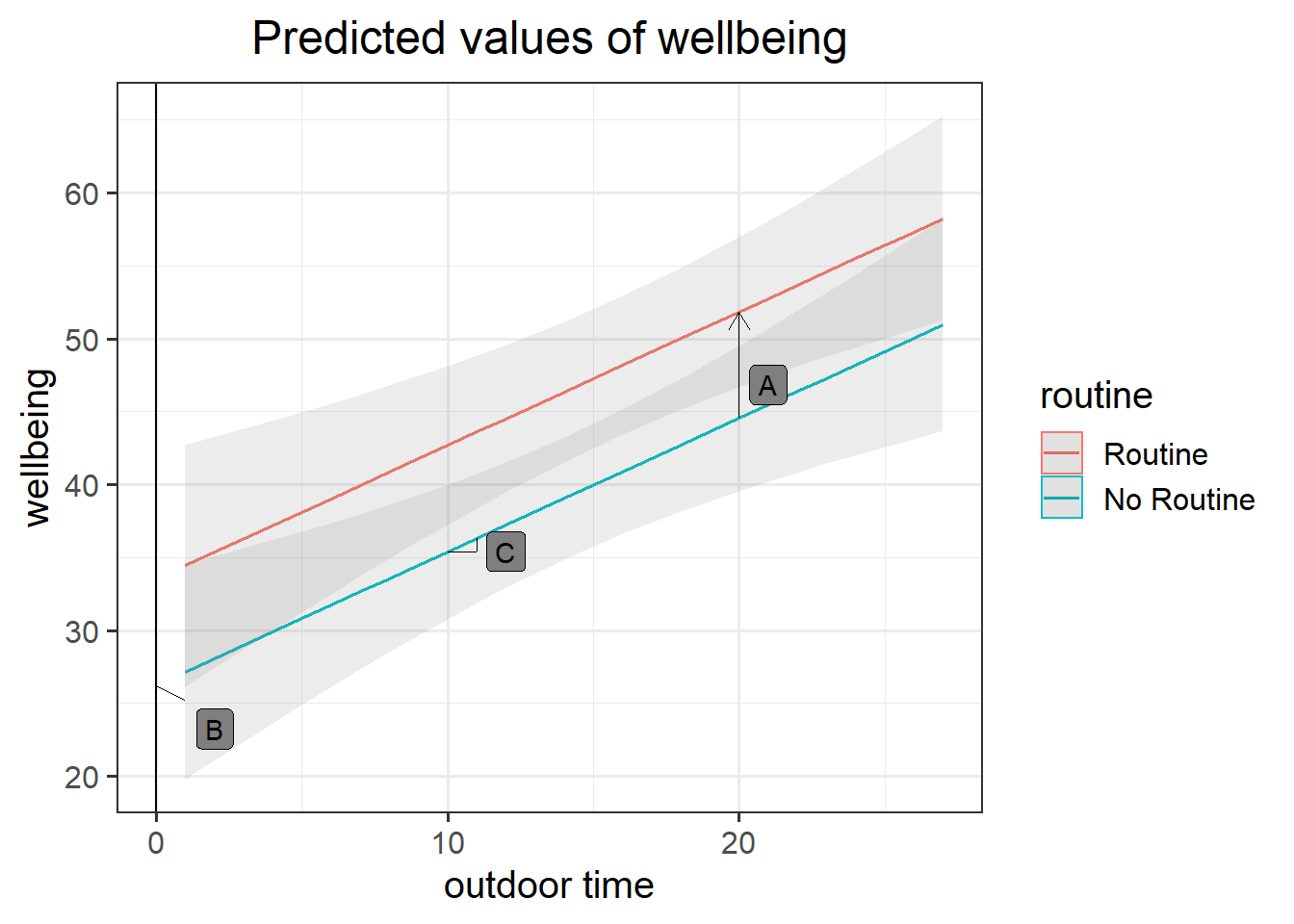
plot_model(mdl2, type = "pred")
plot_model(mdl2, type = "pred", terms=c("outdoor_time","routine"), show.data=TRUE)What do you think each one is showing?
The plot_model function (and the sjPlot package) can do a lot of different things. Most packages in R come with tutorials (or “vignettes”), for instance: https://strengejacke.github.io/sjPlot/articles/plot_model_estimates.html
Categorical Predictors with \(k\) levels
We saw that a binary categorical variable gets inputted into our model as a variable of 0s and 1s (these typically get called “dummy variables”).
Dummy variables are numeric variables that represent categorical data.
When we have a categorical explanatory variable with more than 2 levels, our model gets a bit more - it needs not just one, but a number of dummy variables. For a categorical variable with \(k\) levels, we can express it in \(k-1\) dummy variables.
For example, the “species” column below has three levels, and can be expressed by the two variables “species_dog” and “species_parrot”:
## species species_dog species_parrot
## 1 cat 0 0
## 2 cat 0 0
## 3 dog 1 0
## 4 parrot 0 1
## 5 dog 1 0
## 6 cat 0 0
## 7 ... ... ...- The “cat” level is expressed whenever both the “species_dog” and “species_parrot” variables are 0.
- The “dog” level is expressed whenever the “species_dog” variable is 1 and the “species_parrot” variable is 0.
- The “parrot” level is expressed whenever the “species_dog” variable is 0 and the “species_parrot” variable is 1.
R will do all of this re-expression for us. If we include in our model a categorical explanatory variable with 4 different levels, the model will estimate 3 parameters - one for each dummy variable. We can interpret the parameter estimates (the coefficients we obtain using coefficients(),coef() or summary()) as the estimated increase in the outcome variable associated with an increase of one in each dummy variable (holding all other variables equal).
| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 60.28 | 1.209 | 49.86 | 5.273e-39 |
| speciesdog | -11.47 | 1.71 | -6.708 | 3.806e-08 |
| speciesparrot | -4.916 | 1.71 | -2.875 | 0.006319 |
Note that in the above example, an increase in 1 of “species_dog” is the difference between a “cat” and a “dog.” An increase in one of “species_parrot” is the difference between a “cat” and a “parrot.” We think of the “cat” category in this example as the reference level - it is the category against which other categories are compared against.
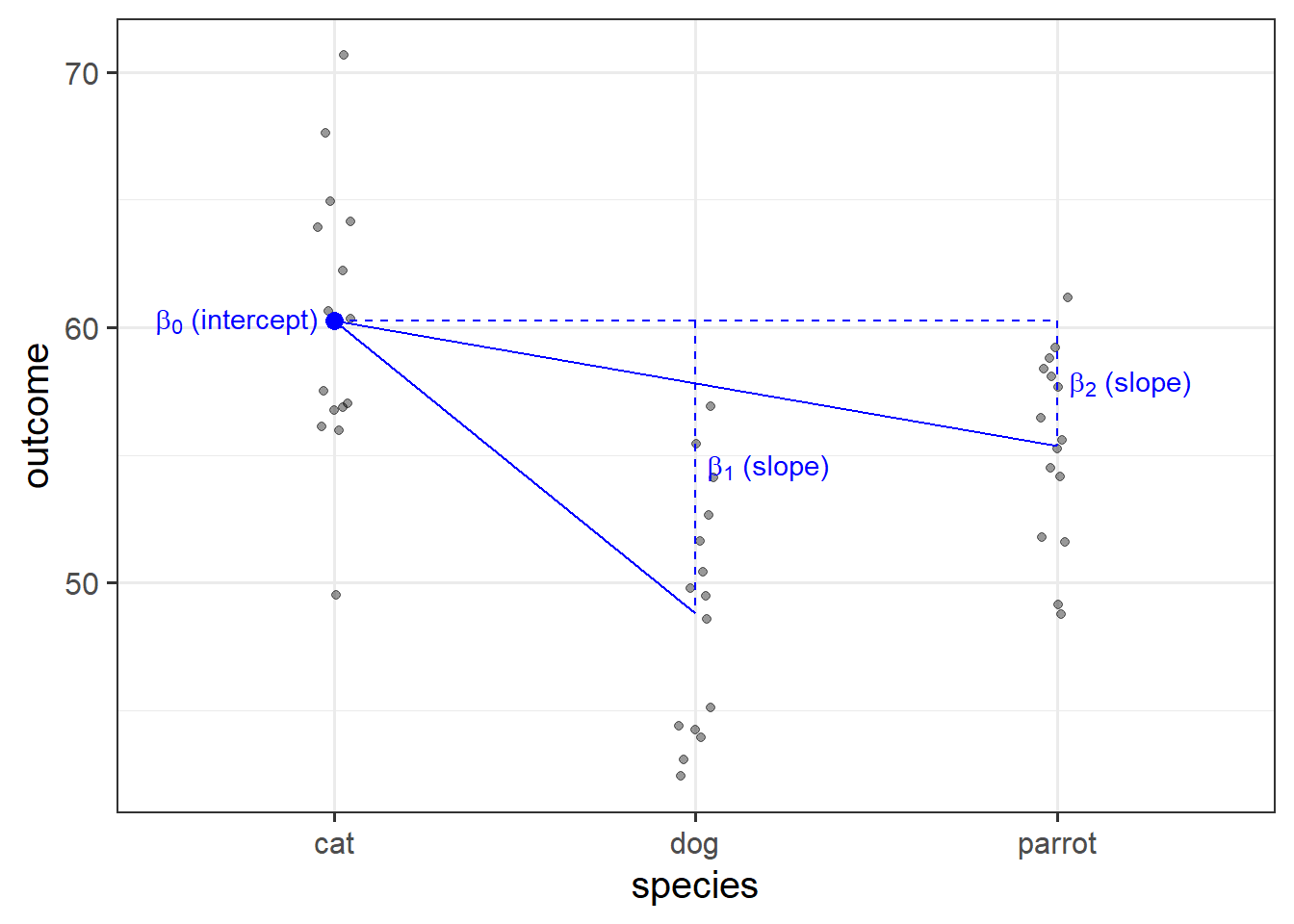

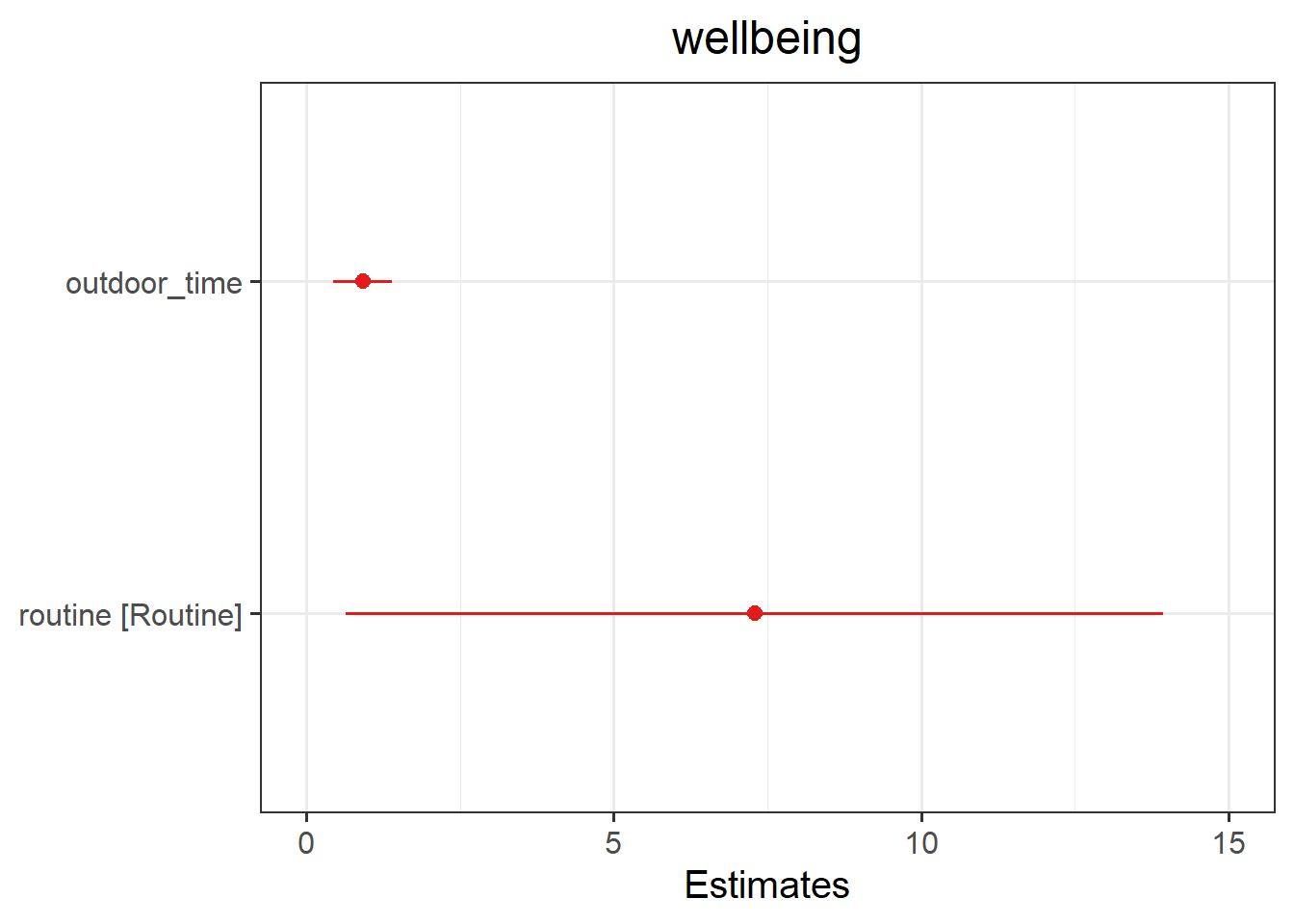 These are the parameter estimates (the
These are the parameter estimates (the