| variable | description |
|---|---|
| id | Unique ID number |
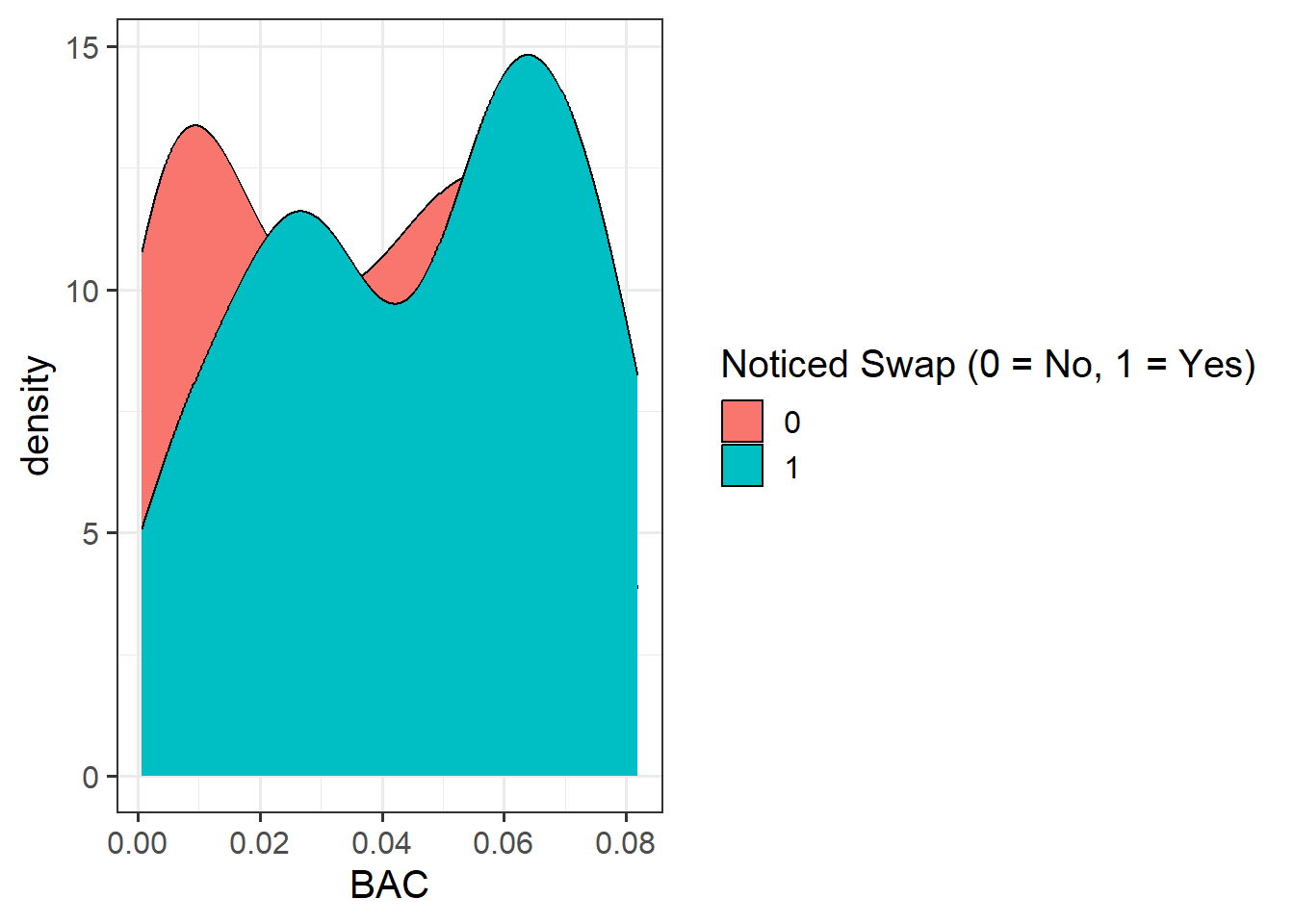
| bac | Blood Alcohol Content (BAC), a BAC of 0.0 is sober, while in the United States 0.08 is legally intoxicated, and above that is very impaired. BAC levels above 0.40 are potentially fatal. |
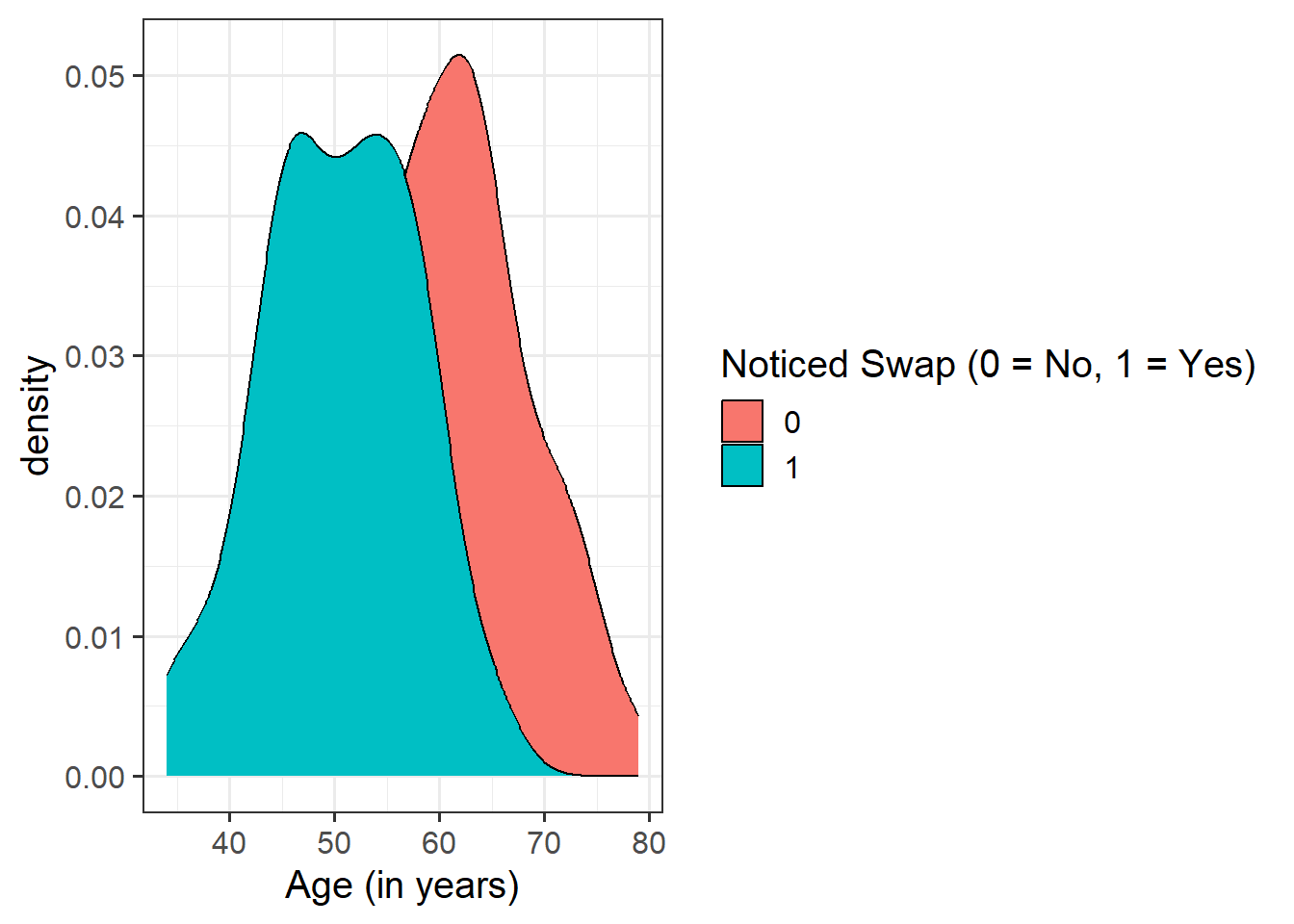
| age | Age (in years) |
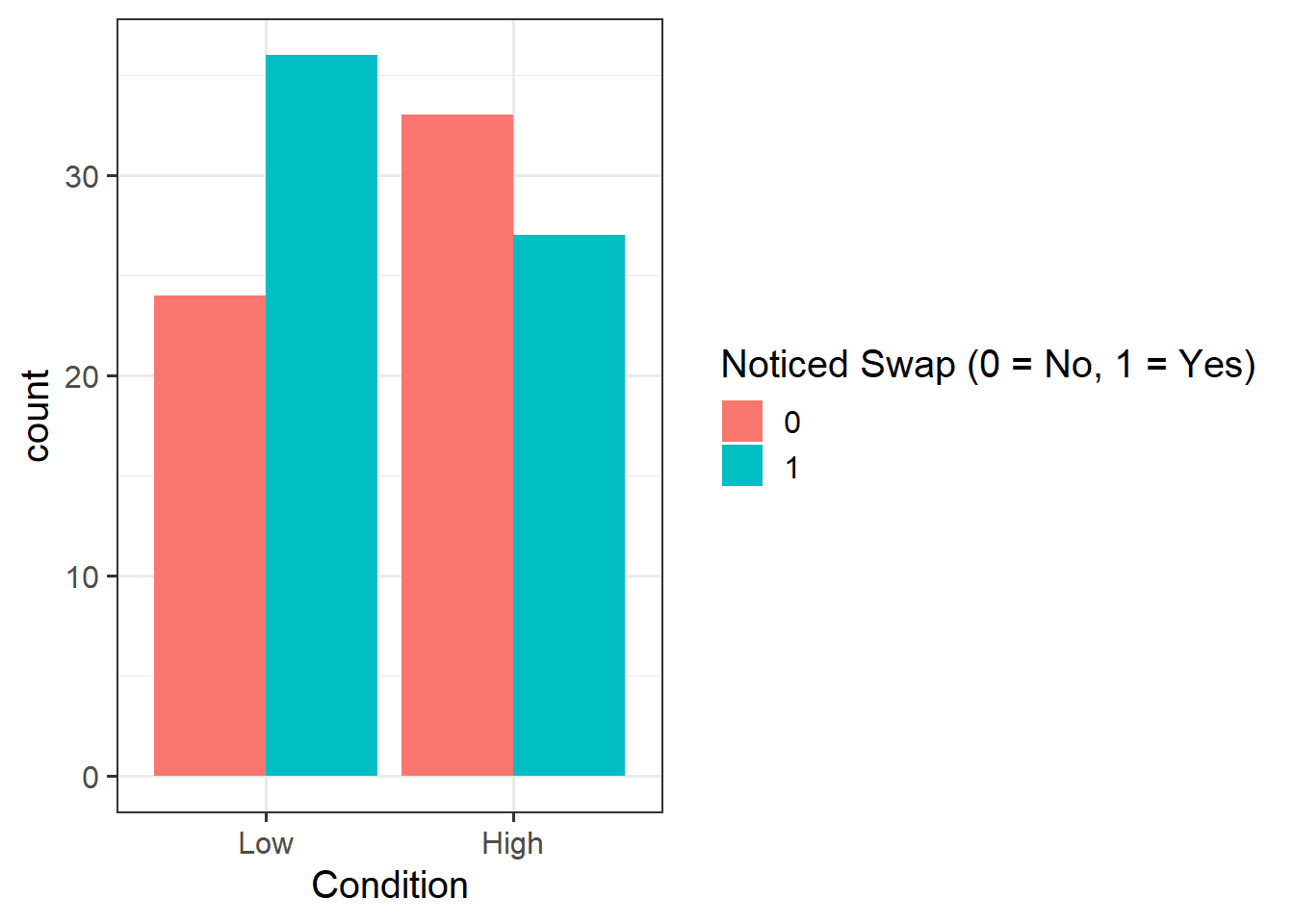
| condition | Condition - Perceptual load created by distracting oject (door) and details and amount of papers handled in front of participant (Low vs High) |
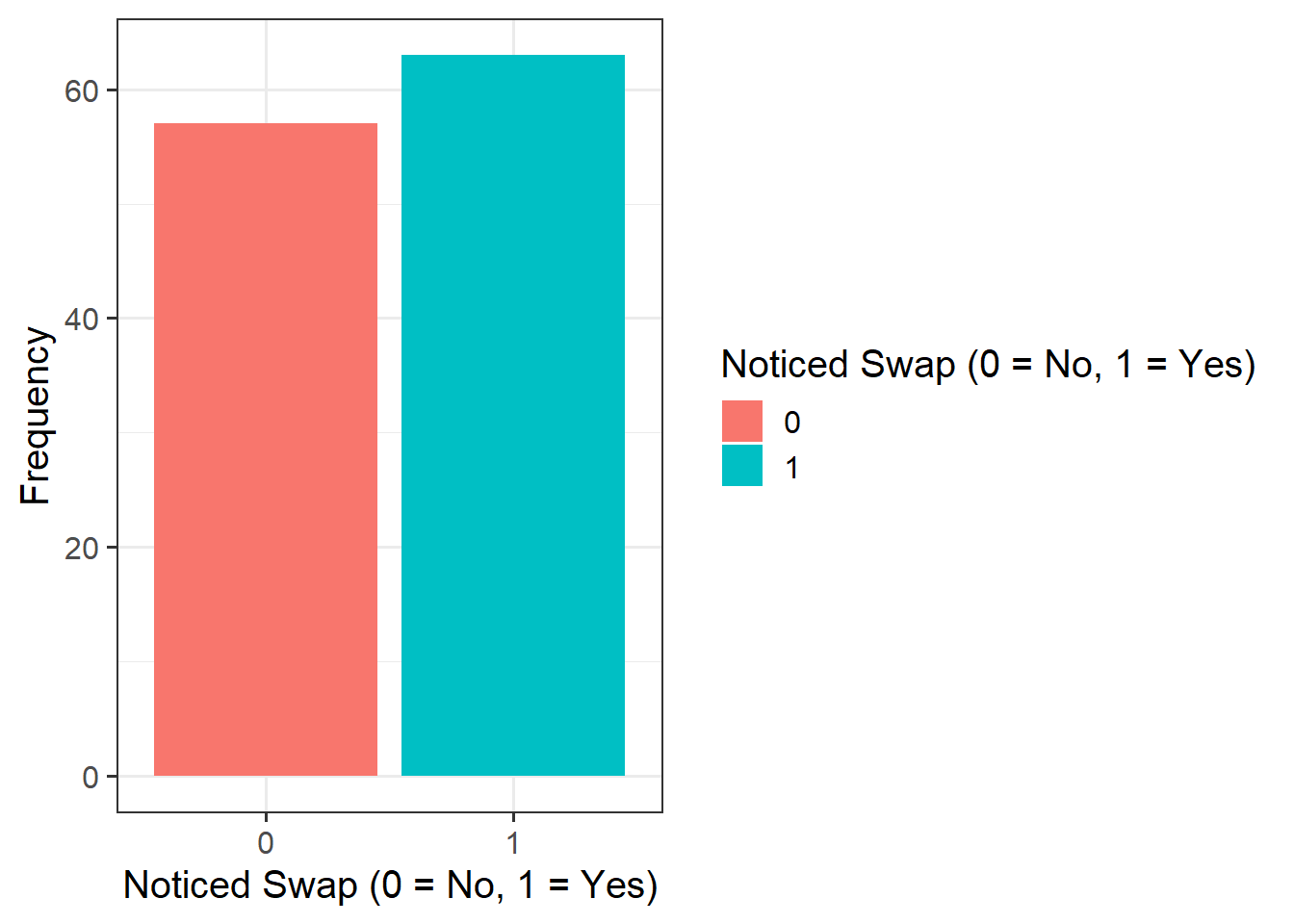
| notice | Whether or not the participant noticed the swap (Yes = 1 vs No = 0) |
Binary Logistic Regression
Learning Objectives
At the end of this lab, you will:
- Understand when to use a logistic model
- Understand how to fit and interpret a logistic model
What You Need
- Be up to date with lectures
- Have completed Labs 1-5
Required R Packages
Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.
For this lab, you will need to load the following package(s):
- tidyverse
- patchwork
- kableExtra
- psych
- sjPlot
Lab Data
You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/drunkdoor.csv.
Study Overview
Research Question
Is susceptibility to change blindness influenced by age, level of alcohol intoxication, and perceptual load?
Watch the following video:
Simons, D. J., & Levin, D. T. (1997). Change blindness. Trends in cognitive sciences, 1(7), 261-267.
You may well have already heard of these series of experiments, or have seen similar things on Netflix.
Setup
- Create a new RMarkdown file
- Load the required package(s)
- Read the drunkdoor dataset into
R, assigning it to an object nameddrunkdoor
Examine the dataset, and perform any necessary and appropriate data management steps.
Provide a table of descriptive statistics and visualise your data.
Remember to interpret your plot in the context of the study.
- For your table of descriptive statistics, both the
group_by()andsummarise()functions will come in handy here - For your visualisations, you will need to specify
as_factor()when plotting the notice variable since this is numeric, but we want it to be treated as a factor only for plotting purposes - Make sure to comment on your observations
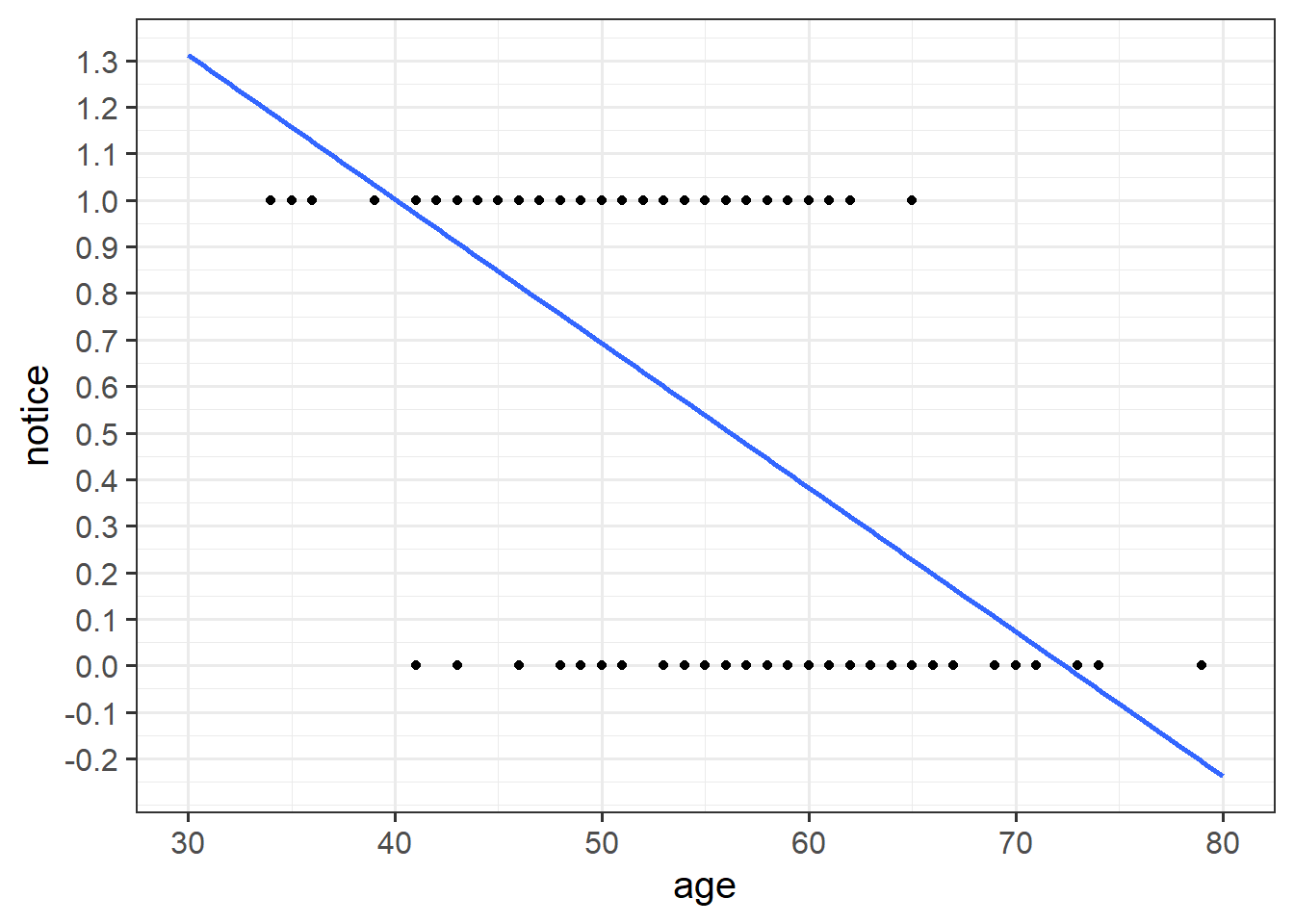
For the moment, lets just consider the association between notice and age. Visually following the line from the plot produced below, what do you think the predicted model value would be for someone who is aged 30? What does this value mean?
Consider the scales that the variables are currently on, with a particular focus on BAC, age, and condition.
- Do you want BAC on the current scale, or could you transform it somehow? Consider that instead of the coefficient representing the difference when moving from 0% to 1% BAC (1% blood alcohol is fatal!), we might want to have the difference associated with 0% to 0.01% BAC (i.e, a we want to talk about effects in terms of changing 1/100th of a percentage of BAC)
- Do you want age to be centred at 0 years (as it currently is), or could you re-centre to make it more meaningful?
- You have hopefully already made condition a factor, but have you considered the reference level? It would likely make most sense for this to be set as “Low”.
Fit your model using glm(), and assign it as an object with the name “changeblind_mdl”.
Conduct a model comparison of your model above against the null model. Report the results of the model comparison in APA format.
Consider whether or not your models are nested. The flowchart in Question 10 of the Semester 2 Week 1 lab may be helpful to revisit.
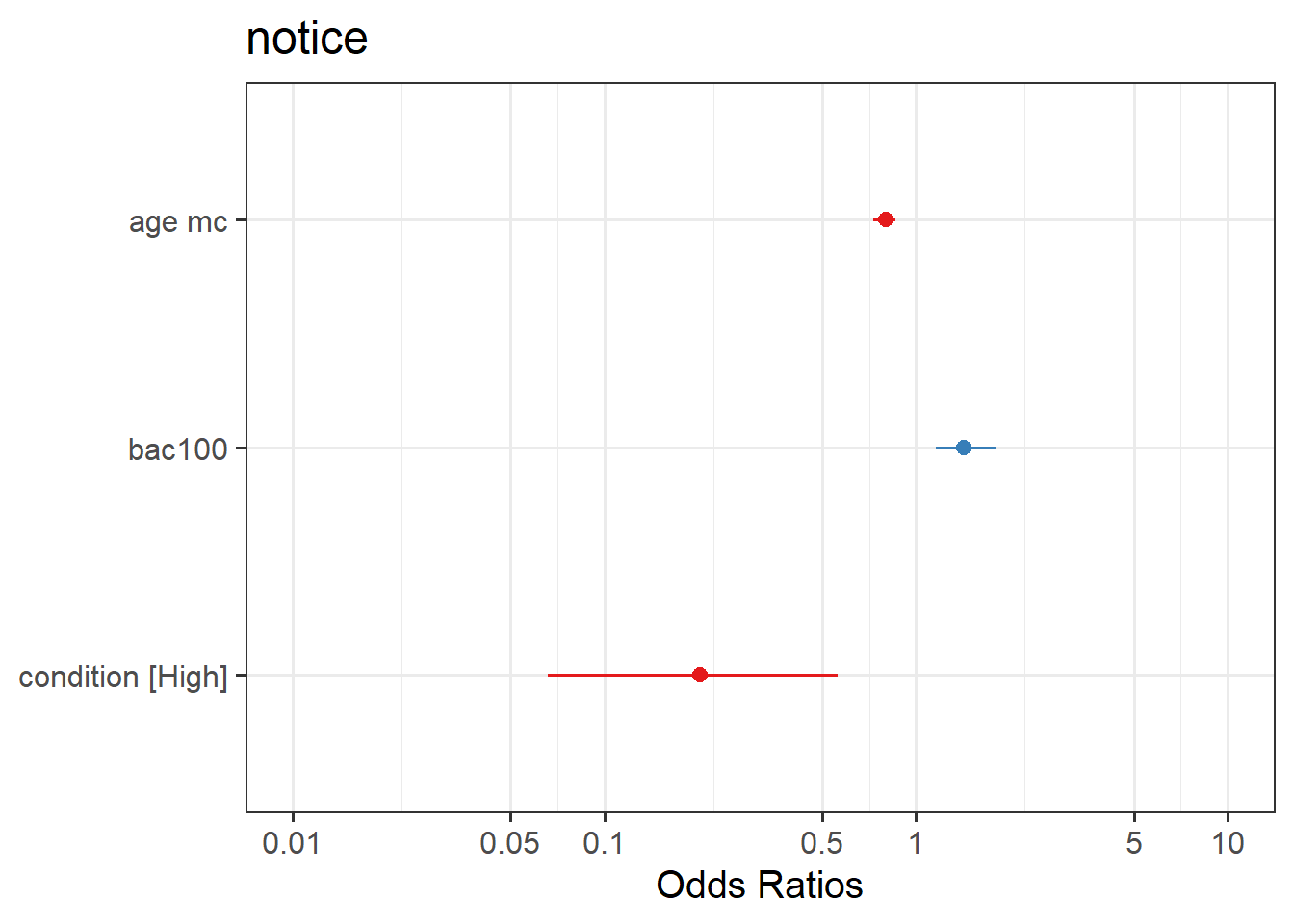
Interpret your coefficients in the context of the study. When doing so, it may be useful to translate the log-odds back into odds.
The opposite of the natural logarithm is the exponential, and in R these functions are log() and exp().
Recall that we can obtain our parameter estimates using various functions such as summary(),coef(), coefficients(), etc. Thus, we want to exponentiate the coefficients from our model in order to translate them back from log-odds.
Plot the predicted model estimates.
Here you will need to use plot_model() from the sjPlot package like you did back in Semester 1. To get your estimates, you will need to specify type = "est".
Provide key model results in a formatted table.
Use tab_model() from the sjPlot package.
Remember that you can rename your DV and IV labels by specifying dv.labels and pred.labels.
Interpret your results in the context of the research question and report your model in full.