Interactions I: Num x Cat

Learning Objectives

At the end of this lab, you will:

1. Understand the concept of an interaction.
2. Be able to interpret the meaning of a numeric \(\times\) categorical interaction.
3. Visualize and probe interactions.

What You Need

1. Be up to date with lectures
2. Have completed all labs from Semester 1 Block 1 (Weeks 1 - 5)

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

• tidyverse
• psych
• patchwork
• sandwich
• interactions

Lab Data

You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/wellbeing_rural.csv.

Study Overview

Research Question

Does the association between number of social interactions and wellbeing differ between rural and non-rural residents?

Researchers were specifically interested in how the number of social interactions might influence mental health and wellbeing differently for those living in rural communities compared to those in cities and suburbs. They want to assess whether the effect of social interactions on wellbeing is moderated by (depends upon) whether or not a person lives in a rural area.

To investigate how the association between the number of social interactions and mental wellbeing might be different for those living in rural communities, the researchers conducted a study, where they collected data from 200 randomly selected residents of the Edinburgh & Lothian postcodes.

Wellbeing/Rurality data codebook.

Description

From the Edinburgh & Lothians, 100 city/suburb residences and 100 rural residences were chosen at random and contacted to participate in the study. The Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), was used to measure mental health and well-being.

Participants filled out a questionnaire including items concerning: estimated average number of hours spent outdoors each week, estimated average number of social interactions each week (whether on-line or in-person), whether a daily routine is followed (yes/no). For those respondents who had an activity tracker app or smart watch, they were asked to provide their average weekly number of steps.

The data in wellbeing.csv contain seven attributes collected from a random sample of \(n=200\) hypothetical residents over Edinburgh & Lothians, and include:

• wellbeing: Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70.
  
• outdoor_time: Self report estimated number of hours per week spent outdoors
  
• social_int: Self report estimated number of social interactions per week (both online and in-person)
• routine: Binary 1=Yes/0=No response to the question “Do you follow a daily routine throughout the week?”
• location: Location of primary residence (City, Suburb, Rural)
• steps_k: Average weekly number of steps in thousands (as given by activity tracker if available)
• age: Age in years of respondent

Preview

The first six rows of the data are:

age	outdoor_time	social_int	routine	wellbeing	location	steps_k
28	12	13	1	36	rural	21.6
56	5	15	1	41	rural	12.3
25	19	11	1	35	rural	49.8
60	25	15	0	35	rural	NA
19	9	18	1	32	rural	48.1
34	18	13	1	34	rural	67.3

Setup

Setup

1. Create a new RMarkdown file
2. Load the required package(s)
3. Read the wellbeing_rural dataset into R, assigning it to an object named wrdata

Solution

#Loading the required package(s)
library(tidyverse)
library(psych)
library(patchwork)
library(sandwich)
library(interactions)

#Reading in data and storing in object named 'wrdata'
wrdata <- read_csv("https://uoepsy.github.io/data/wellbeing_rural.csv")

Exercises

Question 1

Formally state:

• a linear model to investigate if the association between wellbeing and social interactions differs among rural and non-rural residents
• your chosen significance level
• the null and alternative hypotheses

“Except in special circumstances, a model including a product term for interaction between two explanatory variables should also include terms with each of the explanatory variables individually, even though their coefficients may not be significantly different from zero. Following this rule avoids the logical inconsistency of saying that the effect of \(X_1\) depends on the level of \(X_2\) but that there is no effect of \(X_1\).”
— Ramsey and Schafer (2012)

Solution

To address the research question, we are going to fit the following model, where \(y\) = wellbeing; \(x_1\) = social interactions; and \(x_2\) = whether or not the respondent lives in a rural location.

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 (x_1 \cdot x_2) + \epsilon \\ \quad \\ \text{where} \quad \epsilon \sim N(0, \sigma) \quad \text{independently} \] or \[ \begin{split} \text{Wellbeing} = \beta_0 + \beta_1 \cdot Social Interactions + \beta_2 \cdot Location_{Rural} \\+ \beta_3 \cdot (Social Interactions \cdot Location_{Rural}) + \epsilon \\ \end{split} \]

Effects will be considered statistically significant at \(\alpha=.05\)

Our hypotheses are:

\(H_0: \beta_3 = 0\)

The association between wellbeing and social interactions is not moderated by whether or not a person lives in a rural area.

\(H_1: \beta_3 \neq 0\)

The association between wellbeing and social interactions is moderated by whether or not a person lives in a rural area.

Question 2

Check coding of variables (e.g., that categorical variables are coded as factors).

Note that the “location” variable currently has three levels (Rural/Suburb/City). In order to address the research question, we only want two (Rural/Not Rural) locations - you will need to fix this.

Specify ‘not rural’ as your reference group.

Hint

One way to do this would be to use ifelse() to define a variable which takes one value (“Rural”) if the observation meets from some condition, or another value (“Not Rural”) if it does not. Type ?ifelse in the console if you want to see the help function. You can use it to add a new variable either inside mutate(), or using data$new_variable_name <- ifelse(test, x, y) syntax.

Solution

Create a new variable for Rural/Not Rural:

#if location is rural, assign name 'rural'. If another value (i.e., city or suburb) assign name 'not rural'.
# In other words, if location = rural assign name rural; if location != rural then assign name not rural.
wrdata <- wrdata %>% 
  mutate(
    isRural = ifelse(location == "rural", "rural", "not rural")
  )

Check coding of variables within wrdata and ensure isRural is a factor with two levels, ‘rural’ and ‘not rural’:

str(wrdata) #returns overall 'structure' of data. Or could run is.factor() for specific variable of interest

tibble [200 × 8] (S3: tbl_df/tbl/data.frame)
 $ age         : num [1:200] 28 56 25 60 19 34 41 41 35 53 ...
 $ outdoor_time: num [1:200] 12 5 19 25 9 18 17 11 12 13 ...
 $ social_int  : num [1:200] 13 15 11 15 18 13 19 12 13 15 ...
 $ routine     : num [1:200] 1 1 1 0 1 1 1 1 0 1 ...
 $ wellbeing   : num [1:200] 36 41 35 35 32 34 39 43 35 37 ...
 $ location    : chr [1:200] "rural" "rural" "rural" "rural" ...
 $ steps_k     : num [1:200] 21.6 12.3 49.8 NA 48.1 67.3 1.9 50.9 NA 35.5 ...
 $ isRural     : chr [1:200] "rural" "rural" "rural" "rural" ...

wrdata$isRural <- as_factor(wrdata$isRural)
is.factor(wrdata$isRural) #check that isRural is now a factor

[1] TRUE

#specify 'not rural' as reference group
wrdata$isRural <- relevel(wrdata$isRural, 'not rural')

Question 3

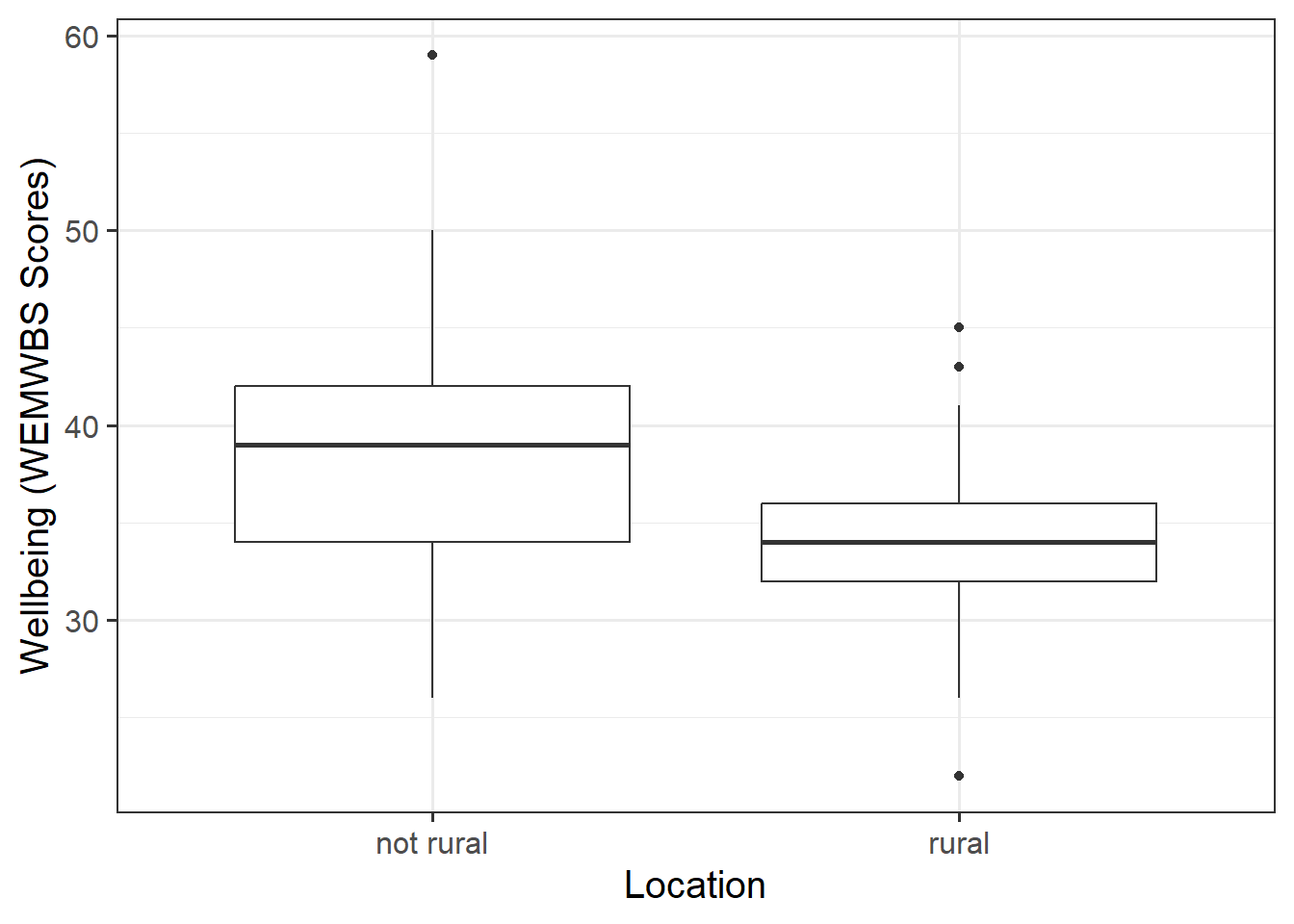
Visualise your data, and interpret your plots.

In particular:

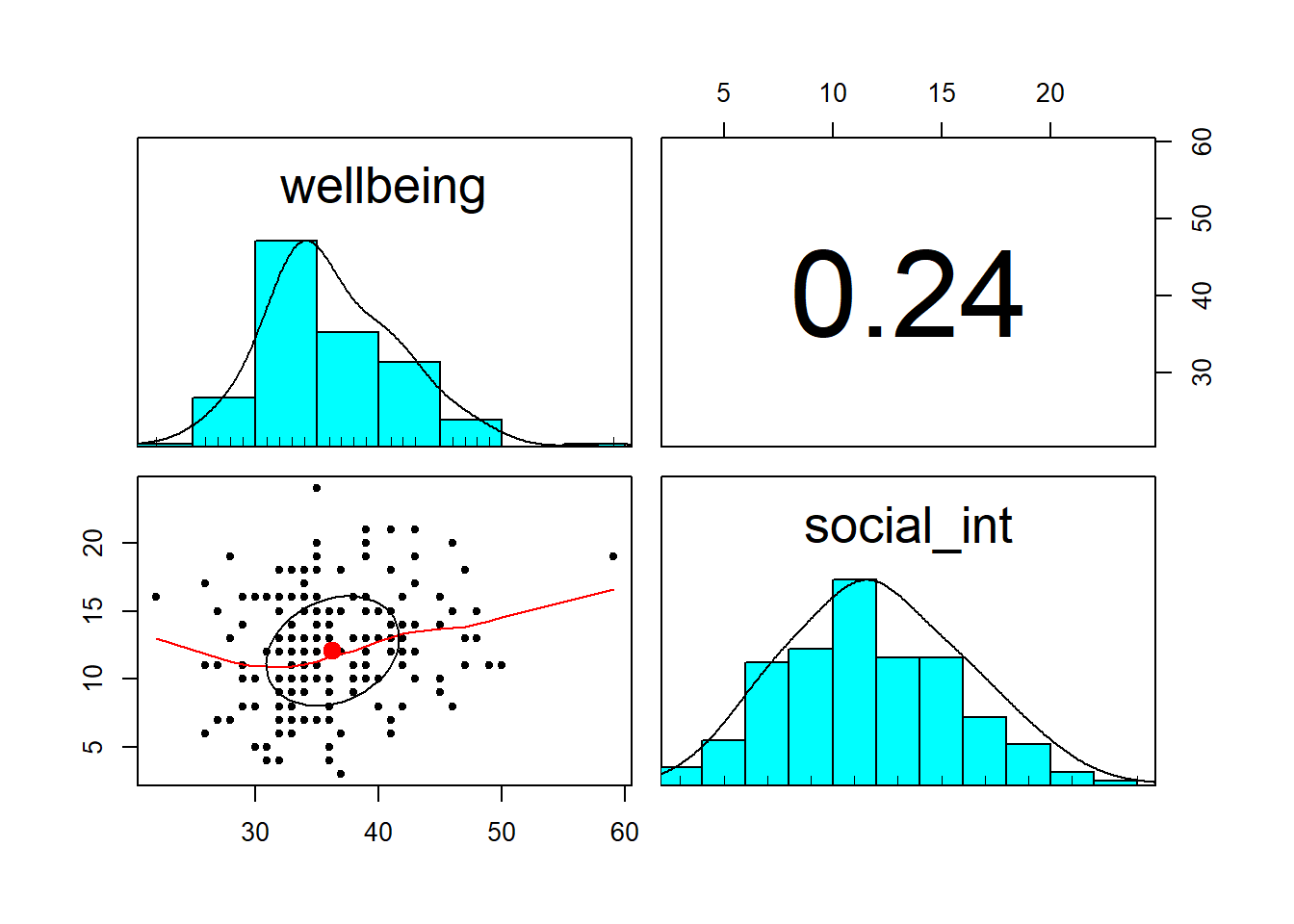
1. Explore the associations among the variables included in your analysis
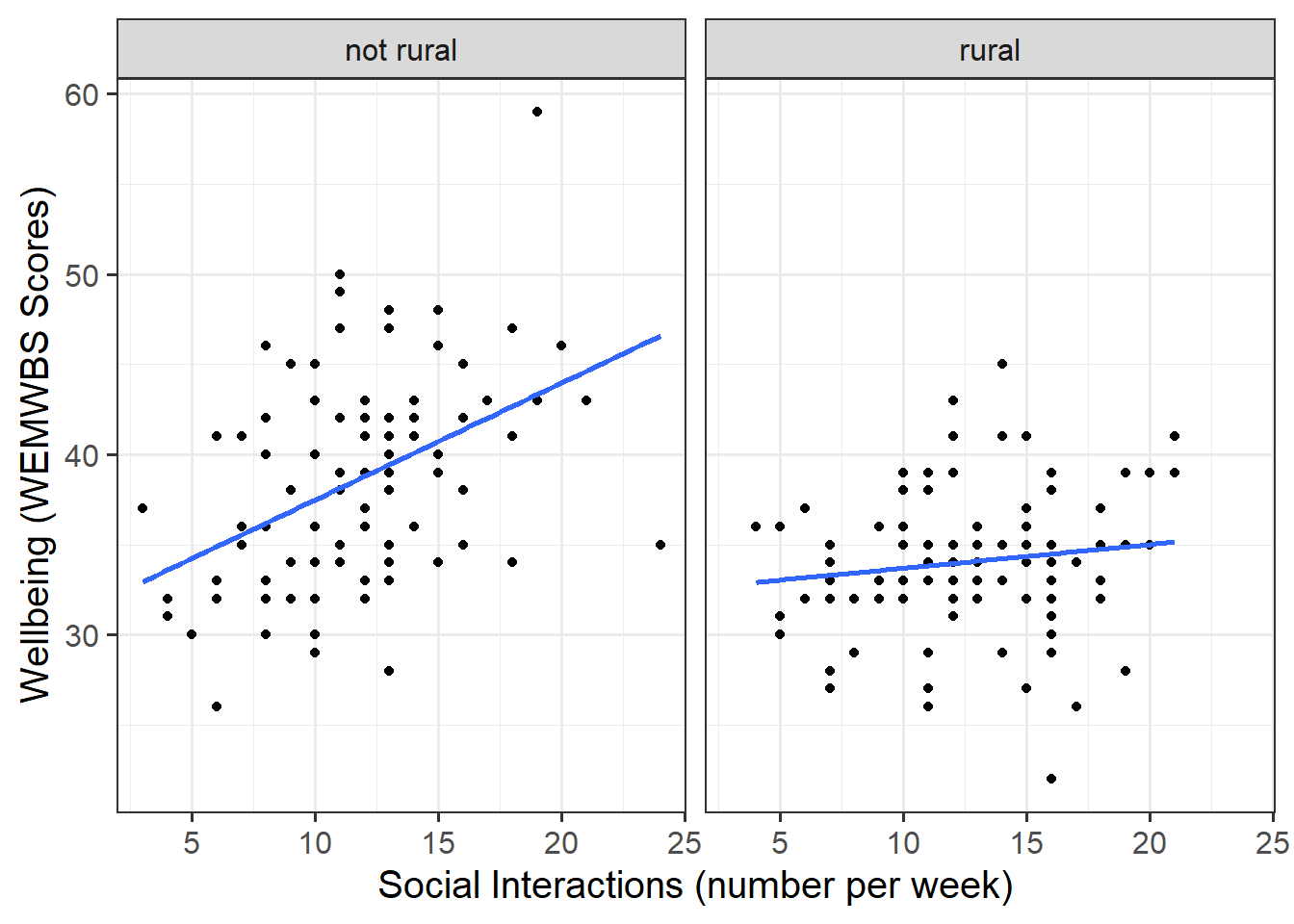
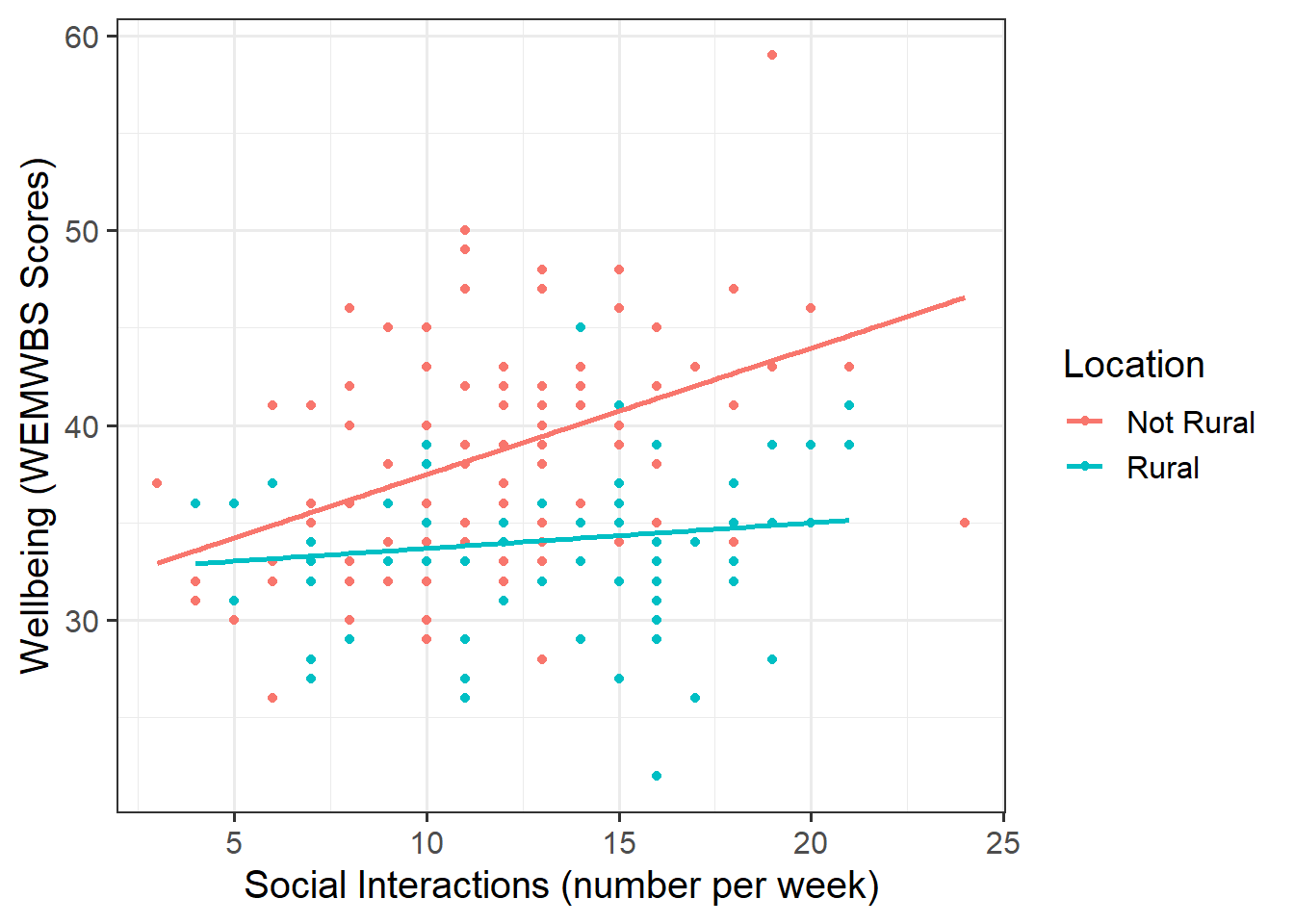
2. Produce a visualisation of the association between weekly number of social interactions and well-being, with separate facets for rural vs non-rural respondents OR with different colours for each level of the isRural variable.

Hint

1. The pairs.panels() function from the psych package will can plot all variables in a dataset against one another. This will save you the time you would have spent creating individual plots, but is only useful for continuous variables.
2. To include facets, Within your ggplot() argument you will need to specify + facet_wrap() in order to produce facets for each location. It would also be useful to specify geom_smooth(method="lm")

Solution

Let’s first plot the continuous variables included within our model (note that we could use this for the whole dataset, but we don’t want to include irrelevant variables):

wrdata %>% 
  select(wellbeing, social_int) %>%
  pairs.panels()

Wellbeing and social interactions appear to follow unimodal distributions. There was a weak, positive association between wellbeing and social interactions (\(r\) = .24).

Now lets look at wellbeing scores by location:

ggplot(data = wrdata, aes(x = isRural, y = wellbeing)) +
  geom_boxplot() + 
  labs(x = "Location", y = "Wellbeing (WEMWBS Scores)")

Those in rural locations appear to have lower wellbeing scores in comparison to those in non-rural locations.

Next, lets produce our plots with a facet for rural vs non-rural residents:

ggplot(data = wrdata, aes(x = social_int, y = wellbeing)) +
  geom_point() +
  geom_smooth(method="lm", se=FALSE) +
  facet_wrap(~isRural) + 
  labs(x = "Social Interactions (number per week)", y = "Wellbeing (WEMWBS Scores)")

Or instead of facets, we could use different colours for each location (rural vs non-rural):

ggplot(data = wrdata, aes(x = social_int, y = wellbeing, colour = isRural)) +
  geom_point() + 
  geom_smooth(method="lm", se=FALSE) +
    scale_colour_discrete(
    name ="Location",
    labels=c("Not Rural", "Rural")) + 
    labs(x = "Social Interactions (number per week)", y = "Wellbeing (WEMWBS Scores)")

Those in non-rural locations appear to have higher wellbeing scores across almost all levels of social interactions. The slopes appear to be different for each location, where the greatest difference in wellbeing scores by location is most visible the highest number of social interactions.

Note

How can we tell that there is an interaction?

The lines in the two plots above are not running in parallel - this suggests the presence of an interaction. Specifically in our example, the non-parallel lines suggest an interaction effect based on location, as the number of social interactions does not appear to have the same influence on rural and non-rural residents’ wellbeing scores.

Question 4

Fit your model using lm(), and assign it as an object with the name “rural_mod”.

Hint

When fitting a regression model in R with two explanatory variables A and B, and their interaction, these three are equivalent:

• y ~ A + B + A:B
• y ~ A + B + A*B
• y ~ A*B

Solution

#fit model including interaction between social_int and isRural
rural_mod <- lm(wellbeing ~  social_int * isRural, data = wrdata)

#check model output
summary(rural_mod)

Call:
lm(formula = wellbeing ~ social_int * isRural, data = wrdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.4845  -2.7975   0.0155   2.4539  15.6743 

Coefficients:
                        Estimate Std. Error t value Pr(>|t|)    
(Intercept)              30.9986     1.4284  21.702  < 2e-16 ***
social_int                0.6488     0.1160   5.593 7.42e-08 ***
isRuralrural              1.3866     2.0510   0.676  0.49981    
social_int:isRuralrural  -0.5176     0.1615  -3.206  0.00157 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.558 on 196 degrees of freedom
Multiple R-squared:  0.2962,    Adjusted R-squared:  0.2854 
F-statistic: 27.49 on 3 and 196 DF,  p-value: 6.97e-15

Question 5

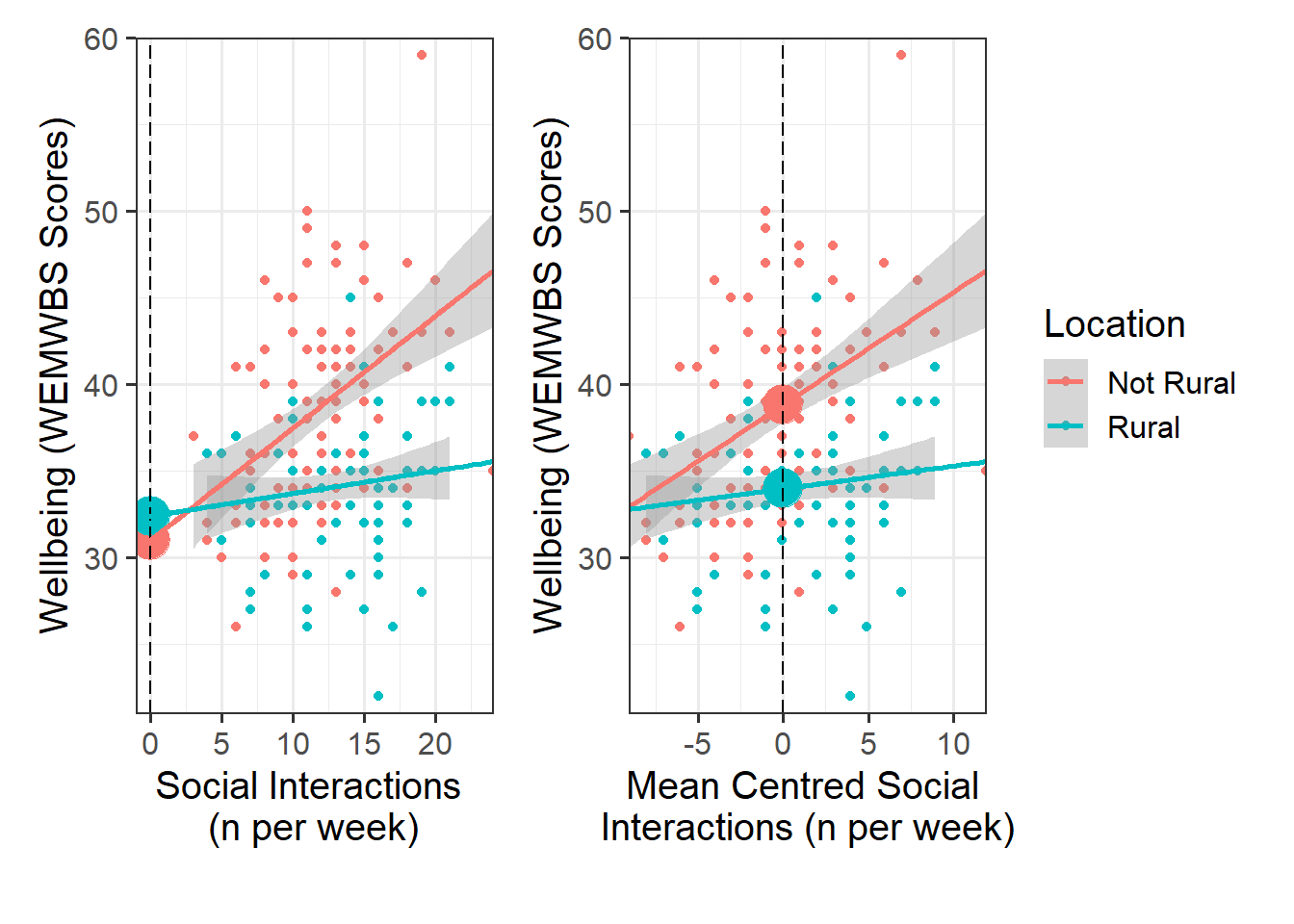
Look at the parameter estimates from your model, and write a description of what each one corresponds to on the plot shown in Figure 1 (it may help to sketch out the plot yourself and annotate it).

Figure 1: Multiple regression model: Wellbeing ~ Social Interactions * is Rural

Options

Here are some options to choose from:

• The point at which the red line cuts the y-axis (where social_int = 0)
• The point at which the blue line cuts the y-axis (where social_int = 0)
• The vertical distance from the red to the blue line at the y-axis (where social_int = 0)
• The vertical distance from the blue to the red line at the y-axis (where social_int = 0)
• The vertical distance from the blue to the red line at the center of the plot
• The vertical distance from the red to the blue line at the center of the plot
• The slope (vertical increase on the y-axis associated with a 1 unit increase on the x-axis) of the red line
• The slope (vertical increase on the y-axis associated with a 1 unit increase on the x-axis) of the blue line
• How the slope of the line changes when you move from the red to the blue line

Solution

Recall that we can obtain our parameter estimates using various functions such as summary(),coef(), coefficients(), etc.

coefficients(rural_mod)

            (Intercept)              social_int            isRuralrural 
             30.9985688               0.6487945               1.3865688 
social_int:isRuralrural 
             -0.5175856 

• \(\beta_0\) = (Intercept) = 31
  • On plot: The point at which the red line cuts the y-axis
  • Interpretation: The intercept, or predicted wellbeing score when the number of social interactions per week is 0, and when location is not rural.
• \(\beta_1\) = social_int = 0.65
  • On plot: The slope (vertical increase on the y-axis associated with a 1 unit increase on the x-axis) of the red line.
  • Interpretation: The simple slope of social interactions (number per week) for location reference group (not rural).
• \(\beta_2\) = isRuralrural = 1.39
  • On plot: The vertical distance from the red to the blue line at the y-axis (where social_int = 0).
    
  • Interpretation: The simple effect of location (or the difference in wellbeing scores between rural and non rural residents) when number of social interactions is 0.
• \(\beta_3\) social_int:isRuralrural = -0.52
  • On plot: How the slope of the line changes when you move from the red to the blue line.
  • Interpretation: The interaction between social interactions (number per week) and location (rural/not rural) - the difference in the simple slopes of social interactions for rural vs non-rural residents.

Question 6

Mean center the continuous IV(s), and re-run your model with mean centered variable(s).

Solution

Create mean centered variable for ‘social_int’:

wrdata <-
 wrdata %>%
  mutate(
   mc_social_int = social_int - mean(social_int)
    )

Re-run model:

#fit model including interaction between social_int and isRural
rural_mod1 <- lm(wellbeing ~  mc_social_int * isRural, data = wrdata)

#check model output
summary(rural_mod1)

Call:
lm(formula = wellbeing ~ mc_social_int * isRural, data = wrdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.4845  -2.7975   0.0155   2.4539  15.6743 

Coefficients:
                           Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 38.8263     0.4581  84.754  < 2e-16 ***
mc_social_int                0.6488     0.1160   5.593 7.42e-08 ***
isRuralrural                -4.8581     0.6478  -7.500 2.17e-12 ***
mc_social_int:isRuralrural  -0.5176     0.1615  -3.206  0.00157 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.558 on 196 degrees of freedom
Multiple R-squared:  0.2962,    Adjusted R-squared:  0.2854 
F-statistic: 27.49 on 3 and 196 DF,  p-value: 6.97e-15

Question 7

Note any differences between the summary() output between the “rural_mod” and “rural_mod1” models. Pay particular attention to your coefficients and their significance values. Why do you think these differences have been observed?

Hint

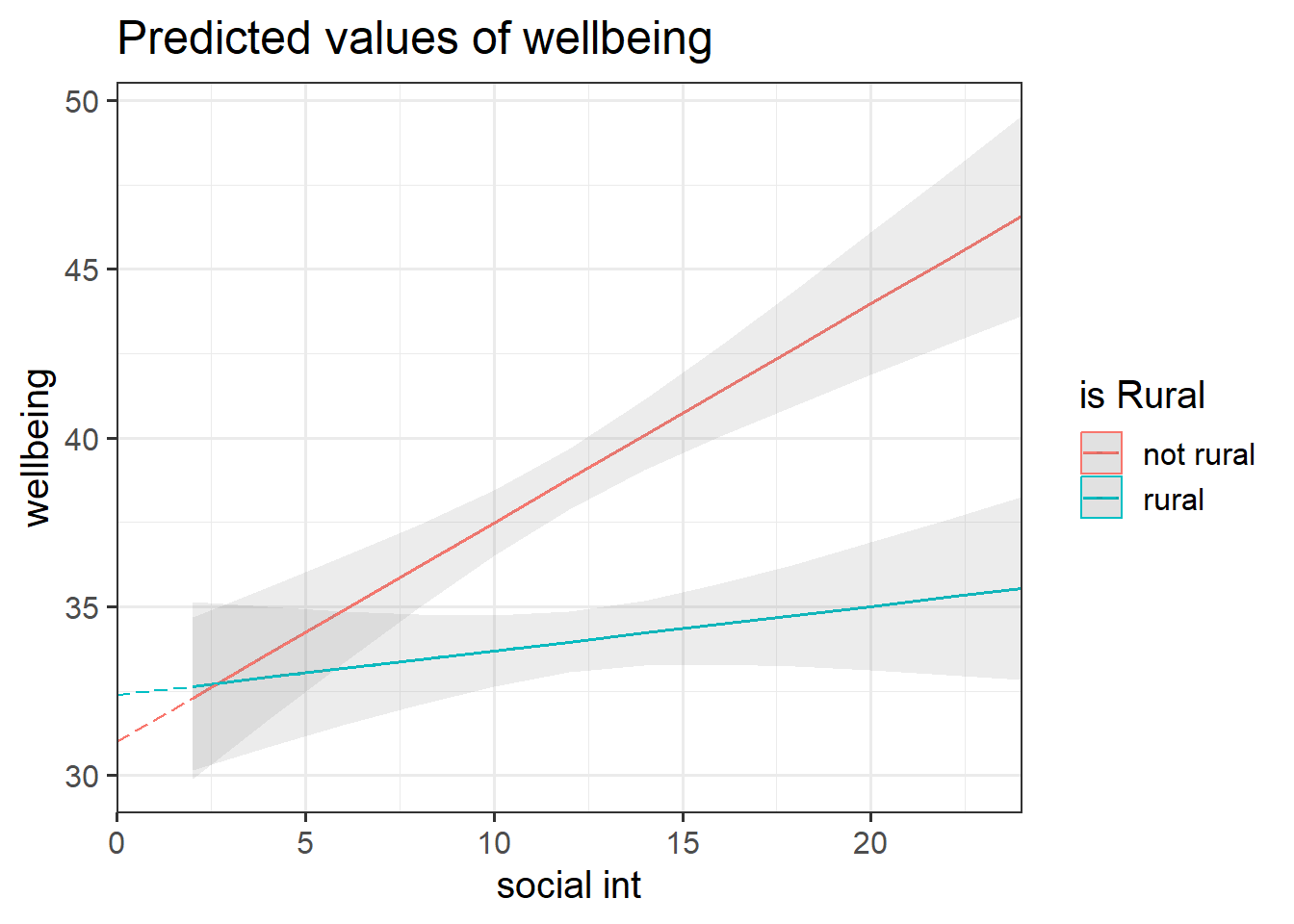
This plot illustrates the difference between the “rural_mod” and “rural_mod1” models.

Figure 2: Difference when social interactions is not vs is mean centered.
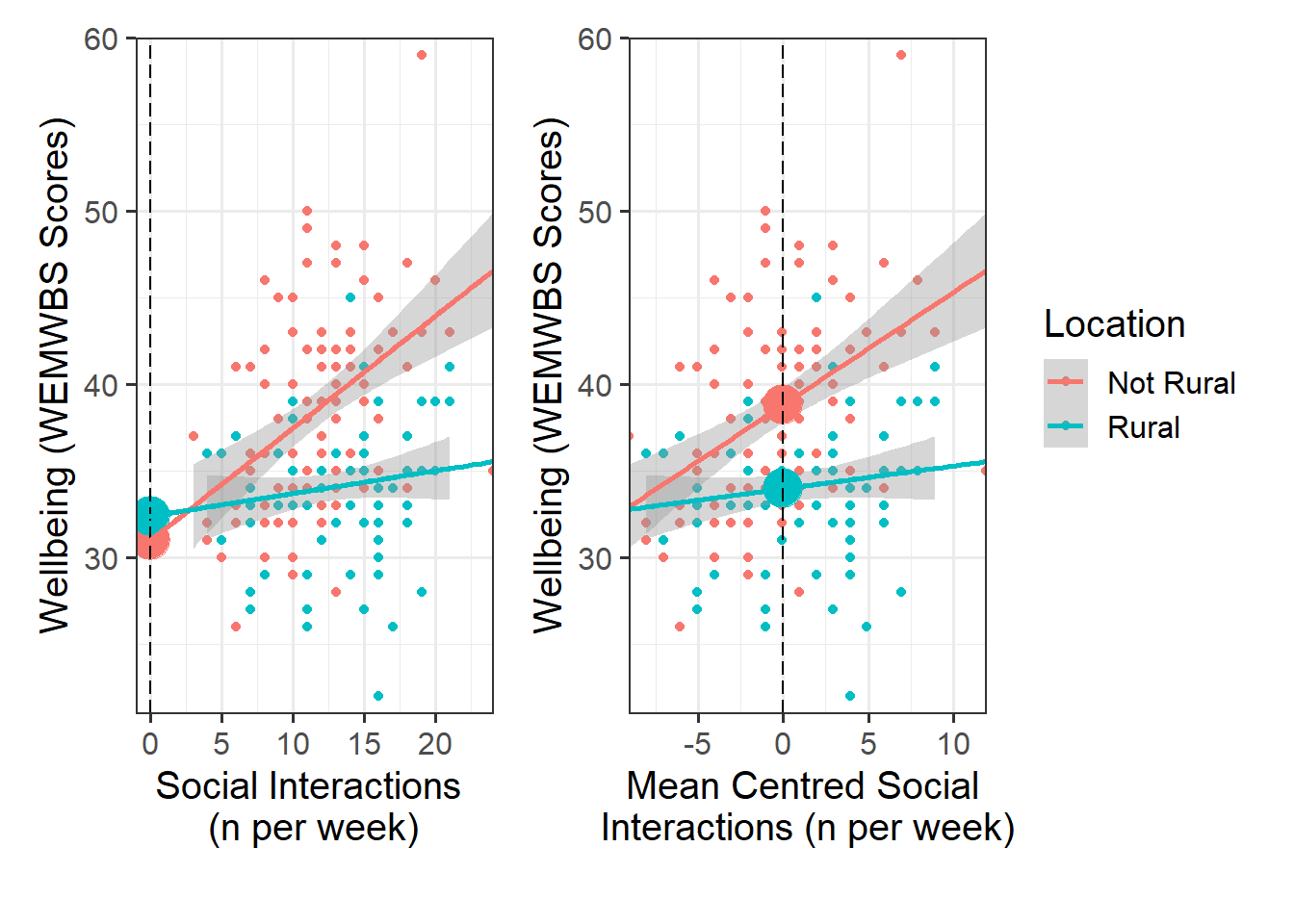
Note that the lines without SE intervals on the left plot represent predicted values below the minimum observed number of social interactions, to ensure that zero on the x-axis is visible

Solution

Recall that when there is an interaction A\(\times\)B, the coefficients A and B are no longer main effects. Instead, they are conditional effects upon the other being zero.

In our “rural_mod”, the isRural coefficient is the difference in rural vs non-rural when social interactions is 0. In our “rural_mod1”, this difference is when social interactions is the mean (12.06).

Whilst the difference in rural vs non-rural may not be significantly different when social interactions is zero, there is a significant difference at the average number of social interactions (as you can see from the plot below - note that this is the same plot as in the hint).

Figure 3: Difference when social interactions is not vs is mean centered

Question 8

Using the probe_interaction() function from the interactions package, visualise the interaction effects from your model.

Try to summarise the interaction effects in a short and concise sentence.

Hint

Make sure to give your plot informative titles/labels. You, for example, likely want to give your plot:

• a clear and concise title (specify main.title =)
• axis labels with units or scale included (specify x.label = and y.label =)
• a legend title (specify legend.main =)

Solution

plt_rural_mod <- probe_interaction(model = rural_mod1, 
                  pred = mc_social_int, 
                  modx = isRural, 
                  interval = T,
                  main.title = "Predicted Wellbeing Scores across \n Social Interactions by Location",
                  x.label = "Number of Social Interactions per Week (mean centred)",
                  y.label = "Wellbeing (WEMWBS Scores)",
                  legend.main = "Location")

Let’s look at our plot:

plt_rural_mod$interactplot

Figure 4: Predicted Wellbeing Scores across Social Interactions by Location

This suggested that for individuals living in non-rural locations, wellbeing scores increased at a steeper rate across the number of social interactions in comparison to those in rural locations.

Question 9

Provide key model results in a formatted table.

Solution

#create table for results
tab_model(rural_mod1,
          dv.labels = "Wellbeing (WEMWBS Scores)",
          pred.labels = c("mc_social_int" = "Social Interactions (number per week)",
                          "isRuralrural" = "Location - Rural",
                          "mc_social_int:isRuralrural" = "Social Interactions * Location - Rural"),
          title = "Regression Table for Wellbeing Model")

Table 1: Regression Table for Wellbeing Model

	Wellbeing (WEMWBS Scores)
Predictors	Estimates	CI	p
(Intercept)	38.83	37.92 – 39.73	<0.001
Social Interactions (number per week)	0.65	0.42 – 0.88	<0.001
Location - Rural	-4.86	-6.14 – -3.58	<0.001
Social Interactions * Location - Rural	-0.52	-0.84 – -0.20	0.002
Observations	200
R2 / R2 adjusted	0.296 / 0.285

Question 10

Interpret your results in the context of the research question and report your model in full.

Make reference to the interaction plot and regression table.

“The best method of communicating findings about the presence of a significant interaction may be to present a table or graph of the estimated means at various combinations of the interacting variables.”
— Ramsey and Schafer (2012)

Solution

Make sure to write your results up following APA guidelines:

Full regression results including 95% Confidence Intervals are shown in Table 1. The \(F\)-test for model utility was significant \((F(3,196) = 27.49, p<.001)\), and the model explained approximately 28.54% of the variability in wellbeing scores.

There was a significant conditional association between wellbeing (WEMWBS Scores) and social interactions (\(\beta\) = 0.65, \(SE\) = 0.12, \(p\) < .001), which suggested that for those living in non-rural locations, wellbeing scores increased by 0.65 for every additional social interaction per week. A significant conditional association was also evident between wellbeing and location (\(\beta\) = -4.86, \(SE\) = 0.65, \(p\) < .001), which suggested that for those with the average number of social interactions per week (\(M\) = 12.06), wellbeing scores were 4.86 points lower for those in rural areas in comparison to those in non-rurual.

The association between wellbeing (WEMWBS Scores) and social interactions was found to be dependent upon location (rural/non-rural), where the slope was less steep for those in rural locations (\(\beta\) = -0.52, \(SE\) = 0.16, \(p\) = .002). This interaction is visually presented in Figure 4. The effect of every additional social interaction per week on wellbeing (WEMWBS Scores) was 0.52 less for those living in rural locations in comparison to those in non-rural locations. Therefore, we have evidence to reject the null hypothesis (that the association between wellbeing and social interactions is not moderated by whether or not a person lives in a rural area).

References

Ramsey, Fred, and Daniel Schafer. 2012. The Statistical Sleuth: A Course in Methods of Data Analysis. Cengage Learning.