Simple Effects, Pairwise Comparisons, Corrections

Learning Objectives

At the end of this lab, you will:

1. Understand how to interpret simple effects for experimental designs
2. Understand how to conduct pairwise comparisons
3. Understand how to apply corrections available for multiple comparisons

What You Need

1. Be up to date with lectures
2. Have completed previous lab exercises from Week 1, Week 2, and Week 3

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

• tidyverse
• psych
• kableExtra
• stargazer
• patchwork
• emmeans

Lab Data

You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/cognitive_experiment.csv. Note, you have already worked with some of this data before - see Semester 1 week 8 lab, but we now have a third Task condition - Classification.

Study Overview

Research Question

Are there differences in types of memory deficits for those experiencing different cognitive impairment(s)?

In this week’s exercises, we will further explore questions such as:

• Does level \(i\) of the first factor have an effect on the response?
• Does level \(j\) of the second factor have an effect on the response?
• Is there a combined effect of level \(i\) of the first factor and level \(j\) of the second factor on the response? In other words, is there interaction of the two factors so that the combined effect is not simply the additive effect of level \(i\) of the first factor plus the effect of level \(j\) of the second factor?

Cognitive Exp 3x3 Codebook

Description

The researchers designed a study yielding a \(3 \times 3\) factorial design to test whether there are differences in types of memory deficits for those experiencing different cognitive impairment(s).

The first factor, “Diagnosis”, classifies the three types of individuals:

• 1 denotes amnesic patients;
• 2 denotes Huntingtons patients; and
• 3 denotes a control group of individuals with no known neurological disorder.

The second factor, “Task”, tells us to which of two tasks each study participant was randomly assigned to:

• 1 = grammar task, which consists of classifying letter sequences as either following or not following grammatical rules;
• 2 = classification task, which consists of classifying stimuli into certain groupings, based on previously indicated information about the groups characteristics; and
• 3 = recognition task, which consists of recognising particular stimuli as stimuli that have previously been presented during the task.

The tasks chosen by the researchers have been picked to map onto the theoretical differences between the three types of research participants. The Grammar and Classification tasks are known to reflect implicit memory processes, whereas the recognition task is known to reflect explicit memory processes. If the theory is correct, we would expect the difference in scores between the recognition and grammar/classification tasks to be relatively similar for the control and amnesiac groups, but relatively larger for the Huntingtons group compared to controls.

Preview

We have data from the 45 participants (15 amnesiacs, 15 Huntington individuals, and 15 controls). Recall that study involves two factors, now with three levels each. For each combination of factor levels we have 5 observations:

The first ten rows of the data are:

	Task
Diagnosis	grammar	classification	recognition
amnesic	44, 63, 76, 72, 45	72, 66, 55, 82, 75	70, 51, 82, 66, 56
huntingtons	24, 30, 51, 55, 40	53, 59, 33, 37, 43	107, 80, 98, 82, 108
control	76, 98, 71, 70, 85	92, 65, 86, 67, 90	107, 80, 101, 82, 105

The five observations are assumed to come from a population having a specific mean. The population means corresponding to each combination of factor levels can be schematically written as:

\[ \begin{matrix} & & & \textbf{Task} & \\ & & (j=1)\text{ grammar} & (j=2)\text{ classification} & (j=3)\text{ recognition} \\ & (i=1)\text{ control} & \mu_{1,1} & \mu_{1,2} & \mu_{1,3} \\ \textbf{Diagnosis} & (i=2)\text{ amnesic} & \mu_{2,1} & \mu_{2,2} & \mu_{2,3} \\ & (i=3)\text{ huntingtons} & \mu_{3,1} & \mu_{3,2} & \mu_{3,3} \end{matrix} \]

Setup

Setup

1. Create a new RMarkdown file
2. Load the required package(s)
3. Read the cognitive_experiment dataset into R, assigning it to an object named cog

Solution

#load packages
library(tidyverse)
library(psych)
library(kableExtra)
library(emmeans)
library(stargazer)
library(patchwork)

#read in data
cog <- read_csv('https://uoepsy.github.io/data/cognitive_experiment.csv')

Question 1

Firstly, examine the dataset, and perform any necessary and appropriate data management steps.

Next, consider would be the most appropriate coding constraint to apply in order to best address the research question - i.e., are we interested in whether group X (e.g., Amnesic) differed from group Y (e.g., Huntingtons), or whether group X (e.g., Amnesic) differed from the global/grand mean?

Make any appropriate changes to reference levels if required based on your decision above.

Solution

First step is to always look at the data we are working with - str() or head() are a good place to start

str(cog)

spc_tbl_ [45 × 3] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ Diagnosis: num [1:45] 1 1 1 1 1 1 1 1 1 1 ...
 $ Task     : num [1:45] 1 1 1 1 1 2 2 2 2 2 ...
 $ Y        : num [1:45] 44 63 76 72 45 72 66 55 82 75 ...
 - attr(*, "spec")=
  .. cols(
  ..   Diagnosis = col_double(),
  ..   Task = col_double(),
  ..   Y = col_double()
  .. )
 - attr(*, "problems")=<externalptr> 

Convert Diagnosis and Task into factors, making the labels of each factor level more meaningful.

According to the data description, the encoding of the factor Diagnosis is: 1 = amnesic patients, 2 = Huntingtons patients, and 3 are control patients. The encoding for the factor Task is: 1 = grammar task, 2 = classification task, and 3 = recognition task.

cog$Diagnosis <- factor(cog$Diagnosis, 
                        labels = c("amnesic", "huntingtons", "control"), 
                        ordered = FALSE)
cog$Task <- factor(cog$Task, 
                   labels = c("grammar", "classification", "recognition"), 
                   ordered = FALSE)

Rename the response so that we have a more meaningful name than “Y”:

cog <- cog %>%
    rename(Score = Y)

Re-examine the data:

head(cog)

# A tibble: 6 × 3
  Diagnosis Task           Score
  <fct>     <fct>          <dbl>
1 amnesic   grammar           44
2 amnesic   grammar           63
3 amnesic   grammar           76
4 amnesic   grammar           72
5 amnesic   grammar           45
6 amnesic   classification    72

Check for NAs:

#check for NAs - there are none - all FALSE
table(is.na(cog))

FALSE 
  135 

Since we are interested in comparing groups, we should use dummy coding. By default, R uses dummy coding, so we do not need to make any changes to the coding constraint. However, if we’re going to have a reference group, we’re likely to want it to be the Control group. Likewise for the Tasks, the recognition task measures ‘explicity memory’ whereas the other two measure ‘implicit memory’, so it arguably makes sense to use that as the reference group.

cog$Diagnosis <- fct_relevel(cog$Diagnosis, "control")
cog$Task <- fct_relevel(cog$Task, "recognition")

Now, let’s summarise our data checks and cleaning:

All participant data was complete, and categorical variables were coded as factors. In terms of reference groups, we re-leveled the Diagnosis factor so that the reference group was Control (since the other two groups have some form of cognitive impairment), and the Task factor to have Recognition as the reference group (since it measures explicit memory whilst the other two task types implicit).

Question 2

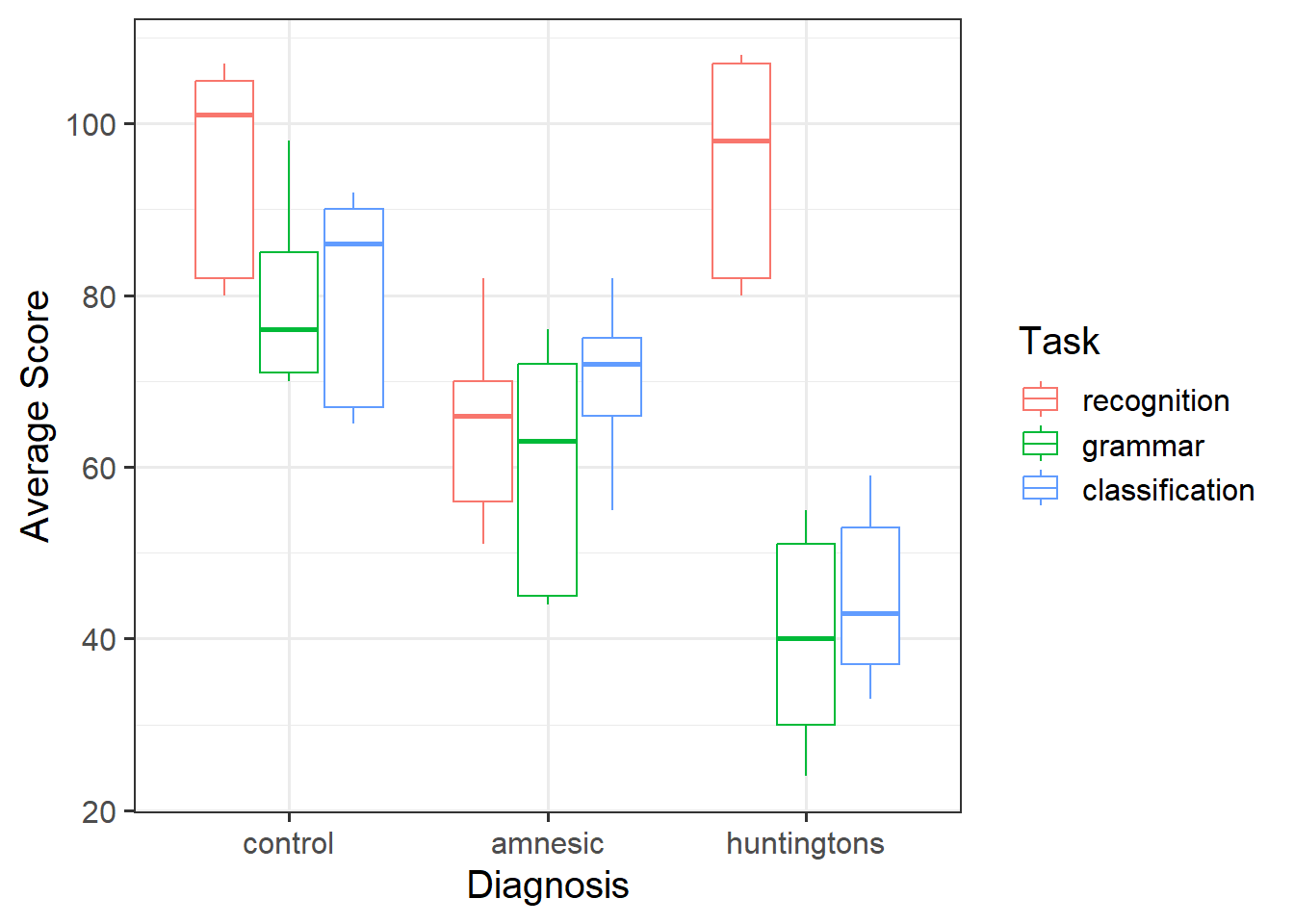
Provide a table of descriptive statistics and visualise your data.

Remember to interpret your plot in the context of the study (i.e., comment on any observed differences among treatment groups).

Hint

1. For your table of descriptive statistics, both the group_by() and summarise() functions will come in handy here.
2. Recall that when visualising a continuous outcome across several groups, geom_boxplot() may be most appropriate to use.
3. Make sure to comment on any observed differences among the sample means of the four treatment conditions.

Solution

Let’s first produce a descriptive statistics table:

cog_stats <- cog %>% 
    group_by(Diagnosis, Task) %>%
    summarise(
        Avg_Score = mean(Score), 
        SD = sd(Score),
        SE = sd(Score) / sqrt(n()),
        Min = min(Score),
        Max = max(Score)) %>%
    kable(caption = "Descriptive Statistics", digits = 2) %>%
    kable_styling()

cog_stats

Table 1: Descriptive Statistics

Diagnosis	Task	Avg_Score	SD	SE	Min	Max
control	recognition	95	12.98	5.81	80	107
control	grammar	80	11.68	5.22	70	98
control	classification	80	12.98	5.81	65	92
amnesic	recognition	65	12.17	5.44	51	82
amnesic	grammar	60	14.92	6.67	44	76
amnesic	classification	70	10.17	4.55	55	82
huntingtons	recognition	95	13.38	5.98	80	108
huntingtons	grammar	40	13.25	5.92	24	55
huntingtons	classification	45	10.86	4.86	33	59

Since we have a continuous outcome and 2 categorical predictors - a boxplot would be most appropriate for visualisations:

cog_plt <- ggplot(data = cog, aes(x = Diagnosis, y = Score, color = Task)) +
  geom_boxplot() +
  labs(x = 'Diagnosis', y = 'Average Score')
cog_plt

Figure 1: Association between Task Condition, Diagnosis, and Average Score

• Control patients consistently perform best across all tasks. They don’t seem to differ substantially in their scores between grammar and classification tasks, but they clearly perform better in the recognition task than the grammar and classification ones.

• Amnesic patients appear to perform better than Huntingtons patients in grammar an classification tasks (reflecting intrinsic memory processes) and perform worse than Huntingtons patients in the recognition task (reflecting extrinsic memory processes).

Question 3

Formally state:

• the linear model(s) to investigate whether there are differences in Score based on Diagnosis and Task conditions
• your chosen significance level
• the null and alternative hypotheses

Solution

Based on previous plotting, it does seem that there is a clear interaction between diagnosis and task. However, we have not statistically compared our interaction model to an additive model (same model but without the interaction). This is what the RQ warrants, and until we make this comparison, we cannot confidently progress on the assumption that the interaction model is the most suitable for answering the research question. Thus, we need to fit both models:

\[ \begin{aligned} Additive Model: Score &= \beta_0 \\ &+ \beta_1 D_\text{Amnseic} + \beta_2 D_\text{Huntingtons} \\ &+ \beta_3 T_\text{Grammar} + \beta_4 T_\text{Classification} \\ &+ \epsilon \end{aligned} \]

\[ \begin{aligned} Interaction Model: Score &= \beta_0 \\ &+ \beta_1 D_\text{Amnseic} + \beta_2 D_\text{Huntingtons} \\ &+ \beta_3 T_\text{Grammar} + \beta_4 T_\text{Classification} \\ &+ \beta_5 (D_\text{Amnseic} * T_\text{Grammar}) + \beta_6 (D_\text{Huntingtons} * T_\text{Grammar}) \\ &+ \beta_7 (D_\text{Amnseic} * T_\text{Classification}) + \beta_8 (D_\text{Huntingtons} * T_\text{Classification}) \\ &+ \epsilon \end{aligned} \]

Effects will be considered statistically significant at \(\alpha=.05\)

Our hypotheses are:

\(H_0:\) All \(\beta_j = 0\) (for \(j = 5, 6, 7, 8\))

There are no significant differences in performance between explicit and implicit memory tasks for patients different cognitive impairment(s).

\(H_1:\) At least one \(\beta_j \neq 0\) (for \(j = 5, 6, 7, 8\))

There are significant differences in performance between explicit and implicit memory tasks for patients different cognitive impairment(s).

We will statistically compare the additive and interaction model using anova() in order to determine which model best explains our data (i.e., the assocation between memory deficits and different cognitive impairments)

Question 4

Fit the specified models, and assign them the names “mdl_add” and “mdl_int” as appropriate.

Provide key model results from the two models in a single formatted table, and report the results of the model comparison in APA format.

Solution

Let’s first fit our two models, and compare via anova():

#Additive Model
mdl_add <- lm(Score ~ Diagnosis + Task, data = cog)
summary(mdl_add)

Call:
lm(formula = Score ~ Diagnosis + Task, data = cog)

Residuals:
   Min     1Q Median     3Q    Max 
   -29    -12      1     10     33 

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)           100.000      5.447  18.360  < 2e-16 ***
Diagnosisamnesic      -20.000      5.967  -3.352 0.001762 ** 
Diagnosishuntingtons  -25.000      5.967  -4.190 0.000149 ***
Taskgrammar           -25.000      5.967  -4.190 0.000149 ***
Taskclassification    -20.000      5.967  -3.352 0.001762 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 16.34 on 40 degrees of freedom
Multiple R-squared:  0.4958,    Adjusted R-squared:  0.4453 
F-statistic: 9.831 on 4 and 40 DF,  p-value: 1.233e-05

#Interaction Model
mdl_int <- lm(Score ~ Diagnosis * Task, data = cog)
summary(mdl_int)

Call:
lm(formula = Score ~ Diagnosis * Task, data = cog)

Residuals:
   Min     1Q Median     3Q    Max 
   -16    -12      2     11     18 

Coefficients:
                                          Estimate Std. Error t value Pr(>|t|)
(Intercept)                              9.500e+01  5.617e+00  16.912  < 2e-16
Diagnosisamnesic                        -3.000e+01  7.944e+00  -3.776 0.000576
Diagnosishuntingtons                     2.605e-15  7.944e+00   0.000 1.000000
Taskgrammar                             -1.500e+01  7.944e+00  -1.888 0.067085
Taskclassification                      -1.500e+01  7.944e+00  -1.888 0.067085
Diagnosisamnesic:Taskgrammar             1.000e+01  1.123e+01   0.890 0.379329
Diagnosishuntingtons:Taskgrammar        -4.000e+01  1.123e+01  -3.560 0.001063
Diagnosisamnesic:Taskclassification      2.000e+01  1.123e+01   1.780 0.083490
Diagnosishuntingtons:Taskclassification -3.500e+01  1.123e+01  -3.115 0.003597
                                           
(Intercept)                             ***
Diagnosisamnesic                        ***
Diagnosishuntingtons                       
Taskgrammar                             .  
Taskclassification                      .  
Diagnosisamnesic:Taskgrammar               
Diagnosishuntingtons:Taskgrammar        ** 
Diagnosisamnesic:Taskclassification     .  
Diagnosishuntingtons:Taskclassification ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 12.56 on 36 degrees of freedom
Multiple R-squared:  0.7318,    Adjusted R-squared:  0.6722 
F-statistic: 12.28 on 8 and 36 DF,  p-value: 2.844e-08

#Compare models using anova
anova(mdl_add, mdl_int)

Analysis of Variance Table

Model 1: Score ~ Diagnosis + Task
Model 2: Score ~ Diagnosis * Task
  Res.Df   RSS Df Sum of Sq      F    Pr(>F)    
1     40 10680                                  
2     36  5680  4      5000 7.9225 0.0001092 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Use the stargazer package to create table (note, you can also use tab_model() if you prefer:

stargazer(mdl_add, mdl_int,
          title="Regression Model",
          dep.var.labels=c("Score"),
          covariate.labels=c("Intercept", "Diagnosis - Amnesic", "Diagnosis - Huntingtons", "Task - Grammar", "Task - Classification", "Diagnosis - Amnesic : Task - Grammar", "Diagnosis - Huntingtons : Task - Grammar", "Diagnosis - Amnesic : Task - Classification", "Diagnosis - Huntingtons : Task - Classification"),
          type = "html", 
          digits = 2,
          single.row=TRUE, 
          align=TRUE,
          intercept.bottom = FALSE)

Regression Model

	Dependent variable:
	Score
	(1)	(2)
Intercept	100.00*** (5.45)	95.00*** (5.62)
Diagnosis - Amnesic	-20.00*** (5.97)	-30.00*** (7.94)
Diagnosis - Huntingtons	-25.00*** (5.97)	0.00 (7.94)
Task - Grammar	-25.00*** (5.97)	-15.00* (7.94)
Task - Classification	-20.00*** (5.97)	-15.00* (7.94)
Diagnosis - Amnesic : Task - Grammar		10.00 (11.23)
Diagnosis - Huntingtons : Task - Grammar		-40.00*** (11.23)
Diagnosis - Amnesic : Task - Classification		20.00* (11.23)
Diagnosis - Huntingtons : Task - Classification		-35.00*** (11.23)
Observations	45	45
R2	0.50	0.73
Adjusted R2	0.45	0.67
Residual Std. Error	16.34 (df = 40)	12.56 (df = 36)
F Statistic	9.83*** (df = 4; 40)	12.28*** (df = 8; 36)
Note:	p<0.1; p<0.05; p<0.01

We performed an \(F\)-test to compare two nested models: an additive two-factor model against a two-factor model with interaction. The test results are \(F(4, 36) = 7.92, p < .001\).

At the 5% significance level, the probability of obtaining an \(F\)-statistic as large as 7.92 or larger is <.001.

Hence, the comparison of nested models provided evidence against the additive effects model, suggesting that we should use the interaction model as each factor has a different effect on the response depending the level of the other factor.

Contrast analysis

We will now begin by looking at each factor separately.

Question 5

In terms of the diagnostic groups, we want to compare the amnesiacs to the Huntington individuals. This corresponds to a contrast with coefficients of 0, 1, and −1, for control, amnesic, and Huntingtons, respectively.

Similarly, in terms of the tasks, we want to compare the average of the two implicit memory tasks with the explicit memory task. This corresponds to a contrast with coefficients of 0.5, 0.5, and −1 for the three tasks.

When we are in presence of a significant interaction, the coefficients for a contrast between the means are found by multiplying each row coefficient with all column coefficients as shown below:

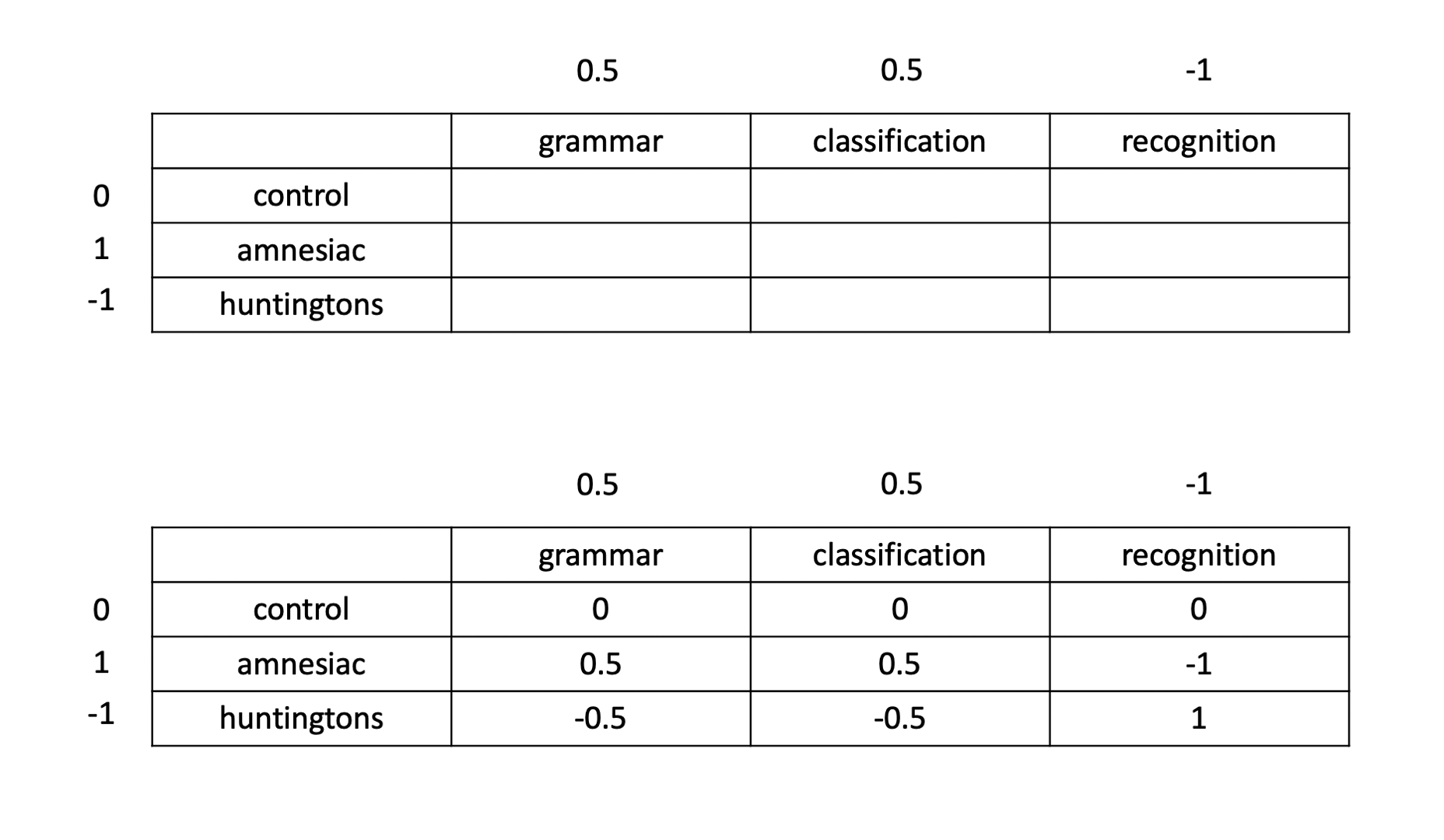
Specify the contrast weights in R, and state the null hypothesis of your contrast analysis.

Solution

This can be done in R using:

Option 1

diag_coef  <- c('control' = 0, 'amnesic' = 1, 'huntingtons' = -1)
task_coef  <- c('grammar' = 0.5, 'classification' = 0.5, 'recognition' = -1)
contr_coef <- outer(diag_coef, task_coef)
contr_coef

            grammar classification recognition
control         0.0            0.0           0
amnesic         0.5            0.5          -1
huntingtons    -0.5           -0.5           1

Option 2

diag_coef  <- c('control' = 0, 'amnesic' = 1, 'huntingtons' = -1)
task_coef  <- c('grammar' = 0.5, 'classification' = 0.5, 'recognition' = -1)
contr_coef <- diag_coef %o% task_coef
contr_coef

            grammar classification recognition
control         0.0            0.0           0
amnesic         0.5            0.5          -1
huntingtons    -0.5           -0.5           1

The above coefficients correspond to testing the null hypothesis

\[ H_0 : \frac{\mu_{2,1} + \mu_{2,2}}{2} - \mu_{2,3} - \left( \frac{\mu_{3,1} + \mu_{3,2}}{2} - \mu_{3,3} \right) = 0 \]

or, equivalently,

\[ H_0 : \frac{\mu_{2,1} + \mu_{2,2}}{2} - \mu_{2,3} = \frac{\mu_{3,1} + \mu_{3,2}}{2} - \mu_{3,3} \]

which says that, in the population, the difference between the mean implicit memory and the explicit memory score is the same for amnesic patients and Huntingtons individuals. Note that the scores for the grammar and classification tasks have been averaged to obtain a single measure of ‘implicit memory’ score.

Question 6

Run the contrast analysis, and interpret your output in the context of the research question.

Solution

Now that we have the coefficients, let’s firstly call the emmeans function (this is helpful to look at the ordering of the groups):

emm <- emmeans(mdl_int, ~ Diagnosis*Task)
emm

 Diagnosis   Task           emmean   SE df lower.CL upper.CL
 control     recognition        95 5.62 36     83.6    106.4
 amnesic     recognition        65 5.62 36     53.6     76.4
 huntingtons recognition        95 5.62 36     83.6    106.4
 control     grammar            80 5.62 36     68.6     91.4
 amnesic     grammar            60 5.62 36     48.6     71.4
 huntingtons grammar            40 5.62 36     28.6     51.4
 control     classification     80 5.62 36     68.6     91.4
 amnesic     classification     70 5.62 36     58.6     81.4
 huntingtons classification     45 5.62 36     33.6     56.4

Confidence level used: 0.95 

Next, from contr_coef, insert the coefficients following the order specified by the rows of emm above. That is, the first one should be for control recognition and have a value of 0, the second for amnesic recognition with a value of -1, and so on…

We also give a name to this contrast, such as ‘Research Hyp’.

comp_res <- contrast(emm, 
                     method = list('Research Hyp' = c(0, -1, 1, 0, 0.5, -0.5, 0, 0.5, -0.5))
                     )

Next, let’s look at the output via one of two ways:

Option 1

comp_res

 contrast     estimate   SE df t.ratio p.value
 Research Hyp     52.5 9.73 36   5.396  <.0001

confint(comp_res)

 contrast     estimate   SE df lower.CL upper.CL
 Research Hyp     52.5 9.73 36     32.8     72.2

Confidence level used: 0.95 

Option 2

summary(comp_res, infer = TRUE)

 contrast     estimate   SE df lower.CL upper.CL t.ratio p.value
 Research Hyp     52.5 9.73 36     32.8     72.2   5.396  <.0001

Confidence level used: 0.95 

The contrast analysis yielded a \(t\)-value of 5.4 and a corresponding \(p\)-value < .001. Thus, there is evidence that the contrast is not zero in the population. In other words, Amnesics and Huntingtons patients differ in the difference between implicit and explicit recognition memory tasks.

The contrast analysis shows that the 95% confidence interval for our contrast stretches from 32.8 to 72.2. This interval does not contain zero. Thus, we can be 95% confident that the task difference is not the same for amnesiacs as for Huntingtons, and therefore can reject the null hypothesis that the difference in differences is equal to zero.

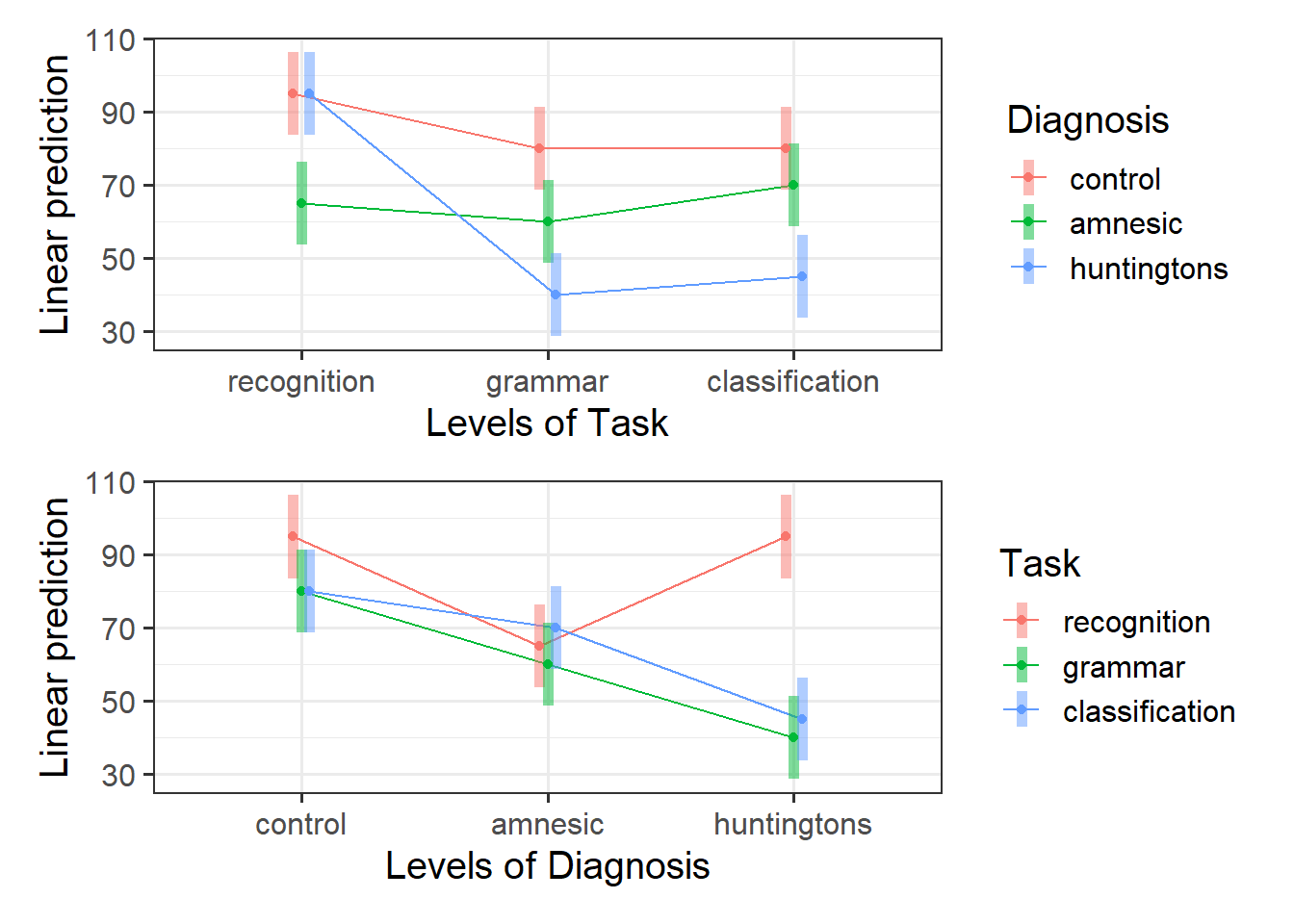
Simple Effects

By considering the simple effects¹, we can identify at which levels of the interacting condition we see different effects.

Question 7

Examine the simple effects for Task at each level of Diagnosis; and then the simple effects for Diagnosis at each level of Task.

Solution

mdl_int_simple1 <- pairs(emm, simple = "Task")
mdl_int_simple1

Diagnosis = control:
 contrast                     estimate   SE df t.ratio p.value
 recognition - grammar              15 7.94 36   1.888  0.1567
 recognition - classification       15 7.94 36   1.888  0.1567
 grammar - classification            0 7.94 36   0.000  1.0000

Diagnosis = amnesic:
 contrast                     estimate   SE df t.ratio p.value
 recognition - grammar               5 7.94 36   0.629  0.8050
 recognition - classification       -5 7.94 36  -0.629  0.8050
 grammar - classification          -10 7.94 36  -1.259  0.4273

Diagnosis = huntingtons:
 contrast                     estimate   SE df t.ratio p.value
 recognition - grammar              55 7.94 36   6.923  <.0001
 recognition - classification       50 7.94 36   6.294  <.0001
 grammar - classification           -5 7.94 36  -0.629  0.8050

P value adjustment: tukey method for comparing a family of 3 estimates 

mdl_int_simple2 <- pairs(emm, simple = "Diagnosis")
mdl_int_simple2

Task = recognition:
 contrast              estimate   SE df t.ratio p.value
 control - amnesic           30 7.94 36   3.776  0.0016
 control - huntingtons        0 7.94 36   0.000  1.0000
 amnesic - huntingtons      -30 7.94 36  -3.776  0.0016

Task = grammar:
 contrast              estimate   SE df t.ratio p.value
 control - amnesic           20 7.94 36   2.518  0.0424
 control - huntingtons       40 7.94 36   5.035  <.0001
 amnesic - huntingtons       20 7.94 36   2.518  0.0424

Task = classification:
 contrast              estimate   SE df t.ratio p.value
 control - amnesic           10 7.94 36   1.259  0.4273
 control - huntingtons       35 7.94 36   4.406  0.0003
 amnesic - huntingtons       25 7.94 36   3.147  0.0091

P value adjustment: tukey method for comparing a family of 3 estimates 

From mdl_int_simple1 we can see the differences between between tasks for each diagnosis group, and from mdl_int_simple2 the differences between diagnoses for each task group.

Question 8

Visualise the interaction, displaying two plots - one with Diagnosis on the x-axis, and the other with Task on the x-axis.

Considering the simple effects that we noted above, identify the significant effects and match them to the parts of your interaction plot.

Hint

To visualise the interaction, you can use emmip().

Recall that the patchwork package allows us to arrange multiple plots using either / or | or +

Solution

First create our plots:

plt_1 <- emmip(mdl_int, Diagnosis ~ Task, CIs = TRUE)
plt_2 <- emmip(mdl_int, Task ~ Diagnosis, CIs = TRUE)
plt_1 / plt_2

• Simple Effects of Task

For the simple effects of task (see plt_1), we saw the significant differences (those for which \(p<.05\)):

• Only in the Huntingtons group, between recognition & grammar and recognition & classification tasks (top plot: left-most blue point compared to the middle blue point, and then compared to the right-most blue point)

• Simple Effects of Diagnosis

For the simple effects of Diagnosis (see plt_2), we saw significant differences:

• in the recognition task, between control & amnesic
  (bottom plot: left-most red point to middle red point)
  
• in the recognition task, between amnesic & huntingtons
  (bottom plot: middle red-point to right-most red point)
  
• in the grammar task, between control & amnesic
  (bottom plot: left-most green point to middle green point)
• in the grammar task, between control & huntingtons
  (bottom plot: left-most green point to right-most green point)
• in the grammar task, between amnesic & huntingtons
  (bottom plot: middle green point to right-most green point)
• in the classification task, between control & huntingtons
  (bottom plot: left-most blue point to right-most blue point)
• in the classification task, between amnesic & huntingtons
  (bottom plot: middle blue point to right-most blue point)

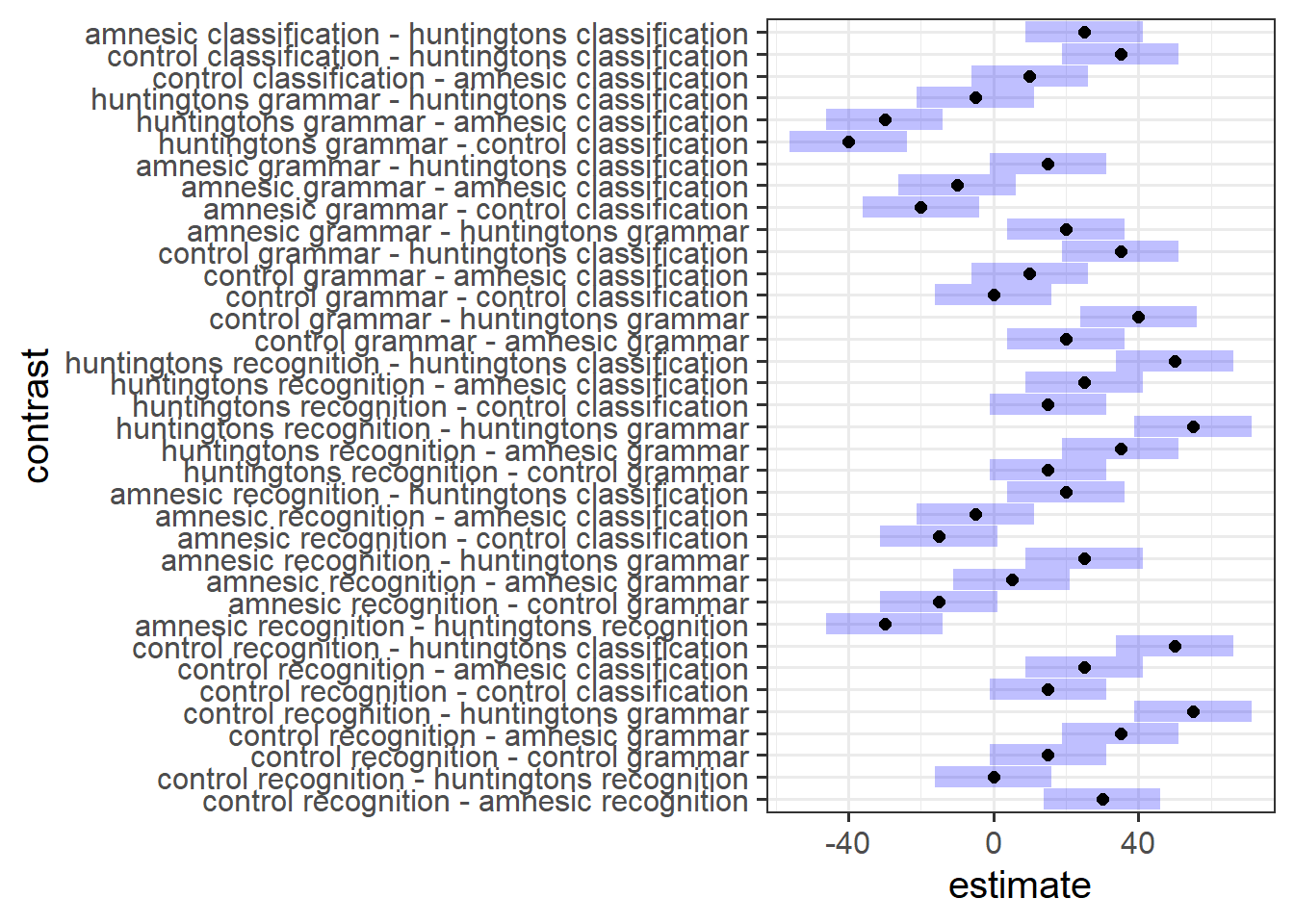
Pairwise Comparisons & Multiple Corrections

Question 9

Conduct exploratory pairwise comparisons to compare all levels of Diagnosis with all levels of Task, applying no correction (note that Tukey will be automatically applied since we are comparing groups of means, so you will need to overwrite this).

Without adjusting our \(\alpha\) (or \(p\)-value), why might any inferences drawn from your output be problematic?

Hint

You can specify the adjustment using adjust = ". Possible options include:

• adjust = "none"
• adjust = "bonferroni"
• adjust = "sidak"
• adjust = "Tukey"
• adjust = scheffe"

Solution

pairs_res <- pairs(emm, adjust = "none")
pairs_res

 contrast                                             estimate   SE df t.ratio
 control recognition - amnesic recognition                  30 7.94 36   3.776
 control recognition - huntingtons recognition               0 7.94 36   0.000
 control recognition - control grammar                      15 7.94 36   1.888
 control recognition - amnesic grammar                      35 7.94 36   4.406
 control recognition - huntingtons grammar                  55 7.94 36   6.923
 control recognition - control classification               15 7.94 36   1.888
 control recognition - amnesic classification               25 7.94 36   3.147
 control recognition - huntingtons classification           50 7.94 36   6.294
 amnesic recognition - huntingtons recognition             -30 7.94 36  -3.776
 amnesic recognition - control grammar                     -15 7.94 36  -1.888
 amnesic recognition - amnesic grammar                       5 7.94 36   0.629
 amnesic recognition - huntingtons grammar                  25 7.94 36   3.147
 amnesic recognition - control classification              -15 7.94 36  -1.888
 amnesic recognition - amnesic classification               -5 7.94 36  -0.629
 amnesic recognition - huntingtons classification           20 7.94 36   2.518
 huntingtons recognition - control grammar                  15 7.94 36   1.888
 huntingtons recognition - amnesic grammar                  35 7.94 36   4.406
 huntingtons recognition - huntingtons grammar              55 7.94 36   6.923
 huntingtons recognition - control classification           15 7.94 36   1.888
 huntingtons recognition - amnesic classification           25 7.94 36   3.147
 huntingtons recognition - huntingtons classification       50 7.94 36   6.294
 control grammar - amnesic grammar                          20 7.94 36   2.518
 control grammar - huntingtons grammar                      40 7.94 36   5.035
 control grammar - control classification                    0 7.94 36   0.000
 control grammar - amnesic classification                   10 7.94 36   1.259
 control grammar - huntingtons classification               35 7.94 36   4.406
 amnesic grammar - huntingtons grammar                      20 7.94 36   2.518
 amnesic grammar - control classification                  -20 7.94 36  -2.518
 amnesic grammar - amnesic classification                  -10 7.94 36  -1.259
 amnesic grammar - huntingtons classification               15 7.94 36   1.888
 huntingtons grammar - control classification              -40 7.94 36  -5.035
 huntingtons grammar - amnesic classification              -30 7.94 36  -3.776
 huntingtons grammar - huntingtons classification           -5 7.94 36  -0.629
 control classification - amnesic classification            10 7.94 36   1.259
 control classification - huntingtons classification        35 7.94 36   4.406
 amnesic classification - huntingtons classification        25 7.94 36   3.147
 p.value
  0.0006
  1.0000
  0.0671
  0.0001
  <.0001
  0.0671
  0.0033
  <.0001
  0.0006
  0.0671
  0.5331
  0.0033
  0.0671
  0.5331
  0.0164
  0.0671
  0.0001
  <.0001
  0.0671
  0.0033
  <.0001
  0.0164
  <.0001
  1.0000
  0.2162
  0.0001
  0.0164
  0.0164
  0.2162
  0.0671
  <.0001
  0.0006
  0.5331
  0.2162
  0.0001
  0.0033

#can also plot if you'd like:
plot(pairs_res)

From the above, we can see comparisons for all different possible pairs of diagnosis-task combinations.

In total, there are 9 different estimates, but comparing them all means that we have 36 comparisons being tested! By not adjusting our \(p\)-value, we are increasing the experimentwise Type I error rate - we could wrongly reject the null hypothesis at a much higher rate than 5/100 (or 1/20 as is assumed when \(\alpha = .05\)). To overcome this, we might adjust and determine a result to be statistically significant if \(p < .005\), as opposed to \(p < .05\), depending on how many tests are in our family of tests).

Question 10

Select an appropriate method to adjust for multiple comparisons, and then obtain confidence intervals.

Comment on how these \(p\)-values differ from your raw (i.e., unadjusted) \(p\)-values.

Solution

Note what the functions in R do is adjust the \(p\)-value, rather than the \(\alpha\).

Since we’re interested in all pairwise comparisons of means, the Tukey adjustment might be a sensible approach. However, we’ll also show the Bonferroni to show how it differs (note, in practice you would only apply one correction and justify this choice based on your design - we are only applying two to note how they differ!)

Let’s start with Tukey:

contrast(emm, method = "pairwise", adjust="Tukey")

 contrast                                             estimate   SE df t.ratio
 control recognition - amnesic recognition                  30 7.94 36   3.776
 control recognition - huntingtons recognition               0 7.94 36   0.000
 control recognition - control grammar                      15 7.94 36   1.888
 control recognition - amnesic grammar                      35 7.94 36   4.406
 control recognition - huntingtons grammar                  55 7.94 36   6.923
 control recognition - control classification               15 7.94 36   1.888
 control recognition - amnesic classification               25 7.94 36   3.147
 control recognition - huntingtons classification           50 7.94 36   6.294
 amnesic recognition - huntingtons recognition             -30 7.94 36  -3.776
 amnesic recognition - control grammar                     -15 7.94 36  -1.888
 amnesic recognition - amnesic grammar                       5 7.94 36   0.629
 amnesic recognition - huntingtons grammar                  25 7.94 36   3.147
 amnesic recognition - control classification              -15 7.94 36  -1.888
 amnesic recognition - amnesic classification               -5 7.94 36  -0.629
 amnesic recognition - huntingtons classification           20 7.94 36   2.518
 huntingtons recognition - control grammar                  15 7.94 36   1.888
 huntingtons recognition - amnesic grammar                  35 7.94 36   4.406
 huntingtons recognition - huntingtons grammar              55 7.94 36   6.923
 huntingtons recognition - control classification           15 7.94 36   1.888
 huntingtons recognition - amnesic classification           25 7.94 36   3.147
 huntingtons recognition - huntingtons classification       50 7.94 36   6.294
 control grammar - amnesic grammar                          20 7.94 36   2.518
 control grammar - huntingtons grammar                      40 7.94 36   5.035
 control grammar - control classification                    0 7.94 36   0.000
 control grammar - amnesic classification                   10 7.94 36   1.259
 control grammar - huntingtons classification               35 7.94 36   4.406
 amnesic grammar - huntingtons grammar                      20 7.94 36   2.518
 amnesic grammar - control classification                  -20 7.94 36  -2.518
 amnesic grammar - amnesic classification                  -10 7.94 36  -1.259
 amnesic grammar - huntingtons classification               15 7.94 36   1.888
 huntingtons grammar - control classification              -40 7.94 36  -5.035
 huntingtons grammar - amnesic classification              -30 7.94 36  -3.776
 huntingtons grammar - huntingtons classification           -5 7.94 36  -0.629
 control classification - amnesic classification            10 7.94 36   1.259
 control classification - huntingtons classification        35 7.94 36   4.406
 amnesic classification - huntingtons classification        25 7.94 36   3.147
 p.value
  0.0149
  1.0000
  0.6257
  0.0026
  <.0001
  0.6257
  0.0711
  <.0001
  0.0149
  0.6257
  0.9993
  0.0711
  0.6257
  0.9993
  0.2575
  0.6257
  0.0026
  <.0001
  0.6257
  0.0711
  <.0001
  0.2575
  0.0004
  1.0000
  0.9367
  0.0026
  0.2575
  0.2575
  0.9367
  0.6257
  0.0004
  0.0149
  0.9993
  0.9367
  0.0026
  0.0711

P value adjustment: tukey method for comparing a family of 9 estimates 

Note that 8 of the comparisons are no longer significant when using Tukey’s adjustment, suggesting that these might have (when using no adjustment) been Type I errors!

Next, lets look at Bonferroni:

contrast(emm, method = "pairwise", adjust="bonferroni")

 contrast                                             estimate   SE df t.ratio
 control recognition - amnesic recognition                  30 7.94 36   3.776
 control recognition - huntingtons recognition               0 7.94 36   0.000
 control recognition - control grammar                      15 7.94 36   1.888
 control recognition - amnesic grammar                      35 7.94 36   4.406
 control recognition - huntingtons grammar                  55 7.94 36   6.923
 control recognition - control classification               15 7.94 36   1.888
 control recognition - amnesic classification               25 7.94 36   3.147
 control recognition - huntingtons classification           50 7.94 36   6.294
 amnesic recognition - huntingtons recognition             -30 7.94 36  -3.776
 amnesic recognition - control grammar                     -15 7.94 36  -1.888
 amnesic recognition - amnesic grammar                       5 7.94 36   0.629
 amnesic recognition - huntingtons grammar                  25 7.94 36   3.147
 amnesic recognition - control classification              -15 7.94 36  -1.888
 amnesic recognition - amnesic classification               -5 7.94 36  -0.629
 amnesic recognition - huntingtons classification           20 7.94 36   2.518
 huntingtons recognition - control grammar                  15 7.94 36   1.888
 huntingtons recognition - amnesic grammar                  35 7.94 36   4.406
 huntingtons recognition - huntingtons grammar              55 7.94 36   6.923
 huntingtons recognition - control classification           15 7.94 36   1.888
 huntingtons recognition - amnesic classification           25 7.94 36   3.147
 huntingtons recognition - huntingtons classification       50 7.94 36   6.294
 control grammar - amnesic grammar                          20 7.94 36   2.518
 control grammar - huntingtons grammar                      40 7.94 36   5.035
 control grammar - control classification                    0 7.94 36   0.000
 control grammar - amnesic classification                   10 7.94 36   1.259
 control grammar - huntingtons classification               35 7.94 36   4.406
 amnesic grammar - huntingtons grammar                      20 7.94 36   2.518
 amnesic grammar - control classification                  -20 7.94 36  -2.518
 amnesic grammar - amnesic classification                  -10 7.94 36  -1.259
 amnesic grammar - huntingtons classification               15 7.94 36   1.888
 huntingtons grammar - control classification              -40 7.94 36  -5.035
 huntingtons grammar - amnesic classification              -30 7.94 36  -3.776
 huntingtons grammar - huntingtons classification           -5 7.94 36  -0.629
 control classification - amnesic classification            10 7.94 36   1.259
 control classification - huntingtons classification        35 7.94 36   4.406
 amnesic classification - huntingtons classification        25 7.94 36   3.147
 p.value
  0.0207
  1.0000
  1.0000
  0.0033
  <.0001
  1.0000
  0.1190
  <.0001
  0.0207
  1.0000
  1.0000
  0.1190
  1.0000
  1.0000
  0.5907
  1.0000
  0.0033
  <.0001
  1.0000
  0.1190
  <.0001
  0.5907
  0.0005
  1.0000
  1.0000
  0.0033
  0.5907
  0.5907
  1.0000
  1.0000
  0.0005
  0.0207
  1.0000
  1.0000
  0.0033
  0.1190

P value adjustment: bonferroni method for 36 tests 

The first Bonferroni adjusted \(p\)-value is 0.0207. The raw (unadjusted) \(p\)-value from the previous question was 0.0005759265. The Bonferroni method simply multiplies the ‘raw’ \(p\)-value by the number of the tests, which we know is 36.

0.0005759265 * 36

[1] 0.02073335

In terms of differences in Bonferroni to raw \(p\)-values, they are thus 36 times the size.

One benefit of Bonferroni is that it can be applied to any set of \(p\)-values, whereas Tukey only applies when comparing the means of levels of a factor. The downside, however, is that it may be overly conservative (i.e. reduce our power to detect an effect that is truly there).

Footnotes

1. simple effects are the effects of one variable at a specific level of another variable