Sample Size and Power Analysis

Learning Objectives

At the end of this lab, you will:

  1. Understand how varying factors can influence power
  2. Be able to conduct power analyses using the pwr package

What You Need

  1. Be up to date with lectures

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

  • tidyverse
  • kableExtra
  • pwr

Presenting Results

All results should be presented following APA guidelines. If you need a reminder on how to hide code, format tables/plots, etc., make sure to review the rmd bootcamp.

The example write-up sections included as part of the solutions are not perfect - they instead should give you a good example of what information you should include and how to structure this. Note that you must not copy any of the write-ups included below for future reports - if you do, you will be committing plagiarism, and this type of academic misconduct is taken very seriously by the University. You can find out more here.

Lab Data

You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/recall_med_coast.csv

Study Overview

Research Question

Do the association between recall and age differ by intervention type?

Recall codebook

Setup

Setup
  1. Create a new RMarkdown file
  2. Load the required package(s)
  3. Read in the recall_med_coast dataset into R, assigning it to an object named recdata 

#Loading the required package(s)
library(tidyverse)
library(kableExtra)
library(pwr)

#Reading in data and storing in object named `recdata`
recdata <- read_csv("https://uoepsy.github.io/data/recall_med_coast.csv")

Exercises

Study Overview & Data Management

Question 1

First, examine the dataset and perform any necessary and appropriate data management steps.

Next, provide a brief overview of the study design and data.

  • Give the reader some background on the context of the study
  • State what type of analysis you will conduct in order to address the research question
  • Specify the model to be fitted to address the research question
  • Specify your chosen significance (\(\alpha\)) level
  • State your hypotheses

Much of the information required can be found in the Study Overview codebook.

The statistical models flashcards may also be useful to refer to. Specifically the interaction models flashcards and numeric x categorical example flashcards might be of most use.

#look at structure of data:
str(recdata)
spc_tbl_ [100 × 3] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ perc_recall: num [1:100] 47.4 61.4 50.1 56.4 57 ...
 $ group      : num [1:100] 0 1 0 1 1 0 1 1 1 0 ...
 $ age        : num [1:100] 52 37 46 72 46 69 70 53 41 26 ...
 - attr(*, "spec")=
  .. cols(
  ..   perc_recall = col_double(),
  ..   group = col_double(),
  ..   age = col_double()
  .. )
 - attr(*, "problems")=<externalptr> 
#check for NAs - there are none - all FALSE:
table(is.na(recdata))

FALSE 
  300 
#Group should be a factor:
recdata$group <- factor(recdata$group, 
                        levels = c(0, 1), 
                        labels = c('rollercoaster', 'meditation'))

The recdata dataset contained information on 100 hypothetical participants who participated in a between-subjects experiment exploring the associations among recall, age, and intervention type. Participants were aged 18-75 years old, and were randomly allocated to one of two intervention groups (exciting - 1-hour long roller-coaster session; or relaxing - 1-hour long meditation session) before completing a free-recall test (% correct).

The ‘group’ variable denoting which intervention type participants were allocated to was coded as a factor with two levels - ‘rollercoaster’ and ‘meditation’, where ‘rollercoaster’ was designated as the reference group. There were no NAs contained within the dataset, and recall scores were within range (i.e., within possible values of 0-100), as were ages (i.e., all ages ranged from 18-75).

To address the research question of whether age and intervention type influence recall, we can specify our model as follows:

\[ \text{Recall} = \beta_0 + \beta_1 \cdot \text{Age} + \beta_2 \cdot \text{Intervention Group}_{\text{Meditation}} + \beta_3 \cdot (\text{Age} \cdot \text{Intervention Group}_{\text{Meditation}}) + \epsilon \] Effects will be considered statistically significant at \(\alpha=.05\).

Our hypotheses are:

\(H_0: \beta_3 = 0\)

The association between recall and age does not differ by intervention type.

\(H_1: \beta_3 \neq 0\)

The association between recall and age does differ by intervention type.

Descriptive Statistics & Visualisations

Question 2

Provide a table of descriptive statistics and visualise your data.

Remember to interpret your findings in the context of the study.

Review the many ways to numerically and visually explore your data by reading over the data exploration flashcards.

For examples, see flashcards on descriptives statistics tables - categorical and numeric values examples and data visualisation - bivariate examples, paying particular attention to the type of data that you’re working with.

More specifically:
1. For your table of descriptive statistics, both the group_by() and summarise() functions will come in handy here.

  1. If you use the select() function and get an error along the lines of Error in select...unused arguments..., you will need to specify dplyr::select() (this just tells R which package to use the select function from).

Descriptive statistics presented in a well formatted table:

recall_stats <- recdata %>%
    group_by(group) %>%
    summarise(
       n = n(),
       M_Age = mean(age),
       SD_Age = sd(age),
       M_Recall = mean(perc_recall),
       SD_Recall = sd(perc_recall)
       ) %>%
    kable(caption = "Descriptive Statistics", digits = 2) %>%
    kable_styling()

recall_stats
Table 1: Descriptive Statistics
group n M_Age SD_Age M_Recall SD_Recall
rollercoaster 53 47.85 14.93 50.11 4.35
meditation 47 46.57 15.29 59.46 2.89

We can visually explore the association between Recall and the two predictor variables as follows:

recall_plt1 <- ggplot(data = recdata, aes(x = group, y = perc_recall, fill = group)) +
    geom_boxplot() + 
    labs(x = "Intervention Group", y = "Recall (%)")
recall_plt1

Figure 1: Association between Recall and Intervention Group
recall_plt2 <- ggplot(data = recdata, aes(x = age, y = perc_recall)) +
    geom_point() + 
    geom_smooth(method = "lm", se = FALSE) + 
    labs(x = "Age (in years)", y = "Recall (%)")
recall_plt2

Figure 2: Association between Recall and Age

From Table 1, Figure 1, and Figure 2 we can see:

  • there were more participants in the rollercoaster condition than meditation
  • participants in the meditation condition had higher recall scores than those in the rollercoaster condition
  • there was less variability in scores in the meditation condition in comparison to the rollercoaster condition
  • older age appeared to be associated with lower recall scores


Question 3

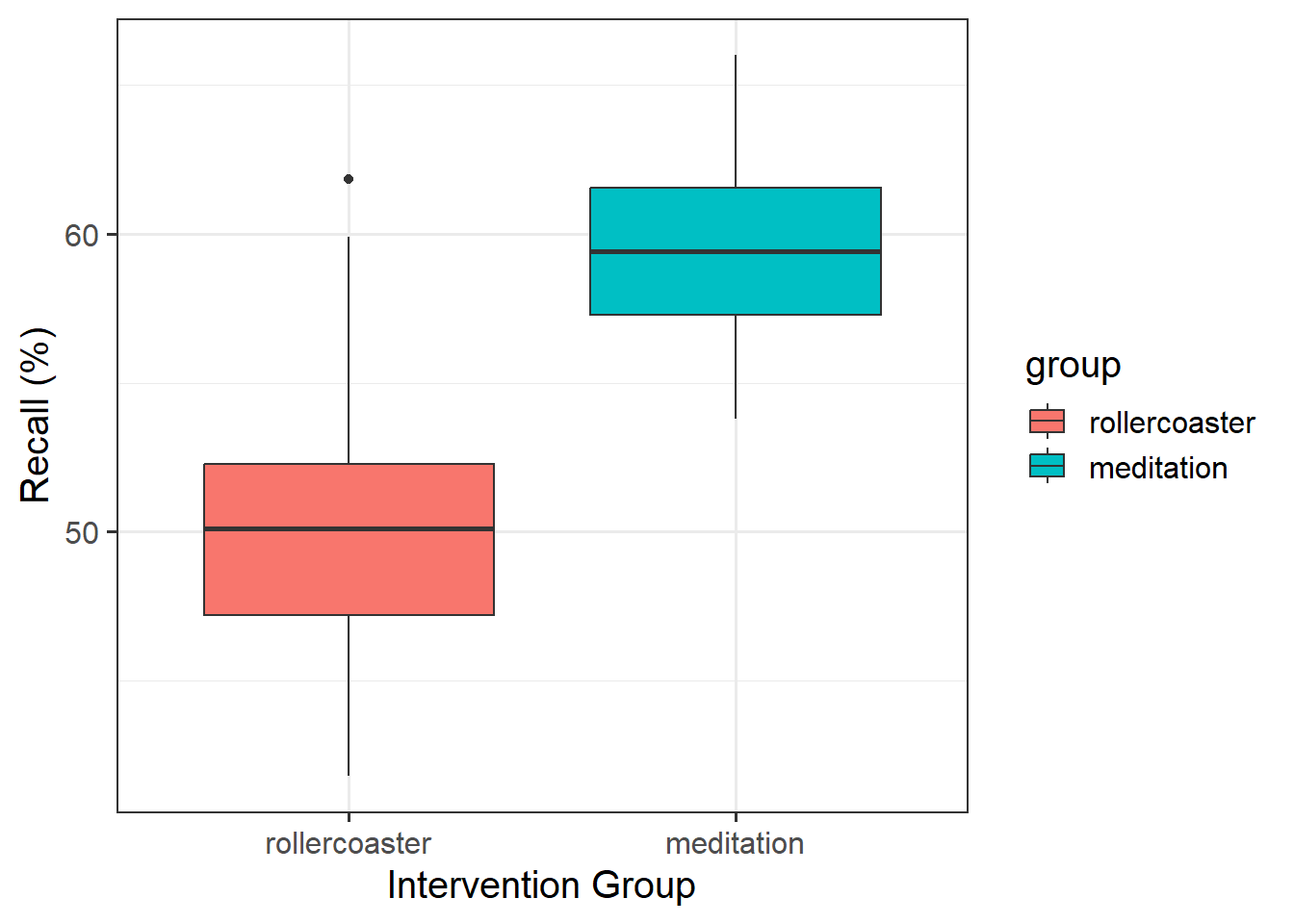
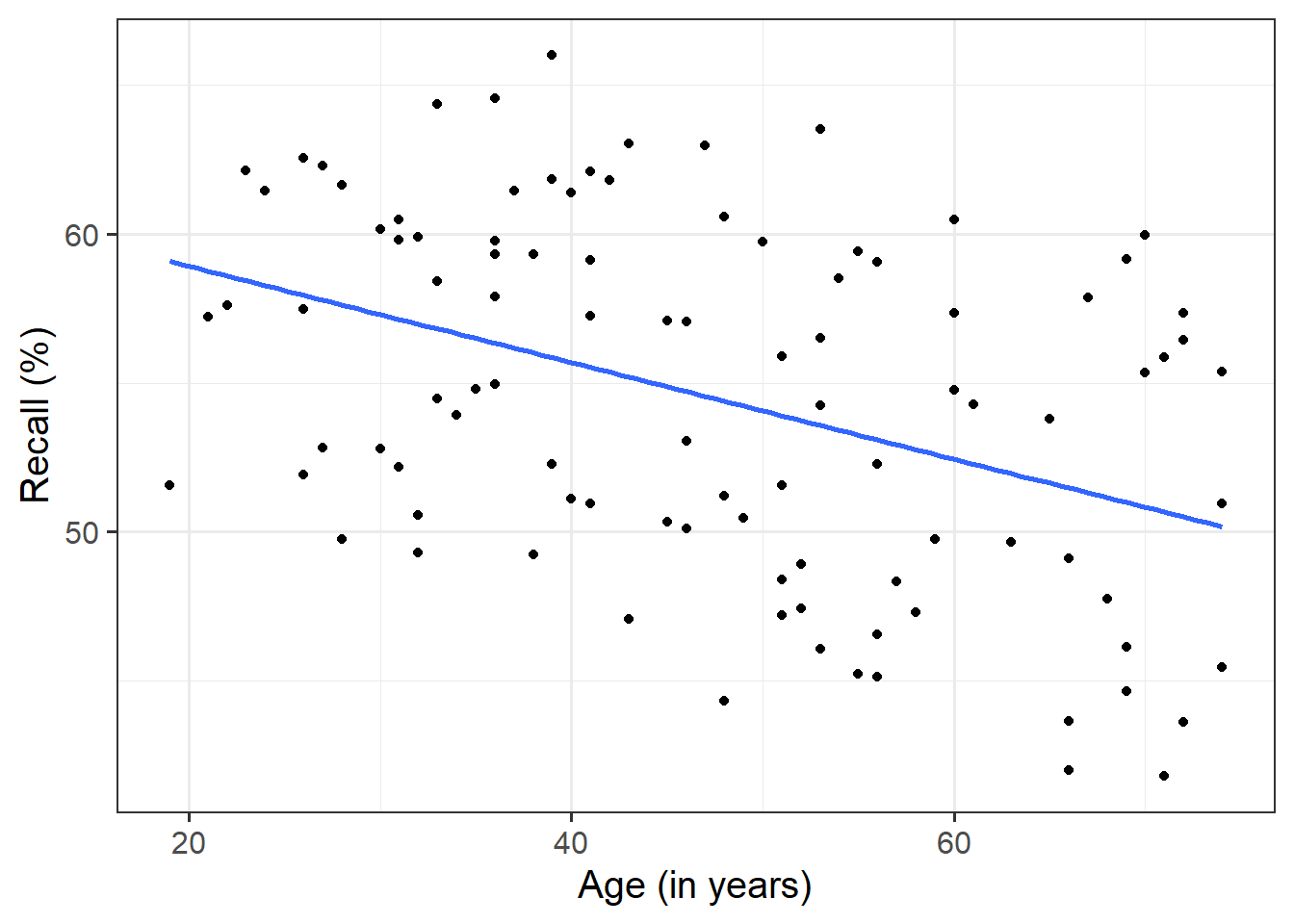
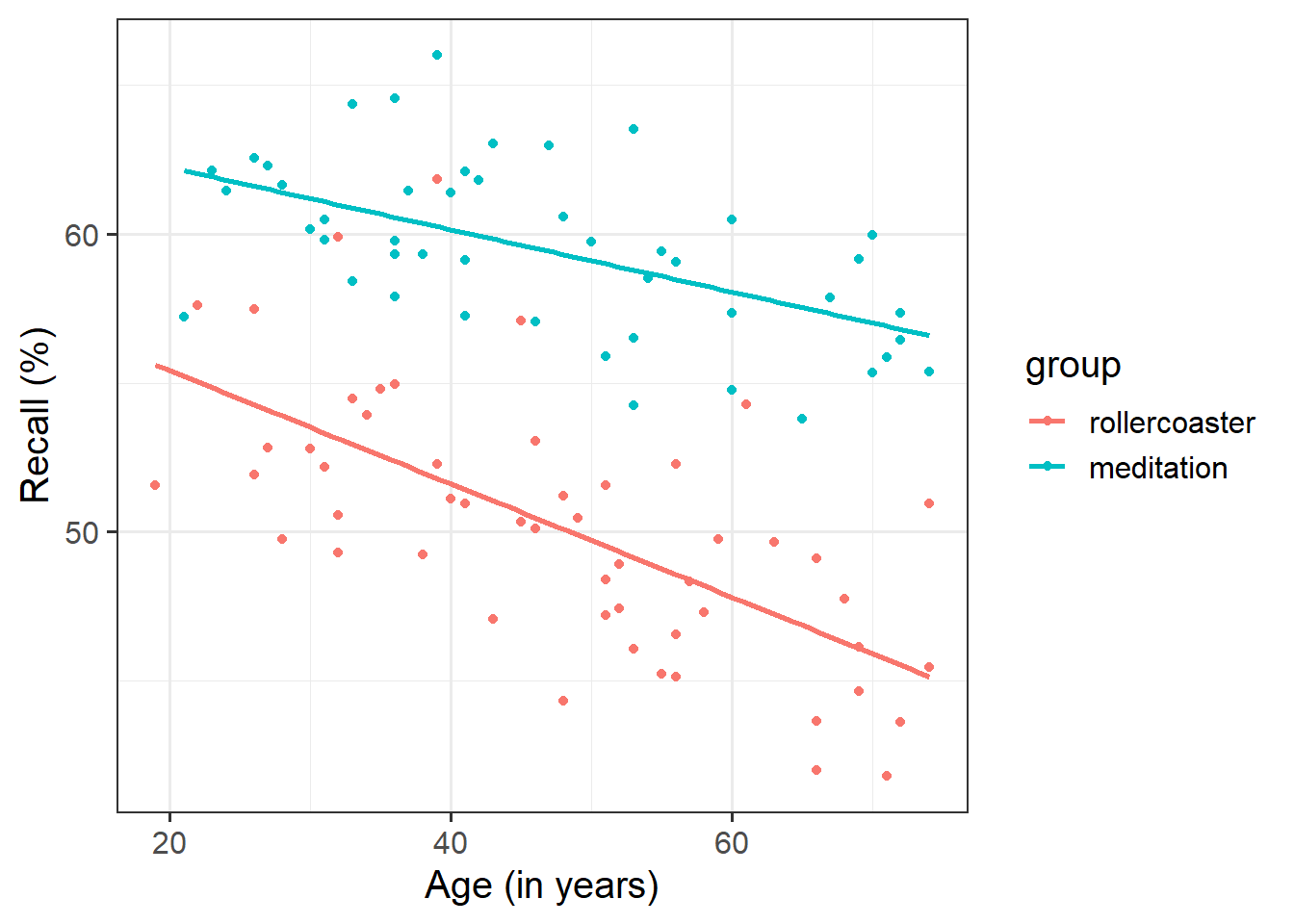
Use a scatterplot to visualise the association between recall and age by group.

Is there any evidence of an interaction between age and group?

For a recap on how to create a scatterplot, review the data visualisation - bivariate examples.

  • It might be useful to specify the color = argument for your grouping variable
  • Consider using geom_smooth() to superimpose the best-fitting line describing the association of interest for each intervention group.

recall_plt3 <- ggplot(data = recdata, aes(x = age, y = perc_recall, color = group)) +
    geom_point() + 
    geom_smooth(method = "lm", se = FALSE) + 
    labs(x = "Age (in years)", y = "Recall (%)")
recall_plt3

Figure 3: Scatterplot displaying the association between age, intervention group, and recall

The slope in Figure 3 appears to be steeper in the roller coaster intervention group than the meditation group - this suggested that there could be an interaction.

Sample Size & Power

Question 4

Using a significance level (\(\alpha\)) of .05, what sample size (\(n\)) would you require to check whether any of the predictors (including their interaction) influenced recall scores with a 90% chance?

Because you do not know the effect size, assume Cohen’s guideline for linear regression and, to be on the safe side, consider the ‘small’ value.

Review the following flashcards on statistical power & effect size, paying particular attention to the following two flashcards - The pwr Package and Power for Linear Regression.

k <- 3
f2 <- .02
pwr.f2.test(u = k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 3
              v = 708.495
             f2 = 0.02
      sig.level = 0.05
          power = 0.9

A power analysis for a multiple regression model \((k = 3)\) was conducted (via the pwr package) to determine the minimum sample size using an \(\alpha\) = .05, power = .90, and small effect size \((f^2 = .02)\).

The required sample size is \(n = \text v + k + 1 = 709 + 3 + 1 = 713\).


Question 5

Using the same \(\alpha\) and power, what would be the sample size if you assumed effect size to be ‘medium’?

Review the following flashcards on statistical power & effect size, paying particular attention to the following two flashcards - The pwr Package and Power for Linear Regression.

k <- 3
f2 <- .15
pwr.f2.test(u = k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 3
              v = 94.48157
             f2 = 0.15
      sig.level = 0.05
          power = 0.9

A power analysis for a multiple regression model \((k = 3)\) was conducted (via the pwr package) to determine the minimum sample size using an \(\alpha\) = .05, power = .90, and moderate effect size \((f^2 = .15)\).

The required sample size is \(n = \text v + k + 1 = 95 + 3 + 1 = 99\).


Question 6

Using the same \(\alpha\) and power, what would be the sample size if you assumed effect size to be ‘large’?

Review the following flashcards on statistical power & effect size, paying particular attention to the following two flashcards - The pwr Package and Power for Linear Regression.

k <- 3
f2 <- .35
pwr.f2.test(u = k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 3
              v = 40.61744
             f2 = 0.35
      sig.level = 0.05
          power = 0.9

A power analysis for a multiple regression model \((k = 3)\) was conducted (via the pwr package) to determine the minimum sample size using an \(\alpha\) = .05, power = .90, and large effect size \((f^2 = .35)\).

The required sample size is \(n = \text v + k + 1 = 41 + 3 + 1 = 45\).


Question 7

Fit the following model using lm(), and assign it as an object with the name “recall_mdl1”.

\[ \text{Recall} = \beta_0 + \beta_1 \cdot \text{Age} + \epsilon \\ \]

How much variance in recall scores does the model explain?

For a recap on how to specify a simple linear model, review the statistical models flashcards.

The proportion of the total variability explained is given by \(R^2\). For a more detailed overview, see the R-squared and Adjusted R-squared flashcard.

recall_mdl1 <- lm(perc_recall ~ age, data = recdata)
summary(recall_mdl1)

Call:
lm(formula = perc_recall ~ age, data = recdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.0850  -4.7474   0.7331   4.6758  10.1733 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 62.16336    1.81984  34.159  < 2e-16 ***
age         -0.16206    0.03672  -4.414 2.61e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.494 on 98 degrees of freedom
Multiple R-squared:  0.1658,    Adjusted R-squared:  0.1573 
F-statistic: 19.48 on 1 and 98 DF,  p-value: 2.614e-05

We can see both the \(R^2\) and Adjusted \(R^2\) from the model summary() output. We can use either since we only have a single predictor. To be conservative, we might want to use the adjusted \(R^2\) (0.16).

The model, with Age as a single predictor, explained approximately 16% of the variance in recall scores.


Question 8

Imagine you found the \(R^2\) that you computed above (Q7) in a paper, and you are using that to base your next study.

A researcher believes that the inclusion of intervention group and its interaction with age should explain an extra 50% of the variation in recall scores.

Using a significance level of 5%, what sample size should you use for your next data collection in order to discover that effect with a power of 0.90?

Review the following flashcards on statistical power & effect size, paying particular attention to the following two flashcards - The pwr Package and Power for Linear Regression.

# restricted model m: number of predictors & R-squared
k <- 1
R2m <- 0.16

# full model M: number of predictors & R-squared
K <- 3
R2M <- 0.16 + 0.5

# effect size: calculate f2
f2 <- (R2M - R2m) / (1 - R2M)

#run test
pwr.f2.test(u = K - k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 2
              v = 9.211914
             f2 = 1.470588
      sig.level = 0.05
          power = 0.9

The sample size should be:

\[ n = \text v + K + 1 \quad \quad n = 10 + 3 + 1 \quad \quad n = 14 \]

With such a big effect size, don’t be surprised it’s so small. When the effect size is much smaller, that will be harder to detect and you will require a bigger sample size.


Question 9

Suppose that the aforementioned researcher made a mistake, and issues a corrected statement in which they state that the inclusion of intervention group and its interaction with age should explain an extra 5% of the variation in recall scores.

Using a significance level of 5%, what sample size should you use for your next data collection in order to discover that effect with a power of 0.90?

Review the following flashcards on statistical power & effect size, paying particular attention to the following two flashcards - The pwr Package and Power for Linear Regression.

# restricted model m: number of predictors & R-squared
k <- 1
R2m <- 0.16

# full model M: number of predictors & R-squared
K <- 3
R2M <- 0.16 + 0.05

# effect size: calculate f2
f2 <- (R2M - R2m) / (1 - R2M)

# run test
pwr.f2.test(u = K - k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 2
              v = 199.9608
             f2 = 0.06329114
      sig.level = 0.05
          power = 0.9

The sample size should be:

\[ n = \text v + K + 1 \quad \quad n = 200 + 3 + 1 \quad \quad n = 204 \]

With such a small effect size, we need a bigger sample size for us to detect it with high confidence.


Question 10

A colleague produces a visualisation of the joint relationship between sample size and effect size via a power curve (with coloured lines representing large, medium, and small effect sizes).

Based on this, what feedback/comments might you share with them regarding sample size for their prospective study, and its relation to effect size?

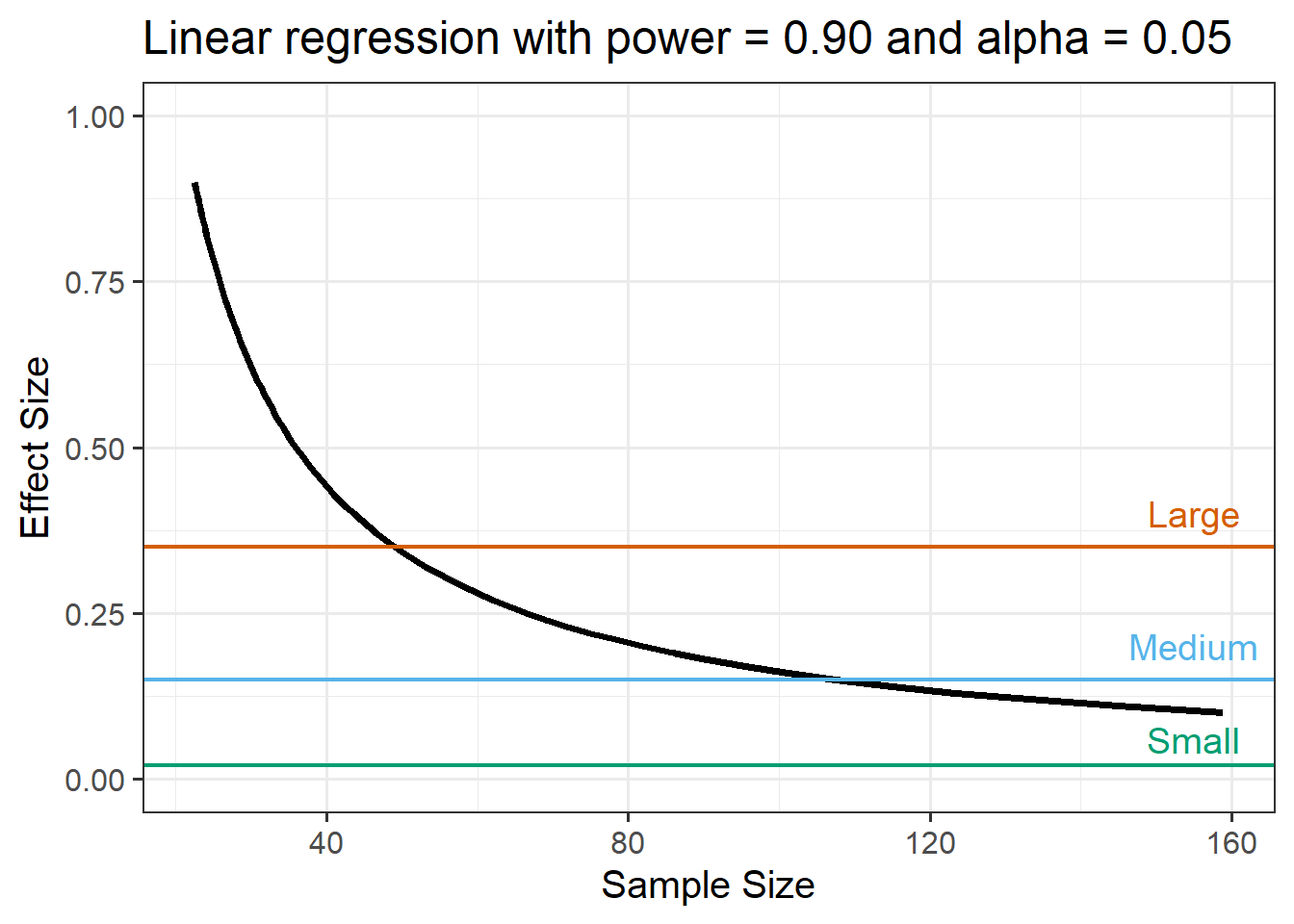
Figure 4: Linear Regression with power = 0.90 and alpha = 0.05

Review the following flashcards on statistical power & effect size, paying particular attention to the following flashcard Factors Affecting Power.

From Figure 4, to detect a large effect size (red line), they should aim to recruit ~50 participants, for a medium effect size ~100 (blue line). It is impossible to judge how many participants would be required to detect a small effect size (green line) - we would suggest that they conduct their own power calculation as it is too difficult to judge based on the figure alone.

Generally, if they want to be able to detect a medium-large effect with 90% power using \(\alpha = .05\), it appears that there is little gain in recruiting a sample size > ~110. However, if they want to be able to detect a small effect with 90% power using \(\alpha = .05\), they are likely going to require a very large sample size.

To summarise the association between effect size and sample size, it appears that the smaller the effect you are trying to detect, the larger the sample size you will require.

Compile Report

Compile Report

Knit your report to PDF, and check over your work. To do so, you should make sure:

  • Only the output you want your reader to see is visible (e.g., do you want to hide your code?)
  • Check that the tinytex package is installed
  • Ensure that the ‘yaml’ (bit at the very top of your document) looks something like this:
---
title: "this is my report title"
author: "B1234506"
date: "07/09/2024"
output: bookdown::pdf_document2
---

If you are having issues knitting directly to PDF, try the following:

  • Knit to HTML file
  • Open your HTML in a web-browser (e.g. Chrome, Firefox)
  • Print to PDF (Ctrl+P, then choose to save to PDF)
  • Open file to check formatting

To not show the code of an R code chunk, and only show the output, write:

```{r, echo=FALSE}
# code goes here
```

To show the code of an R code chunk, but hide the output, write:

```{r, results='hide'}
# code goes here
```

To hide both code and output of an R code chunk, write:

```{r, include=FALSE}
# code goes here
```

You must make sure you have tinytex installed in R so that you can “Knit” your Rmd document to a PDF file:

install.packages("tinytex")
tinytex::install_tinytex()

You should end up with a PDF file. If you have followed the above instructions and still have issues with knitting, speak with a Tutor.