Assumptions and Diagnostics

Learning Objectives

At the end of this lab, you will:

1. Be able to state the assumptions underlying a linear model
2. Specify the assumptions underlying a linear model with multiple predictors
3. Assess if a fitted model satisfies the assumptions of your model
4. Assess the effect of influential cases on linear model coefficients and overall model evaluations

What You Need

1. Be up to date with lectures
2. Have completed Week 2 lab exercises

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

• tidyverse
• car
• performance
• kableExtra
• sjPlot

Presenting Results

All results should be presented following APA guidelines.If you need a reminder on how to hide code, format tables/plots, etc., make sure to review the rmd bootcamp.

The example write-up sections included as part of the solutions are not perfect - they instead should give you a good example of what information you should include and how to structure this. Note that you must not copy any of the write-ups included below for future reports - if you do, you will be committing plagiarism, and this type of academic misconduct is taken very seriously by the University. You can find out more here.

Lab Data

You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/wellbeing_rural.csv

Lab Overview

In the previous labs, we have fitted a number of regression models, including some with multiple predictors. In each case, we first specified the model, then visually explored the marginal distributions and associations among variables which would be used in the analysis. Finally, we fit the model, and began to examine the fit by studying what the various parameter estimates represented, and the spread of the residuals.

But before we draw inferences using our model estimates or use our model to make predictions, we need to be satisfied that our model meets a specific set of assumptions. If these assumptions are not satisfied, the results will not hold.

In this lab, we will check the assumptions of one of the multiple linear regression models that we have previously fitted in Block 1 using the ‘mwdata’ dataset (see Week 2).

Study Overview

Research Question

Is there an association between wellbeing and time spent outdoors after taking into account the association between wellbeing and social interactions?

Wellbeing/Rurality data codebook.

Description

From the Edinburgh & Lothians, 100 city/suburb residences and 100 rural residences were chosen at random and contacted to participate in the study. The Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), was used to measure mental health and well-being.

Participants filled out a questionnaire including items concerning: estimated average number of hours spent outdoors each week, estimated average number of social interactions each week (whether on-line or in-person), whether a daily routine is followed (yes/no). For those respondents who had an activity tracker app or smart watch, they were asked to provide their average weekly number of steps.

Data Dictionary

The data in wellbeing_rural.csv contain seven attributes collected from a random sample of \(n=200\) hypothetical residents over Edinburgh & Lothians, and include:

variable	description
age	Age in years of respondent
outdoor_time	Self report estimated number of hours per week spent outdoors
social_int	Self report estimated number of social interactions per week (both online and in-person)
routine	Binary 1=Yes/0=No response to the question 'Do you follow a daily routine throughout the week?'
wellbeing	Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70
location	Location of primary residence (City, Suburb, Rural)
steps_k	Average weekly number of steps in thousands (as given by activity tracker if available)

Preview

The first six rows of the data are:

age	outdoor_time	social_int	routine	wellbeing	location	steps_k
28	12	13	1	36	rural	21.6
56	5	15	1	41	rural	12.3
25	19	11	1	35	rural	49.8
60	25	15	0	35	rural	NA
19	9	18	1	32	rural	48.1
34	18	13	1	34	rural	67.3

Setup

Setup

1. Create a new RMarkdown file
2. Load the required package(s)
3. Read the wellbeing dataset into R, assigning it to an object named mwdata
4. Fit the following model:

\[ \text{Wellbeing} = \beta_0 + \beta_1 \cdot \text{Social Interactions} + \beta_2 \cdot \text{Outdoor Time} + \epsilon \]

Solution

#Loading the required package(s)
library(tidyverse)
library(car)
library(performance)
library(kableExtra)
library(sjPlot)

# Reading in data and storing to an object named 'mwdata'
mwdata <- read_csv("https://uoepsy.github.io/data/wellbeing_rural.csv")

# wellbeing model
wb_mdl1 <- lm(wellbeing ~ outdoor_time + social_int, data = mwdata) 

Exercises

Assumptions

Question 1

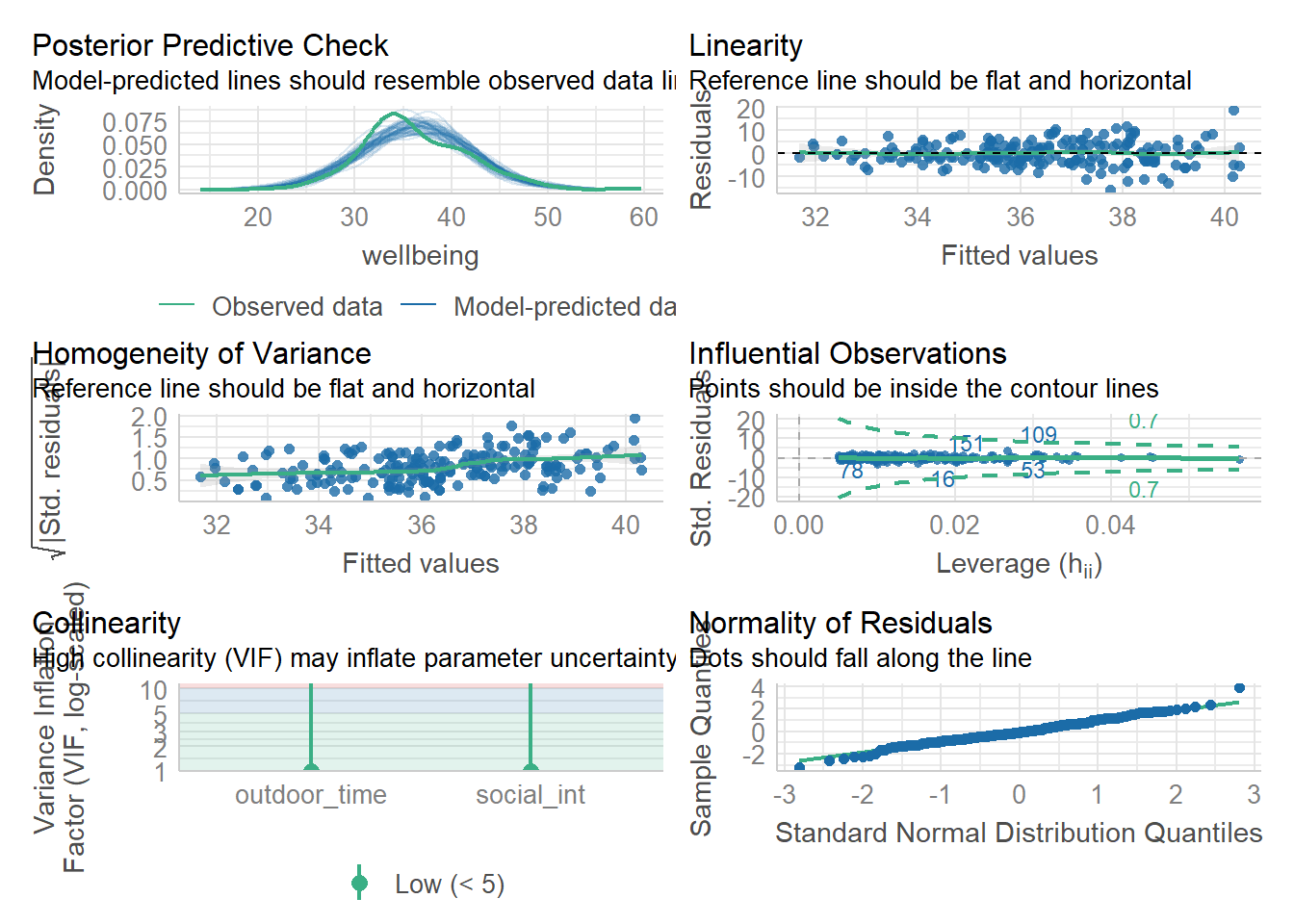
Let’s start by using check_model() for our wb_mdl1 model - we can refer to these plots as a guide as we work through the assumptions questions of the lab.

Hint

See the useful assumptions plots > check_model() flaschard.

These plots cannot be used in your reports - they are to be used as a guide only.

Solution

check_model(wb_mdl1)

The check_model() function is a useful way to check the assumptions of models, as it also returns some useful notes to aid your interpretation. There does appear to be evidence that some assumptions may have been violated, but to be sure we need to check each assumption individually with plots that are more suitable for a statistics report.

Question 2

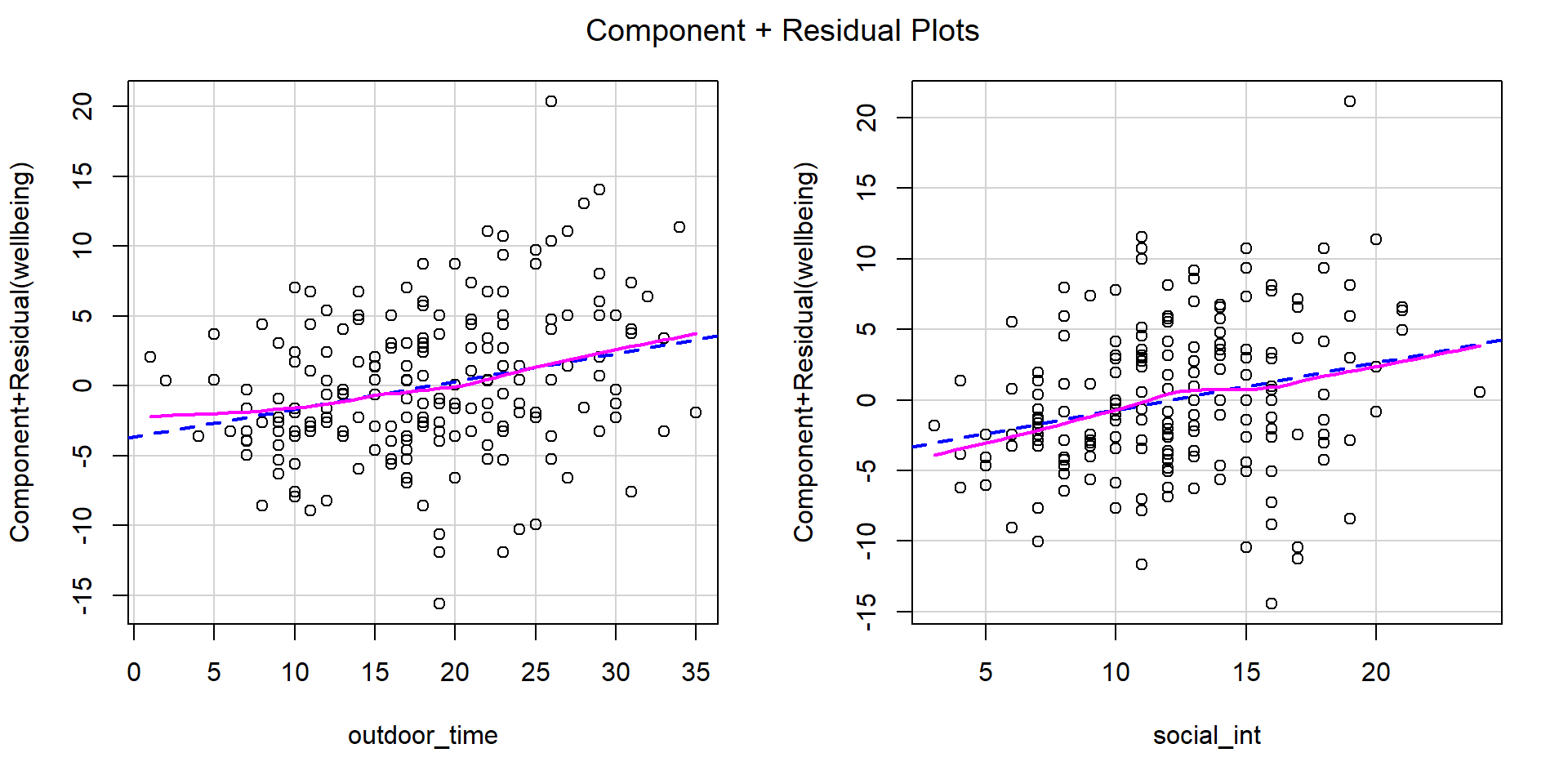
Check if the fitted model satisfies the linearity assumption for wb_mdl1.

Write a sentence summarising whether or not you consider the assumption to have been met. Justify your answer with reference to the plots.

Hint

How you check this assumption depends on the number of predictors in your model:

• Single predictor: Use either residual vs fitted values plot (plot(model, which = 1)), and/or a scatterplot with loess lines
  
• Multiple predictors: Use component-residual plots (also known as partial-residual plots) to check the assumption of linearity

For more information, as well as tips to aid your interpretation, review the linearity flashcard.

Solution

crPlots(wb_mdl1)

The smoother (the pink line) follows quite closely to a linear relationship (the dashed blue line), though there was some deviation. Overall, the evidence suggested that the linearity assumption was met.

Question 3

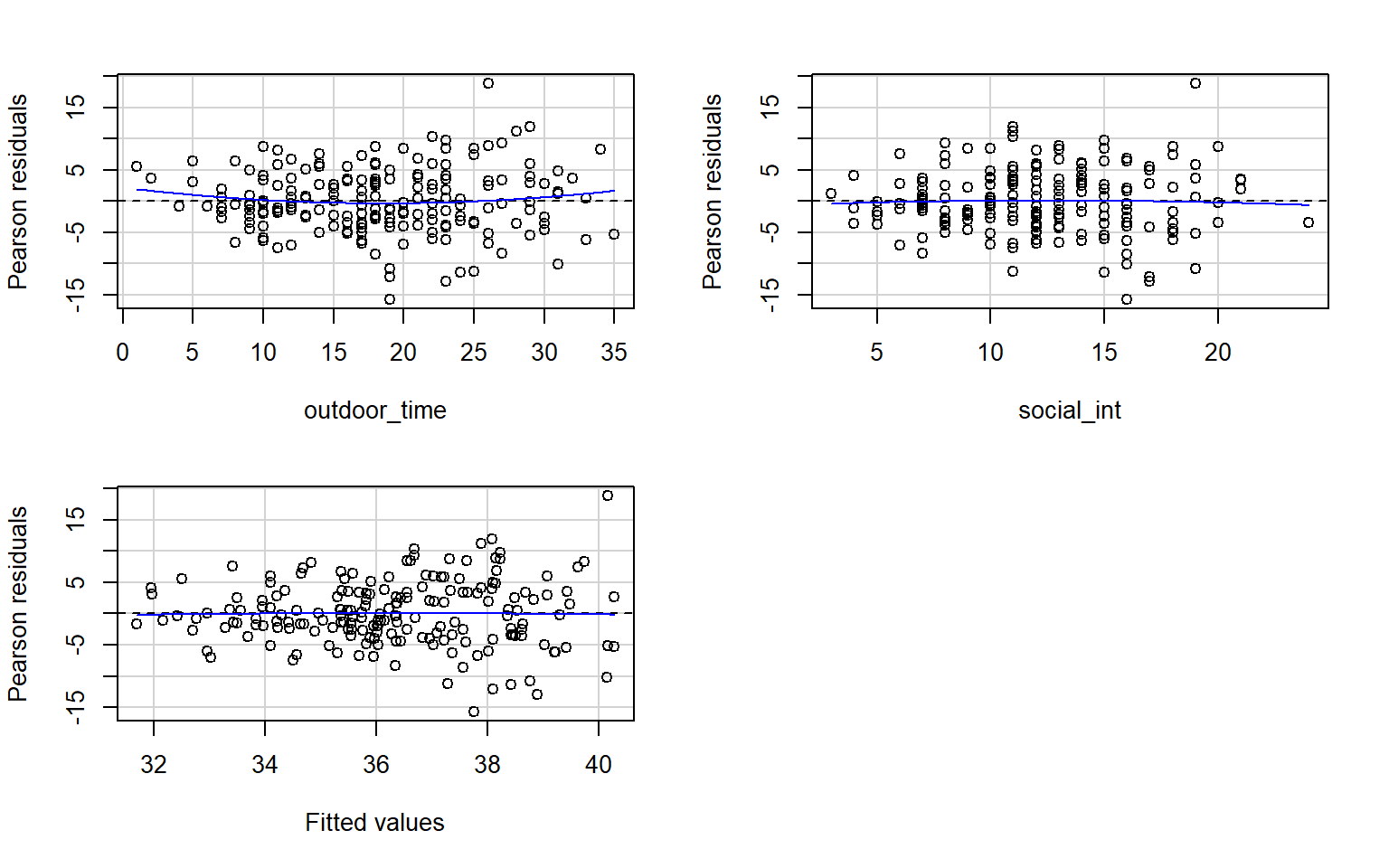
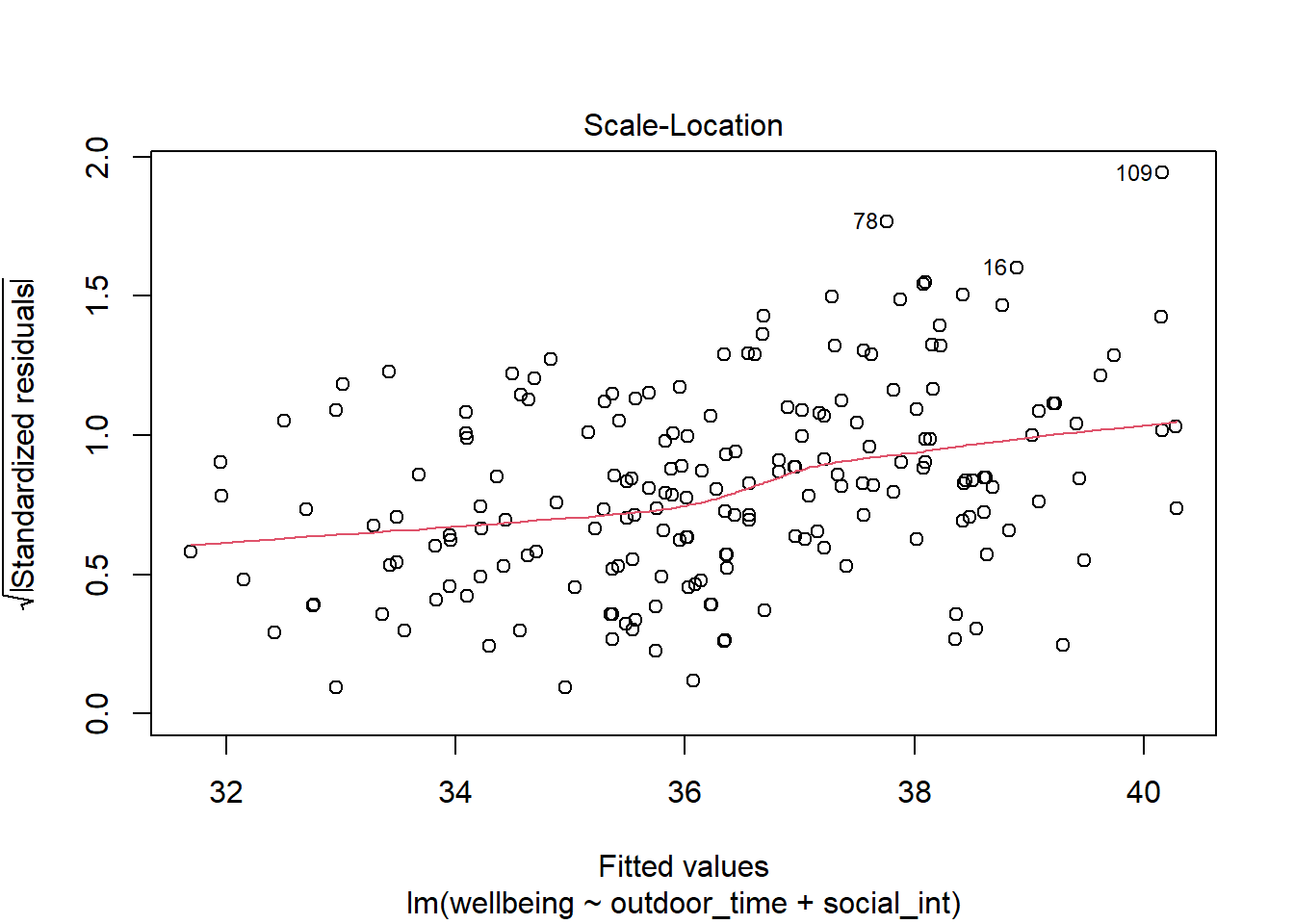
Check if the fitted model wb_mdl1 satisfy the equal variance (homoscedasticity) assumption.

Write a sentence summarising whether or not you consider the assumption to have been met. Justify your answer with reference to the plot.

Hint

Use residualPlots() to plot residuals against the predictor. Since we are only interested in visually assessing our assumption checks, we can suppress the curvature test output by specifying tests = FALSE.

For more information, as well as tips to aid your interpretation, review the equal variances (homoscedasticity) flashcard.

Quick Tip if plotting using plot(model)

As the residuals can be positive or negative, we can make it easier to assess equal spread by improving the ‘resolution’ of the points.

We can make all residuals positive by discarding the sign (take the absolute value), and then take the square root to make them closer to each other.

A plot of \(\sqrt{|\text{Standardized residuals}|}\) against the fitted values can be obtained via plot(model, which = 3).

Solution

We can visually assess by plotting the Pearson residuals against the fitted values:

residualPlots(wb_mdl1, tests = FALSE)

Or by plotting the \(\sqrt{|\text{Standardized residuals}|}\) against the fitted values:

plot(wb_mdl1, which = 3)

Partial residual plots did show non-linear trends between residuals and predictors, hence there is evidence of non-constant variance i.e., heteroscedasticity. Thus, the data did not meet the assumption of equal variance, as the spread of the standardized residuals did not appear to be constant (for the most part) as the fitted values varied.

In the second plot, all points are above 0, but the majority of the points are not very close to each other. The line does not appear to be relatively flat, and so this also suggested that the error variance does change across the fitted values.

Question 4

Assess whether there is autocorrelation in the error terms.

Write a sentence summarising whether or not you consider the assumption of independence to have been met (you may have to assume certain aspects of the study design).

Hint

Review the independence (of errors) flashcard.

Solution

Since our data were collected from a between-persons study design, we can assume (i.e., based on design, we believe) the errors to be independent.

Question 5

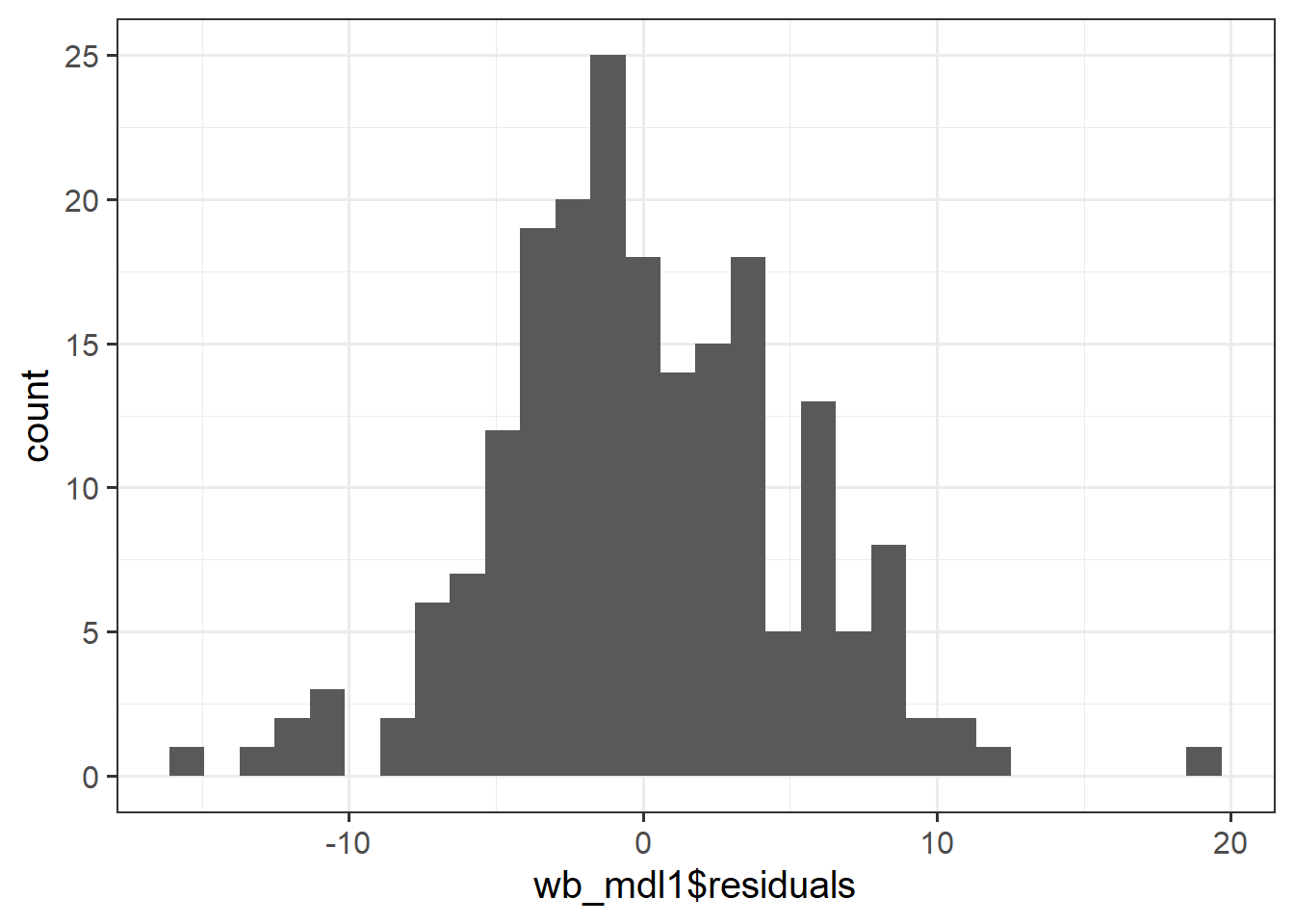
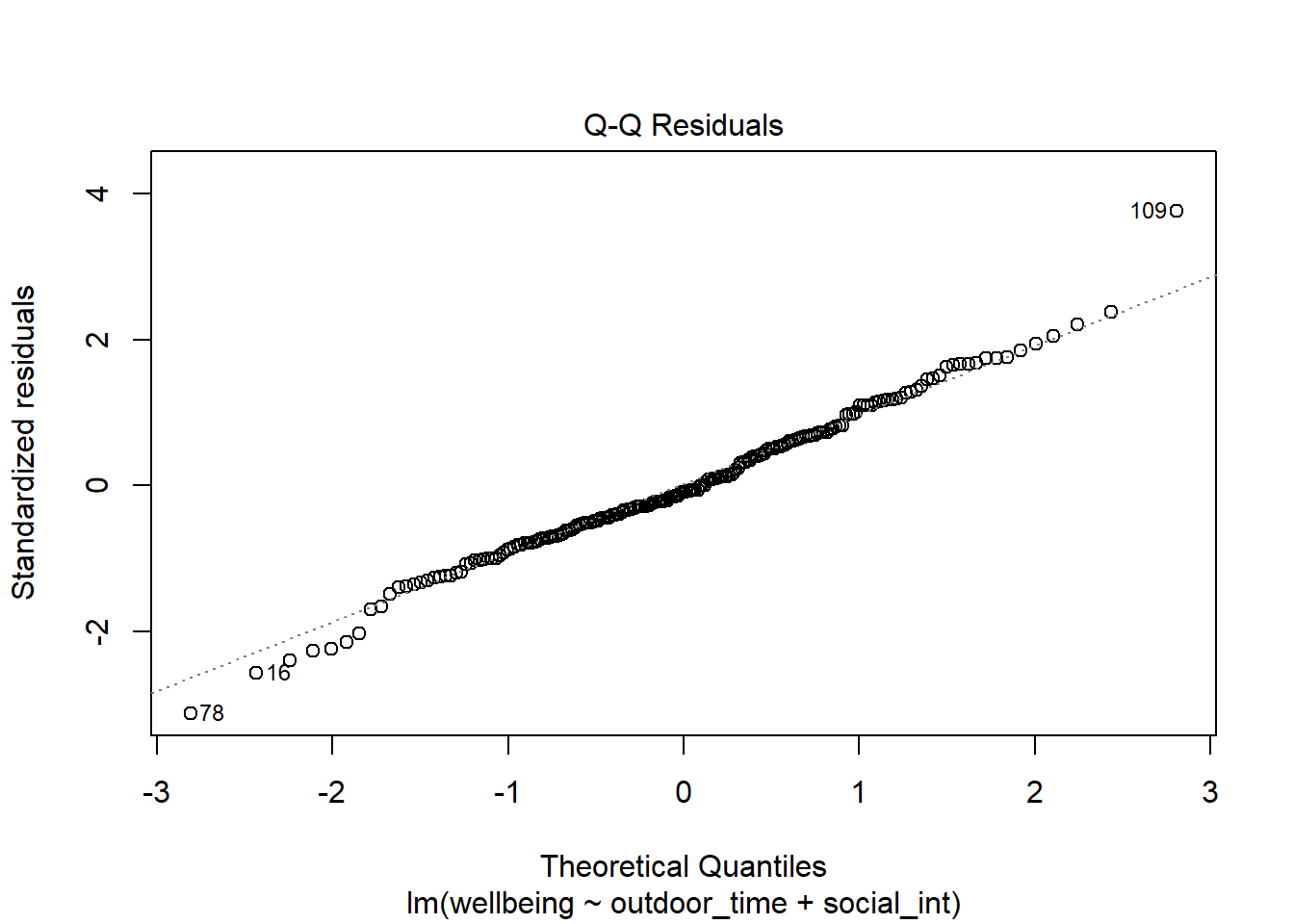
Check if the fitted model wb_mdl1 satisfies the normality assumption.

Write a sentence summarising whether or not you consider the assumption to have been met. Justify your answer with reference to the plots.

Hint

For more information, as well as tips to aid your interpretation, review the normality (of errors) flashcard.

Solution

Histogram

ggplot(data = mwdata, aes(x = wb_mdl1$residuals)) +
    geom_histogram() 

The histogram indicated that the residuals (the differences between observed and predicted values) followed close to a normal distribution.

QQ Plot

plot(wb_mdl1, which = 2)

The QQplot indicated that the residuals followed close to a normal distribution, as the points followed a linear pattern and there was no substantial skew or departure from normality. There was some evidence of heavier tails, and we may want to examine some observations more closely (i.e., 16, 78, 109).

Multicollinearity

Question 6

For wb_mdl1, calculate the variance inflation factor (VIF) for the predictors in the model.

Write a sentence summarising whether or not you consider multicollinearity to be a problem here.

Hint

For more information, as well as tips to aid your interpretation, review the multicollinearity flashcard.

Solution

vif(wb_mdl1)

outdoor_time   social_int 
    1.001306     1.001306 

The VIF values for all predictors are <5, indicating that multicollinearity is not adversely affecting model estimates.

Diagnostics

Question 7

Create a new tibble which contains:

1. The original variables from the model (Hint, what does wb_mdl1$model give you?)
2. The fitted values from the model \(\hat y\)
   
3. The residuals \(\hat \epsilon\)
4. The studentised residuals
5. The hat values
6. The Cook’s Distance values

Hint

For following will likely be useful to consider when creating your tibble():

1. Think about what wb_mdl1$model gives you
2. fitted()
3. residuals()
4. rstudent()
5. hatvalues()
6. cooks.distance()

Solution

mdl_diagnost <- 
  tibble(
  wb_mdl1$model,
  fitted = fitted(wb_mdl1),
  resid = residuals(wb_mdl1),
  studres = rstudent(wb_mdl1),
  hats = hatvalues(wb_mdl1),
  cooksd = cooks.distance(wb_mdl1)
)

Question 8

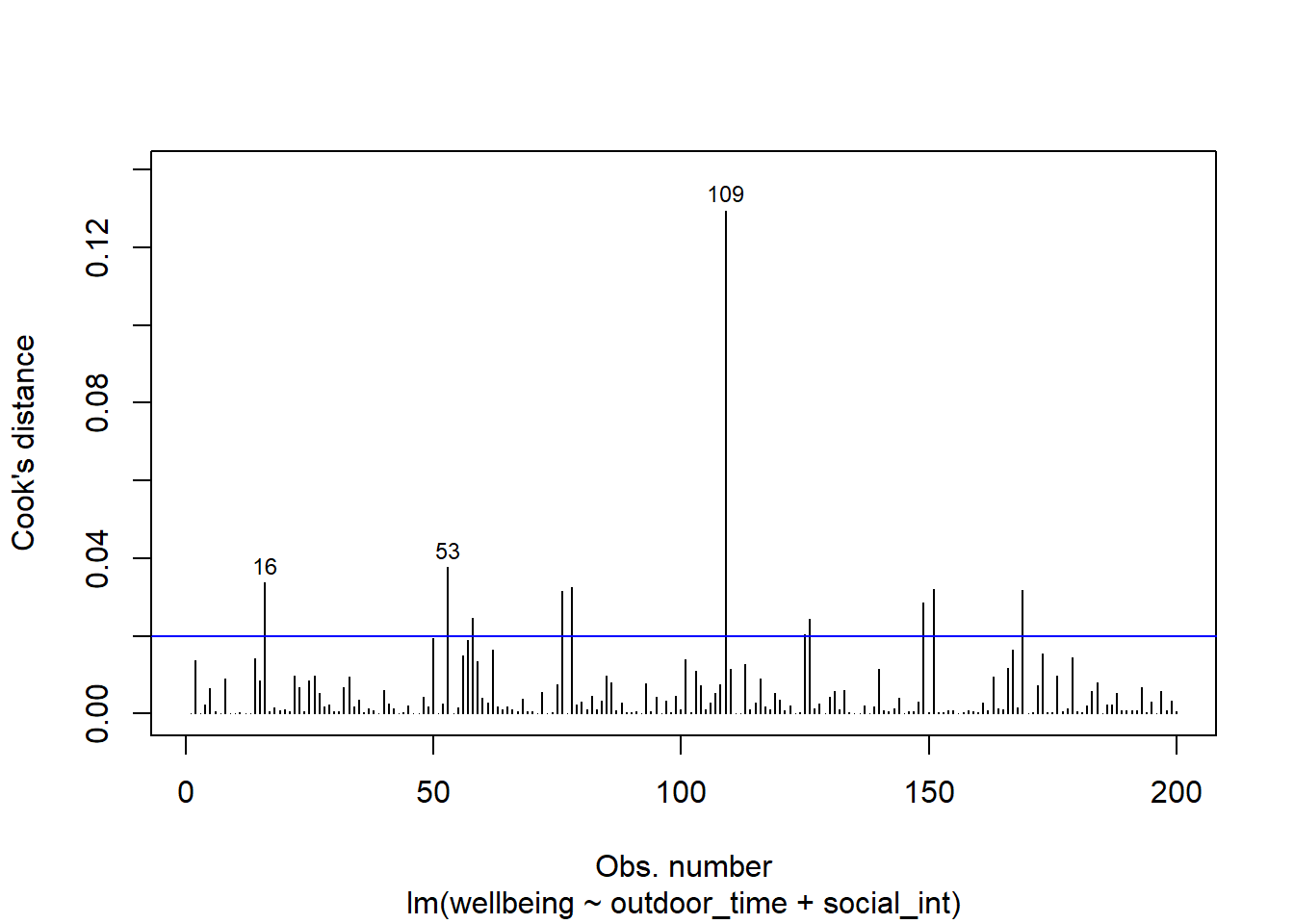
From the tibble above, comment on the following:

• Looking at the studentised residuals, are there any outliers?
• Looking at the hat values, are there any observations with high leverage?
• Looking at the Cook’s Distance values, are there any highly influential points?

Hint

Alongside the lecture materials, review the individual case diagnostics flashcards and consider the commonly used cut-off criteria.

Solution

Outliers

In a standard normal distribution, 95% of the values are roughly between -2 and 2. Because of this, studentised residuals of \(>2\) or \(< -2\) indicate potential outlyingness.

We can ask R how many of the absolute values (by specifying abs()) are \(>2\):

table(abs(mdl_diagnost$studres) > 2)

FALSE  TRUE 
  189    11 

We have 11 TRUE observations, which tells us that they have |studentised residuals| \(>2\).

We can identify which of our observations have these values:

which(abs(mdl_diagnost$studres) > 2)

 16  50  53  58  62  76  78 109 126 151 163 
 16  50  53  58  62  76  78 109 126 151 163 

So we know that observations (or rows) 16, 50, 53, 58, 62, 76, 78, 109, 126, 151, and 163 have absolute values that have studentised residuals of \(>2\) or \(< -2\).

We could also filter our newly created tibble to these observations to examine the values further:

mwdata %>%
    mutate(
    studres = rstudent(wb_mdl1)) %>%
  dplyr::filter(., studres > 2 | studres < -2) %>%
  arrange(., desc(studres)) %>%
  kable(.)  %>%   
    kable_styling(., full_width = F)

age	outdoor_time	social_int	routine	wellbeing	location	steps_k	studres
23	26	19	1	59	city	NA	3.904186
34	29	11	1	50	suburb	61.1	2.402389
39	28	11	1	49	suburb	65.6	2.234367
22	22	11	1	47	city	80.1	2.060351
58	31	16	1	30	rural	46.6	-2.047644
46	19	19	1	28	rural	34.8	-2.167219
44	25	11	0	26	rural	66.6	-2.261542
47	24	15	0	27	rural	53.5	-2.292089
35	19	17	0	26	rural	66.1	-2.433253
19	23	17	0	26	rural	60.0	-2.602129
36	19	16	0	22	rural	51.6	-3.199777

There were 11 observations identified as potential outliers.

High Leverage

Hat values of more than \(2 \bar{h}\) (2 times the average hat value) are considered high leverage. The average hat value, \(\bar{h}\) is calculated as \(\frac{k + 1}{n}\), where \(k\) is the number of predictors, and \(n\) is the sample size.

For our model: \[ \bar h = \frac{k+1}{n} = \frac{2+1}{200} = \frac{3}{200} = 0.015 \] We can ask whether any of observations have hat values which are greater than \(2 \bar h\):

table(mdl_diagnost$hats > (2*0.015))

FALSE  TRUE 
  184    16 

We have 16 TRUE observations, which tells us that they have high leverage.

We can identify which of our observations have these values:

which(mdl_diagnost$hats > (2*0.015))

 25  56  59  60  72  73  75  79 127 131 149 159 165 169 176 197 
 25  56  59  60  72  73  75  79 127 131 149 159 165 169 176 197 

So we know that observations (or rows) 25, 56, 59, 60, 72, 73, 75, 79, 127, 131, 149, 159, 165, 169, 176, and 197 have hat values which are greater than \(2 \bar h\).

We could also filter our newly created tibble to these observations to examine the values further:

mwdata %>%
    mutate(
    hats = hatvalues(wb_mdl1)) %>%
  dplyr::filter(., hats > (2*0.015)) %>%
  arrange(., desc(hats)) %>%
  kable(.)  %>%   
    kable_styling(., full_width = F)

age	outdoor_time	social_int	routine	wellbeing	location	steps_k	hats
21	9	24	1	35	suburb	NA	0.0564084
62	31	3	1	37	city	49.2	0.0452765
69	2	19	0	39	rural	5.9	0.0448793
19	7	21	0	39	rural	40.0	0.0411712
63	10	21	1	41	rural	24.3	0.0356713
27	1	11	1	38	rural	NA	0.0352975
53	35	14	1	35	rural	24.4	0.0345566
21	7	5	1	30	suburb	3.3	0.0341635
18	28	4	0	32	city	71.6	0.0336901
30	10	4	1	36	rural	29.7	0.0328599
44	5	7	1	35	rural	15.1	0.0313589
69	11	4	0	31	suburb	15.6	0.0312095
23	29	5	1	36	rural	NA	0.0310672
56	32	7	1	41	city	58.6	0.0309399
35	10	20	1	46	city	NA	0.0305338
21	34	13	1	48	suburb	35.1	0.0301977

There were 16 observations that had high leverage (> \(2 \bar h\)).

Influential Points

We are using a Cook’s Distance cut-off of \(\frac{4}{n-k-1}\), where \(k\) is the number of predictors, and \(n\) is the sample size.

For our model: \[ D_{cutoff} = \frac{4}{n-k-1} = \frac{4}{200 - 2 - 1} = \frac{4}{197} = 0.020 \]

We can ask whether any of observations have a high influence on our model estimates:

table(mdl_diagnost$cooksd > 0.020)

FALSE  TRUE 
  189    11 

Yes, we have 11 TRUE observations, which tells us that they are above the \(D_{cutoff} = 0.020\).

We can identify which of our observations have these values:

which(mdl_diagnost$cooksd > 0.020)

 16  53  58  76  78 109 125 126 149 151 169 
 16  53  58  76  78 109 125 126 149 151 169 

So we know that observations (or rows) 16, 53, 58, 76, 78, 109, 125, 126, 149, 151, and 169 have \(D > 0.020\).

We could also filter our newly created tibble to these observations to examine the values further:

mwdata %>%
    mutate(
    cooksd = cooks.distance(wb_mdl1)) %>%
  dplyr::filter(., cooksd > 4/(200-2-1)) %>%
  arrange(., desc(cooksd)) %>%
  kable(.)  %>%   
    kable_styling(., full_width = F)

age	outdoor_time	social_int	routine	wellbeing	location	steps_k	cooksd
23	26	19	1	59	city	NA	0.1295568
58	31	16	1	30	rural	46.6	0.0376693
19	23	17	0	26	rural	60.0	0.0336478
36	19	16	0	22	rural	51.6	0.0326114
34	29	11	1	50	suburb	61.1	0.0319559
35	10	20	1	46	city	NA	0.0318858
46	19	19	1	28	rural	34.8	0.0314694
21	34	13	1	48	suburb	35.1	0.0284437
35	19	17	0	26	rural	66.1	0.0247096
39	28	11	1	49	suburb	65.6	0.0243298

You can also display the Cook’s Distance values themselves using plot(model, which = 4), and add a horizontal line at the \(D_{cutoff} = 0.020\) using abline(h = ???):

plot(wb_mdl1, which = 4, abline(h=0.020, col="blue"))

There were 11 observations that had a high influence on our model estimates.

Question 9

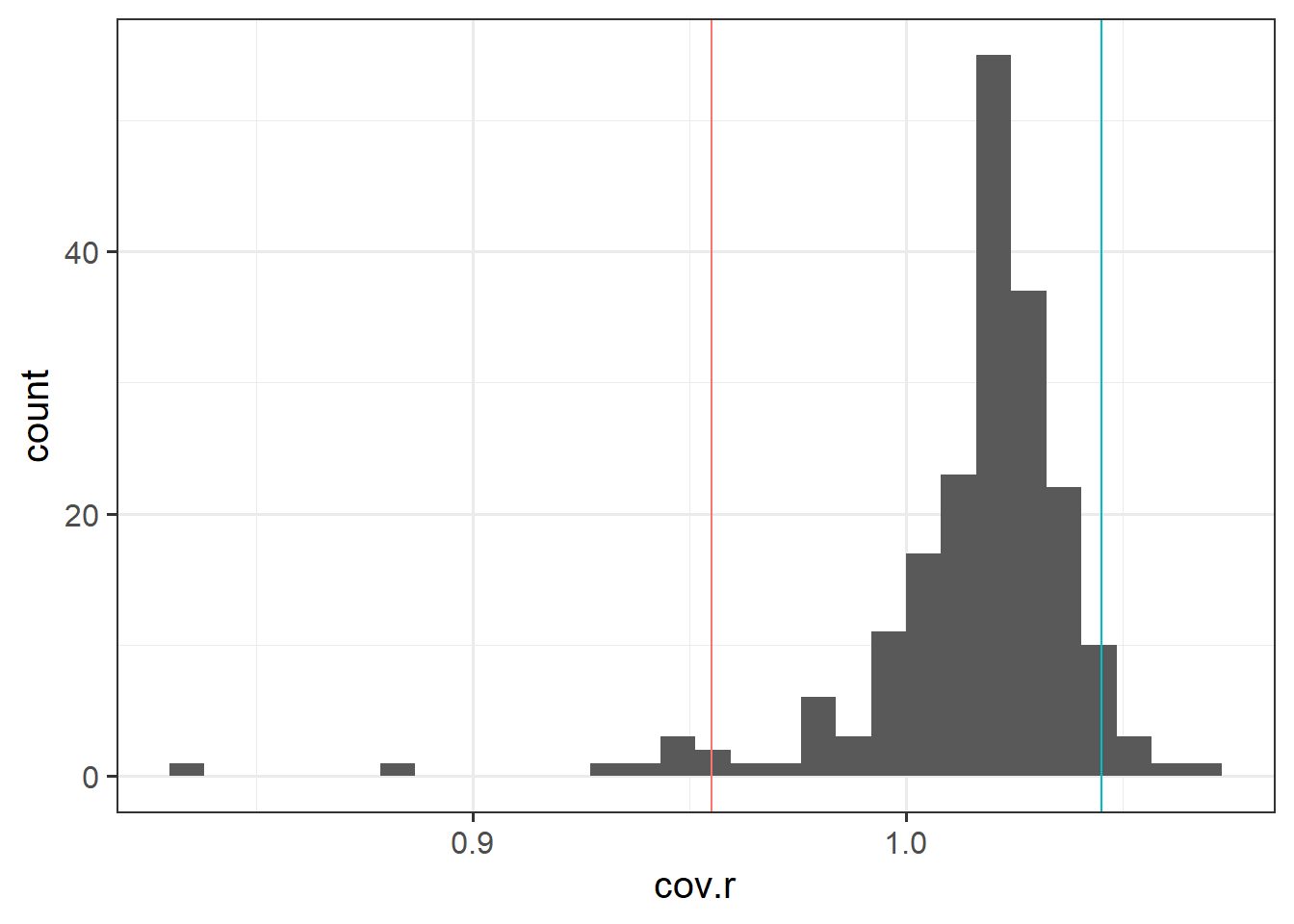
Use the function influence.measures() to extract these delete-1 measures¹ of influence.

Choose a couple of these measures to focus on, exploring in more detail (you may want to examine values or even try plotting distributions).

Hint

Review the individual case diagnostics flashcards.

The function influence.measures() returns an infl-type object. To plot this, we need to find a way to extract the actual numbers from it.

What do you think names(influence.measures(wb_mdl1)) shows you? How can we use influence.measures(wb_mdl1)$<insert name here> to extract the matrix of numbers?

Solution

Extracting influence.measures()

#extract measures
inf_mes <- influence.measures(wb_mdl1)

#examine top ten rows, and round to 3 decimal places
round(inf_mes$infmat[1:10,], 3)

   dfb.1_ dfb.otd_ dfb.scl_  dffit cov.r cook.d   hat
1   0.006   -0.008    0.002  0.012 1.024  0.000 0.009
2   0.083   -0.168    0.061  0.203 1.016  0.014 0.025
3  -0.006   -0.001    0.004 -0.016 1.020  0.000 0.005
4   0.047   -0.050   -0.039 -0.081 1.020  0.002 0.012
5   0.001    0.080   -0.091 -0.138 1.028  0.006 0.024
6  -0.003    0.001   -0.008 -0.037 1.017  0.000 0.005
7  -0.008   -0.001    0.015  0.018 1.036  0.000 0.020
8   0.106   -0.119   -0.006  0.166 0.985  0.009 0.010
9  -0.003    0.004   -0.001 -0.007 1.025  0.000 0.009
10  0.002   -0.008    0.008  0.015 1.026  0.000 0.010

Examine DFBETA values

DFbeta represents the difference in the beta coefficients when a case is excluded from the model versus when it’s included. A large DFbeta value would suggest that a case has a substantial impact on the estimated coefficients, and thus a high influence on the model results; a small DFbeta value would suggest that the case has less influence on the estimated coefficients.

A commonly used cut-off or threshold to compare \(|DFBETA|\) values (absolute values) against is \(\frac{2}{\sqrt{n}}\) (see Belsley et al., (1980) p. 28 for more info)².

For our model:

\[ |DFBETA_{cutoff}| \quad = \quad \frac{2}{\sqrt{n}} \quad = \quad \frac{2}{\sqrt{200}} = 0.141 \]

In order to extract these in order to arrange in descending order, we need to save our delete-1 measures of influence as a dataframe (via as.data.frame()). Then we can then arrange our DFBETA values in descending order (via arrange(desc(???))). To avoid returning 200 rows of output (i.e., the length of the dataframe), we can ask for the first 15 rows via (head(., 15)):

#save as a dataframe
inf_mes1 <- as.data.frame(inf_mes$infmat)

#arrange dfbeta values in descending order using the absolute value, and show first 10 rows
inf_mes1 %>%
    arrange(desc(abs(dfb.1_))) %>%
    head(., 15)

        dfb.1_    dfb.otd_    dfb.scl_      dffit     cov.r      cook.d
109 -0.4918246  0.32363373  0.49483157  0.6455776 0.8332377 0.129556799
53   0.2430892 -0.26944443 -0.15351312 -0.3388798 0.9790122 0.037669317
16   0.2060412 -0.13252138 -0.23259175 -0.3223359 0.9310954 0.033647762
101 -0.1947109  0.09412063  0.15487642 -0.2046876 1.0063119 0.013897196
179  0.1902832 -0.07096434 -0.16598552  0.2085435 0.9990240 0.014401828
76   0.1730591 -0.02595756 -0.26823452 -0.3101290 0.9651183 0.031469445
85  -0.1646134  0.10294561  0.11084731 -0.1711913 1.0143158 0.009748336
149 -0.1638458  0.26658339  0.03742045  0.2934205 1.0039126 0.028443695
56   0.1604565 -0.19478940 -0.02813891  0.2114811 1.0330872 0.014891276
173 -0.1561237  0.10614219  0.15969174  0.2161367 1.0033339 0.015479111
75   0.1457701 -0.07234892 -0.11988282  0.1497178 1.0393526 0.007484738
50   0.1353661 -0.13659118 -0.12403587 -0.2437762 0.9485325 0.019390273
26   0.1300856 -0.08559983 -0.13088097 -0.1707527 1.0263050 0.009715555
58   0.1291280 -0.02591707 -0.21369424 -0.2756455 0.9405759 0.024709605
78   0.1272542 -0.03198691 -0.22393152 -0.3200349 0.8802619 0.032611416
            hat
109 0.026614646
53  0.026659223
16  0.015112834
101 0.020817727
179 0.018565852
76  0.020066684
85  0.020304231
149 0.030197659
56  0.035297538
173 0.020995260
75  0.032859874
50  0.011184976
26  0.026614646
58  0.012670376
78  0.009904492

We can see that we have 11 \(|DFBETA|\) values > \(\frac{2}{\sqrt{200}}\), from observations (or rows) 16, 53, 56, 75, 76, 85, 101, 109, 149, 173, and 179 that we may want to examine further:

which(abs(inf_mes1$dfb.1_) > (2/sqrt(200)))

 [1]  16  53  56  75  76  85 101 109 149 173 179

Plotting COVRATIO statistics

Values which are \(>1+\frac{3(k+1)}{n}\) or \(<1-\frac{3(k+1)}{n}\) are considered as having strong influence.

For our model, this is: \[ 1 \pm \frac{3(k+1)}{n} \quad = \quad 1 \pm\frac{3(2+1)}{200} \quad = \quad 1\pm \frac{9}{200} \quad = \quad 1\pm0.045 \]

The “infmat” bit of an infl-type object contains the numbers, as we can see from out output above. To use it with ggplot(), we will need to turn it into a dataframe (as.data.frame()), or a tibble (as_tibble()):

infdata <- inf_mes$infmat %>%
  as_tibble()

Now we can build our plot. It would be useful to add vertical lines at the values \(\quad 1\pm0.045\). To do so, we can use the geom_vline() function:

ggplot(data = infdata, aes(x = cov.r)) + 
  geom_histogram() +
  geom_vline(aes(xintercept = c(1-0.045), col = "blue")) +
  geom_vline(aes(xintercept = c(1+0.045), col = "red")) + 
  theme(legend.position = "none")  #remove legend

It looks like a few observations may be having quite a strong influence on the standard errors here. We can check specifically how many observations are potentially having a having strong influence using the cut off \(1\pm0.045\):

table(infdata$cov.r < 1 - 0.045 | infdata$cov.r > 1 + 0.045)

FALSE  TRUE 
  185    15 

We can identify these 15 observations to investigate further:

which(infdata$cov.r < 1 - 0.045 | infdata$cov.r > 1 + 0.045)

 [1]  16  25  50  58  62  72  73  78  79 109 127 151 159 165 176

We know that observations (or rows) 16, 25, 50, 58, 62, 72, 73, 78, 79, 109, 127, 151, 159, 165, and 176 have \(\text{COVRATIO } 1\pm0.045\).

Question 10

What approaches would be appropriate to take given the issues highlighted above with the violations of assumptions and case diagnostic results?

Solution

There are lots of different options available to us. We may want to consider one of the approaches described in the next steps: what to do with violations of assumptions / problematic case diagnostic results flashcard.

Compile Report

Compile Report

Knit your report to PDF, and check over your work. To do so, you should make sure:

• Only the output you want your reader to see is visible (e.g., do you want to hide your code?)
• Check that the tinytex package is installed
• Ensure that the ‘yaml’ (bit at the very top of your document) looks something like this:

---
title: "this is my report title"
author: "B1234506"
date: "07/09/2024"
output: bookdown::pdf_document2
---

What to do if you cannot knit to PDF

If you are having issues knitting directly to PDF, try the following:

• Knit to HTML file
  
• Open your HTML in a web-browser (e.g. Chrome, Firefox)
  
• Print to PDF (Ctrl+P, then choose to save to PDF)
  
• Open file to check formatting

Hiding Code and/or Output

Hiding R Code

To not show the code of an R code chunk, and only show the output, write:

```{r, echo=FALSE}
# code goes here
```

Hiding R Output

To show the code of an R code chunk, but hide the output, write:

```{r, results='hide'}
# code goes here
```

Hiding R Code and Output

To hide both code and output of an R code chunk, write:

```{r, include=FALSE}
# code goes here
```

Tinytex

You must make sure you have tinytex installed in R so that you can “Knit” your Rmd document to a PDF file:

install.packages("tinytex")
tinytex::install_tinytex()

Solution

You should end up with a PDF file. If you have followed the above instructions and still have issues with knitting, speak with a Tutor.

Footnotes

1. leave-one-out deletion diagnostics

2. Belsley, D. A., Kuh, E., & Welsch, R. E. (2005). Regression diagnostics: Identifying influential data and sources of collinearity. John Wiley & Sons. DOI: 10.1002/0471725153