Block 2 Analysis & Write-Up Example

Learning Objectives

At the end of this lab, you will:

1. Understand how to write-up and provide interpretation of a linear model with multiple predictors (including categorical)
2. Understand how to specify dummy and sum-to-zero coding and interpret the model output
3. Understand how to specify contrasts to test specific effects
4. Be able to specify and assess the assumptions underlying a linear model with multiple predictors
5. Be able to assess the effect of influential cases on linear model coefficients and overall model evaluations

What You Need

1. Be up to date with lectures
2. Have completed Labs 7 - 10

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

• tidyverse
• psych
• patchwork
• sjPlot
• kableExtra
• emmeans
• car

Lab Data

You can download the data required for this lab here and here or read the datasets in via these links https://uoepsy.github.io/data/DapR2_S1B2_PracticalPart1.csv and https://uoepsy.github.io/data/DapR2_S1B2_PracticalPart2.csv

Section A: Write-Up

In this lab you will be presented with the output from a statistical analysis, and your job will be to write-up and present the results. We’re going to use two simulated datasets based on a paper (the same two that you have worked on in lectures this week) concerning academic outcomes, student/class characteristics, and attendance.

The aim in writing should be that a reader is able to more or less replicate your analyses without referring to your R code. This requires detailing all of the steps you took in conducting the analysis. The point of using RMarkdown is that you can pull your results directly from the code. If your analysis changes, so does your report!

Make sure that your final report doesn’t show any R functions or code. Remember you are interpreting and reporting your results in text, tables, or plots, targeting a generic reader who may use different software or may not know R at all. If you need a reminder on how to hide code, format tables, etc., make sure to review the rmd bootcamp.

Important - Write-Up Examples & Plagiarism

The example write-up sections included below are not perfect - they instead should give you a good example of what information you should include within each section, and how to structure this. For example, some information is missing (e.g., description of data checks, interpretation of descriptive statistics), some information could be presented more clearly (e.g., variable names in tables, table/figure titles/captions, and rationales for choices), and writing could be more concise in places (e.g., discussion section could be more succinct and more focused on the research questions in places).

Further, you must not copy any of the write-up included below for future reports - if you do, you will be committing plagiarism, and this type of academic misconduct is taken very seriously by the University. You can find out more here.

Study Overview

Research Aim

Explore the associations among academic outcomes, student/course characteristics (e.g., class time, online access), and attendance.

Research Questions

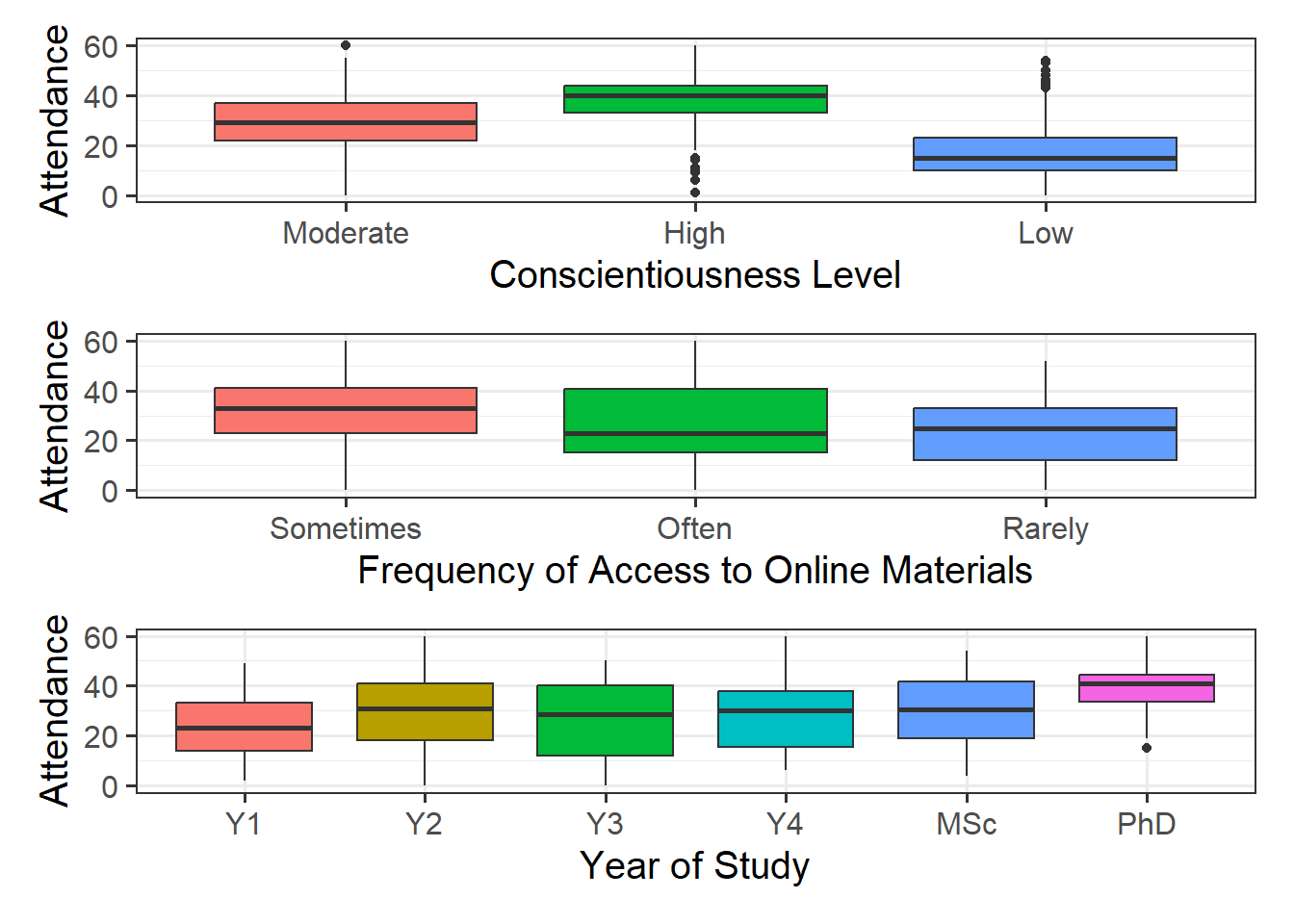
• RQ1: Does conscientiousness, frequency of access to online materials, and year of study in University predict course attendance?
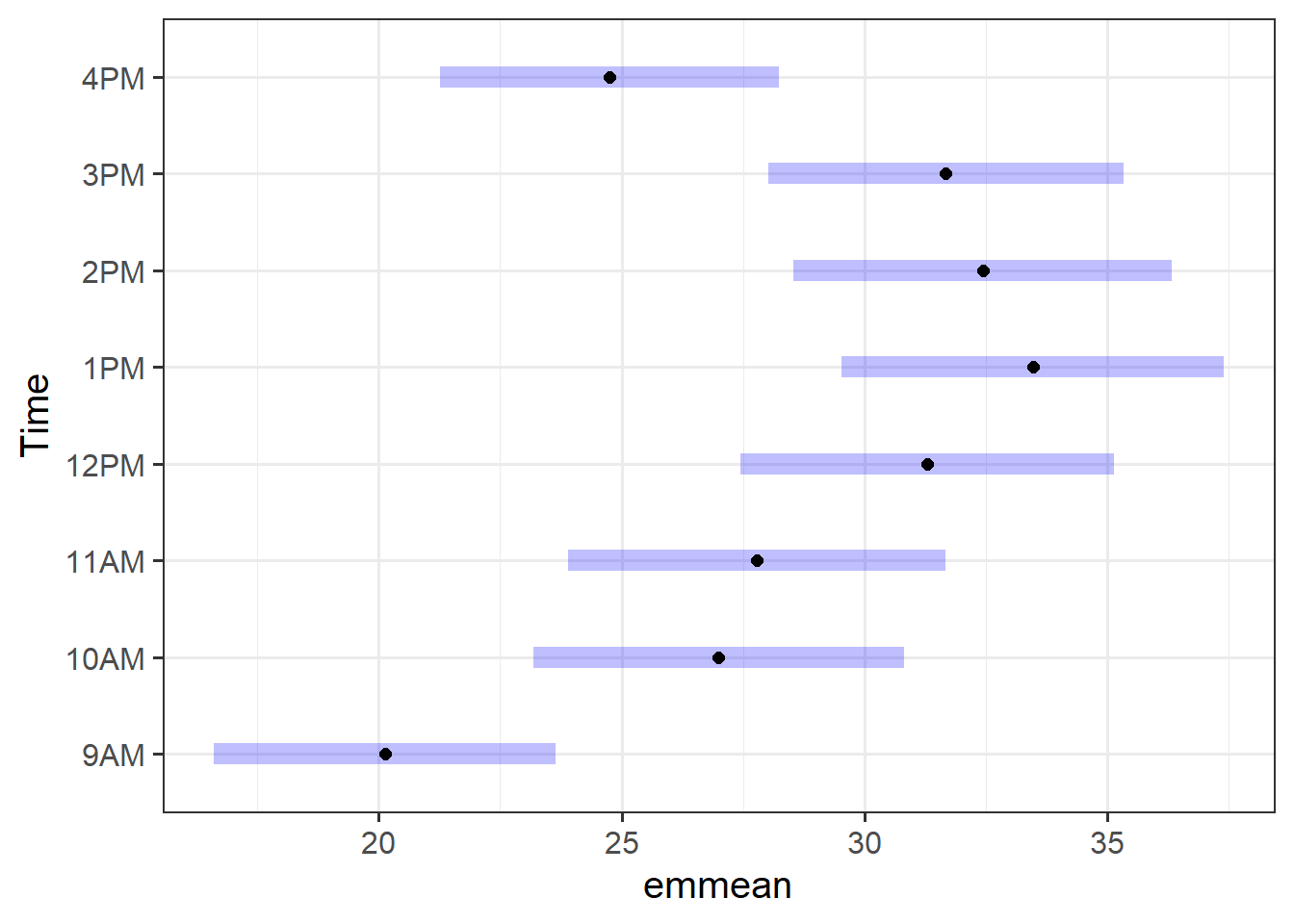
• RQ2: Is there a difference in attendance between those with early/late classes in comparison to those with midday classes?
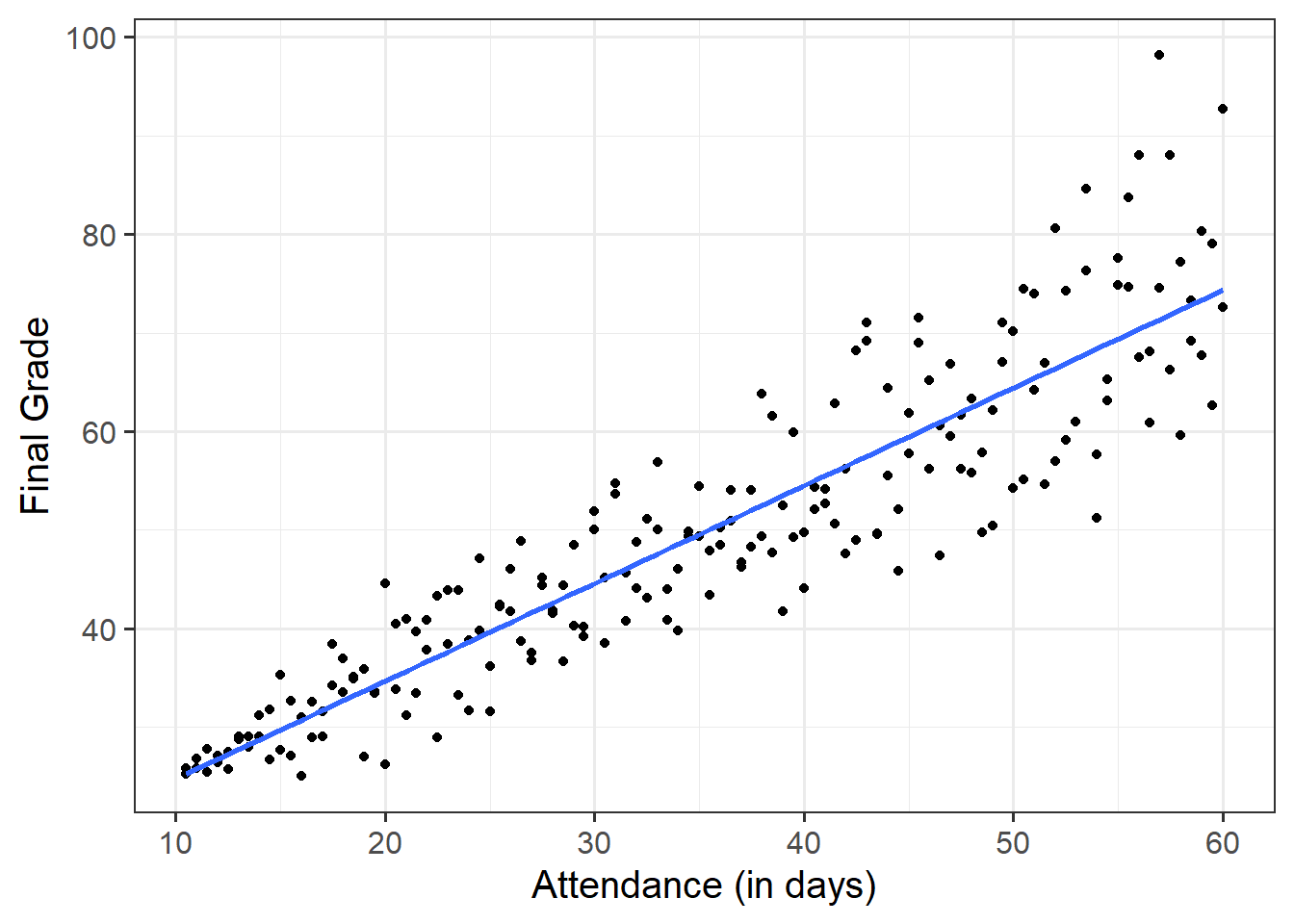
• RQ3: Is class attendance associated with final grades?

Academics data codebook.

Description

The data used for this write-up exercise are simulated, drawing on a meta-analysis that explored the association between student characteristics and grades. The simulated data are loosely based on the findings of this work, and acted to expand upon the methods and results reported in the paper:

Credé, M., Roch, S. G., & Kieszczynka, U. M. (2010). Class attendance in college: A meta-analytic review of the relationship of class attendance with grades and student characteristics. Review of Educational Research, 80(2), 272-295. https://doi.org/10.3102/0034654310362998

The current study was split into two parts. In the first, researchers were interested in further exploring possible predictors of attendance in university courses. They collected information from 397 students across all years of study (i.e., UG (Y1 - Y4), MSc, and PhD), and recorded their class attendance across the academic year, their level of Conscientiousness (categorized as Low, Moderate, or High), the frequency of which they accessed online course materials (categorized as Rarely, Sometimes, or Often), and the timing of class (categorized as 9AM, 10AM, 11AM, 12PM 1PM, 2PM, 3PM, 4PM). In the second, researchers collected data from 200 students, and recorded their class attendance across the academic year and their final course grade.

Data Dictionary: Part 1

The data in DapR2_S1B2_PracticalPart1 contain six attributes collected from a simulated sample of \(n=397\) hypothetical individuals, and includes:

Variable	Description
pid	Participant ID number
Attendance	Total attendance (in days)
Conscientiousness	Conscientiousness (Levels: Low, Moderate, High)
Time	Time of Class (Levels: 9AM, 10AM, 11AM, 12PM, 1PM, 2PM, 3PM, 4PM)
OnlineAccess	Frequency of access to online course materials (Levels: Rarely, Sometimes, Often)
Year	Year of Study in University (Y1, Y2, Y3, Y4, MsC, PhD)

Preview: Part 1

The first six rows of the data are:

pid	Attendance	Conscientiousness	Time	OnlineAccess	Year
1	9	High	3PM	Often	Y3
2	10	High	2PM	Often	Y3
3	0	Low	10AM	Rarely	Y2
4	8	Low	4PM	Often	Y4
5	6	High	4PM	Sometimes	Y1
6	6	High	9AM	Sometimes	Y1

Data Dictionary: Part 2

The data in DapR2_S1B2_PracticalPart2 contain two attributes collected from a simulated sample of \(n=200\) hypothetical individuals, and includes:

Variable	Description
Marks	Final grade (0-100)
Attendance	Total attendance (in days)

Preview: Part 2

The first six rows of the data are:

Marks	Attendance
25.18480	10.5
25.83144	11.0
25.42314	11.5
26.36523	12.0
27.44285	12.5
29.04029	13.0

Setup

Setup

1. Create a new RMarkdown file
2. Load the required package(s)
3. Read the DapR2_S1B2_PracticalPart1 and DapR2_S1B2_PracticalPart2 datasets into R, assigning them to objects named data1 and data2

#Loading the required package(s)
library(tidyverse)
library(patchwork)
library(sjPlot)
library(kableExtra)
library(psych)
library(emmeans)
library(car)

#Reading in two datasets and store in objects named 'data1' and  'data2'
data1 <- read_csv("https://uoepsy.github.io/data/DapR2_S1B2_PracticalPart1.csv")
data2 <- read_csv("https://uoepsy.github.io/data/DapR2_S1B2_PracticalPart2.csv")

#check first six rows of each dataset
head(data1)

# A tibble: 6 × 6
    pid Attendance Conscientiousness Time  OnlineAccess Year 
  <dbl>      <dbl> <chr>             <chr> <chr>        <chr>
1     1          9 High              3PM   Often        Y3   
2     2         10 High              2PM   Often        Y3   
3     3          0 Low               10AM  Rarely       Y2   
4     4          8 Low               4PM   Often        Y4   
5     5          6 High              4PM   Sometimes    Y1   
6     6          6 High              9AM   Sometimes    Y1   

head(data2)

# A tibble: 6 × 2
  Marks Attendance
  <dbl>      <dbl>
1  25.2       10.5
2  25.8       11  
3  25.4       11.5
4  26.4       12  
5  27.4       12.5
6  29.0       13  

Provided Analysis Code

Below you will find the code required to conduct the analysis to address the research questions. This should look similar (in most areas) to what you worked through in lecture.

Provided Analysis Code

Data Management

# load libraries
library(tidyverse) # for all things!
library(psych) # good for descriptive stats
library(patchwork) # grouping plots together
library(kableExtra) # useful for creating nice tables
library(sjPlot) #regression tables & plots
library(emmeans) #for contrasts
library(car) #for assumptions (crPlots, residualPlots, VIF) and bootstrapping

# read in datasets
data1 <- read_csv("https://uoepsy.github.io/data/DapR2_S1B2_PracticalPart1.csv")
data2 <- read_csv("https://uoepsy.github.io/data/DapR2_S1B2_PracticalPart2.csv")

Overall & RQ1

#######
# Coding of Variables
#######

#check coding
str(data1)

spc_tbl_ [397 × 6] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ pid              : num [1:397] 1 2 3 4 5 6 7 8 9 10 ...
 $ Attendance       : num [1:397] 9 10 0 8 6 6 9 14 5 10 ...
 $ Conscientiousness: chr [1:397] "High" "High" "Low" "Low" ...
 $ Time             : chr [1:397] "3PM" "2PM" "10AM" "4PM" ...
 $ OnlineAccess     : chr [1:397] "Often" "Often" "Rarely" "Often" ...
 $ Year             : chr [1:397] "Y3" "Y3" "Y2" "Y4" ...
 - attr(*, "spec")=
  .. cols(
  ..   pid = col_double(),
  ..   Attendance = col_double(),
  ..   Conscientiousness = col_character(),
  ..   Time = col_character(),
  ..   OnlineAccess = col_character(),
  ..   Year = col_character()
  .. )
 - attr(*, "problems")=<externalptr> 

str(data2)

spc_tbl_ [200 × 2] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ Marks     : num [1:200] 25.2 25.8 25.4 26.4 27.4 ...
 $ Attendance: num [1:200] 10.5 11 11.5 12 12.5 13 13.5 14 14.5 15 ...
 - attr(*, "spec")=
  .. cols(
  ..   Marks = col_double(),
  ..   Attendance = col_double()
  .. )
 - attr(*, "problems")=<externalptr> 

#check for NAs - none in dataset, so no missing values
table(is.na(data1))

FALSE 
 2382 

table(is.na(data2))

FALSE 
  400 

# make variables factors
data1 <- data1 %>%
    mutate(OnlineAccess = as_factor(OnlineAccess),
           Time = as_factor(Time),
           Conscientiousness = as_factor(Conscientiousness),
           Year = as_factor(Year))

#specify reference levels (alternatively use the below tidyverse way like Year - see lecture example code)
data1$OnlineAccess <- relevel(data1$OnlineAccess, "Sometimes")
data1$Conscientiousness <- relevel(data1$Conscientiousness, "Moderate")

#ordering of year variable - make chronological, Y1 as reference group
data1$Year <- data1$Year %>% 
  factor(., levels = c('Y1', 'Y2', 'Y3', 'Y4', 'MSc', 'PhD'))

Part 1 Data

RQ1

###########
# Descriptive Stats - Data Viz
###########

# Look at the marginal distributions of variables - use histograms for continuous outcomes, and barplots for categorical: 

p1 <- ggplot(data1, aes(Attendance)) + 
    geom_histogram() + 
    labs(x = "Attendance", y = "Frequency")

p2 <- ggplot(data1, aes(Conscientiousness)) + 
    geom_bar() + 
    labs(x = "Conscientiousness Level", y = "Frequency")

p3 <- ggplot(data1, aes(Year)) + 
    geom_bar() + 
    labs(x = "Year of Study", y = "Frequency")

p4 <- ggplot(data1, aes(OnlineAccess)) + 
    geom_bar()  + 
    labs(x = "Frequency of Access to Online Materials", y = "Frequency")

p1 / p2 / p3 / p4

# Look at the bivariate associations (note we are also removing the legend - it does not offer the reader any additional information and takes up space):

p5 <- ggplot(data1, aes(x = Conscientiousness, y = Attendance, fill = Conscientiousness)) + 
    geom_boxplot() + 
    labs(x = "Conscientiousness Level", y = "Attendance") + 
    theme(legend.position = "none")

p6 <- ggplot(data1, aes(x = OnlineAccess, y = Attendance, fill = OnlineAccess)) + 
    geom_boxplot() + 
    labs(x = "Frequency of Access to Online Materials", y = "Attendance") + 
    theme(legend.position = "none")

p7 <- ggplot(data1, aes(x = Year, y = Attendance, fill = Year)) + 
    geom_boxplot() + 
    labs(x = "Year of Study", y = "Attendance") + 
    theme(legend.position = "none")

p5 / p6 / p7

#######
#Descriptive Stats - Numeric
#######

# check how many observations in each category
table(data1$Conscientiousness)

Moderate     High      Low 
     146      124      127 

table(data1$OnlineAccess)

Sometimes     Often    Rarely 
      170       126       101 

table(data1$Year)

 Y1  Y2  Y3  Y4 MSc PhD 
 89 100  66  71  48  23 

data1 %>%
  group_by(Year, OnlineAccess, Conscientiousness) %>%
  summarise(n = n(), 
            Mean = mean(Attendance), 
            SD = sd(Attendance),
            Minimum = min(Attendance),
            Maximum = max(Attendance)) %>%
    kable(., caption = "Attendance and Academic Year, Frequency of Online Material Access, Conscientiousness Descriptive Statistics", digits = 2) %>%
    kable_styling()   

Attendance and Academic Year, Frequency of Online Material Access, Conscientiousness Descriptive Statistics

Year	OnlineAccess	Conscientiousness	n	Mean	SD	Minimum	Maximum
Y1	Sometimes	Moderate	18	25.33	7.31	14	41
Y1	Sometimes	High	12	27.92	15.41	6	43
Y1	Sometimes	Low	7	19.43	8.98	5	33
Y1	Often	Moderate	12	24.67	7.66	11	36
Y1	Often	High	7	36.29	10.89	21	49
Y1	Often	Low	5	18.60	15.27	7	45
Y1	Rarely	Moderate	7	25.57	11.28	8	40
Y1	Rarely	High	5	31.60	13.52	9	43
Y1	Rarely	Low	16	14.19	10.70	2	42
Y2	Sometimes	Moderate	20	34.00	12.19	5	60
Y2	Sometimes	High	14	41.36	5.17	32	52
Y2	Sometimes	Low	11	21.27	20.51	0	54
Y2	Often	Moderate	13	30.62	11.62	14	51
Y2	Often	High	10	42.80	9.51	24	53
Y2	Often	Low	6	15.33	4.68	10	23
Y2	Rarely	Moderate	8	24.00	6.12	14	31
Y2	Rarely	High	9	31.33	8.87	15	43
Y2	Rarely	Low	9	10.33	5.96	0	18
Y3	Sometimes	Moderate	8	34.62	7.60	27	46
Y3	Sometimes	High	10	38.60	14.01	1	50
Y3	Sometimes	Low	8	20.00	17.03	3	41
Y3	Often	Moderate	3	19.33	19.01	0	38
Y3	Often	High	6	30.17	16.22	9	43
Y3	Often	Low	12	14.83	7.41	8	33
Y3	Rarely	Moderate	7	25.86	8.69	11	39
Y3	Rarely	High	4	35.00	4.40	30	40
Y3	Rarely	Low	8	23.38	14.72	9	46
Y4	Sometimes	Moderate	12	37.25	10.57	22	55
Y4	Sometimes	High	10	38.70	5.19	30	45
Y4	Sometimes	Low	9	23.78	10.23	11	38
Y4	Often	Moderate	8	21.62	12.65	9	42
Y4	Often	High	7	34.57	16.21	11	60
Y4	Often	Low	12	17.75	14.59	6	48
Y4	Rarely	Moderate	5	29.00	11.55	9	38
Y4	Rarely	High	4	34.75	12.84	22	52
Y4	Rarely	Low	4	13.50	5.97	6	20
MSc	Sometimes	Moderate	5	34.80	11.78	25	53
MSc	Sometimes	High	8	42.00	6.99	31	51
MSc	Sometimes	Low	8	19.12	9.39	8	38
MSc	Often	Moderate	5	22.00	13.34	9	44
MSc	Often	High	8	43.00	5.81	37	54
MSc	Often	Low	5	19.20	1.92	16	21
MSc	Rarely	Moderate	4	31.00	12.83	16	44
MSc	Rarely	High	2	45.00	5.66	41	49
MSc	Rarely	Low	3	12.67	9.61	4	23
PhD	Sometimes	Moderate	4	38.50	9.11	25	44
PhD	Sometimes	High	4	42.75	3.50	39	47
PhD	Sometimes	Low	2	47.00	4.24	44	50
PhD	Often	Moderate	3	39.00	19.31	22	60
PhD	Often	High	2	48.00	4.24	45	51
PhD	Often	Low	2	34.50	27.58	15	54
PhD	Rarely	Moderate	4	34.25	7.14	24	40
PhD	Rarely	High	2	25.50	9.19	19	32

#######
# Model Building
#######

#build model
m1 <- lm(Attendance ~ Conscientiousness + OnlineAccess + Year, data = data1)

#check model summary
summary(m1)

Call:
lm(formula = Attendance ~ Conscientiousness + OnlineAccess + 
    Year, data = data1)

Residuals:
    Min      1Q  Median      3Q     Max 
-37.657  -6.990  -0.279   6.085  31.844 

Coefficients:
                      Estimate Std. Error t value Pr(>|t|)    
(Intercept)             27.874      1.533  18.179  < 2e-16 ***
ConscientiousnessHigh    7.366      1.392   5.292 2.03e-07 ***
ConscientiousnessLow   -10.292      1.399  -7.359 1.12e-12 ***
OnlineAccessOften       -3.533      1.339  -2.639 0.008649 ** 
OnlineAccessRarely      -5.378      1.441  -3.732 0.000218 ***
YearY2                   4.574      1.657   2.760 0.006049 ** 
YearY3                   3.418      1.853   1.844 0.065926 .  
YearY4                   4.266      1.817   2.347 0.019418 *  
YearMSc                  5.649      2.046   2.760 0.006051 ** 
YearPhD                 12.484      2.661   4.692 3.76e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 11.35 on 387 degrees of freedom
Multiple R-squared:  0.3574,    Adjusted R-squared:  0.3424 
F-statistic: 23.91 on 9 and 387 DF,  p-value: < 2.2e-16

#######
# Check Assumptions of m1
#######

# Linearity: Can be assumed as working with categorical predictors

# Independence of Errors: Using a between-subjects design, so can assume this

# Normality (either use plot(model, which = 2) or hist(model$residuals))
plot(m1, which = 2, main = "Normality Assumption Check for m1")

# Equal Variances
residualPlot(m1, main = "Equal Variances Assumption Check for m1")

#### Overall, assumption checks look fine

#######
#Table for Results
#######

tab_model(m1,
          pred.labels = c('Intercept', 'Conscientiousness - High', 'Conscientiousness - Low', 'Online Access - Often', 'Online Access - Rarely', 
                              'UG Y2', 'UG Y3', 'UG Y4', 'MSc', 'PhD'),
          title = "RQ1: Regression Table for Attendance Model")

RQ1: Regression Table for Attendance Model

	Attendance
Predictors	Estimates	CI	p
Intercept	27.87	24.86 – 30.89	<0.001
Conscientiousness - High	7.37	4.63 – 10.10	<0.001
Conscientiousness - Low	-10.29	-13.04 – -7.54	<0.001
Online Access - Often	-3.53	-6.16 – -0.90	0.009
Online Access - Rarely	-5.38	-8.21 – -2.54	<0.001
UG Y2	4.57	1.32 – 7.83	0.006
UG Y3	3.42	-0.23 – 7.06	0.066
UG Y4	4.27	0.69 – 7.84	0.019
MSc	5.65	1.63 – 9.67	0.006
PhD	12.48	7.25 – 17.72	<0.001
Observations	397
R2 / R2 adjusted	0.357 / 0.342

RQ2

#######
# Coding of Variables
#######

#ordering of time variable - make chronological
data1$Time <- data1$Time %>% 
  factor(., levels = c('9AM', '10AM', '11AM','12PM', '1PM', '2PM', '3PM', '4PM'))

#######
#Descriptive Stats
#######

# Numeric
data1 %>%
  group_by(Time) %>%
  summarise(n = n(), 
            Mean = mean(Attendance), 
            SD = sd(Attendance),
            Minimum = min(Attendance),
            Maximum = max(Attendance)) %>%
    kable(., caption = "Attendance & Class Time Descriptive Statistics", digits = 2) %>%
    kable_styling()    

Attendance & Class Time Descriptive Statistics

Time	n	Mean	SD	Minimum	Maximum
9AM	56	20.12	10.08	1	49
10AM	48	27.00	14.23	0	60
11AM	46	27.78	14.57	2	52
12PM	47	31.30	14.11	0	55
1PM	45	33.47	14.44	4	60
2PM	46	32.43	12.44	0	60
3PM	52	31.67	13.58	5	54
4PM	57	24.75	13.78	4	54

# check how many observations in each category
table(data1$Time)

 9AM 10AM 11AM 12PM  1PM  2PM  3PM  4PM 
  56   48   46   47   45   46   52   57 

# Visual
p8 <- ggplot(data1, aes(Time)) + 
    geom_bar()

p9 <- ggplot(data1, aes(x = Time, y = Attendance, fill = Time)) + 
    geom_boxplot()

p8 / p9

#######
#Model Building
#######

#build model 
m2 <- lm(Attendance ~ Time, data = data1)

#check summary
summary(m2)

Call:
lm(formula = Attendance ~ Time, data = data1)

Residuals:
    Min      1Q  Median      3Q     Max 
-32.435 -10.298   1.327  10.246  33.000 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   20.125      1.793  11.226  < 2e-16 ***
Time10AM       6.875      2.639   2.605  0.00953 ** 
Time11AM       7.658      2.669   2.869  0.00435 ** 
Time12PM      11.173      2.654   4.210 3.17e-05 ***
Time1PM       13.342      2.686   4.968 1.02e-06 ***
Time2PM       12.310      2.669   4.611 5.43e-06 ***
Time3PM       11.548      2.583   4.470 1.03e-05 ***
Time4PM        4.629      2.524   1.834  0.06740 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 13.41 on 389 degrees of freedom
Multiple R-squared:  0.0974,    Adjusted R-squared:  0.08116 
F-statistic: 5.997 on 7 and 389 DF,  p-value: 1.196e-06

#######
# Check Assumptions of m2
#######

# Linearity: Can be assumed as working with categorical predictors

# Independence of Errors: Using a between-subjects design, so can assume this

# Normality (either use plot(model, which = 2) or hist(model$residuals))
plot(m2, which = 2)

# Equal Variances
residualPlot(m2)

#### Overall, assumption checks look fine

#######
#Contrast
#######

#Morning/Evening vs Afternoon

#check order
levels(data1$Time)

[1] "9AM"  "10AM" "11AM" "12PM" "1PM"  "2PM"  "3PM"  "4PM" 

#table of weights to present in table 1 analysis strategy
TimePeriod <- c("Early/Late", "Early/Late", "Midday", "Midday", "Midday", "Midday", "Early/Late", "Early/Late")
Time <- c("9AM", "10AM", "11AM", "12PM", "1PM", "2PM", "3PM", "4PM")
Weight <- c(1/4, 1/4, -1/4, -1/4, -1/4, -1/4, 1/4, 1/4)
weights <- tibble(TimePeriod, Time, Weight)


#get means
time_mean <- emmeans(m2, ~Time)

#look at means
time_mean

 Time emmean   SE  df lower.CL upper.CL
 9AM    20.1 1.79 389     16.6     23.6
 10AM   27.0 1.94 389     23.2     30.8
 11AM   27.8 1.98 389     23.9     31.7
 12PM   31.3 1.96 389     27.5     35.1
 1PM    33.5 2.00 389     29.5     37.4
 2PM    32.4 1.98 389     28.5     36.3
 3PM    31.7 1.86 389     28.0     35.3
 4PM    24.8 1.78 389     21.3     28.2

Confidence level used: 0.95 

#plot means
plot(time_mean)

#specify weights for contrast
time_comp <- list('Early or Late vs Middle of the Day' = c(-1/4,-1/4, 1/4, 1/4, 1/4, 1/4, -1/4, -1/4))

#run contrast analysis
time_comp_test <- contrast(time_mean, method = time_comp)

#examine output
time_comp_test

 contrast                           estimate   SE  df t.ratio p.value
 Early or Late vs Middle of the Day     5.36 1.35 389   3.963  0.0001

#obtain confidence intervals
confint(time_comp_test)

 contrast                           estimate   SE  df lower.CL upper.CL
 Early or Late vs Middle of the Day     5.36 1.35 389      2.7     8.01

Confidence level used: 0.95 

Part 2 Data

RQ3

#######
#Descriptive Stats
#######

data2 %>%
    describe() %>%
    select(2:4, 8:9) %>%
    rename("N" = n, "Mean" = mean, "SD" = sd, "Minimum" = min, "Maximum" = max) %>%    
        kable(., caption = "Final Grades & Attendance Descriptive Statistics", digits = 2) %>%
        kable_styling()  

Final Grades & Attendance Descriptive Statistics

	N	Mean	SD	Minimum	Maximum
Marks	200	49.79	15.84	25.01	98.2
Attendance	200	35.25	14.47	10.50	60.0

data2 %>%
    select(Attendance, Marks) %>%
    cor() %>%
    round(digits = 2)

           Attendance Marks
Attendance       1.00  0.91
Marks            0.91  1.00

ggplot(data = data2, aes(x = Attendance, y = Marks)) + 
    geom_point() + 
    geom_smooth(method = "lm", se = FALSE) + 
    labs(x = "Attendance (in days)", y = "Final Grade")

#######
#Model Building
#######

#specify model
m3 <- lm(Marks ~ Attendance, data = data2)

#check summary
summary(m3)

Call:
lm(formula = Marks ~ Attendance, data = data2)

Residuals:
     Min       1Q   Median       3Q      Max 
-17.1477  -4.5210  -0.1861   4.2501  26.8415 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 14.83270    1.25534   11.82   <2e-16 ***
Attendance   0.99163    0.03296   30.09   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.727 on 198 degrees of freedom
Multiple R-squared:  0.8205,    Adjusted R-squared:  0.8196 
F-statistic: 905.3 on 1 and 198 DF,  p-value: < 2.2e-16

#######
# Check Assumptions of m3
#######

# Linearity (can also use plot(model, which = 1) in place of below)
ggplot(data2, aes(x = Attendance, y = Marks)) + 
    geom_point() + 
    geom_smooth(method = 'lm', se = F) + 
    geom_smooth(method = 'loess', se = F, colour = 'red') + 
    labs(x = "Attendance", y = "Final Grade", title = "Scatterplot with linear (blue) and loess (red) lines")

# Independence of Errors: Using a between-subjects design, so can assume this

# Normality (either use plot(model, which = 2) or hist(model$residuals))
plot(m3, which = 2)

# Equal Variances
residualPlot(m3)

#######
# Bootstrap Model
#######

# use 1000 resamples
boot_m3 <- Boot(m3, R = 1000)

#check summary
summary(boot_m3)

Number of bootstrap replications R = 1000 
            original   bootBias  bootSE bootMed
(Intercept) 14.83270  0.0598374 1.02249 14.9135
Attendance   0.99163 -0.0022338 0.03595  0.9882

#confidence intervals
confint(boot_m3)

Bootstrap bca confidence intervals

                 2.5 %    97.5 %
(Intercept) 12.5939583 16.644285
Attendance   0.9294931  1.074284

The 3-Act Structure

We need to present our report in three clear sections - think of your sections like the 3 key parts of a play or story - we need to (1) provide some background and scene setting for the reader, (2) present our results in the context of the research question, and (3) present a resolution to our story - relate our findings back to the question we were asked and provide our answer.

Act I: Analysis Strategy

Question 1

Attempt to draft an analysis strategy section based on the above research question and analysis provided.

Analysis Strategy - What to Include*

Your analysis strategy will contain a number of different elements detailing plans and changes to your plan. Remember, your analysis strategy should not contain any results. You may wish to include the following sections:

• Very brief data and design description:
  • Give the reader some background on the context of your write-up. For example, you may wish to describe the data source, data collection strategy, study design, number of observational units.
  • Specify the variables of interest in relation to the research question, including their unit of measurement, the allowed range (e.g., for Likert scales), and how they are scored. If you have categorical data, you will need to specify the levels and coding of your variables, and what was specified as your reference level and the justification for this choice.
• Data management:
  • Describe any data cleaning and/or recoding.
  • Are there any observations that have been excluded based on pre-defined criteria? How/why, and how many?
  • Describe any transformations performed to aid your interpretation (i.e., mean centering, standardisation, etc.).
• Model specification:
  • Clearly state your hypotheses and specify your chosen significance level.
  • What type of statistical analysis do you plan to use to answer the research question (e.g., simple linear regression, multiple linear regression, binary logistic regression, etc.)?
  • In some cases, you may wish to include some visualisations and descriptive tables to motivate your model specification.
  • Specify the model(s) to be fitted to answer your given research question and analysis structure. Clearly specify the response and explanatory variables included in your model(s). This includes specifying the type of coding scheme applied if using categorical data.
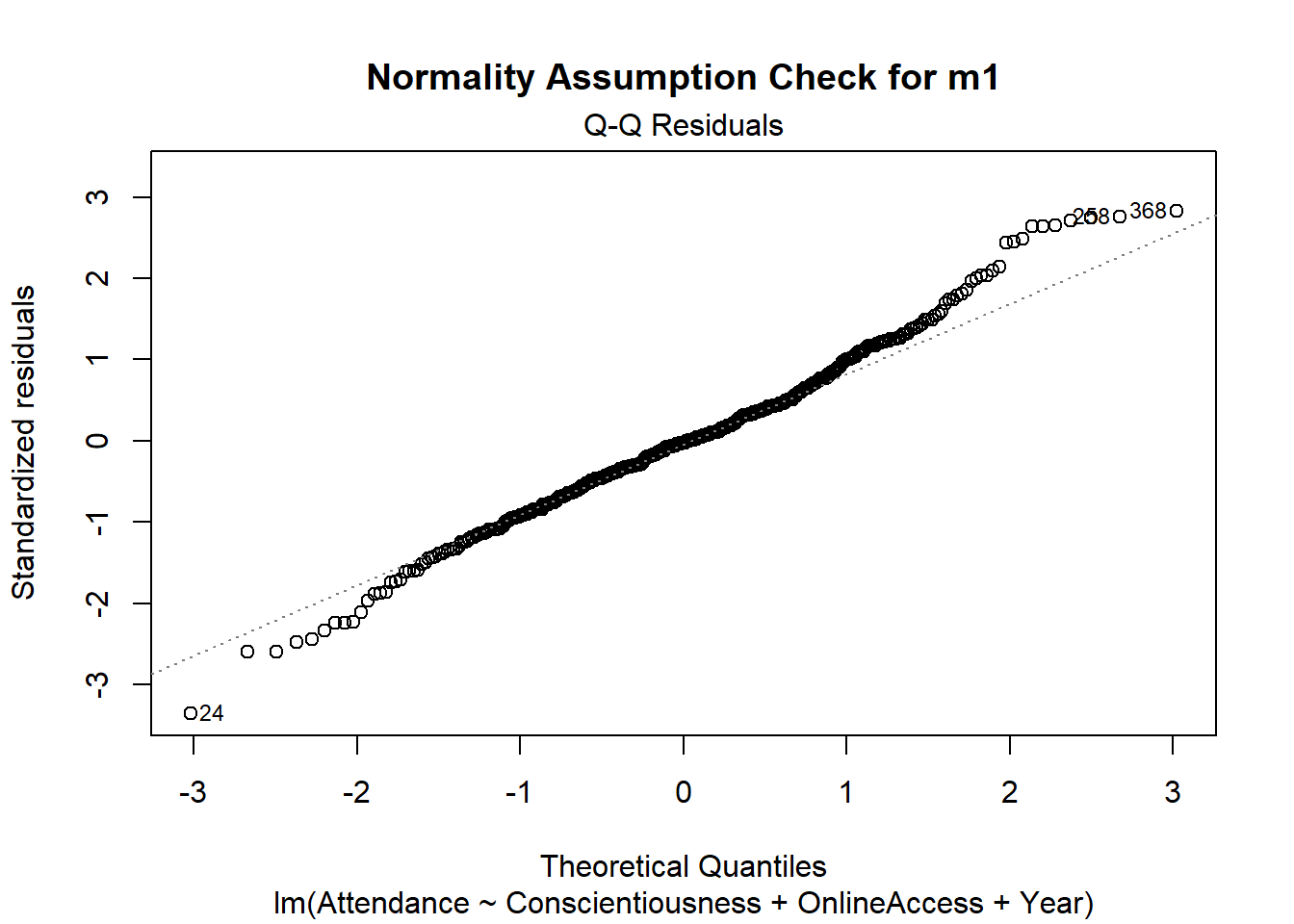
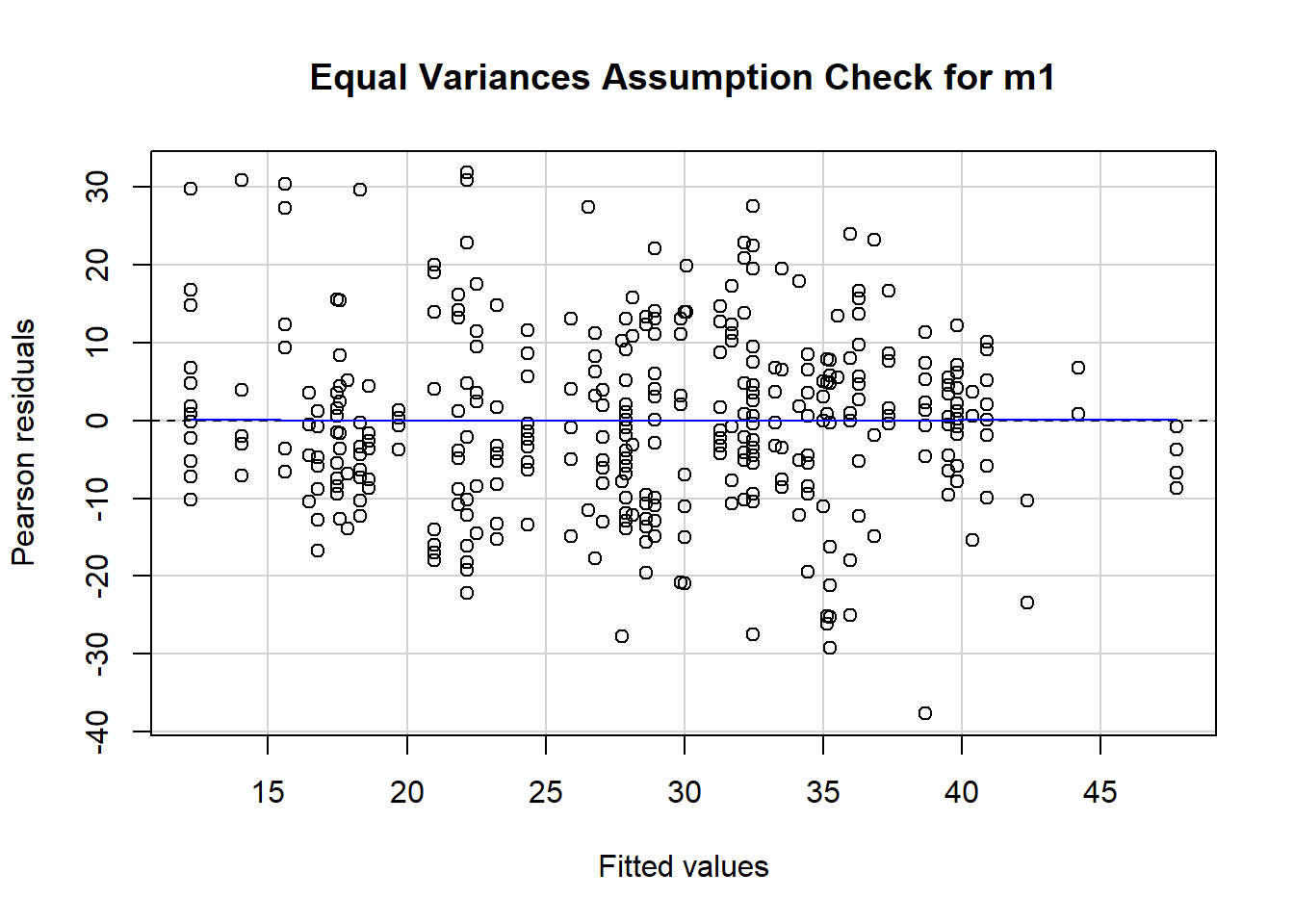
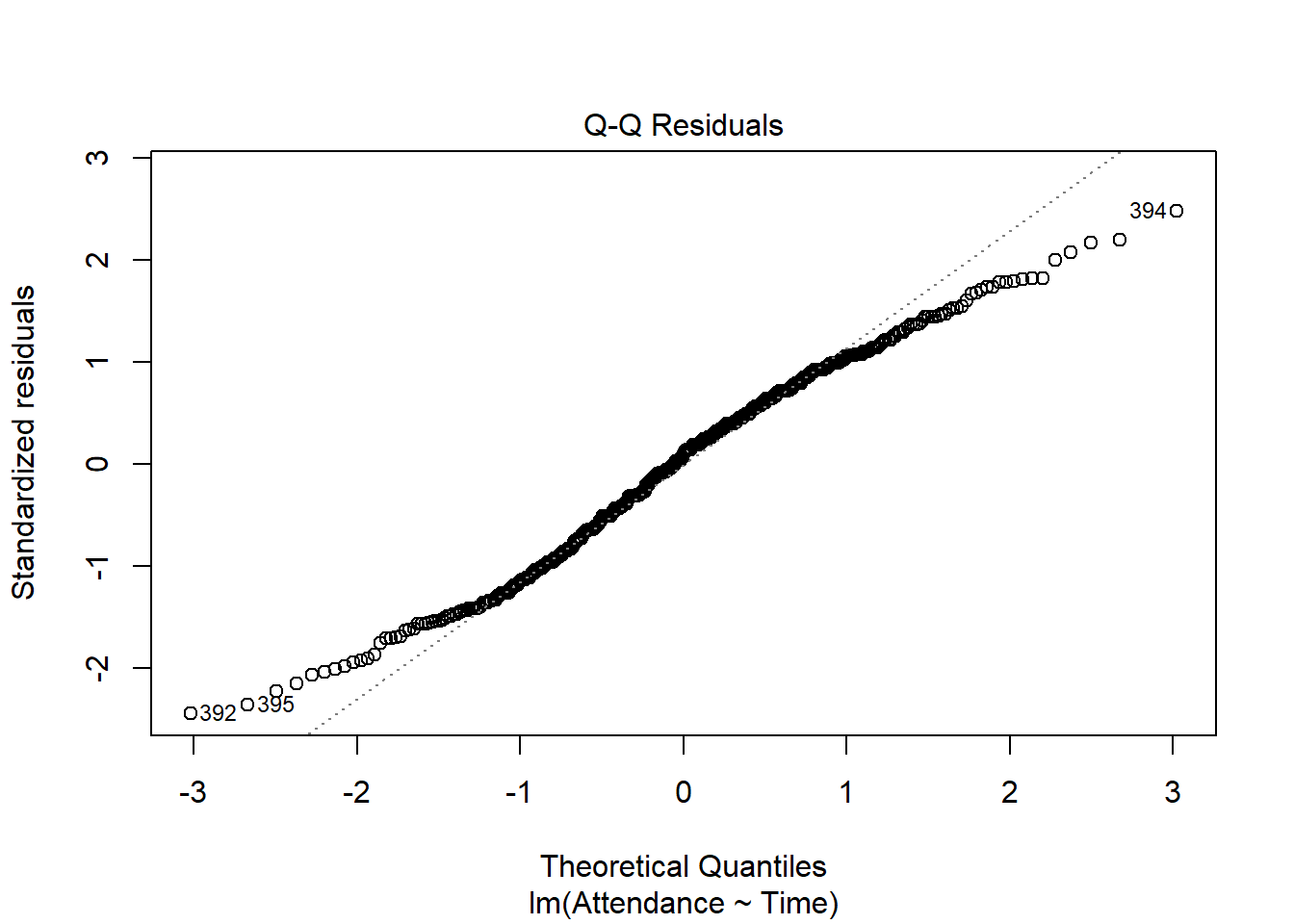
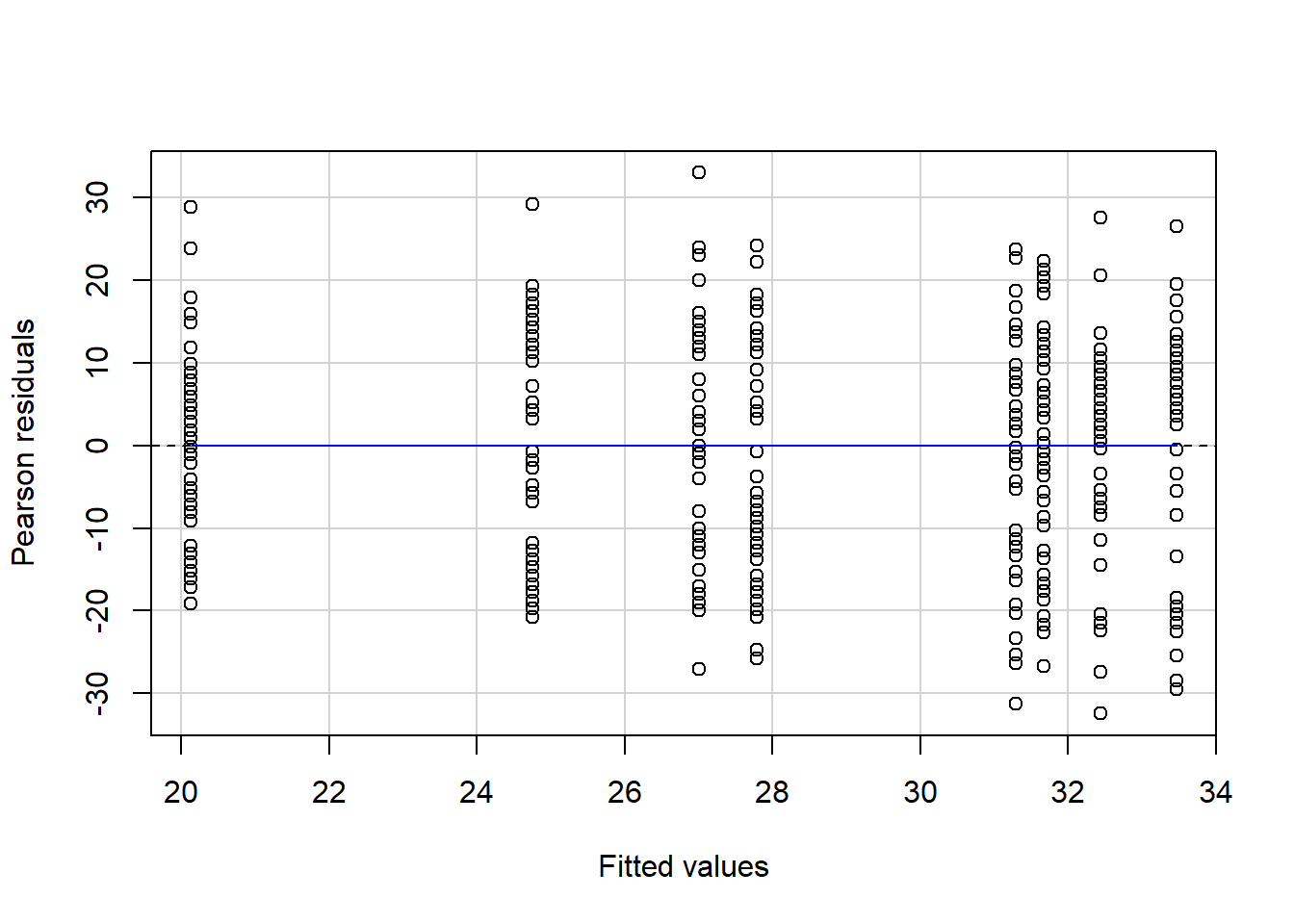
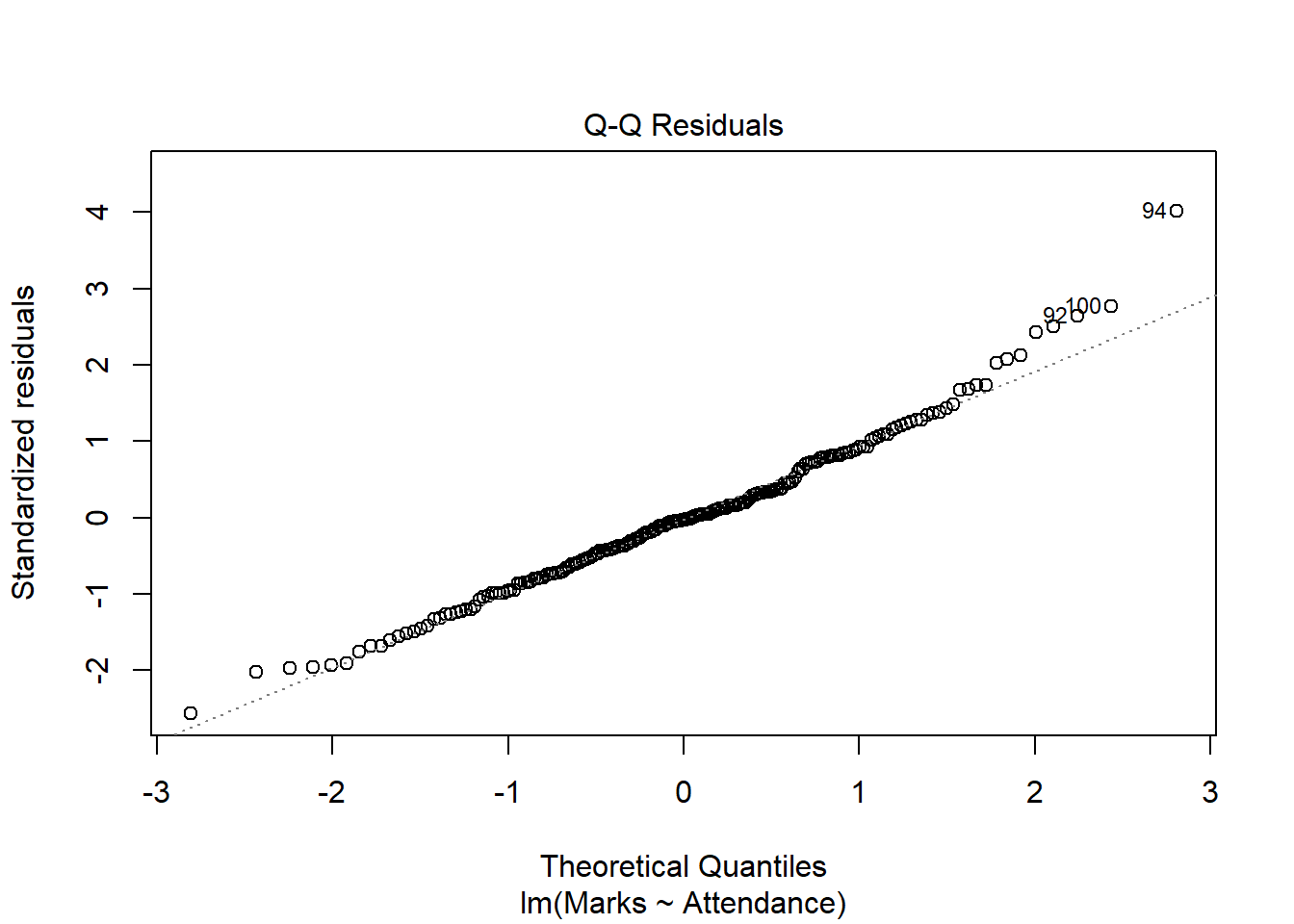
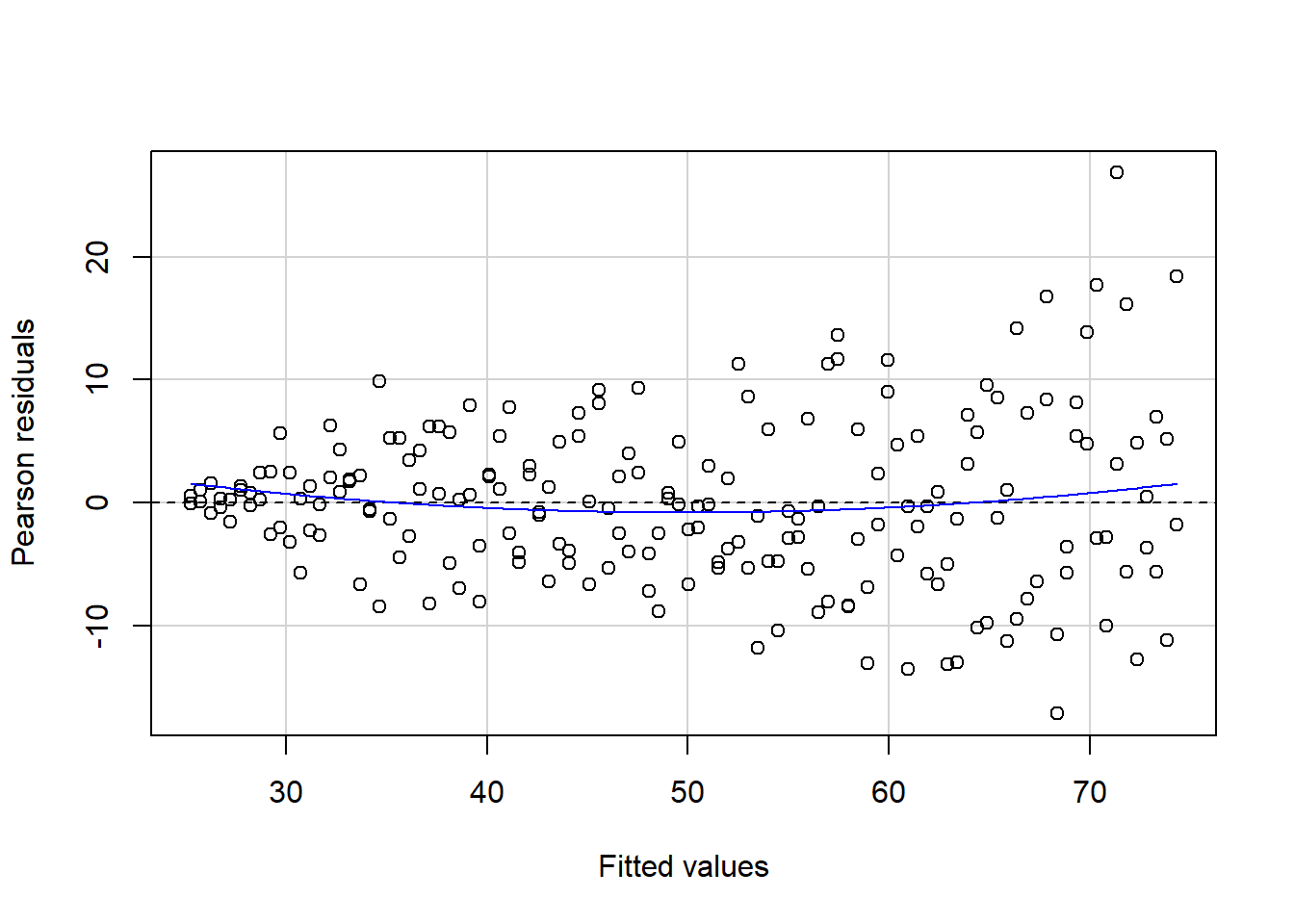
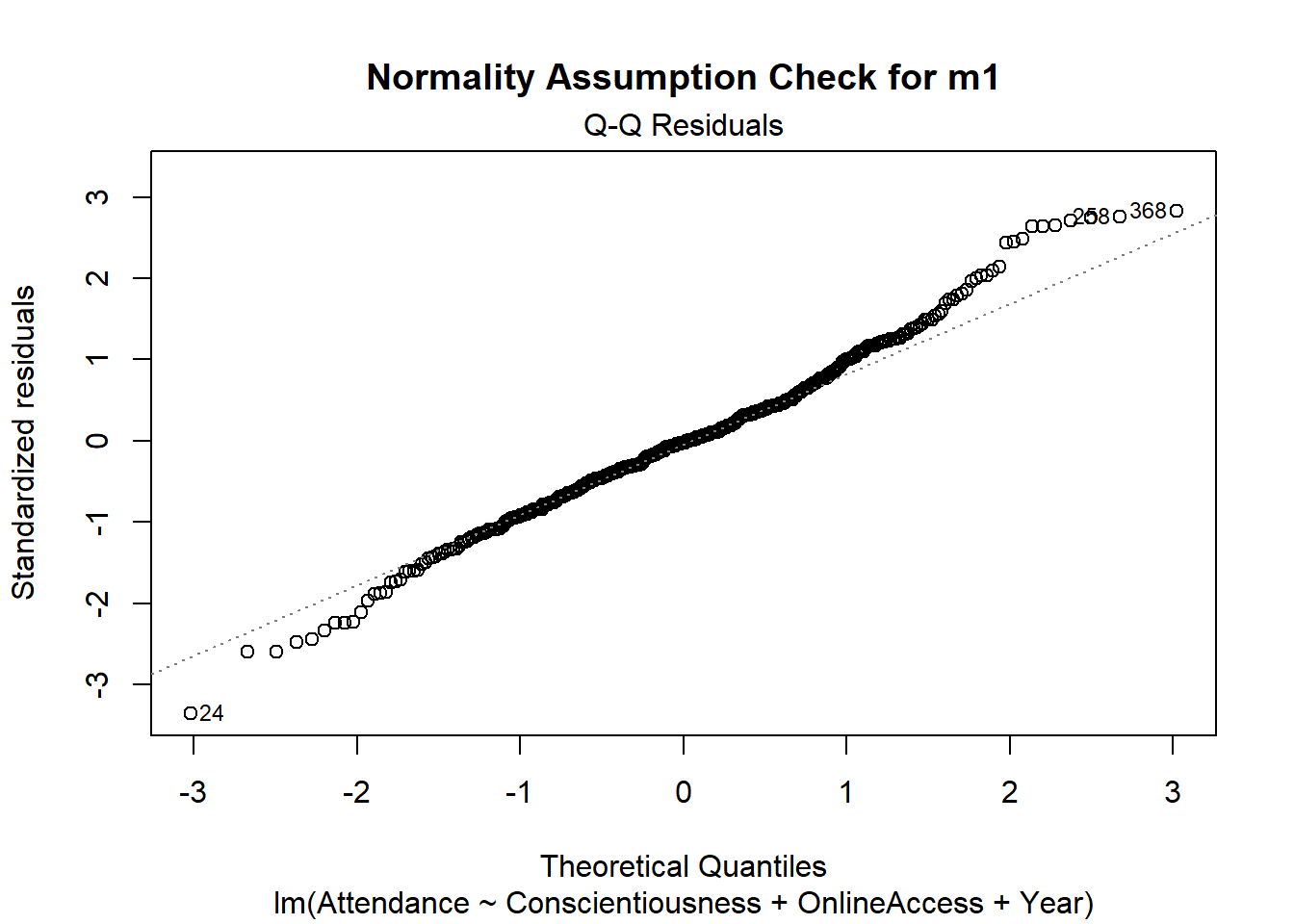
  • * Specify the assumption and diagnostic checks that you will conduct. Specify what plots you will use, and how you will evaluate these.

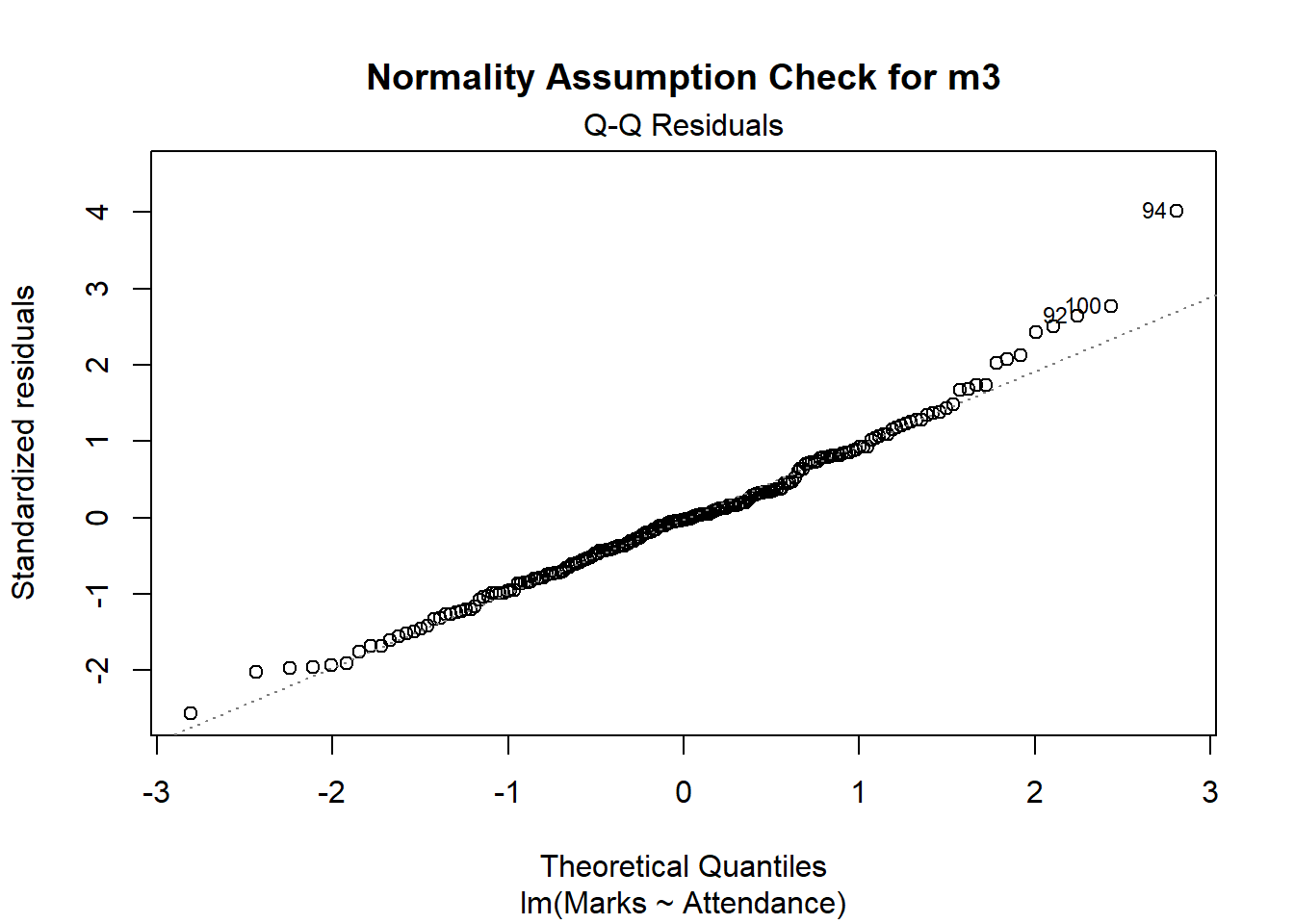
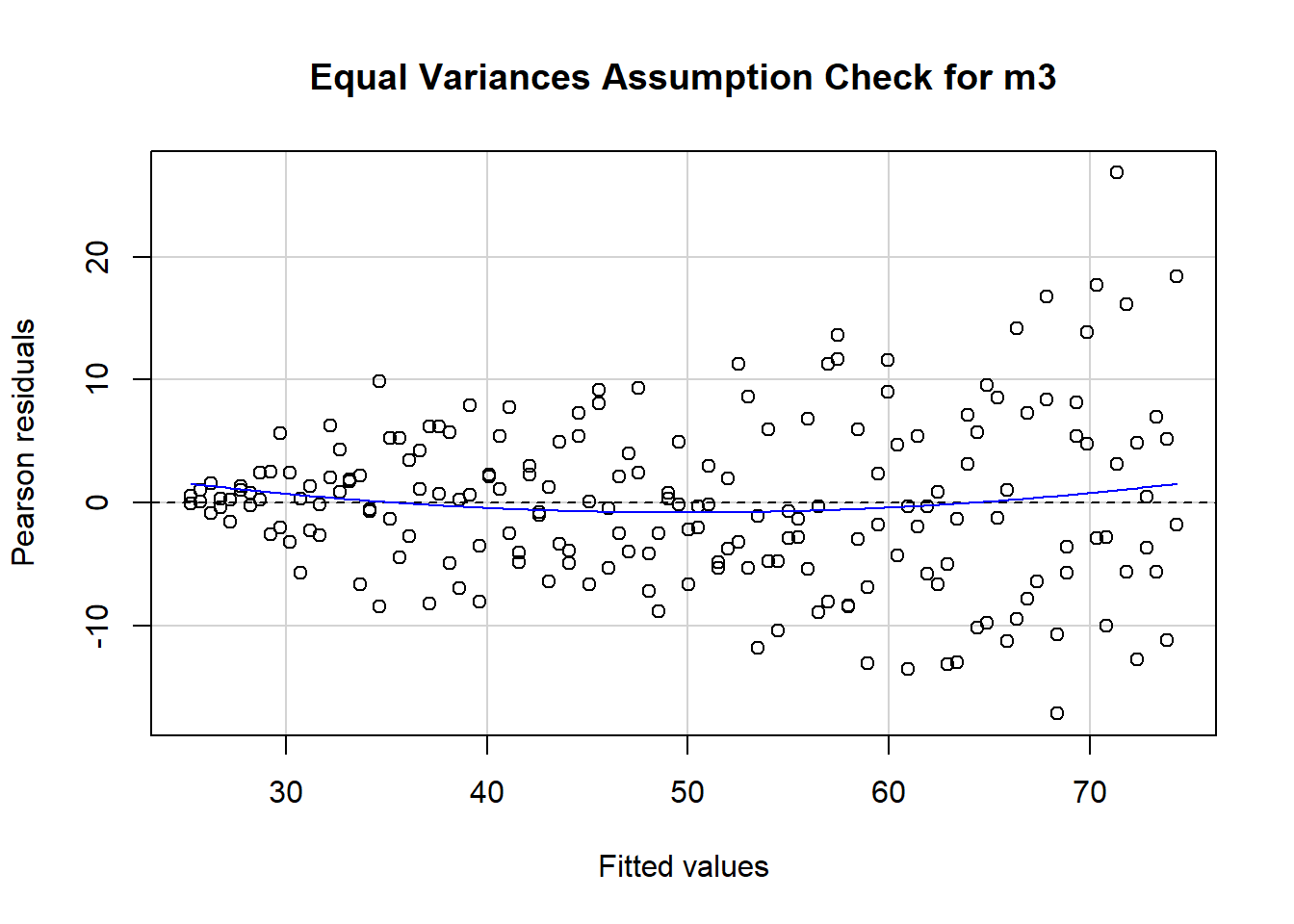
• Note, given time constraints in lab, we have not included any reference to diagnostic checks in this write-up example - you would be expected to include this in your report. You can find more information on diagnostic checks in the S1 Week 9 Lab and S1 Week 9 Lectures.

As noted and encouraged throughout the course, one of the main benefits of using RMarkdown is the ability to include inline R code in your document. Try to incorporate this in your write up so you can automatically pull the specified values from your code. If you need a reminder on how to do this, see Lesson 3 of the Rmd Bootcamp.

The first dataset contained information on 397 participants, including their attendance records (in days), class times (ranging from 9AM-4PM, starting on the hour), year of study (UG Y1-Y4, MSc, PhD), levels of conscientiousness (categorized as low, moderate or high), and the frequency of which they accessed online course materials (categorized as rarely, sometimes, or often). The second dataset contained information on 200 participants, including their attendance records (in days) and their final course grades (ranging from 0 - 100). All participant data was complete (no missing values), with all values within possible ranges.

The aim of this report was to address three research questions (the first two RQs using dataset 1, and RQ3 using dataset 2):

1. Does conscientiousness, frequency of access of online access, and year of study influence class attendance?
2. Is there a difference in attendance between those with early/late classes in comparison to those with midday classes?
3. Does class attendance influence grades?

To allow visual examination of the bivariate associations between attendance and the other variables of interest, a series of boxplots were used for RQs 1 and 2, and a scatterplot for RQ3. In order to comment on the strength of the linear association between attendance and grades in RQ3, we will also compute the correlation coefficient.

To address RQ1, the following multiple regression model was used. We applied dummy coding for Conscientiousness (where ‘Moderate’ was designated as the reference group), OnlineAccess (where ‘Sometimes’ was designated as the reference group), and Year of study (where ‘Y1’ was designated as the reference group).

\[ \begin{align*} \text{Class Attendance} ~=~ & \beta_0 + \beta_1 \cdot \text{Consc}_{\text{High}} + \beta_2 \cdot \text{Consc}_{\text{Low}} \\ & + \beta_3 \cdot \text{Online Access}_\text{Often} + \beta_4 \cdot \text{Online Access}_\text{Rarely} \\ & + \beta_5 \cdot \text{Year}_\text{2} + \beta_6 \cdot \text{Year}_\text{3} + \beta_7 \cdot \text{Year}_\text{4} \\ & + \beta_8 \cdot \text{Year}_\text{MSc} + \beta_9 \cdot \text{Year}_\text{PhD} + \epsilon \end{align*} \quad \]

\[ \begin{align} & \text{Where:} \\ & \text{Consc } = \text{Conscientiousness} \\ & \text{OnlineAccess } = \text{Frequency of Access to Online Material} \\ & \text{Year } = \text{Year of Study} \\ \end{align} \]

where we tested whether there was a significant association between attendance and conscientiousness, frequency of access to online materials and/or year of study:

\[ H_0: \text{All}~~ \beta_j = 0 ~\text{(for j = 1, 2, 3, 4, 5, 6, 7, 8, 9)} \]

\[ H_1: \text{At least one}~ \beta_j \neq 0 ~\text{(for j = 1, 2, 3, 4, 5, 6, 7, 8, 9)} \]

To address RQ2, we first specified the following multiple regression model, where the Time variable was dummy coded (‘9AM’ was set as the reference group):

\[ \begin{align*} \text{Class Attendance} ~=~ & \beta_0 + \beta_1 \cdot \text{Time}_{10\text{AM}} + \beta_2 \cdot \text{Time}_{11\text{AM}} + \beta_3 \cdot \text{Time}_{12\text{PM}} \\ & + \beta_4 \cdot \text{Time}_{1\text{PM}} + \beta_5 \cdot \text{Time}_{2\text{PM}} + \beta_6 \cdot \text{Time}_{3\text{PM}} \\ & + \beta_7 \cdot \text{Time}_{4\text{PM}} + \epsilon \end{align*} \quad \]

Next, in order to determine whether there was a significant difference in attendance between early/late classes and midday classes, we conducted a contrast analysis using the following weights (see Table 1).

Table 1: Contrast Weights

Contrast Weights

TimePeriod	Time	Weight
Early/Late	9AM	0.25
Early/Late	10AM	0.25
Midday	11AM	-0.25
Midday	12PM	-0.25
Midday	1PM	-0.25
Midday	2PM	-0.25
Early/Late	3PM	0.25
Early/Late	4PM	0.25

Here we wanted to formally test the following hypothesis:

\[ \begin{aligned} \quad H_0 &: \mu_\text{Early/Late Class} = \mu_\text{Midday Class} \\ \quad H_0 &: \frac{1}{4}(\mu_1+\mu_2+\mu_7+\mu_8) = \frac{1}{4}(\mu_3+\mu_4+\mu_5+\mu_6) \\ \\ \quad H_1 &: \mu_\text{Early/Late Class} \neq \mu_\text{Midday Class} \\ \quad H_1 &: \frac{1}{4}(\mu_1+\mu_2+\mu_7+\mu_8) \neq \frac{1}{4}(\mu_3+\mu_4+\mu_5+\mu_6) \\ \end{aligned} \]

To address RQ3, the following simple linear regression model was used:

\[ \text{Final Grade} = \beta_0 + \beta_1 \cdot \text{Attendance} + \epsilon \quad \]

where we tested whether there was a significant association between final grade and attendance. Formally, this corresponded to testing whether the attendance coefficient was equal to zero:

\[ H_0: \beta_1 = 0 \]

\[ H_0: \beta_1 \neq 0 \]

For models related to all RQs, as we were using between-subjects datasets, we assumed independence of our error terms. For RQ1 and RQ2 models, we assumed linearity as all predictor variables were categorical. For the RQ3 model, we visually assessed linearity using a scatterplot with loess lines (where the loess line should closely follow the data). For models related to all RQs, equal variances was assessed via partial residual plots (residuals should be evenly spread across the range of fitted values, where the spread should be constant across the range of fitted values), and normality was assessed via a qqplot of the residuals (points should follow along the diagonal line). If assumptions are found to be violated, we will consider either conducting a sensitivity analysis or bootstrapping our model (depending on which assumption(s) are violated).

Throughout the report, effects were considered statistically significant at \(\alpha = .05\).

Act II: Results

Question 2

Attempt to draft a results section based on your detailed analysis strategy and the analysis provided.

Results - What To Include*

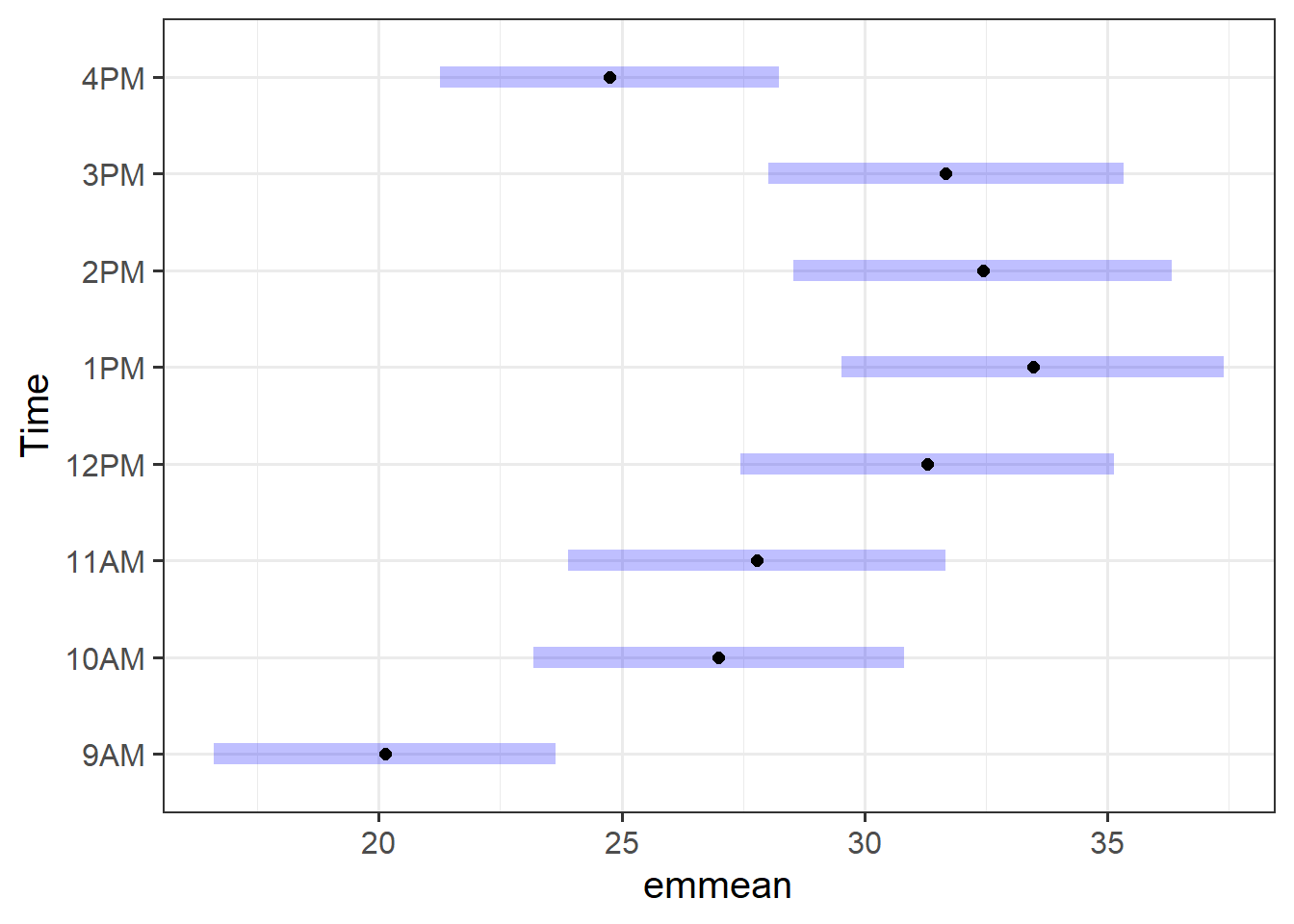
The results section should follow from your analysis strategy. This is where you would present the evidence and results that will be used to answer the research questions and can support your conclusions. Make sure that you address all aspects of the approach you outlined in the analysis strategy (including the evaluation of assumptions and diagnostics).

In this section, it is useful to include tables and/or plots to clearly present your findings to your reader. It is important, however, to carefully select what is the key information that should be presented. You do not want to overload the reader with unnecessary or duplicate information (e.g., do not present print outs of the head of a dataset, or the same information in tables and plots, etc.), and you also want to save space in case there is a page limit. Make use of figures with multiple panels where you can. You can also make use of an Appendix to present your assumption and diagnostic* plots/tables, but remember that you must evaluate these in-text within the results section and clearly refer the reader to the relevant plots within the Appendix.

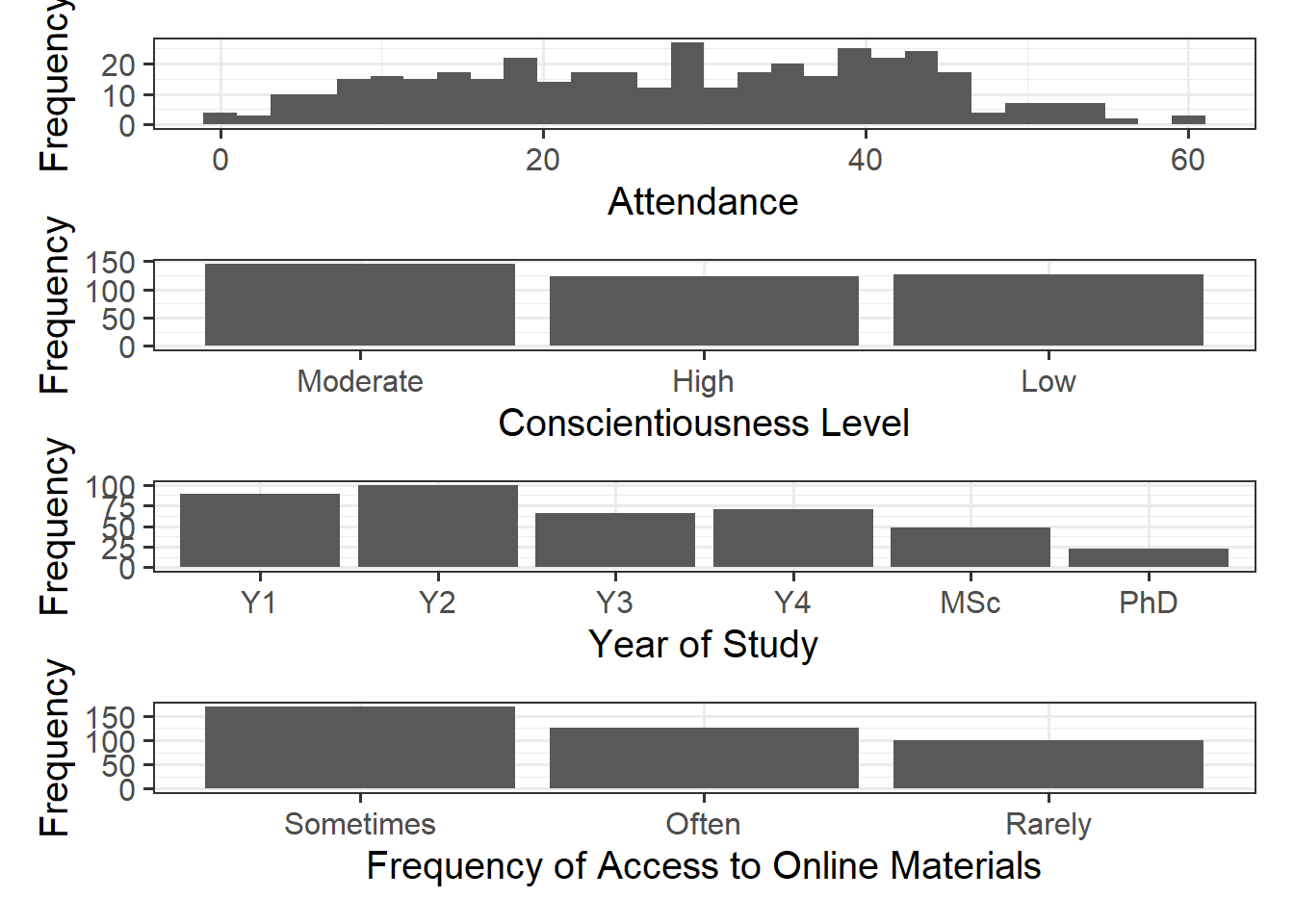
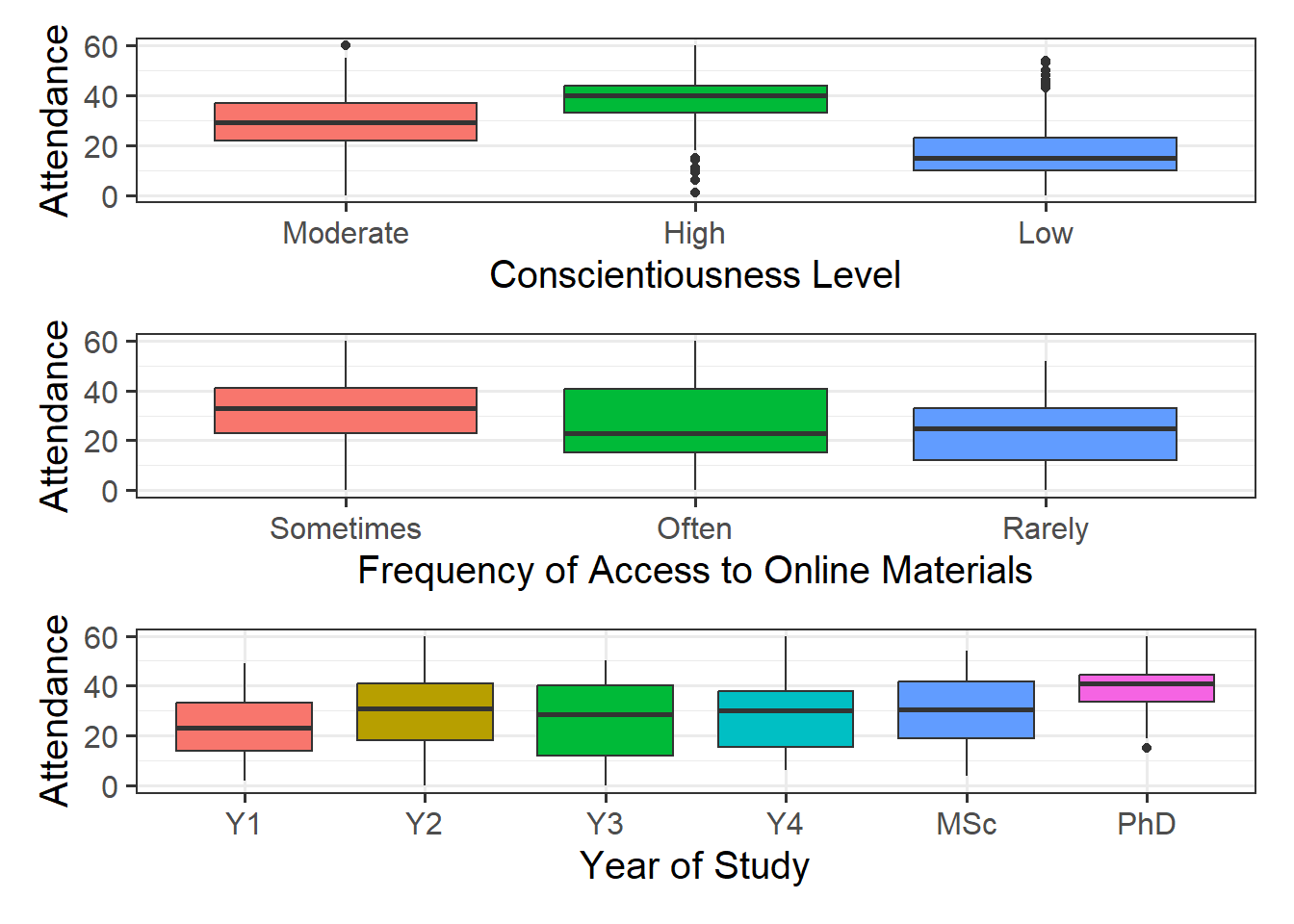
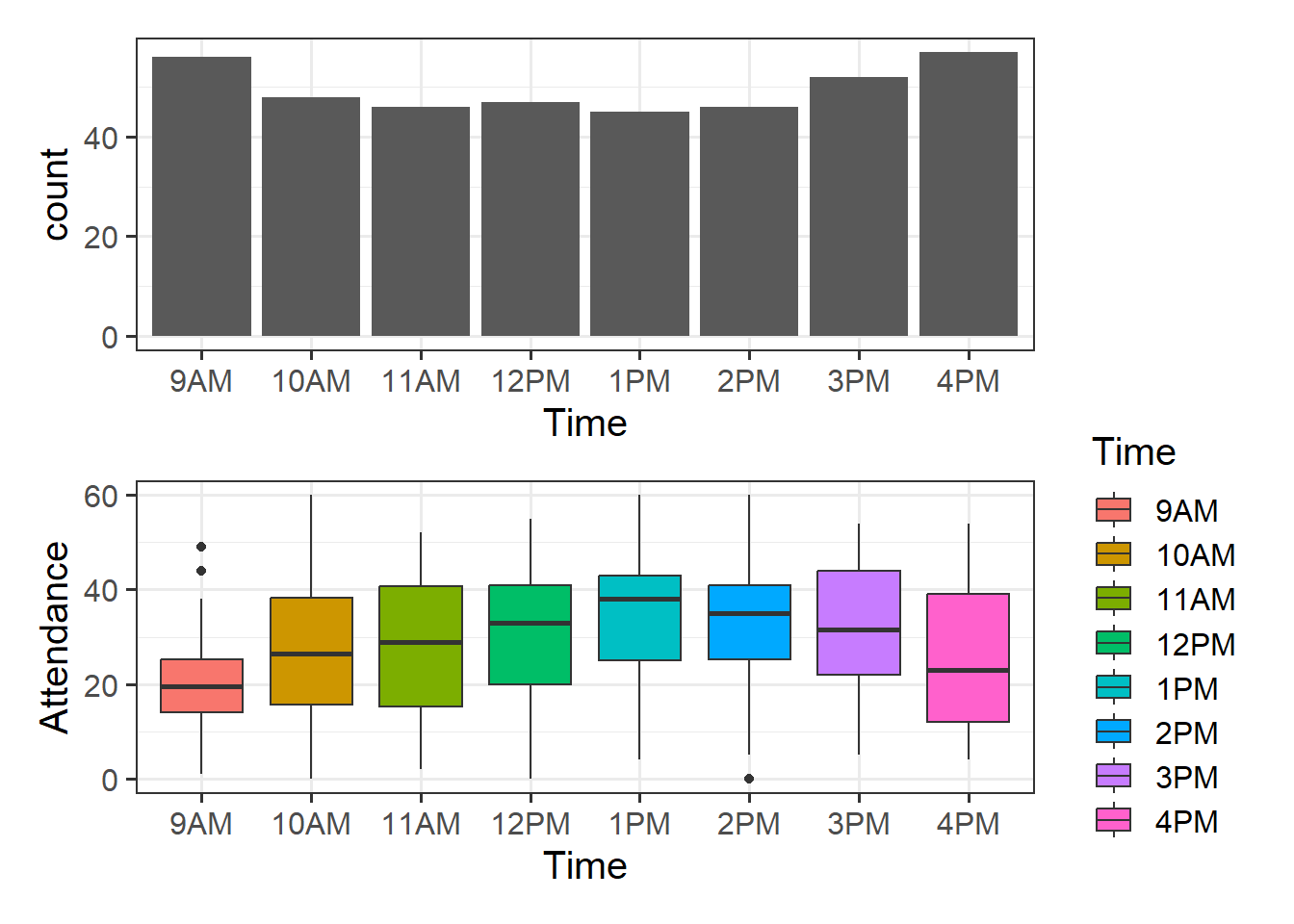
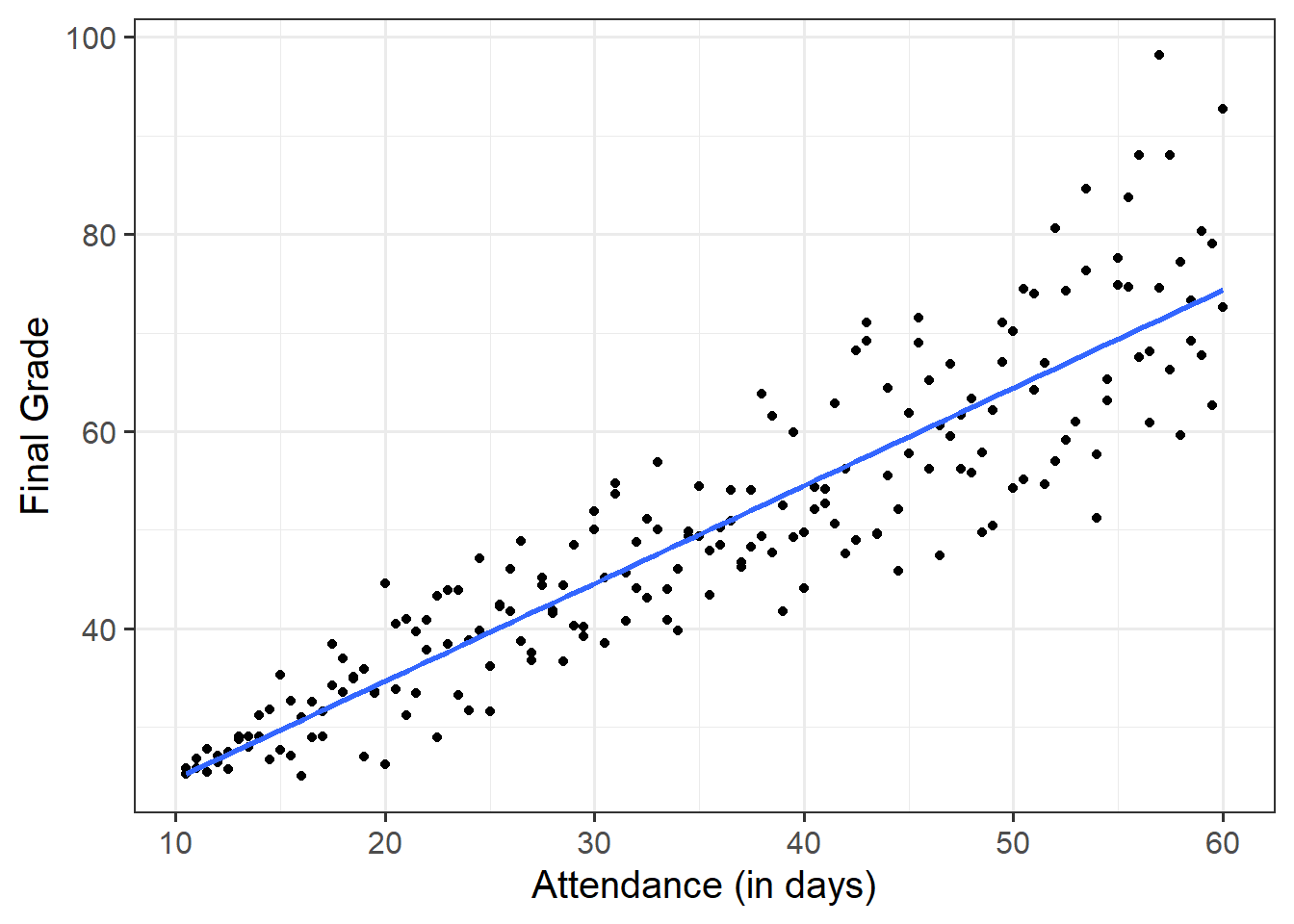
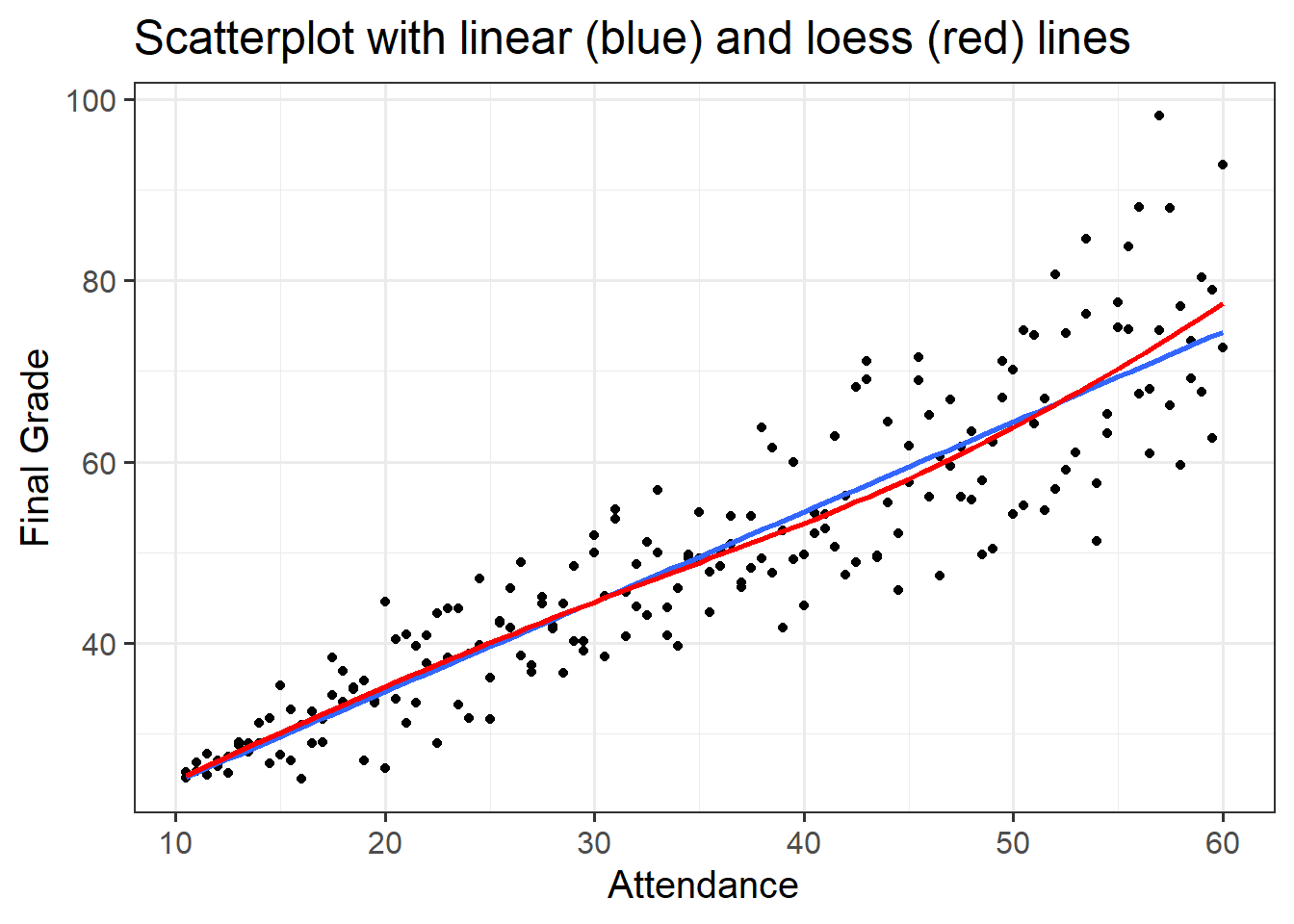
As a broad guideline, you want to start with the results of any exploratory data analysis, presenting tables of summary statistics and exploratory plots. You may also want to visualise associations between/among variables and report covariances or correlations. Then, you should move on to the results from your model.

• Note, given time constraints in lab, we have not included any reference to diagnostic checks in this write-up example - you would be expected to include this in your report. You can find more information on diagnostic checks in the S1 Week 9 Lab and S1 Week 9 Lectures.

Descriptive statistics related to RQ1 are displayed in Table 2.

Table 2: Attendance and Academic Year, Frequency of Online Material Access, Conscientiousness Descriptive Statistics

Attendance and Academic Year, Frequency of Online Material Access, Conscientiousness Descriptive Statistics

Year	OnlineAccess	Conscientiousness	n	Mean	SD	Minimum	Maximum
Y1	Sometimes	Moderate	18	25.33	7.31	14	41
Y1	Sometimes	High	12	27.92	15.41	6	43
Y1	Sometimes	Low	7	19.43	8.98	5	33
Y1	Often	Moderate	12	24.67	7.66	11	36
Y1	Often	High	7	36.29	10.89	21	49
Y1	Often	Low	5	18.60	15.27	7	45
Y1	Rarely	Moderate	7	25.57	11.28	8	40
Y1	Rarely	High	5	31.60	13.52	9	43
Y1	Rarely	Low	16	14.19	10.70	2	42
Y2	Sometimes	Moderate	20	34.00	12.19	5	60
Y2	Sometimes	High	14	41.36	5.17	32	52
Y2	Sometimes	Low	11	21.27	20.51	0	54
Y2	Often	Moderate	13	30.62	11.62	14	51
Y2	Often	High	10	42.80	9.51	24	53
Y2	Often	Low	6	15.33	4.68	10	23
Y2	Rarely	Moderate	8	24.00	6.12	14	31
Y2	Rarely	High	9	31.33	8.87	15	43
Y2	Rarely	Low	9	10.33	5.96	0	18
Y3	Sometimes	Moderate	8	34.62	7.60	27	46
Y3	Sometimes	High	10	38.60	14.01	1	50
Y3	Sometimes	Low	8	20.00	17.03	3	41
Y3	Often	Moderate	3	19.33	19.01	0	38
Y3	Often	High	6	30.17	16.22	9	43
Y3	Often	Low	12	14.83	7.41	8	33
Y3	Rarely	Moderate	7	25.86	8.69	11	39
Y3	Rarely	High	4	35.00	4.40	30	40
Y3	Rarely	Low	8	23.38	14.72	9	46
Y4	Sometimes	Moderate	12	37.25	10.57	22	55
Y4	Sometimes	High	10	38.70	5.19	30	45
Y4	Sometimes	Low	9	23.78	10.23	11	38
Y4	Often	Moderate	8	21.62	12.65	9	42
Y4	Often	High	7	34.57	16.21	11	60
Y4	Often	Low	12	17.75	14.59	6	48
Y4	Rarely	Moderate	5	29.00	11.55	9	38
Y4	Rarely	High	4	34.75	12.84	22	52
Y4	Rarely	Low	4	13.50	5.97	6	20
MSc	Sometimes	Moderate	5	34.80	11.78	25	53
MSc	Sometimes	High	8	42.00	6.99	31	51
MSc	Sometimes	Low	8	19.12	9.39	8	38
MSc	Often	Moderate	5	22.00	13.34	9	44
MSc	Often	High	8	43.00	5.81	37	54
MSc	Often	Low	5	19.20	1.92	16	21
MSc	Rarely	Moderate	4	31.00	12.83	16	44
MSc	Rarely	High	2	45.00	5.66	41	49
MSc	Rarely	Low	3	12.67	9.61	4	23
PhD	Sometimes	Moderate	4	38.50	9.11	25	44
PhD	Sometimes	High	4	42.75	3.50	39	47
PhD	Sometimes	Low	2	47.00	4.24	44	50
PhD	Often	Moderate	3	39.00	19.31	22	60
PhD	Often	High	2	48.00	4.24	45	51
PhD	Often	Low	2	34.50	27.58	15	54
PhD	Rarely	Moderate	4	34.25	7.14	24	40
PhD	Rarely	High	2	25.50	9.19	19	32

In relation to RQ1, full regression results, including 95% Confidence Intervals, are shown in Table 3.

Table 3: RQ1 - Regression Table for Attendance Model

RQ1: Regression Table for Attendance Model

	Attendance
Predictors	Estimates	CI	p
Intercept	27.87	24.86 – 30.89	<0.001
Conscientiousness - High	7.37	4.63 – 10.10	<0.001
Conscientiousness - Low	-10.29	-13.04 – -7.54	<0.001
Online Access - Often	-3.53	-6.16 – -0.90	0.009
Online Access - Rarely	-5.38	-8.21 – -2.54	<0.001
UG Y2	4.57	1.32 – 7.83	0.006
UG Y3	3.42	-0.23 – 7.06	0.066
UG Y4	4.27	0.69 – 7.84	0.019
MSc	5.65	1.63 – 9.67	0.006
PhD	12.48	7.25 – 17.72	<0.001
Observations	397
R2 / R2 adjusted	0.357 / 0.342

The model met assumptions of normality (see Appendix A Figure 4; the QQplot showed some deviation from the diagonal line at the tails, but this was not of concern) and equal variances (there was a constant spread of residuals; see Appendix A Figure 5).

The overall model was significant, \(F(9, 387) = 23.91, p < .001\). Conscientiousness, frequency of online access, and year in university explained approximately 34% of the variance in attendance. Both those with high and low levels of conscientiousness exhibited attendance rates that were significantly different than those with moderate levels of conscientiousness (see Figure 1(a)), when controlling for year of study and online access. Specifically, those with high levels of conscientiousness attended class significantly more often than those with moderate levels \((\beta = 7.37,~ SE = 1.39,~ t = 5.29,~ p < .001)\). Conversely, in comparison to those with moderate levels of conscientiousness, those with low levels attended class significantly less \((\beta = -10.29,~ SE = 1.4,~ t = -7.36,~ p < .001\)). Both those who rarely \((\beta = -5.38,~ SE = 1.44,~ t = -3.73,~ p < .001)\) or often \((\beta = -3.53,~ SE = 1.34,~ t = -2.64,~ p = .009)\) accessed online materials had significantly lower attendance rates than those who accessed only sometimes regardless of Conscientiousness levels and year of study (see Figure 1(b)). Holding constant conscientiousness and frequency of online access to materials, all years of study, with the exception of Y3, had significantly higher attendance rates than those in Y1 (see Figure 1(c)).

Figure 1: Association between Attendance and (a) Conscientiousness (b) Online Access (c) Year of Study

Descriptive statistics related to RQ2 are displayed in Table 4.

Table 4: Attendance & Class Time Descriptive Statistics

Attendance & Class Time Descriptive Statistics

Time	n	Mean	SD	Minimum	Maximum
9AM	56	20.12	10.08	1	49
10AM	48	27.00	14.23	0	60
11AM	46	27.78	14.57	2	52
12PM	47	31.30	14.11	0	55
1PM	45	33.47	14.44	4	60
2PM	46	32.43	12.44	0	60
3PM	52	31.67	13.58	5	54
4PM	57	24.75	13.78	4	54

To determine whether there was a difference in attendance between those with early/late classes in comparison to those with midday classes, we performed a test against \(H_0: \frac{1}{4}(\mu_1+\mu_2+\mu_7+\mu_8) -\frac{1}{4}(\mu_3+\mu_4+\mu_5+\mu_6) = 0\). The model met the assumptions of normality (there was no extreme deviation from the diagonal line; see Appendix B Figure 6) and equal variances (there was a constant spread of residuals; see Appendix B Figure 7).

At the 5% significance level, there was evidence that class attendance did significantly differ between those who had early/late classes and those who had classes in the middle of the day \((t(389) = 3.96,~ p < .001, \text{two-sided})\), where students with midday classes attended, on average, 5.36 \((SE = 1.35)\) more classes (see Figure 2). We are 95% confident that those who had midday classes attended approximately 2-8 classes more than those who had classes in the morning or late afternoon (\(CI_{95}[2.70, 8.01]\)).

Figure 2: Estimated Attendance Means by Year of Study

In relation to RQ3, there was a strong positive correlation between attendance and marks \((r_{(Attendance,~Grade)} = .91)\). Our fitted model failed to satisfy all regression assumptions (see Appendix C). Although our model met the linearity (though there was a slight curve in the loess line; see Appendix C Figure 8), and normality of residuals assumptions (there was a slight skew, but not of concern; see Appendix C Figure 9), the assumption of equal variances was violated as the spread of residuals was not constant and suggested that there was evidence of heteroscedasticity (see Appendix C Figure 10). Therefore, since we could not trust that the SEs in our model results were reliable, we bootstrapped. Results suggested that there was a significant positive association between marks and attendance (see Figure 3). Specifically, we are 95% confident that for every day one attends class, their final mark will increase, on average, between 0.93 and 1.07 points. As the 95% CI did not contain zero, we rejected the null hypothesis as there was evidence of a significant association between student’ attendance and their final marks.

Figure 3: Association between Final Grades and Attendance

Act III: Discussion

Question 3

Attempt to draft a discussion section based on your results and the analysis provided.

Discussion - What To Include

In the discussion section, you should summarise the key findings from the results section and provide the reader with a few take-home sentences drawing the analysis together and relating it back to the original question.

The discussion should be relatively brief, and should not include any statistical analysis - instead think of the discussion as a conclusion, providing an answer to the research question(s).

Previous research had identified strong associations between attendance and both class grades and GPA, as well as associations between class attendance and a variety of student characteristics. In the first part of our analysis, we examined the associations of attendance with (1) conscientiousness, frequency of access to online materials, and year of study; and (2) class time. In the second part of our analysis, we examined the association between final grade and attendance.

Our results suggested that: (1) level of conscientiousness, frequency of access to online materials, and year of study were all significant predictors of attendance. Specifically, higher conscientiousness and more advanced year of study were associated with higher attendance rates. In relation to online materials, it appeared that an over-reliance or lack of use was negatively associated with attendance - those who accessed regularly had the best attendance rates. (2) there were differences in attendance depending upon class time, where students with classes in the middle of the day were more likely to attend than those who had classes either early in the morning or later in the afternoon. (3) attendance was a significant predictor of final marks, where higher attendance was associated with higher grades. Therefore, we rejected the null hypotheses for each of our research questions.

Assumptions & Diagnostics Appendix

Question 4

Given that the report should be kept as concise as possible, you may wish to utilize the appendix to present assumption and diagnostic plots. You must however ensure that you have:

• Described what assumptions you will check in the analysis strategy, including how you will evaluate them.
• Summarized the evaluations of your assumptions and diagnostic checks in the results section of the main report.
• Accurately referred to the figures and tables labels presented in the appendix in the main report (if you don’t refer to them, the reader won’t know what they are relevant to!).

Appendix A

Figure 4: Normality Assumption Check for m1

Figure 5: Equal Variances Assumption Check for m1

Appendix B

Figure 6: Normality Assumption Check for m2

Figure 7: Equal Variances Assumption Check for m2

Appendix C

Figure 8: Linearity Assumption Check for m3

Figure 9: Normality Assumption Check for m3

Figure 10: Equal Variances Assumption Check for m3

Section B: Block 2 (Weeks 7 - 11) Recap

In the second part of the lab, there is no new content - the purpose of the recap section is for you to revisit and revise the concepts you have learned over the last 4 weeks (or the full semester if you feel that it would be beneficial to revise the materials from block 1).

We would encourage you to complete any outstanding work on these exercises (e.g., complete partial write-ups), and review solutions. Doing so will allow you to have good quality materials to refer to during the assessed report (released in Semester 2).

Given that we are now \(\frac{1}{2}\) of the way through the DAPR2 course, we would also strongly encourage you to start creating your revision materials in advance of the exam. You can access all the flashcards that you’ve been presented with in this block here. These will provide a good starting point for collating your notes together on the contents of blocks 1 & 2. We also suggest that you review your weekly quiz feedback (as many of you have learned in Psychology 2A, it is important to provide feedback to allow learners to improve their learning and retention of information, as well as correct any misunderstandings!).