Week 10 Exercises: Logistic Regression

Odd Probability

Question 1

The probability of a coin landing on heads if 0.5, or 50%. What are the odds, and what are the log-odds?
Last year’s Tour de France winner, Tadej Pogacar, was given odds of 11 to 4 by a popular gambling site (i.e., if we could run the race over and over again, for every 4 he won he would lose 11). Translate this into the implied probability of him winning.

Hints:

$odds = \frac{p}{1-p}$
See 10A#introducing-the-glm

Drunkdoor

Research Questions Is susceptibility to change blindness influenced by level of alcohol intoxication and perceptual load?

Method Researchers conducted a study in which they approached 120 people, recruited from within the vicinity of a number of establishments with licenses to sell alcohol to be consumed on-premises. Initially, experimenter A approached participants and asked if they were interested in participating in a short study, and obtained their written consent. While experimenter A subsequently talked each participant through a set of questions on multiple pieces of paper (with the pretense of explaining what the participant was required to do), experimenters B and C carrying a door passed between the participant and experimenter A, with experimenter C replacing A (as can be viewed in the video below).

Simons, D. J., & Levin, D. T. (1997). Change blindness. Trends in cognitive sciences, 1(7), 261-267.

The perceptual load of the experiment was manipulated via a) the presentation of the door and b) the papers held by the experimenters. For 60 of these participants, the door was painted with some detailed graffiti and had a variety of pieces of paper and notices attached to the side facing the participants. Additionally, for these participants, the experimenters handled a disorganised pile of 30 papers, with the top pages covered in drawings around the printed text. For the remaining 60, the door was a standard MDF construction painted a neutral grey, and the experimenters handled only 2 sheets of paper which had minimal printed text on them and nothing else.

Measures
After experimenters A and C had successfully swapped positions, the participant was asked (now by C) to complete small number of questions taking approximately 1 minute. Either after this set of questions, or if the participant made an indication that they had noticed the swap, the experimenters regrouped and the participant was explicitly asked whether they had noticed the swap.
Immediately after this, participants were breathalysed, and their blood alcohol content was recorded. In addition, participants’ age was recorded, as previous research suggests that change-blindness increases with age.

Data

The data can be downloaded from https://uoepsy.github.io/data/drunkdoor.csv.
A description of the variables included is presented below.

variable	description
id	Unique ID number
bac	Blood Alcohol Content (BAC), A BAC of 0.0 is sober, while in the United States 0.08 is legally intoxicated, and above that is very impaired. BAC levels above 0.40 are potentially fatal.
age	Age (in years)
condition	Condition - Perceptual load created by distracting oject (door) and details and amount of papers handled in front of participant (Low vs High)
notice	Whether or not the participant noticed the swap (Yes = 1 vs No = 0)

Age effects

Question 2

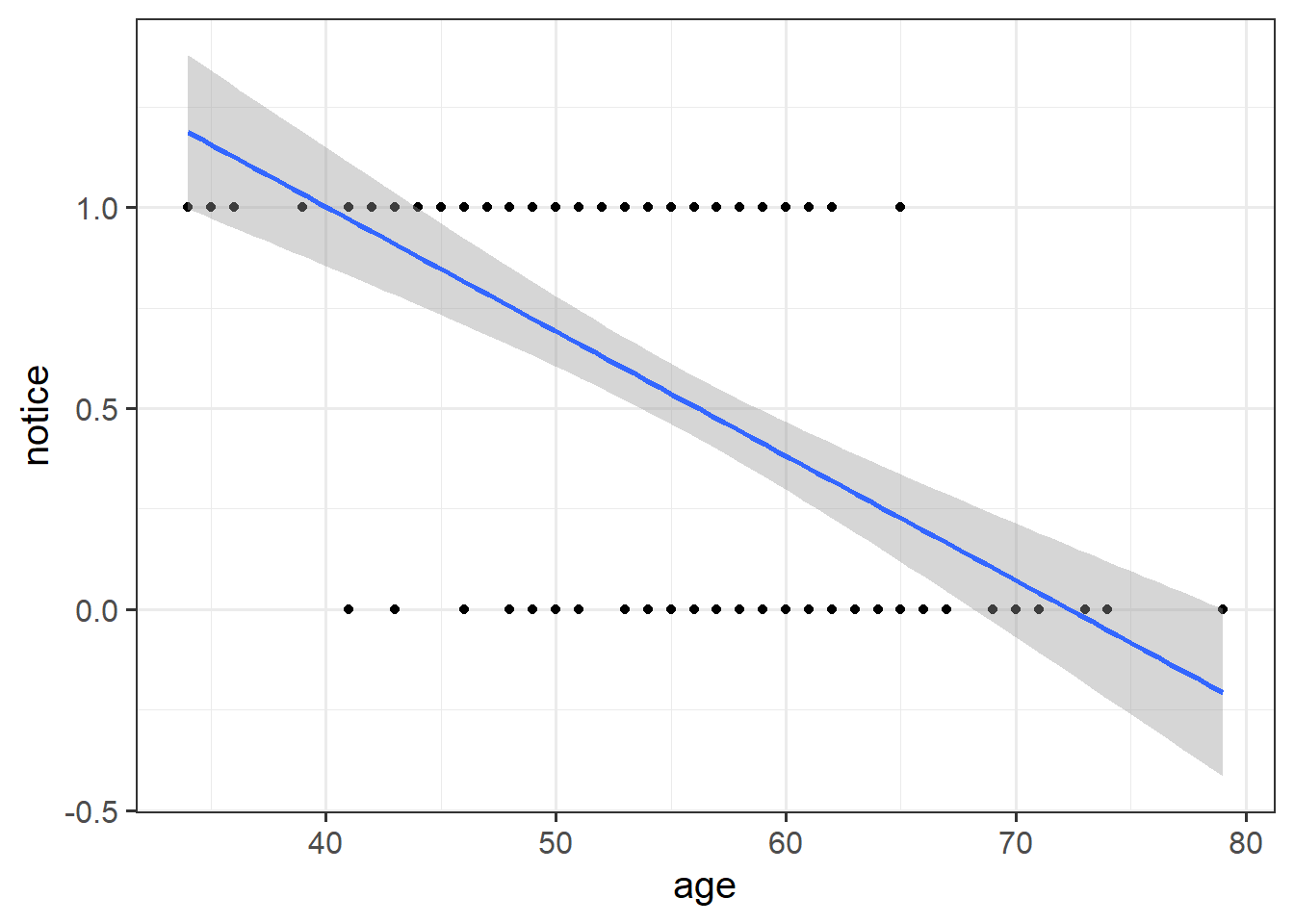
To begin with, we’re going to ignore the research question, and just look at the relationship between age and whether or not participants noticed the person-switch.

Make a scatterplot of this relationship, and add to the plot geom_smooth(method="lm"). This will plot the regression line for a simple model of lm(notice ~ age).

Hint: It won’t look very nice!

Question 3

Just visually following the line from the plot produced in the previous question, what do you think the predicted model value would be for someone who is aged 30?
What does this value mean?

Hint: There’s not really an answer to this.

Question 4

Fit a logistic regression model investigating whether participants’ age predicts the log-odds of noticing the person they are talking to being switched out mid-conversation. Look at the summary() output of your model.

Hints:

To fit a logistic regression model, we need to useglm(), a slightly more general form of lm().
The syntax is pretty much the same, but we need to add in a family at the end, to tell it that we are doing a binomial¹ logistic regression.
See 10A#fitting-glm-in-r

Question 5

Based on your model output, complete the following sentence:

“Being 1 year older decreases _________ by 0.18.”

Hint: on what scale (probability, odds, log-odds) are we modelling linear associations?

Question 6

To get this association into something that is (slightly) more easy to understand, exponentiate the coefficients from your model in order to translate them back from log-odds in to “odds ratios”. Provide an interpretation of what the resulting estimates mean.

Hints:

The opposite of the natural logarithm log() is the exponential exp().
See 10A#interpretation-of-coefficients

Question 7

Based on your answer to the previous question, calculate the odds of noticing the swap for a one year-old (for now, forget about the fact that this experiment wouldn’t work on a 1 year old!)
And what about for a 40 year old?

Can you translate the odds back in to probabilities?

Question 8

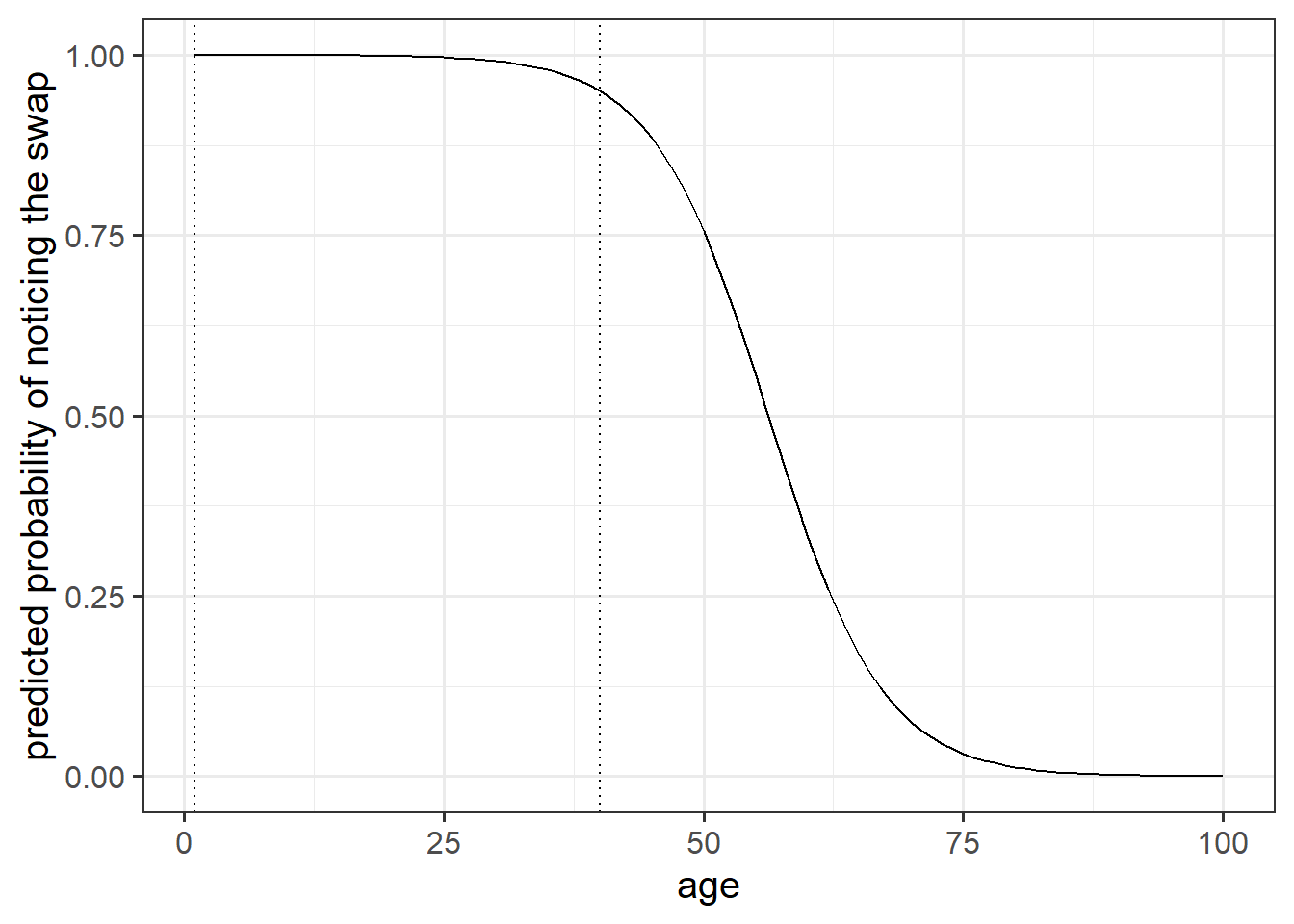
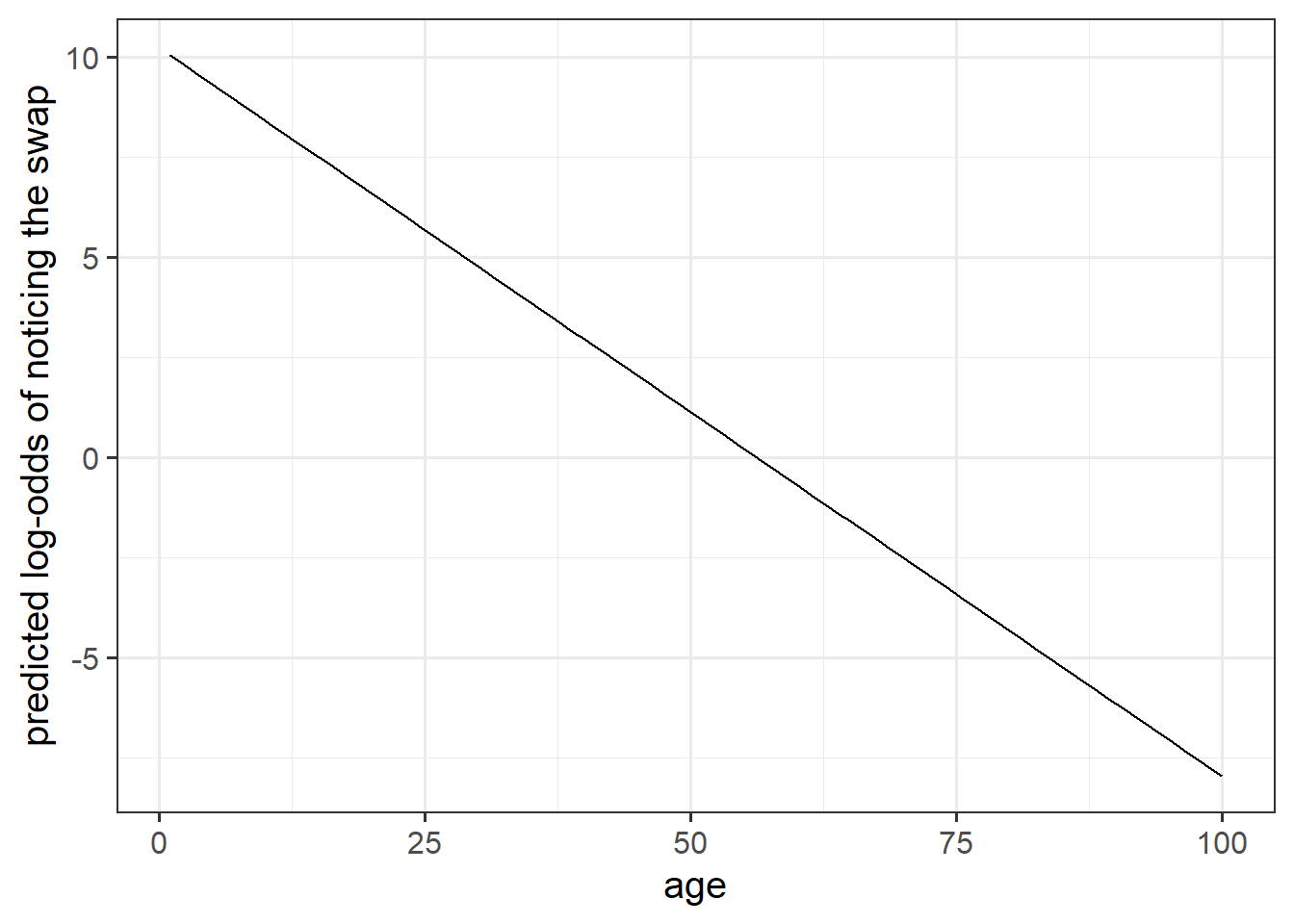
It’s possible to calculate predicted probabilities for a specific value of the predictor(s), but what would be nice is to see how the probability of noticing the swap changes with age.

The code below creates a dataframe with the variable age in it, which has the values 1 to 100. Can you use this object and the predict() function, along with your model, to calculate the predicted probabilities of the outcome (noticing the swap) for each year of age from 1 to 100?
Can you then plot this?

ages100 <- tibble(age = 1:100)

Hints:

predict(model, newdata = ???)
try seeing what happens to the plot when you change between:
- predict(model, newdata = ???, type = "link")
- predict(model, newdata = ???, type = "response")
10A#visualising

Tackling the research question

Question 9

Recall our research question, which we will now turn to:

Research Questions Is susceptibility to change blindness influenced by level of alcohol intoxication and perceptual load?

Try and make a mental list of the different relationships between variables that this question invokes, can you identify one variable as the ‘outcome’ or ‘response’ variable? (it often helps to think about the implicit direction of the relationship in the question)

In addition, are there known things that it might be useful to account for, so that you capture associations that are independent from differences due to these things (hint hint, what have you just been looking at?).

Question 10

Think about our outcome variable and how it is measured. What type of data is it? Numeric? Categorical?

What type of distribution does it follow? For instance, do values vary around a central point, or fall into one of various categories, or follow the count of successes in a number of trials?

Question 11

Think about our explanatory variable(s). Is there more than one? What type of variables are they? Do we want to model these together? Might they be correlated?

Solution

We know that drunkdoor$bac is simply the observed blood alcohol level (BAC). This is technically measured as a proportion, but for the current purposes we can just treat it as any other numeric scale. However, we might consider scaling the variable so that instead of the coefficient representing the change when moving from 0% to 1% BAC (1% blood alcohol is fatal!), we might want to have the change associated with 0% to 0.01% BAC (i.e, a we want to talk about effects in terms of changing 1/100th of a percentage of BAC).

The drunkdoor$condition variable is an experimental manipulation. That is, the researchers had control over what observations fell into which group. We wouldn’t therefore expect any correlation between this and the bac variable (unless researchers did not allocate participants to conditions randomly).

As we’ve talked about already, we have the idea based on previous research that change-blindness appears to vary depending upon age. From the earlier exercises here we have some evidence to corroborate this. We may therefore want to include this in our model. If we don’t, any results might simply be due to, e.g. older people tending to be more highly intoxicated (and so we see an effects of alcohol that might actually be simply the effect of age).

We might also think about any other possible variables which might influence our results, even if we didn’t measure them. This sort of thinking becomes important in the discussion section.

John Stuart Mill - Three Criteria for Causality
To varying extents, all of these criteria can be incredibly difficult to satisfy. Criteria 3 especially is one of the things that makes scientific investigation so interesting.

The cause precedes the effect
The cause is demonstrably related to the effect
There are no plausible alternative explanations

Mill, J. S. (1869). A System of Logic, Ratiocinative and Inductive: Being a Connected View of the Principles of Evidence and the Methods of Scientific Investigation. Harper and brothers.

Question 12

Write a sentence describing the model you will fit. It might help to also describe each variable as you introduce it.
Fit the model.

Hints:

Think of this as writing out the R code but in words.
For instance: glm(outcome ~ predictor1 + predictor2 + Predictor1:Predictor2, family = binomial) might be described as “Outcome (binary,”Level 1” vs “Level 2”) was modelled using logistic regression, predicted by Predictor1, Predictor2 and their interaction”

Do you want BAC on the current scale, or could you transform it somehow?
Is condition a factor? What is your reference level? Have you checked contrasts(drunkdoor$condition)? (Remember that this will only work if you make it a factor first)

Whether or not participants noticed the swap mid-conversation (binary 0 vs 1) is modelled using logistic regression, with blood alcohol content (measured in 100th of percentages blood content) and perceptual load condition (low load vs high load, with low as the reference level) and age (in years, mean centered).

In the sentence above, I stated that I want blood alcohol in terms of 100ths of percentages, rather than percentages. And I want age centered on the mean (this won’t change anything other than the intercept).

drunkdoor <- drunkdoor %>% 
  mutate(
    bac100 = bac*100,
    ageC = age - mean(age)
  )

I also stated that the low-load will be the reference level.
Currently it will be the other way around, because “high” comes before “low” in the alphabet. I can change it:

# make it a factor and give it the levels in the right order
# note this requires getting the levels named exactly as they appear in the variable. 
# if we use lowercase "low", then every "Low" in the variable will turn to NA
drunkdoor$condition <- factor(drunkdoor$condition, levels = c("Low","High"))
# check the contrasts
contrasts(drunkdoor$condition)

     High
Low     0
High    1

Finally, let’s fit our model!

changeblind_model <- glm(notice ~ ageC + bac100 + condition, data = drunkdoor, family = "binomial")
summary(changeblind_model)


Call:
glm(formula = notice ~ ageC + bac100 + condition, family = "binomial", 
    data = drunkdoor)

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -0.51577    0.53536  -0.963  0.33534    
ageC          -0.22584    0.04214  -5.359 8.35e-08 ***
bac100         0.35002    0.11128   3.145  0.00166 ** 
conditionHigh -1.59215    0.54008  -2.948  0.00320 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 166.06  on 119  degrees of freedom
Residual deviance: 100.99  on 116  degrees of freedom
AIC: 108.99

Number of Fisher Scoring iterations: 5

Question 13

Compute 95% confidence intervals for the log-odds coefficients using confint(). Wrap the whole thing in exp() in order to convert all these back into odds and odds-ratios.

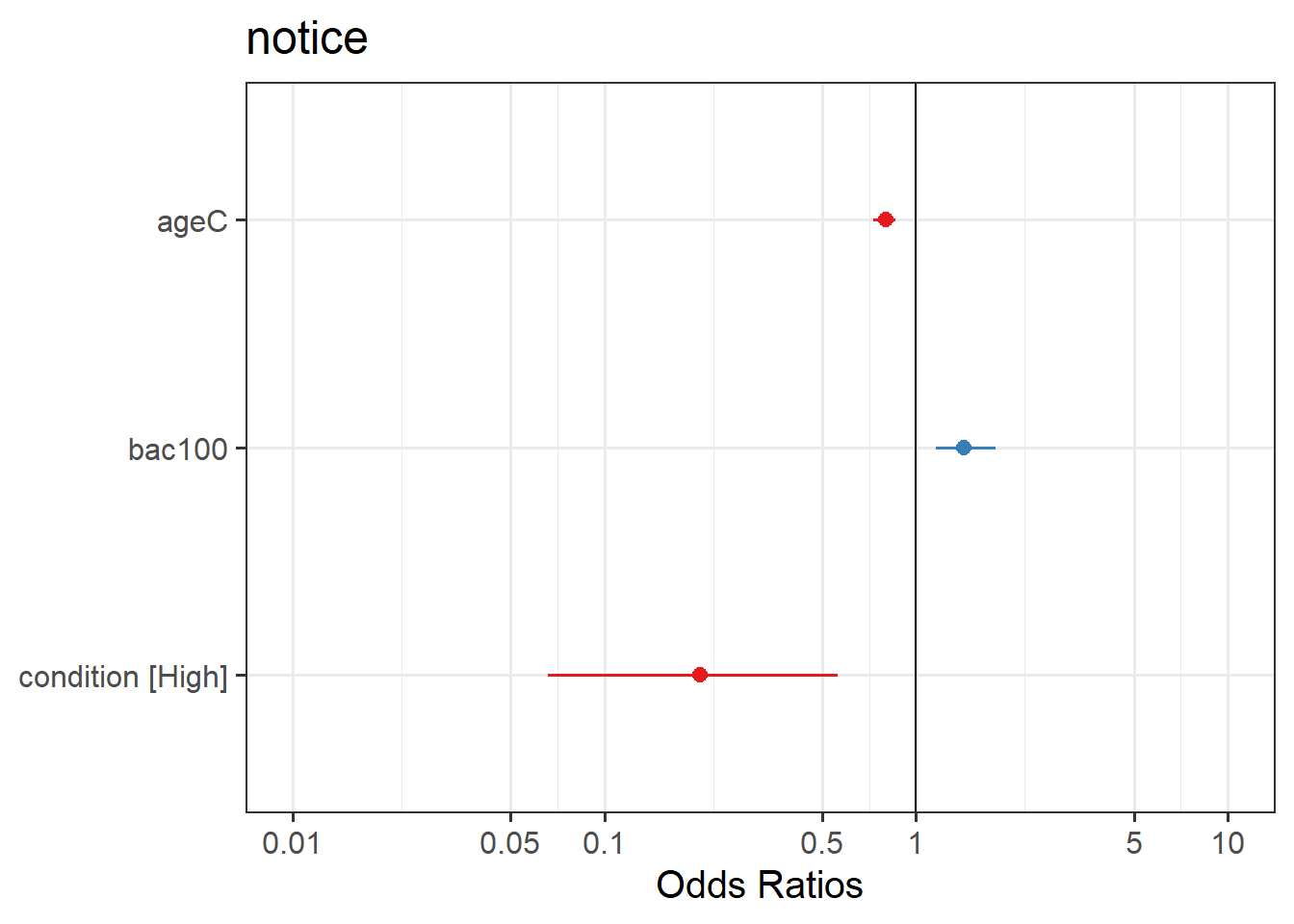
Try the sjPlot package and using tab_model(model) and plot_model(model, type = "est") on your model. What do you get?

Question 14

Write up the results of the study.

Hints:

Often when reporting odds ratios, it’s easiest to interpret them as simply “increased odds of (OR = <??> [95% CI: , ])”. This saves a bit of hassle too! &#128516

Dog people/Cat people

USMR 2022 Data

The data from the USMR 2022 survey (now closed) can be found at https://uoepsy.github.io/data/usmr2022.csv.

note, this is the survey data just from USMR this year, not other students on other courses or in previous years

Question 15

People often talk about personality differences between “cat people” and “dog people” (e.g. if you’re more introverted then you’re more likely to be a cat person).
In our survey, we forced you to choose between “cat” and “dog”, and we also measured a bunch of personality traits from a set of 50 questions (these were aggregated up into scores for ‘extraversion’, ‘conscientiousness’, and so on).

Fit a model that tries to predict whether someone is a cat- or dog- person, based on aspects of their personality.

Hints:

your outcome variable is currently not 0 and 1, but “cat” and “dog”. Remember how R prefers to think of categories - as factors.

Using GLM to classify

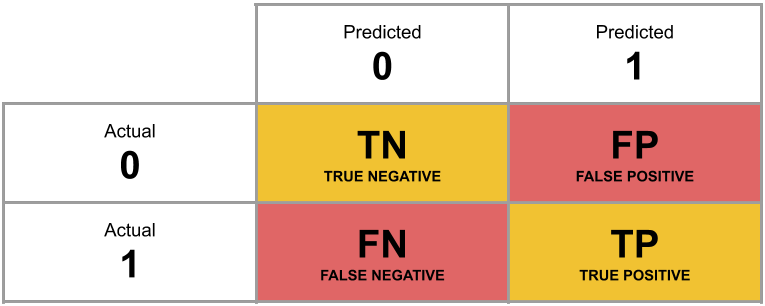
A table of predicted outcome vs observed outcome sometimes gets referred to as a confusion matrix, and we can think of the different cells in general terms (Figure 1).
Another way to think about how our model is fitted is that it aims to maximise (TP + TN)/n, or, put another way, to minimise (FP+FN)/n. Which is equivalent to the good old idea of minimising sums of squares (where we minimise the extend to which the predicted values differ from the observed values).

Question 16

Add new column to the survey dataset which contains the predicted probability of being a cat/dog person for each observation.
Then, using ifelse(), add another column which is these predicted probabilities translated into the predicted binary outcome (0 or 1) based on whether the probability is greater than >.5.
Create a two-way contingency table of the predicted outcome and the observed outcome.
What proportion of observations are correctly predicted?

Hint:

you don’t need the newdata argument for predict() if you want to use the original data the model was fitted on.
if there are NAs in any of the variables in your model (predictors or outcome), then the number of rows in your data will be greater than the number of model predictions.
- if you want a handy function which might help with this, check out what the broom package has to offer. What does augment(model, type.predict = "response") do?

if we just try to add the predictions to the data, we get an error:

usmr %>%
  mutate(
    predprobs = predict(catdogmod)
  )

Error in `mutate()`:
ℹ In argument: `predprobs = predict(catdogmod)`.
Caused by error:
! `predprobs` must be size 80 or 1, not 79.

We could try making our dataset “complete cases” (remove all rows with any missingness), and then refit our model, and then the data and the model would all be the same number of observations.

However, the broom package has a really useful function which will bring us back the data that was fed into the model (i.e. excluding the NAs), and lots of information about the model fit itself such as predictions (.fitted column), residuals, and leverage etc.

library(broom)
augment(catdogmod, type.predict = "response")

# A tibble: 79 × 13
   .rownames catdog extraversion agreeableness conscientiousness emot_stability
   <chr>     <fct>         <dbl>         <dbl>             <dbl>          <dbl>
 1 1         dog              30            42                33             30
 2 2         dog              34            39                36             31
 3 3         cat              22            44                29             27
 4 4         cat              23            40                35             20
 5 5         dog              16            36                31             27
 6 6         dog              34            44                42             37
 7 7         cat              32            43                32             24
 8 8         dog              32            35                43             16
 9 9         cat              31            42                42             20
10 10        cat              31            43                39             36
# ℹ 69 more rows
# ℹ 7 more variables: imagination <dbl>, .fitted <dbl>, .resid <dbl>,
#   .hat <dbl>, .sigma <dbl>, .cooksd <dbl>, .std.resid <dbl>

So we can use this to get out the observed and the predicted!

augment(catdogmod, type.predict = "response") %>%
  mutate(
    prediction = ifelse(.fitted >.5, "pred_dog", "pred_cat")
  ) %>%
  select(catdog, prediction) %>%
  table() %>% prop.table

      prediction
catdog  pred_cat  pred_dog
   cat 0.2405063 0.2151899
   dog 0.1392405 0.4050633

So 19 cat people are predicted as cat people, and 32 dog people are predicted as dog people. But 17 cat people are predicted as dog-people, and 11 dog people are predicted to be cat people.

\[ \frac{19+32}{19+32+17+11} = \frac{51}{79} = 0.65 \]

65% of observations are correctly predicted by our model.

Optional Extra: Red and White

Question 16

People are a lot more difficult to predict than something like, say, the colour of different wines.

You can download a dataset of 6497 different wines (1599 red, 4898 white) from https://uoepsy.github.io/data/usmr_wines.csv.

It contains information on various physiochemical properties such as pH, a measure of level of sulphates, residual sugar, citric acid, volatile acidity and alcohol content, and also quality ratings from a sommelier (wine expert). All the wines are vinho verde from Portugal, and the data was collected between 2004 and 2007.

Build a model that predicts the colour of wine based on all available information.
How accurately can it predict wine colours?

Hints:

glm(outcome ~ ., data = mydata) is a shorthand way of putting all variables in the data in as predictors.
Generally speaking, this question doesn’t reflect how we do research in psychology. Ideally, we would have a theoretical question that motivates the inclusion (and testing of) specific predictors.

Footnotes

In this case it happens to be the special case of a binomial where $n=1$, which sometimes gets referred to as ‘binary logistic regression’↩︎

	notice
Predictors	Odds Ratios	CI	p
(Intercept)	0.60	0.20 – 1.69	0.335
ageC	0.80	0.73 – 0.86	<0.001
bac100	1.42	1.15 – 1.79	0.002
condition [High]	0.20	0.07 – 0.56	0.003
Observations	120
R² Tjur	0.475