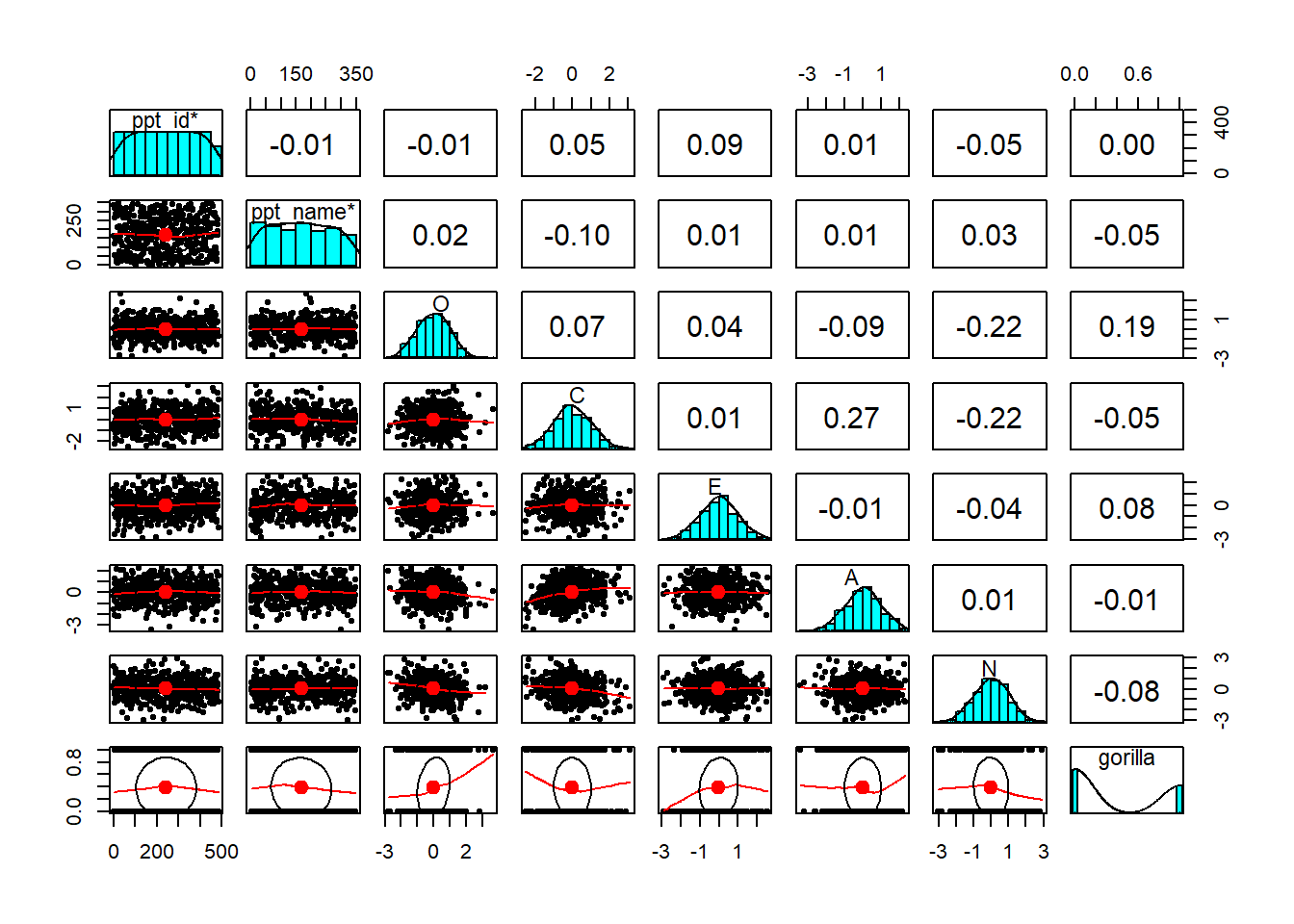
| variable | description |
|---|---|
| ppt_id | Participant ID number |
| ppt_name | Participant Name (if recorded) |
| O | Openness (Z-scored) |
| C | Conscientiousness (Z-scored) |
| E | Extraversion (Z-scored) |
| A | Agreeableness (Z-scored) |
| N | Neuroticism (Z-scored) |
| gorilla | Whether or not participants noticed the gorilla (0 = did not notice, 1 = did notice) |
Exercises: GLM
Before doing anything else, watch this video, and try to count exactly how many times the players wearing white pass the basketball.
Invisible Gorillas
Data: invisibleg.csv
The data here come from a study of 483 participants who completed a Big 5 Personality Inventory (providing standardised scores on 5 personality traits of Openness, Conscientiousness, Extraversion, Agreeableness and Neuroticism), and then completed the selective attention task as seen above, from Simons & Chabris 1999.
We’re interested in whether and how individual differences in personality are associated with susceptibility to inattentional blindness (i.e. not noticing the gorilla).
The data are available at https://uoepsy.github.io/data/invisibleg.csv.
Read in the data, have a look around, plot, describe, and generally explore.
Do any cleaning that you think might be necessary.
There’s nothing new to any of the data cleaning that needs done here. We can do everything that needs doing by using something like ifelse().
Here is an “intercept-only” model of the binary outcome ‘did they notice the gorilla or not’:
glm(gorilla ~ 1, data = invis, family=binomial) |>
summary()...
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.45640 0.09397 -4.857 1.19e-06 ***- Convert the intercept estimate from log-odds into odds
- Convert those odds into probability
- What does that probability represent?
- hint: in
lm(y~1)the intercept is the same asmean(y)
- hint: in
Does personality (i.e. all our measured personality traits collectively) predict inattentional blindness?
We’re wanting to test the influence of a set of predictors here. Sounds like a job for model comparison! (see 10A #comparing-models).
BUT WAIT… we might have some missing data…
(this depends on whether, during your data cleaning, you a) replaced values of -99 with NA, or b) removed those entire rows from the data).
Models like lm() and glm() will exclude any observation (the entire row) if it has a missing value for any variable in the model (outcome or predictor). As we have missing data on the N variable, then when we put that in as a predictor, those rows are omitted from the model.
So we’ll need to ensure that both models that we are comparing are fitted to exactly the same set of observations.
How are different aspects of personality associated with inattentional blindness?
The interpretation of logistic regression coefficients is explained in 10A #coefficient-interpretation.
You might want to explain the key finding(s) in terms of odds ratios.
Compute confidence intervals for your odds ratios.
We haven’t been using confidence intervals very much, but we very easily could have been. Functions like t.test(), cor.test() etc present confidence intervals in their output, and functions like confint() can be used on linear regression models to get confidence intervals for our coefficients.
Confidence intervals (CIs) are often used to make a statement about a null hypothesis just like a p-value (see 3A #inference. If a 95% CI does not contain zero then we can, with that same level of confidence, reject the null hypothesis that the population value is zero. So a 95% confidence interval maps to \(p<.05\), and a 99% CI maps to \(p<.01\), and so on.
However, many people these days prefer confidence intervals to \(p\)-values as they take the focus (slightly) away from the null hypothesis and toward a range of effect sizes that are compatible with the data.
The function confint() will give you confidence intervals. The function car::Confint()1 will do exactly the same but put them alongside the estimates (which saves you scrolling up and down between different outputs).
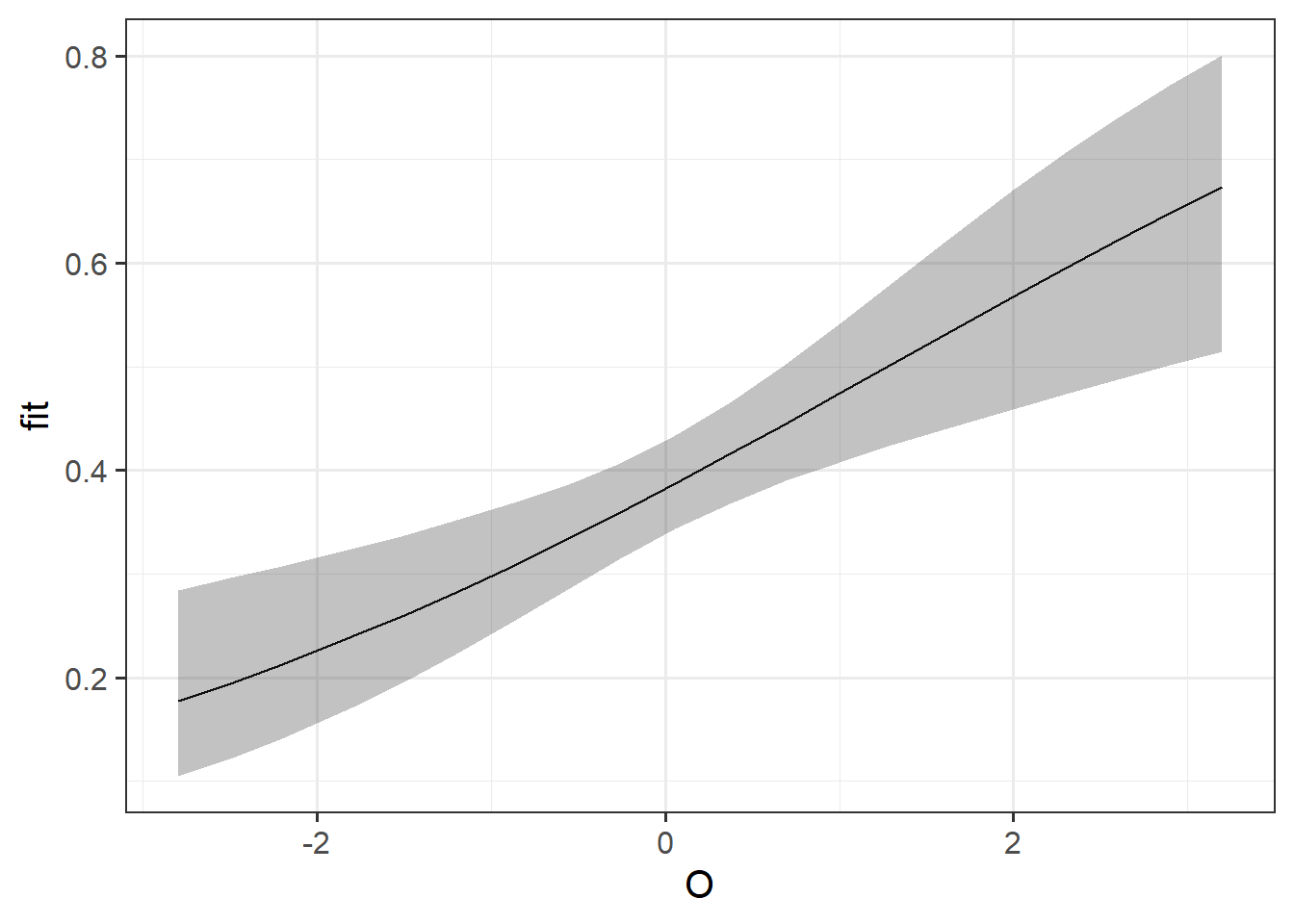
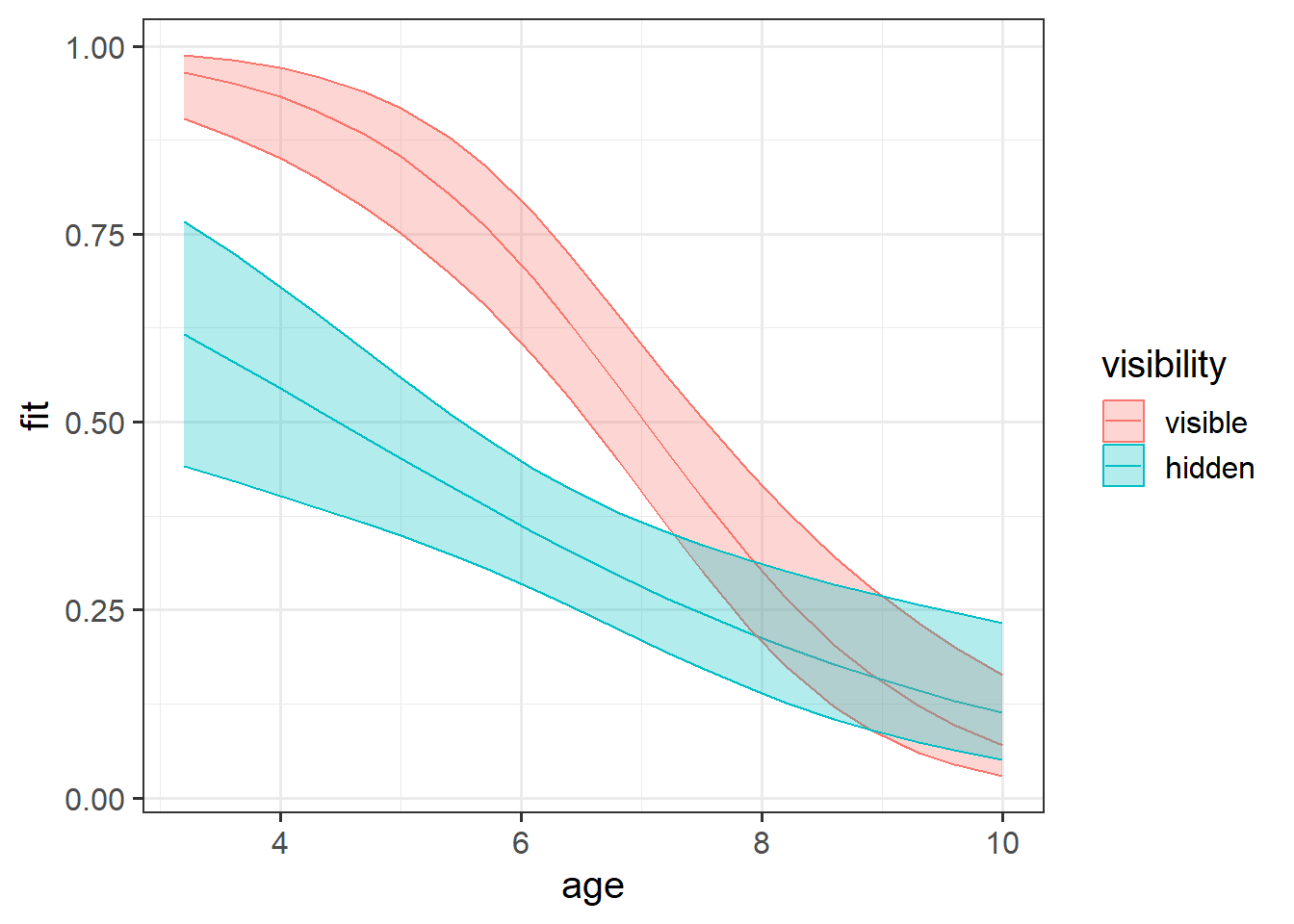
Produce a plot of the predicted probabilities of noticing the gorilla as a function of openness.
There’s an example of this at 10A #visualising. Using the effects package will be handy.
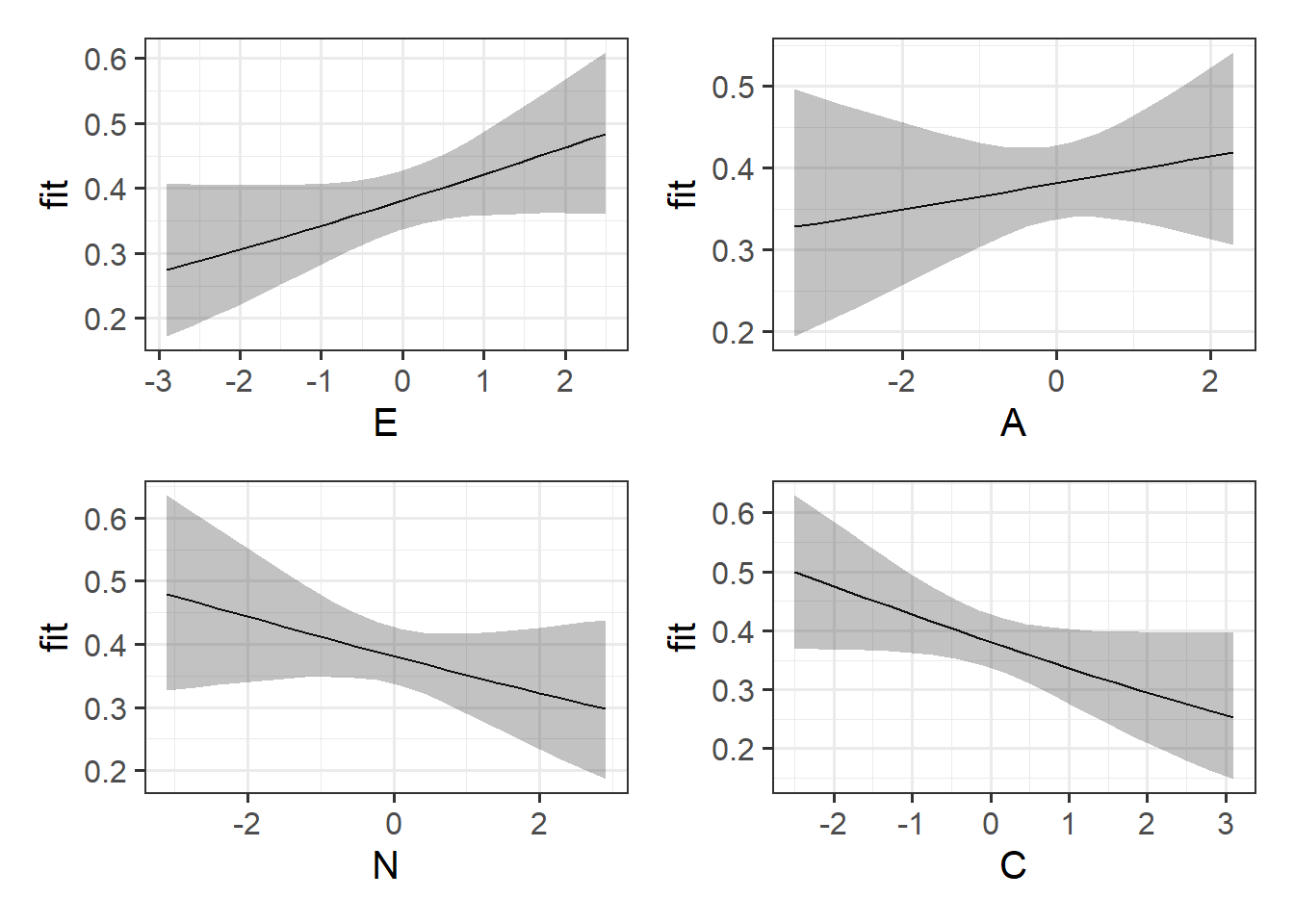
Try creating an equivalent plot for the other personality traits - before you do, what do you expect them to look like?
Invisible Marshmallows
Data: mallow2.csv
We already played with some marshmallow-related data in reading 10A. Here we are extending this study to investigate whether the visibility of the immediate reward moderates age effects on the ability to delay gratification (the ability to forgo an immediate reward for a greater reward at a later point).
304 children took part, ranging in ages from 3 to 10 years old. Each child was shown a marshmallow, and it was explained that they were about to be left alone for 10 minutes. They were told that they were welcome to eat the marshmallow while they were waiting, but if the marshmallow was still there after 10 minutes, they would be rewarded with two marshmallows.
For half of the children who took part, the marshmallow was visible for the entire 10 minutes (or until they ate it!). For the other half, the marshmallow was placed under a plastic cup.
The experiment took part at various times throughout the working day, and researchers were worried about children being more hungry at certain times of day, so they kept track of whether each child completed the task in the morning or the afternoon, so that they could control for this in their analyses.
The data are available at https://uoepsy.github.io/data/mallow2.csv.
| variable | description |
|---|---|
| name | Participant Name |
| agemonths | Age in months |
| timeofday | Time of day that the experiment took place ('am' = morning, 'pm' = afternoon) |
| visibility | Experimental condition - whether the marshmallow was 'visible' or 'hidden' for the 10 minutes |
| taken | Whether or not the participant took the marshmallow within the 10 minutes |
Read in the data, check, clean, plot, describe, explore.
Fit a model that you can use to address the research aims of the study.
Take a look back at the description of the study.
- What are we wanting to find out? How can we operationalise this into a model?
- hint: ‘moderation’ is another word for ‘interaction’.
- hint: ‘moderation’ is another word for ‘interaction’.
- Is there anything that we think it is important to account for?
What do you conclude?
When you have an interaction Y ~ X1 + X2 + X3 + X2:X3 in your model, the coefficients that involved in the interaction (X2 and X3) represent the associations when the other variable in the interaction is zero.
The interaction coefficient itself represents the adjustment to these associations when we move up 1 in the other variable.
Write up the methods and results, providing a plot and regression table.
A template RMarkown file can be found at https://uoepsy.github.io/usmr/2324/misc/marshmallows.Rmd if you want it. It contains a list of questions try and make sure you answer in your write-up.
Optional Extras
Below is the background and design to a study investigating how different types of more active learning strategies improve understanding, in comparison to just studying materials.
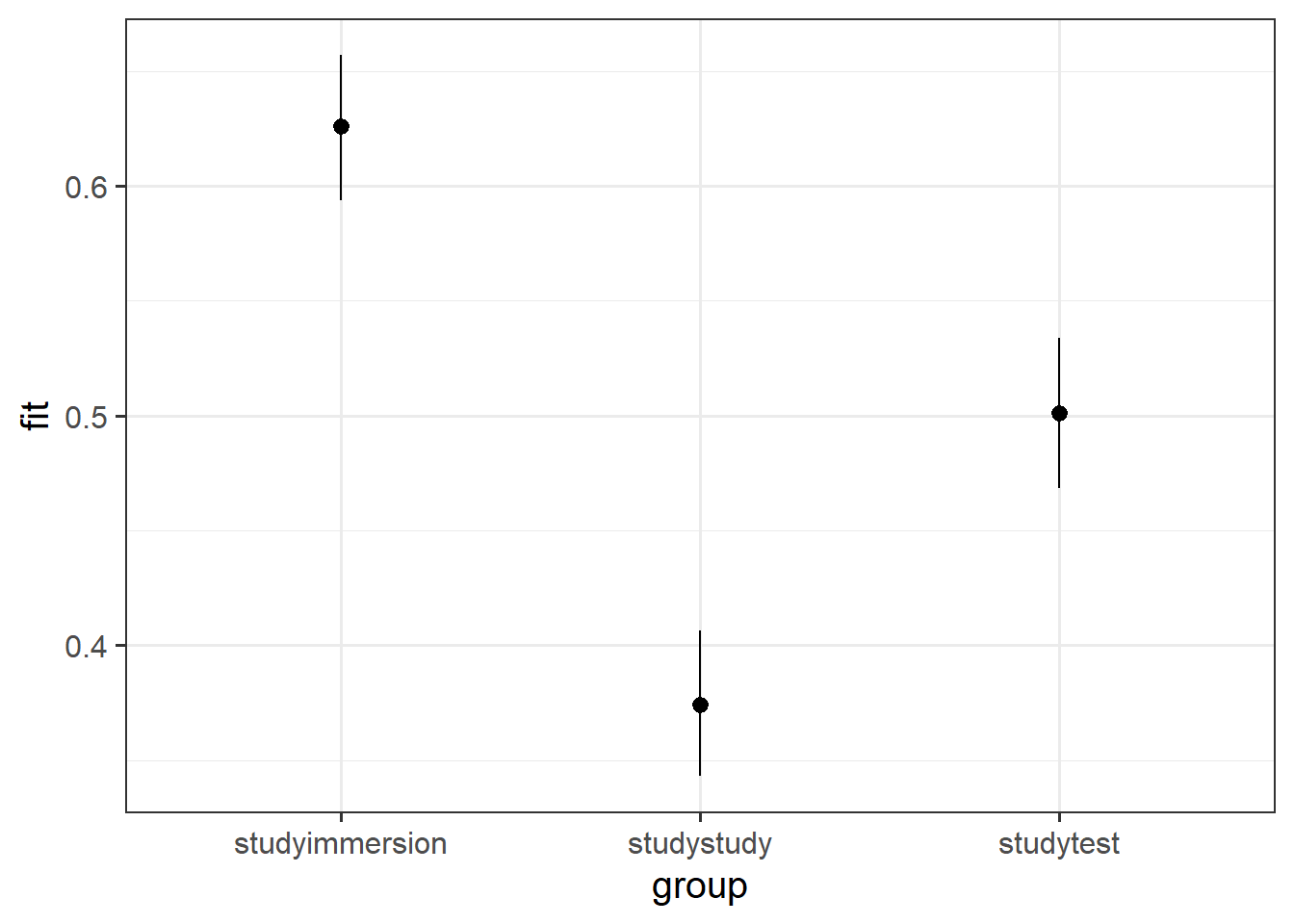
Fit an appropriate model to address the research aims, interpret it, make a plot, etc.
An experiment was run to investigate strategies for learning. Three groups of 30 participants were presented with materials on a novel language to learn.
All groups were given two hours of preparation time, after which their learning was assessed. The first group (studystudy) spent both hours studying the materials. The second group (studytest) spent the first hour studying the materials, and the second hour testing themselves on the materials. The third group (studyimmersion) spent the first hour studying the materials, and the second hour trying to converse with a native speaker of the language (they were not permitted to attempt to converse in any other language during this time).
After the two hours were up, participants were the assessed via a series of 30 communication tasks. The number of tasks each participant got correct was recorded.
Information on two potential covariates was also included - previous language learning experience (novice/experienced), and cognitive aptitude (a 20 item questionnaire leading to a standardised test score).
The data are available at https://uoepsy.github.io/data/immersivelearning.csv.
| variable | description |
|---|---|
| PID | Participant ID number |
| group | Experimental group (studystudy = 2 hours of study, studytest = 1 hour study, 1 hour testing, studyimmersion = 1 hour study, 1 hour conversing) |
| plle | Previous language learning experience (novice or experienced) |
| cog_apt | Cognitive Aptitude (Standardised Z Score) |
| n_correct | Number of the 30 communication tasks that each participant correctly completed |
- This might not be binary (0 or 1), but it’s binomial (“how many success in 30 trials”).
- See the optional box under logistic regression in 10A #fitting-glm-in-r for how to fit a binomial model to data like this.
People and behaviours are a lot more difficult to predict than something like, say, the colour of different wines.
Build a model that predicts the colour of wine based on all available information. How accurately can it predict wine colours?
(Generally speaking, this question doesn’t reflect how we do research in psychology. Ideally, we would have a theoretical question that motivates the inclusion (and testing of) specific predictors.)
You can download a dataset of 6497 different wines (1599 red, 4898 white) from https://uoepsy.github.io/data/usmr_wines.csv.
It contains information on various physiochemical properties such as pH, a measure of level of sulphates, residual sugar, citric acid, volatile acidity and alcohol content, and also quality ratings from a sommelier (wine expert). All the wines are vinho verde from Portugal, and the data was collected between 2004 and 2007.
glm(outcome ~ ., data = mydata)is a shorthand way of putting all variables in the data in as predictors.
- See the lecture slides for an example of how we can get a number for “how accurately can my model predict”.
Footnotes
the colon here means “look in the car package and use the
Confint()function. It saves having to load the package withlibrary(car)↩︎