Exercises: Scaling | Categorical Predictors

Pictures of a Brain

neuronews.csv

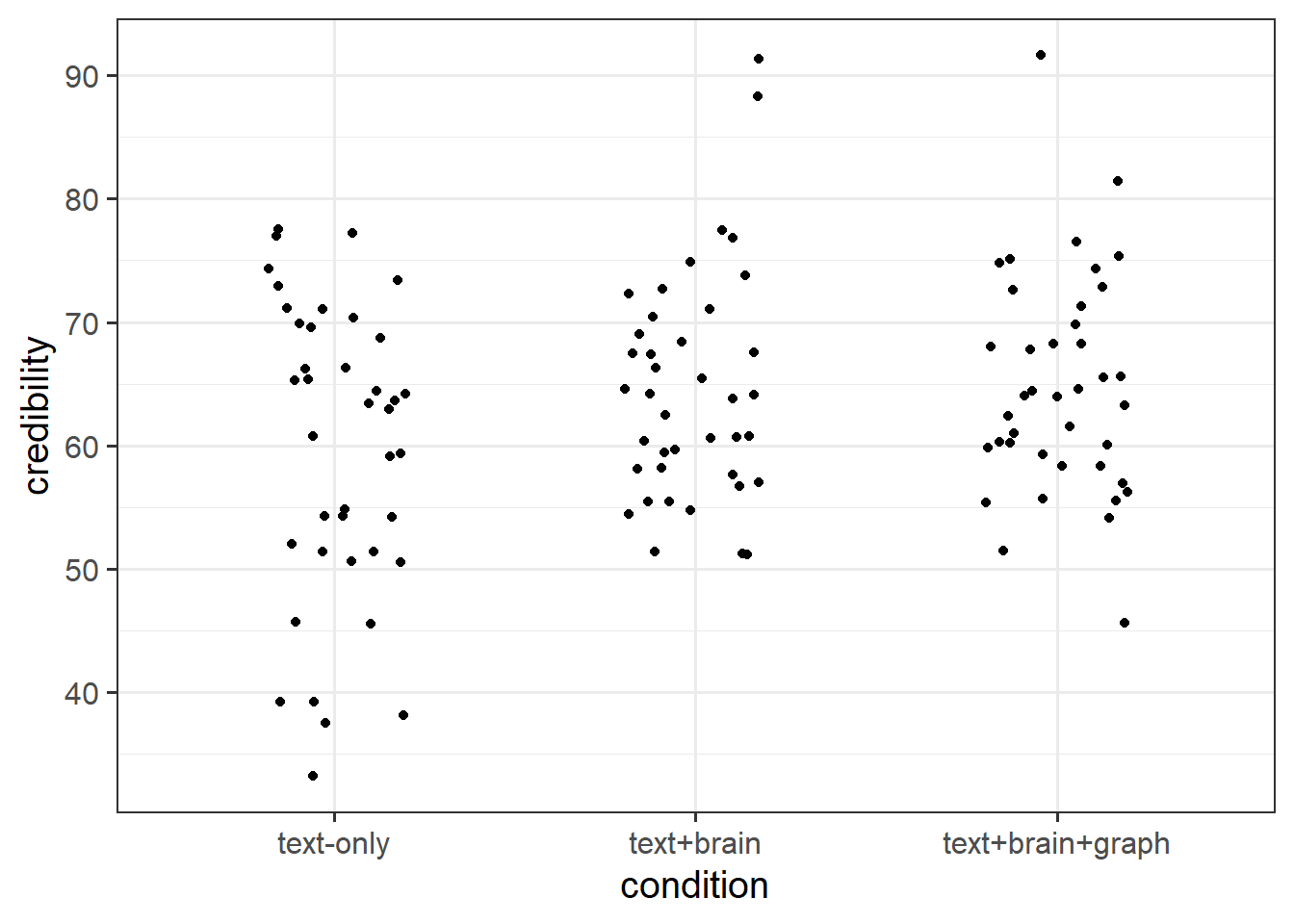
This dataset is from a study¹ looking at the influence of presenting scientific news with different pictures on how believable readers interpret the news.
120 participants took part in the study. Participation involved reading a short article about some research in neuroscience, and then rating how credible they found the research. Participants were randomly placed into one of three conditions, in which the article was presented a) in text alone, b) with a picture of a brain, or c) with a picture of a brain and a fancy looking (but unrelated to the research) graph. They rated credibility using a sliding scale from 0 to 100, with higher values indicating more credibility.

The data is available at https://uoepsy.github.io/data/usmr_neuronews.csv.

usmr_neuronews.csv data dictionary

variable	description
pid	Participant ID
name	Participant Name
condition	Condition (text-only / text+brain / text+brain+graph)
credibility	Credibility rating (0-100)

Question 1

Read in the data and take a look around (this is almost always the first thing to do!)

nndat <- read_csv("https://uoepsy.github.io/data/usmr_neuronews.csv")

hist(nndat$credibility)

# geom jitter is a way of randomly 'jittering' points so that the don't overlap
# i want them to be the right height, so no jitter in height, but i'll give them a little width jitter
ggplot(nndat, aes(x=condition,y=credibility)) +
   geom_jitter(height = 0, width = .2)

Question 2

Fit a model examining whether credibility of the research article differs between conditions.

mod1 <- lm(credibility ~ condition, data = nndat)

Question 3

Do conditions differ in credibility ratings?

Hints

This is an overall question, not asking about differences between specific levels. You can find a way to test this question either at the bottom of the summary() output, or by comparing it with a model without condition differences in it (see 8B #testing-group-differences).

We can either do this as a model comparison:

mod0 <- lm(credibility ~ 1, data = nndat)
anova(mod0, mod1)

Analysis of Variance Table

Model 1: credibility ~ 1
Model 2: credibility ~ condition
  Res.Df   RSS Df Sum of Sq      F  Pr(>F)  
1    119 12820                              
2    117 12146  2    674.03 3.2464 0.04245 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

and this info is also at the bottom of the summary, because we just have one predictor in the model

summary(mod1)

F-statistic: 3.246 on 2 and 117 DF,  p-value: 0.04245

Conditions significantly differed in credibility ratings \(F(2,117) = 3.25, p = .0425\)

Question 4

How do groups differ?

Hints

Note that this is a subtly different question to the previous one. It will require us to look at something that tests between specific groups (8B #testing-differences-between-specific-groups).

summary(mod1)

Call:
lm(formula = credibility ~ condition, data = nndat)

Residuals:
     Min       1Q   Median       3Q      Max 
-26.4476  -6.6086  -0.3778   6.5657  26.8589 

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 59.663      1.611  37.035   <2e-16 ***
conditiontext+brain          4.909      2.278   2.155   0.0332 *  
conditiontext+brain+graph    5.138      2.278   2.255   0.0260 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 10.19 on 117 degrees of freedom
Multiple R-squared:  0.05258,   Adjusted R-squared:  0.03638 
F-statistic: 3.246 on 2 and 117 DF,  p-value: 0.04245

Compared to when presented in text-only, conditions where the article was presented alongside a picture of a brain, or alongside both a brain-picture and a graph, resulted in higher average credibility ratings. Including a picture of a brain was associated with a 4.91 increase in credibility over the text-only article (\(b = 4.91\), \(t(117)=2.15\), \(p=0.033\)), and including both a brain-picture and a graph was associated with a 5.14 higher average credibility rating (\(b = 5.14\), \(t(117)=2.26\), \(p=0.026\)).

Question 5

Let’s prove something to ourselves.
Because we have no other predictors in the model, it should be possible to see how the coefficients from our model map exactly to the group means.

Calculate the mean credibility for each condition, and compare with your model coefficients.

Hints

To calculate group means, we can use group_by() and summarise()!

nndat |> 
  group_by(condition) |>
  summarise(
    meancred = mean(credibility)
  )

# A tibble: 3 × 2
  condition        meancred
  <chr>               <dbl>
1 text+brain           64.6
2 text+brain+graph     64.8
3 text-only            59.7

Here are our model coefficients:

coef(mod1)

              (Intercept)       conditiontext+brain conditiontext+brain+graph 
                59.662662                  4.909058                  5.138197 

And here are our means:

nndat |> 
  group_by(condition) |>
  summarise(
    meancred = mean(credibility)
  )

# A tibble: 3 × 2
  condition        meancred
  <chr>               <dbl>
1 text+brain           64.6
2 text+brain+graph     64.8
3 text-only            59.7

We can see that the intercept is the mean of the text-only group.

The next coefficient - named “conditiontext+brain” is the difference from the text-only group to the text+brain group.

The final coefficient - named “conditiontext+brain+graph” is the difference from the text-only group to the text+brain+graph group.

So this means we can get to our group means by using:

coef(mod1)[c(1,2)] |> sum() # the mean of text+brain

[1] 64.57172

coef(mod1)[c(1,3)] |> sum() # the mean of text+brain+graph

[1] 64.80086

Detectorists

Question 6

We saw this study briefly at the end of last week and we’re going to continue where we left off.

Below is the description of the study, and the code that we had given you to clean the data and fit a model that assessed whether different strategies (e.g. breathing, closing eyes) were associated with changes in heart rate during a lie-detection test. The model also accounts for differences in heart rates due to age and pre-test anxiety.

Run the code given below to ensure that we are all at the same place.

Study: Lie detectors

Law enforcement in some countries regularly rely on ‘polygraph’ tests as a form of ‘lie detection’. These tests involve measuring heart rate, blood pressure, respiratory rate and sweat. However, there is very little evidence to suggest that these methods are remotely accurate in being able to determine whether or not someone is lying.

Researchers are interested in if peoples’ heart rates during polygraph tests can be influenced by various pre-test strategies, including deep breathing, or closing their eyes. They recruited 142 participants (ages 22 to 64). Participants were told they were playing a game in which their task was to deceive the polygraph test, and they would receive financial rewards if they managed successfully. At the outset of the study, they completed a questionnaire which asked about their anxiety in relation to taking part. Participants then chose one of 4 strategies to prepare themselves for the test, each lasting 1 minute. These were “do nothing”, “deep breathing”, “close your eyes” or “cough”². The average heart rate of each participant was recorded during their test.

usmr_polygraph.csv data dictionary

variable	description
age	Age of participant (years)
anx	Anxiety measure (Z-scored)
strategy	Pre-test Strategy (0 = do nothing, 1 = close eyes, 2 = cough, 3 = deep breathing)
hr	Average Heart Rate (bpm) during test

Analysis

Code

# load libraries
library(tidyverse)
library(psych)
# read in the data
liedf <- read_csv("https://uoepsy.github.io/data/usmr_polygraph.csv")

# there seems to be a 5 there.. 
table(liedf$strategy)
# the other variables look okay though
describe(liedf)
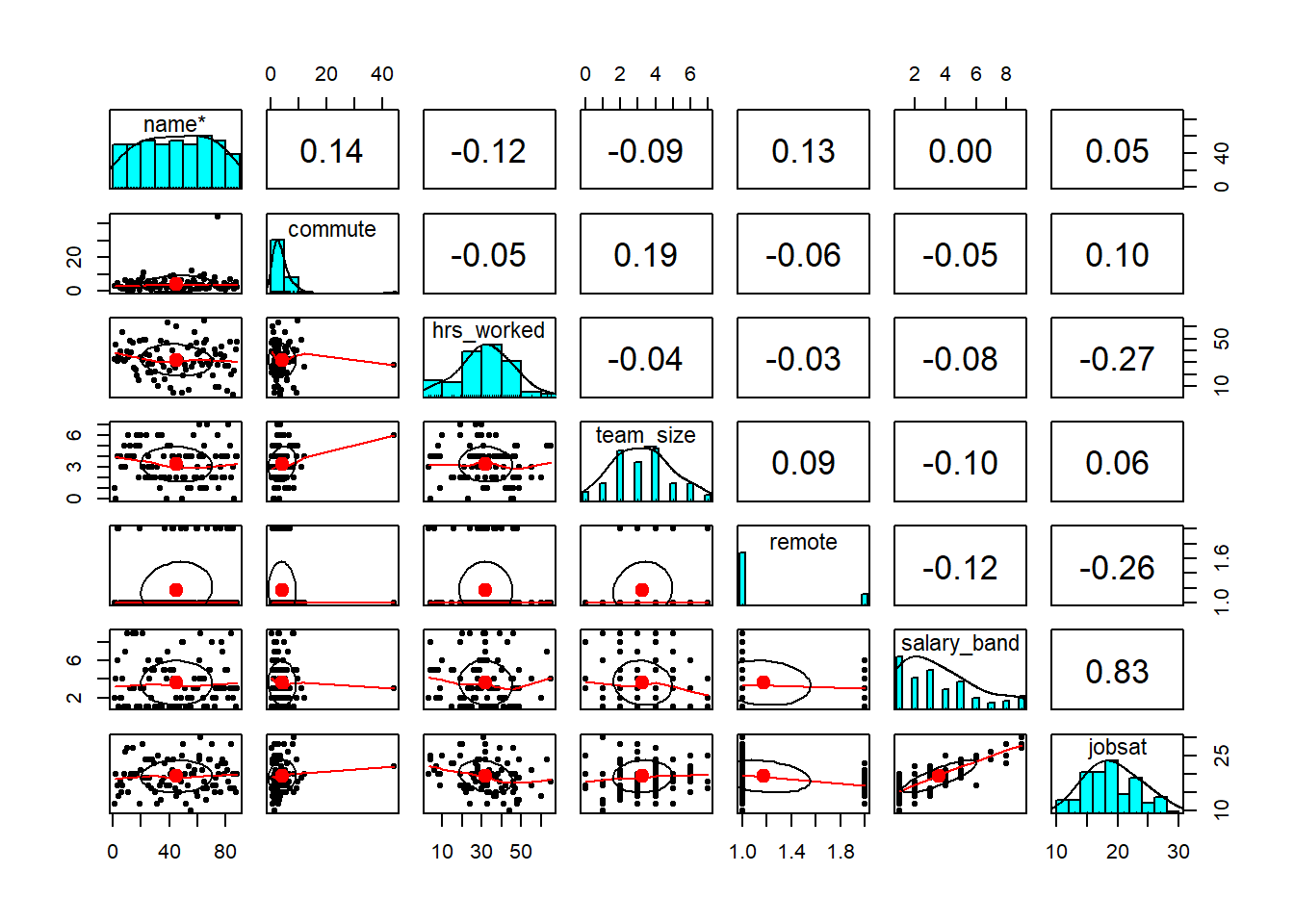
pairs.panels(liedf)

liedf <- liedf |> 
  filter(strategy!=5) |>
  mutate(
    # strategy is a factor. but currently numbers
    # i'm going to give them better labels too.. 
    # to do this is need to tell factor() what "levels" to look for
    # and then give it some "labels" to apply to those.
    strategy = factor(strategy, 
                      levels = c("0","1","2","3"),
                      labels = c("do nothing", "close eyes",
                                 "cough", "deep breathing")
                      )
  )

liemod <- lm(hr ~ age + anx + strategy, data = liedf)

# Does HR differ between strategies?
anova(liemod)
# the above is a shortcut for getting this comparison out:
anova(
  lm(hr ~ age + anx, data = liedf),
  lm(hr ~ age + anx + strategy, data = liedf)
)

Question 7

Our model includes a predictor with 4 levels (the 4 different strategies).

This means we will have 3 coefficients pertaining to this predictor. Take a look at them. Write a brief sentence explaining what each one represents.

Hints

We’re still all using R’s defaults (8B #treatment-contrasts-the-default), so these follow the logic we have seen already above.

coef(liemod)

           (Intercept)                    age                    anx 
            45.5463008              0.2923910              2.9474446 
    strategyclose eyes          strategycough strategydeep breathing 
            -0.8836002             -3.9818287             -5.8436306 

term	estimate	interpretation
(Intercept)	45.55	estimated HR for someone age 0, anxiety 0 (the mean), who 'does nothing' prior to the test
age	0.29	estimated change in HR for an additional year of age, holding constant anxiety and strategy
anx	2.95	estimated change in HR for an additional SD of anxiety, holding constant age and strategy
strategyclose eyes	-0.88	estimated difference in HR between 'doing nothing' strategy and 'close eyes' strategy, holding constant age and anxiety
strategycough	-3.98	estimated difference in HR between 'doing nothing' strategy and 'cough' strategy, holding constant age and anxiety
strategydeep breathing	-5.84	estimated difference in HR between 'doing nothing' strategy and 'deep breathing' strategy, holding constant age and anxiety

Question 8

Calculate the mean heart rate for each strategy group.
Do they match to our model coefficients?

liedf |> 
  group_by(strategy) |>
  summarise(
    meanHR = mean(hr)
  )

# A tibble: 4 × 2
  strategy       meanHR
  <fct>           <dbl>
1 do nothing       54.2
2 close eyes       55.7
3 cough            54.1
4 deep breathing   55.0

They don’t match! For instance, in our group means above the ‘close eyes’ strategy has a higher average heart rate than the ‘do nothing’ strategy. But that’s not what our model coefficients said - they said the opposite!

Why is this? It’s because we have other things in our model, so these model estimated differences are now “holding age and anxiety constant”.

Question 9

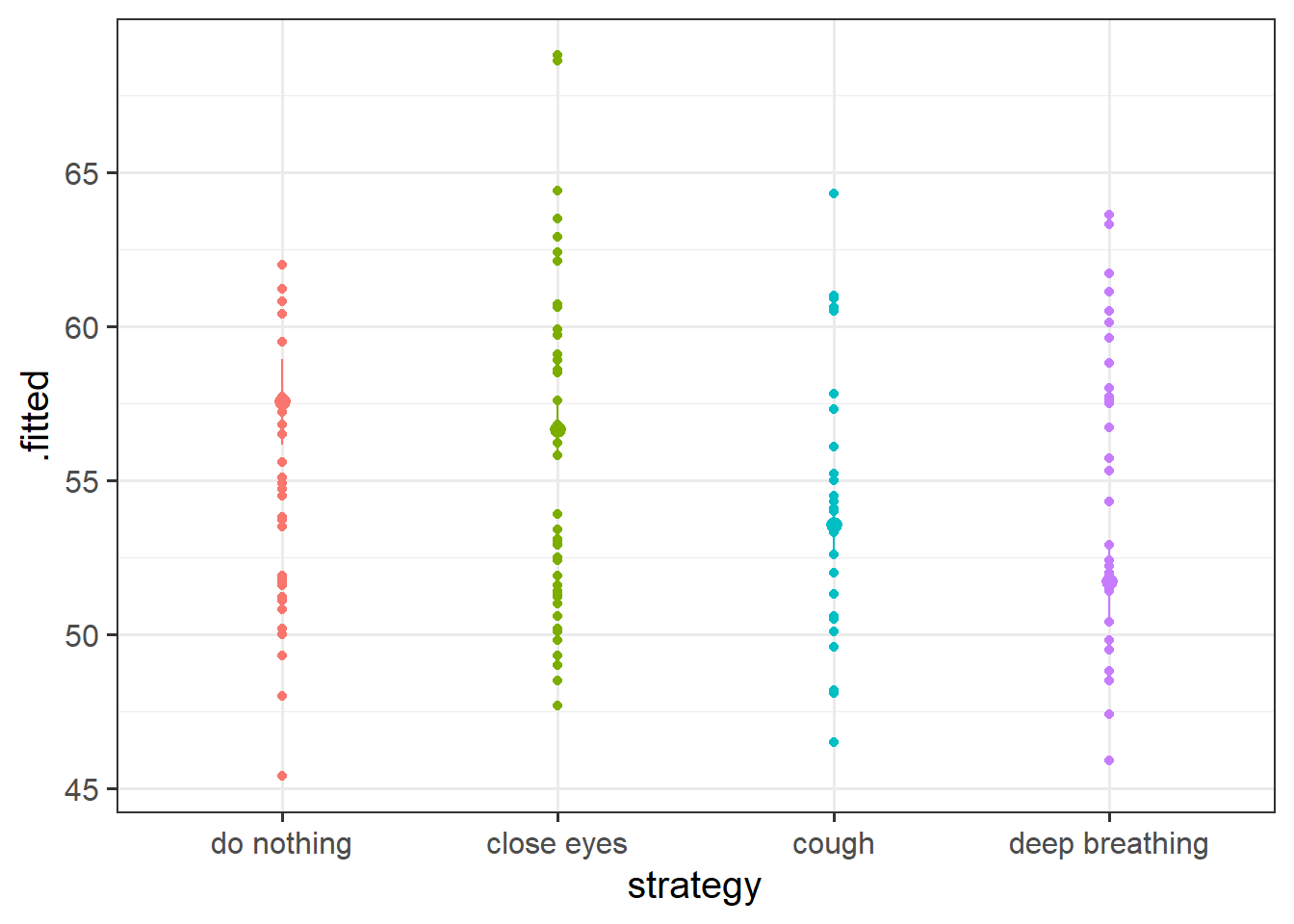
At the end last week’s exercises, we wanted you to make a plot of the model estimated differences in heart rates between the strategies.

Chances are that you followed the logic of 1) create a little plotting data frame, 2) use augment() from the broom package, and 3) shove it into ggplot.

You may have ended up with something like this:

Code

plotdat <- data.frame(
  age = mean(liedf$age),
  anx = mean(liedf$anx),
  strategy = unique(liedf$strategy)
)
broom::augment(liemod, 
               newdata=plotdat, 
               interval="confidence") |>
  ggplot(aes(x=strategy,y=.fitted, col=strategy))+
  geom_pointrange(aes(ymin=.lower,ymax=.upper)) +
  guides(col="none")

These plots are great, but they don’t really show the underlying spread of the data. They make it seem like everybody in the ‘do nothing’ strategy will have a heart rate between 56 and 59bpm. But that interval is where we expect the mean to be, not where we expect the individuals.

Can you add the original raw datapoints to the plot, to present a better picture?

Hints

This is tricky, and we haven’t actually seen it anywhere in the readings or lectures.
The thing that we’re giving to ggplot (the output of the augment function) doesn’t have the data in it.
With ggplot we can actually pull in data from different sources:

ggplot(data1, aes(x=x,y=y)) + 
  geom_point() +
  geom_point(data = data2, aes(x=x,y=newy))

So here was our nice plot:

plotdat <- data.frame(
  age = mean(liedf$age),
  anx = mean(liedf$anx),
  strategy = unique(liedf$strategy)
)
broom::augment(liemod, 
               newdata=plotdat, 
               interval="confidence") |>
  ggplot(aes(x=strategy,y=.fitted, col=strategy))+
  geom_pointrange(aes(ymin=.lower,ymax=.upper)) +
  guides(col="none")

We want to add to that the original data.. but all that original data is in a different dataset!
However, that doesn’t mean we can’t use it.
Let’s try to add points for all our heart rates, and we’ll tell geom_point() to look in the original dataset.
The thing we need to be careful with is that our original dataset doesn’t have anything called .fitted in it, which is currently on our y-axis. So we need to specify the y we want it to use (in this case, the hr variable)

broom::augment(liemod, 
               newdata=plotdat, 
               interval="confidence") |>
  ggplot(aes(x=strategy,y=.fitted, col=strategy))+
  geom_pointrange(aes(ymin=.lower,ymax=.upper)) +
  guides(col="none") +
  geom_point(data = liedf, aes(y = hr))

Okay, the data is on there.. now we just need to make it look nice. My instinct here is to jitter again. I’m also going to make the plots black, and a little transparent, so that we can still see the means.

broom::augment(liemod, 
               newdata=plotdat, 
               interval="confidence") |>
  ggplot(aes(x=strategy,y=.fitted, col=strategy))+
  geom_pointrange(aes(ymin=.lower,ymax=.upper)) +
  guides(col="none") +
  geom_jitter(data = liedf, aes(y = hr), width = .2, height = 0,
              col = "black", alpha = .3)

This is just one way to better visualise our findings.

If you’re feeling adventurous, try:

• a violin plot to show the distributions, rather than jittered points
• what happens when you put position = position_nudge(x=.3) inside the geom_pointrange()?
  
• what happens if you add coord_flip() to the plot?

Job Satisfaction, Guaranteed

jobsatpred.csv

A company is worried about employee turnover, and they are trying to figure out what are the main aspects of work life that predict their employees’ job satisfaction. 86 of their employees complete a questionnaire that leads to a ‘job satisfaction score’, that can range between 6 to 30 (higher scores indicate more satisfaction).

The company then linked their responses on the questionnaire with various bits of information they could get from their human resources department, as seen in Table 1.

The data are available at https://uoepsy.github.io/data/usmr_jobsatpred.csv.

Table 1:

usmr_jobsatpred.csv data dictionary

variable	description
name	Employee Surname
commute	Distance (km) to employee residence (note, records have used a comma in place of a decimal point)
hrs_worked	Hours worked in previous week
team_size	Size of the team in which the employee works
remote	Whether the employee works in the office or remotely (0 = office, 1 = remote)
salary_band	Salary band of employee (range 1 to 10, with those on band 10 earning the most)
jobsat	Job Satisfaction Score (sum of 6 questions each scored on 1-5 likert scale)

Question 10

Read in the data. Look around, do any cleaning that might be needed.

jsdat <- read_csv("https://uoepsy.github.io/data/usmr_jobsatpred.csv")

Just looking at the top of the data, I already know that commute is a problem..

head(jsdat)

# A tibble: 6 × 7
  name          commute hrs_worked team_size remote salary_band jobsat
  <chr>         <chr>        <dbl>     <dbl>  <dbl>       <dbl>  <dbl>
1 Sayavong      44,1            28         6      0           3     22
2 Herman        1,0             60         2      0           2     14
3 el-Nour       2,6             10         6      0           6     25
4 Barnes Saputo 0,4             46         4      0           9     27
5 Laurents      3,0             24         4      1           1     12
6 Lawton        5,3             42         1      0           2     17

The summary shows us a few other things..

• remote has a max of 2, but it should be 0s and 1s, because it’s a binary variable according to our data dictionary.
  
• jobsat should surely be between 6 and 30 (this is that idea of 6 questions where you score between 1 and 6 means your minimum should be 6, and maximum should be 30). Here we have a min of 0 and a max of 31 so something’s amiss there.

summary(jsdat)

     name             commute            hrs_worked      team_size    
 Length:93          Length:93          Min.   : 3.00   Min.   :0.000  
 Class :character   Class :character   1st Qu.:24.00   1st Qu.:2.000  
 Mode  :character   Mode  :character   Median :32.00   Median :3.000  
                                       Mean   :31.99   Mean   :3.269  
                                       3rd Qu.:41.00   3rd Qu.:4.000  
                                       Max.   :65.00   Max.   :7.000  
     remote        salary_band        jobsat     
 Min.   :0.0000   Min.   :1.000   Min.   : 0.00  
 1st Qu.:0.0000   1st Qu.:2.000   1st Qu.:16.00  
 Median :0.0000   Median :3.000   Median :19.00  
 Mean   :0.1935   Mean   :3.602   Mean   :19.11  
 3rd Qu.:0.0000   3rd Qu.:5.000   3rd Qu.:23.00  
 Max.   :2.0000   Max.   :9.000   Max.   :31.00  

Variables are all appropriate types apart from commute.
If we’re being good, we should probably also set remote to be a factor as it is two distinct categories.

For the commute variable, we need to first (prior to making it a numeric variable), replace all the commas with a point - “.”. We can do this using gsub().

For the remote variable, we know it only has two possible levels - 0 and 1. However, we saw earlier that there was a 2 in there as well. But there’s only one of them, so it’s probably a typo or something.

sum(df$remote==2)

[1] 1

We should probably replace that with an NA as it is an impossible value, and we have no idea whether it is supposed to be a 0 or a 1.
As it happens, by giving the factor() function only the levels we want to keep, it will replace any others with NAs.

factor(c("dog","cat","parrot"), levels=c("dog","cat"))

[1] dog  cat  <NA>
Levels: dog cat

We also noted that the jobsat variable had some values that were \(<6\) and \(>30\). We can replace those with NAs as well, using that handy ifelse() function!

x <- c(1,16,50,72)
# if x is less than 10 or x is less than 70, give me an NA, 
# otherwise give me the value of x
ifelse(x<10 | x>70, NA, x)

[1] NA 16 50 NA

Let’s do this bit of cleaning all in one mutate:

jsdat <- 
  jsdat |> 
    mutate(
      commute = as.numeric(gsub(",",".",commute)),
      remote = factor(remote, levels = c("0","1"),
                      labels = c("office","remote")),
      jobsat = ifelse(jobsat < 6 | jobsat > 30, NA, jobsat)
    )

Question 11

Explore! Make some quick plots and calculate some quick descriptives.

library(tableone)
CreateTableOne(data = jsdat |> select(-name))

                         
                          Overall      
  n                          93        
  commute (mean (SD))      4.20 (4.88) 
  hrs_worked (mean (SD))  31.99 (13.37)
  team_size (mean (SD))    3.27 (1.68) 
  remote = remote (%)        16 (17.4) 
  salary_band (mean (SD))  3.60 (2.42) 
  jobsat (mean (SD))      19.40 (4.40) 

library(psych)
pairs.panels(jsdat)

It looks like commute has a big outlier!!

max(jsdat$commute)

[1] 44.1

It’s not impossible though (44 km commute?), it’s just quite different.. chances are this may come out as an influential datapoint in our model, but I have no obvious reason to exclude this observation just because they live far away!

Question 12

Fit a model to examine the independent associations between job satisfaction and all of the aspects of working patterns collected by the company.

Hints

We want to look at the independent associations, so we want a multiple regression model.
We don’t really have any theoretical order in which to put the predictors in our model. However, this mainly matters when we use anova(model) - if we are just going to look at the coefficients (which is what we will be doing), then we can put them in any order for now.

jsmod <- lm(jobsat ~ commute + hrs_worked + team_size + remote + salary_band, jsdat)
summary(jsmod)

Call:
lm(formula = jobsat ~ commute + hrs_worked + team_size + remote + 
    salary_band, data = jsdat)

Residuals:
   Min     1Q Median     3Q    Max 
-5.245 -1.188 -0.010  1.402  3.862 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  14.65369    0.87424  16.762  < 2e-16 ***
commute       0.07175    0.04469   1.605 0.112201    
hrs_worked   -0.06424    0.01627  -3.948 0.000165 ***
team_size     0.43577    0.13337   3.267 0.001579 ** 
remoteremote -2.09258    0.58744  -3.562 0.000612 ***
salary_band   1.52322    0.09385  16.231  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.042 on 83 degrees of freedom
  (4 observations deleted due to missingness)
Multiple R-squared:  0.7982,    Adjusted R-squared:  0.786 
F-statistic: 65.64 on 5 and 83 DF,  p-value: < 2.2e-16

Question 13

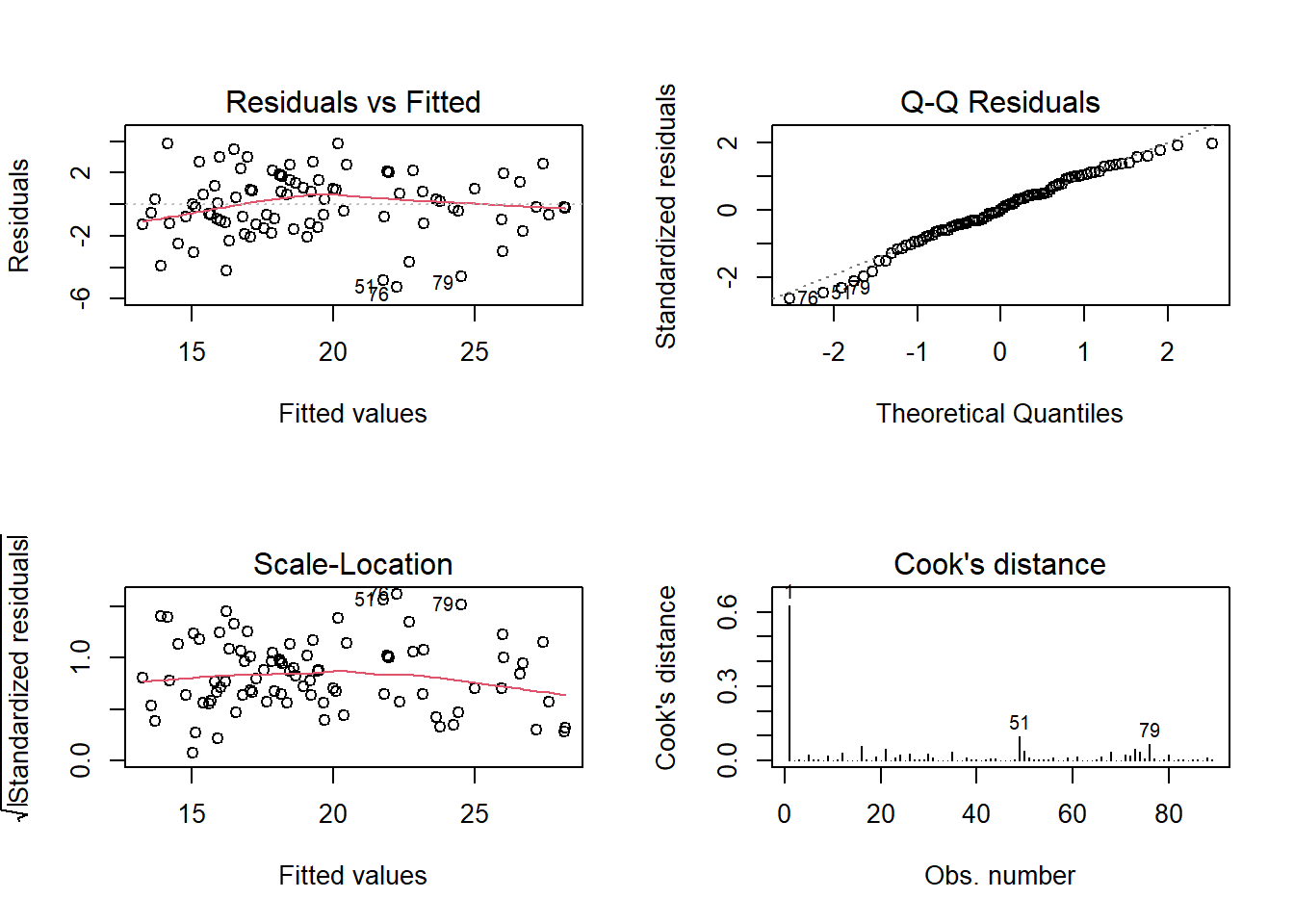
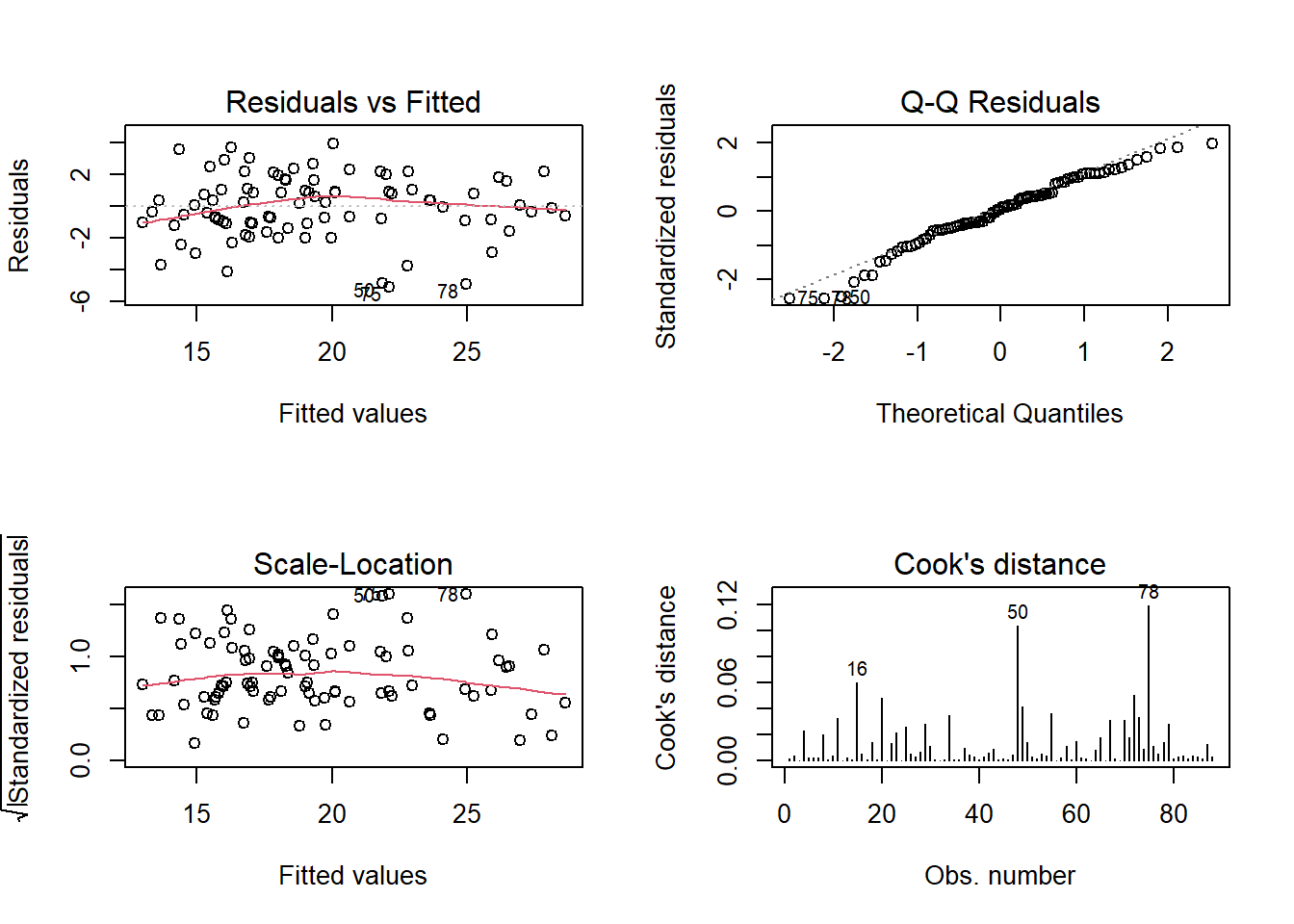
Check the assumption plots from the model. Remember we had that employee who was commuting quite far - are they exerting too much influence on our model?
If so, maybe refit the model without them.

We can see below that there is that one very influential observation (see bottom right plot). It’s almost 6 times more than the next most influential one.

plot(jsmod, which=c(1:4))

We’ll refit the model without that observation:

jsmod1 <- lm(jobsat ~ commute + hrs_worked + 
               team_size + remote + salary_band, 
             data = jsdat[-1,])

And check again. These look much better in terms of influencers. The main assumption plots don’t look terrible, but they’re not perfect (but then nothing ever is!).

plot(jsmod1, which=c(1:4))

Question 14

Now fit a second model, in which the predictors are standardised (those that can be).

Hints

• You can either standardise just the predictors, or standardise both predictors and outcome (see 8A #standardised-coefficients).
• If you’ve excluded some data in the model from the previous question, you should exclude them here too.

jsmodZ <- lm(scale(jobsat) ~ scale(commute) + scale(hrs_worked) + 
               scale(team_size) + remote + scale(salary_band), 
             data = jsdat[-1,])

Question 15

Looking at the standardised coefficients, which looks to have the biggest impact on employees’ job satisfaction?

Salary has a big positive impact. Then remote working (negative impact) Then hours worked (negative impact) Then team size (positive) Then commuting distance (positive, but non-significant)

summary(jsmodZ)

Call:
lm(formula = scale(jobsat) ~ scale(commute) + scale(hrs_worked) + 
    scale(team_size) + remote + scale(salary_band), data = jsdat[-1, 
    ])

Residuals:
     Min       1Q   Median       3Q      Max 
-1.15723 -0.23466  0.03139  0.36020  0.89447 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         0.09466    0.05422   1.746 0.084589 .  
scale(commute)      0.08950    0.04901   1.826 0.071441 .  
scale(hrs_worked)  -0.19522    0.04948  -3.945 0.000167 ***
scale(team_size)    0.16464    0.05008   3.287 0.001490 ** 
remoteremote       -0.47368    0.13289  -3.564 0.000611 ***
scale(salary_band)  0.84099    0.05163  16.288  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4618 on 82 degrees of freedom
  (4 observations deleted due to missingness)
Multiple R-squared:  0.8006,    Adjusted R-squared:  0.7884 
F-statistic: 65.85 on 5 and 82 DF,  p-value: < 2.2e-16

Question 16

The company can’t afford to pay employees anymore, and they are committed to letting staff work remotely. What would you suggest they do to improve job satisfaction?

You might argue here that because hrs_worked has the next biggest effect, we should suggest the company reduces the working hours.

The standardised coefficients are telling us that:

• a person who works 1 SD hours more is .19 SD lower on job satisfaction
• a person in a team 1 SD bigger is .16 SD higher on job satisfaction

So what are the standard deviations of hrs_worked and of team_size? Are they even worth comparing?

sd(jsdat$hrs_worked)

[1] 13.37299

sd(jsdat$team_size)

[1] 1.675526

So what our standardised coefficients are really saying is:

• a person works 13.4 hours more is .19 SD lower on job satisfaction
• a person in a team 1.67 people bigger is .16 SD higher on job satisfaction

You could easily argue from this that a much easier way the company could improve job satisfaction is to make team sizes a bit bigger - rather than letting people work 13 hours less than they currently do!

Footnotes

1. not a real one, but inspired very loosely by this one

2. apparently coughing is a method of immediately lowering heart rate!