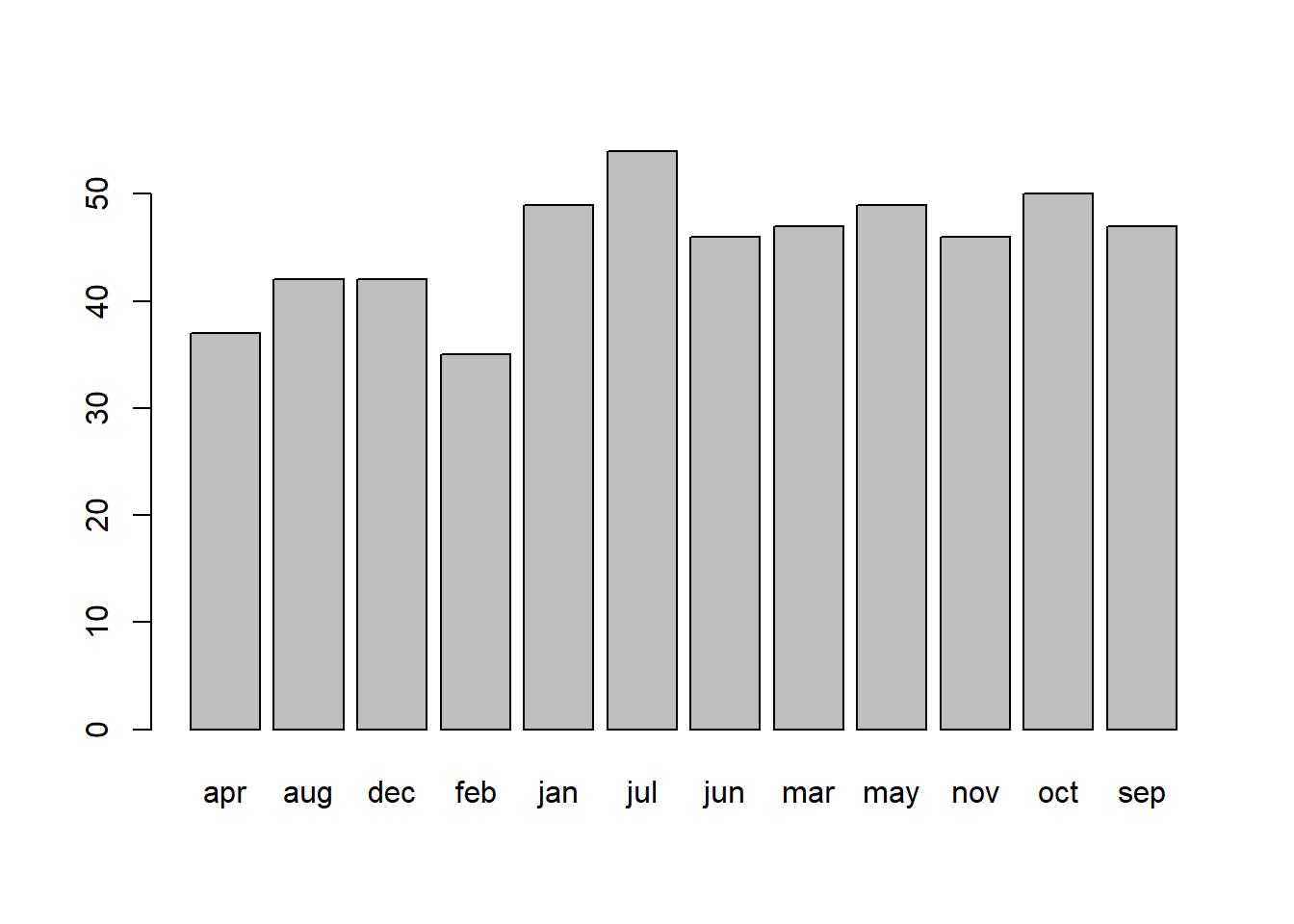Exercises: Chi-Square Tests

Chi-Square Tests

Birth-Months

Research Question: Are students more likely to be born in certain months than others?

Data: Past Surveys
In the last few years, we have asked students of the statistics courses in the Psychology department to fill out a little survey.
Anonymised data are available at https://uoepsy.github.io/data/surveydata_historical.csv.

Note: this does not contain the responses from this year.

surveydata <- 
  read_csv("https://uoepsy.github.io/data/surveydata_historical.csv")

Question 1

What is your intuition about the distribution of all students’ birth-months?
Do you think they will be spread uniformly across all months of the year (like a fair 12-sided dice), or do you think people are more likely to be born in certain months more than others?

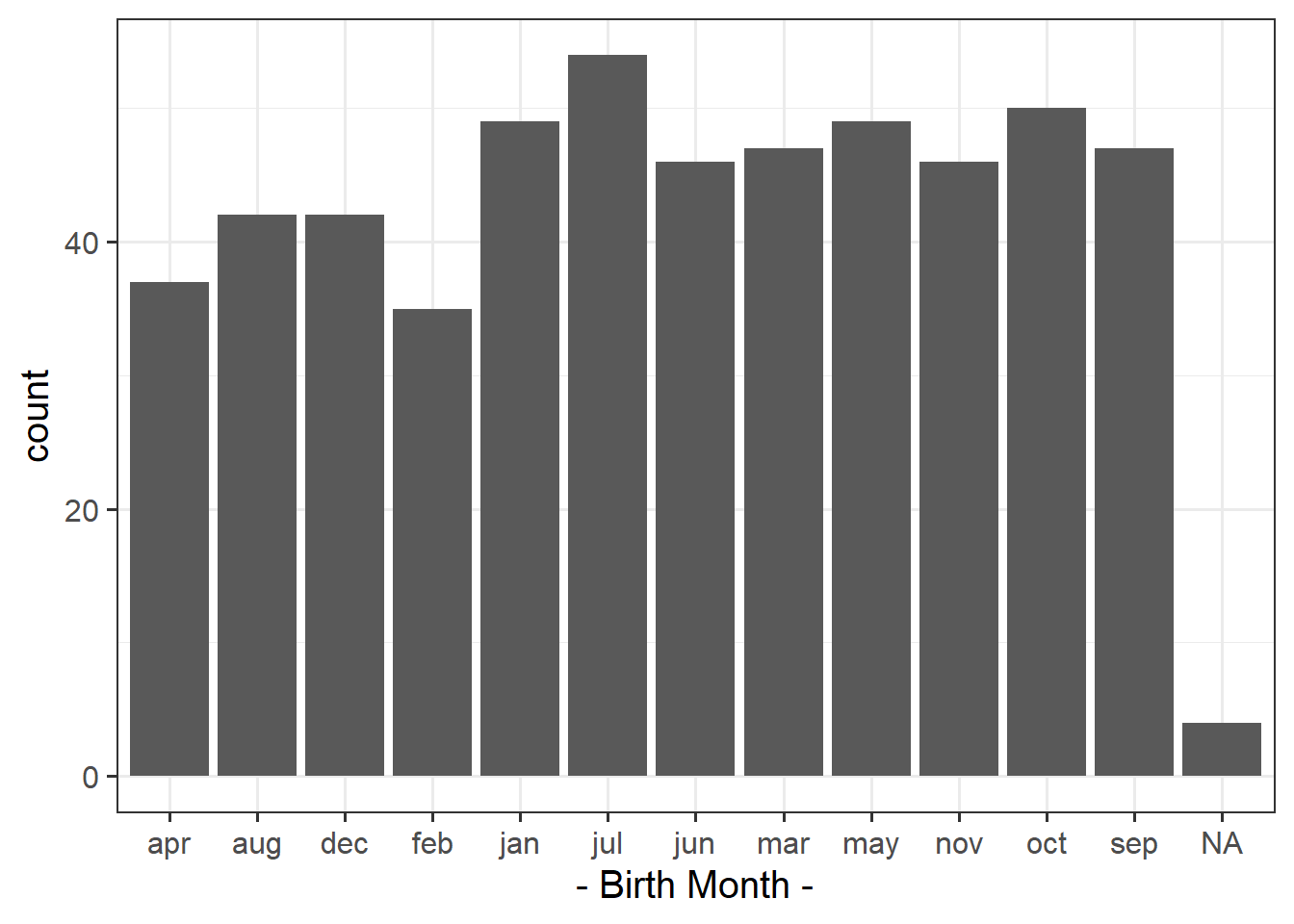
Plot the distribution and get an initial idea of how things are looking.

Hints

You can do this quickly with barplot() and table(), or you could create try using ggplot() and looking into geom_bar().

The quick and dirty way to plot:

barplot(table(surveydata$birthmonth))

A ggplot option:

ggplot(data = surveydata, aes(x = birthmonth)) +
    geom_bar() +
    labs(x = "- Birth Month -")

Question 2

We’re going to perform a statistical test to assess the extent to which our data conforms to the hypothesis that people are no more likely to be born on one month than another.

Under this hypothesis, what would be the proportional breakdown of observed births in each of the months?

If people are no more likely to be born in one month than another, then we would expect the same proportion of observed births in each month.
There are 12 months, so we would expect \(\frac{1}{12}\) observations in each month.

We can write these as: \[ \begin{align} & p_{jan} = 1/12 \\ & p_{feb} = 1/12 \\ & ... \\ & p_{dec} = 1/12 \\ \end{align} \]

Question 3

How many observations in our sample would we expect to find with a birthday in January? And in February? … and so on?

Hints

How many responses (i.e. not missing values) do we have for this question?

There are 470 people who have non-NA values (sum(!is.na(surveydata$birthmonth))).

Under the null hypothesis, we would expect \(\frac{1}{12} \times\) 470 = 39.17 observations born in each month.

Question 4

The code below creates counts for each month. Before doing that, it removes the rows which have an NA in them for birthmonth:

surveydata |>
  filter(!is.na(birthmonth)) |>
  group_by(birthmonth) |>
  summarise(
      observed = n()
  )

(A shortcut for this would be surveydata |> filter(!is.na(birthmonth)) |> count(birthmonth))

Add to the code above to create columns showing:

• the expected counts \(E_i\)
• observed-expected (\(O_i - E_i\))
• the squared differences \((O_i - E_i)^2\)
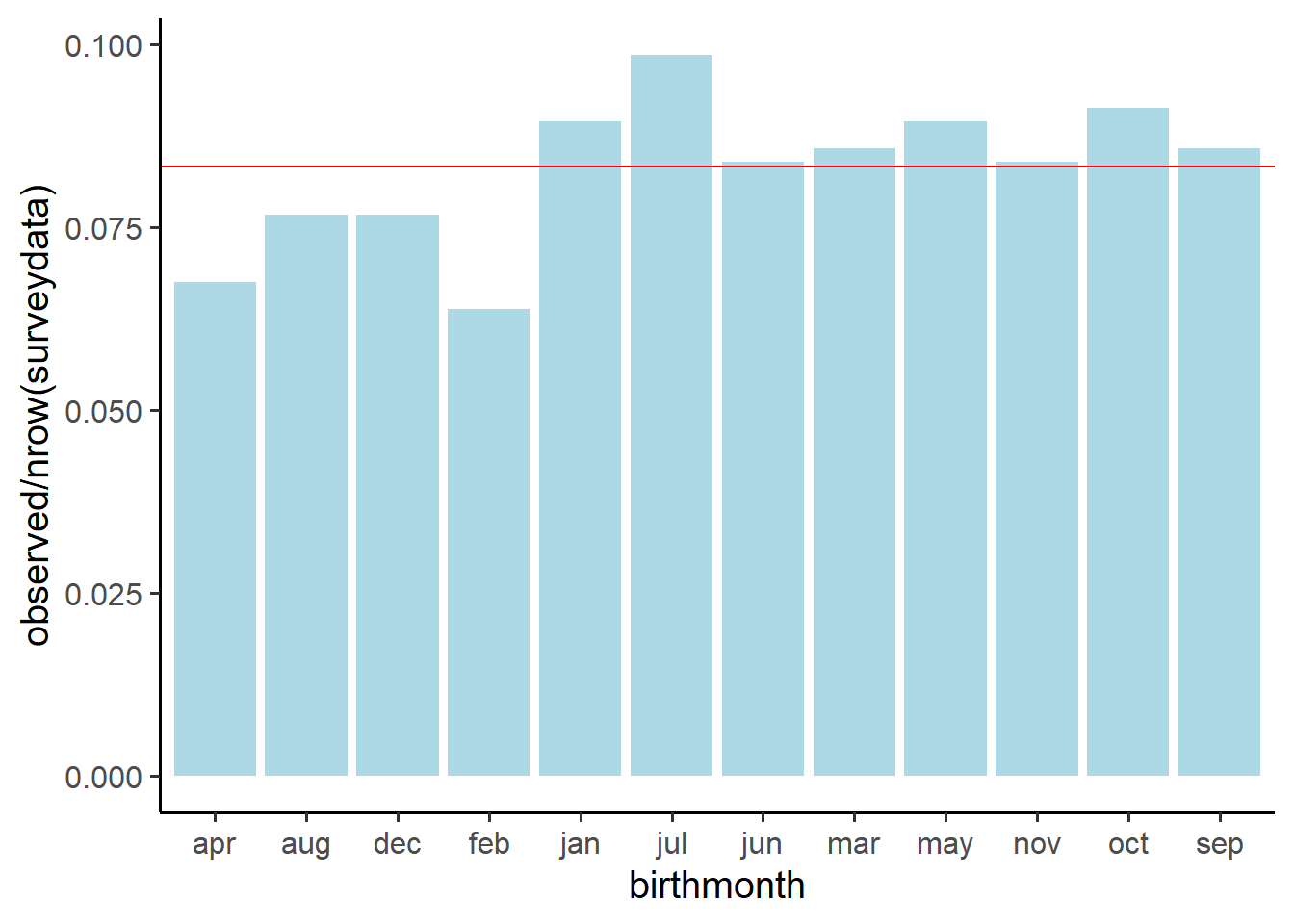
• the standardised square differences \(\frac{(O_i - E_i)^2}{E_i}\)

Then calculate the \(\chi^2\) statistic (the sum of the standardised squared differences).
If your observed counts matched the expected counts perfectly, what would the \(\chi^2\) statistic be?

Hints

This was all done in the step-by-step example of a \(\chi^2\) test in 4A #chi2-goodness-of-fit-test

chi_table <- 
    surveydata |>
    filter(!is.na(birthmonth)) |>
    group_by(birthmonth) |>
    summarise(
        observed = n(),
        expected = sum(!is.na(surveydata$birthmonth))/12,
        diff = observed-expected,
        sq_diff = diff^2,
        std_sq_diff = sq_diff / expected
    )
chi_table

# A tibble: 12 × 6
   birthmonth observed expected   diff sq_diff std_sq_diff
   <chr>         <int>    <dbl>  <dbl>   <dbl>       <dbl>
 1 apr              31     39.2 -8.17   66.7        1.70  
 2 aug              38     39.2 -1.17    1.36       0.0348
 3 dec              37     39.2 -2.17    4.69       0.120 
 4 feb              31     39.2 -8.17   66.7        1.70  
 5 jan              40     39.2  0.833   0.694      0.0177
 6 jul              46     39.2  6.83   46.7        1.19  
 7 jun              41     39.2  1.83    3.36       0.0858
 8 mar              37     39.2 -2.17    4.69       0.120 
 9 may              42     39.2  2.83    8.03       0.205 
10 nov              43     39.2  3.83   14.7        0.375 
11 oct              43     39.2  3.83   14.7        0.375 
12 sep              41     39.2  1.83    3.36       0.0858

And we can calculate our \(\chi^2\) test statistic by simply summing the values in the last column we created:

sum(chi_table$std_sq_diff)

[1] 6.017021

If all our observed counts are equal to our expected counts, then the diff column above will be all \(0\), and \(0^2=0\), and \(\frac{0}{E_i}\) will be \(0\). So \(\chi^2\) will be \(0\).

Question 5

You can see the distribution of \(\chi^2\) statistics with different degrees of freedom below.

Figure 1: Chi-Square Distributions

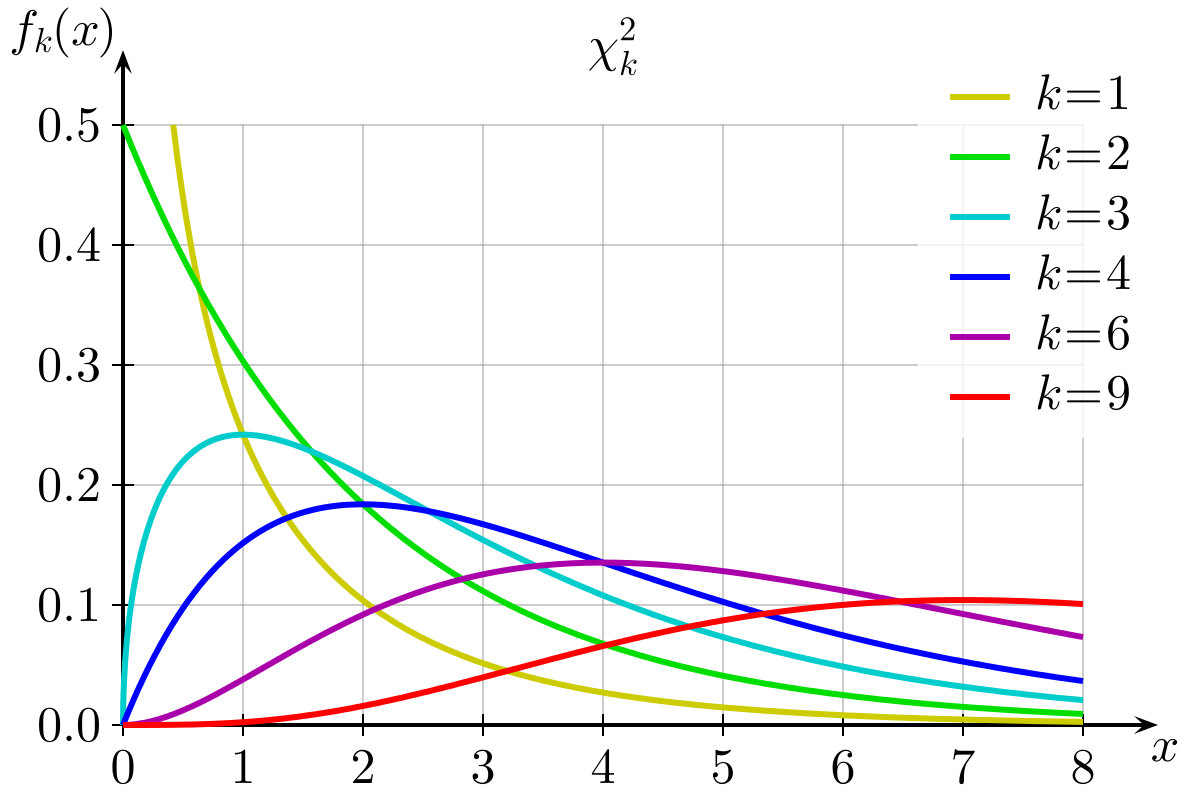
We can find out the proportion of the distribution which falls to either side of a given value of \(\chi^2\) using pchisq(). We need to give it our calculated \(\chi^2\) statistic, our degrees of freedom (df), which is equal to the number of categories minus 1. We also need to specify whether we want the proportion to the left (lower.tail=TRUE) or to the right (lower.tail=FALSE).

1. Using pchisq(), calculate the probability of observing a \(\chi^2\) statistic as least as extreme as the one we have calculated.
   
2. Check that these results match with those provided by R’s built-in function: chisq.test(table(surveydata$birthmonth)) (the table function will ignore NAs by default, so we don’t need to do anything extra for this).

sum(chi_table$std_sq_diff)

[1] 6.017021

pchisq(sum(chi_table$std_sq_diff), df = 11, lower.tail = FALSE)

[1] 0.8722261

chisq.test(table(surveydata$birthmonth))

    Chi-squared test for given probabilities

data:  table(surveydata$birthmonth)
X-squared = 6.017, df = 11, p-value = 0.8722

Question 6

Which months of year had the highest contributions to the chi-square test statistic?

Hints

Think about your standardised squared deviations.

Standardized squared deviations

One possible way to answer this question is to look at the individual contribution of each category to the \(\chi^2\) statistic. We computed these values in an earlier question.

chi_table |>
  select(birthmonth, std_sq_diff)

# A tibble: 12 × 2
   birthmonth std_sq_diff
   <chr>            <dbl>
 1 apr             1.70  
 2 aug             0.0348
 3 dec             0.120 
 4 feb             1.70  
 5 jan             0.0177
 6 jul             1.19  
 7 jun             0.0858
 8 mar             0.120 
 9 may             0.205 
10 nov             0.375 
11 oct             0.375 
12 sep             0.0858

From the barplot we created earlier on, we can see which months make up higher/lower proportions than expected:

ggplot(chi_table, aes(x = birthmonth, y = observed/nrow(surveydata))) +
  geom_col(fill = 'lightblue') +
  geom_hline(yintercept = 1/12, color = 'red') +
  theme_classic(base_size = 15)

Pearson residuals

Equivalently, you could answer by looking at Pearson residuals:

chisq.test(table(surveydata$birthmonth))$residuals

       apr        aug        dec        feb        jan        jul        jun 
-1.3049279 -0.1864183 -0.3462054 -1.3049279  0.1331559  1.0918785  0.2929430 
       mar        may        nov        oct        sep 
-0.3462054  0.4527301  0.6125172  0.6125172  0.2929430 

The greatest absolute values are for apr and feb, showing that for these months the deviations from expected to observed were the greatest.

Children’s Favourite Colours

Research Question: Do childrens’ favourite colours correspond to the those suggested by the internet?

According to one part of the internet, 30% of children have red as their favourite colour, 20% have blue, 15% yellow, 11% purple, 9% green, and 15% prefer some other colour.

We collected data from 50 children aged between 2 and 5, and got them to choose one of a set of objects that were identical apart from colour. You can see the data in Table 1

Table 1:

Colour preferences of 50 children aged between 2 and 5

colour	Freq
blue	10
green	6
other	3
purple	8
red	8
yellow	15

Question 7

Perform a \(\chi^2\) goodness of fit test to assess the extent to which our sample of children conform to this theorised distribution of colour preferences.

No need to do this manually - once is enough. Just go straight to using the chisq.test() function.
However, we will need to get the numbers into R somehow..

Hints

You can make a table from scratch using, for example: as.table(c(1,2,3,4,5)).

For the test, try using chisq.test(..., p = c(?,?,?,...) ).
We saw the use of chisq.test() in the example goodness of fit test, 4A #chi2-goodness-of-fit-test

Let’s get the data in:

childcols <- as.table(c(10,6,3,8,8,15))
names(childcols) <- c("blue","green","other","purple","red","yellow")
childcols

  blue  green  other purple    red yellow 
    10      6      3      8      8     15 

Our theoretical probabilities of different colours must match the order in the table which we give chisq.test(). They must also always sum to 1.

chisq.test(childcols, p = c(.20,.09,.15,.11,.30,.15))

Warning in chisq.test(childcols, p = c(0.2, 0.09, 0.15, 0.11, 0.3, 0.15)):
Chi-squared approximation may be incorrect

    Chi-squared test for given probabilities

data:  childcols
X-squared = 15.103, df = 5, p-value = 0.009931

Note, we get a warning here of “Chi-squared approximation may be incorrect”. This is because some of the expected cell counts are <5.

chisq.test(childcols, 
           p = c(.20,.09,.15,.11,.30,.15))$expected

  blue  green  other purple    red yellow 
  10.0    4.5    7.5    5.5   15.0    7.5 

There are a couple of options here, but the easiest is to use the functionality of chisq.test() that allows us to compute the p-value by using a simulation (similar to the idea we saw in 2B#sampling-&-sampling-distributions), rather than by comparing it to a theoretical \(\chi^2\) distribution. We can do this by using:

chisq.test(childcols, p = c(.20,.09,.15,.11,.30,.15),
           simulate.p.value = TRUE)

    Chi-squared test for given probabilities with simulated p-value (based
    on 2000 replicates)

data:  childcols
X-squared = 15.103, df = NA, p-value = 0.01249

Question 8

What are the observed proportions of our sample with each eyecolour?

Hints

Look up the prop.table() function?

From the help documentation (?prop.table()), we see that we can pass prop.table() the argument x, which needs to be a table.

prop.table(childcols)*100

  blue  green  other purple    red yellow 
    20     12      6     16     16     30 

barplot(prop.table(childcols)*100)

Jokes and Tips

Data: TipJokes

Research Question: Can telling a joke affect whether or not a waiter in a coffee bar receives a tip from a customer?

A study published in the Journal of Applied Social Psychology¹ investigated this question at a coffee bar of a famous seaside resort on the west Atlantic coast of France. The waiter randomly assigned coffee-ordering customers to one of three groups. When receiving the bill, one group also received a card telling a joke, another group received a card containing an advertisement for a local restaurant, and a third group received no card at all.

The data are available at https://uoepsy.github.io/data/TipJoke.csv.
The dataset contains the variables:

• Card: None, Joke, Ad.
• Tip: 1 = The customer left a tip, 0 = The customer did not leave tip.

Question 9

Produce a plot and a table to display the relationship between whether or not the customer left a tip, and what (if any) card they received alongside the bill.

Don’t worry about making it all pretty. Mosaic plots in R are a bit difficult.

Hints

plot(table(...)) will give you something. You can see one in the example \(\chi^2\) test of independence,4A #chi2-test-of-independence.

tipjoke <- read_csv('https://uoepsy.github.io/data/TipJoke.csv')

table(tipjoke$Card, tipjoke$Tip)

      
        0  1
  Ad   60 14
  Joke 42 30
  None 49 16

plot(table(tipjoke$Card, tipjoke$Tip))

Question 10

What would you expect the cell counts to look like if there were no relationship between what the waiter left and whether or not the customer tipped?

Hints

Think about what proportion of customers tipped. Then work out how many customers got each type of card. If there were no relationship, then the proportions would be the same in each group.

In total, 60 customers tipped (14+30+16), and 151 did not. So overall, 0.28 (\(\frac{60}{(60+151)}\)) of customers tip.

74 customers got an Ad card, 72 customers got a Joke, and 65 got None. If this were independent of whether or not they left a tip, we would expect equal proportions of tippers in each group.
So we would expect 0.28 of each group to leave a tip.

some calculations

You can think about observed vs expected by looking at the two-way table along with the marginal row and column totals given:

	0	1
Ad			74
Joke			72
None			65
	151	60	211

For a given cell of the table we can calculate the expected count as \(\text{row total} \times \frac{\text{column total}}{\text{samplesize}}\):

Expected:

	0	1
Ad	52.96	21.04	74
Joke	51.53	20.47	72
None	46.52	18.48	65
	151.00	60.00	211

If you’re wondering how we do this in R.. here’s our table:

t <- tipjoke |>
  select(Card, Tip) |> table()
t

      Tip
Card    0  1
  Ad   60 14
  Joke 42 30
  None 49 16

Here are the row totals:

rowSums(t)

  Ad Joke None 
  74   72   65 

and column totals divided by total:

colSums(t) / sum(t)

        0         1 
0.7156398 0.2843602 

there’s a complicated bit of code using %o% which could do this for us. You don’t need to remember %o%, it’s very rarely used):

e <- rowSums(t) %o% colSums(t) / sum(t)
e

            0        1
Ad   52.95735 21.04265
Joke 51.52607 20.47393
None 46.51659 18.48341

Or, alternatively, do it one by one:

rowSums(t) * (colSums(t) / sum(t))[1]

      Ad     Joke     None 
52.95735 51.52607 46.51659 

rowSums(t) * (colSums(t) / sum(t))[2]

      Ad     Joke     None 
21.04265 20.47393 18.48341 

Question 11

Just like we gave the chisq.test() function a table of observed frequencies when we conducted a goodness of fit test in earlier exercises, we can give it a two-way table of observed frequencies to conduct a test of independence.

Try it now.

chisq.test(table(tipjoke$Card, tipjoke$Tip))

    Pearson's Chi-squared test

data:  table(tipjoke$Card, tipjoke$Tip)
X-squared = 9.9533, df = 2, p-value = 0.006897

Some RMarkdown

Using one of the \(t\)-tests we saw in the previous week’s exercises, we can use an RMarkdown document in which we write our results so that they get compiled to look nice and pretty:

Writing this

Compiles to this

A one-sided one-sample t-test was conducted in order to determine if the average score on the Procrastination Assessment Scale for Students (PASS) for a sample of 20 students at Edinburgh University was significantly lower (\(\alpha = .05\)) than the average score obtained during development of the PASS.

Edinburgh University students scored lower (Mean = 30.7, SD = 3.31) than the score reported by the authors of the PASS (Mean = 33). This difference was statistically significant (t(19)=-3.11, p < .05, one-tailed).

This is one of the huge benefits of RMarkdown. Imagine we collected more data - we wouldn’t have to edit all the results, we could simply recompile and they would update for us!
Note how it works:

• the code chunk saves the results of the t.test() function as a named object res2.
• in text, the backticks `r … … … ` are used to execute small bits of R code, and include the output within the text. For instance, the line `r res2$statistic |> round(2)` gets the t-statistic from the results, and rounds it to 2 decimal places, which get’s printed out as -3.11.
• the bits between the dollar signs, e.g. $\alpha$ will get printed as mathematical symbols such as \(\alpha\).

RMarkdown documents are self-contained.

You need to to put everything that is needed to reproduce your analysis in the correct order.

For instance, if you have used the console (bottom left window) to define an object peppapig <- 30, you will have an object in your environment (top right window) called “peppapig” which has the value 30.

If you were to refer to that object in your RMarkdown document, you will be able to run a line of code such as peppapig/10 because it will find the “peppapig” object in your environment. BUT you won’t be able to compile the document because it “starts fresh” (i.e., compiles within its own environment). In order for it to compile, you would need to define what “peppapig” is inside your document, and before the document then refers to it.

The same applies with using functions in from packages. The RMarkdown document needs to know what packages to load before it uses functions from them. Just because you yourself have loaded a package in your session, it does not mean the compilation process for your RMarkdown has access to it.

If you want some extra explanations on these aspects of RMarkdown, then please see Lessons 0-3 of our Rmd-bootcamp.

Question 12

Can you create an RMarkdown document which:

1. Reads in the https://uoepsy.github.io/data/TipJoke.csv data.
2. Conducts and reports a \(\chi^2\) test of independence examining whether telling a joke affect whether or not a waiter in a coffee bar receives a tip from a customer.
3. Successfully compiles (“knits”) into an .html file.

Optional Extras

Question

Research Question: Do childrens’ favourite colours differ from Adults?

Along with the 50 children from whom we collected data on their favourite colours, we also had 100 adult participants. You can see the data in Table 2

Table 2:

Colour preferences of 50 children aged between 2 and 5, and 50 Adults (aged 18+)

colour	children	adults
blue	10	24
green	6	11
other	3	19
purple	8	7
red	8	24
yellow	15	15

Getting this into R is a little more tricky, so we’re giving you the code below:

as.table(matrix(c(10,6,3,8,8,15,24,11,19,7,24,15), ncol=2))

   A  B
A 10 24
B  6 11
C  3 19
D  8  7
E  8 24
F 15 15

Conduct an appropriate test to address the research question.

childadult <- as.table(matrix(c(10,6,3,8,8,15,24,11,19,7,24,15), ncol=2))

chisq.test(childadult)

    Pearson's Chi-squared test

data:  childadult
X-squared = 11.556, df = 5, p-value = 0.04141

Footnotes

1. Gueaguen, N. (2002). The Effects of a Joke on Tipping When It Is Delivered at the Same Time as the Bill. Journal of Applied Social Psychology, 32(9), 1955-1963.