Week 11 Exercises: More SEM!

Prenatal Stress & IQ data

A researcher is interested in the effects of prenatal stress on child cognitive outcomes.
She has a 5-item measure of prenatal stress and a 5 subtest measure of child cognitive ability, collected for 500 mother-infant dyads.

• The data is available as a .csv file here: https://uoepsy.github.io/data/stressIQ.csv

variable	description
ID	Participant ID
stress1	acute stress
stress2	chronic stress
stress3	environmental stress
stress4	psychological stress
stress5	physiological stress
IQ1	verbal ability
IQ2	verbal memory
IQ3	inductive reasoning
IQ4	spatial orientiation
IQ5	perceptual speed

Question 1

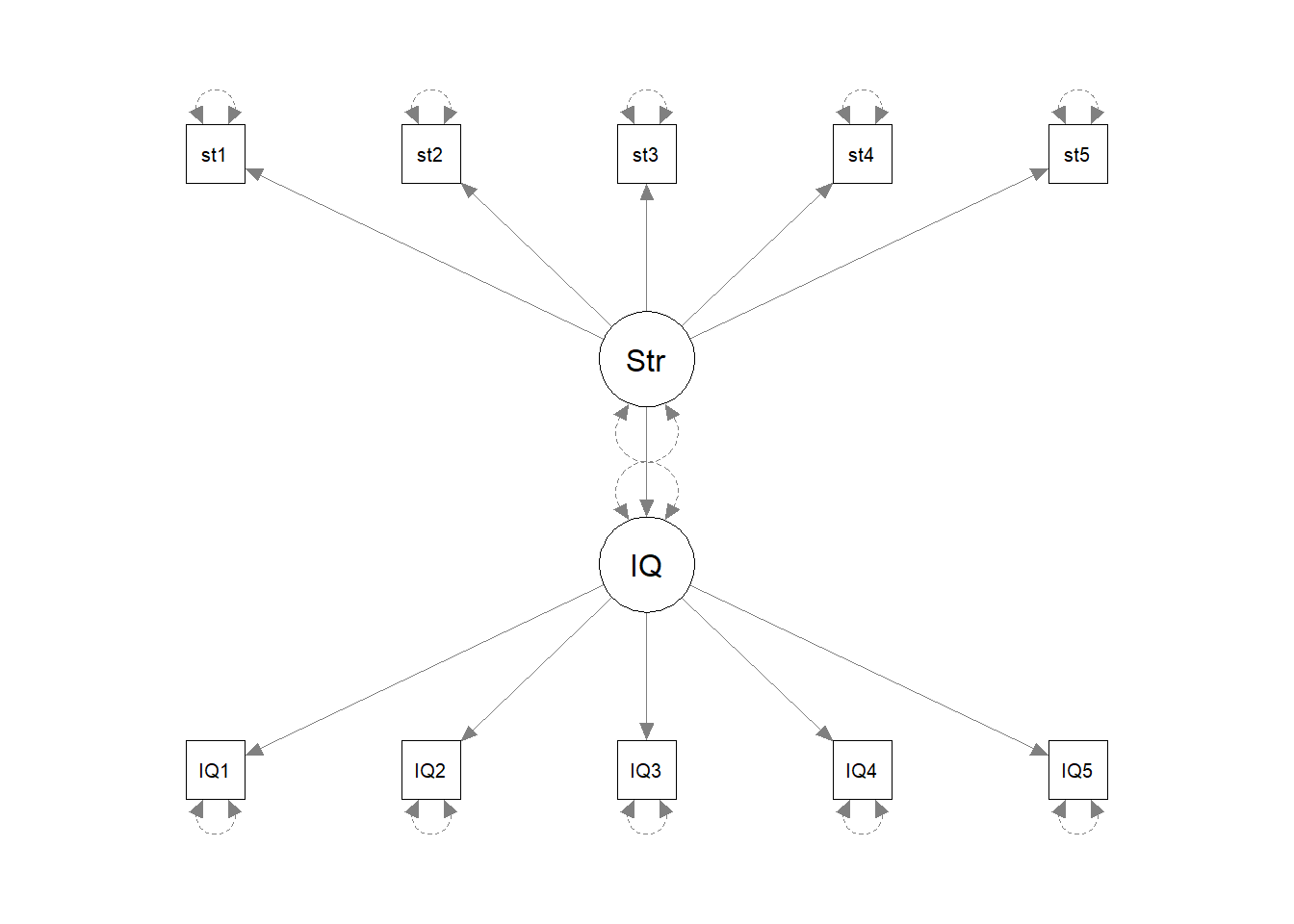
Before we do anything with the data, grab some paper and sketch out the full model that you plan to fit to address the researcher’s question.

Tip: everything you need is in the description of the data. Start by drawing the specific path(s) of interest. Are these between latent variables? If so, add in the paths to the indicators for each latent variable.

The main parameter of interest here is “the effects of prenatal stress on child cognitive outcomes”. So we have an arrow going from Stress to IQ.
Each of these are latent variables, for which we have observed 5 indicator variables, so we have an arrow going from “IQ” to each of the 5 IQ items, and from “Stress” to the 5 stress items.

Question 2

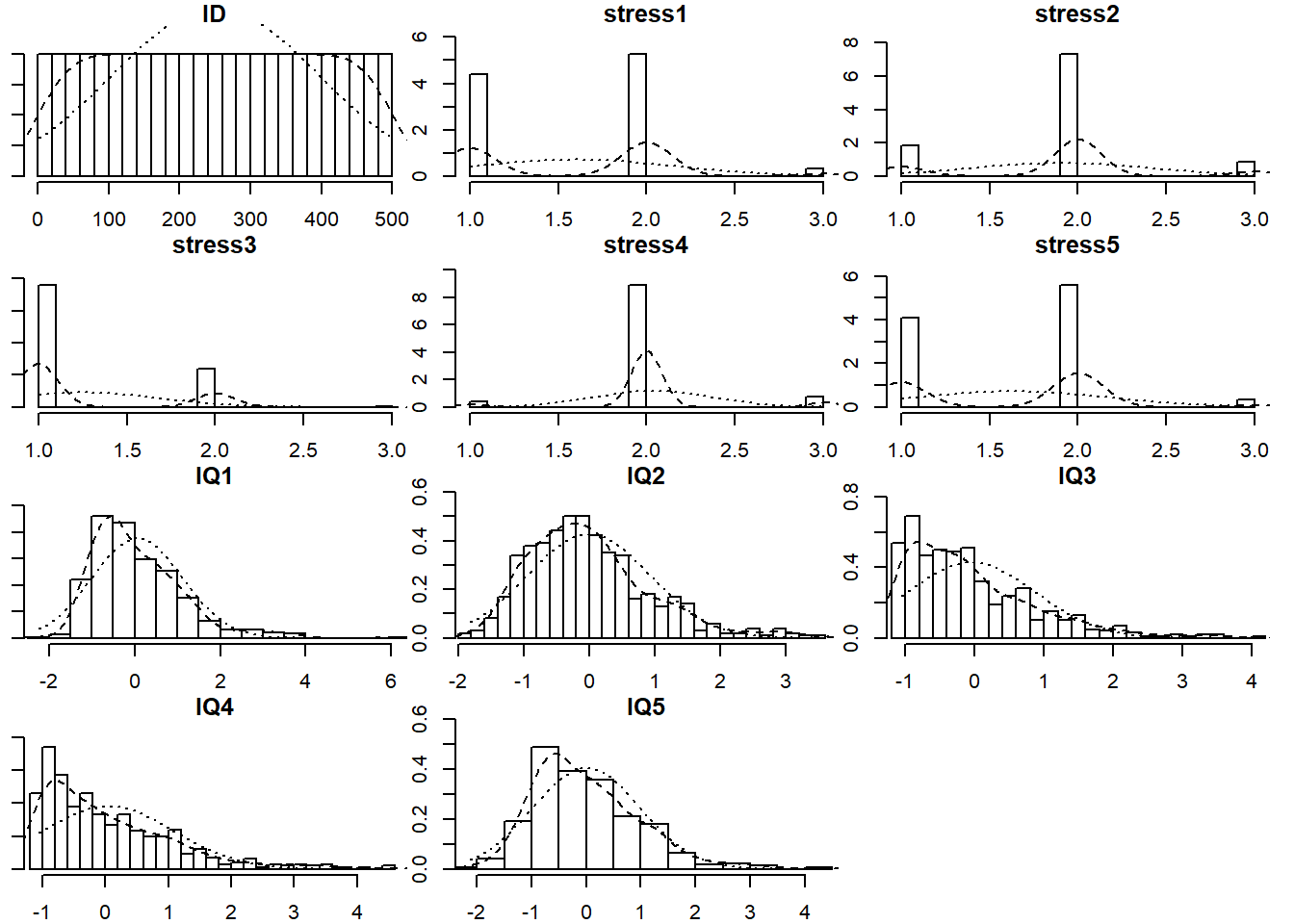
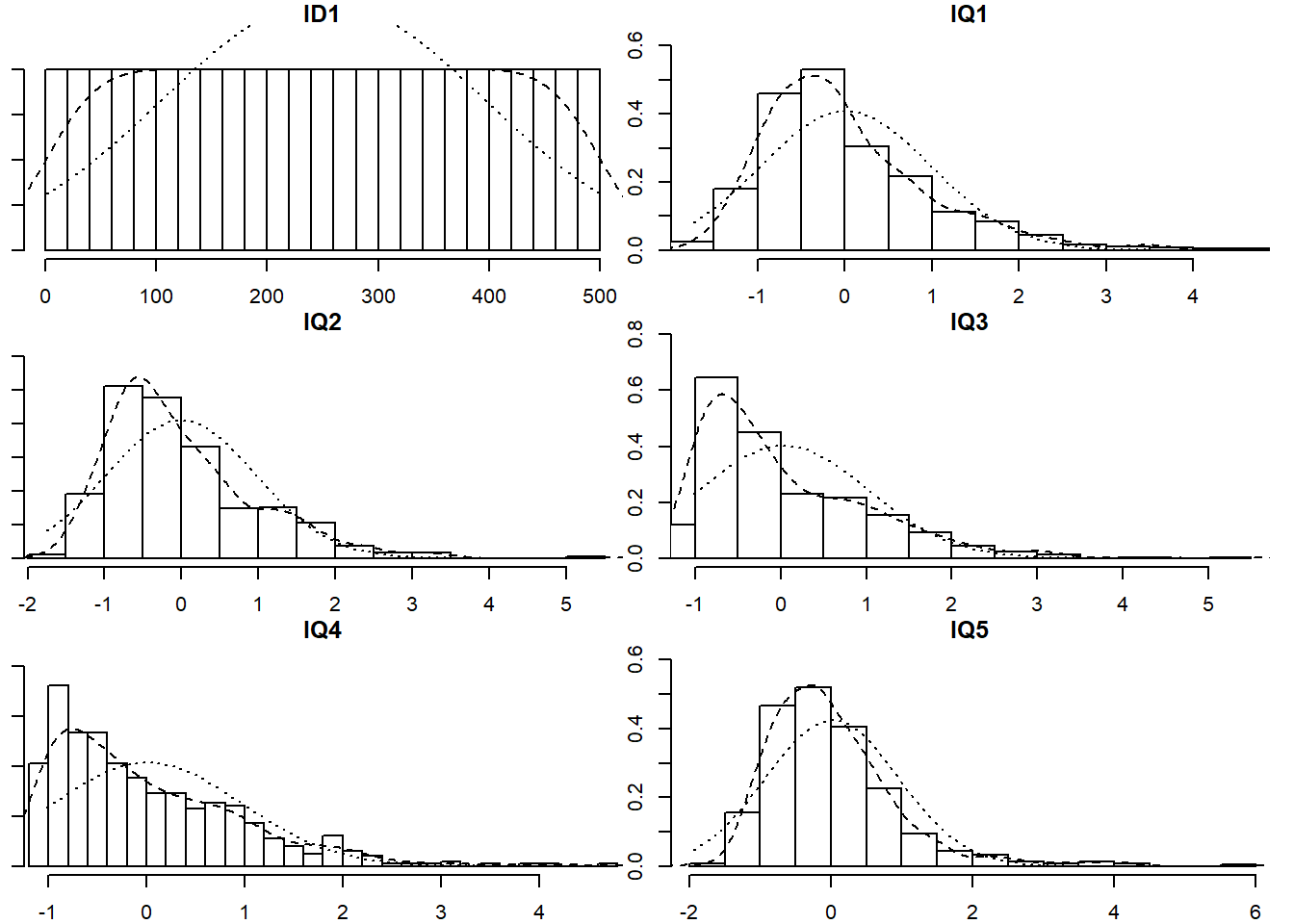
Read in the data and explore it. Look at the individual distributions of each variable to get a sense of univariate normality, as well as the number of response options each item has.

Hints

The multi.hist() function from the psych package is pretty useful for getting quick histograms of multiple variables. If necessary, you can set multi.hist(data, global = FALSE) to let each histogram’s x-axis be on a different scale.

library(tidyverse)
library(psych)

stress_IQ_data <- read_csv("https://uoepsy.github.io/data/stressIQ.csv")

This gives us a whole load of descriptives, means, standard deviations, and other things like skew and kurtosis.

describe(stress_IQ_data) # from psych package

        vars   n   mean     sd median trimmed    mad   min    max  range  skew
ID         1 500 250.50 144.48 250.50  250.50 185.32  1.00 500.00 499.00  0.00
stress1    2 500   1.59   0.56   2.00    1.57   0.00  1.00   3.00   2.00  0.22
stress2    3 500   1.90   0.51   2.00    1.90   0.00  1.00   3.00   2.00 -0.16
stress3    4 500   1.24   0.43   1.00    1.18   0.00  1.00   3.00   2.00  1.26
stress4    5 500   2.03   0.33   2.00    2.00   0.00  1.00   3.00   2.00  0.57
stress5    6 500   1.63   0.55   2.00    1.61   0.00  1.00   3.00   2.00  0.10
IQ1        7 500   0.06   1.06  -0.18   -0.06   0.94 -2.25   6.02   8.28  1.28
IQ2        8 500  -0.01   0.93  -0.13   -0.09   0.83 -1.83   3.58   5.40  0.93
IQ3        9 500  -0.06   0.93  -0.28   -0.19   0.85 -1.07   4.05   5.12  1.34
IQ4       10 500   0.04   1.04  -0.24   -0.11   0.94 -1.07   4.56   5.63  1.40
IQ5       11 500   0.00   0.98  -0.16   -0.08   0.91 -2.14   4.35   6.48  0.95
        kurtosis   se
ID         -1.21 6.46
stress1    -0.90 0.02
stress2     0.65 0.02
stress3    -0.19 0.02
stress4     5.78 0.01
stress5    -0.87 0.02
IQ1         2.72 0.05
IQ2         1.08 0.04
IQ3         1.93 0.04
IQ4         2.17 0.05
IQ5         1.39 0.04

Here we can see the distribution of each variable. Some immediate things of note - the stress items are only measured on 3 response options, and the IQ items are quite positively skewed (we can see this matches with the skew metrics above).

multi.hist(stress_IQ_data, global = FALSE) # from psych package

Non-normality

Question 3

Fit a one factor CFA for the IQ items using an appropriate estimation method.

Be sure to first check their distributions (both numerically and visually). The describe() function from the psych package will give you measures of skew and kurtosis.

Multivariate Normality (MVN)

One of the key assumptions of the models we have been fitting so far is that our variables are all normally distributed, and are continuous. Why?

Recall how we first introduced the idea of estimating a SEM: comparing the observed covariance matrix with our model implied covariance matrix. This heavily relies on the assumption that our observed covariance matrix provides a good representation of our data - i.e., that \(var(x_i)\) and \(cov(x_i,x_j)\) are adequate representations of the relations between variables. While this is true if we have a “multivariate normal distribution”, things become more difficult when our variables are either not continuous or not normally distributed.

The multivariate normal distribution is fundamentally just the extension of our univariate normal (the bell-shaped curve we are used to seeing) to more dimensions. The condition which needs to be met is that every linear combination of the \(k\) variables has a univariate normal distribution. It is denoted by \(N(\boldsymbol{\mu}, \boldsymbol{\Sigma})\) (note that the bold font indicates that \(\boldsymbol{\mu}\) and \(\boldsymbol{\Sigma}\) are, respectively, a vector of means and a matrix of covariances).¹
The idea of the multivariate normal can be a bit difficult to get to grips with in part because there’s not an intuitive way to visualise it once we move beyond 2 or 3 variables.

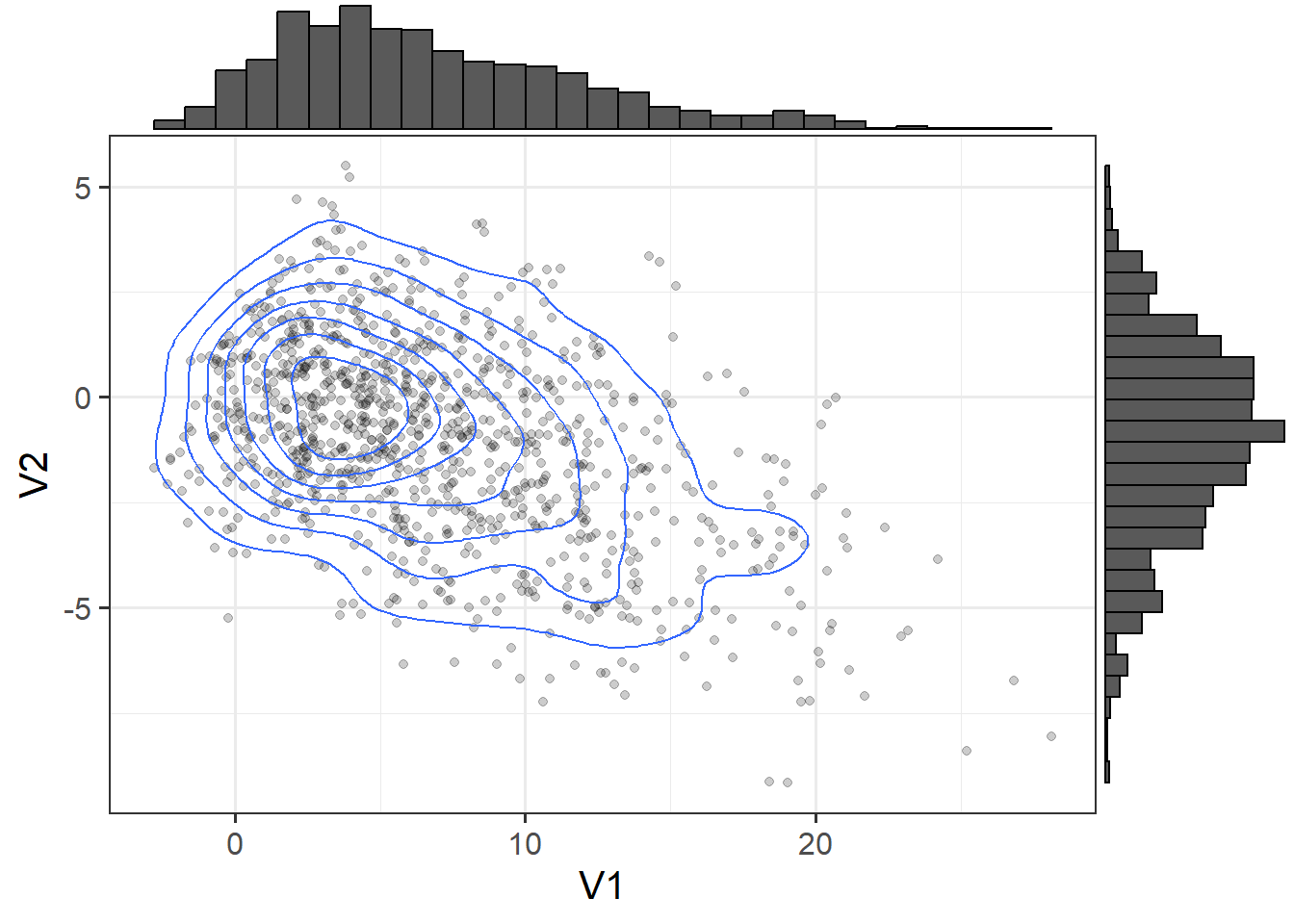
With 2 variables, you can think of it just like a density plot but in 3 dimensions, as in Figure 1. You can also represent this as a “contour” plot, which is like looking down on Figure 1 from above (just like a map!)

Figure 1: Bivariate Normal

Now let’s look at a situation where we have some skewed variables. Figure 2 shows such a distribution, and Figure 3 shows the contour plot (i.e. it is like Figure 2 viewed from above).

3D

Figure 2: Joint distribution of some skewed variables

Contour

Figure 3: Contour plot for a non-normal bivariate distribution. Marginal distributions of each variable are presented along each axis

simulations from a covariance matrix

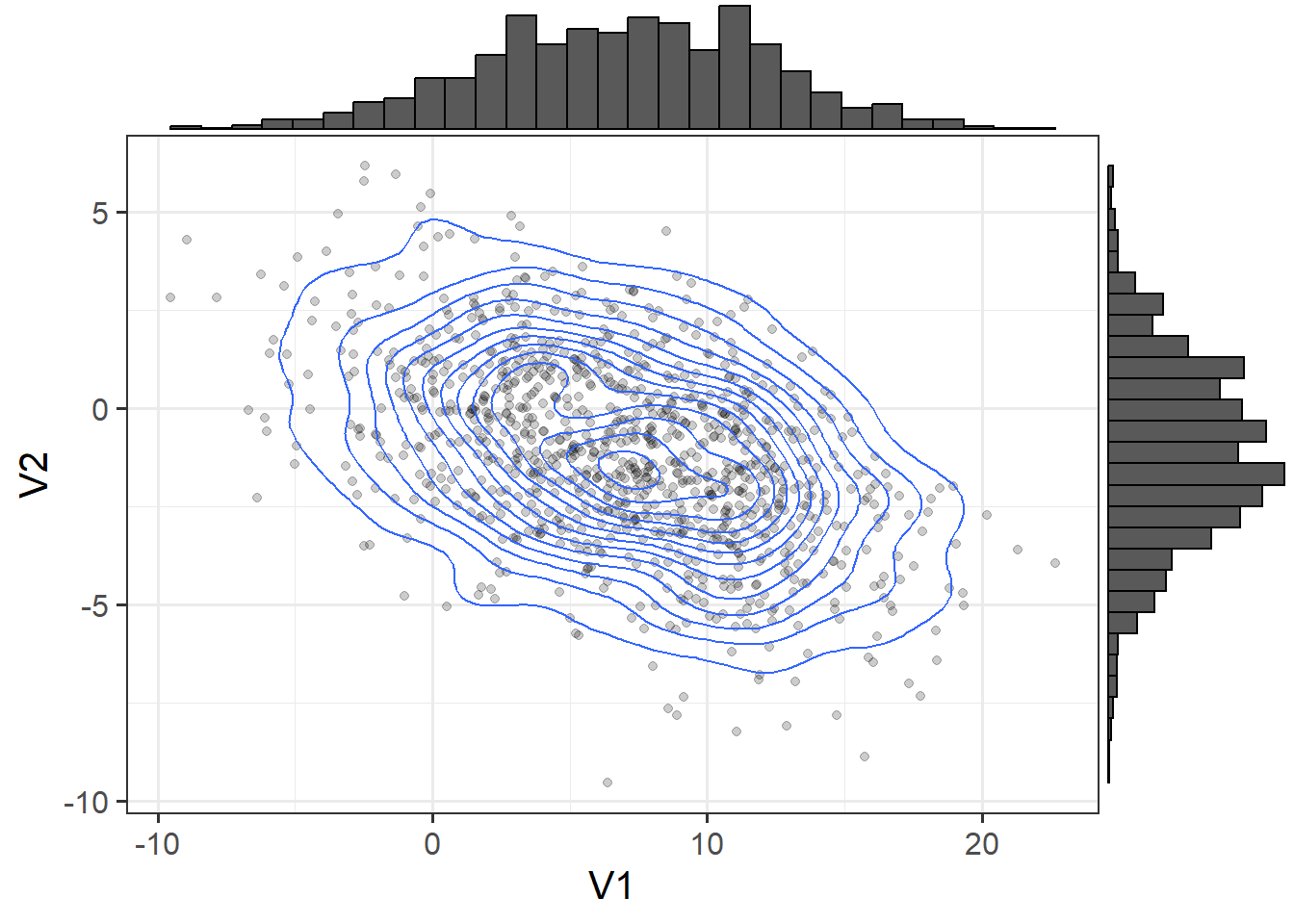
If we compute our covariance matrix from the 2 skewed variables, we get:

          V1        V2
V1 27.822839 -5.770942
V2 -5.770942  5.542513

But this fails to capture information about important properties of the data relating to features such as skew (lop-sided-ness) and kurtosis (pointiness). As an example, if we were to simulate data based on this covariance matrix, we get something like Figure 4, which is clearly limited in its reflection of our actual data.

3D

Figure 4: Probability distribution of simulations based on a covariance matrix (of some skewed variables). The covariance matrix contains only 2 ‘moments’ of the variables: their scale (spread) and location (center)

Contour

Figure 5: Contour plot for simulated data from a covariance matrix

Non-normality & Robust Estimation

For determining what constitutes deviations from normality, there are various ways to calculate the skewness and kurtosis of univariate distributions (see Joanes, D.N. and Gill, C.A (1998). Comparing measures of sample skewness and kurtosis if you’re interested). In addition, there are various suggested rules of thumb we can follow. Below are the most common:

Skewness rules of thumb:

• \(|skew| < 0.5\): fairly symmetrical
• \(0.5 < |skew| < 1\): moderately skewed
• \(1 < |skew|\): highly skewed

Kurtosis rule of thumb:

• \(Kurtosis > 3\): Heavier tails than the normal distribution. Possibly problematic

What we can do

In the event of non-normality, we can still use maximum likelihood to find our estimated factor loadings, coefficients and covariances. However, our standard errors (and our \(\chi^2\) model fit) will be biased. We can use a robust maximum likelihood estimator that essentially applies corrections to the standard errors² and \(\chi^2\) statistic.

There are a few robust estimators in lavaan, but one of the more frequently used ones is “MLR” (maximum likelihood with robust SEs). You can find all the other options at https://lavaan.ugent.be/tutorial/est.html.
We can make use of these with: sem(model, estimator="MLR") or cfa(model, estimator="MLR").

We should check the item distributions for evidence of non-normality (skewness and kurtosis). We can use the describe() function from psych and plot the data using histograms or density curves.

Code

library(kableExtra)

# this is just describe() but dressed up to make a nice table output (the one we see below)
stress_IQ_data |> 
    select(contains("IQ")) |> 
    describe() |> 
    as.data.frame() |>
    rownames_to_column(var = "variable") |> 
    select(variable,mean,sd,skew,kurtosis) |>
    kable(digits = 2) |>
    kable_styling(full_width = FALSE)

variable	mean	sd	skew	kurtosis
IQ1	0.06	1.06	1.28	2.72
IQ2	-0.01	0.93	0.93	1.08
IQ3	-0.06	0.93	1.34	1.93
IQ4	0.04	1.04	1.40	2.17
IQ5	0.00	0.98	0.95	1.39

It looks like some of our IQ items are pretty skewed. Let’s plot them.

multi.hist

stress_IQ_data |> 
  select(contains("IQ")) |> 
  multi.hist()

ggplot

## GGPLOT
# temporarily reshape the data to long format to make it quicker to plot
stress_IQ_data |> 
  pivot_longer(IQ1:IQ5, names_to="variable",values_to="score") |>
  ggplot(aes(x=score))+
  geom_density()+
  facet_wrap(~variable)+
  theme_light()

Because our variables seem to be non-normal, therefore, we should use a robust estimator such as MLR for our CFA

model_IQ <- 'IQ =~ IQ1 + IQ2 + IQ3 + IQ4 + IQ5'

model_IQ.est <- cfa(model_IQ, data=stress_IQ_data, estimator='MLR')

Question 4

Examine the fit of the CFA model of IQ.
If it doesn’t fit very well, consider checking for areas of local misfit (i.e., check your modindices()), and adjust your model accordingly.

We also get out robust fit measures, so we should ask for them:

fitmeasures(model_IQ.est)[c("rmsea.robust","srmr","cfi.robust","tli.robust")]

rmsea.robust         srmr   cfi.robust   tli.robust 
  0.18420861   0.05713656   0.90814181   0.81628363 

The model doesn’t fit very well so we could check the modification indices for local mis-specifications

modindices(model_IQ.est, sort=T) |> head()

   lhs op rhs     mi    epc sepc.lv sepc.all sepc.nox
12 IQ1 ~~ IQ2 82.653  0.302   0.302    0.762    0.762
21 IQ4 ~~ IQ5 48.799  0.224   0.224    0.397    0.397
17 IQ2 ~~ IQ4 29.875 -0.166  -0.166   -0.349   -0.349
14 IQ1 ~~ IQ4 15.906 -0.138  -0.138   -0.268   -0.268
15 IQ1 ~~ IQ5 15.870 -0.132  -0.132   -0.279   -0.279
19 IQ3 ~~ IQ4 15.720  0.122   0.122    0.216    0.216

It looks like we might need to include residual covariances between the items IQ1 and IQ2 and maybe also between items IQ4 and IQ5. As always, we need to double check this makes substantive sense. Items IQ1 and IQ2 measure verbal comprehension and verbal memory - people might be likely to score low/high on both of these due to their verbal ability. IQ4 and IQ5 might be both related due to both being tests requiring visual perception, but it’s less obvious. We’d probably want to know more about the specific tests undertaken.

model2_IQ <- '
    IQ=~IQ1+IQ2+IQ3+IQ4+IQ5
    IQ1~~IQ2
'
model2_IQ.est <- cfa(model2_IQ, data=stress_IQ_data, estimator='MLR')

The fit of the model is now much improved! and our loadings are all significant and \(>|0.3|\).
The RMSEA is still in that grey area between 0.05 and 0.08, so we would probably want to flag this when writing up. We could keep trying to add stuff in order to get it below 0.05, but that means a high risk of overfitting.

fitmeasures(model2_IQ.est)[c("rmsea.robust","srmr","cfi.robust","tli.robust")]

rmsea.robust         srmr   cfi.robust   tli.robust 
  0.07556791   0.02590197   0.98763304   0.96908261 

summary(model2_IQ.est, standardized=T)

lavaan 0.6-18 ended normally after 21 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        11

  Number of observations                           500

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                16.196      13.567
  Degrees of freedom                                 4           4
  P-value (Chi-square)                           0.003       0.009
  Scaling correction factor                                  1.194
    Yuan-Bentler correction (Mplus variant)                       

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  IQ =~                                                                 
    IQ1               1.000                               0.688    0.651
    IQ2               0.842    0.059   14.330    0.000    0.579    0.622
    IQ3               0.889    0.084   10.605    0.000    0.611    0.659
    IQ4               1.136    0.110   10.280    0.000    0.781    0.749
    IQ5               1.069    0.096   11.128    0.000    0.735    0.748

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
 .IQ1 ~~                                                                
   .IQ2               0.275    0.044    6.183    0.000    0.275    0.469

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .IQ1               0.644    0.079    8.191    0.000    0.644    0.577
   .IQ2               0.533    0.049   10.783    0.000    0.533    0.613
   .IQ3               0.487    0.058    8.388    0.000    0.487    0.566
   .IQ4               0.479    0.054    8.807    0.000    0.479    0.440
   .IQ5               0.426    0.046    9.319    0.000    0.426    0.441
    IQ                0.473    0.074    6.364    0.000    1.000    1.000

Ordered Categoricals

Question 5

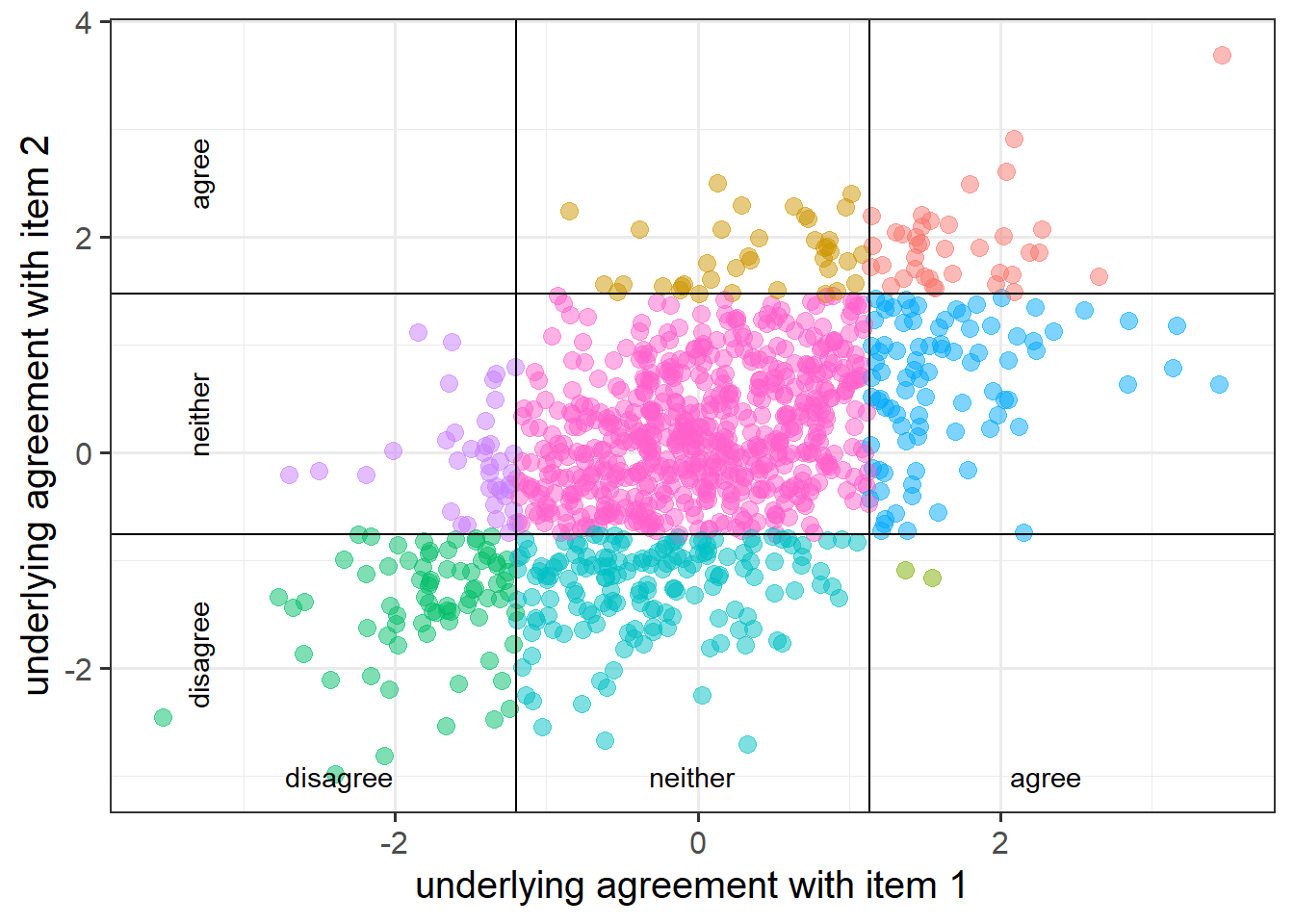
Fit a one-factor confirmatory factor analysis for the latent factor of Stress. Note that the items are measured on a 3-point scale!

Ordered-Categorical Endogenous Variables

Sometimes we can treat ordinal data as if it is continuous. When exactly this is appropriate is a contentious issue - some statisticians might maintain that it is never appropriate to treat ordinal data as continuous. In psychology, much research using SEM centers around questionnaire data, which lends itself to likert data (for instance, “strongly agree”,“agree”,“neither agree nor disagree”,“disagree”,“strongly disagree”). An often used rule of thumb is that likert data with \(\geq 5\) levels can be treated as if they are continuous without unduly influencing results (see Johnson, D.R., & Creech, J.C. (1983). Ordinal measures in multiple indicator models: A simulation study of categorization error).

But what if we don’t have 5+ levels? An important note is that even if your questionnaire included 5 response options for people to choose from, if participants only used 3 of them, then you actually have a variable with just 3 levels.

Estimation techniques exist that allow us to model such variables by considering the set of ordered responses to correspond to portions of an underlying continuum. This involves estimating the ‘thresholds’ of that underlying distribution at which people switch from giving one response to the next.

Rather than working with correlations, this method involves using “polychoric correlations”, which are estimates of the correlation between two theorized normally distributed continuous variables, based on their observed ordinal manifestations.

Figure 6: the idea of polychoric correlation is to estimate the correlation between two unobserved continuous variables by examining the distributions across the set of ordered categories that we do observe

What we can do

In R, lavaan will automatically switch to a categorical estimator (called “DWLS”³) if we tell it that we have some ordered-categorical variables. We can use the ordered = c("item1name","item2name","item3name", ...) argument.
This is true for both the cfa() and sem() functions.

library(lavaan)
library(semPlot)
# specify the model
model_stress <- 'Stress =~ stress1 + stress2 + stress3 + stress4 + stress5'

# estimate the model - cfa will automatically switch to a categorical estimator if we mention that our five variables are ordered-categorical, using the 'ordered' function
model_stress.est <- 
  cfa(model_stress, data=stress_IQ_data,
      ordered=c('stress1','stress2','stress3','stress4','stress5'))

Question 6

Inspect your summary model output. Notice that we have a couple of additional things - we have ‘scaled’ and ‘robust’ values for the fit statistics (we have a second column for all the fit indices but using a scaled version of the \(\chi^2\) statistic, and then we also have some extra rows of ‘robust’ measures), and we have the estimated ‘thresholds’ in our output (there are two thresholds per item in this example because we have a three-point response scale). The estimates themselves are not of great interest to us.

# inspect the output
fitmeasures(model_stress.est)[c("rmsea.robust","srmr","cfi.robust","tli.robust")]

rmsea.robust         srmr   cfi.robust   tli.robust 
  0.00000000   0.01234819   1.00000000   1.06512057 

summary(model_stress.est, standardized=TRUE)

lavaan 0.6-18 ended normally after 18 iterations

  Estimator                                       DWLS
  Optimization method                           NLMINB
  Number of model parameters                        15

  Number of observations                           500

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                 0.520       0.773
  Degrees of freedom                                 5           5
  P-value (Chi-square)                           0.991       0.979
  Scaling correction factor                                  0.740
  Shift parameter                                            0.070
    simple second-order correction                                

Parameter Estimates:

  Parameterization                               Delta
  Standard errors                           Robust.sem
  Information                                 Expected
  Information saturated (h1) model        Unstructured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  Stress =~                                                             
    stress1           1.000                               0.619    0.619
    stress2           1.111    0.121    9.214    0.000    0.688    0.688
    stress3           1.182    0.137    8.614    0.000    0.732    0.732
    stress4           1.049    0.130    8.089    0.000    0.649    0.649
    stress5           1.134    0.129    8.790    0.000    0.702    0.702

Thresholds:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    stress1|t1       -0.151    0.056   -2.680    0.007   -0.151   -0.151
    stress1|t2        1.825    0.108   16.973    0.000    1.825    1.825
    stress2|t1       -0.900    0.065  -13.806    0.000   -0.900   -0.900
    stress2|t2        1.379    0.081   17.124    0.000    1.379    1.379
    stress3|t1        0.700    0.061   11.399    0.000    0.700    0.700
    stress3|t2        2.878    0.315    9.124    0.000    2.878    2.878
    stress4|t1       -1.751    0.102  -17.198    0.000   -1.751   -1.751
    stress4|t2        1.461    0.084   17.324    0.000    1.461    1.461
    stress5|t1       -0.233    0.057   -4.107    0.000   -0.233   -0.233
    stress5|t2        1.825    0.108   16.973    0.000    1.825    1.825

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .stress1           0.616                               0.616    0.616
   .stress2           0.526                               0.526    0.526
   .stress3           0.464                               0.464    0.464
   .stress4           0.578                               0.578    0.578
   .stress5           0.507                               0.507    0.507
    Stress            0.384    0.064    6.011    0.000    1.000    1.000

Question 7

Now its time to build the full SEM.
Estimate the effect of prenatal stress on IQ.

Hints

Remember: We know that IQ is non-normal, so we would like to use a robust estimator (e.g. MLR). However, as lavaan will tell you if you try using estimator="MLR", this is not supported for ordered data (i.e., the Stress items). It suggests instead using the WLSMV (weighted least square mean and variance adjusted) estimator.

As it happens, the WLSMV estimator is just DWLS with a correction to return robust standard errors. If you specify estimator="WLSMV" then your standard errors will be corrected, but don’t be misled by the fact that the summary here will still say that the estimator is DWLS.

SEM_model <- '
    #IQ measurement model
    IQ =~ IQ1 + IQ2 + IQ3 + IQ4 + IQ5 
    IQ1 ~~ IQ2
    IQ4 ~~ IQ5

    #stress measurement model 
    Stress =~ stress1 + stress2 + stress3 + stress4 + stress5 

    #structural part of model
    IQ ~ Stress
'

SEM_model.est <- sem(SEM_model, data=stress_IQ_data,
                     ordered=c('stress1','stress2','stress3','stress4','stress5'),
                     estimator="WLSMV")

Let’s print out the full summary.
Note that when we have a mix of ordered categoricals and continuous variables, then we can’t get the robust estimates of the fit indices. These are now NA. We do still get the scaled versions though:

summary(SEM_model.est, fit.measures=T, standardized=T)

lavaan 0.6-18 ended normally after 31 iterations

  Estimator                                       DWLS
  Optimization method                           NLMINB
  Number of model parameters                        33

  Number of observations                           500

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                16.002      27.058
  Degrees of freedom                                32          32
  P-value (Chi-square)                           0.992       0.715
  Scaling correction factor                                  0.810
  Shift parameter                                            7.300
    simple second-order correction                                

Model Test Baseline Model:

  Test statistic                              2147.504    1242.141
  Degrees of freedom                                45          45
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.756

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    1.000       1.000
  Tucker-Lewis Index (TLI)                       1.011       1.006
                                                                  
  Robust Comparative Fit Index (CFI)                            NA
  Robust Tucker-Lewis Index (TLI)                               NA

Root Mean Square Error of Approximation:

  RMSEA                                          0.000       0.000
  90 Percent confidence interval - lower         0.000       0.000
  90 Percent confidence interval - upper         0.000       0.026
  P-value H_0: RMSEA <= 0.050                    1.000       1.000
  P-value H_0: RMSEA >= 0.080                    0.000       0.000
                                                                  
  Robust RMSEA                                                  NA
  90 Percent confidence interval - lower                        NA
  90 Percent confidence interval - upper                        NA
  P-value H_0: Robust RMSEA <= 0.050                            NA
  P-value H_0: Robust RMSEA >= 0.080                            NA

Standardized Root Mean Square Residual:

  SRMR                                           0.030       0.030

Parameter Estimates:

  Parameterization                               Delta
  Standard errors                           Robust.sem
  Information                                 Expected
  Information saturated (h1) model        Unstructured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  IQ =~                                                                 
    IQ1               1.000                               0.714    0.676
    IQ2               0.841    0.046   18.370    0.000    0.601    0.645
    IQ3               0.889    0.071   12.609    0.000    0.635    0.684
    IQ4               1.025    0.086   11.898    0.000    0.732    0.701
    IQ5               0.961    0.077   12.402    0.000    0.686    0.698
  Stress =~                                                             
    stress1           1.000                               0.612    0.612
    stress2           1.096    0.124    8.812    0.000    0.671    0.671
    stress3           1.253    0.150    8.334    0.000    0.767    0.767
    stress4           1.063    0.152    7.006    0.000    0.651    0.651
    stress5           1.135    0.126    8.993    0.000    0.695    0.695

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  IQ ~                                                                  
    Stress            0.456    0.082    5.575    0.000    0.391    0.391

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
 .IQ1 ~~                                                                
   .IQ2               0.244    0.032    7.667    0.000    0.244    0.440
 .IQ4 ~~                                                                
   .IQ5               0.098    0.037    2.649    0.008    0.098    0.186

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .IQ1               0.059    0.059    1.013    0.311    0.059    0.056
   .IQ2              -0.009    0.049   -0.182    0.856   -0.009   -0.010
   .IQ3              -0.056    0.056   -0.989    0.322   -0.056   -0.060
   .IQ4               0.040    0.064    0.620    0.535    0.040    0.038
   .IQ5               0.001    0.051    0.017    0.987    0.001    0.001

Thresholds:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    stress1|t1       -0.151    0.056   -2.680    0.007   -0.151   -0.151
    stress1|t2        1.825    0.108   16.973    0.000    1.825    1.825
    stress2|t1       -0.900    0.065  -13.806    0.000   -0.900   -0.900
    stress2|t2        1.379    0.081   17.124    0.000    1.379    1.379
    stress3|t1        0.700    0.061   11.399    0.000    0.700    0.700
    stress3|t2        2.878    0.315    9.124    0.000    2.878    2.878
    stress4|t1       -1.751    0.102  -17.198    0.000   -1.751   -1.751
    stress4|t2        1.461    0.084   17.324    0.000    1.461    1.461
    stress5|t1       -0.233    0.057   -4.107    0.000   -0.233   -0.233
    stress5|t2        1.825    0.108   16.973    0.000    1.825    1.825

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .IQ1               0.607    0.046   13.209    0.000    0.607    0.543
   .IQ2               0.507    0.037   13.568    0.000    0.507    0.584
   .IQ3               0.457    0.037   12.242    0.000    0.457    0.532
   .IQ4               0.553    0.045   12.365    0.000    0.553    0.508
   .IQ5               0.495    0.043   11.554    0.000    0.495    0.513
   .stress1           0.625                               0.625    0.625
   .stress2           0.550                               0.550    0.550
   .stress3           0.411                               0.411    0.411
   .stress4           0.576                               0.576    0.576
   .stress5           0.517                               0.517    0.517
   .IQ                0.432    0.053    8.205    0.000    0.847    0.847
    Stress            0.375    0.065    5.783    0.000    1.000    1.000

We can see that the effect of prenatal stress on offspring IQ is \(\beta\) = 0.456 and is statistically significant at \(p<.05\).

Missingness

Question 8

In order to try and replicate the IQ CFA, our researcher collects a new sample of size \(n=500\). However, she has some missing data (specifically, those who scored poorly on earlier tests tended to feel discouraged and chose not to complete further tests).

Read in the new dataset, plot and numerically summarise the univariate distributions of the measured variables, and then conduct a CFA using the new data, taking account of the missingness (don’t forget to also use an appropriate estimator to account for any non-normality). Does the model fit well?

• The data can be found at https://uoepsy.github.io/data/IQdatam.csv, and is in .csv format.

Missingness

It is very common to have missing data. Participants may stop halfway through the study, may decline to be followed up (if it is longitudinal) or may simply decline to answer certain sections. In addition, missing data can occur for all sorts of technical reasons (e.g, website crash and auto-submit a questionnaire, etc.).

It is important to understand the possible reasons for missing data in order to appropriately consider what data you do have. If missing data are missing completely random, then the data you do have should still be representative of the population. But suppose you are studying cognitive decline in an aging population, and people who are suffering from cognitive impairment are less likely to attend the follow-up assessments. Is this missingness random? No. Does it affect how you should consider your available data to represent the population of interest? Yes.

There are three main reasons that we certain data may be missing, and the acronyms are a nightmare:⁴

• MCAR: Missing Completely At Random. Data which are MCAR are missing data for which the propensity for missingness is completely independent of any observed or unobserved variables. It is truly random if the data are missing or not.

• MAR: Missing At Random. Data which are MAR are missing data for which the propensity for missingness is not random, but it can be fully explained by some variables for which there is complete data. In other words, there is a systematic relationship between missing values and observed values. For example, people who are unemployed at time of assessment will likely not respond to questions on work-life satisfaction. Missing values on work-life satisfaction is unrelated to the levels of work-life satisfaction, but related to their employment status.

• MNAR: Missing Not At Random. Data which are MNAR are missing data for which the propensity for missingness is related to the value which is missing. For example, suppose an employer tells employees that there are a limited number of bonuses to hand out, and then employees are asked to fill out a questionnaire. Thos who are less satisfied with their job may not respond to questions on job satisfaction (if they believe it will negatively impact their chances of receiving a bonus).

What we can do

In SEM, there is an extremely useful method known as full information maximum likelihood (FIML) which, allows us to use all our available data (including those that have only some values present).

FIML separates data into the different patterns of missingness (i.e. those that are missing on IQ1, those missing on IQ1 and IQ2, those missing on just IQ2, and so on). The likelihood of each group can be estimated from the parameters that are available for that pattern. The estimation process then finds the set of parameters that maximise the likelihood of the full dataset (we can sum up the loglikelihoods of the datsets with each missingness pattern). This way it utilises all observed variables (hence “full information”) to estimate the model parameters.

A downside, one could argue, is that you may have specific theoretical considerations about which observed variables should weigh in on estimating missingness in variable \(x\) (rather than all variables), in which case imputation techniques may be preferable. FIML only provides unbiased estimates if the data are MAR (i.e. if the missingness depends on other variables present in the data).

In lavaan, we can make use of full information maximum likelihood by using either missing = "FIML" or missing = "ML" (they’re the same) in the functions cfa() and sem().

optional: other approaches to missingness

Thus far in our analyses, we have been simply excluding any row for which there is missingness. This is typically known as “listwise deletion”, and is the default for many modelling approaches. Any person who is missing some data on a variable in our model will simply not be included. This method assumes that the data are “Missing Completely At Random”, because we make the assumption that studying only the people who have complete data does not bias our results in any way.

Other traditional approaches are to use basic imputation methods such as “mean/median imputation” (replace missing values with the average of that variable). These can be okay, but they assume that the imputed values are exactly what we would have observed had it not been missing, rather than estimates. The lack of variability around this imputed value will shrink the standard errors because it is assumed that no deviations exist among the substituted values. Another option is “regression imputation”, where we replace missing values with the predicted values from a regression model of the variable with missingness onto some relevant predictors. This is better because our estimates of the values of missing observations could be much better, but we still make an assumption that these estimates are perfect, when we know they are just estimates.

A more sophisticated approach to this is “Multiple Imputation” (MI). Multiple imputation is similar to the regression imputation approach described above in that it predicts the value of missing observations based on the covariates, but instead of predicting just one value, it predicts many. Rather than saying “the predicted value for this missing observation is 5”, we say “the predicted value for this missing observation is from the distribution \(\sim N(5,2)\)”. So we simulate \(m\) draws from that distribution, and we end up with \(m\) predicted values. We make \(m\) copies of our data and replace the missing observations with each of our \(m\) predicted values. We then do our analysis on each \(m\) imputed dataset, and pool the results!

We can fit the model setting missing='FIML'. If data are missing at random (MAR) - i.e., missingness is related to the measured variables but not the unobserved missing values - then this gives us unbiased parameter estimates. Unfortunately we can never know whether data are MAR for sure as this would require knowledge of the missing values.

IQ_data_new <- read_csv("https://uoepsy.github.io/data/IQdatam.csv")
multi.hist(IQ_data_new, global = FALSE)

IQ_data_new |> select(contains("IQ")) |> 
    describe() |> 
    as.data.frame() |>
    rownames_to_column(var = "variable") |> 
    select(variable,mean,sd,skew,kurtosis) |>
    kable(digits = 2) |>
    kable_styling(full_width = FALSE)

variable	mean	sd	skew	kurtosis
IQ1	0.01	0.98	1.28	2.29
IQ2	-0.01	0.97	1.25	2.33
IQ3	0.03	0.99	1.39	2.40
IQ4	0.01	0.96	1.30	2.05
IQ5	0.01	0.94	1.77	5.70

IQ_model_missing <- '
  IQ=~IQ1+IQ2+IQ3+IQ4+IQ5
  IQ1~~IQ2
  IQ4~~IQ5
'

IQ_model_missing.est <- cfa(IQ_model_missing, 
                            data=IQ_data_new, 
                            missing='FIML', estimator="MLR")

summary(IQ_model_missing.est, fit.measures=T, standardized=T)

lavaan 0.6-18 ended normally after 25 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        17

  Number of observations                           500
  Number of missing patterns                         3

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                 4.218       3.559
  Degrees of freedom                                 3           3
  P-value (Chi-square)                           0.239       0.313
  Scaling correction factor                                  1.185
    Yuan-Bentler correction (Mplus variant)                       

Model Test Baseline Model:

  Test statistic                               914.603     657.484
  Degrees of freedom                                10          10
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.391

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.999       0.999
  Tucker-Lewis Index (TLI)                       0.996       0.997
                                                                  
  Robust Comparative Fit Index (CFI)                         0.999
  Robust Tucker-Lewis Index (TLI)                            0.998

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -2979.748   -2979.748
  Scaling correction factor                                  1.635
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -2977.639   -2977.639
  Scaling correction factor                                  1.568
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                5993.496    5993.496
  Bayesian (BIC)                              6065.145    6065.145
  Sample-size adjusted Bayesian (SABIC)       6011.185    6011.185

Root Mean Square Error of Approximation:

  RMSEA                                          0.028       0.019
  90 Percent confidence interval - lower         0.000       0.000
  90 Percent confidence interval - upper         0.085       0.076
  P-value H_0: RMSEA <= 0.050                    0.658       0.756
  P-value H_0: RMSEA >= 0.080                    0.073       0.035
                                                                  
  Robust RMSEA                                               0.019
  90 Percent confidence interval - lower                     0.000
  90 Percent confidence interval - upper                     0.088
  P-value H_0: Robust RMSEA <= 0.050                         0.682
  P-value H_0: Robust RMSEA >= 0.080                         0.083

Standardized Root Mean Square Residual:

  SRMR                                           0.008       0.008

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  IQ =~                                                                 
    IQ1               1.000                               0.658    0.674
    IQ2               0.994    0.072   13.792    0.000    0.654    0.673
    IQ3               1.033    0.106    9.768    0.000    0.679    0.685
    IQ4               0.989    0.113    8.788    0.000    0.651    0.676
    IQ5               0.958    0.119    8.073    0.000    0.630    0.672

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
 .IQ1 ~~                                                                
   .IQ2               0.248    0.049    5.029    0.000    0.248    0.480
 .IQ4 ~~                                                                
   .IQ5               0.072    0.049    1.452    0.146    0.072    0.146

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .IQ1               0.010    0.044    0.229    0.819    0.010    0.010
   .IQ2              -0.007    0.043   -0.170    0.865   -0.007   -0.008
   .IQ3               0.027    0.044    0.602    0.547    0.027    0.027
   .IQ4               0.002    0.043    0.050    0.960    0.002    0.002
   .IQ5              -0.001    0.042   -0.029    0.977   -0.001   -0.001

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .IQ1               0.519    0.064    8.103    0.000    0.519    0.545
   .IQ2               0.515    0.063    8.222    0.000    0.515    0.546
   .IQ3               0.521    0.063    8.324    0.000    0.521    0.530
   .IQ4               0.504    0.062    8.190    0.000    0.504    0.543
   .IQ5               0.482    0.069    6.998    0.000    0.482    0.549
    IQ                0.433    0.073    5.899    0.000    1.000    1.000

Our fit indices all look very good!

Question 9

Note that the summary of the model output when we used FIML also told us that there are 3 patterns of missingness.

Can you find out a) what the patterns are, and b) how many people are in each pattern?

Hints

is.na() will help a lot here, as will distinct() and count().

This will turn all the NAs into TRUE, and everything else into FALSE:

is.na(IQ_data_new)

If we turn this back to a dataframe, and then pass it to distinct(), we get out the different patterns!

is.na(IQ_data_new) |>
  as.data.frame() |>
  distinct()

    ID1   IQ1   IQ2   IQ3   IQ4   IQ5
1 FALSE FALSE FALSE  TRUE  TRUE  TRUE
2 FALSE FALSE FALSE FALSE FALSE FALSE
3 FALSE FALSE FALSE FALSE FALSE  TRUE

Getting the counts is more difficult, but one way would be to do it with count(), but we have to give it all of the variables, to get all the different combinations:

is.na(IQ_data_new) |>
  as.data.frame() |>
  count(ID1,IQ1,IQ2,IQ3,IQ4,IQ5)

    ID1   IQ1   IQ2   IQ3   IQ4   IQ5   n
1 FALSE FALSE FALSE FALSE FALSE FALSE 485
2 FALSE FALSE FALSE FALSE FALSE  TRUE  12
3 FALSE FALSE FALSE  TRUE  TRUE  TRUE   3

Extras: Equivalent models

Question Extra 10

Returning to our full SEM, adjust your model so that instead of IQ ~ Stress we are fitting Stress ~ IQ (i.e. child cognitive ability \(\rightarrow\) prenatal stress).
Does this model fit better or worse than our first one?

Here’s our first model:

fitmeasures(SEM_model.est)[c("rmsea.scaled","srmr","tli.scaled","cfi.scaled")]

rmsea.scaled         srmr   tli.scaled   cfi.scaled 
  0.00000000   0.03002311   1.00580515   1.00000000 

And here’s the model with the direction reversed:

SEM_model2 <- '
    #IQ measurement model
    IQ =~ IQ1 + IQ2 + IQ3 + IQ4 + IQ5 
    IQ1 ~~ IQ2
    IQ4 ~~ IQ5
    
    #stress measurement model 
    Stress =~ stress1 + stress2 + stress3 + stress4 + stress5 
    
    #structural part of model
    Stress ~ IQ
'

SEM_model.est2 <- sem(SEM_model2, data=stress_IQ_data,
                    ordered = c('stress1', 'stress2', 'stress3', 'stress4', 'stress5'),
                    estimator="WLSMV")

fitmeasures(SEM_model.est2)[c("rmsea.scaled","srmr","tli.scaled","cfi.scaled")]

rmsea.scaled         srmr   tli.scaled   cfi.scaled 
  0.00000000   0.03002311   1.00580515   1.00000000 

The fit is exactly the same!!

One of the strengths of SEM is that we are fitting quantitative models that very closely correspond to theoretical models. In fact, researchers may often start with two slightly different theoretical models, and SEM will allow them to make a formal comparison of the two, because they will lead to differences in model fit.

However, it is important to be aware that for every structural equation model, there are always equivalent representations of the model structure that leads to precisely the same model fit. These are essentially re-parameterisations of our model - they contain the same information, and lead to the exact same model-implied covariance matrix, but they involve different theoretical assumptions. Many of these we can rule out on conceptual grounds (i.e. a child’s cognitive ability cannot influence their mothers’ pre-natal stress levels), but others we cannot.

Extras: Simulating SEM data

Question Extra11

Simulating data as an tool for learning

An extremely useful approach to learning both R and statistics is to create yourself some fake data on which you can try things out. Because you create the data, you can control any relationships, group differences etc. In doing so, you essentially make yourself a target to aim for.

Many of you will currently be in the process of collecting/acquiring data for your thesis. If you are yet to obtain your data, we strongly recommend that you start to simulate some data with the expected distributions in order to play around and test how your analyses works, and how to interpret the results.

I estimate that I generate fake data at least a couple of times every week just to help me work out things I don’t understand. It also enables for easy sharing of reproducible chunks of code which can perfectly replicate issues and help discussions.

While structural equation models are a fairly complex method, simulating data from a pre-defined SEM is actually pretty straightforward. We just specify a population model (i.e. giving it some values of each parameter) and then sample from it.
For example:

popmod <- "
biscuits =~ .7*oreo + .6*digestive + .7*custardcream + 
            .6*jammydodger + .8*bourbon + .3*jaffacake
"

newdata <- simulateData(popmod, sample.nobs = 300)

head(newdata)

         oreo   digestive custardcream jammydodger    bourbon   jaffacake
1  0.06992848 -1.96401881   -0.6930186   0.9031730 -3.7925025  0.24151604
2  1.14049039  0.08674750    1.3059567   0.6697633 -1.2861885  1.07859713
3  1.52744333  0.97322962   -0.1676939   0.8226969  0.9266996 -2.55767075
4 -0.08882437  0.19439799    1.1692537   0.2738211  3.1872644  0.01498641
5 -0.18472543 -0.06220265    0.7107427   0.9779674  1.1212930 -0.87409201
6 -0.68054395 -1.80212884    0.4449138  -2.0590937  0.8689626 -2.29479125

1. Do a little bit of research and find a paper that fits a structural equation model. Simulate some data from it.
   
2. Save the dataset (write_csv() will help), and share it with someone else, along with a description of the theoretical model. Can they estimate a model that fits well?

Extras: Extensions of SEM

We have really only scraped the surface of the different things we can do with SEM. If you are interested in taking you learning further, then some of the next things to start looking into:

• Multigroup analysis (testing the model across two or more populations)
  • Jöreskog, K. G. (1971). Simultaneous factor analysis in several populations. Psychometrika, 36(4), 409-426.
    
  • Sorbom, D. (1974). A general method for studying differences in factor means and factor structures between groups. British Journal of Mathematical and Statistical Psychology, 27, 229-239.
• Latent Growth Curves (actually just the same as a multilevel model!! 🤯 )
  • Michael Clark has a great lot of resources on this, and it makes the link between random effects and latent variables super clear.

Footnotes

1. We’ve actually seen this previously in multilevel modelling, when we had random intercepts, random slopes, and the covariance between the two!

2. These are similar corrections to ones that we apply in a regression world, see LM Troubleshooting

3. Diagonally Weighted Least Squares

4. To me, these are some of the most confusing terms in statistics, because “at random” is used to mean “not completely random”!?? It might be easier to think of “missing at random” as “missing conditionally at random”, but then it gives the same acronym as “completely at random”!