Week 4 Exercises: Nested and Crossed

Psychoeducation Treatment Effects

Data: gadeduc.csv

This is synthetic data from a randomised controlled trial, in which 30 therapists randomly assigned patients (each therapist saw between 4 and 30 patients) to a control or treatment group, and monitored their scores over time on a measure of generalised anxiety disorder (GAD7 - a 7 item questionnaire with 5 point likert scales).

The control group of patients received standard sessions offered by the therapists. For the treatment group, 10 mins of each sessions was replaced with a specific psychoeducational component, and patients were given relevant tasks to complete between each session. All patients had monthly therapy sessions. Generalised Anxiety Disorder was assessed at baseline and then every visit over 4 months of sessions (5 assessments in total).

The data are available at https://uoepsy.github.io/data/msmr_gadeduc.csv

You can find a data dictionary below:

Table 1: Data Dictionary: msmr_gadeduc.csv

variable	description
patient	A patient code in which the labels take the form <Therapist initials>_<group>_<patient number>.
visit_0	Score on the GAD7 at baseline
visit_1	GAD7 at 1 month assessment
visit_2	GAD7 at 2 month assessment
visit_3	GAD7 at 3 month assessment
visit_4	GAD7 at 4 month assessment

Question 1

Uh-oh… these data aren’t in the same shape as the other datasets we’ve been giving you..

Can you get it into a format that is ready for modelling?

Hints

• It’s wide, and we want it long.
  
• Once it’s long. “visit_0”, “visit_1”,.. needs to become the numbers 0, 1, …
• One variable (patient) contains lots of information that we want to separate out. There’s a handy function in the tidyverse called separate(), check out the help docs!

Here’s the data. We have one row per patient, but we have multiple observations for each patient across the columns..

geduc = read_csv("../../data/msmr_gadeduc.csv")
head(geduc)

# A tibble: 6 × 6
  patient        visit_0 visit_1 visit_2 visit_3 visit_4
  <chr>            <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
1 OT_Control_1        26      27      27      27      27
2 OT_Control_2        25      24      27      26      25
3 OT_Treatment_3      26      27      24      23      22
4 OT_Treatment_4      26      26      26      25      25
5 ND_Control_1        25      25      25      25      25
6 ND_Control_2        26      24      25      24      23

We can make it long by taking the all the columns from visit_0 to visit_4 and shoving their values into one variable, and keeping the name of the column they come from as another variable:

geduc |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD")

# A tibble: 2,600 × 3
   patient      visit     GAD
   <chr>        <chr>   <dbl>
 1 OT_Control_1 visit_0    26
 2 OT_Control_1 visit_1    27
 3 OT_Control_1 visit_2    27
 4 OT_Control_1 visit_3    27
 5 OT_Control_1 visit_4    27
 6 OT_Control_2 visit_0    25
 7 OT_Control_2 visit_1    24
 8 OT_Control_2 visit_2    27
 9 OT_Control_2 visit_3    26
10 OT_Control_2 visit_4    25
# ℹ 2,590 more rows

Now we know how to get our data long, we need to sort out our time variable (visit) and make it into numbers.
We can replace all occurrences of the string "visit_" with nothingness "", and then convert them to numeric.

geduc |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD") |>
  mutate(
    visit = as.numeric(gsub("visit_","",visit))
  ) 

# A tibble: 2,600 × 3
   patient      visit   GAD
   <chr>        <dbl> <dbl>
 1 OT_Control_1     0    26
 2 OT_Control_1     1    27
 3 OT_Control_1     2    27
 4 OT_Control_1     3    27
 5 OT_Control_1     4    27
 6 OT_Control_2     0    25
 7 OT_Control_2     1    24
 8 OT_Control_2     2    27
 9 OT_Control_2     3    26
10 OT_Control_2     4    25
# ℹ 2,590 more rows

Finally, we need to sort out the patient variable. It contains 3 bits of information that we will want to have separated out. It has the therapist (their initials), then the group (treatment or control), and then the patient number. These are all separated by an underscore “_“.

The separate() function takes a column and separates it into several things (as many things as we give it), splitting them by some user defined separator such as an underscore:

geduc_long <- geduc |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD") |>
  mutate(
    visit = as.numeric(gsub("visit_","",visit))
  ) |>
  separate(patient, into=c("therapist","group","patient"), sep="_")

And we’re ready to go!

geduc_long

# A tibble: 2,600 × 5
   therapist group   patient visit   GAD
   <chr>     <chr>   <chr>   <dbl> <dbl>
 1 OT        Control 1           0    26
 2 OT        Control 1           1    27
 3 OT        Control 1           2    27
 4 OT        Control 1           3    27
 5 OT        Control 1           4    27
 6 OT        Control 2           0    25
 7 OT        Control 2           1    24
 8 OT        Control 2           2    27
 9 OT        Control 2           3    26
10 OT        Control 2           4    25
# ℹ 2,590 more rows

Question 2

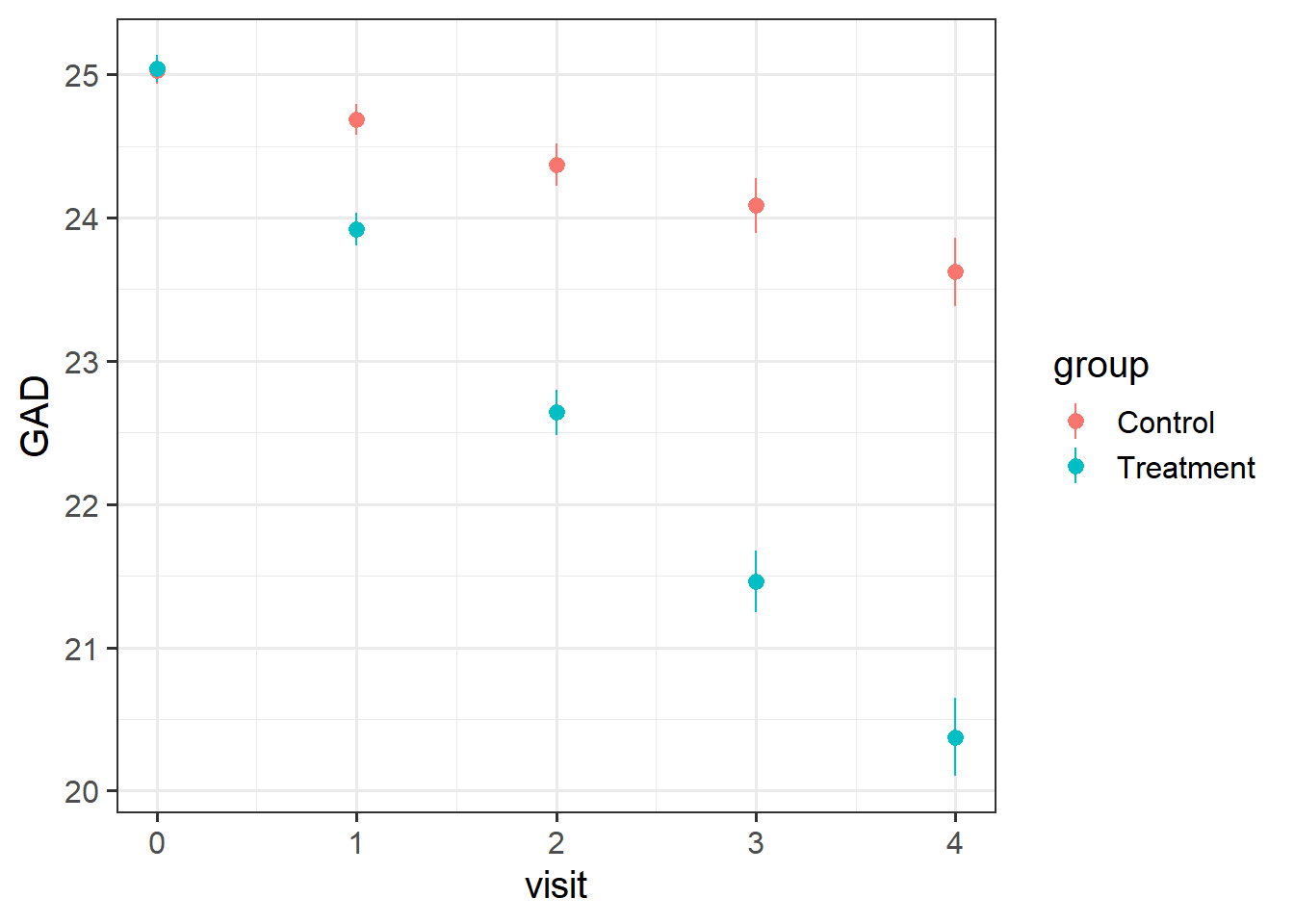
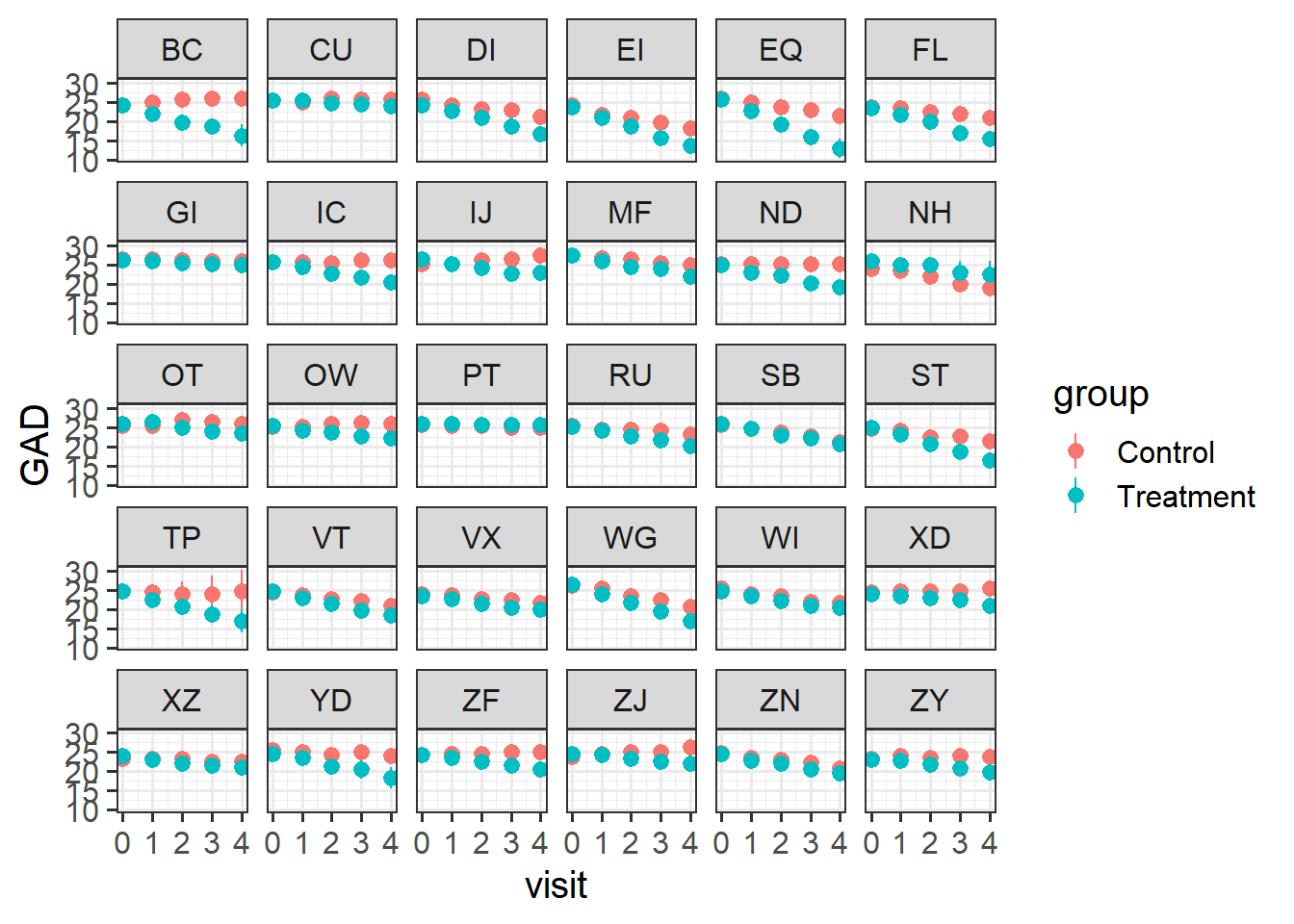
Visualise the data. Does it look like the treatment had an effect?
Does it look like it worked for every therapist?

Hints

• remember, stat_summary() is very useful for aggregating data inside a plot.

Here’s the overall picture. The average score on the GAD7 at each visit gets more and more different between the two groups. The treatment looks effective..

ggplot(geduc_long, aes(x = visit, y = GAD, col = group)) +
  stat_summary(geom="pointrange")

Let’s split this up by therapist, so we can see the averages across each therapist’s set of patients.
There’s clear variability between therapists in how well the treatment worked. For instance, the therapists PT and GI don’t seem to have much difference between their groups of patients.

ggplot(geduc_long, aes(x = visit, y = GAD, col = group)) +
  stat_summary(geom="pointrange") +
  facet_wrap(~therapist)

Question 3

Fit a model to test if the psychoeducational treatment is associated with greater improvement in anxiety over time.

We want to know if how anxiety (GAD) changes over time (visit) is different between treatment and control (group).

Hopefully this should hopefully come as no surprise¹ - it’s an interaction!

lmer(GAD ~ visit * group + ...
       ...
     data = geduc_long)

We have multiple observations for each of the 520 patients, and those patients are nested within 30 therapists.

Note that in our data, the patient variable does not uniquely specify the individual patients. i.e. patient “1” from therapist “OT” is a different person from patient “1” from therapist “ND”. To correctly group the observations into different patients (and not ‘patient numbers’), we need to have therapist:patient.

So we capture therapist-level differences in ( ... | therapist) and the patients-within-therapist-level differences in ( ... | therapist:patient):

lmer(GAD ~ visit * group + ...
       ( ... | therapist) + 
       ( ... | therapist:patient),
     data = geduc_long)

Note that each patient can change differently in their anxiety levels over time - i.e. the slope of visit could vary by participant.

Likewise, some therapists could have patients who change differently from patients from another therapist, so visit|therapist can be included.

Each patient is in one of the two groups - they’re either treatment or control. So we can’t say that “differences in anxiety due to treatment varies between patients”, because for any one patient the “difference in anxiety due to treatment” is not defined in our study design.

However, therapists see multiple different patients, some of which are in the treatment group, and some of which are in the control group. So the treatment effect could be different for different therapists!

mod1 <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist)+
               (1+visit|therapist:patient),
             geduc_long)

Question 4

For each of the models below, what is wrong with the random effect structure?

modelA <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist)+
               (1+visit|patient),
             geduc_long)

modelB <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist/patient),
             geduc_long)

modelA <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist)+
               (1+visit|patient),
             geduc_long)

The patient variable doesn’t capture the different patients within therapists, so this actually fits crossed random effects and treats all data where patient==1 as from the same group (even if this includes several different patients’ worth of data from different therapists!)

modelB <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist/patient),
             geduc_long)

Using the / here means we have the same random slopes fitted for therapists and for patients-within-therapists. but the effect of group can’t vary by patient, so this doesn’t work. hence why we need to split them up into (...|therapist)+(...|therapist:patient).

Question 5

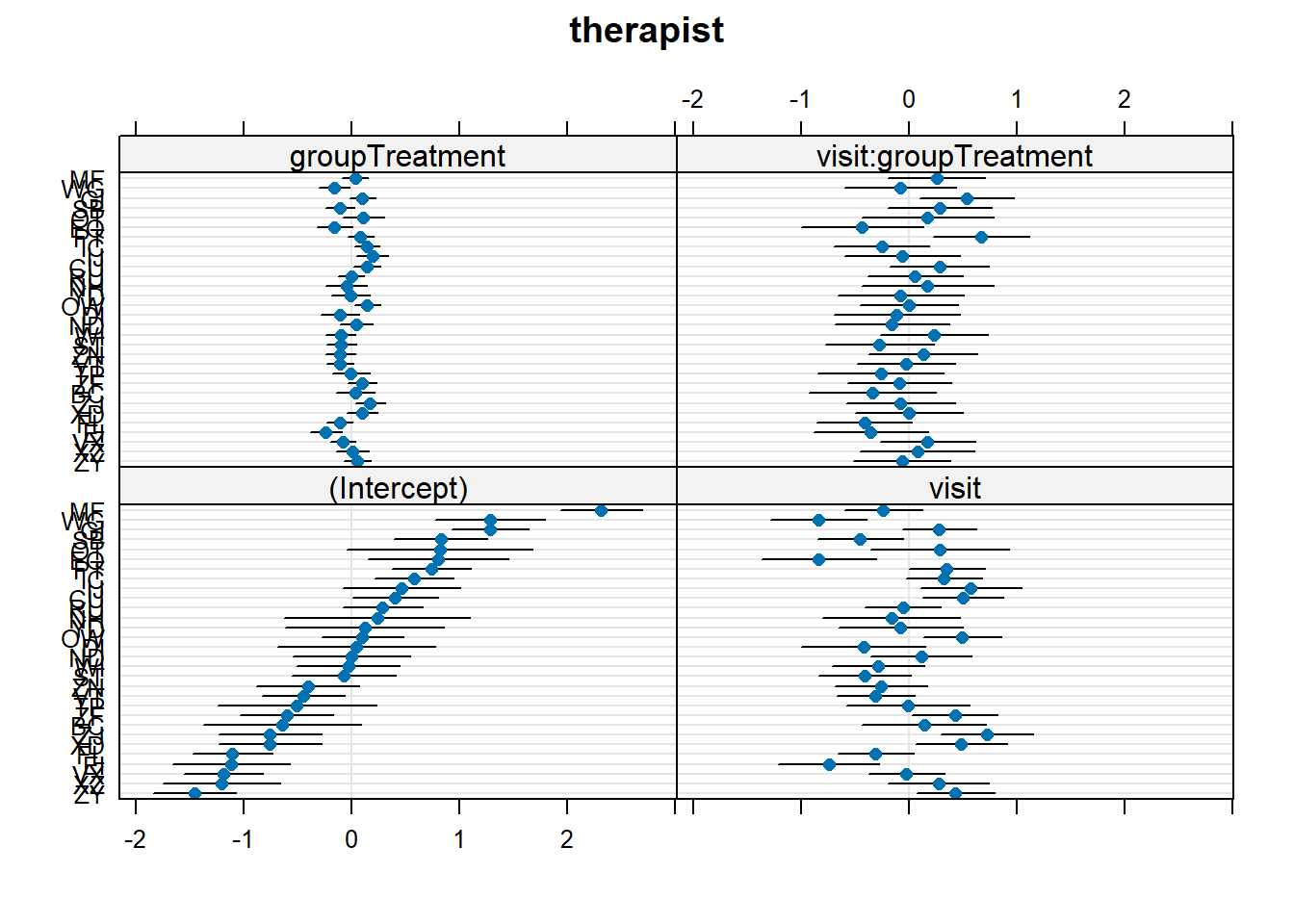
Let’s suppose that I don’t want the psychoeducation treatment, I just want the standard therapy sessions that the ‘Control’ group received. Which therapist should I go to?

Hints

dotplot.ranef.mer() might help here!

It would be best to go to one of the therapists WG, EQ, or EI…

Why? These therapists all have the most negative slope of visit:

dotplot.ranef.mer(ranef(mod1))$therapist

Question 6

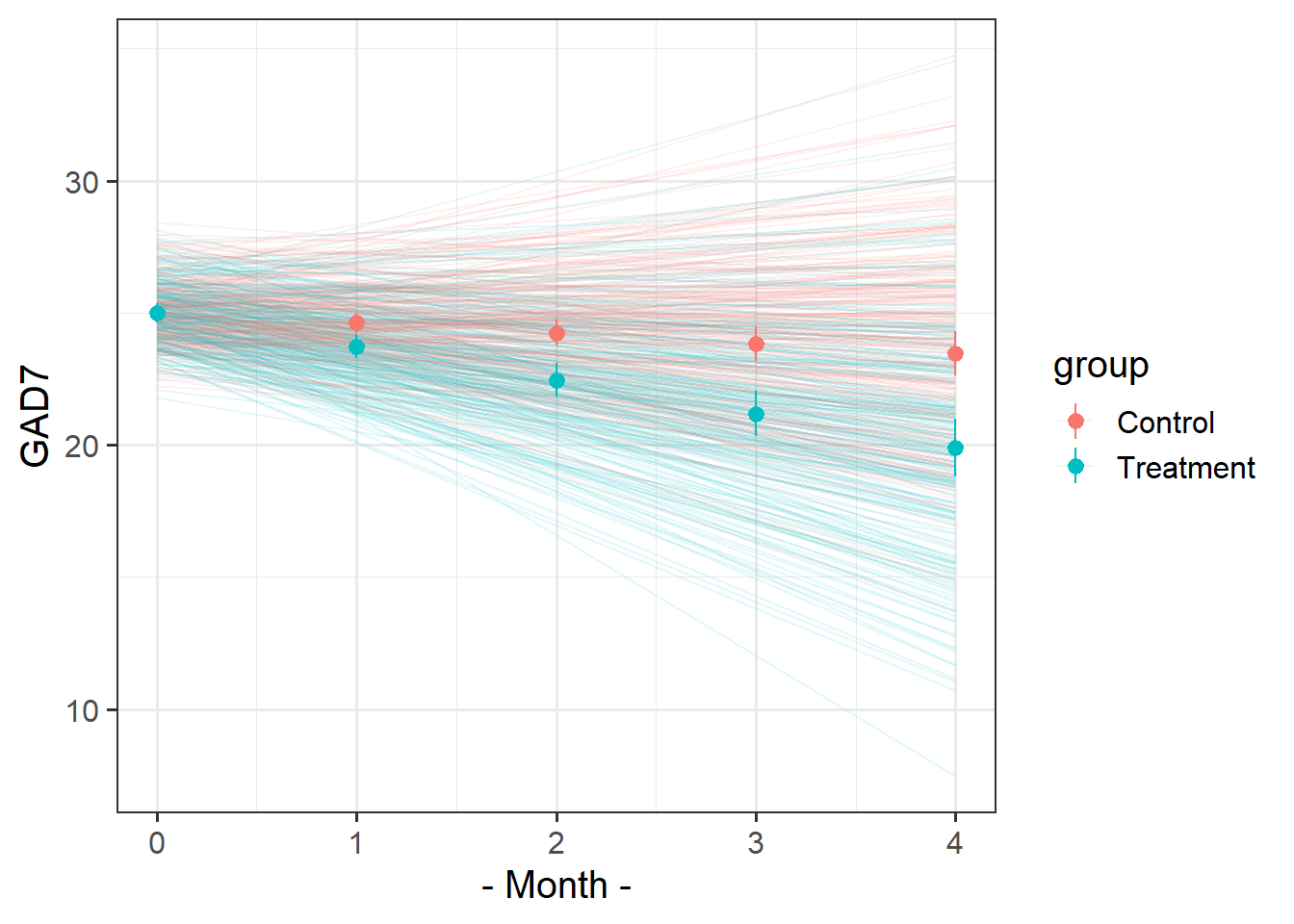
Recreate this plot.

The faint lines represent the model estimated lines for each patient. The points and ranges represent our fixed effect estimates and their uncertainty.

Hints

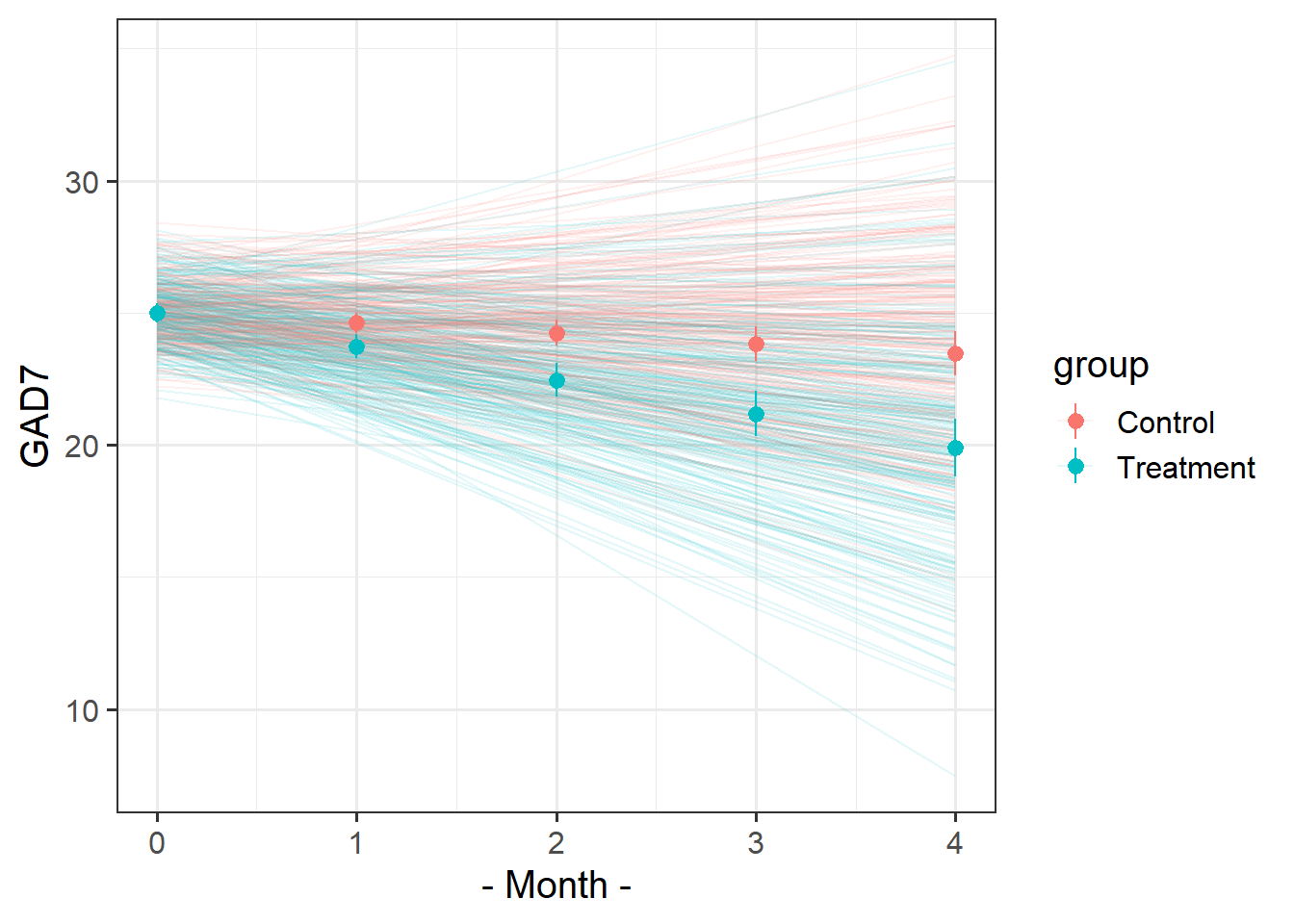
• you can get the patient-specific lines using augment() from the broom.mixed package, and the fixed effects estimates using the effects package.
• remember you can pull multiple datasets into ggplot:

ggplot(data = dataset1, aes(x=x,y=y)) + 
  geom_point() + # points from dataset1
  geom_line(data = dataset2) # lines from dataset2

library(effects)
library(broom.mixed)
effplot <- effect("visit*group",mod1) |>
  as.data.frame()

augment(mod1) |> 
  mutate(
    upatient = paste0(therapist,patient)
  ) |>
  ggplot(aes(x=visit,y=.fitted,col=group))+
  stat_summary(geom="line", aes(group=upatient,col=group), alpha=.1)+
  geom_pointrange(data=effplot, aes(y=fit,ymin=lower,ymax=upper,col=group))+
  labs(x="- Month -",y="GAD7")

Test Enhanced Learning

Data: Test-enhanced learning

An experiment was run to conceptually replicate “test-enhanced learning” (Roediger & Karpicke, 2006): two groups of 25 participants were presented with material to learn. One group studied the material twice (StudyStudy), the other group studied the material once then did a test (StudyTest). Recall was tested immediately (one minute) after the learning session and one week later. The recall tests were composed of 175 items identified by a keyword (Test_word).

The critical (replication) prediction is that the StudyStudy group recall more items on the immediate test, but the StudyTest group will retain the material better and thus perform better on the 1-week follow-up test.

The following code loads the data into your R environment by creating a variable called tel:

load(url("https://uoepsy.github.io/data/testenhancedlearning.RData"))

Table 2: Data Dictionary: testenhancedlearning.Rdata

variable	description
Subject_ID	Unique Participant Identifier
Group	Group denoting whether the participant studied the material twice (StudyStudy), or studied it once then did a test (StudyTest)
Delay	Time of recall test ('min' = Immediate, 'week' = One week later)
Test_word	Word being recalled (175 different test words)
Correct	Whether or not the word was correctly recalled
Rtime	Time to recall word (milliseconds)

Question 7

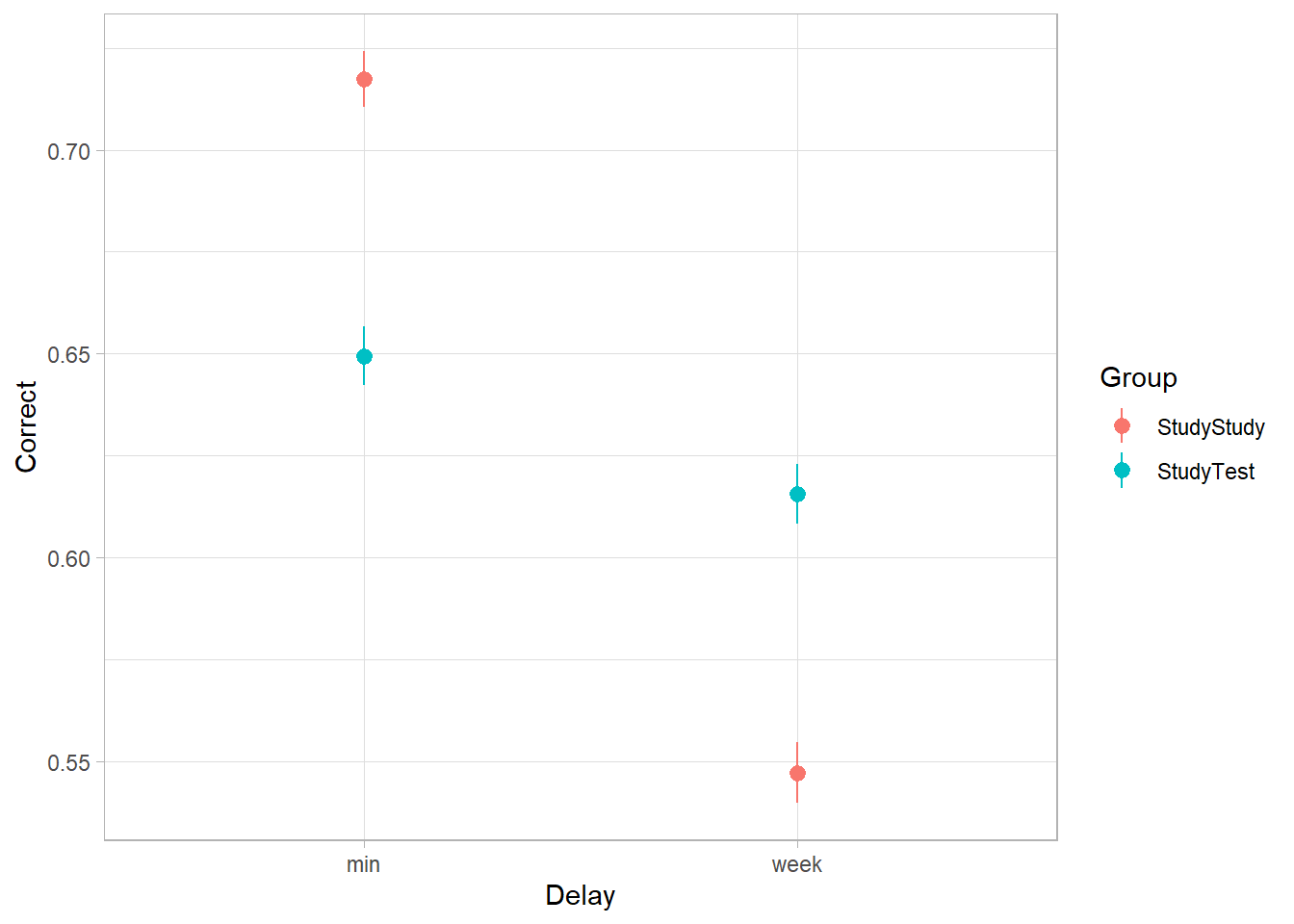
Load and plot the data. Does it look like the effect was replicated?

The critical (replication) prediction is that the StudyStudy group recall more items on the immediate test, but the StudyTest group will retain the material better and thus perform better on the 1-week follow-up test.

Hints

We can actually look at this from a couple of different angles. The most obvious option is to take successful learning as “correctly recalling” an item. This means we take the Correct variable as our outcome.

Note we also have Rtime - the “time-to-recall” of an item. This could also work as an outcome, but note that it also includes the time it took participants to provide an incorrect response too. If this was your own project, you may well want to provide analyses of Correct, and then also of the time-taken, but on the subset of correcty recalled items.

load(url("https://uoepsy.github.io/data/testenhancedlearning.RData"))

ggplot(tel, aes(Delay, Correct, col=Group)) + 
  stat_summary(fun.data=mean_se, geom="pointrange")+
  theme_light()

That looks like test-enhanced learning to me!

Question 8

Test the critical hypothesis using a mixed-effects model.

Fit the maximal random effect structure supported by the experimental design. Simplify the random effect structure until you reach a model that converges.

Note: Some of the models you attempt here might take time to fit. This is normal, and you can cancel the estimation at any time by pressing the escape key.
I suggest that you write your initial model, set it running, and then look at the first solution to see if it converged for me. You can assume that if it didn’t work for me, it also won’t work for you. I’ve shown the random effects for each model, in case it helps in deciding your next step.

Hints

What we’re aiming to do here is to follow Barr et al.’s advice of defining our maximal model and then removing only the terms to allow a non-singular fit.

• What kind of model will you use? What is our outcome? is it binary, or continuous?
• We can expect variability across subjects (some people are better at learning than others) and across items (some of the recall items are harder than others). How should this be represented in the random effects?

We have a crossed random effect structure here. Each participant was tested on every word, and each word was seen by every participant.

Subjects were tested at both the min and week, so Delay|Subject_ID can be included (some people might retain the items better than others).
Likewise the words were seen at both min and week, and some words might be more easy to retain than others (Delay|Test_word).

The participants are in either one group or another, so we can’t have Group|Subject_ID. However, the words were seen by people in both groups, so we can have Group|Test_word.

This one took my computer about 6 minutes.

mod1 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 + Delay * Group | Test_word),
             family=binomial, data=tel)

Warning message:
In checkConv(attr(opt, “derivs”), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0184773 (tol = 0.002, component 1)

VarCorr(mod1)

 Groups     Name                     Std.Dev. Corr                
 Test_word  (Intercept)              1.057208                     
            Delayweek                0.059611 -0.341              
            GroupStudyTest           0.067625 -0.835  0.802       
            Delayweek:GroupStudyTest 0.115439 -0.783  0.852  0.996
 Subject_ID (Intercept)              1.594518                     
            Delayweek                0.210026 -0.623              

Lets remove the interaction in the by-word random effects.
This one took about 5 minutes…

mod2 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 + Delay + Group | Test_word),
             family=binomial, data=tel)

Warning message:
In checkConv(attr(opt, “derivs”), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.00887744 (tol = 0.002, component 1)

VarCorr(mod2)

 Groups     Name           Std.Dev. Corr         
 Test_word  (Intercept)    1.076941              
            Delayweek      0.074697 -0.801       
            GroupStudyTest 0.109342 -0.928  0.966
 Subject_ID (Intercept)    1.589794              
            Delayweek      0.210633 -0.601       

We still have a singular fit here. Thinking about the study, if we are going to remove one of the by-testword random effects (Delay or Group), which one do we consider to be more theoretically justified? Is the effect of Delay likely to vary by test-words? More so than the effect of group is likely to vary by test-words?
Quite possibly - it’s reasonable to think that some words will be more easily retained over a week than others, but I can’t come up with a reason to think why StudyTest vs StudyStudy would have a different effect for some words than others.

Let’s remove the by-testword random effect of group.

mod3 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 + Delay | Test_word),
             family=binomial, data=tel)

This one converges! But we still have a correlation of -1.
Why did we not get a warning message?

VarCorr(mod3)

 Groups     Name        Std.Dev. Corr  
 Test_word  (Intercept) 1.027514       
            Delayweek   0.055424 -1.000
 Subject_ID (Intercept) 1.598967       
            Delayweek   0.208732 -0.599

The isSingular() function allows us to check for when a model is close to singularity (i.e. on the boundary of the feasible parameter space):

isSingular(mod3)

[1] FALSE

This suggests that we’re fine! However, note that this function has a tolerance, which is by default set to 1e-4, or 0.0001. Change this to 1e-3, and it indicates a problem.

isSingular(mod3, tol=1e-3)

[1] TRUE

So we’re kind of in a grey area that suggests we are close to overfitting here, so it might be worth continuing to simplify.

mod4 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 | Test_word),
             family=binomial, data=tel)

Even when we raise the tolerance here, we’re still fine:

isSingular(mod4, tol=1e-3)

[1] FALSE

And here’s our random effects:

VarCorr(mod4)

 Groups     Name        Std.Dev. Corr  
 Test_word  (Intercept) 0.99805        
 Subject_ID (Intercept) 1.58653        
            Delayweek   0.19670  -0.521

In the process of getting to our final model, we’ve just fitted quite a few models that didn’t converge. We definitely don’t want to do anything with these models (i.e. we shouldn’t report them or use them in model comparisons etc).

However, it can sometimes be useful to just check how estimates of fixed effects and their standard errors differ across these models. More often than not, this simply provides us with reassurance that the removal of random effects hasn’t actually had too much of an impact on anything we’re going to conduct inferences on.

For instance, in all these models, the fixed effects estimates are all pretty similar, suggesting that they’ve all found similar estimates of these parameters which have been largely invariant to our refinement of the random effects.

term	mod1	mod2	mod3	mod4
(Intercept)	1.275 (0.332)	1.283 (0.331)	1.267 (0.332)	1.257 (0.329)
Delayweek	-1.065 (0.071)	-1.071 (0.071)	-1.057 (0.07)	-1.047 (0.068)
GroupStudyTest	-0.415 (0.456)	-0.429 (0.454)	-0.401 (0.457)	-0.398 (0.453)
Delayweek:GroupStudyTest	0.781 (0.103)	0.795 (0.102)	0.776 (0.101)	0.776 (0.099)

Question 9

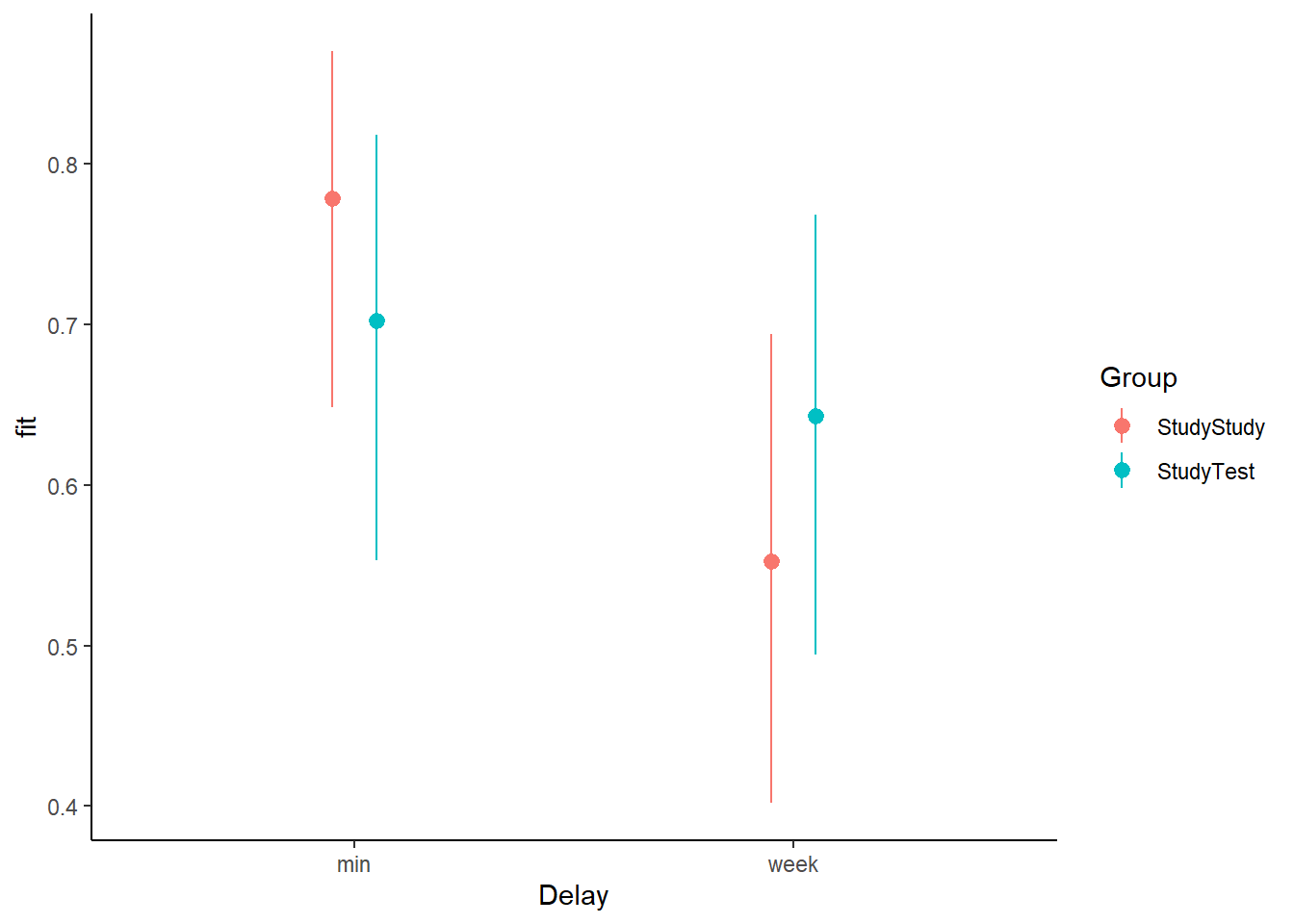
Create a plot of the predicted probabilities and uncertainty for each of the Delay * Group combinations.

library(effects)
effplot <- effect("Delay:Group", mod4) |>
  as.data.frame()

ggplot(effplot, aes(Delay, fit, color=Group)) + 
  geom_pointrange(aes(ymax=upper, ymin=lower), 
                  position=position_dodge(width = 0.2))+
  theme_classic() # just for a change :)

Question 10

Here are odds ratios for our model:

Code

# cbind combines columns
cbind(
  # the odds ratios:
  OR = exp(fixef(mod4)), 
  # the CIs:
  exp(confint(mod4, method="Wald", parm="beta_"))
)

                                OR     2.5 %    97.5 %
(Intercept)              3.5155077 1.8444914 6.7003803
Delayweek                0.3510452 0.3075298 0.4007181
GroupStudyTest           0.6715269 0.2761216 1.6331515
Delayweek:GroupStudyTest 2.1734992 1.7894502 2.6399723

What should we do with this information? How should we apply test-enhanced learning to learning R and statistics?

We’ll get the benefits of test-enhanced learning if we try these exercises before looking at any of the solutions that are visible! If we don’t test ourselves, we’re more likely to forget it in the long run.

Vocab Development

Data: pvt_bilingual.csv

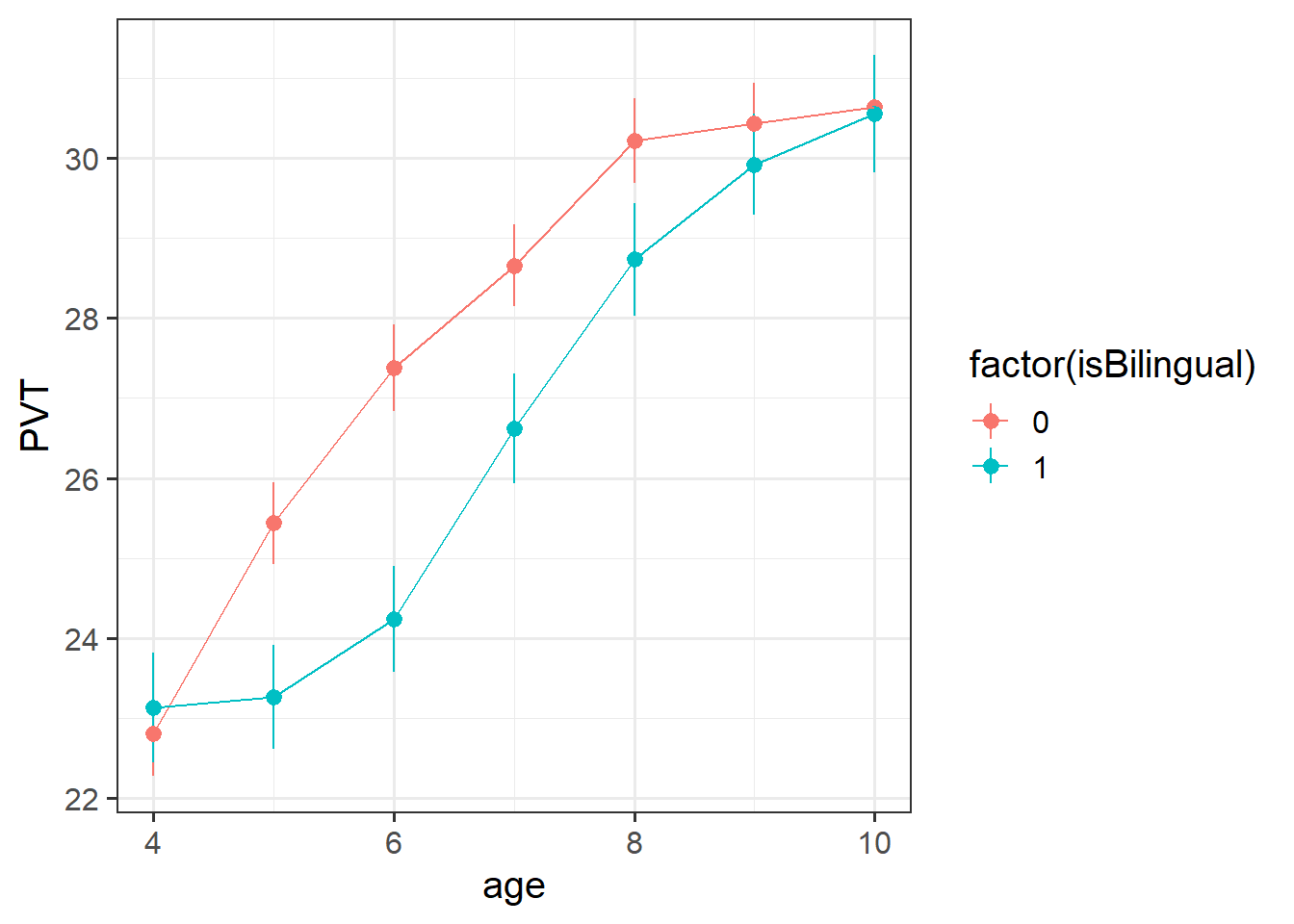
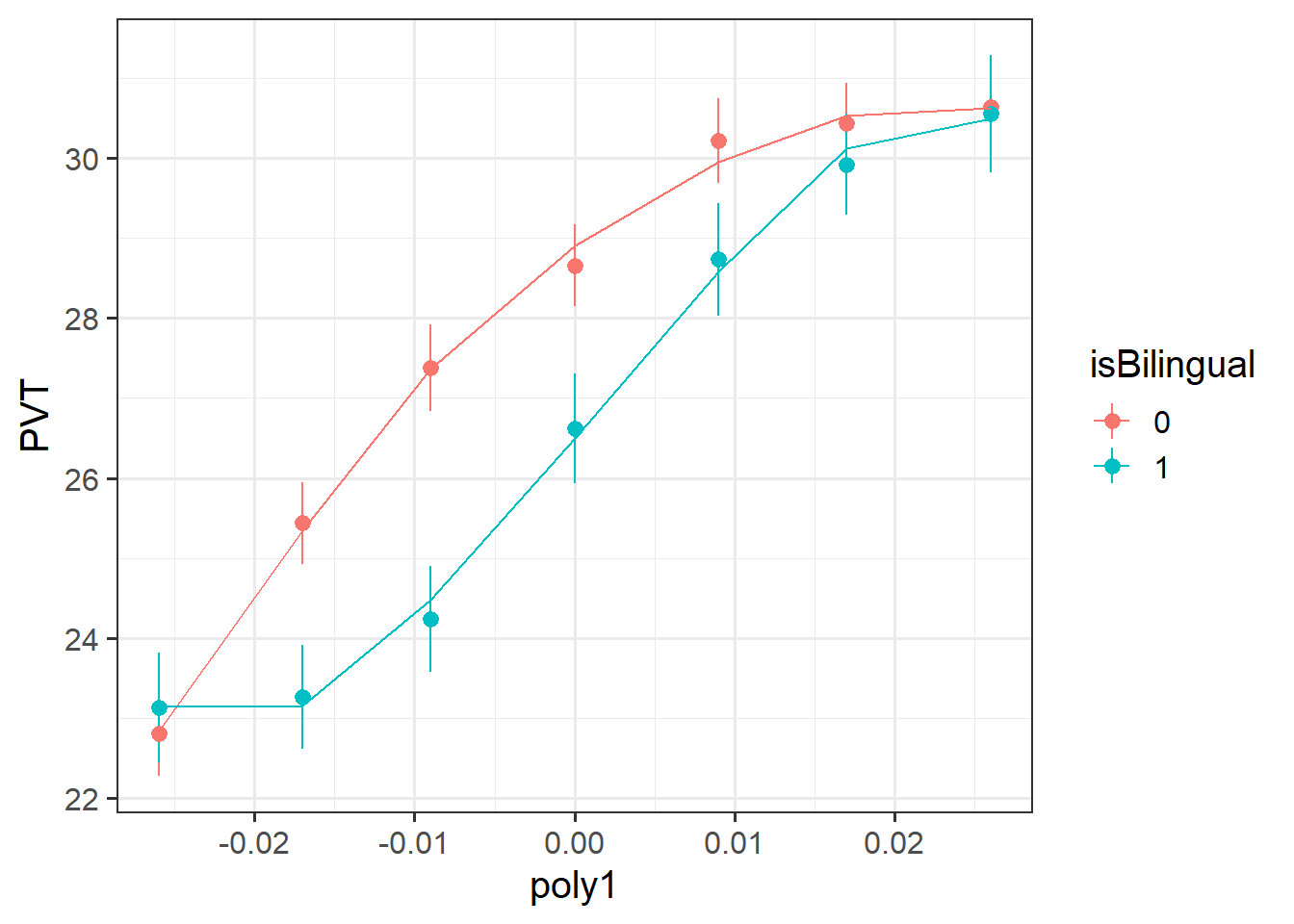
488 children from 30 schools were included in the study. Children were assessed on a yearly basis for 7 years throughout primary school on a measure of vocabulary administered in English, the Picture Vocab Test (PVT). 295 were monolingual English speakers, and 193 were bilingual (english + another language).

Previous research conducted on monolingual children has suggested that that scores on the PVT increase steadily up until the age of approximately 7 or 8 at which point they begin to plateau. The aim of the present study is to investigate differences in the development of vocabulary between monolingual and bilingual children.

The data are available at https://uoepsy.github.io/data/pvt_bilingual.csv.

Table 3: Data Dictionary: pvt_bilingual.csv

variable	description
child	Child's name
school	School Identifier
isBilingual	Binary variable indicating whether the child is monolingual (0) or bilingual (1)
age	Age (years)
PVT	Score on the Picture Vocab Test (PVT). Scores range 0 to 60

Question 11 - Less Guided

Conduct an analysis to estimate the differences in trajectories of vocabulary development between children attending bilingual schools vs those attending monolingual schools.

Write up your results.

Hints

1. make things factors
2. always plot your data!
3. read the study background: “increase steadily … before beginning to plateau” describes a curve!
   
4. plotting the data can give an initial sense of the possible need for higher order polynomials.

Let’s read in the data:

pvt <- read_csv("https://uoepsy.github.io/data/pvt_bilingual.csv")

We have 30 distinct schools:

n_distinct(pvt$school)

[1] 30

And 418 distinct children. Is that right?

n_distinct(pvt$child)

[1] 418

Given that the pvt$child variable is just the first name of the child, it’s entirely likely that there will be, for instance more than one “Martin”.

This says that there are 487!

pvt |> count(school, child) |> nrow()

[1] 487

But wait… we could still have issues. What if there were 2 “Martin”s at the same school??

pvt |> 
  # count the school-children groups
  count(school, child) |> 
  # arrange the output so that the highest 
  # values of the 'n' column are at the top
  arrange(desc(n))

# A tibble: 487 × 3
   school    child        n
   <chr>     <chr>    <int>
 1 School 14 James       14
 2 School 14 Michelle    14
 3 School 15 Michael     14
 4 School 21 Daniel      14
 5 School 3  Jackson     14
 6 School 5  Raven       14
 7 School 9  Kaamil      14
 8 School 1  Allyssa      7
 9 School 1  Armon        7
10 School 1  Dakota       7
# ℹ 477 more rows

Aha! There are 7 cases where schools have two children of the same name. Remember that each child was measured at 7 timepoints. We shouldn’t have people with 14!

If we actually look at the data, we’ll see that it is very neatly organised, with each child’s data together. This means that we could feasibly make an educated guess that, e.g., the “Jackson” from “School 3” in rows 155-161 is different from the “Jackson” from “School 3” at rows 190-196.

Because of the ordering of our data, we can do something like this:

pvt <- 
  pvt |>
  # group by the school and child
  group_by(school, child) |>
  mutate(
    # make a new variable which counts from 1 to 
    # the number of rows for each school-child
    n_obs = 1:n()
  ) |>
  # ungroup the data
  ungroup() |>
  mutate(
    # change it so that if the n_obs is >7, the 
    # child becomes "[name] 2", to indicate they're the second
    # child with that name
    child = ifelse(n_obs>7, paste0(child," 2"), child)
  )

Now we have 494!

pvt |> count(school, child) |> nrow()

[1] 494

And nobody has anything other than 7 observations!

pvt |> count(school, child) |>
  filter(n != 7)

# A tibble: 0 × 3
# ℹ 3 variables: school <chr>, child <chr>, n <int>

Phew!

Okay, let’s just fit an intercept-only model:

# pvt <- read_csv("../../data/bntmono.csv")
pvt_null <- lmer(PVT ~ 1 +  (1 | school/child), data = pvt)
summary(pvt_null)

Linear mixed model fit by REML ['lmerMod']
Formula: PVT ~ 1 + (1 | school/child)
   Data: pvt

REML criterion at convergence: 23844.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.7768 -0.5984  0.0068  0.5744  4.1806 

Random effects:
 Groups       Name        Variance Std.Dev.
 child:school (Intercept) 33.48    5.786   
 school       (Intercept) 19.76    4.445   
 Residual                 43.59    6.602   
Number of obs: 3458, groups:  child:school, 494; school, 30

Fixed effects:
            Estimate Std. Error t value
(Intercept)  27.5263     0.8667   31.76

As we can see from summary(bnt_null), the random intercept variances are 33.48 for child-level, 19.76 for school-level, and the residual variance is 43.59.

So child level differences account for \(\frac{33.48}{33.48 + 19.76 + 43.59} = 0.35\) of the variance in PVT scores, and child & school differences together account for \(\frac{33.48 + 19.76}{33.48 + 19.76 + 43.59} = 0.55\) of the variance.

Here’s an initial plot too:

ggplot(pvt, aes(x=age,y=PVT,col=factor(isBilingual)))+
  stat_summary(geom="pointrange")+
  stat_summary(geom="line")

I feel like either raw or orthogonal polynomials would be fine here - there’s nothing explicit from the study background about stuff “at baseline”. There’s the stuff about the plateau at 7 or 8, but we can get that from the model plots. Orthogonal will allow us to compare the trajectories overall (their linear trend, the ‘curviness’ and ‘wiggliness’).

An additional benefit of orthogonal polynomials is that we are less likely to get singular fits when we include polynomial terms in our random effects. Remember, raw polynomials are correlated, so often the by-participant variances in raw poly terms are highly correlated.

I’ve gone for 3 degrees of polynomials here because the plot above shows a bit of an S-shape for the bilinguals.

pvt <- pvt |> mutate(
  poly1 = poly(age, 3)[,1],
  poly2 = poly(age, 3)[,2],
  poly3 = poly(age, 3)[,3],
  isBilingual = factor(isBilingual)
)

These models do not converge.
I’ve tried to preserve the by-child random effects of time, because while I think Schools probably do vary, School’s all teach the same curriculum, whereas there’s a lot of varied things that can influence a child’s vocabulary, both in and out of school

mod1 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + (poly1 + poly2 + poly3)*isBilingual | school) + 
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod2 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual * (poly1 + poly2) + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod3 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual * poly1 + poly2 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod4 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual + poly1 + poly2 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod5 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
# relative to the variance in time slopes, there's v little by-school variance in bilingual differences in vocab

mod6 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly2 +  poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
# looks like curvature doesn't vary between schools much as linear and wiggliness 

this one does!

mod7 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

library(broom.mixed)
augment(mod7) |> 
  mutate(
    poly1 = round(poly1, 3) # because of rounding errors that make plot weird
  ) |>
  ggplot(aes(x=poly1,col=isBilingual))+
  stat_summary(geom="pointrange",aes(y=PVT))+
  stat_summary(geom="line", aes(y=.fitted))

refitted with lmerTest:

mod7 <- lmerTest::lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

summary(mod7)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + (1 + poly1 +  
    poly3 | school) + (1 + (poly1 + poly2 + poly3) | school:child)
   Data: pvt

REML criterion at convergence: 23076.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.4459 -0.5498 -0.0004  0.5262  4.4199 

Random effects:
 Groups       Name        Variance Std.Dev. Corr             
 school:child (Intercept)   34.86   5.904                    
              poly1       1839.62  42.891    0.01            
              poly2       3945.03  62.810   -0.08  0.23      
              poly3        684.45  26.162    0.19  0.61  0.87
 school       (Intercept)   19.97   4.468                    
              poly1        928.67  30.474   -0.40            
              poly3        335.73  18.323   -0.52 -0.12      
 Residual                   31.94   5.651                    
Number of obs: 3458, groups:  school:child, 494; school, 30

Fixed effects:
                    Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)          27.9464     0.8987   31.1131  31.098  < 2e-16 ***
poly1               157.0432     9.5752   39.5900  16.401  < 2e-16 ***
poly2               -48.9606     8.0943  517.6462  -6.049 2.80e-09 ***
poly3                -1.2783     8.1743   61.5668  -0.156  0.87624    
isBilingual1         -1.2113     0.5863  465.7954  -2.066  0.03939 *  
poly1:isBilingual1   16.6106    12.3112  501.6593   1.349  0.17787    
poly2:isBilingual1   56.2609    12.9499  517.6462   4.345 1.68e-05 ***
poly3:isBilingual1  -34.3285    11.8631 1217.6504  -2.894  0.00387 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) poly1  poly2  poly3  isBln1 pl1:B1 pl2:B1
poly1       -0.215                                          
poly2       -0.013  0.026                                   
poly3       -0.184 -0.003  0.072                            
isBilingul1 -0.250 -0.001  0.020 -0.020                     
ply1:sBlng1  0.000 -0.499 -0.020 -0.022 -0.001              
ply2:sBlng1  0.008 -0.016 -0.625 -0.045 -0.033  0.033       
ply3:sBlng1 -0.009 -0.020 -0.050 -0.566  0.034  0.038  0.079

term	est	p	interpretation
(Intercept)	27.95	*	average vocab score at the mean age (for monolingual)
poly1	157.04	*	vocab increases over time (for monolingual children)
poly2	-48.96	*	the increase in vocab becomes more gradual (for monolingual children)
poly3	-1.28		no significant wiggliness to vocab trajectory of the average monolingual child
isBilingual1	-1.21	*	average vocab score at mean age is lower for bilingual vs monolingual children
poly1:isBilingual1	16.61		no significant difference in linear trend of vocab for bilingual vs monolingual
poly2:isBilingual1	56.26	*	curvature for vocab trajectory of bilingual children significantly differs from that of monolinguals
poly3:isBilingual1	-34.33	*	wiggliness for vocab trajectory of bilingual children significantly differs from that of monolinguals

From the random effects, we get even more information!
School’s vary in the average child vocab score at mean age with an SD of 4.5. More school level variation in linear trends than in curvature. Schools with higher vocab scores at the mean age tend to have lower linear increase, and also a more negative curvature.
Within schools, children vary in the vocab scores at mean age with an SD of 5.9. Lots of child-level variation in curvature and linear increases, slightly less variation in wiggliness.

VarCorr(mod7)

 Groups       Name        Std.Dev. Corr                
 school:child (Intercept)  5.9043                      
              poly1       42.8908   0.005              
              poly2       62.8095  -0.078  0.228       
              poly3       26.1619   0.191  0.610  0.871
 school       (Intercept)  4.4683                      
              poly1       30.4741  -0.403              
              poly3       18.3230  -0.525 -0.116       
 Residual                  5.6511                      

Footnotes

1. if it does, head back to where we learned about interactions in the single level regressions lm(). It’s just the same here.