Recap of multilevel models

No specific exercises this week

This week, there aren’t any exercises, but there is a small recap reading of multilevel models, followed by some ‘flashcard’ type boxes to help you test your understanding of some of the key concepts.

Please use the lab sessions to go over exercises from previous weeks, as well as asking any questions about the content below.

Flashcards: lm to lmer

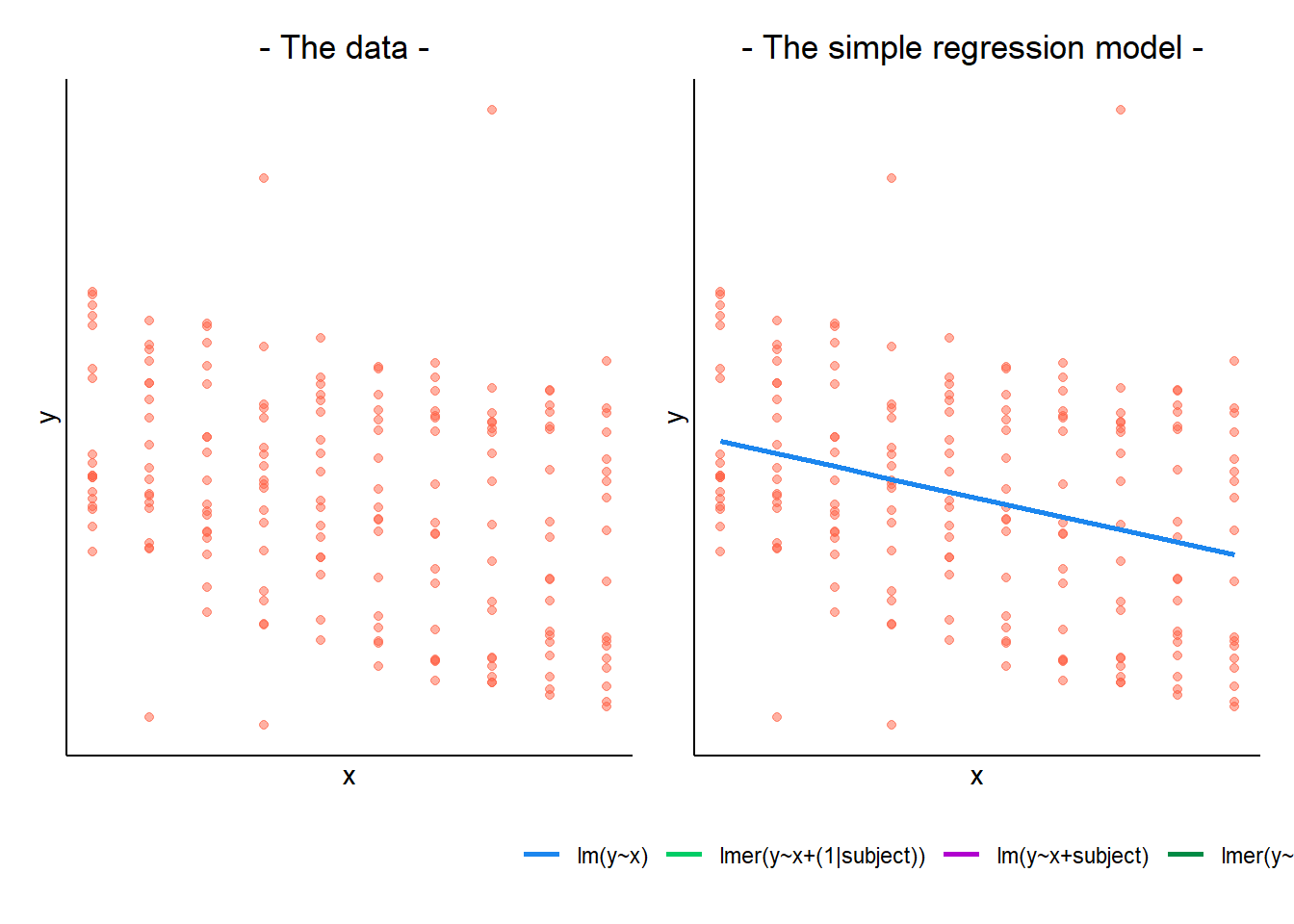
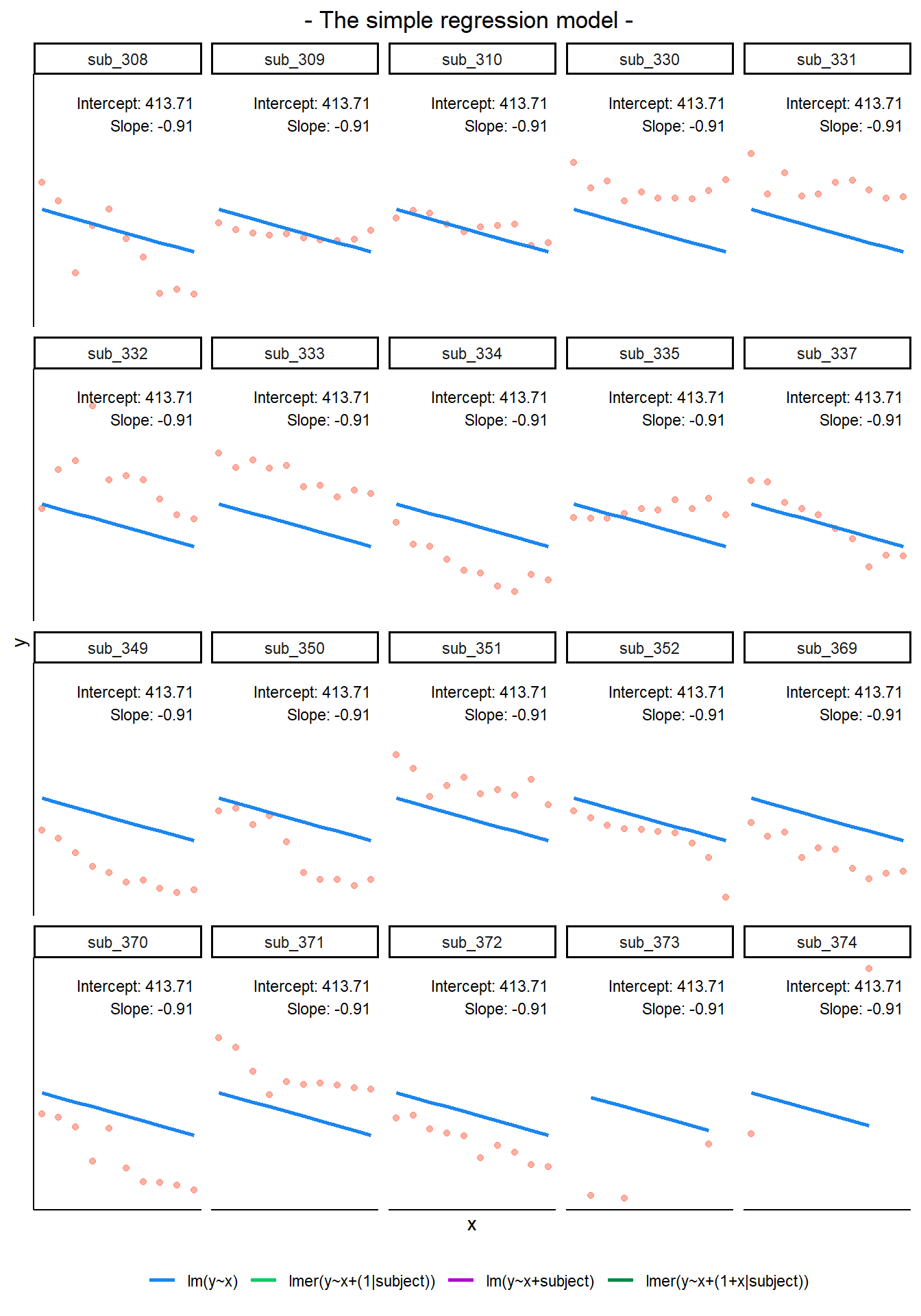
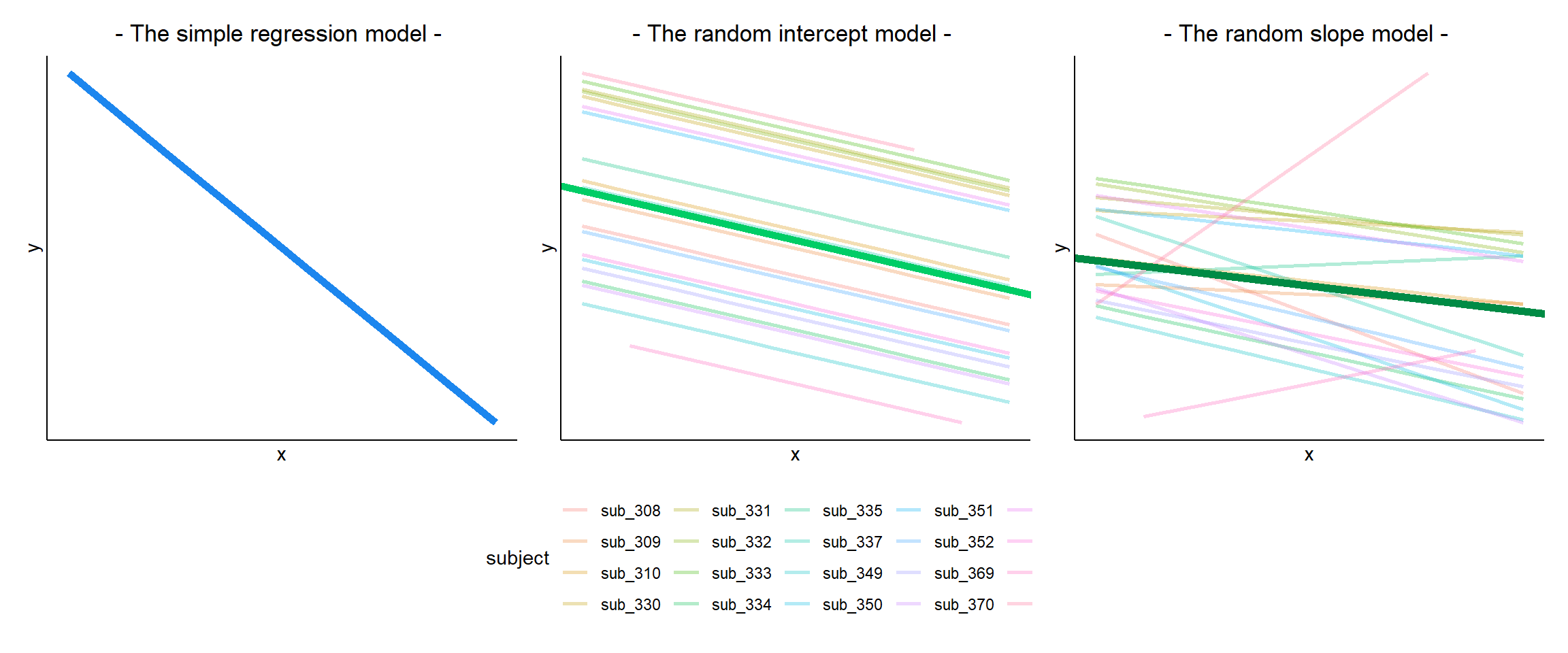
In a simple linear regression, there is only considered to be one source of random variability: any variability left unexplained by a set of predictors (which are modelled as fixed estimates) is captured in the model residuals.

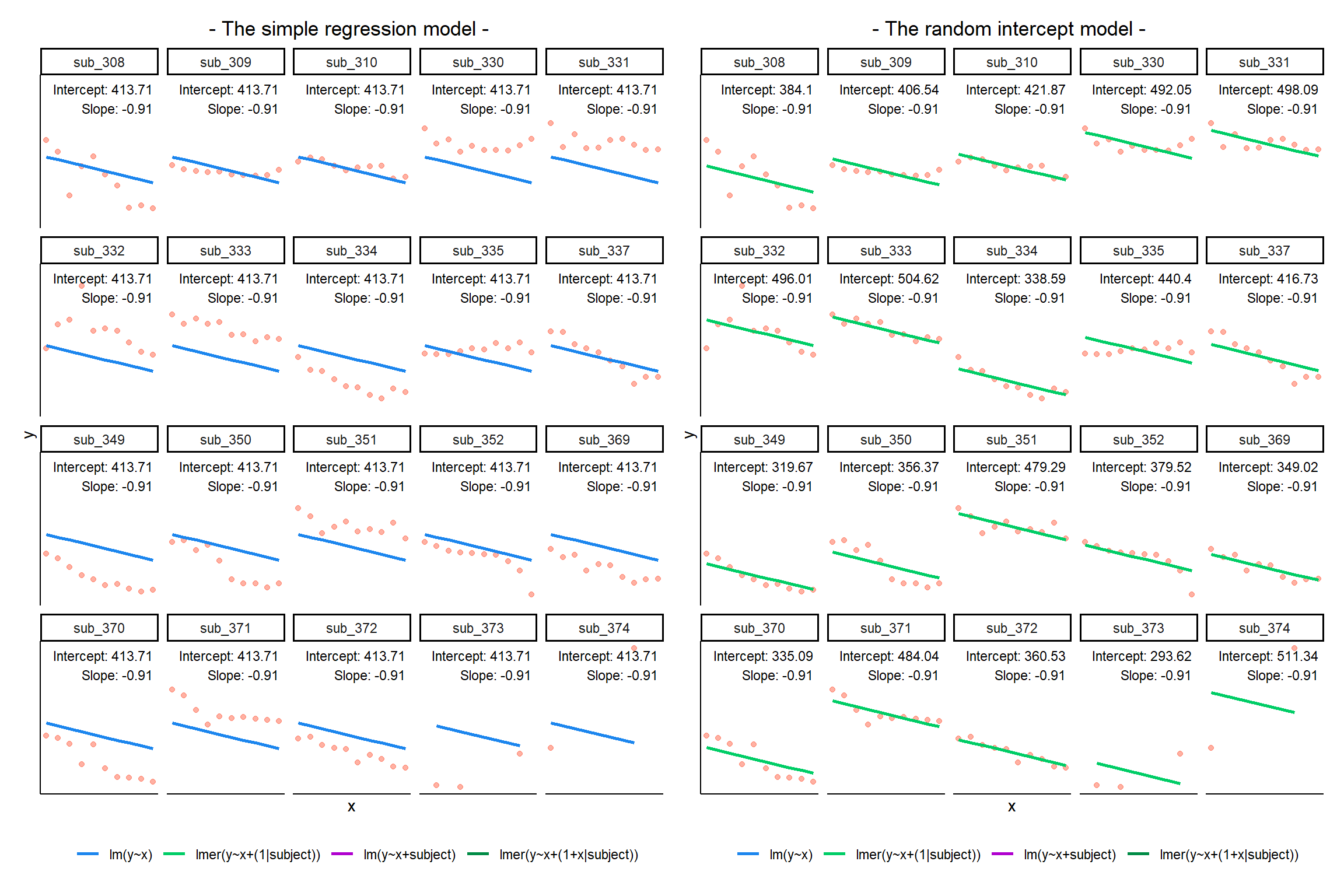
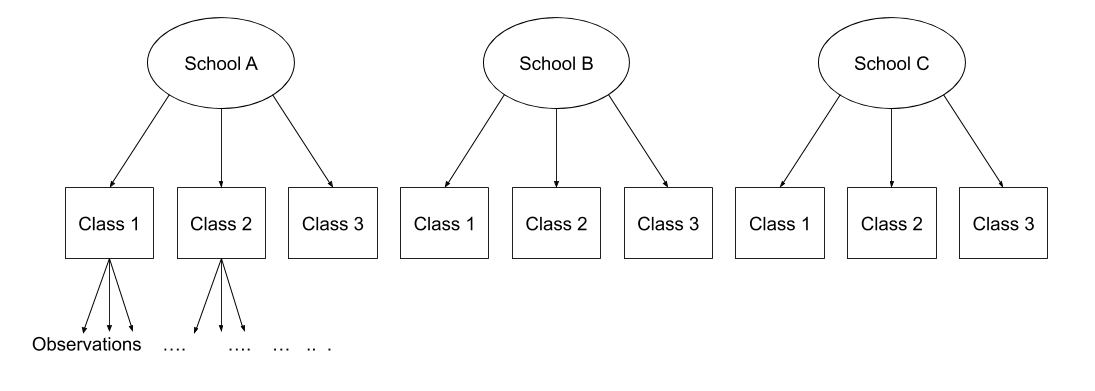
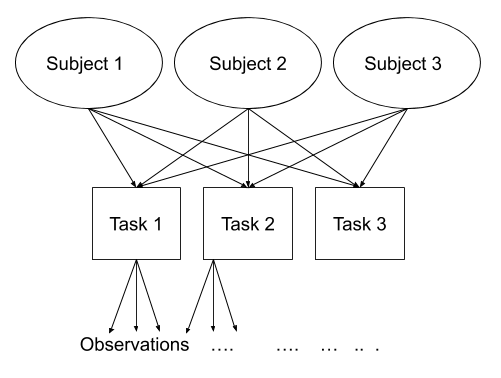
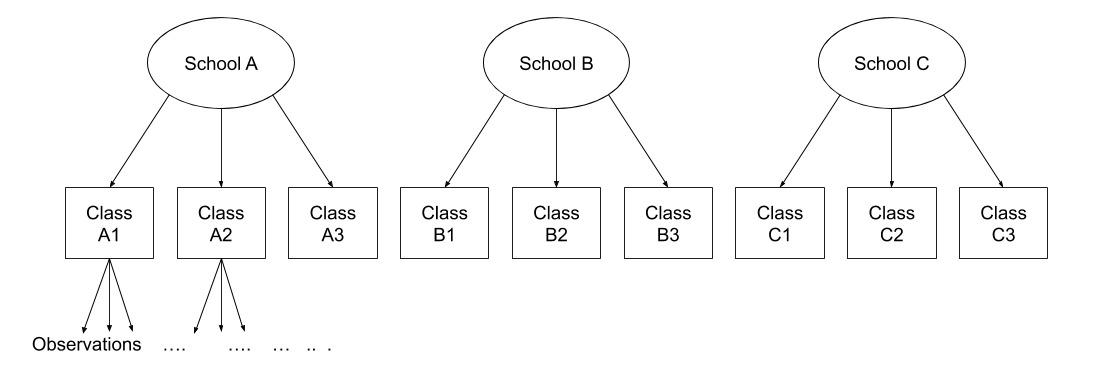
Multi-level (or ‘mixed-effects’) approaches involve modelling more than one source of random variability - as well as variance resulting from taking a random sample of observations, we can identify random variability across different groups of observations. For example, if we are studying a patient population in a hospital, we would expect there to be variability across the our sample of patients, but also across the doctors who treat them.

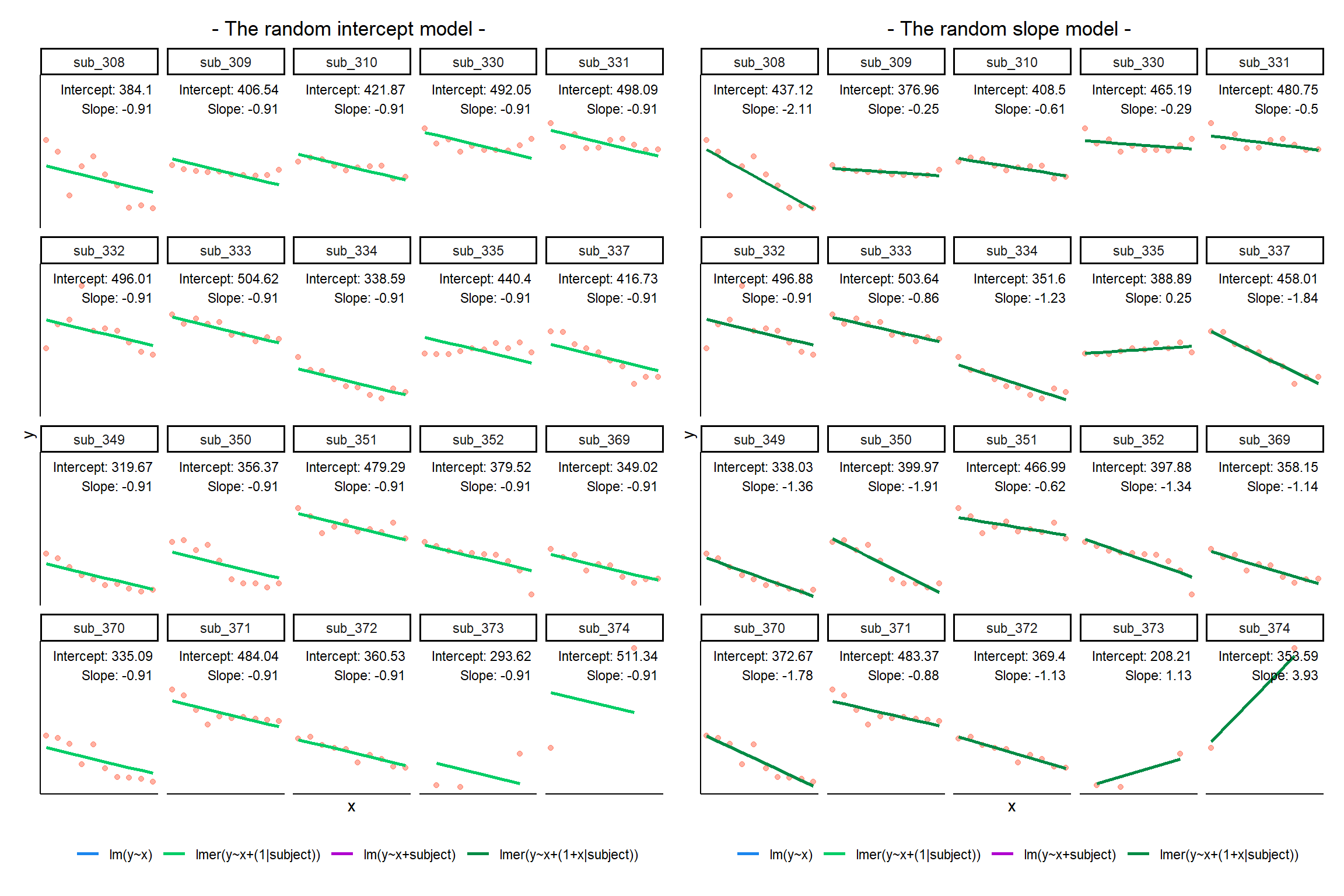
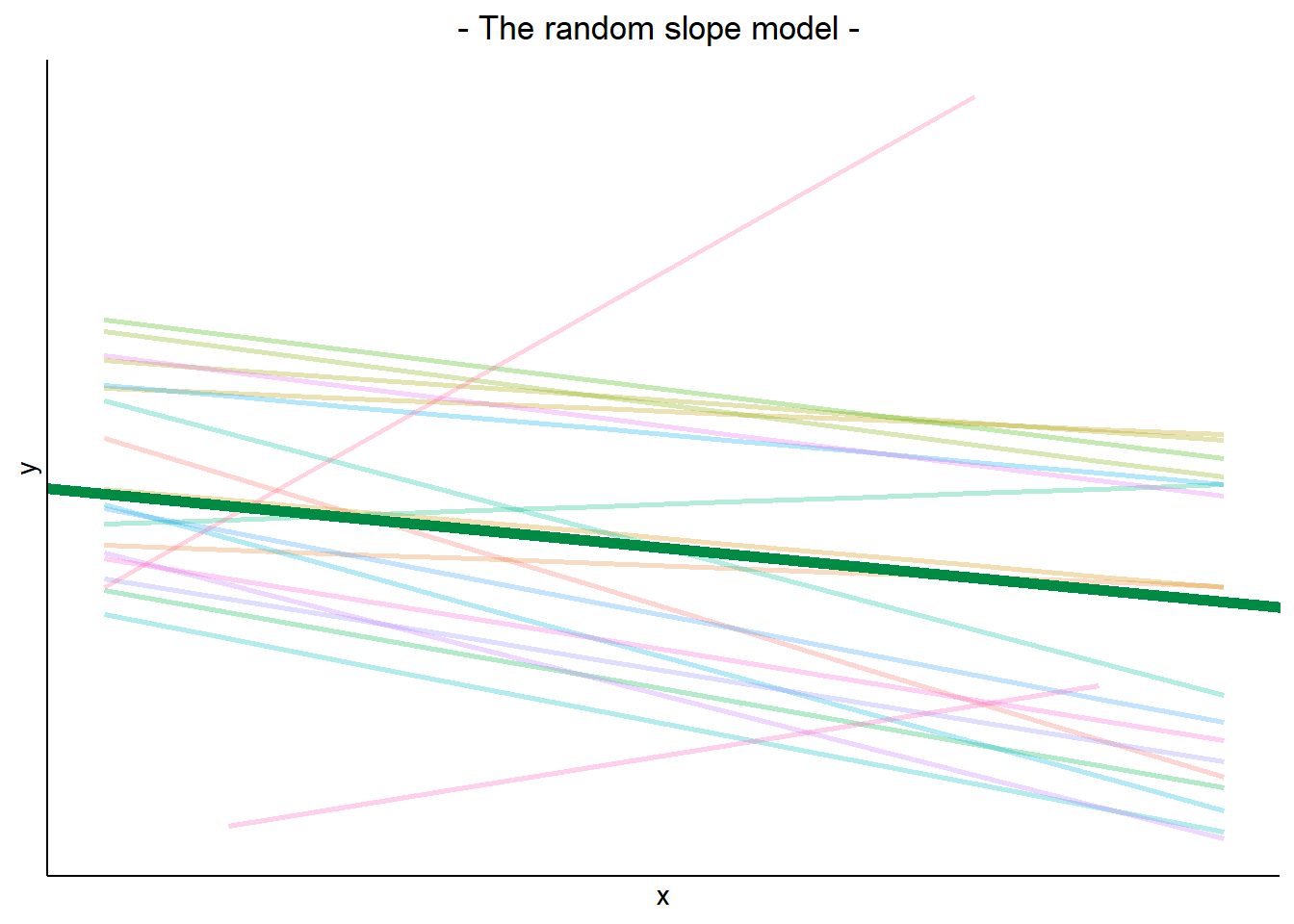
We can account for this variability by allowing the outcome to be lower/higher for each group (a random intercept) and by allowing the estimated effect of a predictor vary across groups (random slopes).

Before you expand each of the boxes below, think about how comfortable you feel with each concept.
This content is very cumulative, which means often going back to try to isolate the place which we need to focus efforts in learning.

Simple Linear Regression

Clustered (multi-level) data

Random intercepts

Shrinkage

Random slopes

Fixed effects

Random effects

Group-level coefficients

Visualising Model Fitted values

Visualising Fixed Effects

Plotting random effects

Nested and Crossed structures

MLM in a nutshell

Model Structure & Notation

MLM allows us to model effects in the linear model as varying between groups. Our coefficients we remember from simple linear models (the \(\beta\)’s) are modelled as a distribution that has an overall mean around which our groups vary. We can see this in Figure 1, where both the intercept and the slope of the line are modelled as varying by-groups. Figure 1 shows the overall line in blue, with a given group’s line in green.

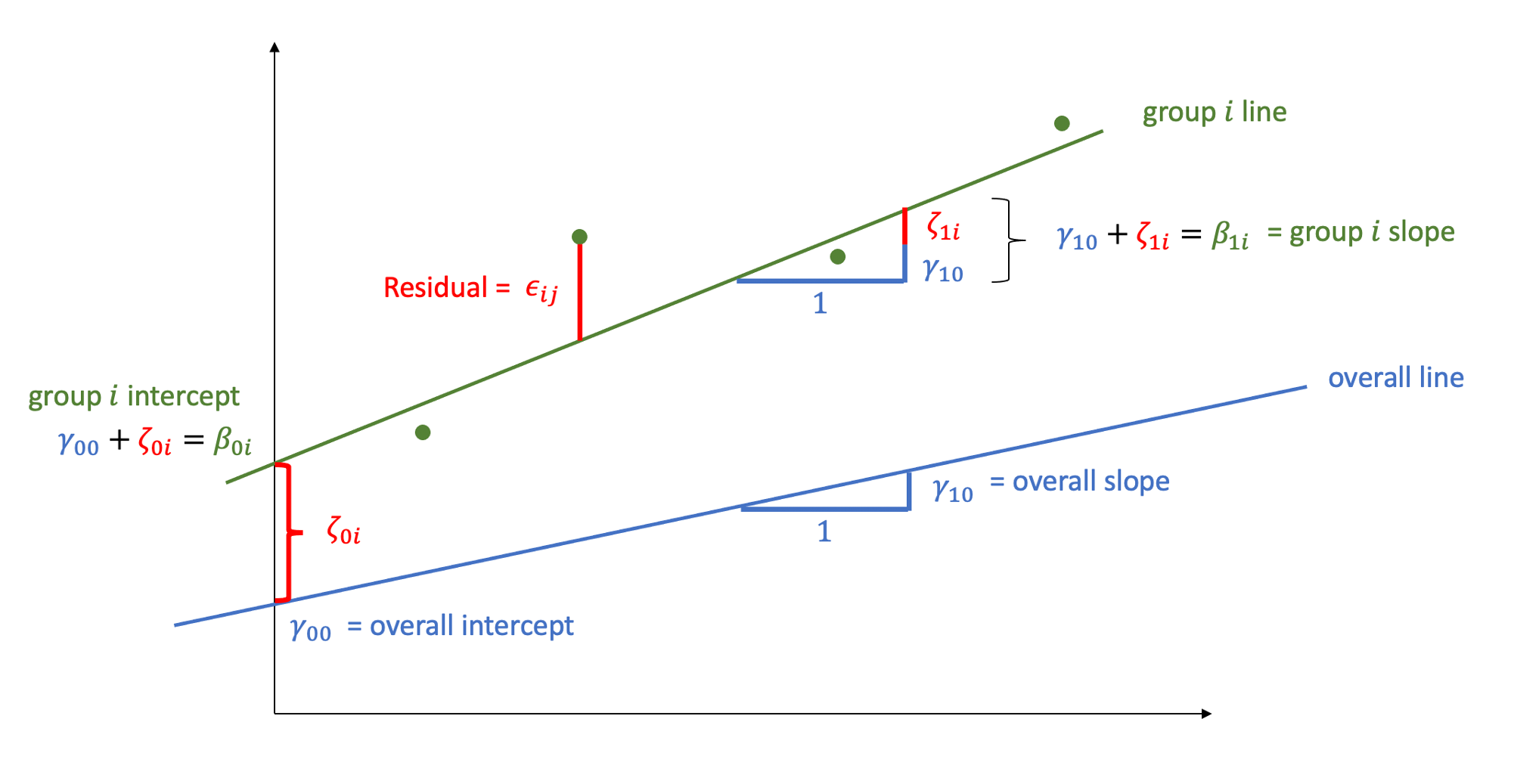
Figure 1: Multilevel Model. Each group (e.g. the group in the green line) deviates from the overall fixed effects (the blue line), and the individual observations (green points) deviate from their groups line

The formula notation for these models involves separating out our effects \(\beta\) into two parts: the overall effect \(\gamma\) + the group deviations \(\zeta_i\):

\[ \begin{align} & \text{for observation }j\text{ in group }i \\ \quad \\ & \text{Level 1:} \\ & \color{red}{y_{ij}}\color{black} = \color{blue}{\beta_{0i} \cdot 1 + \beta_{1i} \cdot x_{ij}}\color{black} + \varepsilon_{ij} \\ & \text{Level 2:} \\ & \color{blue}{\beta_{0i}}\color{black} = \gamma_{00} + \color{orange}{\zeta_{0i}} \\ & \color{blue}{\beta_{1i}}\color{black} = \gamma_{10} + \color{orange}{\zeta_{1i}} \\ \quad \\ & \text{Where:} \\ & \gamma_{00}\text{ is the population intercept, and }\color{orange}{\zeta_{0i}}\color{black}\text{ is the deviation of group }i\text{ from }\gamma_{00} \\ & \gamma_{10}\text{ is the population slope, and }\color{orange}{\zeta_{1i}}\color{black}\text{ is the deviation of group }i\text{ from }\gamma_{10} \\ \end{align} \]

The group-specific deviations \(\zeta_{0i}\) from the overall intercept are assumed to be normally distributed with mean \(0\) and variance \(\sigma_0^2\). Similarly, the deviations \(\zeta_{1i}\) of the slope for group \(i\) from the overall slope are assumed to come from a normal distribution with mean \(0\) and variance \(\sigma_1^2\). The correlation between random intercepts and slopes is \(\rho = \text{Cor}(\zeta_{0i}, \zeta_{1i}) = \frac{\sigma_{01}}{\sigma_0 \sigma_1}\):

\[ \begin{bmatrix} \zeta_{0i} \\ \zeta_{1i} \end{bmatrix} \sim N \left( \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \sigma_0^2 & \rho \sigma_0 \sigma_1 \\ \rho \sigma_0 \sigma_1 & \sigma_1^2 \end{bmatrix} \right) \]

The random errors, independently from the random effects, are assumed to be normally distributed with a mean of zero

\[ \epsilon_{ij} \sim N(0, \sigma_\epsilon^2) \]

MLM in R

We can fit these models using the R package lme4, and the function lmer(). Think of it like building your linear model lm(y ~ 1 + x), and then allowing effects (i.e. things on the right hand side of the ~ symbol) to vary by the grouping of your data. We specify these by adding (vary these effects | by these groups) to the model:

library(lme4)
m1 <- lmer(y ~ x + (1 + x | group), data = df)
summary(m1)
Linear mixed model fit by REML ['lmerMod']
Formula: y ~ x + (1 + x | group)
   Data: df

REML criterion at convergence: 637.9

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.49449 -0.57223 -0.01353  0.62544  2.39122 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 group    (Intercept) 2.2616   1.5038       
          x           0.7958   0.8921   0.55
 Residual             4.3672   2.0898       
Number of obs: 132, groups:  group, 20

Fixed effects:
            Estimate Std. Error t value
(Intercept)   1.7261     0.9673   1.785
x             1.1506     0.2968   3.877

Correlation of Fixed Effects:
  (Intr)
x -0.552

The summary of the lmer output returns estimated values for

Fixed effects:

  • \(\widehat \gamma_{00} = 1.726\)
  • \(\widehat \gamma_{10} = 1.151\)

Variability of random effects:

  • \(\widehat \sigma_{0} = 1.504\)
  • \(\widehat \sigma_{1} = 0.892\)

Correlation of random effects:

  • \(\widehat \rho = 0.546\)

Residuals:

  • \(\widehat \sigma_\epsilon = 2.09\)

Flashcards: Getting p-values/CIs for Multilevel Models

Inference for multilevel models is tricky, and there are lots of different approaches.
You might find it helpful to think of the majority of these techniques as either:

A. Fitting a full model and a reduced model. These differ only with respect to the relevant effect. Comparing the overall fit of these models by some metric allows us to isolate the improvement due to our effect of interest. B. Fitting the full model and - using some method of approximating the degrees of freedom for the tests of whether a coefficient is zero. - constructing some confidence intervals (e.g. via bootstrapping) in order to gain a range of plausible values for the estimate (typically we then ask whether zero is within the interval)

Neither of these is correct or incorrect, but they each have different advantages. In brief:

  • Satterthwaite \(df\) = Very easy to implement, can fit with REML
  • Kenward-Rogers \(df\) = Good when working with small samples, can fit with REML
  • Likelihood Ratio Tests = better with bigger samples (of groups, and of observations within groups), requires REML = FALSE
  • Parametric Bootstrap = takes time to run, but in general a reliable approach. , requires REML = FALSE if doing comparisons, but not for confidence intervals
  • Non-Parametric Bootstrap = takes time, needs careful thought about which levels to resample, but means we can relax distributional assumptions (e.g. about normality of residuals).

For the examples below, we’re investigating how “hours per week studied” influences a child’s reading age. We have data from 132 children from 20 schools, and we have fitted the model:

full_model <- lmer(reading_age ~ 1 + hrs_week + (1 + hrs_week | school), 
                   data = childread)
Use a normal approximation (not advisable)

Satterthwaite df approximation

Kenward Rogers df approximations

Likelihood Ratio Test (LRT)

Parametric Bootstrap LRT

Parametric Bootstrap Confidence Intervals

Non-Parametric Bootstrap Confidence Intervals