Multiple Comparisons

Introduction

This week’s exercises are much lighter than last week, so it might be worth also using it to catch up on previous week’s this term.

Next week :

This week, we’re going to take a brief look at the idea of multiple comparisons.

Refreshing last week:

Last week we learned how to conduct a 2-factor ANOVA. We examined the effects of two variables, Diagnosis (Amnesic, Huntingtons or a Control group) and Task (Grammar, Classification or Recognition).

We incrementally built the 2x2 anova model. Recall, ANOVA is actually a special case of the linear model in which the predictors are categorical variables, so we can build our model using lm(), and presented slightly differently.
Our full model, including the interaction, looked like this:

mdl_int <- lm(Score ~ 1 + Diagnosis + Task + Diagnosis:Task, data = cog)
# Alternatively, we could have used the following shorter version:
# mdl_int <- lm(Score ~ 1 + Diagnosis * Task, data = cog)

And to view the typically presented ANOVA table for this model:

anova(mdl_int)

Analysis of Variance Table

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
Diagnosis	2	5250	2625	16.64	7.64e-06
Task	2	5250	2625	16.64	7.64e-06
Diagnosis:Task	4	5000	1250	7.923	0.0001092
Residuals	36	5680	157.8	NA	NA

The interaction between diagnosis and task is significant. At the 5% level, the probability of obtaining an F-statistic as large as 7.92 or larger, if there was no interaction effect, is <.001. This provides very strong evidence against the null hypothesis that effect of task is constant across the different diagnoses.

(remember: in the presence of a significant interaction it does not make sense to interpret the main effects as their interpretation changes with the level of the other factor)

ANOVA is an “omnibus” test

The results from an ANOVA are often called an ‘omnibus’ test, because we are testing the null hypothesis that a set of group means are equal (or in the interaction case, that the differences between group means are equal across some other factor).

If you have found Semester 1 materials on linear models a bit more intuitive than ANOVA, another way to think of it is that we are testing the improvement of model fit between a full and a reduced model.
For instance, our significant interaction \(F(4, 36) = 7.9225, p < .001\) can also be obtained by comparing the nested models (one with the interaction vs one without):

mdl_add <- lm(Score ~ 1 + Diagnosis + Task, data = cog)
mdl_int <- lm(Score ~ 1 + Diagnosis + Task + Diagnosis:Task, data = cog)
anova(mdl_add, mdl_int)

## Analysis of Variance Table
## 
## Model 1: Score ~ 1 + Diagnosis + Task
## Model 2: Score ~ 1 + Diagnosis + Task + Diagnosis:Task
##   Res.Df   RSS Df Sum of Sq      F    Pr(>F)    
## 1     40 10680                                  
## 2     36  5680  4      5000 7.9225 0.0001092 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

But it is common to want to know more about the details of such an effect. What groups differ, and by how much?

The traditional approach is to conduct an ANOVA, and then only ask this sort of follow-up question if obtaining a significant omnibus test.
You might think of it as:

Question 1: Omnibus: “Are there any differences in group means?”
Question 2: Comparisons: “What are the differences and between which groups?”

If your answer to 1 is “No,” then it doesn’t make much sense to ask question 2.

Multiple Comparisons

In last week’s exercises we began to look at how we compare different groups, by using contrast analysis to conduct tests of specific comparisons between groups. We also saw how we might conduct “pairwise comparisons,” where we test all possible pairs of group means within a given set.

For instance, we compares the means of the different diagnosis groups for each task:

emm_task <- emmeans(mdl_int, ~ Diagnosis | Task)
contr_task <- contrast(emm_task, method = 'pairwise', 
                       adjust = "bonferroni")
contr_task

or we might test all different combinations of task and diagnosis group (if that was something we were theoretically interested in, which is unlikely!) which would equate to conducting 36 comparisons!

emm_task <- emmeans(mdl_int, ~ Diagnosis * Task)
contr_task <- contrast(emm_task, method = 'pairwise', 
                       adjust = "bonferroni")
contr_task

##  contrast                                             estimate   SE df t.ratio
##  control grammar - amnesic grammar                          20 7.94 36  2.518 
##  control grammar - huntingtons grammar                      40 7.94 36  5.035 
##  control grammar - control classification                    0 7.94 36  0.000 
##  control grammar - amnesic classification                   10 7.94 36  1.259 
##  control grammar - huntingtons classification               35 7.94 36  4.406 
##  control grammar - control recognition                     -15 7.94 36 -1.888 
##  control grammar - amnesic recognition                      15 7.94 36  1.888 
##  control grammar - huntingtons recognition                 -15 7.94 36 -1.888 
##  amnesic grammar - huntingtons grammar                      20 7.94 36  2.518 
##  amnesic grammar - control classification                  -20 7.94 36 -2.518 
##  amnesic grammar - amnesic classification                  -10 7.94 36 -1.259 
##  amnesic grammar - huntingtons classification               15 7.94 36  1.888 
##  amnesic grammar - control recognition                     -35 7.94 36 -4.406 
##  amnesic grammar - amnesic recognition                      -5 7.94 36 -0.629 
##  amnesic grammar - huntingtons recognition                 -35 7.94 36 -4.406 
##  huntingtons grammar - control classification              -40 7.94 36 -5.035 
##  huntingtons grammar - amnesic classification              -30 7.94 36 -3.776 
##  huntingtons grammar - huntingtons classification           -5 7.94 36 -0.629 
##  huntingtons grammar - control recognition                 -55 7.94 36 -6.923 
##  huntingtons grammar - amnesic recognition                 -25 7.94 36 -3.147 
##  huntingtons grammar - huntingtons recognition             -55 7.94 36 -6.923 
##  control classification - amnesic classification            10 7.94 36  1.259 
##  control classification - huntingtons classification        35 7.94 36  4.406 
##  control classification - control recognition              -15 7.94 36 -1.888 
##  control classification - amnesic recognition               15 7.94 36  1.888 
##  control classification - huntingtons recognition          -15 7.94 36 -1.888 
##  amnesic classification - huntingtons classification        25 7.94 36  3.147 
##  amnesic classification - control recognition              -25 7.94 36 -3.147 
##  amnesic classification - amnesic recognition                5 7.94 36  0.629 
##  amnesic classification - huntingtons recognition          -25 7.94 36 -3.147 
##  huntingtons classification - control recognition          -50 7.94 36 -6.294 
##  huntingtons classification - amnesic recognition          -20 7.94 36 -2.518 
##  huntingtons classification - huntingtons recognition      -50 7.94 36 -6.294 
##  control recognition - amnesic recognition                  30 7.94 36  3.776 
##  control recognition - huntingtons recognition               0 7.94 36  0.000 
##  amnesic recognition - huntingtons recognition             -30 7.94 36 -3.776 
##  p.value
##  0.5907 
##  0.0005 
##  1.0000 
##  1.0000 
##  0.0033 
##  1.0000 
##  1.0000 
##  1.0000 
##  0.5907 
##  0.5907 
##  1.0000 
##  1.0000 
##  0.0033 
##  1.0000 
##  0.0033 
##  0.0005 
##  0.0207 
##  1.0000 
##  <.0001 
##  0.1190 
##  <.0001 
##  1.0000 
##  0.0033 
##  1.0000 
##  1.0000 
##  1.0000 
##  0.1190 
##  0.1190 
##  1.0000 
##  0.1190 
##  <.0001 
##  0.5907 
##  <.0001 
##  0.0207 
##  1.0000 
##  0.0207 
## 
## P value adjustment: bonferroni method for 36 tests

36? how do we know there are 36?

There are 3 diagnosis groups, and 3 tasks, meaning there are 9 different group means.
All possible pairwise comparisons would is all different possible combinations of 2 from a set of 9.
We can work this out using the rule:

$$ _nC_r = \ \[\begin{align} \\ & \text{Where:} \\ & n = \text{total number in the set} \\ & r = \text{number chosen} \\ & _nC_r = \text{number of combinations of r from n} \\ \end{align}\]

$$ In R:

factorial(9)/(factorial(2)*(factorial(9-2)))

## [1] 36

Or, easier still:

dim(combn(9, 2))

## [1]  2 36

Why does the number of tests matter?

As discussed briefly in last week’s exercises, we will ideally ensure that our error rate is 0.05 (i.e., the chance that we reject a null hypothesis when it actually true, is 5%).

refresher on making errors in hypothesis tests

Think back to “Type 1 errors” from DAPR1 - when we conduct an hypothesis test, and we set \(\alpha=0.05\), we will reject the null hypothesis \(H_0\) when we find a \(p < .05\). Now remember what a \(p\)-value represents - it is the chance of observing a statistic at least as extreme as the one we do have, assuming the null hypothesis to be true. This means that if \(H_0\) is true, then we will still observe a \(p < .05\) 5% of the time. So our chance of making this error = the threshold (\(\alpha\)) at which below a p-value results in us rejecting \(H_0\).

But this error-rate applies to each statistical hypothesis we test. So if we conduct an experiment in which we plan on conducting lots of tests of different comparisons, the chance of an error being made increases substantially. Across the family of tests performed that chance will be much higher than 5%.¹

Each test conducted at \(\alpha = 0.05\) has a 0.05 (or 5%) probability of Type I error (wrongly rejecting the null hypothesis). If we do 9 tests, that experimentwise error rate is \(\alpha_{ew} \leq 9 \times 0.05\), where 9 is the number of comparisons made as part of the experiment. Thus, if nine independent comparisons were made at the \(\alpha = 0.05\) level, the experimentwise Type I error rate \(\alpha_{ew}\) would be at most \(9 \times 0.05 = 0.45\). That is, we could wrongly reject the null hypothesis on average 45 times out of 100. To make this more confusing, many of the tests in a family are not independent (see the lecture slides for the calculation of error rate for dependent tests).

Here, we go through some of the different options available to us to control, or ‘correct’ for this problem. The first we look at was used in the solutions to last week’s exercises, and is perhaps the most well-known.

Bonferroni

Bonferroni

• Use Bonferroni’s method when you are interested in a small number of planned contrasts (or pairwise comparisons).
• Bonferroni’s method is to divide alpha by the number of tests/confidence intervals.
• Assumes that all comparisons are independent of one another.
  
• It sacrifices slightly more power than Tukey’s method (discussed below), but it can be applied to any set of contrasts or linear combinations (i.e., it is useful in more situations than Tukey).
• It is usually better than Tukey if we want to do a small number of planned comparisons.

Question 1

Load the data from last week, and re-acquaint yourself with it. Provide a plot of the Diagnosis*Task group mean scores.
The data is at https://uoepsy.github.io/data/cognitive_experiment.csv.

Solution

cog <- read_csv('https://uoepsy.github.io/data/cognitive_experiment.csv')
# head(df)

cog$Diagnosis <- factor(cog$Diagnosis, 
                       labels = c("amnesic", "huntingtons", "control"),
                       ordered = FALSE)

cog$Task <- factor(cog$Task, 
                  labels = c("grammar", "classification", "recognition"), 
                  ordered = FALSE)

cog$Diagnosis <- fct_relevel(cog$Diagnosis, "control")

cog <- cog %>%
    rename(Score = Y)

Question 2

Fit the interaction model, using lm(). Pass your model to the anova() function, to remind yourself that there is a significant interaction present.

Solution

mdl_int <- lm(Score ~ Task*Diagnosis, data = cog)
anova(mdl_int)

## Analysis of Variance Table
## 
## Response: Score
##                Df Sum Sq Mean Sq F value    Pr(>F)    
## Task            2   5250 2625.00 16.6373  7.64e-06 ***
## Diagnosis       2   5250 2625.00 16.6373  7.64e-06 ***
## Task:Diagnosis  4   5000 1250.00  7.9225 0.0001092 ***
## Residuals      36   5680  157.78                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Question 3

There are various ways to make nice tables in RMarkdown.
Some of the most well known are:

• The knitr package has kable()
  
• The pander package has pander()

Pick one (or find go googling and find a package you like the look of), install the package (if you don’t already have it), then try to create a nice pretty ANOVA table rather than the one given by anova(model).

Solution

library(knitr)
kable(anova(mdl_int))

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
Task	2	5250	2625.0000	16.637324	0.0000076
Diagnosis	2	5250	2625.0000	16.637324	0.0000076
Task:Diagnosis	4	5000	1250.0000	7.922535	0.0001092
Residuals	36	5680	157.7778	NA	NA

library(pander)
pander(anova(mdl_int))

Analysis of Variance Table

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
Task	2	5250	2625	16.64	7.64e-06
Diagnosis	2	5250	2625	16.64	7.64e-06
Task:Diagnosis	4	5000	1250	7.923	0.0001092
Residuals	36	5680	157.8	NA	NA

Question 4

As in the previous week’s exercises, let us suppose that we are specifically interested in comparisons of the mean score across the different diagnosis groups for a given task.

Edit the code below to obtain the pairwise comparisons of diagnosis groups for each task. Use the Bonferroni method to adjust for multiple comparisons, and then obtain confidence intervals.

library(emmeans)
emm_task <- emmeans(mdl_int, ? )
contr_task <- contrast(emm_task, method = ?, adjust = ? )

Solution

emm_task <- emmeans(mdl_int, ~ Diagnosis | Task)
contr_task <- contrast(emm_task, method = "pairwise", adjust="bonferroni")
contr_task

## Task = grammar:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           20 7.94 36  2.518  0.0492 
##  control - huntingtons       40 7.94 36  5.035  <.0001 
##  amnesic - huntingtons       20 7.94 36  2.518  0.0492 
## 
## Task = classification:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           10 7.94 36  1.259  0.6486 
##  control - huntingtons       35 7.94 36  4.406  0.0003 
##  amnesic - huntingtons       25 7.94 36  3.147  0.0099 
## 
## Task = recognition:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           30 7.94 36  3.776  0.0017 
##  control - huntingtons        0 7.94 36  0.000  1.0000 
##  amnesic - huntingtons      -30 7.94 36 -3.776  0.0017 
## 
## P value adjustment: bonferroni method for 3 tests

confint(contr_task)

## Task = grammar:
##  contrast              estimate   SE df lower.CL upper.CL
##  control - amnesic           20 7.94 36   0.0517     39.9
##  control - huntingtons       40 7.94 36  20.0517     59.9
##  amnesic - huntingtons       20 7.94 36   0.0517     39.9
## 
## Task = classification:
##  contrast              estimate   SE df lower.CL upper.CL
##  control - amnesic           10 7.94 36  -9.9483     29.9
##  control - huntingtons       35 7.94 36  15.0517     54.9
##  amnesic - huntingtons       25 7.94 36   5.0517     44.9
## 
## Task = recognition:
##  contrast              estimate   SE df lower.CL upper.CL
##  control - amnesic           30 7.94 36  10.0517     49.9
##  control - huntingtons        0 7.94 36 -19.9483     19.9
##  amnesic - huntingtons      -30 7.94 36 -49.9483    -10.1
## 
## Confidence level used: 0.95 
## Conf-level adjustment: bonferroni method for 3 estimates

adjusting \(\alpha\), adjusting p

In the lecture we talked about adjusting the \(\alpha\) level (i.e., instead of determining significance at \(p < .05\), we might adjust and determine a result to be statistically significant if \(p < .005\), depending on how many tests are in our family of tests).

Note what the functions in R do is adjust the \(p\)-value, rather than the \(\alpha\). The Bonferroni method simply multiplies the ‘raw’ p-value by the number of the tests.

Question 5

In question 4, above, there are 9 tests being performed, but there are 3 in each ‘family’ (each Task).

Try changing your answer to question 4 to use adjust = "none", rather than "bonferroni", and confirm that the p-values are 1/3 of the size.

Solution

The first Bonferroni adjusted p-value is 0.0492.

0.0492/3

## [1] 0.0164

Let’s check that this is the raw p-value:

contrast(emm_task, method = "pairwise", adjust="none")

## Task = grammar:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           20 7.94 36  2.518  0.0164 
##  control - huntingtons       40 7.94 36  5.035  <.0001 
##  amnesic - huntingtons       20 7.94 36  2.518  0.0164 
## 
## Task = classification:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           10 7.94 36  1.259  0.2162 
##  control - huntingtons       35 7.94 36  4.406  0.0001 
##  amnesic - huntingtons       25 7.94 36  3.147  0.0033 
## 
## Task = recognition:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           30 7.94 36  3.776  0.0006 
##  control - huntingtons        0 7.94 36  0.000  1.0000 
##  amnesic - huntingtons      -30 7.94 36 -3.776  0.0006

Šídák

Šídák

• (A bit) more powerful than the Bonferroni method.
• Assumes that all comparisons are independent of one another.
• Less common than Bonferroni method, largely because it is more difficult to calculate (not a problem now we have computers).

Question 6

The Sidak approach is slightly less conservative than the Bonferroni adjustment.
Doing this with the emmeans package is easy, can you guess how?

Hint: you just have to change the adjust argument in contrast() function.

Solution

contrast(emm_task, method = "pairwise", adjust = "sidak")

## Task = grammar:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           20 7.94 36  2.518  0.0484 
##  control - huntingtons       40 7.94 36  5.035  <.0001 
##  amnesic - huntingtons       20 7.94 36  2.518  0.0484 
## 
## Task = classification:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           10 7.94 36  1.259  0.5185 
##  control - huntingtons       35 7.94 36  4.406  0.0003 
##  amnesic - huntingtons       25 7.94 36  3.147  0.0099 
## 
## Task = recognition:
##  contrast              estimate   SE df t.ratio p.value
##  control - amnesic           30 7.94 36  3.776  0.0017 
##  control - huntingtons        0 7.94 36  0.000  1.0000 
##  amnesic - huntingtons      -30 7.94 36 -3.776  0.0017 
## 
## P value adjustment: sidak method for 3 tests

Tukey

Tukey

• It specifies an exact family significance level for comparing all pairs of treatment means.
  
• Use Tukey’s method when you are interested in all (or most) pairwise comparisons of means.

As for Šídák, In R we can easily change to Tukey. For instance, if we wanted to conduct pairwise comparisons of the scores of different Diagnosis groups on different Task types (i.e., the interaction):

emm_task <- emmeans(mdl_int, ~ Diagnosis*Task)
contr_task <- contrast(emm_task, method = "pairwise", adjust="tukey")
contr_task

##  contrast                                             estimate   SE df t.ratio
##  control grammar - amnesic grammar                          20 7.94 36  2.518 
##  control grammar - huntingtons grammar                      40 7.94 36  5.035 
##  control grammar - control classification                    0 7.94 36  0.000 
##  control grammar - amnesic classification                   10 7.94 36  1.259 
##  control grammar - huntingtons classification               35 7.94 36  4.406 
##  control grammar - control recognition                     -15 7.94 36 -1.888 
##  control grammar - amnesic recognition                      15 7.94 36  1.888 
##  control grammar - huntingtons recognition                 -15 7.94 36 -1.888 
##  amnesic grammar - huntingtons grammar                      20 7.94 36  2.518 
##  amnesic grammar - control classification                  -20 7.94 36 -2.518 
##  amnesic grammar - amnesic classification                  -10 7.94 36 -1.259 
##  amnesic grammar - huntingtons classification               15 7.94 36  1.888 
##  amnesic grammar - control recognition                     -35 7.94 36 -4.406 
##  amnesic grammar - amnesic recognition                      -5 7.94 36 -0.629 
##  amnesic grammar - huntingtons recognition                 -35 7.94 36 -4.406 
##  huntingtons grammar - control classification              -40 7.94 36 -5.035 
##  huntingtons grammar - amnesic classification              -30 7.94 36 -3.776 
##  huntingtons grammar - huntingtons classification           -5 7.94 36 -0.629 
##  huntingtons grammar - control recognition                 -55 7.94 36 -6.923 
##  huntingtons grammar - amnesic recognition                 -25 7.94 36 -3.147 
##  huntingtons grammar - huntingtons recognition             -55 7.94 36 -6.923 
##  control classification - amnesic classification            10 7.94 36  1.259 
##  control classification - huntingtons classification        35 7.94 36  4.406 
##  control classification - control recognition              -15 7.94 36 -1.888 
##  control classification - amnesic recognition               15 7.94 36  1.888 
##  control classification - huntingtons recognition          -15 7.94 36 -1.888 
##  amnesic classification - huntingtons classification        25 7.94 36  3.147 
##  amnesic classification - control recognition              -25 7.94 36 -3.147 
##  amnesic classification - amnesic recognition                5 7.94 36  0.629 
##  amnesic classification - huntingtons recognition          -25 7.94 36 -3.147 
##  huntingtons classification - control recognition          -50 7.94 36 -6.294 
##  huntingtons classification - amnesic recognition          -20 7.94 36 -2.518 
##  huntingtons classification - huntingtons recognition      -50 7.94 36 -6.294 
##  control recognition - amnesic recognition                  30 7.94 36  3.776 
##  control recognition - huntingtons recognition               0 7.94 36  0.000 
##  amnesic recognition - huntingtons recognition             -30 7.94 36 -3.776 
##  p.value
##  0.2575 
##  0.0004 
##  1.0000 
##  0.9367 
##  0.0026 
##  0.6257 
##  0.6257 
##  0.6257 
##  0.2575 
##  0.2575 
##  0.9367 
##  0.6257 
##  0.0026 
##  0.9993 
##  0.0026 
##  0.0004 
##  0.0149 
##  0.9993 
##  <.0001 
##  0.0711 
##  <.0001 
##  0.9367 
##  0.0026 
##  0.6257 
##  0.6257 
##  0.6257 
##  0.0711 
##  0.0711 
##  0.9993 
##  0.0711 
##  <.0001 
##  0.2575 
##  <.0001 
##  0.0149 
##  1.0000 
##  0.0149 
## 
## P value adjustment: tukey method for comparing a family of 9 estimates

We can also use the following, which doesn’t require the emmeans package. You might see this when you look online for resources. The aov() function is fitting an ANOVA model, and then TukeyHSD() compares between Diagnosis group; between Task type; and between Diagnosis*Task.
Run the code below yourself to see the ouput.

TukeyHSD(aov(Score ~ Diagnosis * Task, data = cog))

Scheffe

Scheffe

• It is the most conservative (least powerful) of all tests.
• It controls the family alpha level for testing all possible contrasts.
• It should be used if you have not planned contrasts in advance.
• For testing pairs of treatment means it is too conservative (you should use Bonferroni or Šídák).

emm_task <- emmeans(mdl_int, ~ Diagnosis * Task)
contr_task <- contrast(emm_task, method = "pairwise", adjust="scheffe")
contr_task

##  contrast                                             estimate   SE df t.ratio
##  control grammar - amnesic grammar                          20 7.94 36  2.518 
##  control grammar - huntingtons grammar                      40 7.94 36  5.035 
##  control grammar - control classification                    0 7.94 36  0.000 
##  control grammar - amnesic classification                   10 7.94 36  1.259 
##  control grammar - huntingtons classification               35 7.94 36  4.406 
##  control grammar - control recognition                     -15 7.94 36 -1.888 
##  control grammar - amnesic recognition                      15 7.94 36  1.888 
##  control grammar - huntingtons recognition                 -15 7.94 36 -1.888 
##  amnesic grammar - huntingtons grammar                      20 7.94 36  2.518 
##  amnesic grammar - control classification                  -20 7.94 36 -2.518 
##  amnesic grammar - amnesic classification                  -10 7.94 36 -1.259 
##  amnesic grammar - huntingtons classification               15 7.94 36  1.888 
##  amnesic grammar - control recognition                     -35 7.94 36 -4.406 
##  amnesic grammar - amnesic recognition                      -5 7.94 36 -0.629 
##  amnesic grammar - huntingtons recognition                 -35 7.94 36 -4.406 
##  huntingtons grammar - control classification              -40 7.94 36 -5.035 
##  huntingtons grammar - amnesic classification              -30 7.94 36 -3.776 
##  huntingtons grammar - huntingtons classification           -5 7.94 36 -0.629 
##  huntingtons grammar - control recognition                 -55 7.94 36 -6.923 
##  huntingtons grammar - amnesic recognition                 -25 7.94 36 -3.147 
##  huntingtons grammar - huntingtons recognition             -55 7.94 36 -6.923 
##  control classification - amnesic classification            10 7.94 36  1.259 
##  control classification - huntingtons classification        35 7.94 36  4.406 
##  control classification - control recognition              -15 7.94 36 -1.888 
##  control classification - amnesic recognition               15 7.94 36  1.888 
##  control classification - huntingtons recognition          -15 7.94 36 -1.888 
##  amnesic classification - huntingtons classification        25 7.94 36  3.147 
##  amnesic classification - control recognition              -25 7.94 36 -3.147 
##  amnesic classification - amnesic recognition                5 7.94 36  0.629 
##  amnesic classification - huntingtons recognition          -25 7.94 36 -3.147 
##  huntingtons classification - control recognition          -50 7.94 36 -6.294 
##  huntingtons classification - amnesic recognition          -20 7.94 36 -2.518 
##  huntingtons classification - huntingtons recognition      -50 7.94 36 -6.294 
##  control recognition - amnesic recognition                  30 7.94 36  3.776 
##  control recognition - huntingtons recognition               0 7.94 36  0.000 
##  amnesic recognition - huntingtons recognition             -30 7.94 36 -3.776 
##  p.value
##  0.6128 
##  0.0080 
##  1.0000 
##  0.9894 
##  0.0329 
##  0.8852 
##  0.8852 
##  0.8852 
##  0.6128 
##  0.6128 
##  0.9894 
##  0.8852 
##  0.0329 
##  0.9999 
##  0.0329 
##  0.0080 
##  0.1131 
##  0.9999 
##  0.0001 
##  0.3060 
##  0.0001 
##  0.9894 
##  0.0329 
##  0.8852 
##  0.8852 
##  0.8852 
##  0.3060 
##  0.3060 
##  0.9999 
##  0.3060 
##  0.0003 
##  0.6128 
##  0.0003 
##  0.1131 
##  1.0000 
##  0.1131 
## 
## P value adjustment: scheffe method with rank 8

When to use which

For ease of scrolling, we have provided the bulletpoints for each correction below in one place:

Bonferroni

• Use Bonferroni’s method when you are interested in a small number of planned contrasts (or pairwise comparisons).
• Bonferroni’s method is to divide alpha by the number of tests/confidence intervals.
• Assumes that all comparisons are independent of one another.
  
• It sacrifices slightly more power than Tukey’s method (discussed below), but it can be applied to any set of contrasts or linear combinations (i.e., it is useful in more situations than Tukey).
• It is usually better than Tukey if we want to do a small number of planned comparisons.

Šídák

• (A bit) more powerful than the Bonferroni method.
• Assumes that all comparisons are independent of one another.
• Less common than Bonferroni method, largely because it is more difficult to calculate (not a problem now we have computers).

Tukey

• It specifies an exact family significance level for comparing all pairs of treatment means.
  
• Use Tukey’s method when you are interested in all (or most) pairwise comparisons of means.

Scheffe

• It is the most conservative (least powerful) of all tests.
• It controls the family alpha level for testing all possible contrasts.
• It should be used if you have not planned contrasts in advance.
• For testing pairs of treatment means it is too conservative (you should use Bonferroni or Šídák).

Lie detecting experiment

Lie detectors: Data Codebook

120 participants took part in a study in which they were presented with 100 recordings, and were tasked with guessing whether the speaker in each recording was lying or whether they were telling the truth.
Participants scored points every time they correctly identified a truth or a lie, and lost points whenever they mistook a lie for a truth (or vice versa). The maximum possible points to be scored was 100.

Half of the participants (60) were shown recordings in audio and video, the other half were presented with only the audio track. Prior to taking the experimen, participants were given material to read for 10 minutes. Half of the participants in each condition (30 in the audio-only condition, and 30 in the audiovideo condition) were given instructional material used by the Police Force to train detectives to pick up on dishonesty during interrogations via various verbal and non-verbal cues. The remaining 30 participants in each condition were given a series of cartoon strips to read.

The data is available at https://uoepsy.github.io/data/lietraining.csv

Research Questions

Do the Police training materials and the mode of communication (audio vs audiovideo) interact to influence the accuracy of veracity judgements?

Question 7

Load the data.
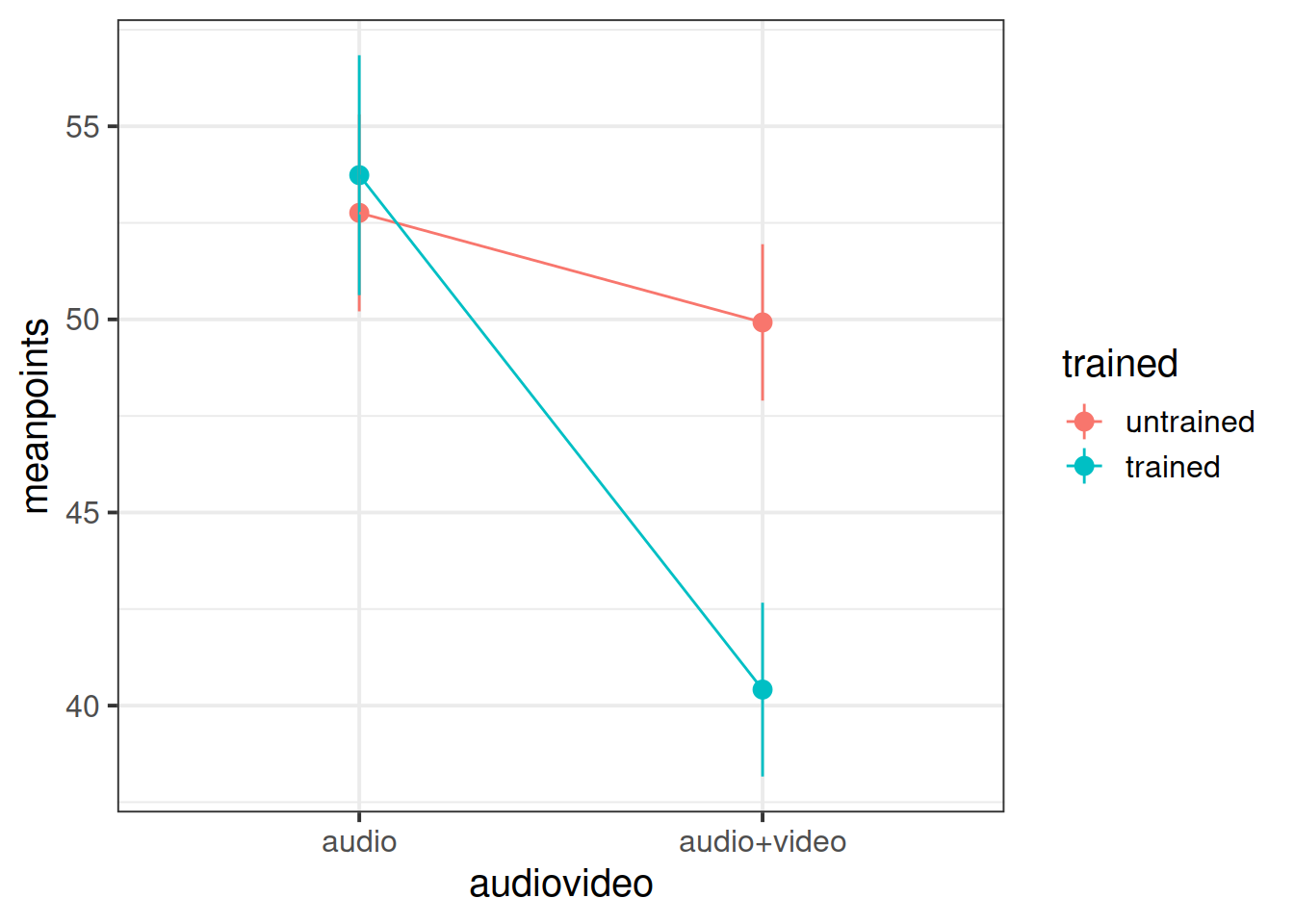
Produce a descriptives table for the variables of interest. Produce a plot showing the mean points for each condition.

Solution

liedat <- read_csv("https://uoepsy.github.io/data/lietraining.csv")

liedat$audiovideo <- factor(liedat$audiovideo, labels=c("audio","audio+video"))
liedat$trained <- factor(liedat$trained, labels = c("untrained","trained"))


liestats <- 
  liedat %>% group_by(audiovideo, trained) %>%
  summarise(meanpoints = mean(points),
            se = sd(points)/sqrt(n())
  )

ggplot(liestats, aes(x = audiovideo, y = meanpoints, color = trained)) + 
  geom_point(size = 3) +
  geom_linerange(aes(ymin = meanpoints - 2 * se, ymax = meanpoints + 2 * se)) +
  geom_path(aes(x = as.numeric(audiovideo)))

Question 8

Conduct a two-way ANOVA to investigate research question above.
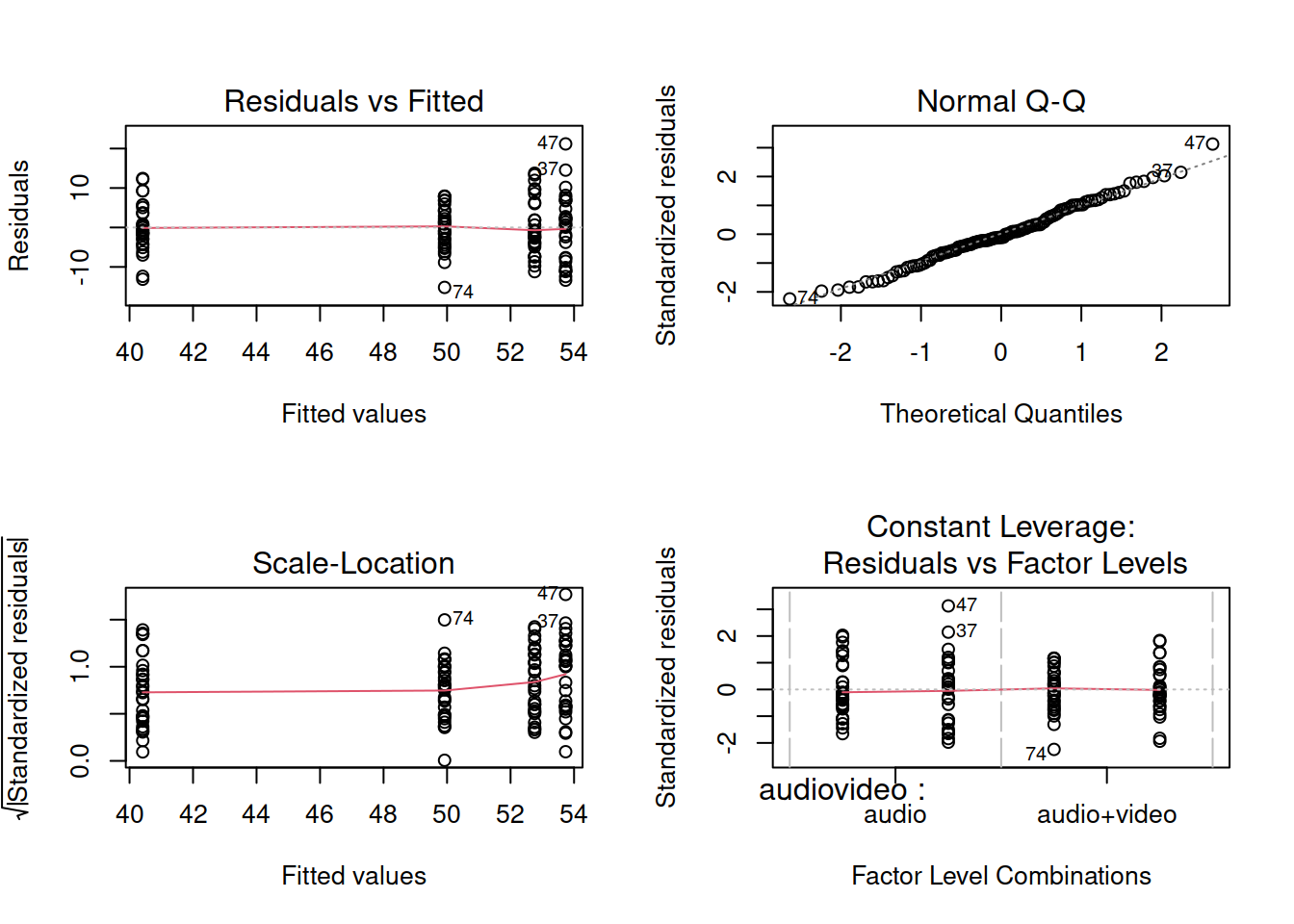
Be sure to check the assumptions!

Write up your results in a paragraph.

Solution

lie_mdl <- lm(points ~ audiovideo * trained, data = liedat)

plot(lie_mdl)

shapiro.test(residuals(lie_mdl))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(lie_mdl)
## W = 0.99122, p-value = 0.6469

car::ncvTest(lie_mdl)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 2.138705, Df = 1, p = 0.14362

anova(lie_mdl)

## Analysis of Variance Table
## 
## Response: points
##                     Df Sum Sq Mean Sq F value    Pr(>F)    
## audiovideo           1 1957.7 1957.71  41.263 3.046e-09 ***
## trained              1  545.8  545.85  11.505   0.00095 ***
## audiovideo:trained   1  824.2  824.20  17.372 5.949e-05 ***
## Residuals          116 5503.6   47.45                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Accuracy of veracity judgements (measured by points scored in lie-detecting game) were analysed with a 2 (audio vs audiovideo) \(\times\) 2 (untrained vs trained) between-subjects ANOVA. Residuals did not show significant departure from normality (Shapiro-Wilk \(W=0.99, p = .65\)), nor unequal variances across groups (Breusch-Pagan \(\chi^2(1)=2.14, p = .14\)). There was a significant interaction between presentation mode and whether or not participants had received training for detecting lies \(F(1, 116) = 17.37, p <. 001\).

Please note that these are short example write ups that may not be complete for every question you are asked. It is intended to give you a sense of the style.

Question 9

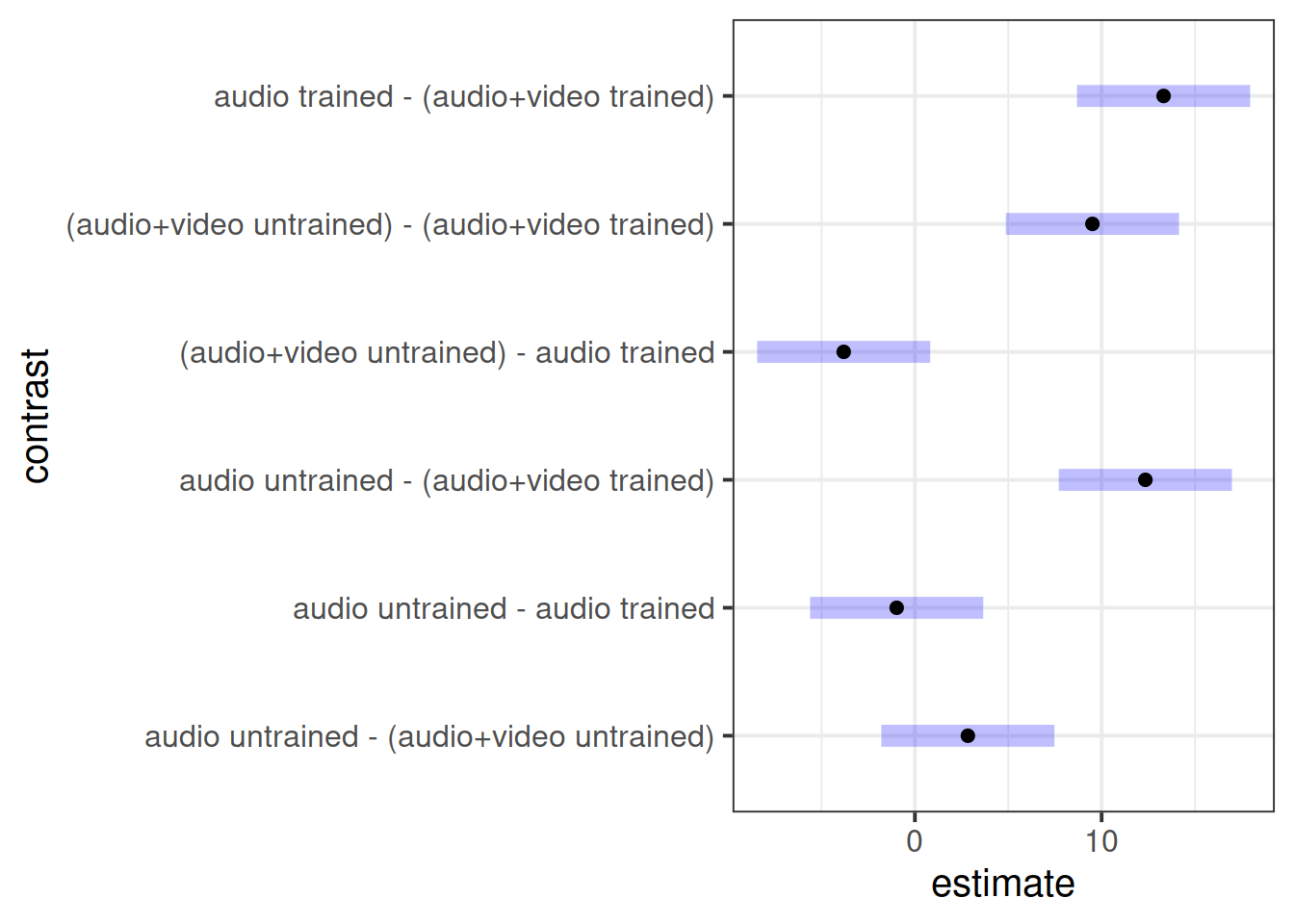
Perform a pairwise comparison of the mean accuracy (as measured by points accrued) across the 2×2 factorial design, making sure to adjust for multiple comparisons by the method of your choice.

Write up your results in a paragraph. Combined with your plot of group means, what do you feel about the Police training materials on using behavioural cues to detect lying?

Solution

emms_lie <- emmeans(lie_mdl, ~ audiovideo * trained)
lie_con <- contrast(emms_lie, method = "pairwise", adjust="tukey")
lie_con

##  contrast                                        estimate   SE  df t.ratio
##  audio untrained - (audio+video untrained)          2.837 1.78 116  1.595 
##  audio untrained - audio trained                   -0.976 1.78 116 -0.549 
##  audio untrained - (audio+video trained)           12.344 1.78 116  6.941 
##  (audio+video untrained) - audio trained           -3.813 1.78 116 -2.144 
##  (audio+video untrained) - (audio+video trained)    9.507 1.78 116  5.346 
##  audio trained - (audio+video trained)             13.320 1.78 116  7.489 
##  p.value
##  0.3855 
##  0.9467 
##  <.0001 
##  0.1456 
##  <.0001 
##  <.0001 
## 
## P value adjustment: tukey method for comparing a family of 4 estimates

confint(lie_con)

##  contrast                                        estimate   SE  df lower.CL
##  audio untrained - (audio+video untrained)          2.837 1.78 116    -1.80
##  audio untrained - audio trained                   -0.976 1.78 116    -5.61
##  audio untrained - (audio+video trained)           12.344 1.78 116     7.71
##  (audio+video untrained) - audio trained           -3.813 1.78 116    -8.45
##  (audio+video untrained) - (audio+video trained)    9.507 1.78 116     4.87
##  audio trained - (audio+video trained)             13.320 1.78 116     8.68
##  upper.CL
##     7.473
##     3.660
##    16.980
##     0.823
##    14.143
##    17.956
## 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 4 estimates

plot(lie_con)

Tukey’s Honestly Significant Difference comparisons indicated that, contrary to what one might expect, participants who were presented with audiovisual recordings scored on average 9.5 points lower when they had read the police training materials compared to when they had received no training (95% CI [4.87 — 14.14]). The presentation mode (audio vs audiovideo) was not found to result in a significantly different average score for those who were untrained (95% CI [-1.80 — 7.47]), and nor did training appear to have any effect on detecting lies in the audio-only condition (95% CI [-5.61 — 3.66]).

The findings indicate that, on the whole, people are bad at determining whether they are being presented with a lie or the truth, as the overall mean score was 49.2 out of 100 (SD = 8.61), where a series of completely random guesses expected to score 50/100. The police training materials did not appear to improve lie detection, in fact with trained participants performing worse (compared to untrained) in the audiovisual condition. This may indicate that the training materials focus too heavily on visual cues, which perhaps are not actually associated with dishonesty in the appropriate way.

Please note that these are short example write ups that may not be complete for every question you are asked. It is intended to give you a sense of the style.

---

1. what defines a ‘family’ of tests is debateable.↩︎