Two-way ANOVA
Introduction
In this week’s exercises, you will learn how to measure the effect of two factors on a response variable of interest. We will try to answer questions such as:
- Does level \(i\) of the first factor have an effect on the response?
- Does level \(j\) of the second factor have an effect on the response?
- Is there a combined effect of level \(i\) of the first factor and level \(j\) of the second factor on the response? In other words, is there interaction of the two factors so that the combined effect is not simply the additive effect of level \(i\) of the first factor plus the effect of level \(j\) of the second factor?
To that end, we will consider an example cognitive neuroscience study comparing the performance of different patient groups on a series of tasks.
Research question and data
A group of researchers wants to test an hypothesised theory according to which patients with amnesia will have a deficit in explicit memory but not on implicit memory. Huntingtons patients, on the other hand, will be just the opposite: they will have no deficit in explicit memory, but will have a deficit in implicit memory.
The researchers designed a study yielding a \(3 \times 3\) factorial design to test this theory. The first factor, “Diagnosis,” classifies the three types of individuals:
- 1 denotes amnesic patients;
- 2 denotes Huntingtons patients; and
- 3 denotes a control group of individuals with no known neurological disorder.
The second factor, “Task,” tells us to which of three tasks each study participant was randomly assigned to:
- 1 = artificial grammar task, which consists of classifying letter sequences as either following or not following grammatical rules;
- 2 = classification learning task, which consists of classifying hypothetical patients as either having or not having a certain disease based on symptoms probabilistically related to the disease; and
- 3 = recognition memory task, which consists of recognising particular stimuli as stimuli that have previously been presented during the task.
The following table presents the recorded data for 15 amnesiacs, 15 Huntington individuals, and 15 controls.
| Diagnosis | grammar | classification | recognition |
|---|---|---|---|
| amnesic | 44, 63, 76, 72, 45 | 72, 66, 55, 82, 75 | 70, 51, 82, 66, 56 |
| huntingtons | 24, 30, 51, 55, 40 | 53, 59, 33, 37, 43 | 107, 80, 98, 82, 108 |
| control | 76, 98, 71, 70, 85 | 92, 65, 86, 67, 90 | 107, 80, 101, 82, 105 |
Keep in mind that each person has been randomly assigned to one of the three tasks, so there are five observations per cell of the design.1
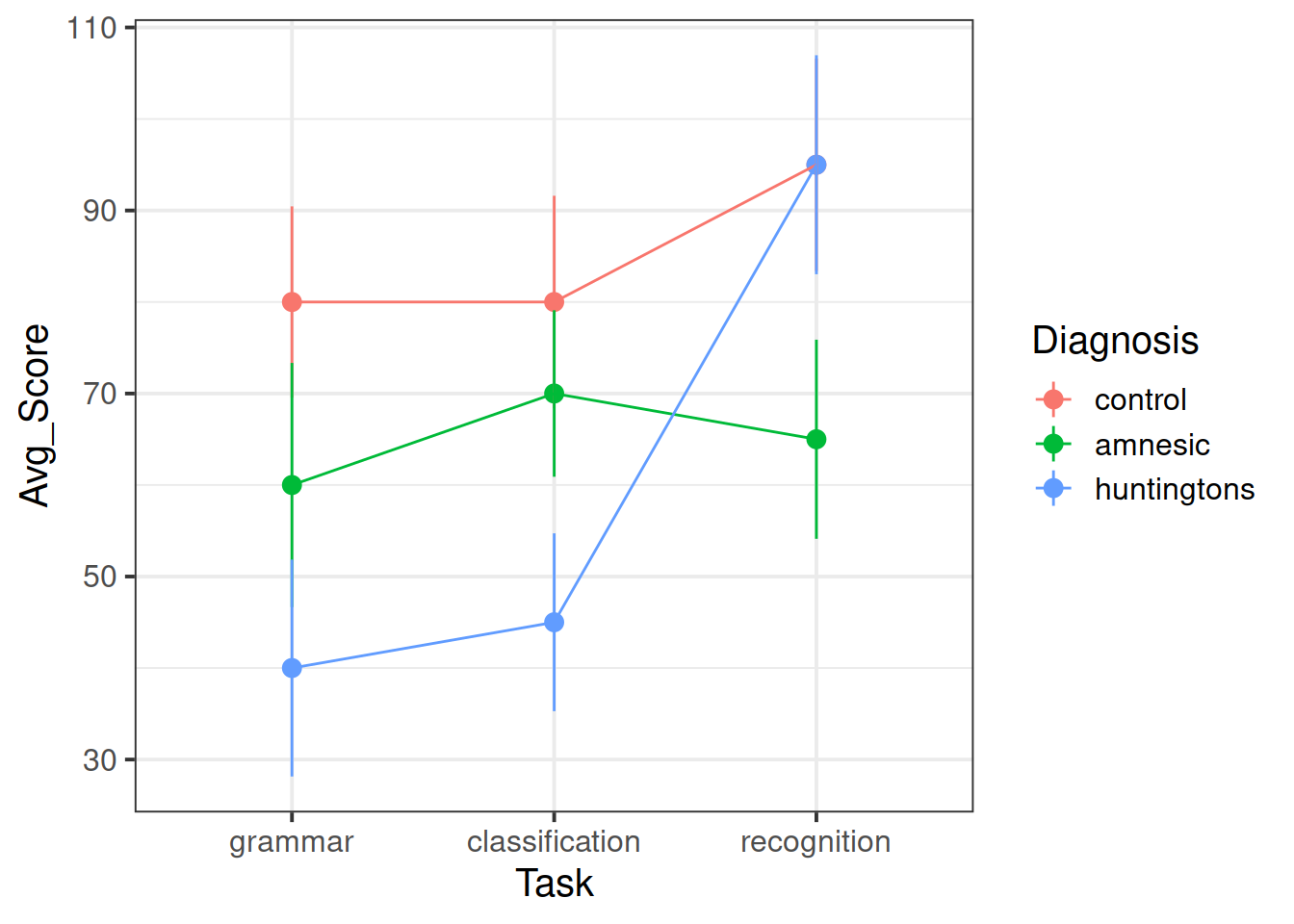
The tasks chosen by the researchers have been picked to map onto the theoretical differences between the three types of research participants. The first two tasks (grammar and classification) are known to reflect implicit memory processes, whereas the recognition task is known to reflect explicit memory processes. If the theory is correct, we would expect to see relatively higher scores on the first two tasks for the amnesiac group but relatively higher scores on the third task for the Huntington group.
Exploratory analysis
Load the tidyverse library and read the cognitive experiment data into R.
Convert categorical variables into factors, and assign more informative labels to the factor levels according to the data description provided above.
Relevel the Diagnosis factor to have “Control” as the reference group. (Hint: Use the fct_relevel function).
Rename the response variable from Y to Score.
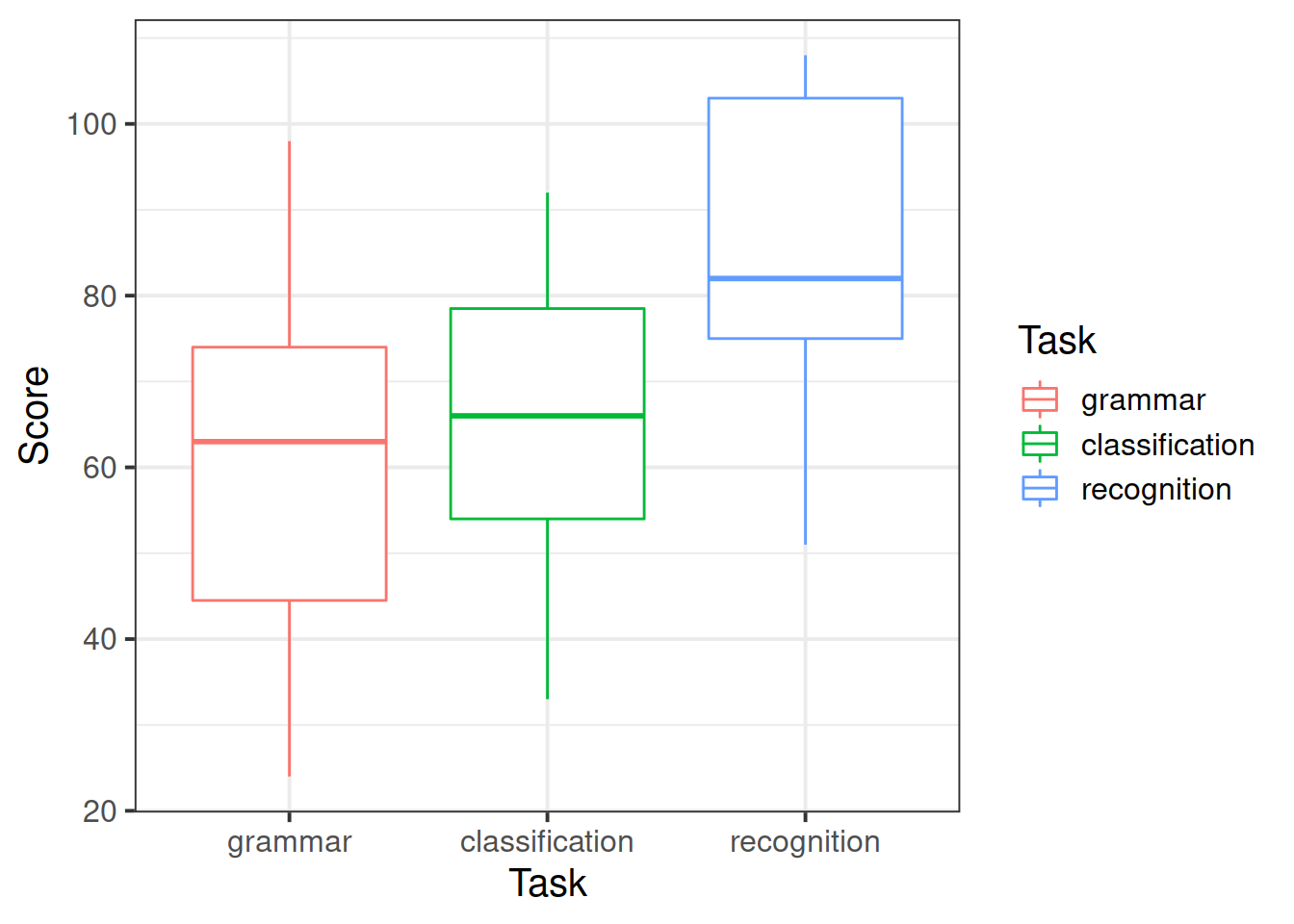
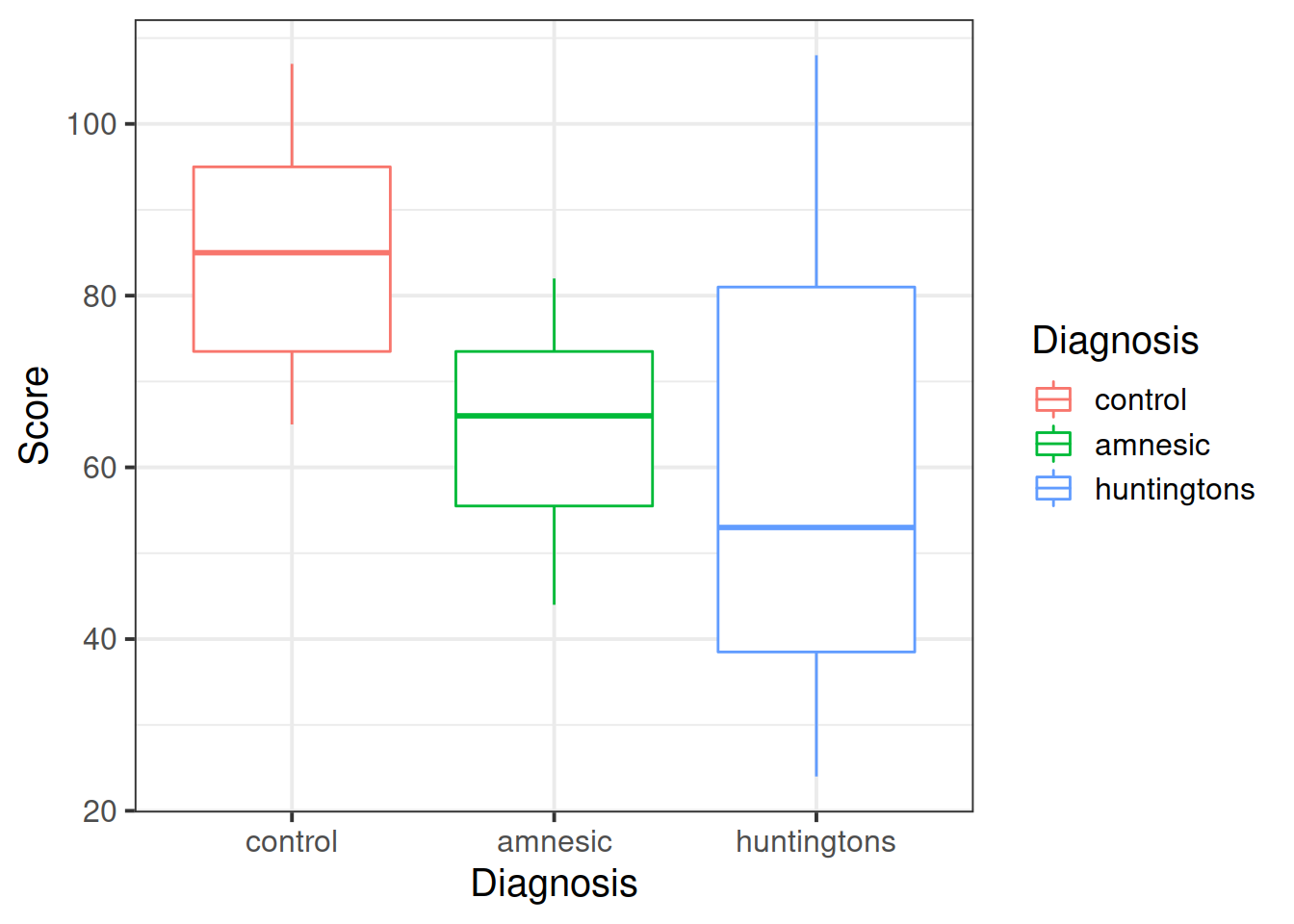
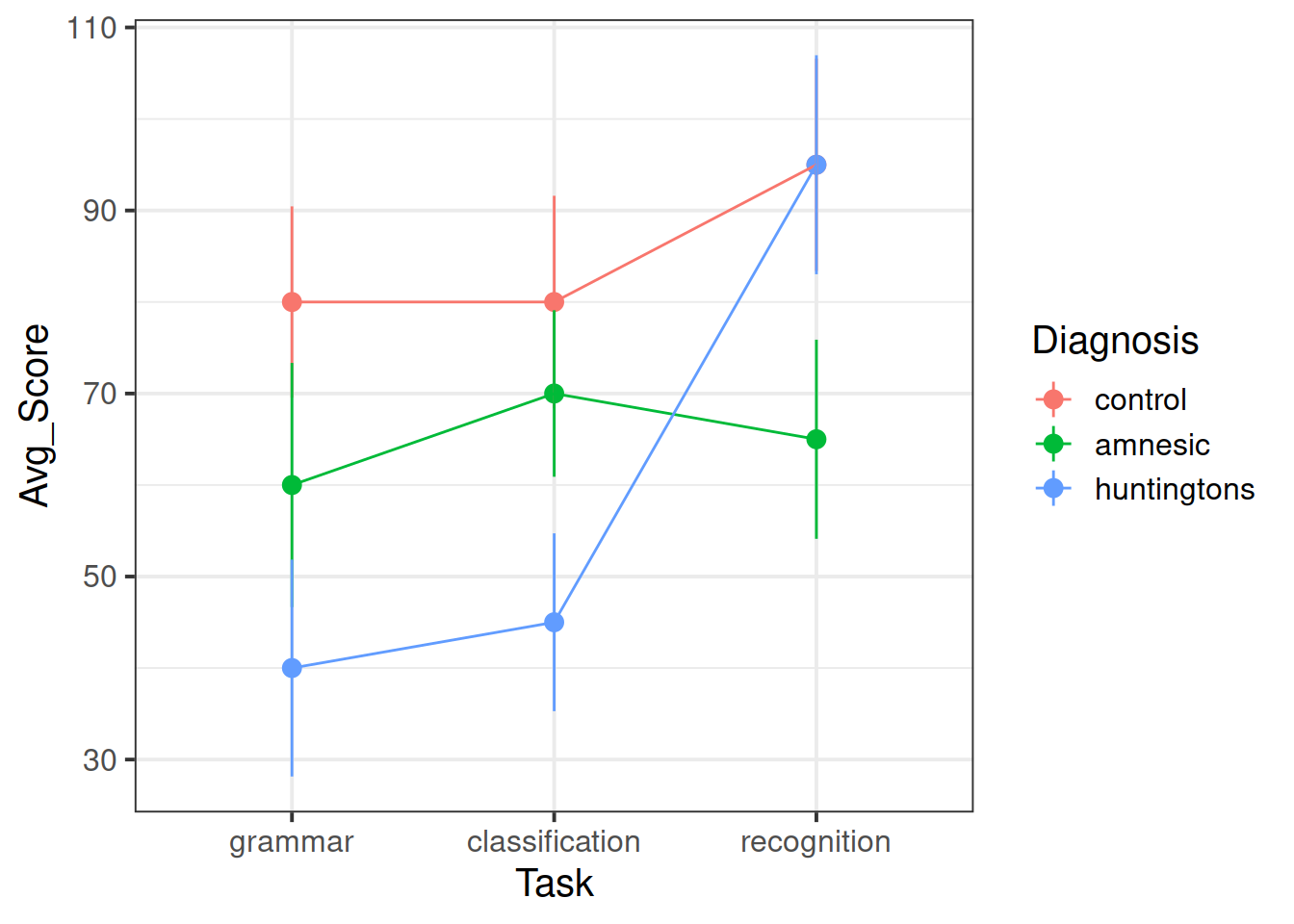
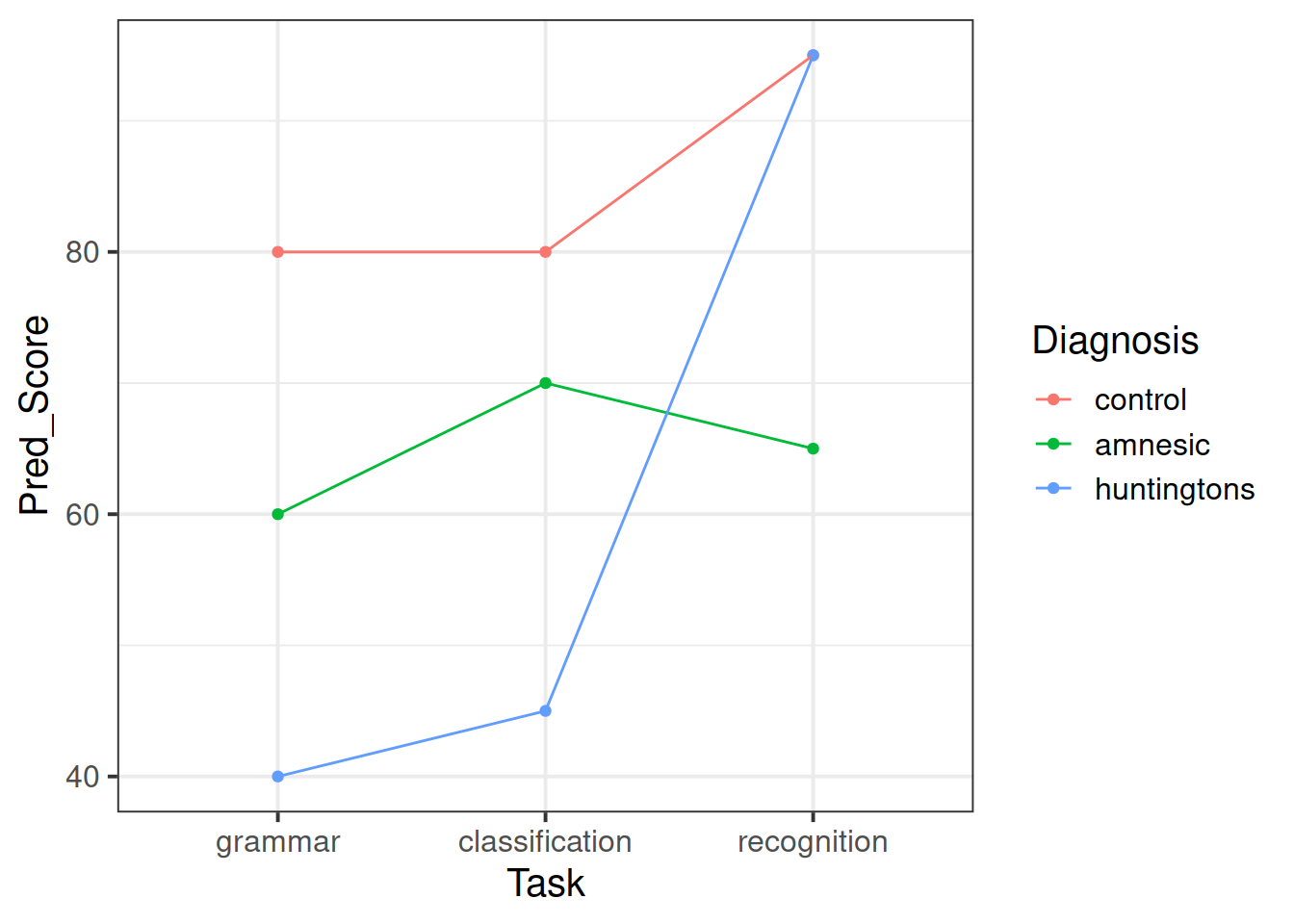
Create some exploratory plots showing
- the joint distribution of diagnosis and task;
- how the patient scores vary across the tasks;
- how the patient scores vary across the diagnoses;
- how the patient scores vary between the different diagnostic groups and tasks. This is called an interaction plot.
Model fitting
The study involves two factors with three levels each. For each combination of factor levels we have 5 observations. The five observations are assumed to come from a population having a specific mean. The population means corresponding to each combination of factor levels can be schematically written as:
\[ \begin{matrix} & & & \textbf{Task} & \\ & & (j=1)\text{ grammar} & (j=2)\text{ classification} & (j=3)\text{ recognition} \\ & (i=1)\text{ control} & \mu_{1,1} & \mu_{1,2} & \mu_{1,3} \\ \textbf{Diagnosis} & (i=2)\text{ amnesic} & \mu_{2,1} & \mu_{2,2} & \mu_{2,3} \\ & (i=3)\text{ huntingtons} & \mu_{3,1} & \mu_{3,2} & \mu_{3,3} \end{matrix} \]
Additive model
The additive two-way ANOVA model has the form \[ Score_{i,j,k} = Intercept + DiagnosisEffect_i + TaskEffect_j + Error_{i,j,k} \qquad \begin{cases} i = 1, 2, 3 \\ j = 1, 2, 3 \\ k = 1, ..., 5 \end{cases} \] where:
- \(i = 1, 2, 3\) counts the levels of the first factor (Diagnosis);
- \(j = 1, 2, 3\) counts the levels of the second factor (Task);
- \(k = 1, ..., 5\) counts the observations within each combination of factor levels;
- \(Score_{i,j,k}\) is the \(k\)th score measured at level \(i\) of Diagnosis and level \(j\) of Task;
- \(Intercept\) is the model intercept;
- \(DiagnosisEffect_i\) represents the effect of level \(i\) of Diagnosis;
- \(TaskEffect_j\) represents the effect of level \(j\) of Task.
As last week, the interpretation of \(Intercept\) will change depending on the side-constraint used.
This week we will be using the reference group constraint (contr.treatment), which is what R uses by default.
Reference group constraint
Under the reference group constraint, the intercept represents the mean response at the first level of each factor, that is when Diagnosis is “control” and Task = “grammar.”
The terms \(DiagnosisEffect_i\) and \(TaskEffect_j\) correspond, respectively, to the effect of level \(i\) of the first factor and level \(j\) of the second factor.
The reference group constraint in the two-factor case is a simple generalisation of the constraint we saw last week:
\[ \begin{aligned} Intercept &= \mu_{1,1} \\ DiagnosisEffect_1 &= 0 \\ TaskEffect_1 &= 0 \end{aligned} \]
The cell means are obtained as:
\[ { \scriptsize \begin{matrix} & & \textbf{Task} & \\ \textbf{Diagnosis} & (j=1)\text{ grammar} & (j=2)\text{ classification} & (j=3)\text{ recognition} \\ (i=1)\text{ control} & Intercept & Intecept + TaskEffect_2 & Intercept + TaskEffect_3 \\ (i=2)\text{ amnesic} & Intercept + DiagnosisEffect_2 & Intercept + DiagnosisEffect_2 + TaskEffect_2 & Intercept + DiagnosisEffect_2 + TaskEffect_3 \\ (i=3)\text{ huntingtons} & Intercept + DiagnosisEffect_3 & Intercept + DiagnosisEffect_3 + TaskEffect_2 & Intercept + DiagnosisEffect_3 + TaskEffect_3 \end{matrix} } \]
Sum to zero constraint
If, instead, we use the sum to zero constraint, we would have that
\[ \begin{aligned} Intercept &= \frac{\mu_{1,1} + \mu_{1,2} + \cdots + \mu_{3,3}}{9} = \text{global mean} \\ DiagnosisEffect_3 &= -(DiagnosisEffect_1 + DiagnosisEffect_2) \\ TaskEffect_3 &= -(TaskEffect_1 + TaskEffect_2) \end{aligned} \]
meaning that the intercept would now represent the overall or global mean, and the last effect for each factor would not be shown in the R output as it can be found using the side-constraint as minus the sum of the remaining effects for that factor.
Cognitive experiment continued
Let’s go back to the cognitive experiment data…
From the exploratory analysis performed in question 2, it seems that both task and diagnosis factors might help predict a patient score.
Fit a linear model which makes use of the two factors Diagnosis and Task to predict the patients’ Score. Call the fitted model mdl_add.
Comment on the F-test for model utility returned by summary(mdl_add), as well as the t-test for the significance of the model coefficients.
Furthermore, look at the anova(mdl_add) and comment on whether Diagnosis impacts scores on the test and whether each Task affects the score.
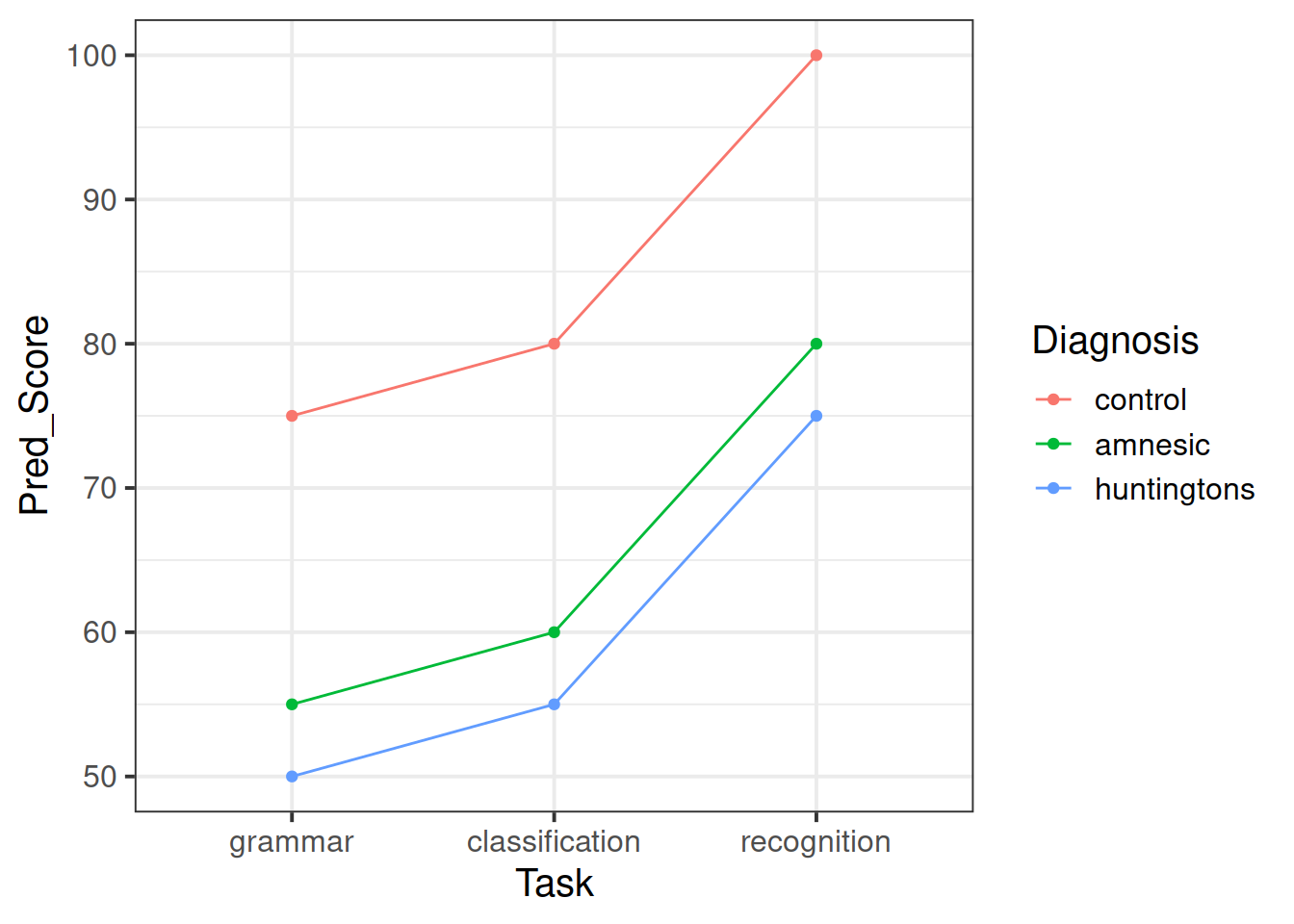
Use the additive model fitted above to predict the average score for each combination of the factor levels. (Hint: use the predict() function)
Create a plot showing how the predicted averages vary by diagnosis and task.
Does this match to the last plot created in question 2?
Interaction model
An interaction model also allows for the interaction of the two factors. That is, the effect of level \(i\) of one factor can be different depending on level \(j\) of the second factor. For example, the effect of amnesia (\(i=2\)) might increase the response in grammar tasks (\(j=1\)), while it might decrease the response in recognition tasks (\(j=3\)).
The two-way ANOVA model with interaction is:
\[ Score_{i,j,k} = Intercept + DiagnosisEffect_i + TaskEffect_j + InteractionEffect_{i,j} + Error_{i,j,k} \]
where the constraints on the interaction are such that whenever \(i=1\) OR \(j=1\), the coefficient is 0:
\[ \begin{aligned} InteractionEffect_{1,1} &= 0 \qquad InteractionEffect_{1,2} = 0 \qquad \qquad InteractionEffect_{1,3} = 0 \\ InteractionEffect_{2,1} &= 0 \\ InteractionEffect_{3,1} &= 0 \end{aligned} \]
Update the previously fitted additive model to also include an interaction term for Diagnosis and Task. Call the fitted model mdl_int.
Comment on the model output.
Perform a model comparison between the additive model and the interaction model using the anova() function.
Interpret the result of the model comparison.
Which model will you use to answer the research questions of interest?
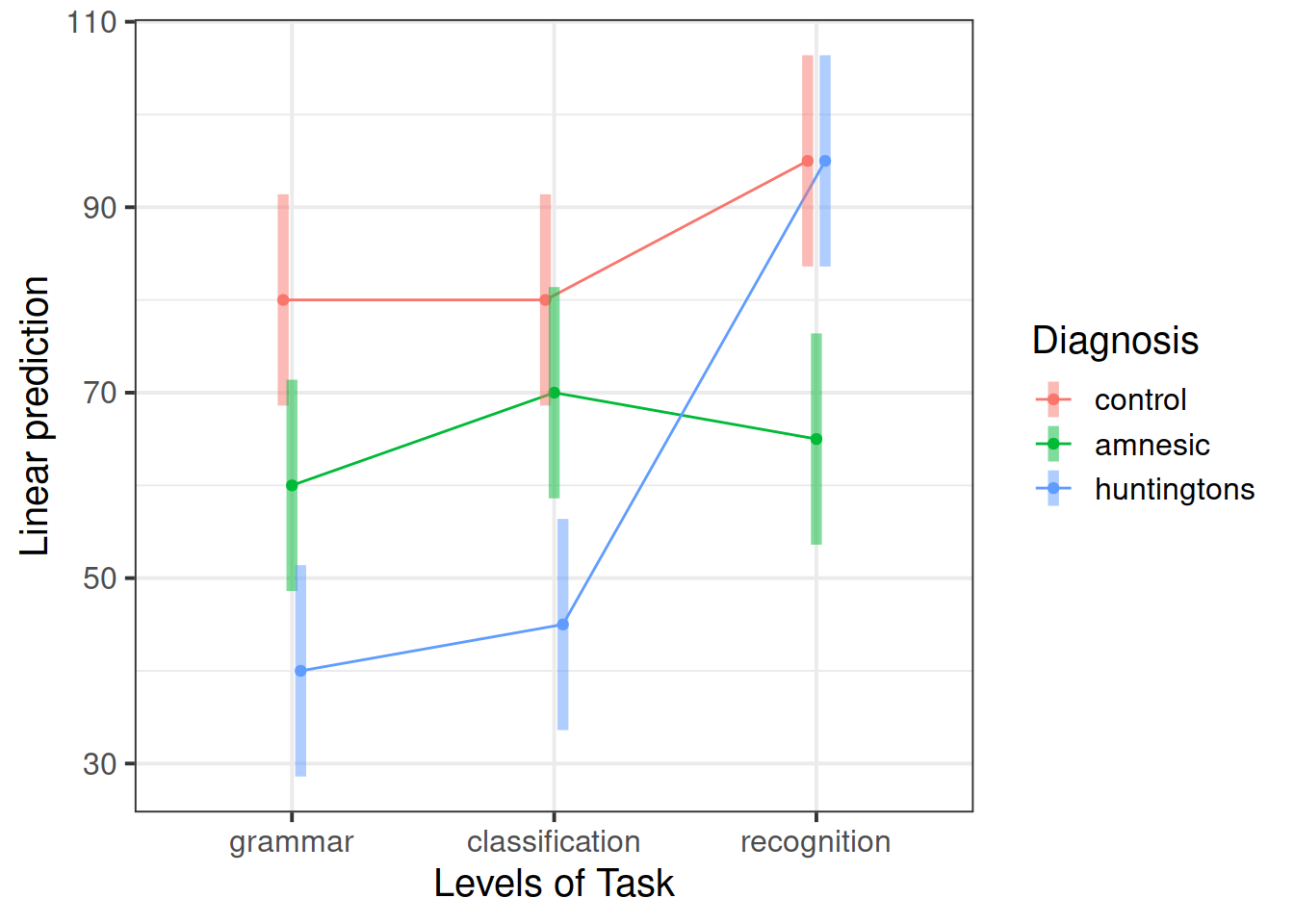
Generate again a plot showing the predicted mean scores for each combination of levels of the diagnosis and task factors.
Do the predicted values better match the interaction plot created in question 2?
Assumption checking
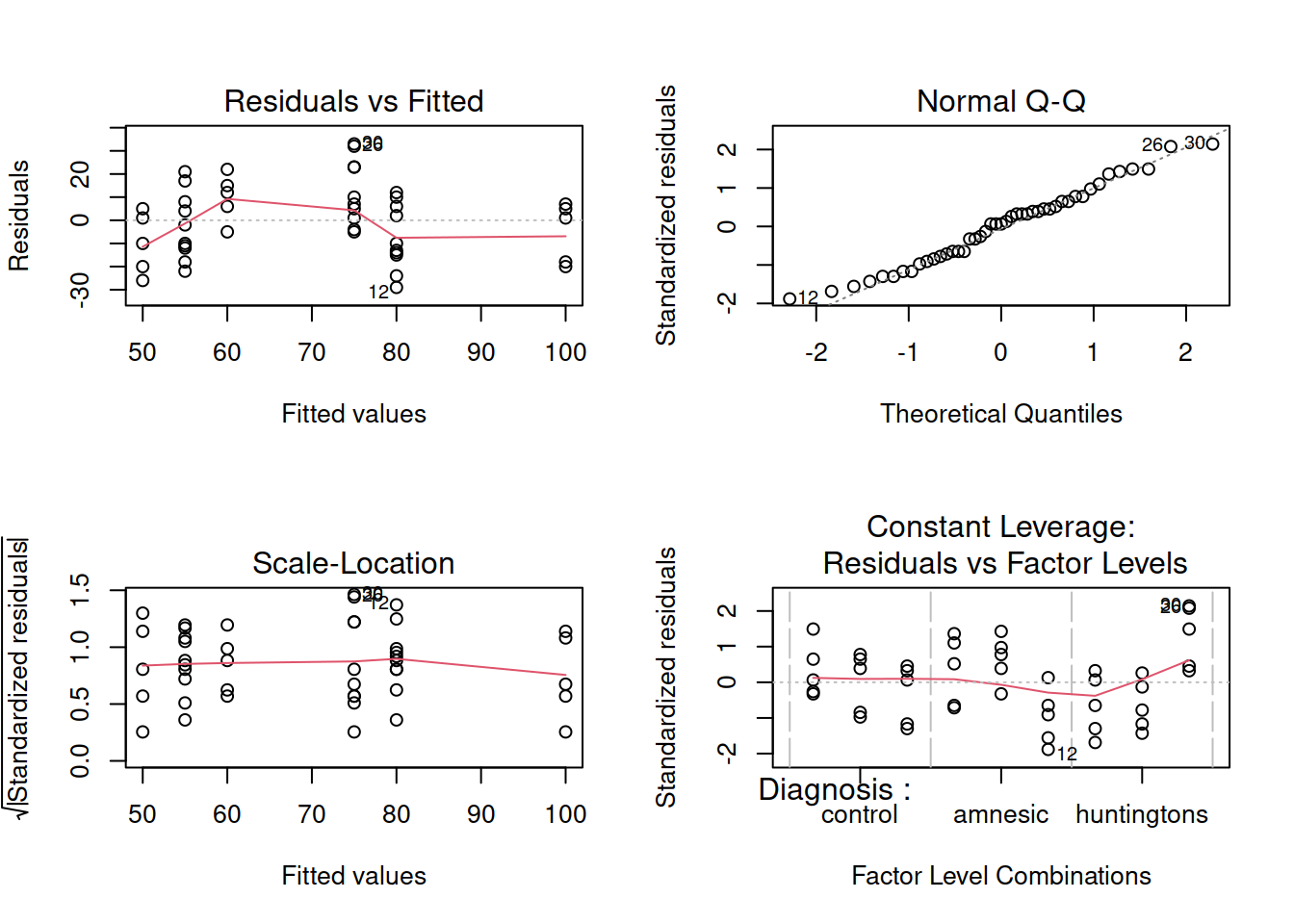
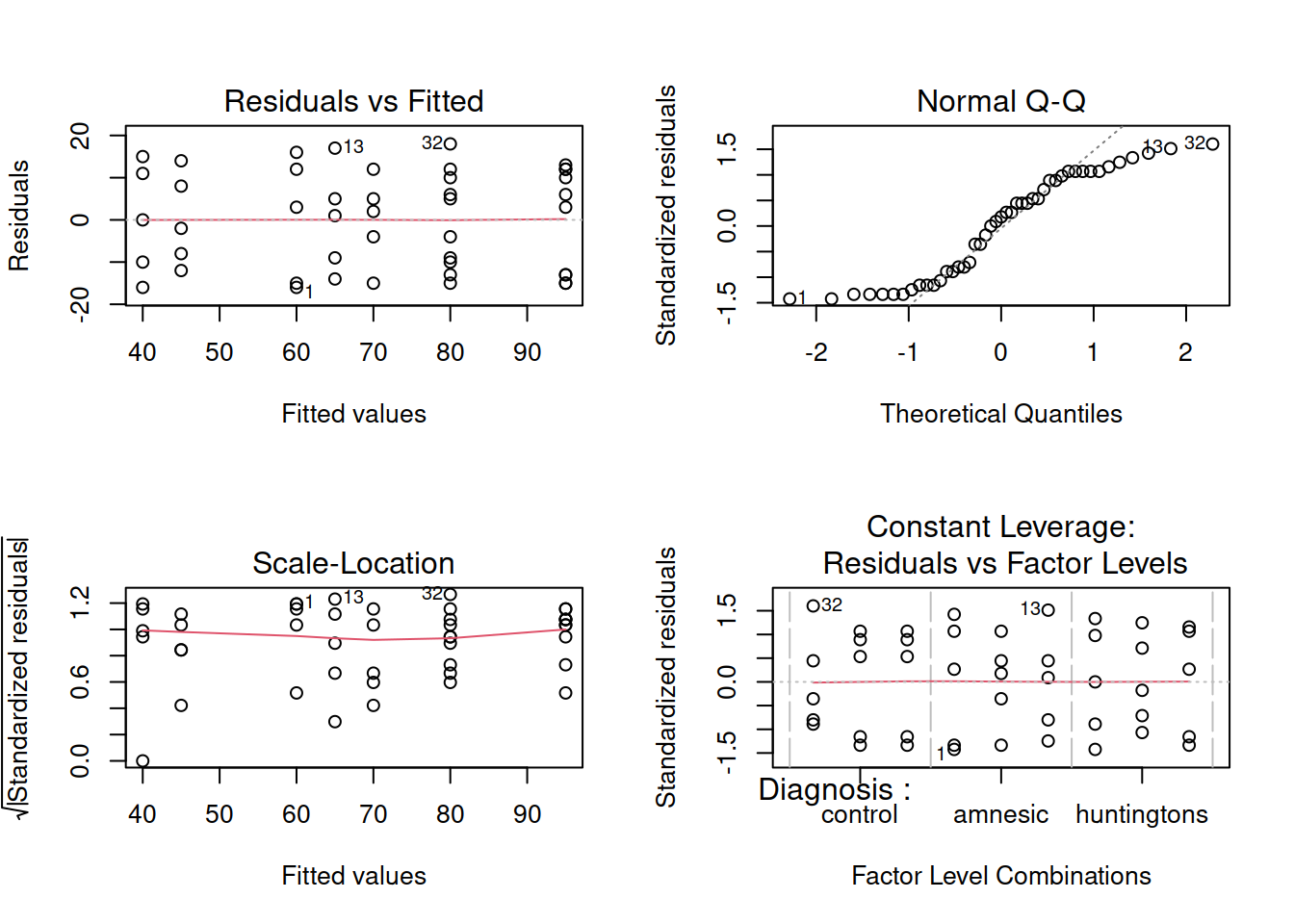
Before interpreting the results of the model it is important to check that the model doesn’t violate the assumptions.
Are the errors independent?
Do the errors have a mean of zero?
Are the group variances equal?
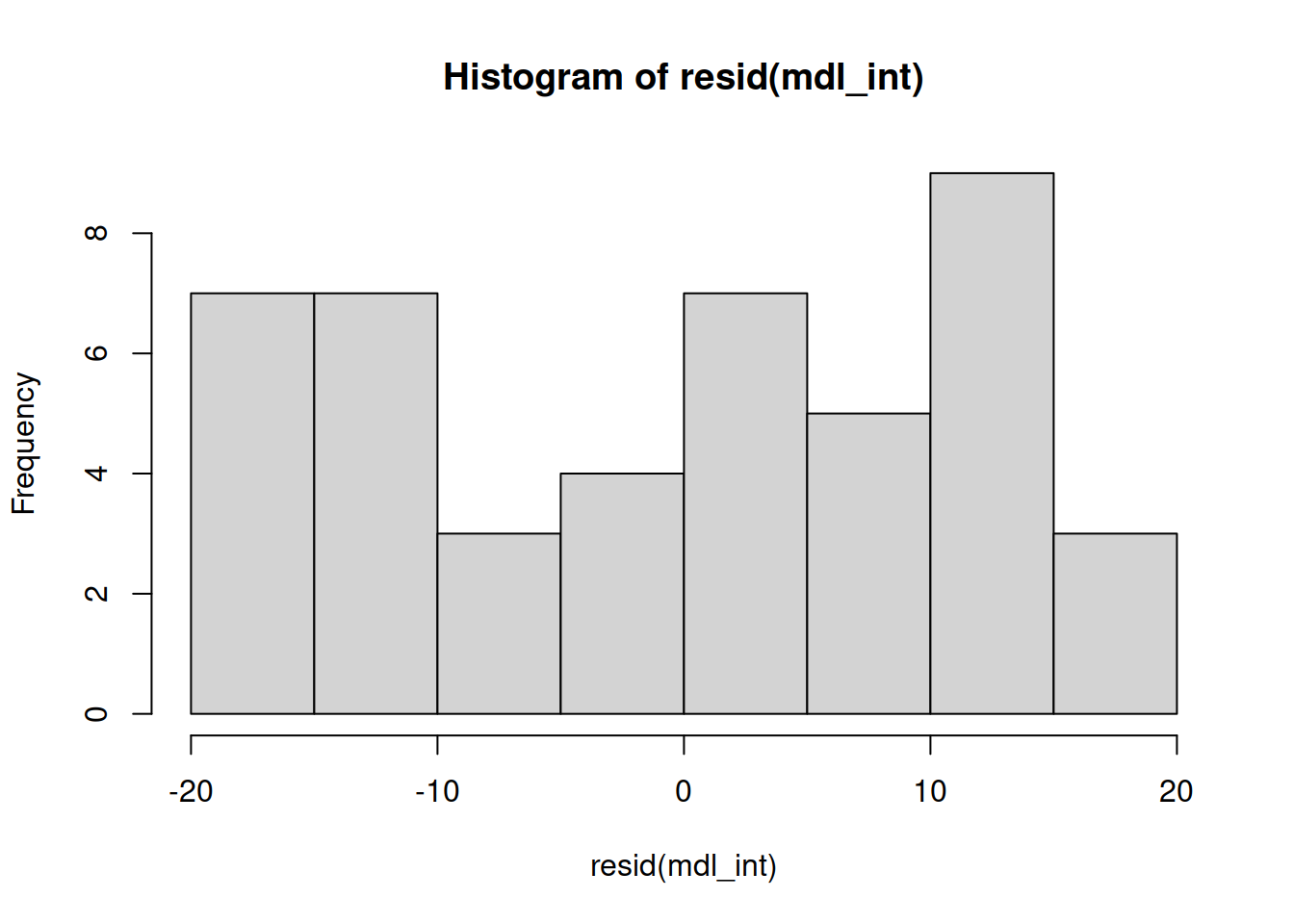
Is the distribution of the errors normal?
WARNING
The residuals don’t look like a sample from a normal population. For this reason, we can’t trust the model results and we should not generalise the results to the population as the hypothesis tests to be valid require all the assumptions to be met, including normality.
We will nevertheless carry on and finish this example so that we can exploring the remaining functions relevant for carrying out a two-way ANOVA.
Contrast analysis
We will begin by looking at each factor separately. In terms of the diagnostic groups, recall that we want to compare the amnesiacs to the Huntington individuals. This corresponds to a contrast with coefficients of 0, 1, and −1, for control, amnesic, and Huntingtons, respectively. Similarly, in terms of the tasks, we want to compare the average of the two implicit memory tasks with the explicit memory task. This corresponds to a contrast with coefficients of 0.5, 0.5, and −1 for the three tasks.
When we are in presence of a significant interaction, the coefficients for a contrast between the means are found by multiplying each row coefficient with all column coefficients as shown below:
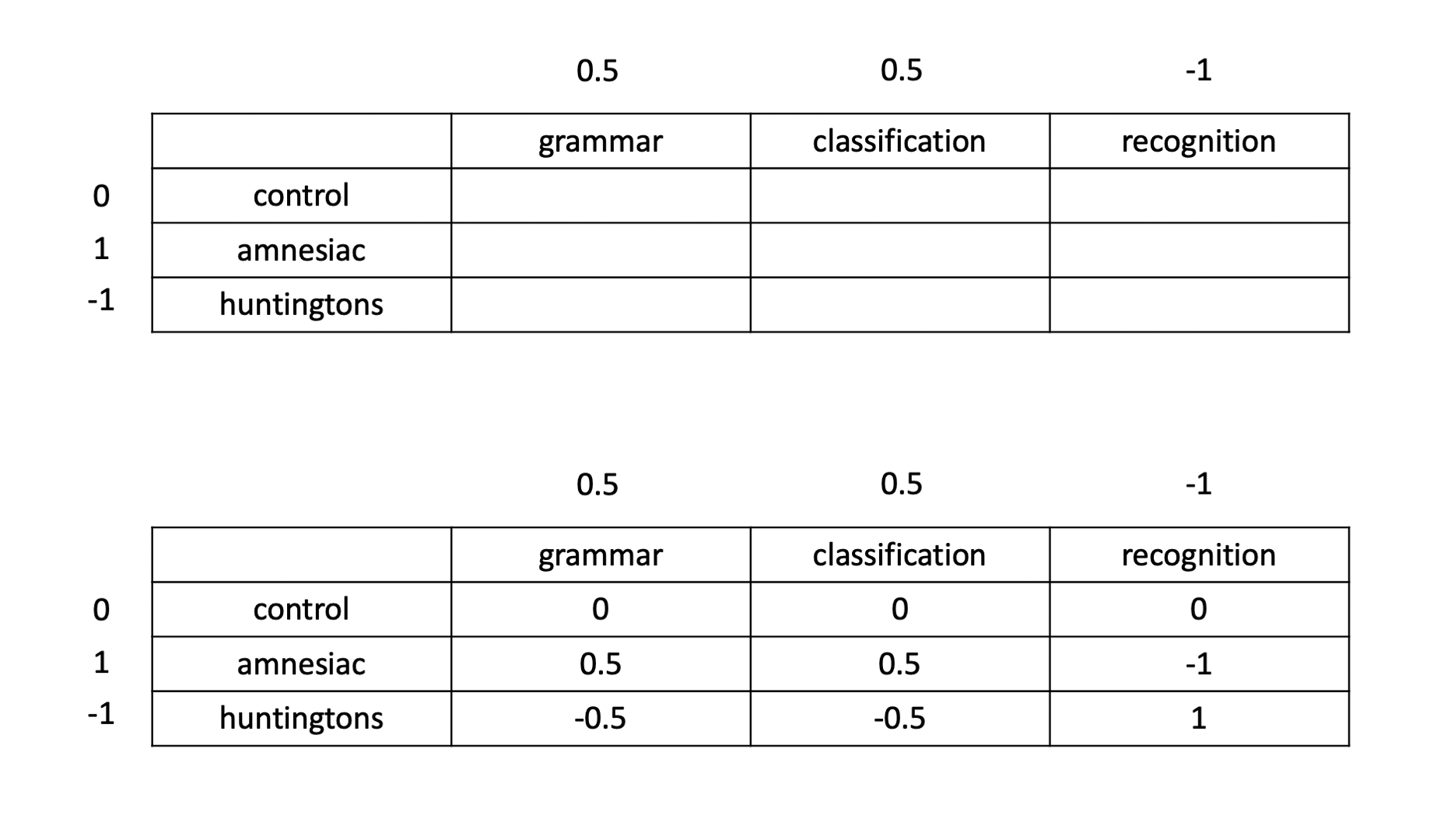
This can be done in R using:
diag_coef <- c('control' = 0, 'amnesic' = 1, 'huntingtons' = -1)
task_coef <- c('grammar' = 0.5, 'classification' = 0.5, 'recognition' = -1)
contr_coef <- outer(diag_coef, task_coef) # or: diag_coef %o% task_coef
contr_coef## grammar classification recognition
## control 0.0 0.0 0
## amnesic 0.5 0.5 -1
## huntingtons -0.5 -0.5 1The above coefficients correspond to testing the null hypothesis
\[ H_0 : \frac{\mu_{2,1} + \mu_{2,2}}{2} - \mu_{2,3} - \left( \frac{\mu_{3,1} + \mu_{3,2}}{2} - \mu_{3,3} \right) = 0 \]
or, equivalently,
\[ H_0 : \frac{\mu_{2,1} + \mu_{2,2}}{2} - \mu_{2,3} = \frac{\mu_{3,1} + \mu_{3,2}}{2} - \mu_{3,3} \] which says that, in the population, the difference between the mean implicit memory and the explicit memory score is the same for amnesic patients and Huntingtons individuals. Note that the scores for the grammar and classification tasks have been averaged to obtain a single measure of “implicit memory” score.
Now that we have the coefficients, let’s call the emmeans function:
emm <- emmeans(mdl_int, ~ Diagnosis*Task)
emm## Diagnosis Task emmean SE df lower.CL upper.CL
## control grammar 80 5.62 36 68.6 91.4
## amnesic grammar 60 5.62 36 48.6 71.4
## huntingtons grammar 40 5.62 36 28.6 51.4
## control classification 80 5.62 36 68.6 91.4
## amnesic classification 70 5.62 36 58.6 81.4
## huntingtons classification 45 5.62 36 33.6 56.4
## control recognition 95 5.62 36 83.6 106.4
## amnesic recognition 65 5.62 36 53.6 76.4
## huntingtons recognition 95 5.62 36 83.6 106.4
##
## Confidence level used: 0.95Next, insert the coefficients following the order specified by the rows of emm above. That is, the first one should be for control grammar, the second for amnesic grammar, and so on…
We also give a name to this contrast, such as ‘Research Hyp.’
comp_res <- contrast(emm,
method = list('Research Hyp' = c(0, 0.5, -0.5, 0, 0.5, -0.5, 0, -1, 1)))
comp_res## contrast estimate SE df t.ratio p.value
## Research Hyp 52.5 9.73 36 5.396 <.0001confint(comp_res)## contrast estimate SE df lower.CL upper.CL
## Research Hyp 52.5 9.73 36 32.8 72.2
##
## Confidence level used: 0.95or:
summary(comp_res, infer = TRUE)## contrast estimate SE df lower.CL upper.CL t.ratio p.value
## Research Hyp 52.5 9.73 36 32.8 72.2 5.396 <.0001
##
## Confidence level used: 0.95Interpret the results of the contrast analysis.
The following code compares the means of the different diagnosis groups for each task.
Furthermore, it adjusts for multiple comparisons using the Bonferroni method. This makes sure that the experimentwise error rate is 5%. If we do not control for multiple comparisons, the more t-tests we do, the higher the chance of wrongly rejecting the null, and across the family of t-tests performed that chance will be much higher than 5%.2
emm_task <- emmeans(mdl_int, ~ Diagnosis | Task)
emm_task## Task = grammar:
## Diagnosis emmean SE df lower.CL upper.CL
## control 80 5.62 36 68.6 91.4
## amnesic 60 5.62 36 48.6 71.4
## huntingtons 40 5.62 36 28.6 51.4
##
## Task = classification:
## Diagnosis emmean SE df lower.CL upper.CL
## control 80 5.62 36 68.6 91.4
## amnesic 70 5.62 36 58.6 81.4
## huntingtons 45 5.62 36 33.6 56.4
##
## Task = recognition:
## Diagnosis emmean SE df lower.CL upper.CL
## control 95 5.62 36 83.6 106.4
## amnesic 65 5.62 36 53.6 76.4
## huntingtons 95 5.62 36 83.6 106.4
##
## Confidence level used: 0.95contr_task <- contrast(emm_task, method = 'pairwise',
adjust = "bonferroni")
contr_task## Task = grammar:
## contrast estimate SE df t.ratio p.value
## control - amnesic 20 7.94 36 2.518 0.0492
## control - huntingtons 40 7.94 36 5.035 <.0001
## amnesic - huntingtons 20 7.94 36 2.518 0.0492
##
## Task = classification:
## contrast estimate SE df t.ratio p.value
## control - amnesic 10 7.94 36 1.259 0.6486
## control - huntingtons 35 7.94 36 4.406 0.0003
## amnesic - huntingtons 25 7.94 36 3.147 0.0099
##
## Task = recognition:
## contrast estimate SE df t.ratio p.value
## control - amnesic 30 7.94 36 3.776 0.0017
## control - huntingtons 0 7.94 36 0.000 1.0000
## amnesic - huntingtons -30 7.94 36 -3.776 0.0017
##
## P value adjustment: bonferroni method for 3 testsplot(contr_task)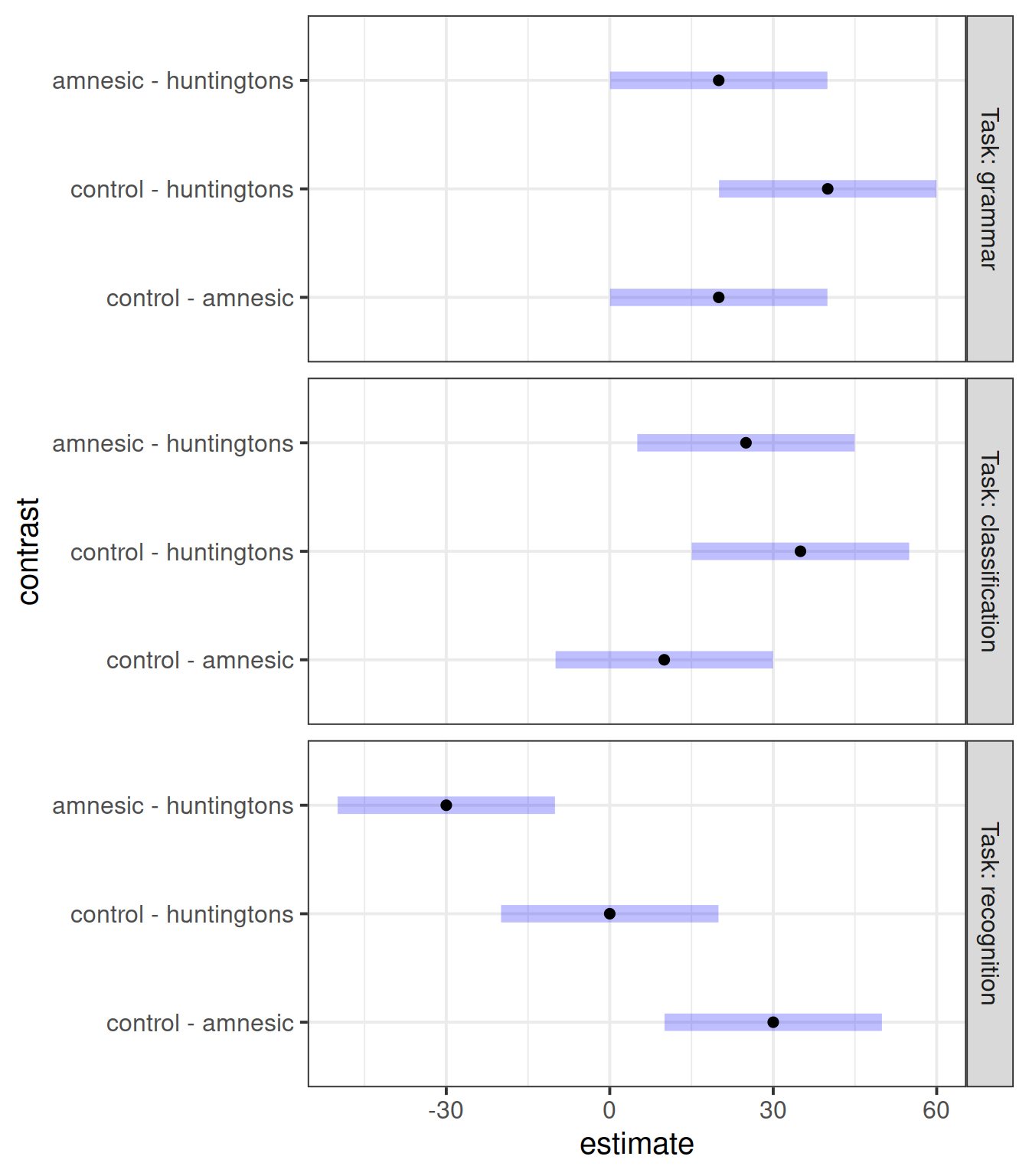
Discuss what the plot tells us.
References
Some researchers may point out that a design where each person was assessed on all three tasks might have been more efficient. However, the task factor in such design would then be within-subjects, meaning that the scores corresponding to the same person would be correlated. To analyse such design we will need a different method which is discussed next year!
↩︎Each t-test comes with a \(\alpha = 0.05\) probability of Type I error (wrongly rejecting the null hypothesis). If we do 9 t-tests, we will have that the experimentwise error rate is \(\alpha_{ew} \leq 9 \times 0.05\), where 9 is the number of comparisons made as part of the experiment. Thus, if nine independent comparisons were made at the \(\alpha = 0.05\) level, the experimentwise Type I error rate \(\alpha_{ew}\) would be at most \(9 \times 0.05 = 0.45\). That is, we could wrongly reject the null hypothesis up to 45 times out of 100.↩︎