~ Numeric * Categorical
Question 1
Reseachers have become interested in how the number of social interactions might influence mental health and wellbeing differently for those living in rural communities compared to those in cities and suburbs. They want to assess whether the effect of social interactions on wellbeing is moderated by (depends upon) whether or not a person lives in a rural area.
Create a new RMarkdown, load the tidyverse package read in the wellbeing data into R.
The data is available at https://uoepsy.github.io/data/wellbeing.csv".
Count the number of respondents in each location (City/Location/Rural).
Open-ended: Do you think there is enough data to answer this question?
Solution
library(tidyverse)
mwdata <- read_csv("https://uoepsy.github.io/data/wellbeing.csv")
mwdata %>% count(location)
## # A tibble: 3 x 2
## location n
## <chr> <int>
## 1 City 15
## 2 Rural 7
## 3 Suburb 10
- We have only 7 respondents who are from a rural location, and 25 from the city & suburbs. Intuitively, this doesn’t seem very many to rely on as representative of the population of those living in rural areas in Edinburgh & Lothians. Another thing to think about is that we probably don’t expect large differences between rural and city dwellers in the effect of social interaction on wellbeing (i.e., we might not expect differences in these sub-groups to be stronger than the overall relationship between social interaction and wellbeing).
Research Question:
Does the relationship between number of social interactions and mental wellbeing differ between rural and non-rural residents?
To investigate how the relationship between the number of social interactions and mental wellbeing might be different for those living in rural communities, the researchers conduct a new study, collecting data from 200 randomly selected residents of the Edinburgh & Lothian postcodes.
Wellbeing/Rurality data codebook. Click the plus to expand →
Download link
The data is available at https://uoepsy.github.io/data/wellbeing_rural.csv.
Description
From the Edinburgh & Lothians, 100 city/suburb residences and 100 rural residences were chosen at random and contacted to participate in the study. The Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), was used to measure mental health and well-being.
Participants filled out a questionnaire including items concerning: estimated average number of hours spent outdoors each week, estimated average number of social interactions each week (whether on-line or in-person), whether a daily routine is followed (yes/no). For those respondents who had an activity tracker app or smart watch, they were asked to provide their average weekly number of steps.
The data in wellbeing_rural.csv contain seven attributes collected from a random sample of \(n=200\) hypothetical residents over Edinburgh & Lothians, and include:
wellbeing: Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70.
outdoor_time: Self report estimated number of hours per week spent outdoors
social_int: Self report estimated number of social interactions per week (both online and in-person)routine: Binary 1=Yes/0=No response to the question “Do you follow a daily routine throughout the week?”location: Location of primary residence (City, Suburb, Rural)steps_k: Average weekly number of steps in thousands (as given by activity tracker if available)age: Age in years of respondent
Preview
The first six rows of the data are:
| age |
outdoor_time |
social_int |
routine |
wellbeing |
location |
steps_k |
| 28 |
12 |
13 |
1 |
36 |
rural |
21.6 |
| 56 |
5 |
15 |
1 |
41 |
rural |
12.3 |
| 25 |
19 |
11 |
1 |
35 |
rural |
49.8 |
| 60 |
25 |
15 |
0 |
35 |
rural |
NA |
| 19 |
9 |
18 |
1 |
32 |
rural |
48.1 |
| 34 |
18 |
13 |
1 |
34 |
rural |
67.3 |
Question 2
Specify a multiple regression model to answer the research question.
Read in the data, and assign it the name “mwdata2.” Then fully explore the variables and relationships which are going to be used in your analysis.
“Except in special circumstances, a model including a product term for interaction between two explanatory variables should also include terms with each of the explanatory variables individually, even though their coefficients may not be significantly different from zero. Following this rule avoids the logical inconsistency of saying that the effect of \(X_1\) depends on the level of \(X_2\) but that there is no effect of \(X_1\).”
Ramsey and Schafer (2012)
- Tip 1: Install the
psych package (remember to use the console, not your script to install packages), and then load it (load it in your script). The pairs.panels() function will plot all variables in a dataset against one another. This will save you the time you would have spent creating individual plots.
- Tip 2: Check the “location” variable. It currently has three levels (Rural/Suburb/City), but we only want two (Rural/Not Rural). You’ll need to fix this. One way to do this would be to use
ifelse() to define a variable which takes one value (“Rural”) if the observation meets from some condition, or another value (“Not Rural”) if it does not. Type ?ifelse in the console if you want to see the help function. You can use it to add a new variable either inside mutate(), or using data$new_variable_name <- ifelse(test, x, y) syntax.
Solution
To address the research question, we are going to fit the following model, where \(y\) = wellbeing; \(x_1\) = weekly outdoor time; and \(x_2\) = whether or not the respondent lives in a rural location or not.
\[
y = \beta_0 + \beta_1 \cdot x_1 + \beta_2 \cdot x_2 + \beta_3 \cdot x_1 \cdot x_2 + \epsilon \\
\quad \\ \text{where} \quad \epsilon \sim N(0, \sigma) \text{ independently}
\]
First we read in the data, and take a quick look at our variables:
mwdata2 <- read_csv("https://uoepsy.github.io/data/wellbeing_rural.csv")
summary(mwdata2)
## age outdoor_time social_int routine wellbeing
## Min. :18.00 Min. : 1.00 Min. : 3.00 Min. :0.000 Min. :22.0
## 1st Qu.:30.00 1st Qu.:12.75 1st Qu.: 9.00 1st Qu.:0.000 1st Qu.:33.0
## Median :42.00 Median :18.00 Median :12.00 Median :1.000 Median :35.0
## Mean :42.30 Mean :18.25 Mean :12.06 Mean :0.565 Mean :36.3
## 3rd Qu.:54.25 3rd Qu.:23.00 3rd Qu.:15.00 3rd Qu.:1.000 3rd Qu.:40.0
## Max. :70.00 Max. :35.00 Max. :24.00 Max. :1.000 Max. :59.0
##
## location steps_k
## Length:200 Min. : 0.00
## Class :character 1st Qu.: 24.00
## Mode :character Median : 42.45
## Mean : 44.93
## 3rd Qu.: 65.28
## Max. :111.30
## NA's :66
First let’s create a new variable for Rural/Not Rural
mwdata2 <-
mwdata2 %>%
mutate(
isRural = ifelse(location == "rural", "rural","not rural")
)
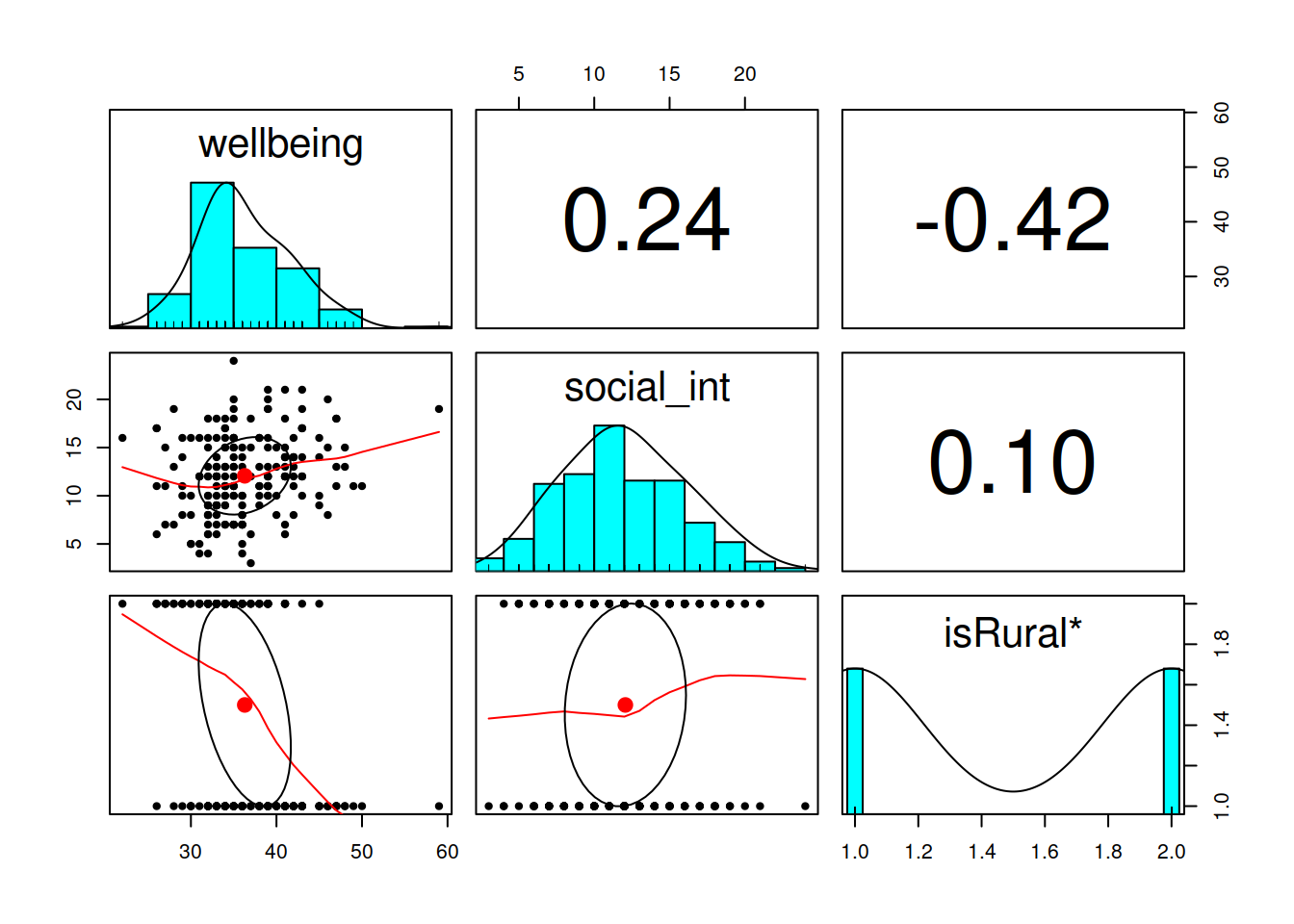
Now let’s use psych::pairs.panels() function.
We could use it on the whole dataset, but for now we’ll just do it on the variables we’re interested in:
library(psych)
pairs.panels(mwdata2 %>% select(wellbeing, social_int, isRural))
Question 3
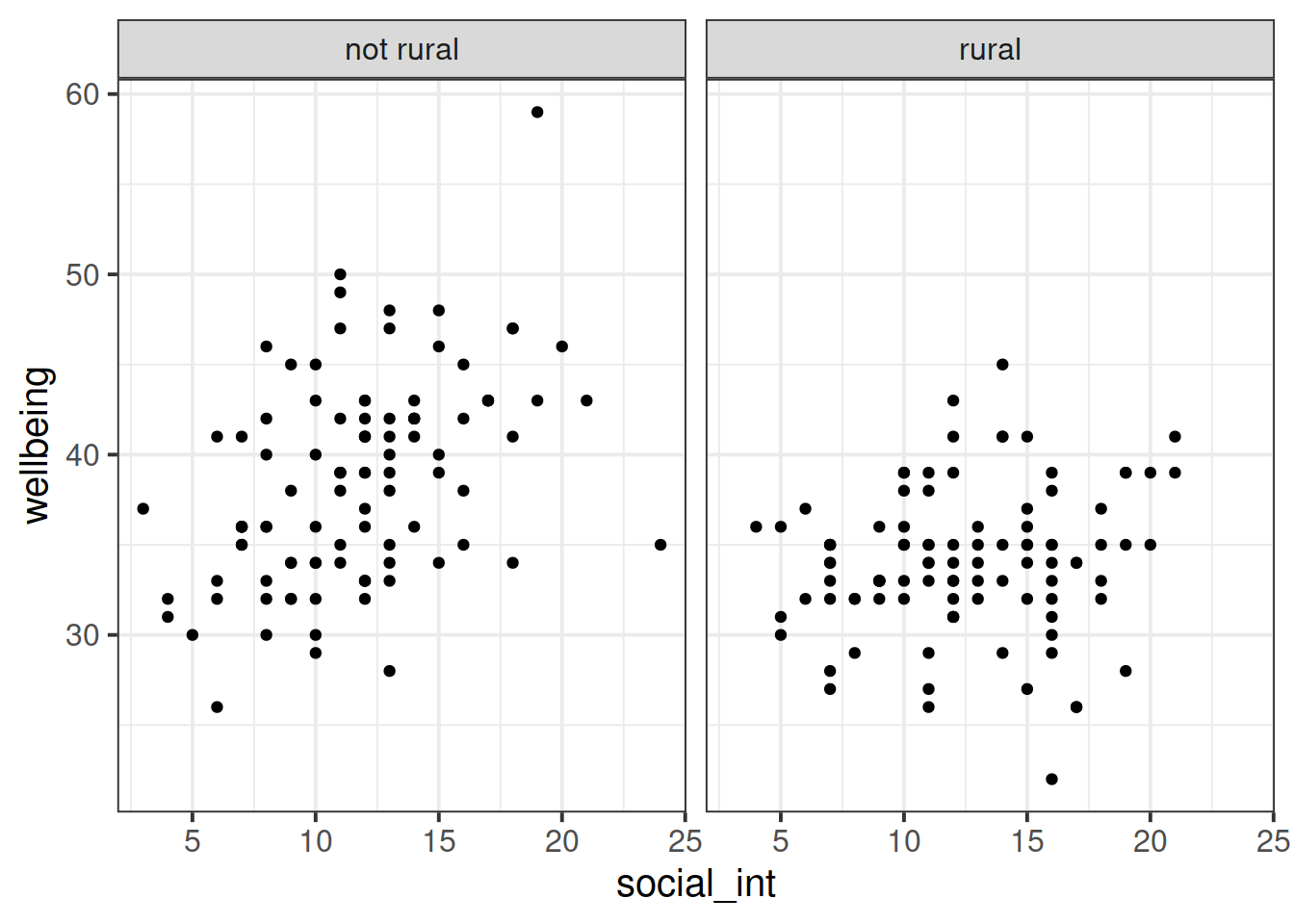
Produce a visualisation of the relationship between weekly number of social interactions and well-being, with separate facets for rural vs non-rural respondents.
Solution
ggplot(data = mwdata2, aes(x = social_int, y = wellbeing)) +
geom_point() +
facet_wrap(~isRural)
Question 4
Fit your model using lm(), and assign it as an object with the name “rural_mod.”
Hint: When fitting a regression model in R with two explanatory variables A and B, and their interaction, these two are equivalent:
Solution
rural_mod <- lm(wellbeing ~ 1 + social_int * isRural, data = mwdata2)
Interpreting coefficients for A and B in the presence of an interaction A:B
When you include an interaction between \(x_1\) and \(x_2\) in a regression model, you are estimating the extent to which the effect of \(x_1\) on \(y\) is different across the values of \(x_2\).
What this means is that the effect of \(x_1\) on \(y\) depends on/is conditional upon the value of \(x_2\).
(and vice versa, the effect of \(x_2\) on \(y\) is different across the values of \(x_1\)).
This means that we can no longer talk about the “effect of \(x_1\) holding \(x_2\) constant.” Instead we can talk about a marginal effect of \(x_1\) on \(y\) at a specific value of \(x_2\).
When we fit the model \(y = \beta_0 + \beta_1\cdot x_1 + \beta_2 \cdot x_2 + \beta_3 \cdot x_1 \cdot x_2 + \epsilon\) using lm():
- the parameter estimate \(\hat \beta_1\) is the marginal effect of \(x_1\) on \(y\) where \(x_2 = 0\)
- the parameter estimate \(\hat \beta_2\) is the marginal effect of \(x_2\) on \(y\) where \(x_1 = 0\)
side note: Regardless of whether or not there is an interaction term in our model, all parameter estimates in multiple regression are “conditional” in the sense that they are dependent upon the inclusion of other variables in the model. For instance, in \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon\) the coefficient \(\hat \beta_1\) is conditional upon holding \(x_2\) constant.
Interpreting the interaction term A:B
The coefficient for an interaction term can be thought of as providing an adjustment to the slope.
In our model: \(\text{wellbeing} = \beta_0 + \beta_1\cdot\text{social-interactions} + \beta_2\cdot\text{isRural} + \beta_3\cdot\text{social-interactions}\cdot\text{isRural} + \epsilon\), we have a numeric*categorical interaction.
The estimate \(\hat \beta_3\) is the adjustment to the slope \(\hat \beta_1\) to be made for the individuals in the \(\text{isRural}=1\) group.
Question 5
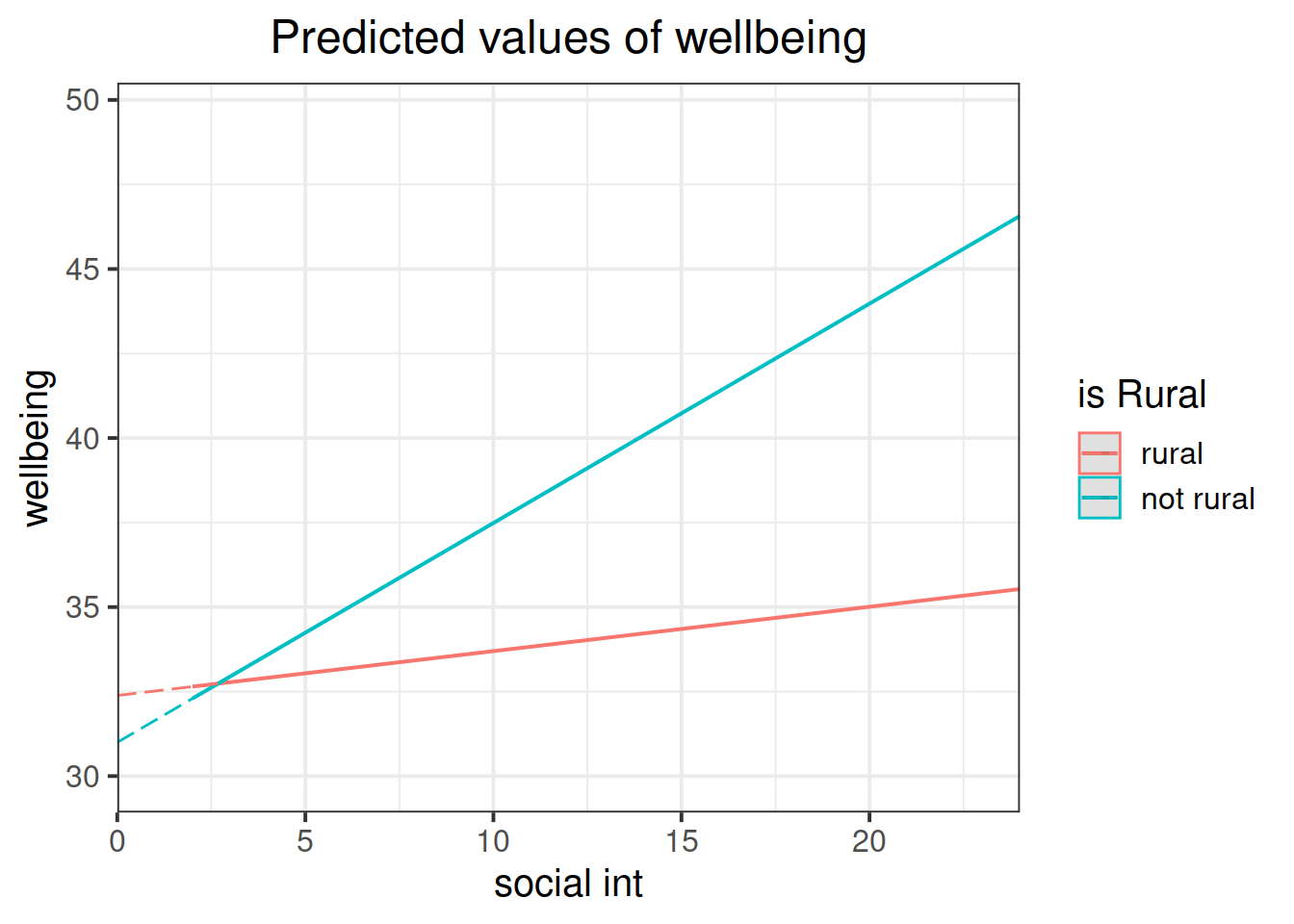
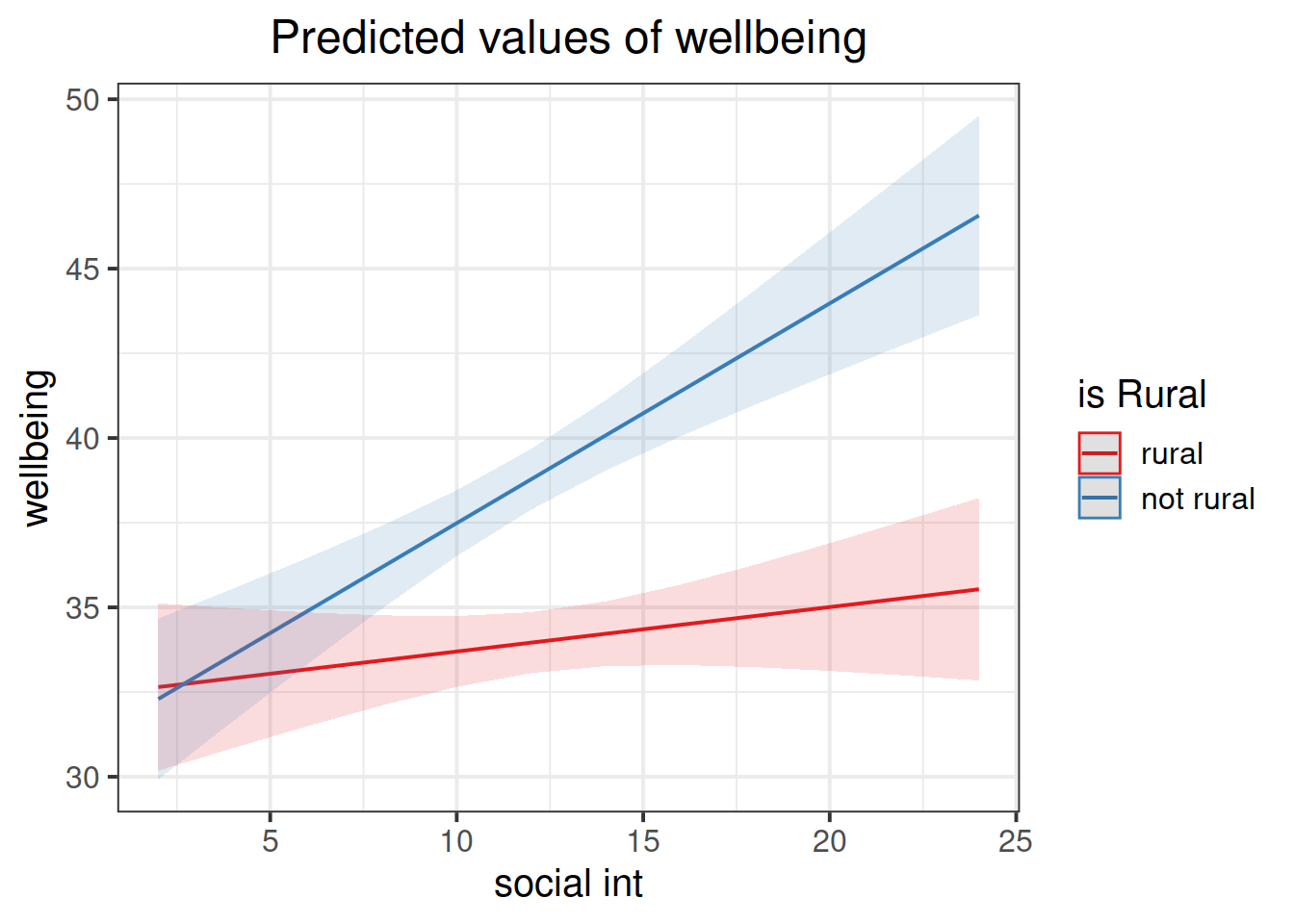
Look at the parameter estimates from your model, and write a description of what each one corresponds to on the plot shown in Figure 1 (it may help to sketch out the plot yourself and annotate it).
“The best method of communicating findings about the presence of significant interaction may be to present a table of graph of the estimated means at various combinations of the interacting variables.”
Ramsey and Schafer (2012)
Hints. Click the plus to expand →
Here are some options to choose from:
- The point at which the blue line cuts the y-axis (where social_int = 0)
- The point at which the red line cuts the y-axis (where social_int = 0)
- The average vertical distance between the red and blue lines.
- The vertical distance from the blue to the red line at the y-axis (where social_int = 0)
- The vertical distance from the red to the blue line at the y-axis (where social_int = 0)
- The vertical distance from the blue to the red line at the center of the plot
- The vertical distance from the red to the blue line at the center of the plot
- The slope (vertical increase on the y-axis associated with a 1 unit increase on the x-axis) of the blue line
- The slope of the red line
- How the slope of the line changes when you move from the blue to the red line
- How the slope of the line changes when you move from the red to the blue line
Solution
We can obtain our parameter estimates using various functions such as summary(rural_mod),coef(rural_mod), coefficients(rural_mod) etc.
coefficients(rural_mod)
## (Intercept) social_int isRuralrural
## 30.9985688 0.6487945 1.3865688
## social_int:isRuralrural
## -0.5175856
- \(\hat \beta_0\) =
(Intercept) = 31: The point at which the blue line cuts the y-axis (where social_int = 0).
- \(\hat \beta_1\) =
social_int = 0.65: The slope (vertical increase on the y-axis associated with a 1 unit increase on the x-axis) of the blue line.
- \(\hat \beta_2\) =
isRuralrural = 1.39: The vertical distance from the blue to the red line at the y-axis (where social_int = 0).
- \(\hat \beta_3\) =
social_int:isRuralrural = -0.52: How the slope of the line changes when you move from the blue to the red line.
Question 6
Load the sjPlot package and try using the function plot_model().
The default behaviour of plot_model() is to plot the parameter estimates and their confidence intervals. This is where type = "est".
Try to create a plot like Figure 1, which shows the two lines (Hint: what are this weeks’ exercises all about? type = ???.)
Solution
library(sjPlot)
plot_model(rural_mod, type="int")
~ Numeric * Numeric
We will now look at a multiple regression model with an interaction betweeen two numeric explanatory variables.
Research question
Previous research has identified an association between an individual’s perception of their social rank and symptoms of depression, anxiety and stress. We are interested in the individual differences in this relationship.
Specifically:
- Does the effect of social comparison on symptoms of depression, anxiety and stress vary depending on level of neuroticism?
Social Comparison Study data codebook. Click the plus to expand →
Download link
The data is available at https://uoepsy.github.io/data/scs_study.csv
Description
Data from 656 participants containing information on scores on each trait of a Big 5 personality measure, their perception of their own social rank, and their scores on a measure of depression.
The data in scs_study.csv contain seven attributes collected from a random sample of \(n=656\) participants:
zo: Openness (Z-scored), measured on the Big-5 Aspects Scale (BFAS)zc: Conscientiousness (Z-scored), measured on the Big-5 Aspects Scale (BFAS)ze: Extraversion (Z-scored), measured on the Big-5 Aspects Scale (BFAS)za: Agreeableness (Z-scored), measured on the Big-5 Aspects Scale (BFAS)zn: Neuroticism (Z-scored), measured on the Big-5 Aspects Scale (BFAS)scs: Social Comparison Scale - An 11-item scale that measures an individual’s perception of their social rank, attractiveness and belonging relative to others. The scale is scored as a sum of the 11 items (each measured on a 5-point scale), with higher scores indicating more favourable perceptions of social rank.dass: Depression Anxiety and Stress Scale - The DASS-21 includes 21 items, each measured on a 4-point scale. The score is derived from the sum of all 21 items, with higher scores indicating higher a severity of symptoms.
Preview
The first six rows of the data are:
| zo |
zc |
ze |
za |
zn |
scs |
dass |
| 0.7587304 |
1.5838564 |
-0.79153841 |
-0.09104726 |
1.32023703 |
30 |
56 |
| 0.3033394 |
-0.2698774 |
-0.08636742 |
0.08849465 |
-0.40280445 |
30 |
48 |
| -0.1347251 |
0.6566343 |
-0.79796588 |
-0.94759192 |
0.92927138 |
35 |
48 |
| 1.0640775 |
-1.0218540 |
-0.16475623 |
-0.50409122 |
-0.02021664 |
29 |
48 |
| 1.7411706 |
-0.7773205 |
-1.55003059 |
-2.86050116 |
-1.14145028 |
41 |
43 |
| 0.2203023 |
-0.4054477 |
0.78397367 |
0.90388509 |
-0.24641819 |
37 |
60 |
Refresher: Z-scores
When we standardise a variable, we re-express each value as the distance from the mean in units of standard deviations. These transformed values are called z-scores.
To transform a given value \(x_i\) into a z-score \(z_i\), we simply calculate the distance from \(x_i\) to the mean, \(\bar{x}\), and divide this by the standard deviation, \(s\):
\[
z_i = \frac{x_i - \bar{x}}{s}
\]
A Z-score of a value is the number of standard deviations below/above the mean that the value falls.
Question 7
Specify the model you plan to fit in order to answer the research question (e.g., \(\text{??} = \beta_0 + \beta_1 \cdot \text{??} + .... + \epsilon\))
Solution
\[
\text{DASS-21 Score} = \beta_0 + \beta_1 \cdot \text{SCS Score} + \beta_2 \cdot \text{Neuroticism} + \beta_3 \cdot \text{SCS score} \cdot \text{Neuroticism} + \epsilon
\]
Question 8
Read in the data and assign it the name “scs_study.” Produce plots of the relevant distributions and relationships involved in the analysis.
Solution
scs_study <- read_csv("https://uoepsy.github.io/data/scs_study.csv")
summary(scs_study)
## zo zc ze za
## Min. :-2.81928 Min. :-3.21819 Min. :-3.00576 Min. :-2.94429
## 1st Qu.:-0.63089 1st Qu.:-0.66866 1st Qu.:-0.68895 1st Qu.:-0.69394
## Median : 0.08053 Median : 0.00257 Median :-0.04014 Median :-0.01854
## Mean : 0.09202 Mean : 0.01951 Mean : 0.00000 Mean : 0.00000
## 3rd Qu.: 0.80823 3rd Qu.: 0.71215 3rd Qu.: 0.67085 3rd Qu.: 0.72762
## Max. : 3.55034 Max. : 3.08015 Max. : 2.80010 Max. : 2.97010
## zn scs dass
## Min. :-1.4486 Min. :27.00 Min. :23.00
## 1st Qu.:-0.7994 1st Qu.:33.00 1st Qu.:41.00
## Median :-0.2059 Median :35.00 Median :44.00
## Mean : 0.0000 Mean :35.77 Mean :44.72
## 3rd Qu.: 0.5903 3rd Qu.:38.00 3rd Qu.:49.00
## Max. : 3.3491 Max. :54.00 Max. :68.00
ggplot(data = scs_study, aes(x=dass)) +
geom_density() +
geom_boxplot(width = 1/50) +
labs(title="Marginal distribution of DASS-21 Scores",
x = "Depression Anxiety and Stress Scale", y = "Probability density")
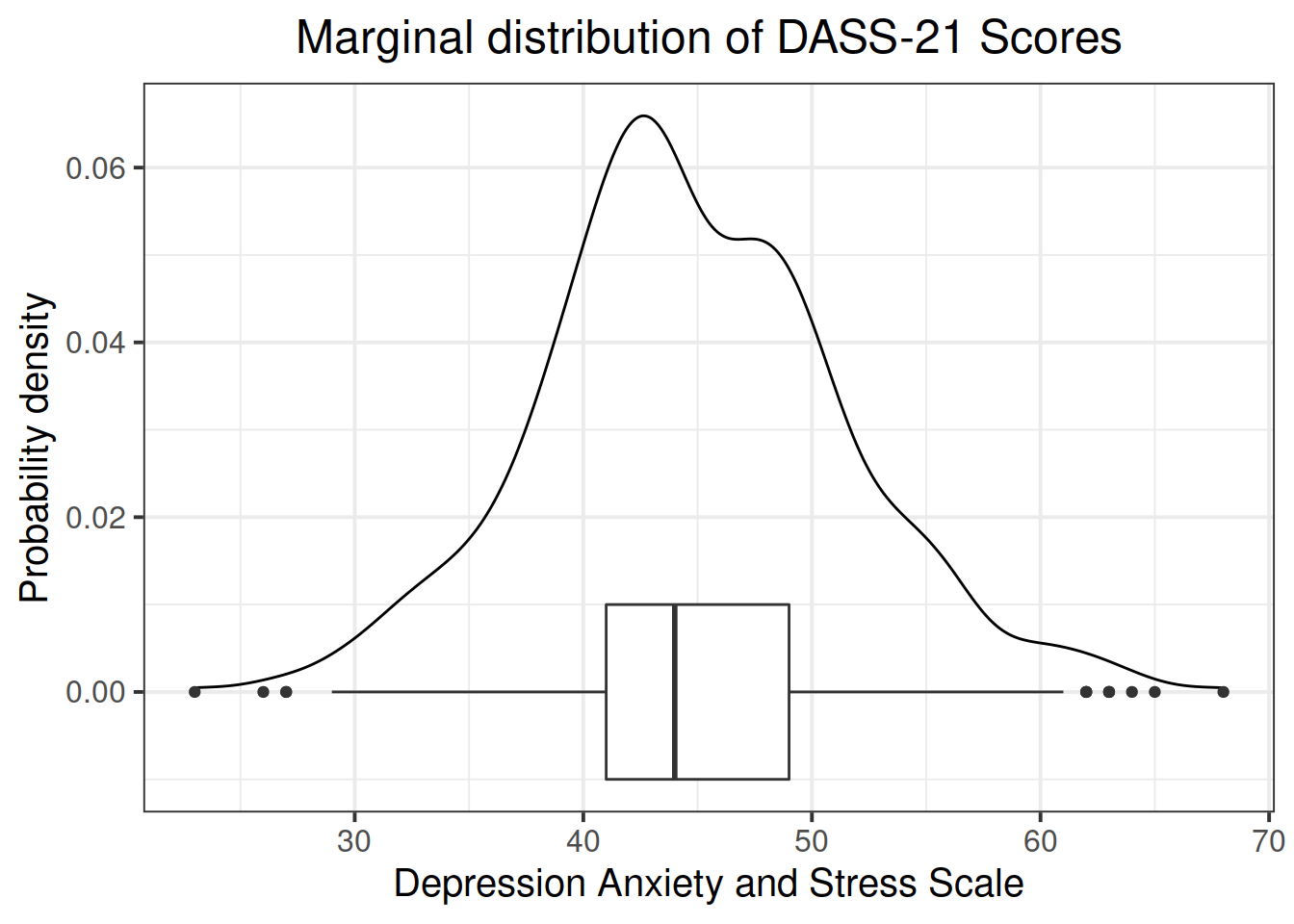
The marginal distribution of scores on the Depression, Anxiety and Stress Scale (DASS-21) is unimodal with a mean of approximately 45 and a standard deviation of 7.
ggplot(data = scs_study, aes(x=scs)) +
geom_density() +
geom_boxplot(width = 1/50) +
labs(title="Marginal distribution of Social Comparison Scale (SCS) scores",
x = "Social Comparison Scale Score", y = "Probability density")
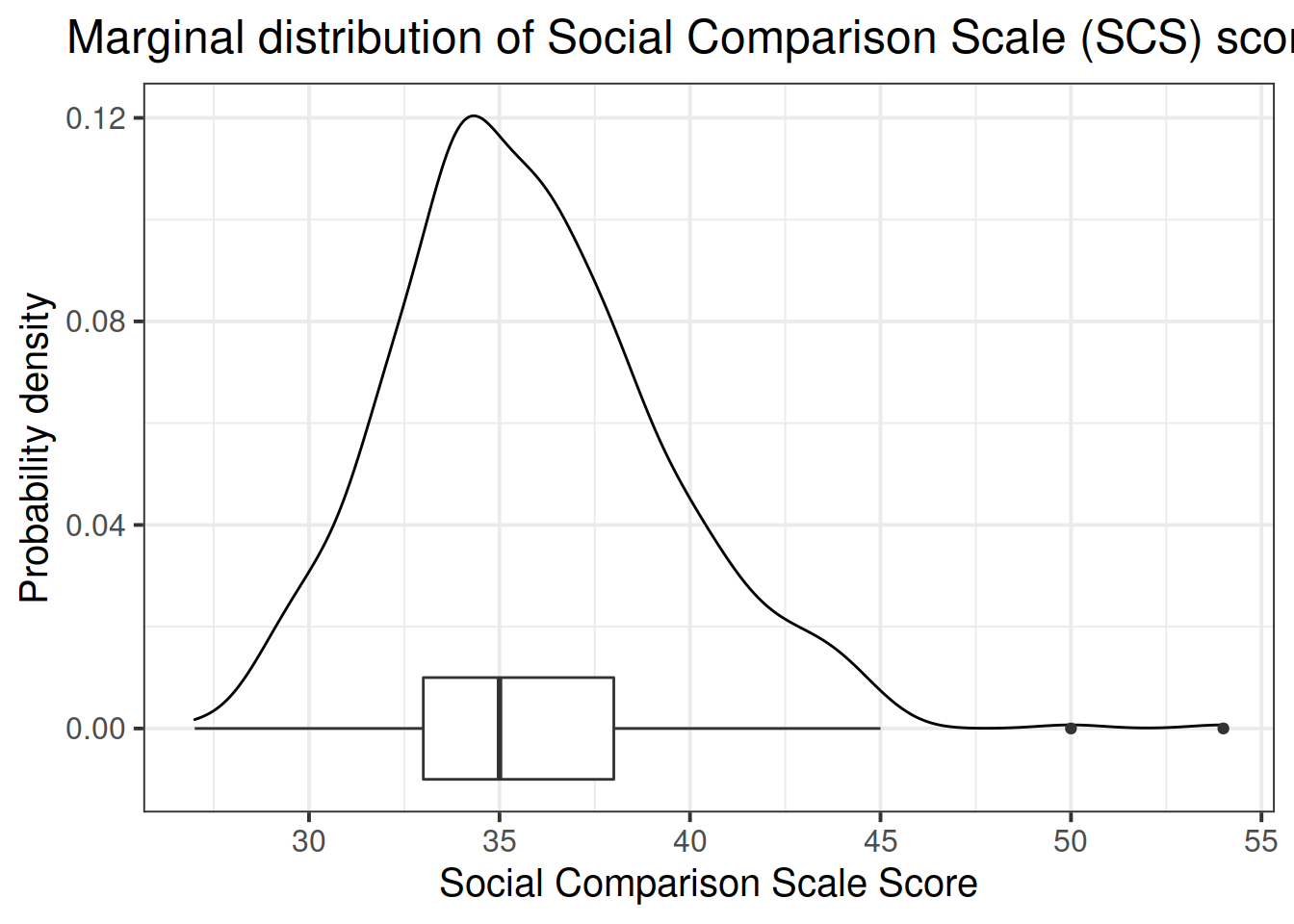
The marginal distribution of score on the Social Comparison Scale (SCS) is unimodal with a mean of approximately 36 and a standard deviation of 4. There look to be a number of outliers at the upper end of the scale.
ggplot(data = scs_study, aes(x=zn)) +
geom_density() +
geom_boxplot(width = 1/50) +
labs(title="Marginal distribution of Neuroticism (Z-Scored)",
x = "Neuroticism (Z-Scored)", y = "Probability density")
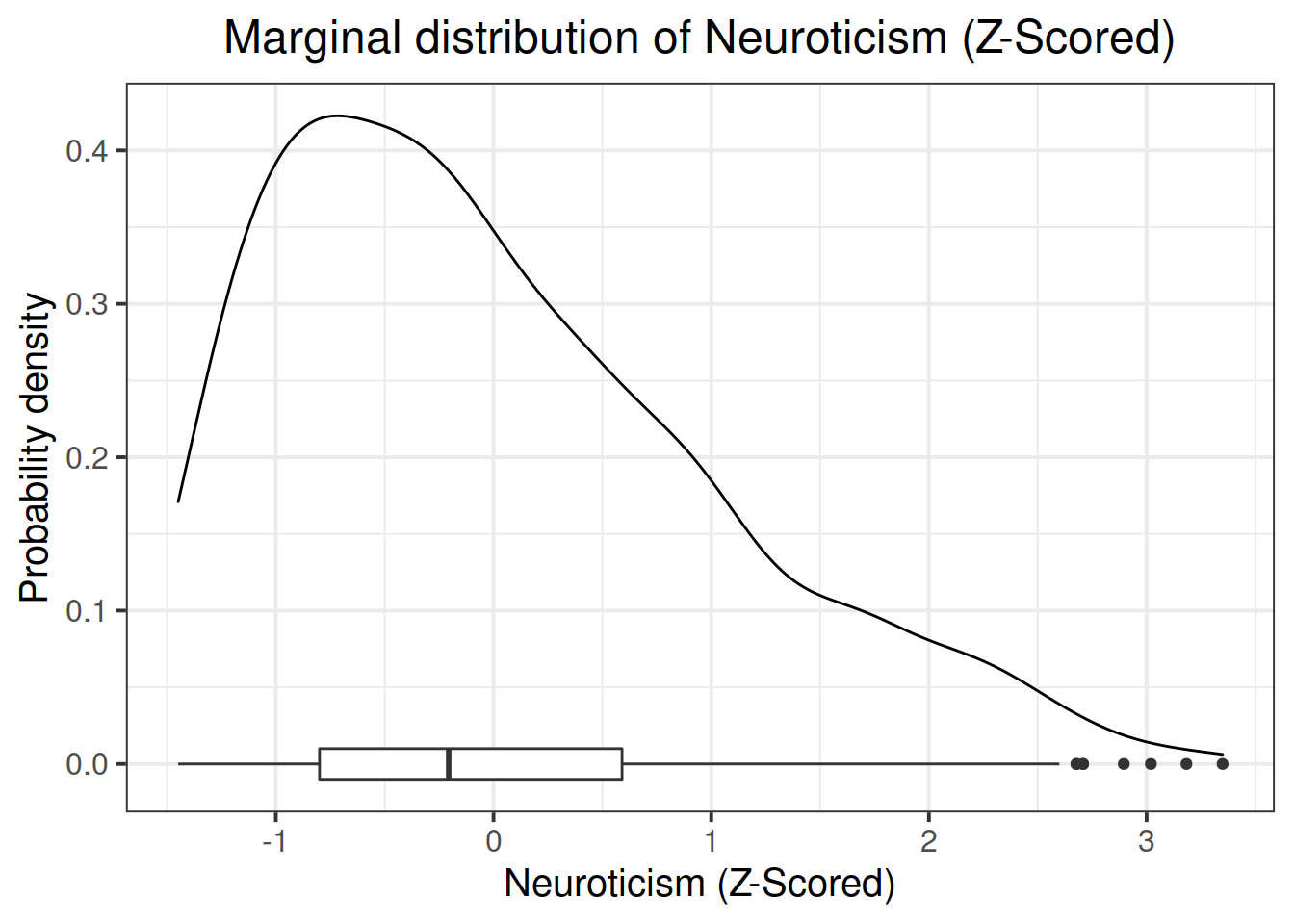
The marginal distribution of Neuroticism (Z-scored) is positively skewed, with the 25% of scores falling below -0.8, 75% of scores falling below 0.59.
library(patchwork) # for arranging plots side by side
library(knitr) # for making tables look nice
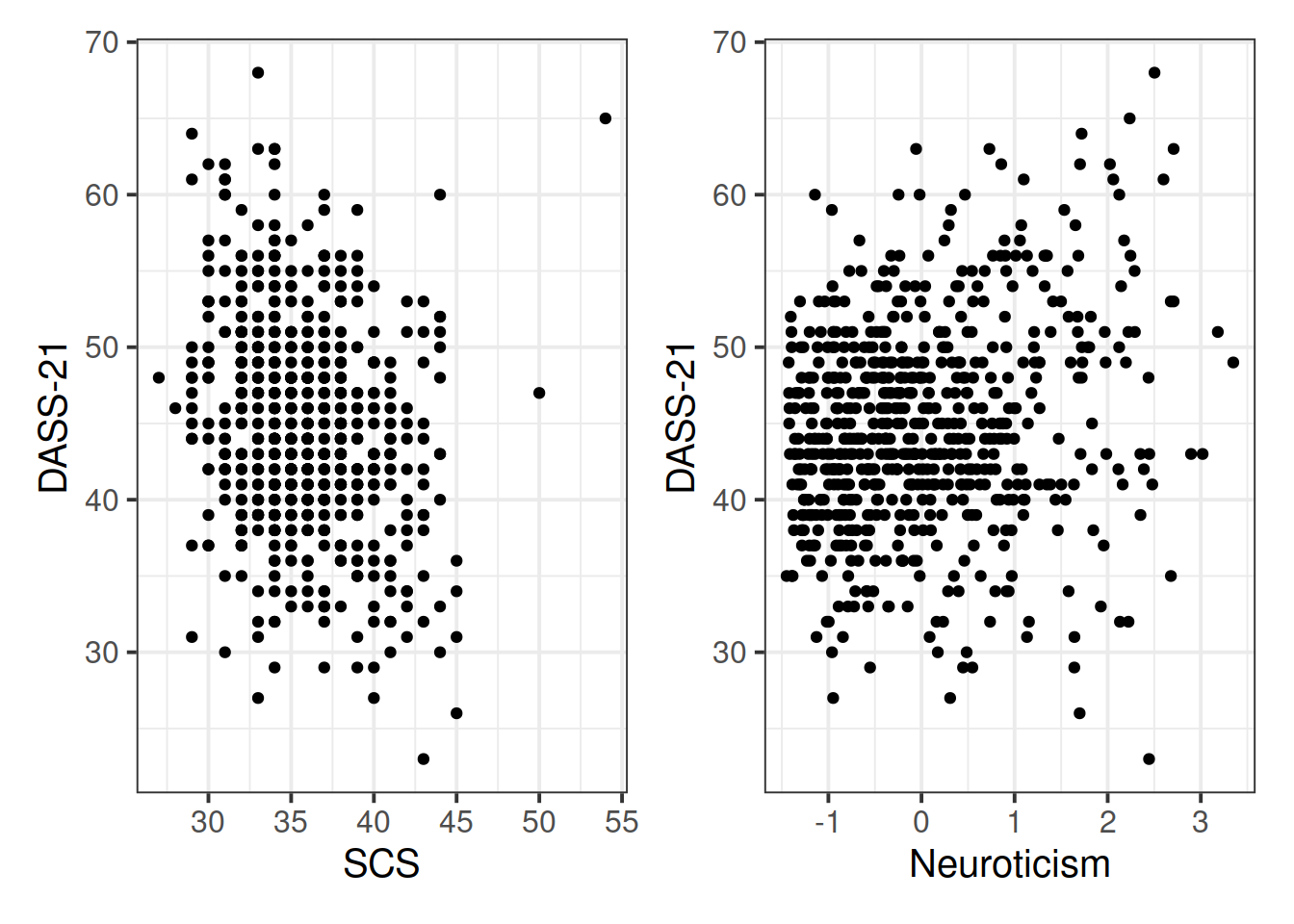
p1 <- ggplot(data = scs_study, aes(x=scs, y=dass)) +
geom_point()+
labs(x = "SCS", y = "DASS-21")
p2 <- ggplot(data = scs_study, aes(x=zn, y=dass)) +
geom_point()+
labs(x = "Neuroticism", y = "DASS-21")
p1 | p2
# the kable() function from the knitr package can make table outputs print nicely into html.
scs_study %>%
select(dass, scs, zn) %>%
cor %>%
kable
|
|
dass
|
scs
|
zn
|
|
dass
|
1.0000000
|
-0.2280126
|
0.2001885
|
|
scs
|
-0.2280126
|
1.0000000
|
0.1146687
|
|
zn
|
0.2001885
|
0.1146687
|
1.0000000
|
There is a weak, negative, linear relationship between scores on the Social Comparison Scale and scores on the Depression Anxiety and Stress Scale for the participants in the sample. Severity of symptoms measured on the DASS-21 tend to decrease, on average, the more favourably participants view their social rank.
There is a weak, positive, linear relationship between the levels of Neuroticism and scores on the DASS-21. Participants who are more neurotic tend to, on average, display a higher severity of symptoms of depression, anxiety and stress.
Question 9
Run the code below. It takes the dataset, and uses the
cut() function to add a new variable called “zn_group,” which is the “zn” variable split into 4 groups.
Remember: we have re-assign this output as the name of the dataset (the scs_study <- bit at the beginning) to make these changes occur in our environment (the top-right window of Rstudio). If we didn’t have the first line, then it would simply print the output.
scs_study <-
scs_study %>%
mutate(
zn_group = cut(zn, 4)
)
We can see how it has split the “zn” variable by plotting the two against one another:
(Note that the levels of the new variable are named according to the cut-points).
ggplot(data = scs_study, aes(x = zn_group, y = zn)) +
geom_point()
Plot the relationship between scores on the SCS and scores on the DASS-21, for each group of the variable we just created.
How does the pattern change? Does it suggest an interaction?
Tip: Rather than creating four separate plots, you might want to map some feature of the plot to the variable we created in the data, or make use of facet_wrap()/facet_grid().
Solution
ggplot(data = scs_study, aes(x = scs, y = dass, col = zn_group)) +
geom_point() +
facet_grid(~zn_group) +
theme(legend.position = "none") # remove the legend
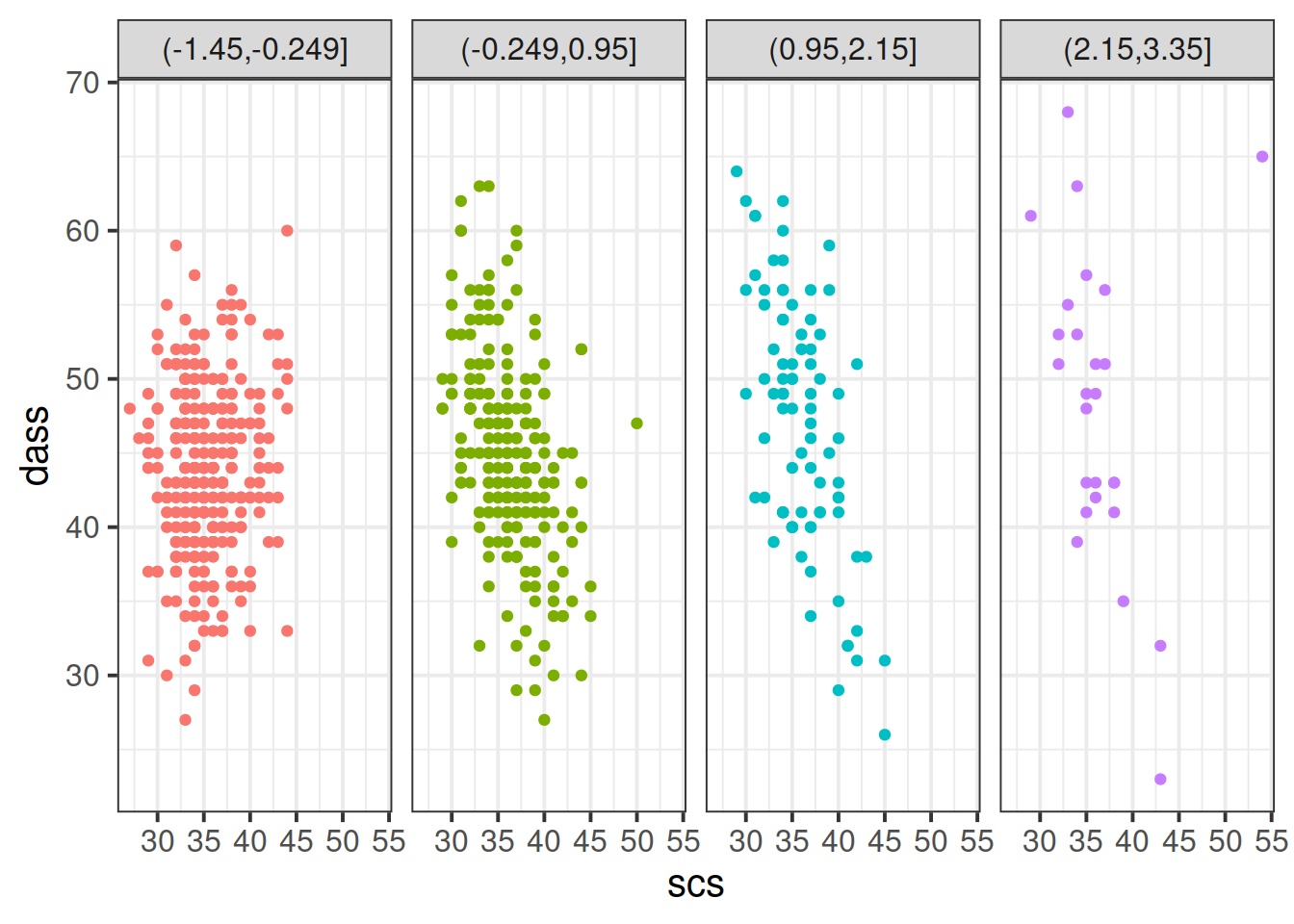
The relationship between SCS scores and DASS-21 scores appears to be different between these groups. For those with a relatively high neuroticism score, the relationship seems stronger, while for those with a low neuroticism score there is almost no discernable relationship.
This suggests an interaction - the relationship of DASS-21 ~ SCS differs across the values of neuroticism!
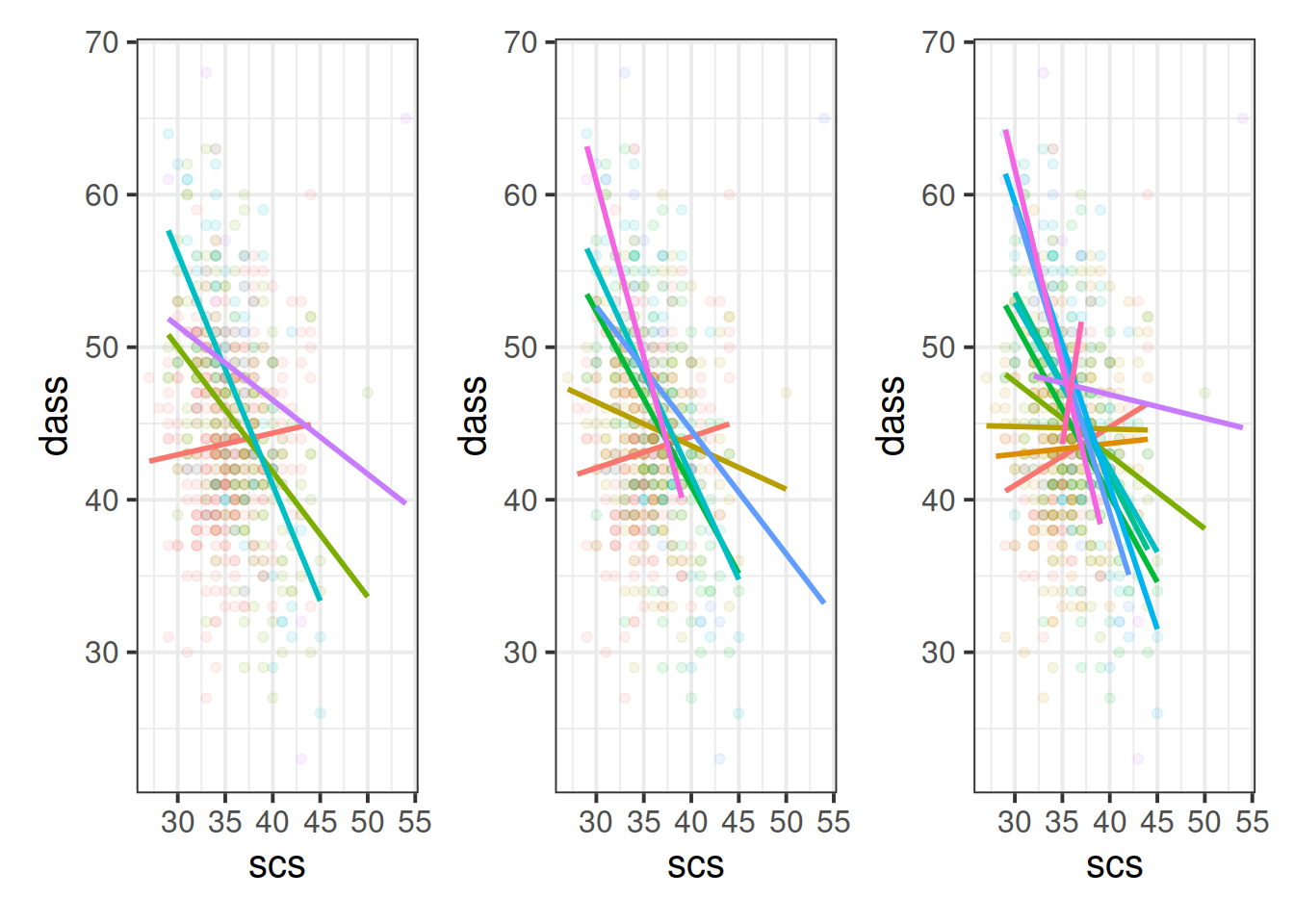
Cutting one of the explanatory variables up into groups essentially turns a numeric variable into a categorical one. We did this just to make it easier to visualise how a relationship changes across the values of another variable, because we can imagine a separate line for the relationship between SCS and DASS-21 scores for each of the groups of neuroticism. However, in grouping a numeric variable like this we lose information. Neuroticism is measured on a continuous scale, and we want to capture how the relationship between SCS and DASS-21 changes across that continuum (rather than cutting it into chunks).
We could imagine cutting it into more and more chunks (see Figure 2), until what we end up with is a an infinite number of lines - i.e., a three-dimensional plane/surface (recall that in for a multiple regression model with 2 explanatory variables, we can think of the model as having three-dimensions). The inclusion of the interaction term simply results in this surface no longer being necessarily flat. You can see this in Figure 3.
Question 10
Fit your model using lm().
Solution
dass_mdl <- lm(dass ~ 1 + scs*zn, data = scs_study)
summary(dass_mdl)
##
## Call:
## lm(formula = dass ~ 1 + scs * zn, data = scs_study)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.301 -3.825 -0.173 3.733 45.777
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 60.80887 2.45399 24.780 < 2e-16 ***
## scs -0.44391 0.06834 -6.495 1.64e-10 ***
## zn 20.12813 2.35951 8.531 < 2e-16 ***
## scs:zn -0.51861 0.06552 -7.915 1.06e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.123 on 652 degrees of freedom
## Multiple R-squared: 0.1825, Adjusted R-squared: 0.1787
## F-statistic: 48.5 on 3 and 652 DF, p-value: < 2.2e-16
Question 11
|
|
Estimate
|
Std. Error
|
t value
|
Pr(>|t|)
|
|
(Intercept)
|
60.8088736
|
2.4539924
|
24.779569
|
0
|
|
scs
|
-0.4439065
|
0.0683414
|
-6.495431
|
0
|
|
zn
|
20.1281319
|
2.3595133
|
8.530629
|
0
|
|
scs:zn
|
-0.5186142
|
0.0655210
|
-7.915236
|
0
|
Recall that the coefficients zn and scs from our model now reflect the estimated change in the outcome associated with an increase of 1 in the explanatory variables, when the other variable is zero.
Think - what is 0 in each variable? what is an increase of 1? Are these meaningful? Would you suggest recentering either variable?
Solution
The neuroticism variable zn is Z-scored, which means that 0 is the mean (it is mean-centered), and 1 is a standard deviation.
The Social Comparison Scale variable scs is the raw-score. Looking back at the description of the variables, we can work out that the minimum possible score is 11 (if people respond 1 for each of the 11 questions) and the maximum is 55 (if they respond 5 for all questions). Is it meaningful/useful to talk about estimated effects for people who score 0? Not really.
But we can make it so that zero represents something else, such as the minimum score, or the mean score. For instance, scs_study$scs - 11 will subtract 11 from the scores, making zero the minimum possible score on the scale.
Question 12
Recenter one or both of your explanatory variables to ensure that 0 is a meaningful value
Solution
We’re going to mean-center the scores on the SCS. Think about what someone who now scores zero on the zn variable and zero on the mean-centered SCS?
scs_study <-
scs_study %>%
mutate(
scs_mc = scs - mean(scs)
)
Question 13
We re-fit the model using mean-centered SCS scores instead of the original variable. Here are the parameter estimates:
dass_mdl2 <- lm(dass ~ 1 + scs_mc * zn, data = scs_study)
# pull out the coefficients from the summary():
summary(dass_mdl2)$coefficients
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 44.9324476 0.24052861 186.807079 0.000000e+00
## scs_mc -0.4439065 0.06834135 -6.495431 1.643265e-10
## zn 1.5797687 0.24086372 6.558766 1.105118e-10
## scs_mc:zn -0.5186142 0.06552100 -7.915236 1.063297e-14
Fill in the blanks in the statements below.
- For those of average neuroticism and who score average on the SCS, the estimated DASS-21 Score is ???
- For those who who score ??? on the SCS, an increase of ??? in neuroticism is associated with a change of 1.58 in DASS-21 Scores
- For those of average neuroticism, an increase of ??? on the SCS is associated with a change of -0.44 in DASS-21 Scores
- For every increase of ??? in neuroticism, the change in DASS-21 associated with an increase of ??? on the SCS is asjusted by ???
- For every increase of ??? in SCS, the change in DASS-21 associated with an increase of ??? in neuroticism is asjusted by ???
Solution
- For those of average neuroticism and who score average on the SCS, the estimated DASS-21 Score is 44.93
- For those who who score average (mean) on the SCS, an increase of 1 standard deviation in neuroticism is associated with a change of 1.58 in DASS-21 Scores
- For those of average neuroticism, an increase of 1 on the SCS is associated with a change of -0.44 in DASS-21 Scores
- For every increase of 1 standard deviation in neuroticism, the change in DASS-21 associated with an increase of 1 on the SCS is asjusted by -0.52
- For every increase of 1 in SCS, the change in DASS-21 associated with an increase of 1 standard deviation in neuroticism is asjusted by -0.52
Ramsey, Fred, and Daniel Schafer. 2012. The Statistical Sleuth: A Course in Methods of Data Analysis. Cengage Learning.