Be sure to check the solutions to last week’s exercises.
You can still ask any questions about previous weeks’ materials if things aren’t clear!

LEARNING OBJECTIVES

Specify the assumptions underlying a LM with multiple predictors.
Assess if a fitted model satisfies the assumptions.
Test and assess the effect of influential cases on LM coefficients and overall model evaluations.

Refresher: LM assumptions

In the previous labs, we have fitted a number of multiple regression models. In each case, we first specified the model, then visually explored the marginal distributions and relationships of variables which would be used in the analysis. Finally, we fit the model, and began to examine the fit by studying what the various parameter estimates represented, and the spread of the residuals (the parts of the output inside the red boxes in Figure 1)

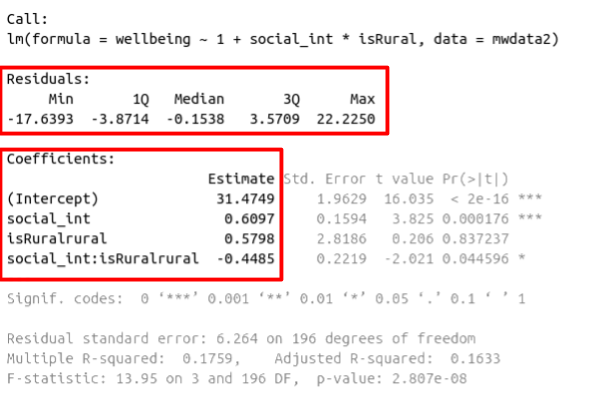
Figure 1: Multiple regression output in R, summary.lm(). Residuals and Coefficients highlighted

You will recall that before we draw inferences using our model estimates or use our model to make predictions, we need to be satisfied that our model meets the set of assumptions.

All of the estimates, intervals and hypothesis tests (see Figure 2) resulting from a regression analysis assume a certain set of conditions have been met. Meeting these conditions is what allows us to generalise our findings beyond our sample (i.e., to the population).

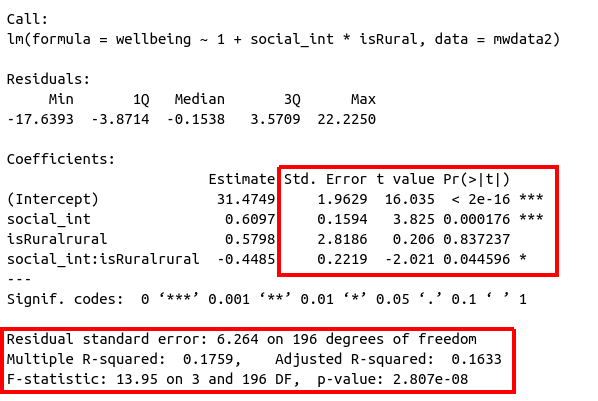
Figure 2: Multiple regression output in R, summary.lm(). Hypothesis tests highlighted

Recall the assumptions of the linear model:

Linearity: The relationship between $y$ and $x$ is linear.
Independence of errors: The error terms should be independent from one another.
Normality: The errors $\epsilon$ are normally distributed
Equal variances (“Homoscedasticity”): The scale of the variability of the errors $\epsilon$ is constant at all values of $x$.

When we fit a model, we evaluate many of these assumptions by looking at the residuals (the deviations from the observed values $y_i$ and the model estimated value $\hat y_i$). The residuals, $\hat \epsilon$ are our estimates of the actual unknown true error term $\epsilon$.
Because these same assumptions hold for a regression model with multiple predictors, we can assess them in a similar way. However, there are a number of important considerations.

Question 1

Open a new RMarkdown document. Copy the code below to load in the tidyverse packages, read in the wellbeing.csv data and fit the following model:

\[ \text{Wellbeing} = \beta_0 + \beta_1 \cdot \text{Outdoor Time} + \beta_2 \cdot \text{Social Interactions} + \epsilon \]

library(tidyverse) 

# read in the wellbeing data
mwdata = read_csv(file = "https://uoepsy.github.io/data/wellbeing.csv")
# fit the linear model: 
wb_mdl1 <- lm(wellbeing ~ outdoor_time + social_int, data = mwdata)

Note: We have have forgone writing the 1 in lm(y ~ 1 + x.... The 1 just tells R that we want to estimate the Intercept, and it will do this by default even if we leave it out.

Guided exercises

Linearity

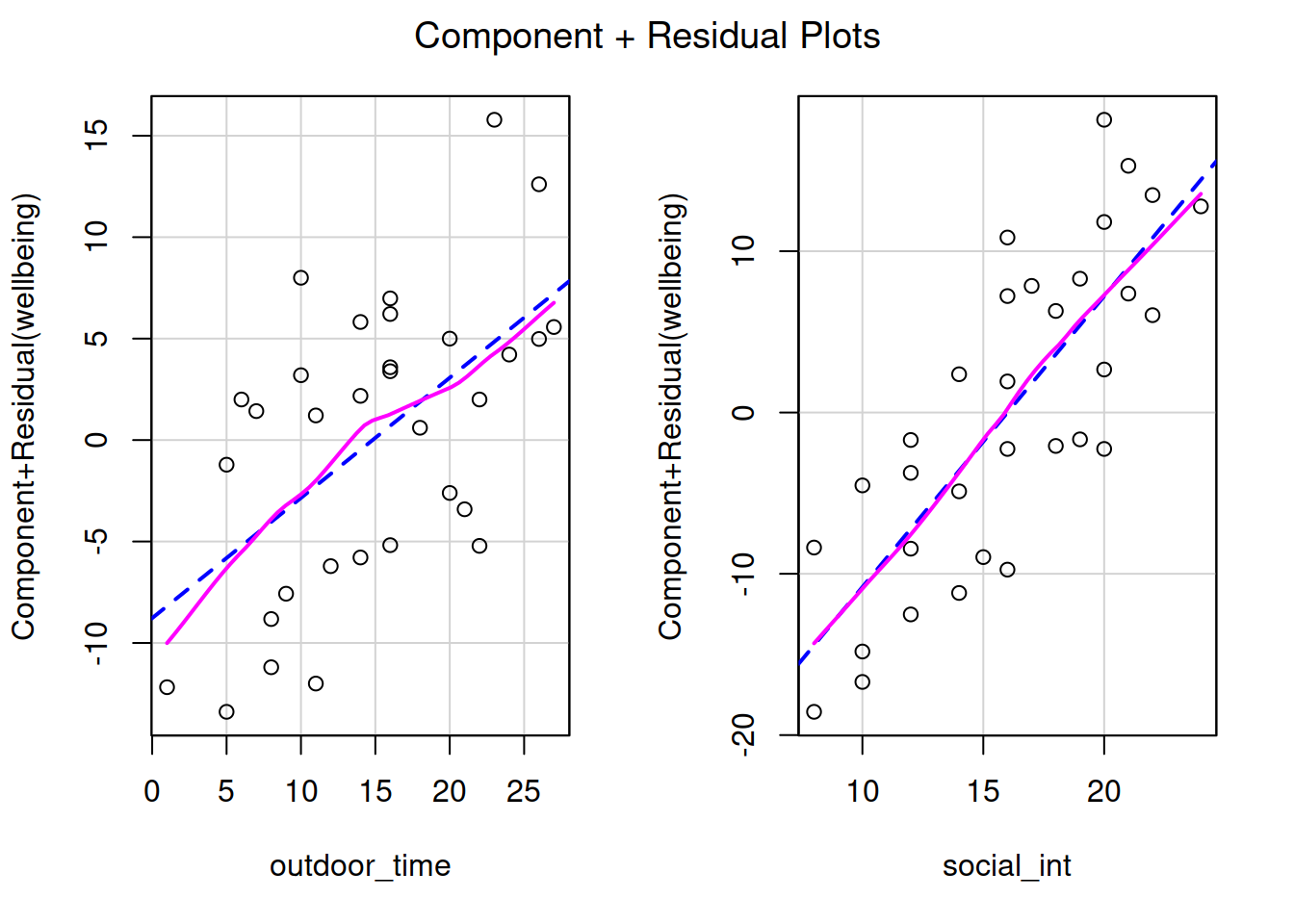
In simple linear regression (SLR) with only one explanatory variable, we could assess linearity through a simple scatterplot of the outcome variable against the explanatory. In multiple regression, however, it becomes more necessary to rely on diagnostic plots of the model residuals. This is because we need to know whether the relations are linear between the outcome and each predictor after accounting for the other predictors in the model.

In order to assess this, we use partial-residual plots (also known as ‘component-residual plots’). This is a plot with each explanatory variable $x_j$ on the x-axis, and partial residuals on the y-axis.

Partial residuals for a predictor $x_j$ are calculated as: \[ \hat \epsilon + \hat \beta_j x_j \]

In R we can easily create these plots for all predictors in the model by using the crPlots() function from the car package.

Question 2

Create partial-residual plots for the wb_mdl1 model.
Remember to load the car package first. If it does not load correctly, it might mean that you have need to install it.

Write a sentence summarising whether or not you consider the assumption to have been met. Justify your answer with reference to the plots.

Solution

library(car)
crPlots(wb_mdl1)

The smoother (the pink line) follows quite closely to a linear relationship (the dashed blue line), suggesting that the linearity assumption is met.

Equal variances (Homoscedasticity)

The equal variances assumption is that the error variance $\sigma^2$ is constant across values of the predictors $x_1$, … $x_k$, and across values of the fitted values $\hat y$. This sometimes gets termed “Constant” vs “Non-constant” variance. Figures 3 & 4 shows what these look like visually.

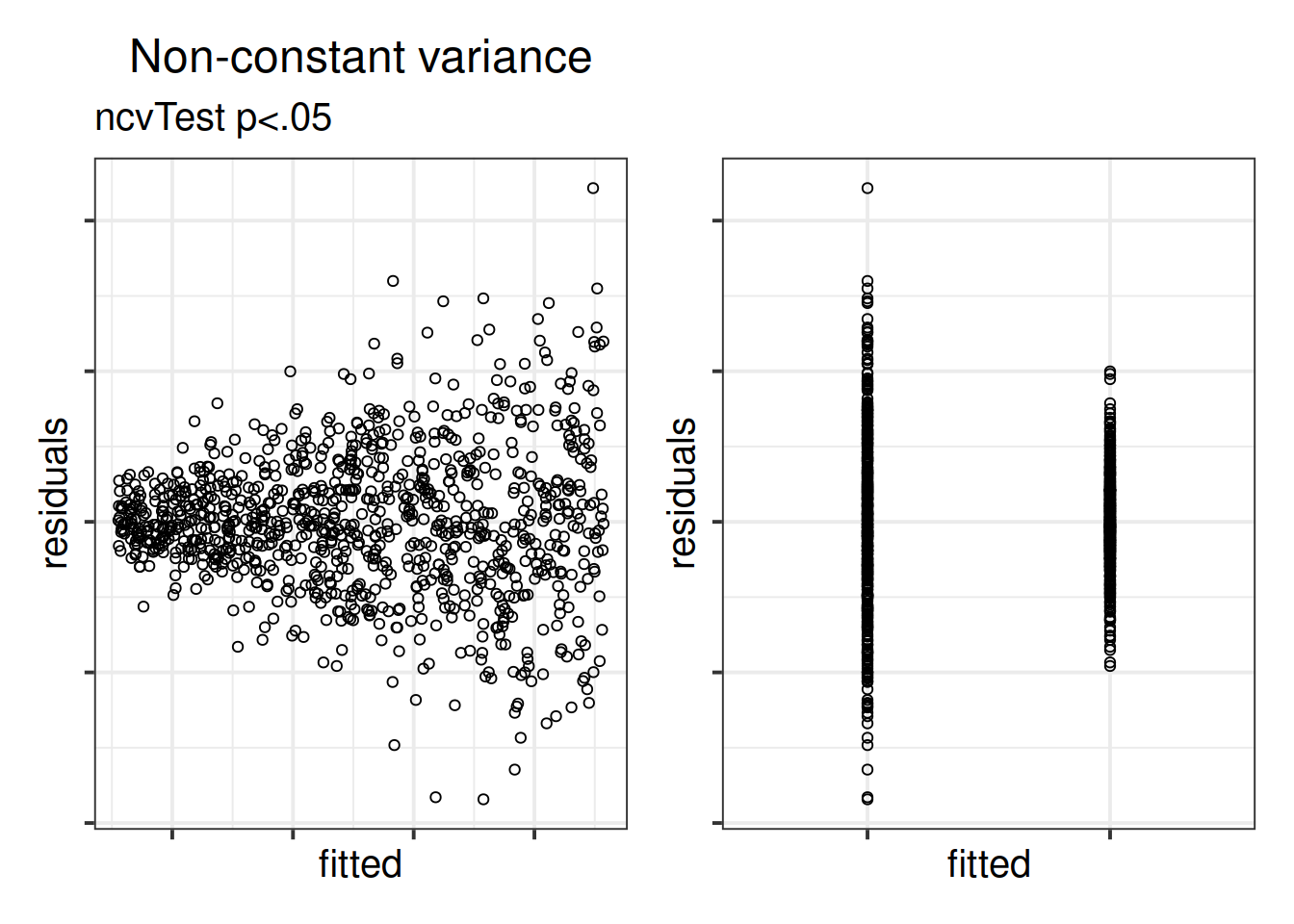
Figure 3: Non-constant variance for numeric and categorical x

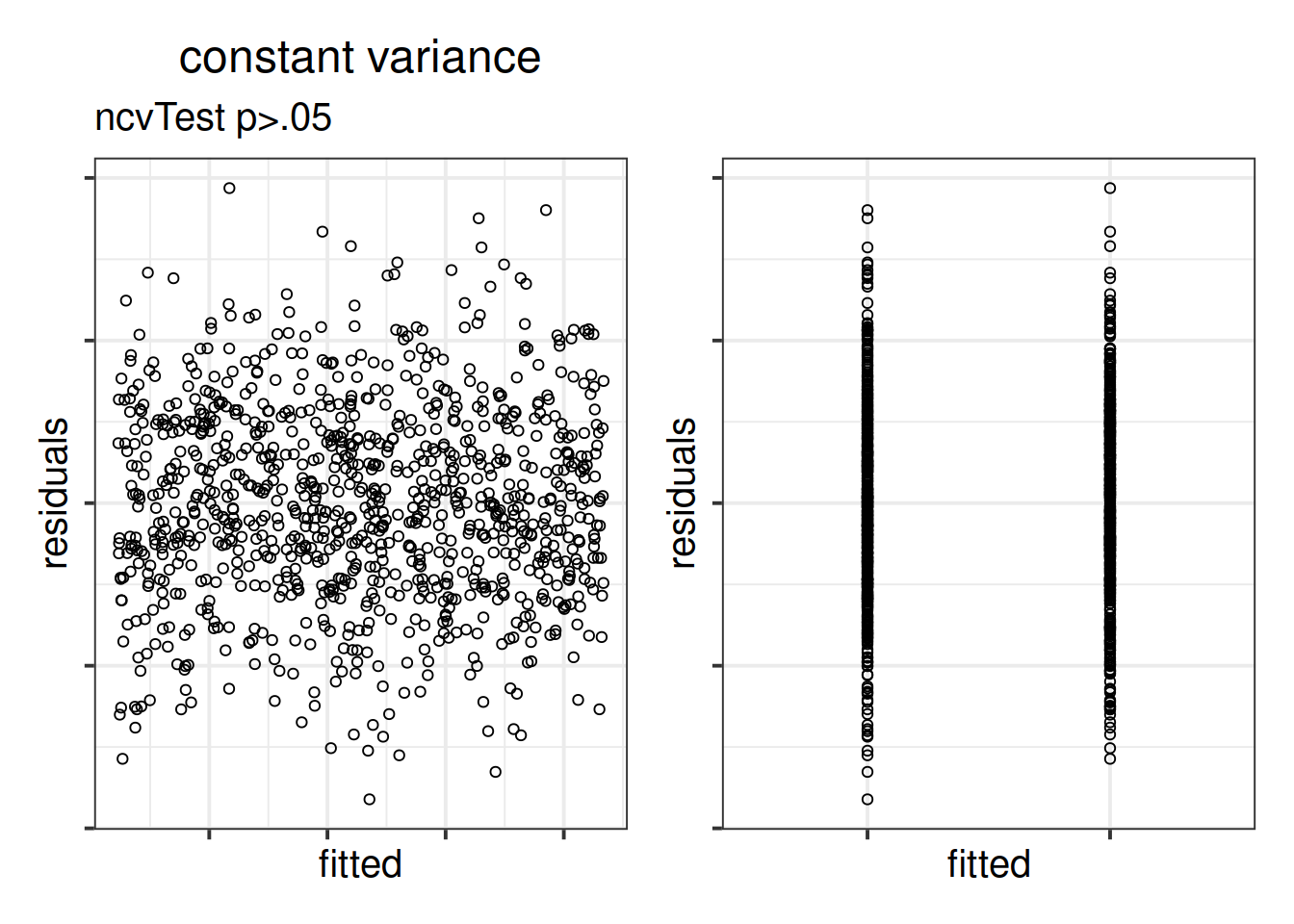
Figure 4: Constant variance for numeric and categorical x

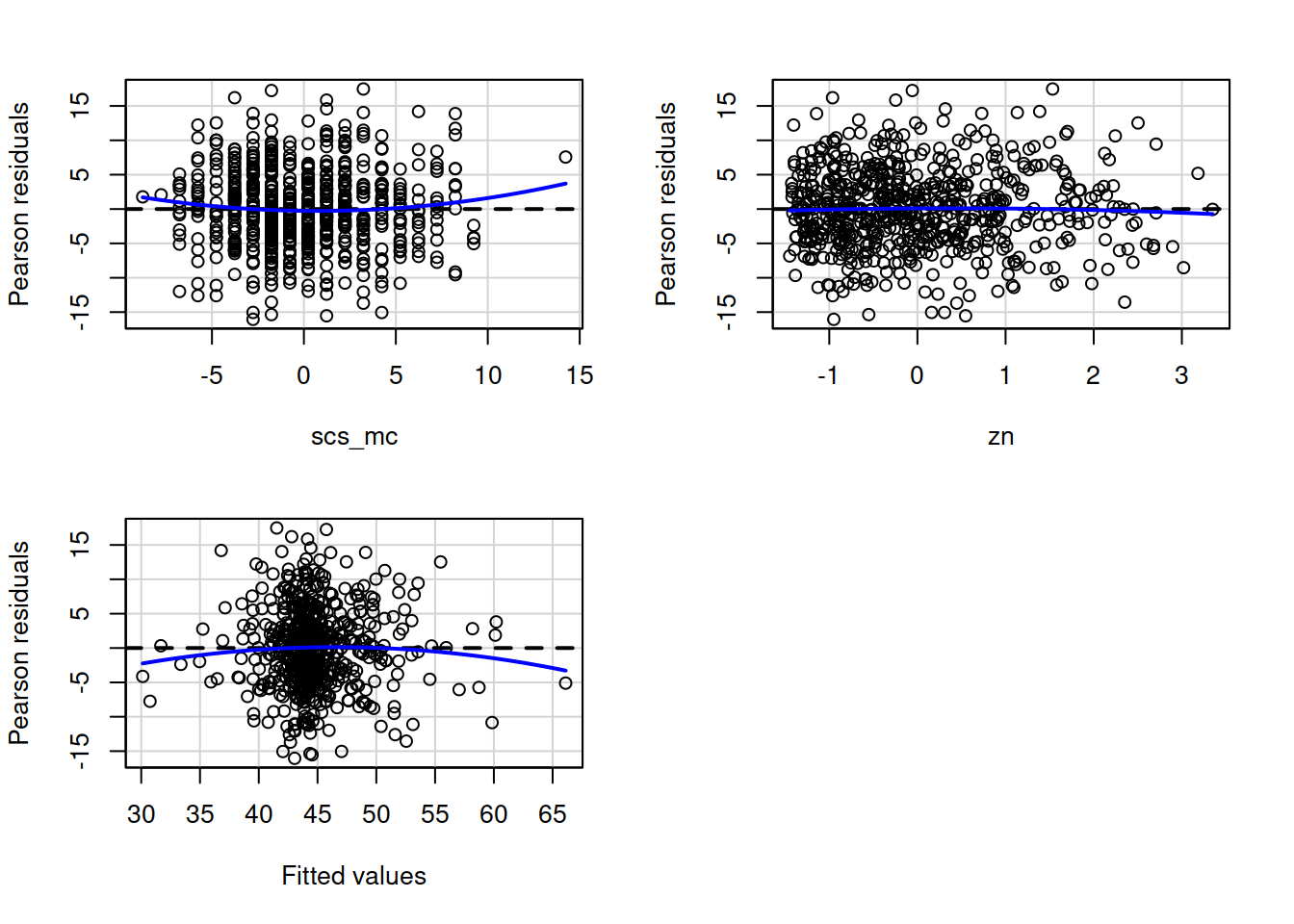
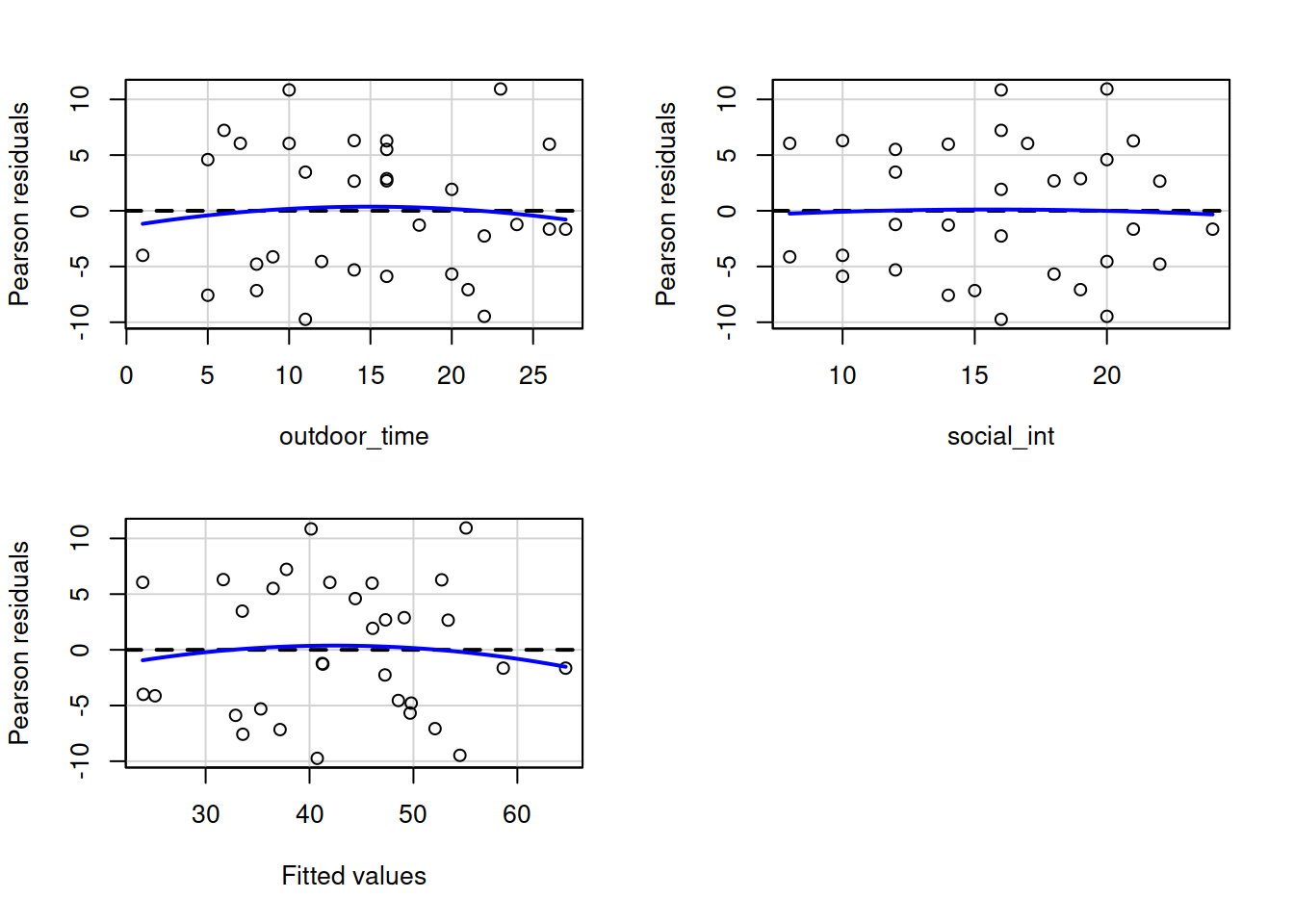
In R we can create plots of the Pearson residuals against the predicted values $\hat y$ and against the predictors $x_1$, … $x_k$ by using the residualPlots() function from the car package. This function also provides the results of a lack-of-fit test for each of these relationships (note when it is the fitted values $\hat y$ it gets called “Tukey’s test”).

ncvTest(model) (also from the car package) performs a test against the alternative hypothesis that the error variance changes with the level of the fitted value (also known as the “Breusch-Pagan test”). $p >.05$ indicates that we do not have evidence that the assumption has been violated.

Question 3

Use residualPlots() to plot residuals against each predictor, and use ncvTest() to perform a test against the alternative hypothesis that the error variance changes with the level of the fitted value.

Write a sentence summarising whether or not you consider the assumption to have been met. Justify your answer with reference to plots and/or formal tests where available.

Solution

residualPlots(wb_mdl1)

##              Test stat Pr(>|Test stat|)
## outdoor_time   -0.3478           0.7306
## social_int     -0.1068           0.9157
## Tukey test     -0.4189           0.6753

#test against the alternative hypothesis that error variance changes with level of fitted value
ncvTest(wb_mdl1)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.001925809, Df = 1, p = 0.965

Partial residual plots show no clear non-linear trends between residuals and predictors. Visual inspection of suggested little sign of non-constant variance, with the Breusch-Pagan test failing to reject the null that error varance does not change across the fitted values ($\chi^2(1)=0.002$, $p = .965$).

Question 4

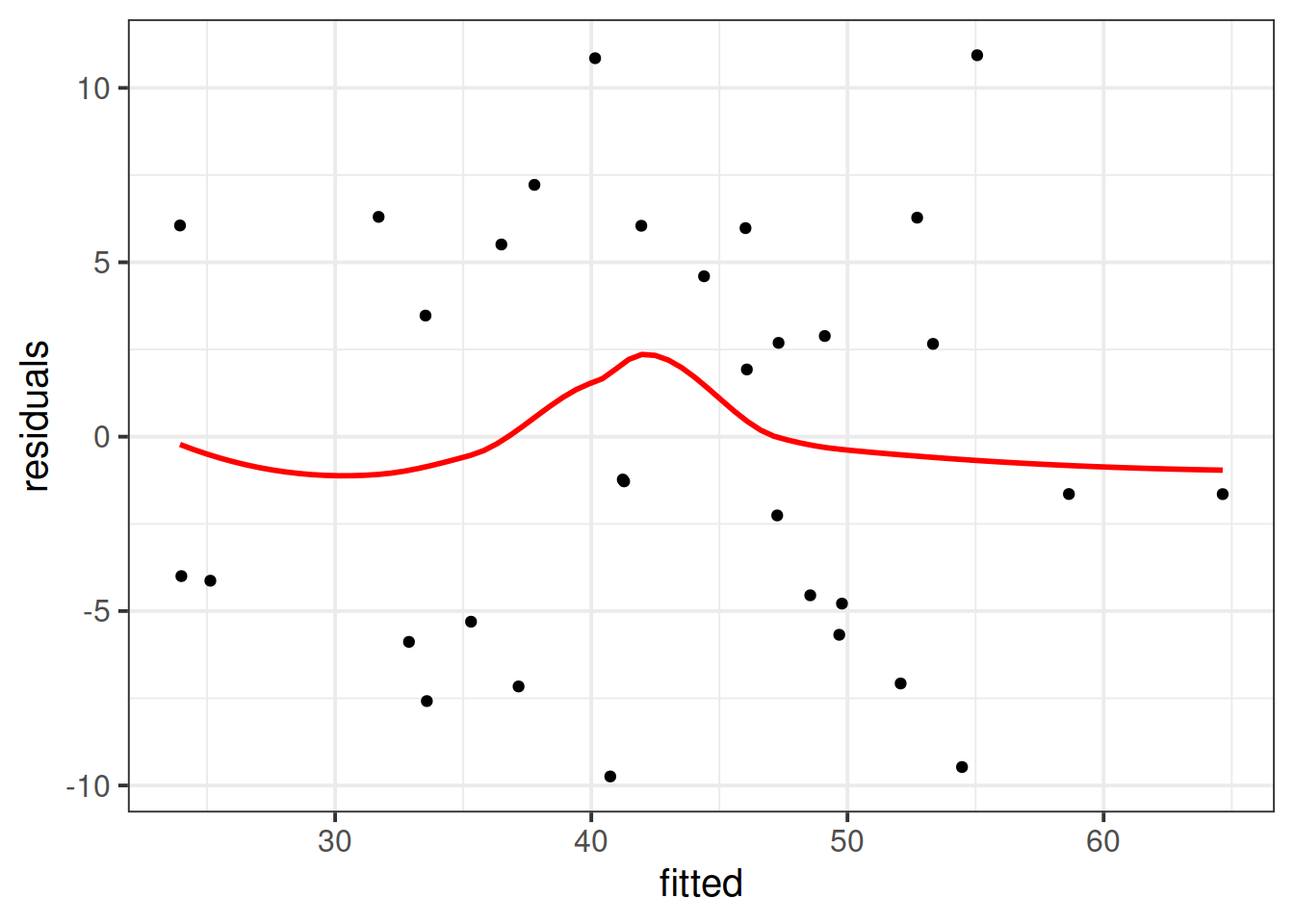
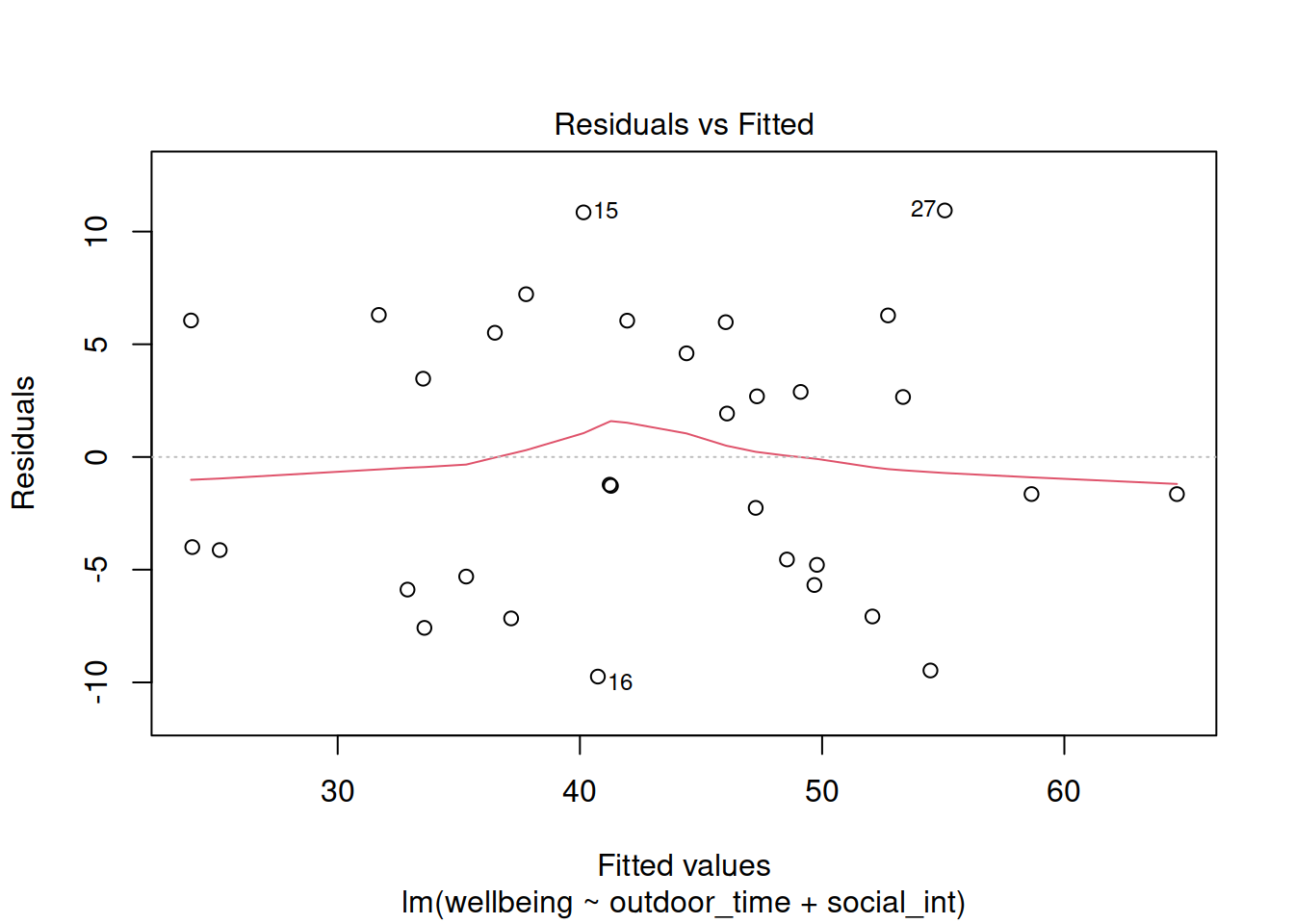
Create the “residuals vs. fitted plot” - a scatterplot with the residuals $\hat \epsilon$ on the y-axis and the fitted values $\hat y$ on the x-axis.

You can either do this:

manually, using the functions residuals() and fitted(), or
quickly by giving the plot() function your model. Be sure to specify which plot you want to return - e.g., plot(wb_mdl1, which = ???)

You can use this plot to visually assess:

Linearity: Does the average of the residuals $\hat \epsilon$ remain close to 0 across the plot?
Equal Variance: does the spread of the residuals $\hat \epsilon$ remain constant across the predicted values $\hat y$?

Solution

The long way:

# Notice that we create a tibble and pass it directly to ggplot()
# using the %>%.
# This means we don't have to store it as an object in the environment,
# it is just being used to create the plot
tibble(
  residuals = residuals(wb_mdl1),
  fitted = fitted(wb_mdl1)
) %>% 
  ggplot(aes(x = fitted, y = residuals)) + 
  geom_point() + 
  geom_smooth(color="red",se=FALSE)

The quick way:

plot(wb_mdl1, which=1)

The horizontal red line shows that the average of the residual remains close to zero across the fitted values.
The spread of the residuals remains reasonably constant across the fitted values.

Independence

The “independence of errors” assumption is the condition that the errors do not have some underlying relationship which is causing them to influence one another.
There are many sources of possible dependence, and often these are issues of study design. For example, we may have groups of observations in our data which we would expect to be related (e.g., multiple trials from the same participant). Our modelling strategy would need to take this into account.
One form of dependence is autocorrelation - this is when observations influence those adjacent to them. It is common in data for which time is a variable of interest (e.g, the humidity today is dependent upon the rainfall yesterday).

In R we can test against the alternative hypothesis that there is autocorrelation in our errors using the durbinWatsonTest() (an abbreviated function dwt() is also available) in the car package.

Question 5

Perform a test against the alternative hypothesis that there is autocorrelation in the error terms.

Write a sentence summarising whether or not you consider the assumption of independence to have been met (you may have to assume certain aspects of the study design).

Solution

dwt(wb_mdl1)

##  lag Autocorrelation D-W Statistic p-value
##    1       -0.318249      2.600574   0.146
##  Alternative hypothesis: rho != 0

A Durbin-Watson test of autocorrelation failed to reject the null hypothesis that there was no serial dependence in the error ($DW = 2.6$, $p = .138$). We will also assume that observations to be randomly sampled during study recruitment.

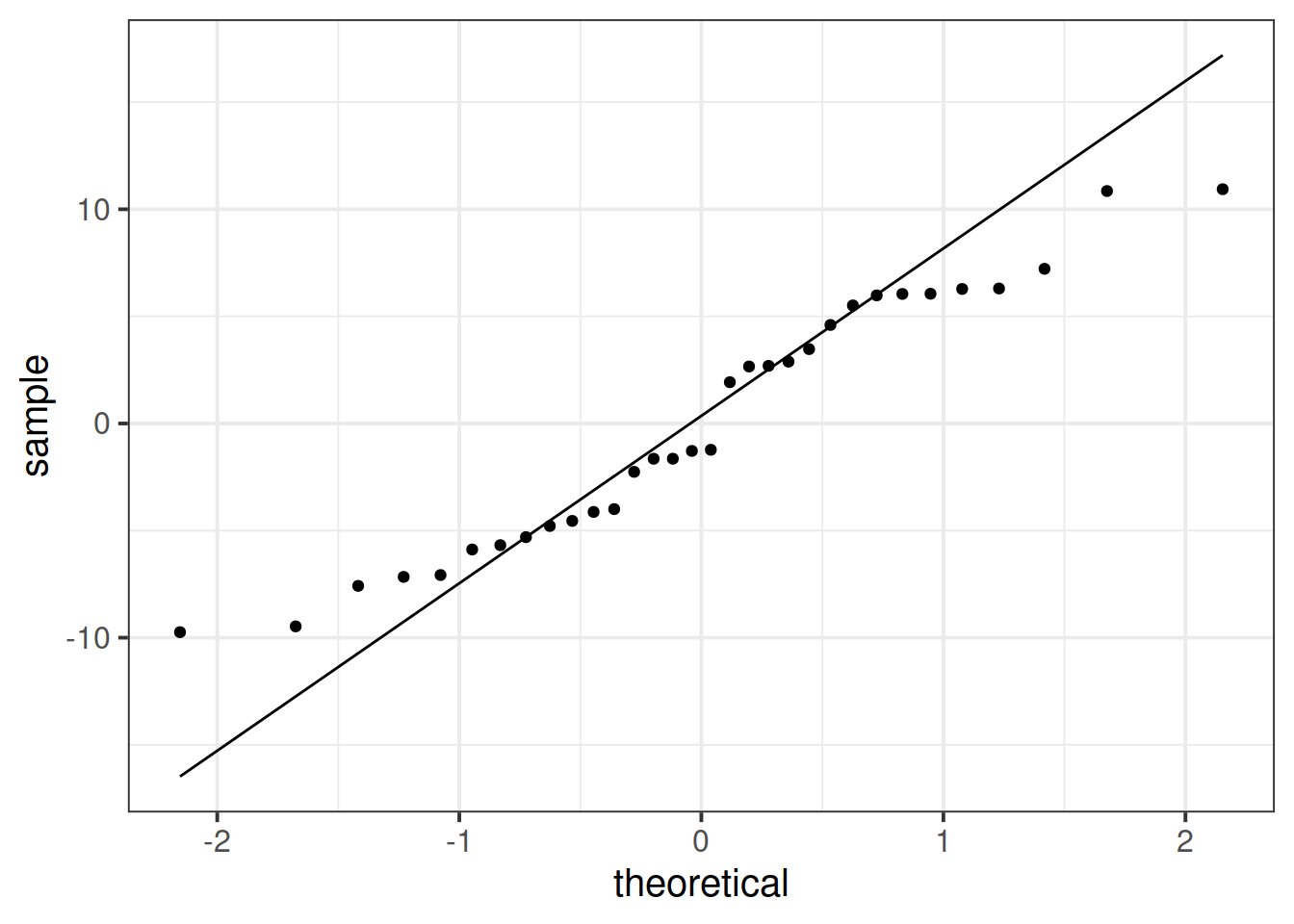
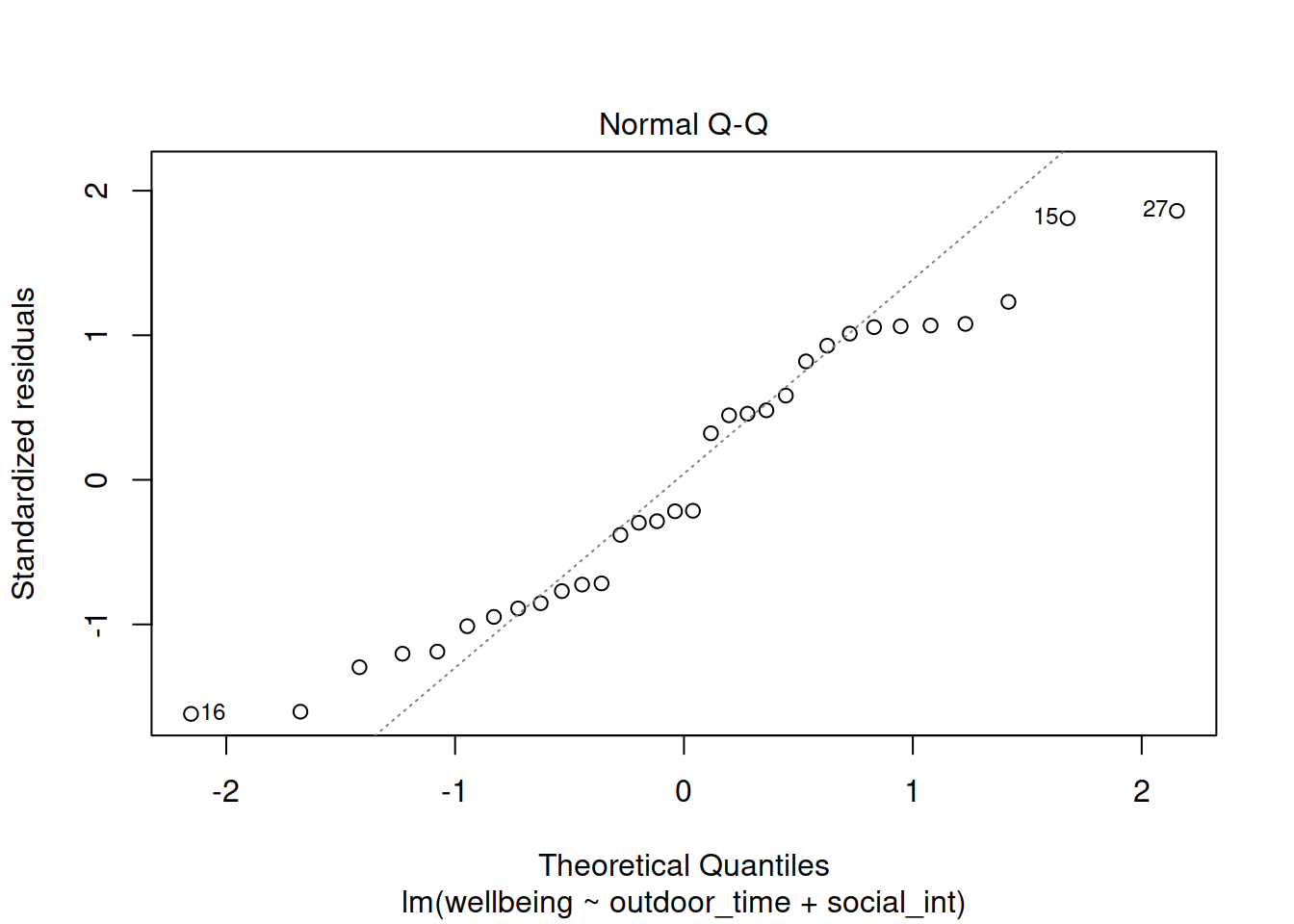
Normality of errors

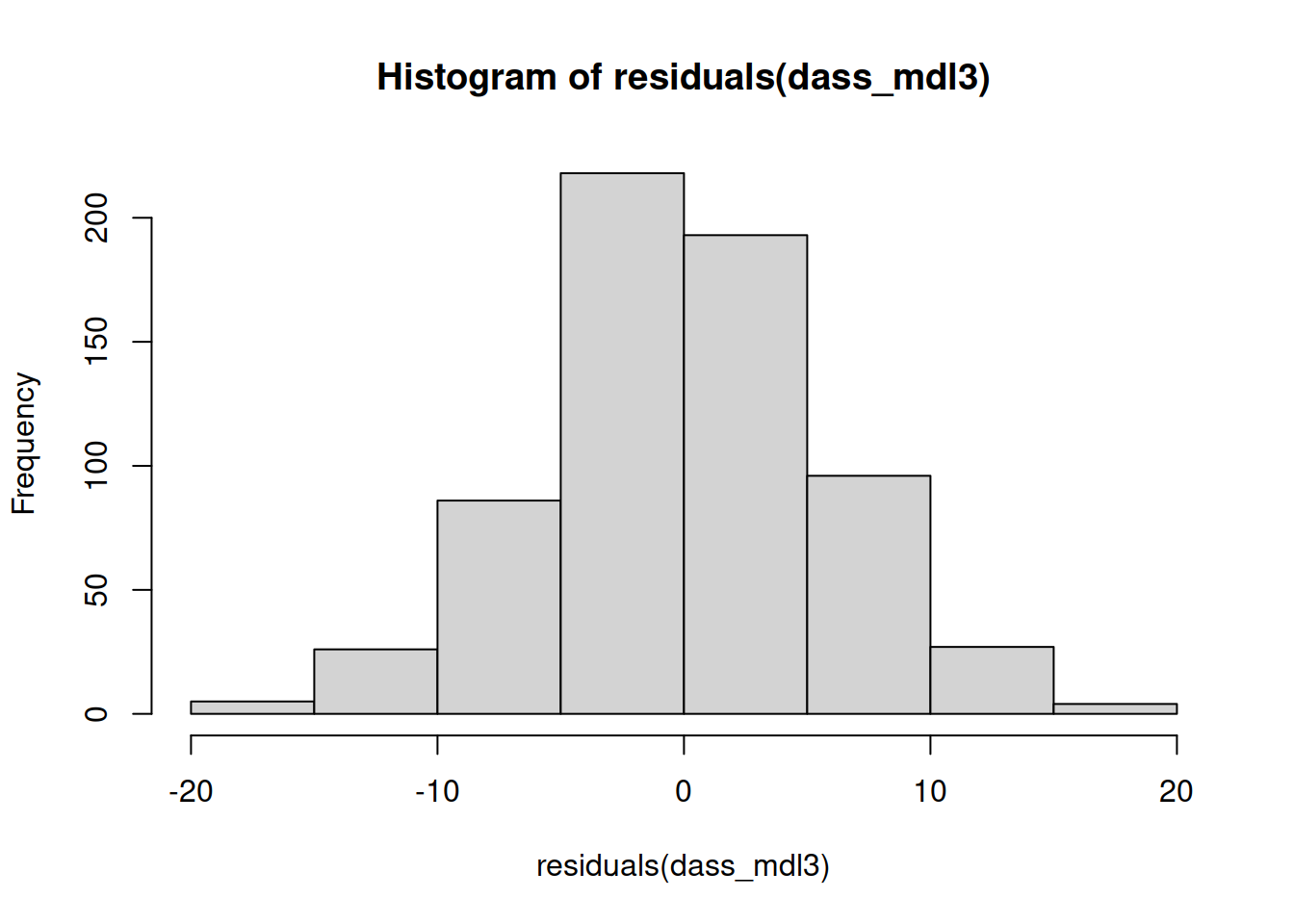
The normality assumption is the condition that the errors $\epsilon$ are normally distributed.

We can visually assess this condition through histograms, density plots, and quantile-quantile plots (QQplots) of our residuals $\hat \epsilon$.
We can also perform a Shapiro-Wilk test against the alternative hypothesis that the residuals were not sampled from a normally distributed population. The shapiro.test() function in R.

Question 6

Assess the normality assumption by producing a qqplot of the residuals (either manually or using plot(model, which = ???)), and conducting a Shapiro-Wilk test.

Write a sentence summarising whether or not you consider the assumption to have been met. Justify your answer with reference to plots and/or formal tests where available.

Solution

We can get the QQplot from one of the plot(model) plots:

plot(wb_mdl1, which = 2)

Or we can make our own:

tibble(
  resids = residuals(wb_mdl1)
) %>% ggplot(aes(sample=resids))+
  geom_qq()+
  geom_qq_line()

shapiro.test(residuals(wb_mdl1))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(wb_mdl1)
## W = 0.94831, p-value = 0.129

The QQplot indicates that the residuals follow close to a normal distribution, although with evidence of heavier tails. A Shapiro-Wilk test failed to reject the null hypothesis that the residuals were drawn from a normally distributed population ($W = 0.95$, $p = .129$)

Multicollinearity

For the linear model with multiple explanatory variables, we need to also think about multicollinearity - this is when two (or more) of the predictors in our regression model are moderately or highly correlated.
Recall our interpretation of multiple regression coefficients as
“the effect of $x_1$ on $y$ when holding the values of $x_2$, $x_3$, … $x_k$ constant”

This interpretation falls down if predictors are highly correlated because if, e.g., predictors $x_1$ and $x_2$ are highly correlated, then changing the value of $x_1$ necessarily entails a change the value of $x_2$ meaning that it no longer makes sense to talk about holding $x_2$ constant.

We can assess multicollinearity using the variance inflation factor (VIF), which for a given predictor $x_j$ is calculated as:
\[ VIF_j = \frac{1}{1-R_j^2} \\ \] Where $R_j^2$ is the coefficient of determination (the R-squared) resulting from a regression of $x_j$ on to all the other predictors in the model ($x_j = x_1 + ... x_k + \epsilon$).
The more highly correlated $x_j$ is with other predictors, the bigger $R_j^2$ becomes, and thus the bigger $VIF_j$ becomes.

The square root of VIF indicates how much the SE of the coefficient has been inflated due to multicollinearity. For example, if the VIF of a predictor variable were 4.6 ($\sqrt{4.6} = 2.1$), then the standard error of the coefficient of that predictor is 2.1 times larger than if the predictor had zero correlation with the other predictor variables. Suggested cut-offs for VIF are varied. Some suggest 10, others 5. Define what you will consider an acceptable value prior to calculating it.

In R, the vif() function from the car package will provide VIF values for each predictor in your model.

Question 7

Calculate the variance inflation factor (VIF) for the predictors in the model.

Write a sentence summarising whether or not you consider multicollinearity to be a problem here.

Solution

vif(wb_mdl1)

## outdoor_time   social_int 
##      1.13023      1.13023

VIF values <5 indicate that multicollinearity is not adversely affecting model estimates.

Individual cases

We have seen in the case of the simple linear regression that individual cases in our data can influence our model more than others. We know about:

Regression outliers: A large residual $\hat \epsilon_i$ - i.e., a big discrepancy between their predicted y-value and their observed y-value.
- Standardised residuals: For residual $\hat \epsilon_i$, divide by the estimate of the standard deviation of the residuals. In R, the rstandard() function will give you these
- Studentised residuals: For residual $\hat \epsilon_i$, divide by the estimate of the standard deviation of the residuals excluding case $i$. In R, the rstudent() function will give you these.
High leverage cases: These are cases which have considerable potential to influence the regression model (e.g., cases with an unusual combination of predictor values).
- Hat values: are used to assess leverage. In R, The hatvalues() function will retrieve these.
High influence cases: When a case has high leverage and is an outlier, it will have a large influence on the regression model.
- Cook’s Distance: combines leverage (hatvalues) with outlying-ness to capture influence. In R, the cooks.distance() function will provide these.

Question 8

Create a new tibble which contains:

The original variables from the model (Hint, what does wb_mdl1$model give you?)
The fitted values from the model $\hat y$
The residuals $\hat epsilon$
The studentised residuals
The hat values
The Cook’s Distance values.

Solution

mdl_diagnost <- 
  tibble(
  wb_mdl1$model,
  fitted = fitted(wb_mdl1),
  resid = residuals(wb_mdl1),
  studres = rstudent(wb_mdl1),
  hats = hatvalues(wb_mdl1),
  cooksd = cooks.distance(wb_mdl1)
)

Question 9

Looking at the studentised residuals, are there any outliers?

Solution

Recall from the lectures, studentised residuals of $>2$ or $< -2$ indicate potential outlyingness.

We can ask R whether the absolute values are $>2$:

abs(mdl_diagnost$studres) > 2

##     1     2     3     4     5     6     7     8     9    10    11    12    13 
## FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE 
##    14    15    16    17    18    19    20    21    22    23    24    25    26 
## FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE 
##    27    28    29    30    31    32 
## FALSE FALSE FALSE FALSE FALSE FALSE

We could filter our newly created tibble to these observations:

mdl_diagnost %>% 
  filter(abs(studres)>2)

## # A tibble: 0 x 8
## # … with 8 variables: wellbeing <dbl>, outdoor_time <dbl>, social_int <dbl>,
## #   fitted <dbl>, resid <dbl>, studres <dbl>, hats <dbl>, cooksd <dbl>

There are zero rows.

Question 10

Looking at the hat values, are there any observations with high leverage?

Solution

Recall from the lectures, hat values of more than $2 \bar{h}$ (2 times the average hat value) are considered high leverage.

The average hat value, $\bar{h}$ is calculated as $\frac{k + 1}{n}$, where $k$ is the number of predictors, and $n$ is the sample size. For our model: \[ \bar h = \frac{k+1}{n} = \frac{2+1}{32} = \frac{3}{32} = 0.094 \]

We can ask whether any of observations have hat values which are greater than $2 \bar h$:

mdl_diagnost %>%
  filter(hats > (2*0.094))

## # A tibble: 0 x 8
## # … with 8 variables: wellbeing <dbl>, outdoor_time <dbl>, social_int <dbl>,
## #   fitted <dbl>, resid <dbl>, studres <dbl>, hats <dbl>, cooksd <dbl>

Note that 0 observations have high leverage.

Question 11

Looking at the Cook’s Distance values, are there any highly influential points?
You can also display these graphically using plot(model, which = 4) and plot(model, which = 5).

Solution

Recall from the lectures that we have a Cook’s Distance cut-off of $\frac{4}{n-k-1}$, where $k$ is the number of predictors, and $n$ is the sample size.
For our model: \[ D_{cutoff} = \frac{4}{n-k-1} = \frac{4}{32 - 2 - 1} = \frac{4}{29} = 0.138 \]

There are no observations which have a high influence on our model estimates:

mdl_diagnost %>%
  filter(cooksd > 0.138)

## # A tibble: 0 x 8
## # … with 8 variables: wellbeing <dbl>, outdoor_time <dbl>, social_int <dbl>,
## #   fitted <dbl>, resid <dbl>, studres <dbl>, hats <dbl>, cooksd <dbl>

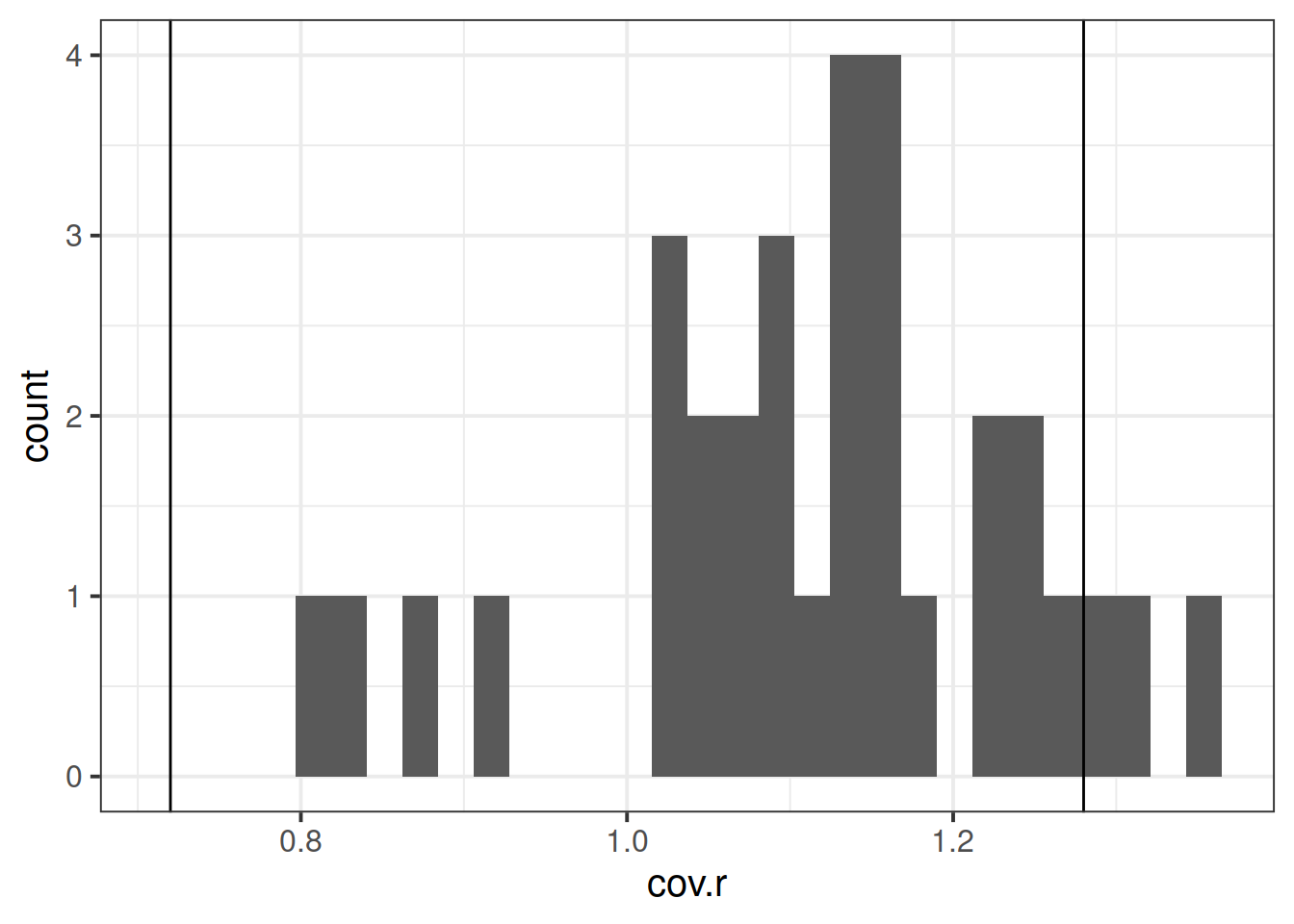
Other influence.measures()

Alongside Cook’s Distance, we can examine the extent to which model estimates and predictions are affected when an entire case is dropped from the dataset and the model is refitted.

DFFit: the change in the predicted value at the $i^{th}$ observation with and without the $i^{th}$ observation is included in the regression.
DFbeta: the change in a specific coefficient with and without the $i^{th}$ observation is included in the regression.
DFbetas: the change in a specific coefficient divided by the standard error, with and without the $i^{th}$ observation is included in the regression.
COVRATIO: measures the effect of an observation on the covariance matrix of the parameter estimates. In simpler terms, it captures an observation’s influence on standard errors.

Question 12

Use the function influence.measures() to extract these delete-1 measures of influence.

Try plotting the distributions of some of these measures.

Tip: the function influence.measures() returns an infl-type object. To plot this, we need to find a way to extract the actual numbers from it.
What do you think names(influence.measures(wb_mdl1)) shows you? How can we use influence.measures(wb_mdl1)$<insert name here> to extract the matrix of numbers?

Solution

influence.measures(wb_mdl1)

## Influence measures of
##   lm(formula = wellbeing ~ outdoor_time + social_int, data = mwdata) :
## 
##      dfb.1_ dfb.otd_ dfb.scl_   dffit cov.r   cook.d    hat inf
## 1   0.43653 -0.11116 -0.32167  0.4477 1.157 0.066470 0.1489    
## 2  -0.28160  0.03170  0.22954 -0.2917 1.225 0.028838 0.1414    
## 3   0.29581  0.07604 -0.29025  0.3540 1.088 0.041520 0.0967    
## 4  -0.26445 -0.13055  0.29341 -0.3508 1.117 0.040991 0.1071    
## 5  -0.27084  0.22733  0.10472 -0.3290 1.279 0.036700 0.1766    
## 6   0.12462 -0.02693 -0.08288  0.1460 1.141 0.007277 0.0604    
## 7  -0.17361 -0.03392  0.15313 -0.2235 1.087 0.016770 0.0597    
## 8  -0.02879 -0.07259  0.06069 -0.0918 1.309 0.002906 0.1556    
## 9   0.16925  0.08820 -0.17834  0.2477 1.088 0.020553 0.0668    
## 10 -0.24768  0.33112 -0.00551 -0.4267 1.027 0.059217 0.0956    
## 11 -0.02018 -0.02535  0.02534 -0.0492 1.166 0.000834 0.0518    
## 12  0.04644  0.38731 -0.22045  0.4474 1.164 0.066462 0.1517    
## 13 -0.15606  0.21587 -0.02477 -0.3135 1.017 0.032241 0.0626    
## 14  0.13390 -0.31537  0.10705  0.3905 1.039 0.049887 0.0899    
## 15  0.14774 -0.25595  0.08688  0.4273 0.815 0.055918 0.0487    
## 16 -0.11881  0.17855 -0.06061 -0.3502 0.873 0.038519 0.0422    
## 17  0.00121 -0.07684  0.02608 -0.1031 1.177 0.003653 0.0703    
## 18  0.00329  0.04637 -0.01574  0.0739 1.159 0.001877 0.0516    
## 19  0.04301 -0.15310  0.09227  0.2432 1.055 0.019693 0.0546    
## 20  0.05819 -0.10961 -0.03803 -0.2189 1.065 0.016025 0.0508    
## 21 -0.01498  0.00131  0.03428  0.0875 1.131 0.002622 0.0380    
## 22  0.12553 -0.15510 -0.09098 -0.3084 1.020 0.031247 0.0622    
## 23 -0.03324 -0.00580  0.05840  0.1049 1.138 0.003770 0.0466    
## 24  0.24606 -0.23731 -0.18568 -0.4783 0.911 0.071967 0.0774    
## 25  0.06123  0.10878 -0.16017 -0.2209 1.131 0.016498 0.0771    
## 26 -0.02732 -0.29363  0.23790  0.3643 1.243 0.044752 0.1666    
## 27 -0.30514  0.33726  0.20108  0.5966 0.830 0.108234 0.0858    
## 28  0.06176 -0.07036 -0.03455 -0.1080 1.263 0.004013 0.1280    
## 29 -0.15327 -0.04611  0.23001  0.3039 1.067 0.030646 0.0754    
## 30  0.11226  0.25745 -0.30386 -0.3826 1.238 0.049262 0.1686    
## 31 -0.07637 -0.05313  0.12879  0.1542 1.214 0.008153 0.1047    
## 32  0.10249 -0.07000 -0.07662 -0.1399 1.353 0.006736 0.1864   *

Let’s plot the distribution of COVRATIO statistics.
Recall that values which are $>1+\frac{3(k+1)}{n}$ or $<1-\frac{3(k+1)}{n}$ are considered as having strong influence.
For our model: \[ 1 \pm \frac{3(k+1)}{n} \quad = \quad 1 \pm\frac{3(2+1)}{32} \quad = \quad 1\pm \frac{9}{32} \quad = \quad 1\pm0.28 \]

The “infmat” bit of an infl-type object contains the numbers. To use it with ggplot, we will need to turn it into a dataframe (as.data.frame()), or a tibble (as_tibble()):

infdata <- influence.measures(wb_mdl1)$infmat %>%
  as_tibble()

ggplot(data = infdata, aes(x = cov.r)) + 
  geom_histogram() +
  geom_vline(aes(xintercept = c(1-0.28)))+
  geom_vline(aes(xintercept = c(1+0.28)))

It looks like a few observations may be having quite a high influence here. This is perhaps not that surprising as we only have 32 datapoints.

Less guided exercises

Question 13

Create a new section header in your Rmarkdown document, as we are moving onto a different dataset.

The code below loads the dataset of 656 participants’ scores on Big 5 Personality traits, perceptions of social ranks, and scores on a depression and anxiety scale.

scs_study <- read_csv("https://uoepsy.github.io/data/scs_study.csv")

Fit the following interaction model:
- $\text{DASS-21 Score} = \beta_0 + \beta_1 \cdot \text{SCS Score} + \beta_2 \cdot \text{Neuroticism} + \beta_3 \cdot \text{SCS score} \cdot \text{Neuroticism} + \epsilon$
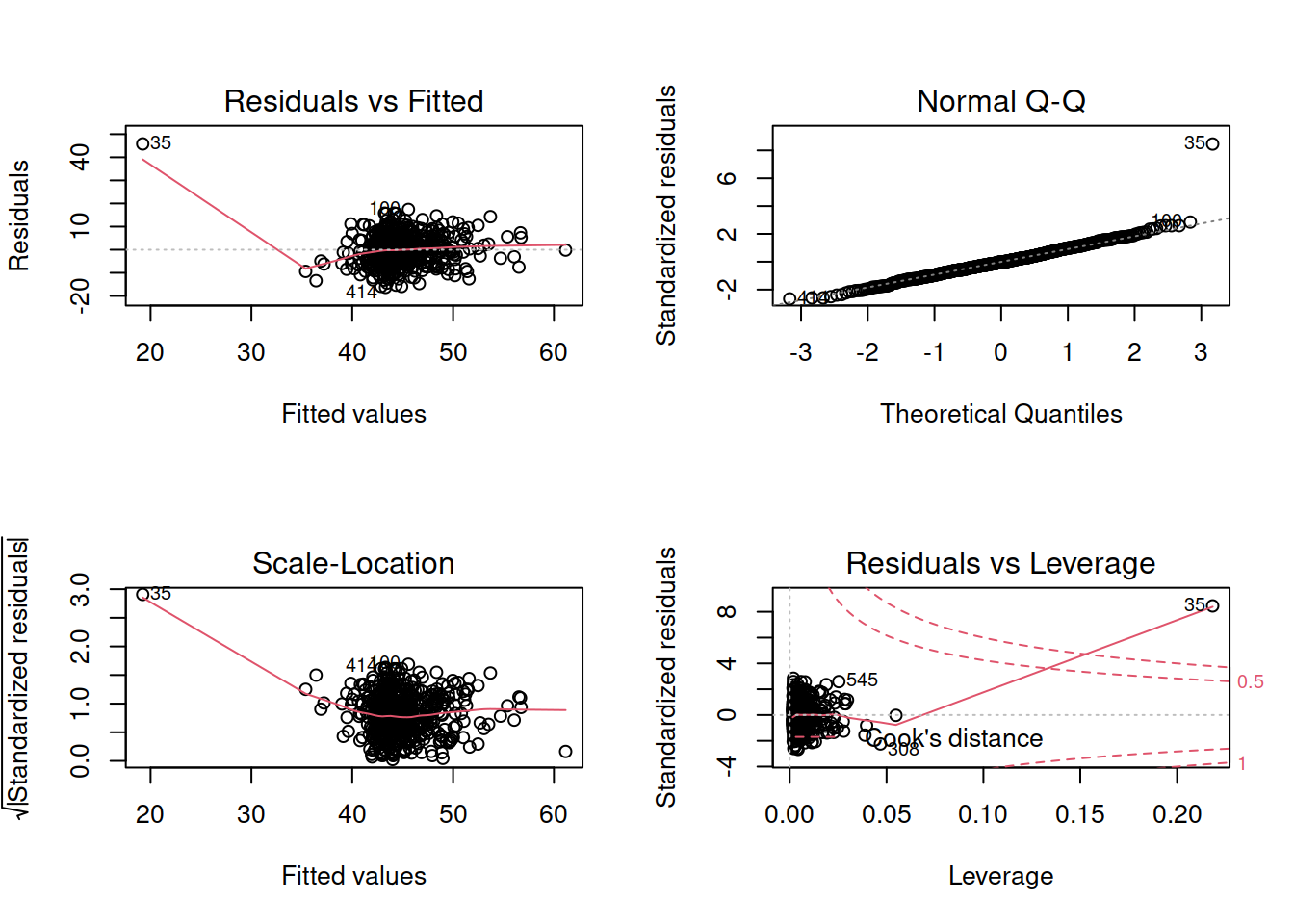
Check that the model meets the assumptions of the linear model (Tip: to get a broad overview you can pass your model to the plot() function to get a series of plots).
If you notice any violated assumptions:
- address the issues by, e.g., excluding observations from the analysis, or replacing outliers with the next most extreme value (Winsorisation).
- after fitting a new model which you hope addresses violations, you need to check all of your assumptions again. It can be an iterative process, and the most important thing is that your final model (the one you plan to use) meets all the assumptions.

Tips:

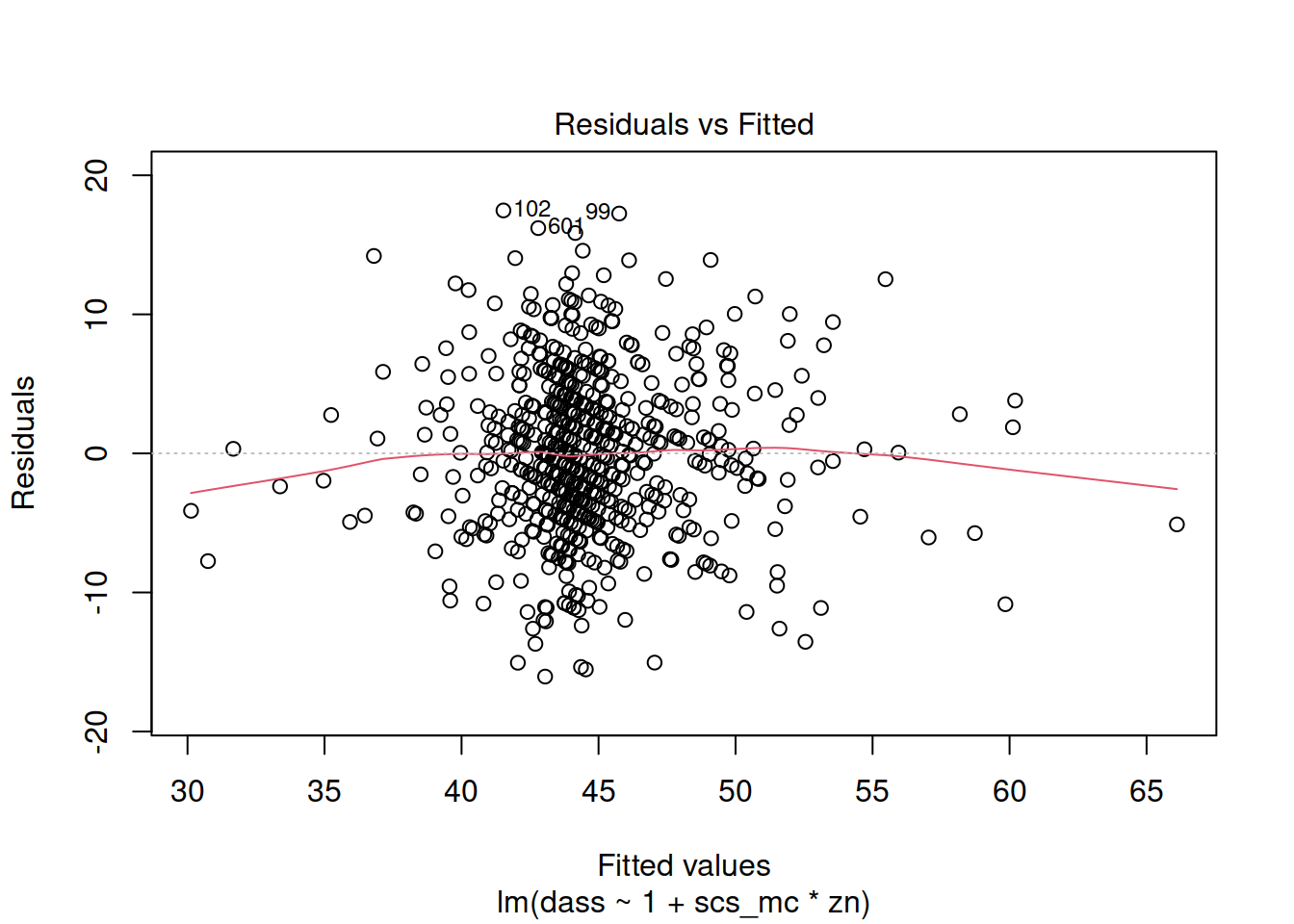
When there is an interaction in the model, assessing linearity becomes difficult. In fact, crPlots() will not work. To assess, you can create a residuals-vs-fitted plot like we saw in the guided exercises above.
Interaction terms often result in multicollinearity, because these terms are made up of the product of some ‘main effects.’ Mean-centering the variables like we have here will reduce this source of structural multicollinearity (“structural” here refers to the fact that multicollinearity is due to our model specification, rather than the data itself)
You can fit a model and exclude specific observations. For instance, to remove the 3rd and 5th rows of the dataset: lm(y ~ x1 + x2, data = dataset[-c(3,5),]). Be careful to remember that these values remain in the dataset, they have simply been excluded from the model fit.

Solution

We’re going to mean-center the scs variable from the outset.

scs_study <- read_csv("https://uoepsy.github.io/data/scs_study.csv")  

scs_study <-
  scs_study %>%
  mutate(
    scs_mc = scs - mean(scs)
  )

dass_mdl2 <- lm(dass ~ 1 + scs_mc * zn, data = scs_study)

plot(dass_mdl2)

From quick visual inspection, it looks like there is at least one very influential point, which has been labelled for us as case number 35.

scs_study[35,]

## # A tibble: 1 x 8
##      zo    zc    ze     za    zn   scs  dass scs_mc
##   <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>  <dbl>
## 1 0.645 -1.49 0.970 -0.121  2.24    54    65   18.2

The code below fits a new model and assigns it the name dass_mdl3. How is it different from the previous model?

dass_mdl3 <- lm(dass ~ 1 + scs_mc * zn, data = scs_study[-35, ])

Does this new model meet the assumptions of multiple regression?

Linearity

plot(dass_mdl3, which = 1)

Equal variances (Homoscedasticity)

residualPlots(dass_mdl3)

##            Test stat Pr(>|Test stat|)
## scs_mc        1.6260           0.1044
## zn           -0.5074           0.6121
## Tukey test   -1.3170           0.1878

ncvTest(dass_mdl3)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.3706851, Df = 1, p = 0.54263

Independence of errors

# we assume independence of observations was considered during study design (e.g., participants are not related, or influence one another in some way). We can test for autocorrelation:
durbinWatsonTest(dass_mdl3)

##  lag Autocorrelation D-W Statistic p-value
##    1     -0.04018765      2.079286    0.34
##  Alternative hypothesis: rho != 0

Normality

hist(residuals(dass_mdl3))

shapiro.test(residuals(dass_mdl3))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(dass_mdl3)
## W = 0.99762, p-value = 0.4801

Check for multicollinearity

vif(dass_mdl3)

##    scs_mc        zn scs_mc:zn 
##  1.010026  1.010174  1.000240

Assumptions & Diagnostics

Refresher: LM assumptions

Guided exercises

Linearity

Equal variances (Homoscedasticity)

Independence

Normality of errors

Multicollinearity

Individual cases

Other influence.measures()

Less guided exercises