Sample Size and Power Analysis

Learning Objectives

At the end of this lab, you will:

1. Understand how varying factors can influence power
2. Be able to conduct power analyses using the pwr package

What You Need

1. Be up to date with lectures

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

• tidyverse
• kableExtra
• pwr

Presenting Results

All results should be presented following APA guidelines. If you need a reminder on how to hide code, format tables/plots, etc., make sure to review the rmd bootcamp.

The example write-up sections included as part of the solutions are not perfect - they instead should give you a good example of what information you should include and how to structure this. Note that you must not copy any of the write-ups included below for future reports - if you do, you will be committing plagiarism, and this type of academic misconduct is taken very seriously by the University. You can find out more here.

Lab Data

You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/recall_med_coast.csv

Study Overview

Research Question

Do age and intervention type influence recall?

Recall Codebook

Description

A sample of 100 individuals aged 18-75 years old was randomly allocated to one of two intervention groups, and completed a free-recall test after their intervention. There were two types of intervention - exciting (1-hour long roller-coaster session; group = 0) or relaxing (1-hour long meditation session; group = 1).

Data Dictionary

variable	description
perc_recall	Percentage Recall - the percentage of correctly recalled items
group	Group - whether the individual was assigned to the roller-coaster (group = 0) or the meditation (group = 1) intervention condition
age	Age - individual's age (in years)

Preview

The first six rows of the data are:

perc_recall	group	age
47.42891	0	52
61.44327	1	37
50.08974	0	46
56.44092	1	72
57.04786	1	46
46.11492	0	69

Setup

Setup

1. Create a new RMarkdown file
2. Load the required package(s)
3. Read in the recall_med_coast dataset into R, assigning it to an object named recdata

Solution

#load packages
library(tidyverse)
library(kableExtra)
library(pwr)

#read in data
recdata <- read_csv("https://uoepsy.github.io/data/recall_med_coast.csv")

Exercises

Study Overview & Data Management

Question 1

First, provide a brief overview of the study design and data.

Next examine the dataset, and perform any necessary and appropriate data management steps.

Solution

Study design and data

The recdata dataset contained information on 100 hypothetical participants who participated in a between-subjects experiment exploring the associations among recall, age, and intervention type. Participants were aged 18-75 years old, and were randomly allocated to one of two intervention groups (exciting - 1-hour long roller-coaster session; or relaxing - 1-hour long meditation session) before completing a free-recall test (% correct).

Data checks & management

#look at structure of data:
str(recdata)

spc_tbl_ [100 × 3] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ perc_recall: num [1:100] 47.4 61.4 50.1 56.4 57 ...
 $ group      : num [1:100] 0 1 0 1 1 0 1 1 1 0 ...
 $ age        : num [1:100] 52 37 46 72 46 69 70 53 41 26 ...
 - attr(*, "spec")=
  .. cols(
  ..   perc_recall = col_double(),
  ..   group = col_double(),
  ..   age = col_double()
  .. )
 - attr(*, "problems")=<externalptr> 

#check for NAs - there are none - all FALSE:
table(is.na(recdata))

FALSE 
  300 

#Group should be a factor:
recdata$group <- factor(recdata$group, 
                        levels = c(0, 1), 
                        labels = c('rollercoaster', 'meditation'))

The ‘group’ variable denoting which intervention type participants were allocated to was coded as a factor with two levels - ‘rollercoaster’ and ‘meditation’, where ‘rollercoaster’ was designated as the reference group. There were no NAs contained within the dataset, and recall scores were within range (i.e., within possible values of 0-100), as were ages (i.e., all ages ranged from 18-75).

Descriptive Statistics & Visualisations

Question 2

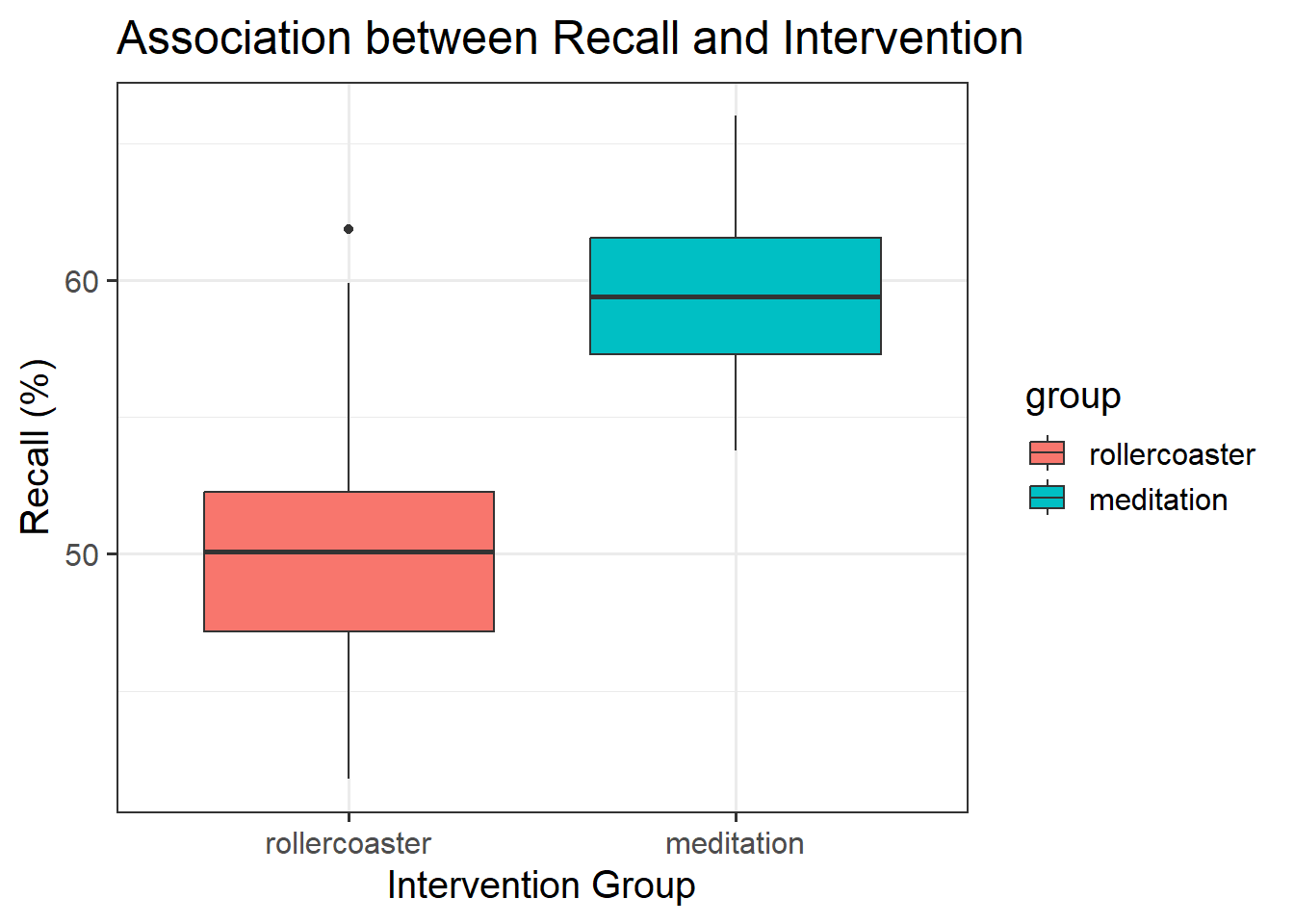
Provide a table of descriptive statistics and visualise your data.

Remember to interpret these in the context of the study.

Hint

1. For your table of descriptive statistics, both the group_by() and summarise() functions will come in handy here.
2. Recall that when visualising a continuous outcome across groups, geom_boxplot() may be most appropriate to use.
3. Make sure to comment on any observed differences among the sample means of the four treatment conditions.

Solution

Numeric

Descriptive statistics presented in a well formatted table:

recall_stats <- recdata %>%
    group_by(group) %>%
    summarise(
       n = n(),
       M_Age = mean(age),
       SD_Age = sd(age),
       M_Recall = mean(perc_recall)
       ) %>%
    kable(caption = "Descriptive Statistics", digits = 2) %>%
    kable_styling()

recall_stats

Table 1: Descriptive Statistics

group	n	M_Age	SD_Age	M_Recall
rollercoaster	53	47.85	14.93	50.11
meditation	47	46.57	15.29	59.46

Visual

We can visually explore the association between Recall and the two predictor variables as follows:

Recall & Intervention Group

recall_plt1 <- ggplot(data = recdata, aes(x = group, y = perc_recall, fill = group)) +
    geom_boxplot() + 
    labs(x = "Intervention Group", y = "Recall (%)", title = "Association between Recall and Intervention")
recall_plt1

Figure 1: Association between Recall and Intervention Group

Recall & Age

recall_plt2 <- ggplot(data = recdata, aes(x = age, y = perc_recall)) +
    geom_point() + 
    geom_smooth(method = "lm", se = FALSE) + 
    labs(x = "Age (in years)", y = "Recall (%)", title = "Association between Recall and Age")
recall_plt2

Figure 2: Association between Recall and Age

From Table 1, Figure 1, and Figure 2 we can see:

• there were more participants in the rollercoaster condition than meditation
  
• participants in the meditation condition had higher recall scores than those in the rollercoaster condition
  
• there was less variability in scores in the meditation condition in comparison to the rollercoaster condition
  
• older age appeared to be associated with lower recall scores

Question 3

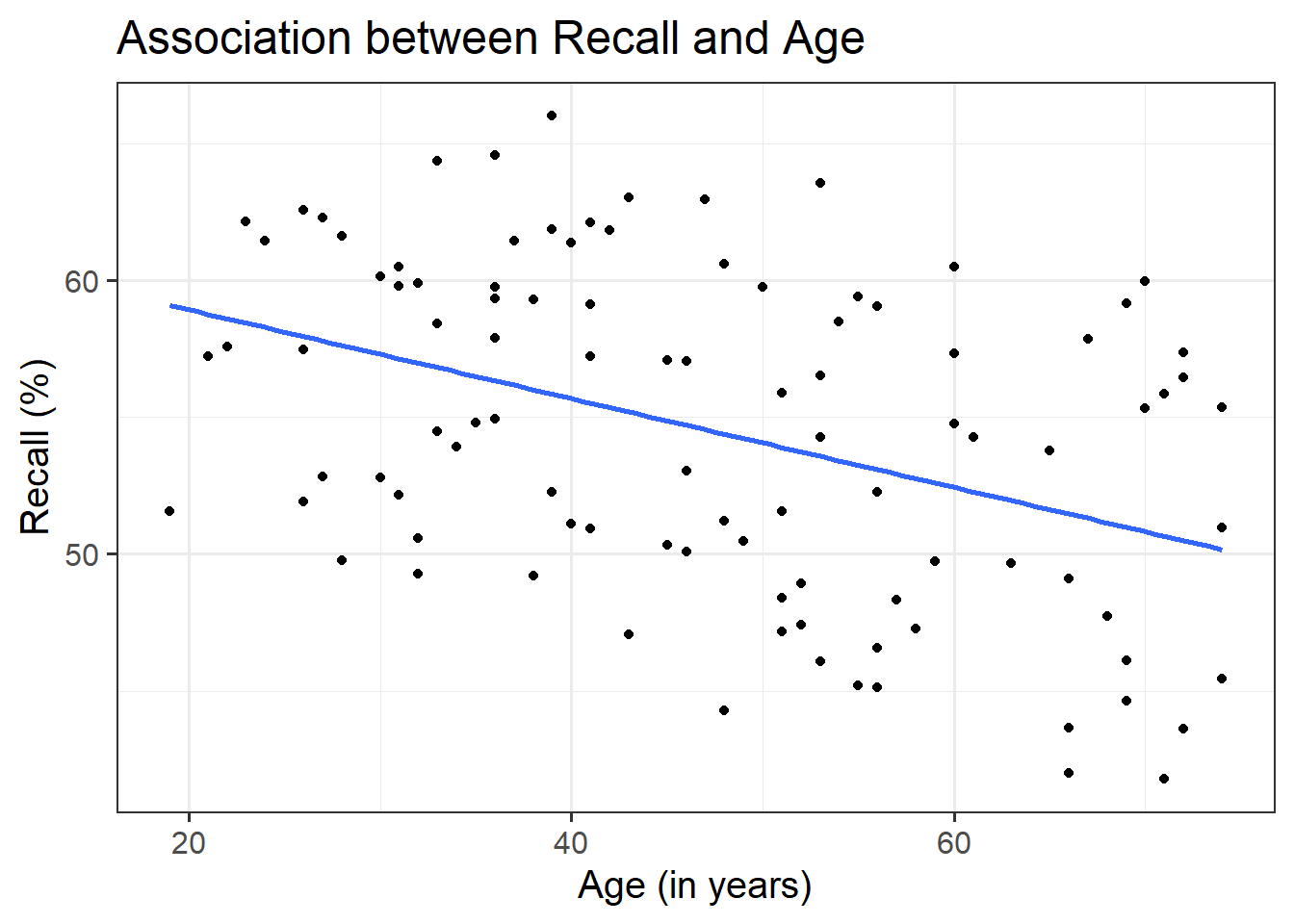
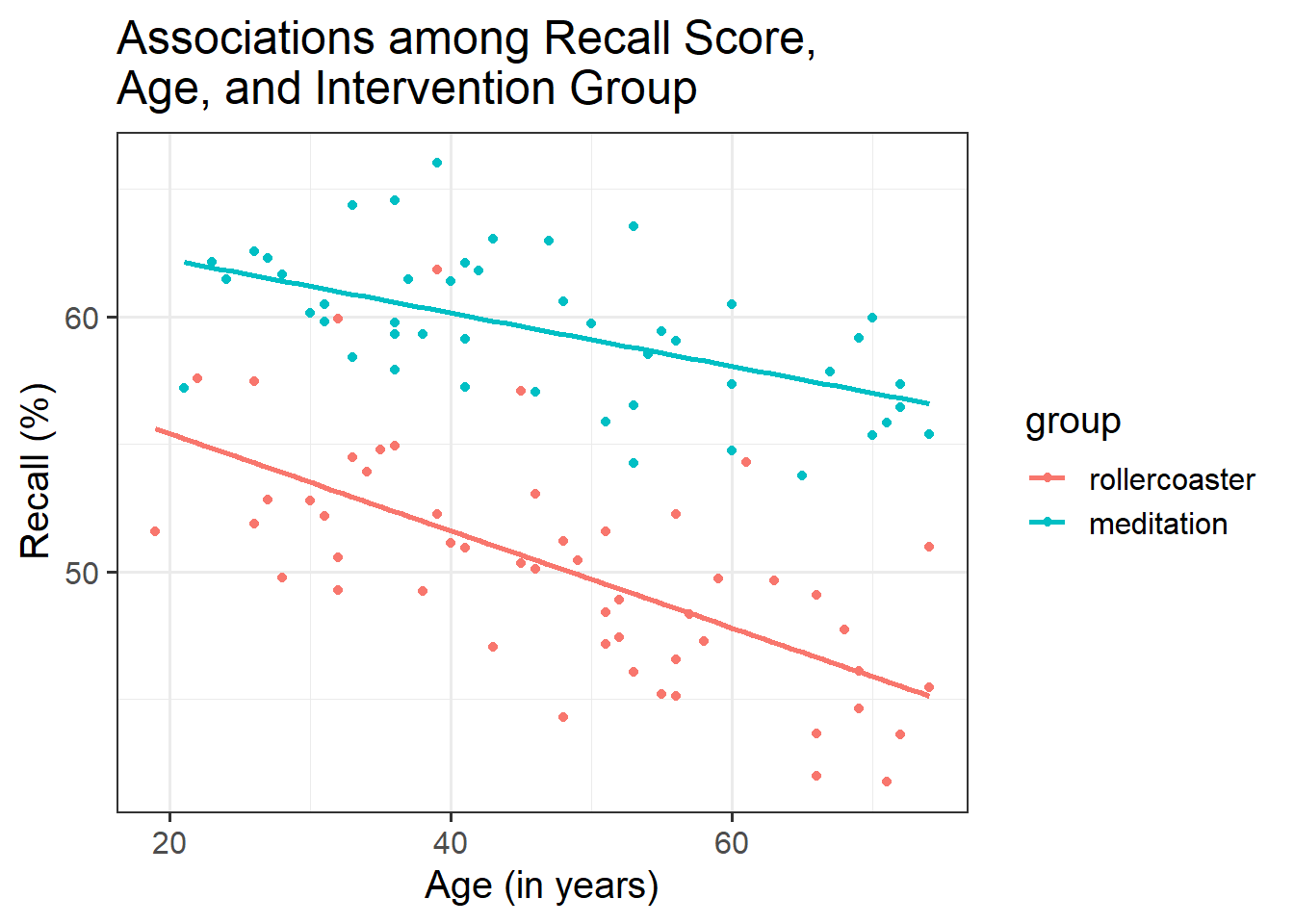
Use a scatterplot to visualise the association between recall and age by group.

Is there any evidence of an interaction between age and group?

Hint

• It might be useful to specify the color = argument for your grouping variable
• Consider using geom_smooth() to superimpose the best-fitting line describing the association of interest for each intervention group.

Solution

recall_plt3 <- ggplot(data = recdata, aes(x = age, y = perc_recall, color = group)) +
    geom_point() + 
    geom_smooth(method = "lm", se = FALSE) + 
    labs(x = "Age (in years)", y = "Recall (%)", title = "Associations among Recall Score, \nAge, and Intervention Group")
recall_plt3

Figure 3: Scatterplot displaying the association between age, intervention group, and recall

The slope in Figure 3 appears to be stepper in the roller coaster intervention group than the meditation group - this suggested that there could be an interaction.

Sample Size & Power

Question 4

Using a significance level (\(\alpha\)) of .05, what sample size (\(n\)) would you require to check whether any of the predictors (including their interaction) influenced recall scores with a 90% chance?

Because you do not know the effect size, assume Cohen’s guideline for linear regression and, to be on the safe side, consider the ‘small’ value.

Hint

In linear regression, the relevant function in R is:

pwr.f2.test(u = , v = , f2 = , sig.level = , power = )

Where:

• u = numerator degrees of freedom = number predictors in the model (\(k\))
• v = denominator degrees of freedom = \(v = n-k-1\)
• f2 = effect size. Cohen suggests effect size cut-off values of \(.02\) (small), \(.15\) (moderate), and \(.35\) (large)
• sig.level = significance level
• power = level of power

where one of the above the parameters - u, v, f2,power, or sig.level - must be passed as NULL (or in other words not specified), as that parameter will be determined from the others.

Solution

k <- 3
f2 <- .02
pwr.f2.test(u = k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 3
              v = 708.495
             f2 = 0.02
      sig.level = 0.05
          power = 0.9

A power analysis for a multiple regression model \((k = 3)\) was conducted (via the pwr package) to determine the minimum sample size using an \(\alpha\) = .05, power = .90, and small effect size \((f^2 = .02)\). The required sample size is \(n = \text v + k + 1 = 709 + 3 + 1 = 713\).

Question 5

Using the same \(\alpha\) and power, what would be the sample size if you assumed effect size to be ‘medium’?

Hint

In linear regression, the relevant function in R is:

pwr.f2.test(u = , v = , f2 = , sig.level = , power = )

Where:

• u = numerator degrees of freedom = number predictors in the model (\(k\))
• v = denominator degrees of freedom = \(v = n-k-1\)
• f2 = effect size. Cohen suggests effect size cut-off values of \(.02\) (small), \(.15\) (moderate), and \(.35\) (large)
• sig.level = significance level
• power = level of power

where one of the above the parameters - u, v, f2,power, or sig.level - must be passed as NULL (or in other words not specified), as that parameter will be determined from the others.

Solution

k <- 3
f2 <- .15
pwr.f2.test(u = k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 3
              v = 94.48157
             f2 = 0.15
      sig.level = 0.05
          power = 0.9

A power analysis for a multiple regression model \((k = 3)\) was conducted (via the pwr package) to determine the minimum sample size using an \(\alpha\) = .05, power = .90, and moderate effect size \((f^2 = .15)\). The required sample size is \(n = \text v + k + 1 = 95 + 3 + 1 = 99\).

Question 6

Using the same \(\alpha\) and power, what would be the sample size if you assumed effect size to be ‘large’?

Hint

In linear regression, the relevant function in R is:

pwr.f2.test(u = , v = , f2 = , sig.level = , power = )

Where:

• u = numerator degrees of freedom = number predictors in the model (\(k\))
• v = denominator degrees of freedom = \(v = n-k-1\)
• f2 = effect size. Cohen suggests effect size cut-off values of \(.02\) (small), \(.15\) (moderate), and \(.35\) (large)
• sig.level = significance level
• power = level of power

where one of the above the parameters - u, v, f2,power, or sig.level - must be passed as NULL (or in other words not specified), as that parameter will be determined from the others.

Solution

k <- 3
f2 <- .35
pwr.f2.test(u = k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 3
              v = 40.61744
             f2 = 0.35
      sig.level = 0.05
          power = 0.9

A power analysis for a multiple regression model \((k = 3)\) was conducted (via the pwr package) to determine the minimum sample size using an \(\alpha\) = .05, power = .90, and large effect size \((f^2 = .35)\). The required sample size is \(n = \text v + k + 1 = 41 + 3 + 1 = 45\).

Question 7

Fit the following model using lm(), and assign it as an object with the name “recall_mdl1”.

\[ \text{Recall} = \beta_0 + \beta_1 \cdot Age + \epsilon \\ \]

How much variance in recall scores does the model explain?

Solution

recall_mdl1 <- lm(perc_recall ~ age, data = recdata)
summary(recall_mdl1)

Call:
lm(formula = perc_recall ~ age, data = recdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.0850  -4.7474   0.7331   4.6758  10.1733 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 62.16336    1.81984  34.159  < 2e-16 ***
age         -0.16206    0.03672  -4.414 2.61e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.494 on 98 degrees of freedom
Multiple R-squared:  0.1658,    Adjusted R-squared:  0.1573 
F-statistic: 19.48 on 1 and 98 DF,  p-value: 2.614e-05

We can see both the R-squared and Adjusted R-squared from the model summary() output. We can use either since we only have a single predictor. To be conservative, we might want to use the adjusted R-squared (0.16).

The model, with Age as a single predictor, explained approximately 16% of the variance in recall scores.

Question 8

Imagine you found the R-squared that you computed above (Q7) in a paper, and you are using that to base your next study.

A researcher believes that the inclusion of intervention group and its interaction with age should explain an extra 50% of the variation in recall scores.

Using a significance level of 5%, what sample size should you use for your next data collection in order to discover that effect with a power of 0.90?

Solution

# restricted model m - number of predictors & R-squared
k <- 1
R2m <- 0.16

# full model M - number of predictors & R-squared
K <- 3
R2M <- 0.16 + 0.5

# effect size - calculate f2
f2 <- (R2M - R2m) / (1 - R2M)

#run test
pwr.f2.test(u = K - k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 2
              v = 9.211914
             f2 = 1.470588
      sig.level = 0.05
          power = 0.9

The sample size should be:

\[ n = \text v + K + 1 \quad \quad n = 10 + 3 + 1 \quad \quad n = 14 \]

With such a big effect size, don’t be surprised it’s so small. When the effect size is much smaller, that will be harder to detect and you will require a bigger sample size.

Question 9

Suppose that the aforementioned researcher made a mistake, and issues a corrected statement in which they state that the inclusion of intervention group and its interaction with age should explain an extra 5% of the variation in recall scores.

Using a significance level of 5%, what sample size should you use for your next data collection in order to discover that effect with a power of 0.90?

Solution

# restricted model m - number of predictors & R-squared
k <- 1
R2m <- 0.16

# full model M - number of predictors & R-squared
K <- 3
R2M <- 0.16 + 0.05

# effect size - calculate f2
f2 <- (R2M - R2m) / (1 - R2M)

# run test
pwr.f2.test(u = K - k, f2 = f2, sig.level = 0.05, power = 0.9)

     Multiple regression power calculation 

              u = 2
              v = 199.9608
             f2 = 0.06329114
      sig.level = 0.05
          power = 0.9

The sample size should be:

\[ n = \text v + K + 1 \quad \quad n = 200 + 3 + 1 \quad \quad n = 204 \]

With such a small effect size, we need a bigger sample size for us to detect it with high confidence.

Question 10

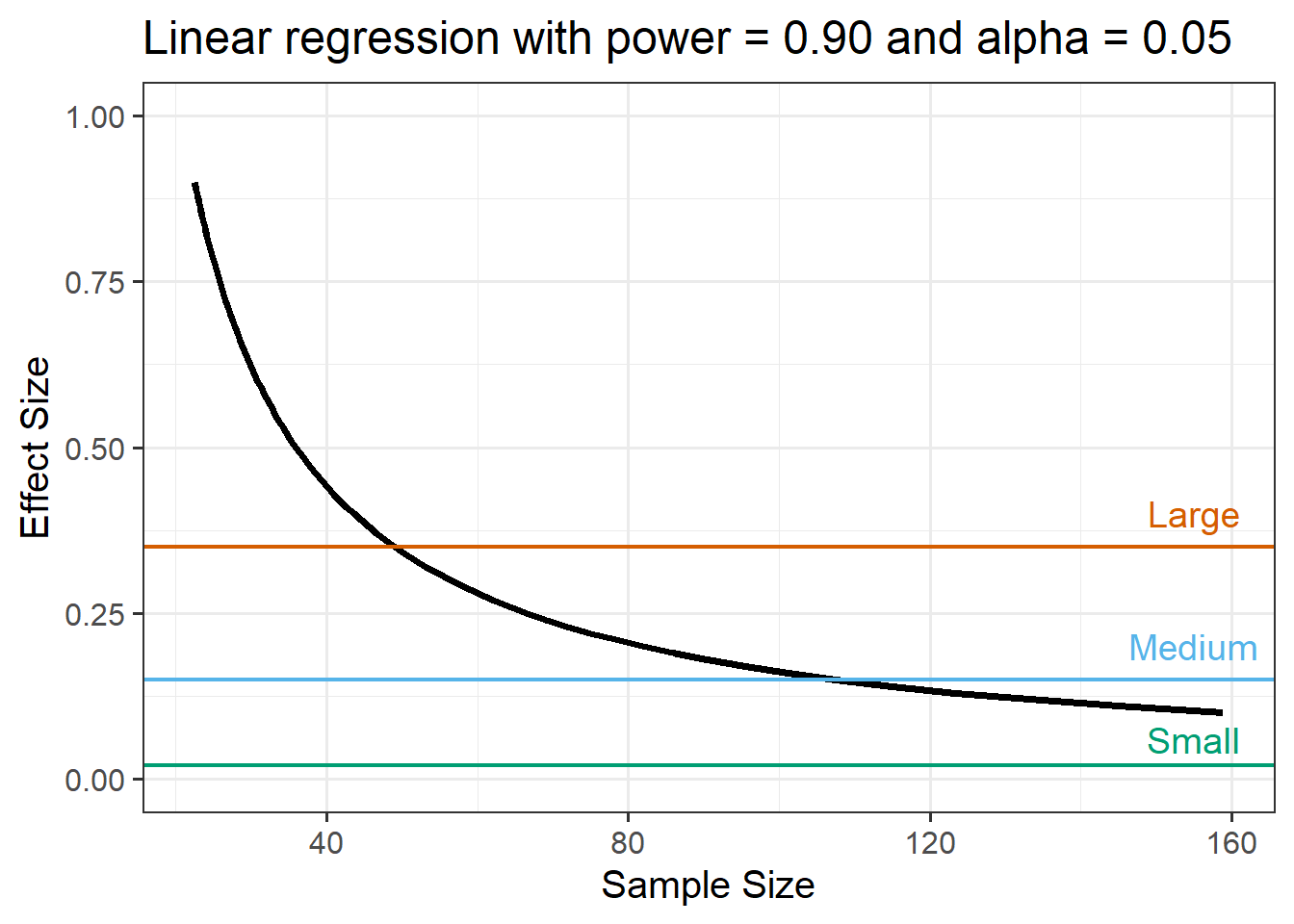
A colleague produces a visualisation of the joint relationship between sample size and effect size via a power curve (with coloured lines representing large, medium, and small effect sizes).

Based on this, what feedback/comments might you share with them regarding sample size for their prospective study, and its relation to effect size?

Figure 4: Linear Regression with power = 0.90 and alpha = 0.05

Solution

From Figure 4, to detect a large effect size (red line), they should aim to recruit ~50 participants, for a medium effect size ~100 (blue line). It is impossible to judge how many participants would be required to detect a small effect size (green line) - we would suggest that they conduct their own power calculation as it is too difficult to judge based on the figure alone.

Generally, if they want to be able to detect a medium-large effect with 90% power using \(\alpha = .05\), it appears that there is little gain in recruiting a sample size > ~110. However, if they want to be able to detect a small effect with 90% power using \(\alpha = .05\), they are likely going to require a very large sample size.

To summarise the association between effect size and sample size, it appears that the smaller the effect you are trying to detect, the larger the sample size you will require.

Compile Report

Compile Report

Knit your report to PDF, and check over your work. To do so, you should make sure:

• Only the output you want your reader to see is visible (e.g., do you want to hide your code?)
• Check that the tinytex package is installed
• Ensure that the ‘yaml’ (bit at the very top of your document) looks something like this:

---
title: "this is my report title"
author: "B1234506"
date: "07/09/2024"
output: bookdown::pdf_document2
---

What to do if you cannot knit to PDF

If you are having issues knitting directly to PDF, try the following:

• Knit to HTML file
  
• Open your HTML in a web-browser (e.g. Chrome, Firefox)
  
• Print to PDF (Ctrl+P, then choose to save to PDF)
  
• Open file to check formatting

Hiding Code and/or Output

Hiding R Code

To not show the code of an R code chunk, and only show the output, write:

```{r, echo=FALSE}
# code goes here
```

Hiding R Output

To show the code of an R code chunk, but hide the output, write:

```{r, results='hide'}
# code goes here
```

Hiding R Code and Output

To hide both code and output of an R code chunk, write:

```{r, include=FALSE}
# code goes here
```

Tinytex

You must make sure you have tinytex installed in R so that you can “Knit” your Rmd document to a PDF file:

install.packages("tinytex")
tinytex::install_tinytex()

Solution

You should end up with a PDF file. If you have followed the above instructions and still have issues with knitting, speak with a Tutor.