| variable | description |
|---|---|
| age | Age in years of respondent |
| outdoor_time | Self report estimated number of hours per week spent outdoors |
| social_int | Self report estimated number of social interactions per week (both online and in-person) |
| routine | Binary 1=Yes/0=No response to the question 'Do you follow a daily routine throughout the week?' |
| wellbeing | Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70 |
| location | Location of primary residence (City, Suburb, Rural) |
| steps_k | Average weekly number of steps in thousands (as given by activity tracker if available) |
Model Fit and Comparisons
Learning Objectives
At the end of this lab, you will:
- Understand how to calculate the interpret \(R^2\) and adjusted-\(R^2\) as a measure of model quality.
- Understand the calculation and interpretation of the \(F\)-test of model utility.
- Understand measures of model fit using F.
- Understand the principles of model selection and how to compare models via F tests.
- Understand AIC and BIC.
What You Need
Required R Packages
Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.
For this lab, you will need to load the following package(s):
- tidyverse
- sjPlot
- kableExtra
Presenting Results
All results should be presented following APA guidelines. If you need a reminder on how to hide code, format tables/plots, etc., make sure to review the rmd bootcamp.
The example write-up sections included as part of the solutions are not perfect - they instead should give you a good example of what information you should include and how to structure this. Note that you must not copy any of the write-ups included below for future reports - if you do, you will be committing plagiarism, and this type of academic misconduct is taken very seriously by the University. You can find out more here.
Lab Data
You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/wellbeing_rural.csv.
Study Overview
Research Question(s)
Section I
- Is there an association between wellbeing and time spent outdoors after taking into account the association between wellbeing and social interactions?
Section II
- RQ1: Is the number of weekly social interactions a useful predictor of wellbeing scores?
- RQ2: Does weekly outdoor time explain a significant amount of variance in wellbeing scores over and above social interactions?
Setup
- Create a new RMarkdown file
- Load the required package(s)
- Read the wellbeing dataset into R, assigning it to an object named
mwdata
Exercises
Section I: Model Fit
In the first section of this lab, you will focus on the statistics contained within the highlighted sections of the summary() output below. You will be both calculating these by hand and deriving via R before interpreting these values in the context of the research question.
Fit the following multiple linear regression model, and assign the output to an object called mdl, and examine the summary output.
\[ \text{Wellbeing} = \beta_0 + \beta_1 \cdot Social~Interactions + \beta_2 \cdot Outdoor~Time + \epsilon \]
What is the proportion of the total variability in wellbeing scores explained by the model?
The proportion of the total variability explained is given by \(R^2\). Since the model includes 2 predictors, you should report the Adjusted-\(R^2\).
The \(R^2\) coefficient is defined as:
\[ R^2 = \frac{SS_{Model}}{SS_{Total}} = 1 - \frac{SS_{Residual}}{SS_{Total}} \]
The Adjusted-\(R^2\) coefficient is defined as:
\[ \hat R^2 = 1 - \frac{(1 - R^2)(n-1)}{n-k-1} \quad \\ \]
\[ \begin{align} & \text{Where:} \\ & n = \text{sample size} \\ & k = \text{number of explanatory variables} \\ \end{align} \]
What do you notice about the unadjusted and adjusted R-squared values?
Are they similar or quite different? Why might this be?
Perform a model utility test at the 5% significance level and report your results.
In other words, conduct an \(F\)-test against the null hypothesis that the model is ineffective at predicting wellbeing scores using social interactions and outdoor time by computing the \(F\)-statistic using its definition.
The \(F\)-ratio is used to test the null hypothesis that all regression slopes are zero.
It is called the \(F\)-ratio because it is the ratio of the how much of the variation is explained by the model (per parameter) versus how much of the variation is left unexplained in the residuals (per remaining degrees of freedom).
\[ F_{df_{model},df_{residual}} = \frac{MS_{Model}}{MS_{Residual}} = \frac{SS_{Model}/df_{Model}}{SS_{Residual}/df_{Residual}} \\ \quad \\ \]
\[ \begin{align} & \text{Where:} \\ & df_{model} = k \\ & df_{residual} = n-k-1 \\ & n = \text{sample size} \\ & k = \text{number of explanatory variables} \\ \end{align} \]
Section II: Model Comparisons
In the second section of this lab, you will focus on model comparison where you will formally test a number of research questions:
- RQ1: Is the number of weekly social interactions a useful predictor of wellbeing scores?
- RQ2: Does weekly outdoor time explain a significant amount of variance in wellbeing scores over and above the number of weekly social interactions?
Fit the below 3 models required to address the 2 research questions stated above. Note down which model(s) will be used to address each research question, and examine the results of each model.
Name the models as follows: “wb_mdl0”, “wb_mdl1”, “wb_mdl2”
\[
\text{Wellbeing} = \beta_0 + \epsilon
\]
\[ \text{Wellbeing} = \beta_0 + \beta_1 \cdot Social~Interactions + \epsilon \]
\[
\text{Wellbeing} = \beta_0 + \beta_1 \cdot Social~Interactions + \beta_2 \cdot Outdoor~Time + \epsilon
\]
The summary() function will be useful to examine the model output.
RQ1: Is the number of weekly social interactions a useful predictor of wellbeing scores?
Check that the \(F\)-statistic and the \(p\)-value are the the same from the model comparison as that which are given at the bottom of summary(wb_mdl1).
Provide the key model results from the two models in a single formatted table.
Use the anova() function to perform a model comparison between your model with social interactions (wb_mdl1) to the null model (wb_mdl0). Remember that the null model tests the null hypothesis that all beta coefficients are zero. By comparing wb_mdl0 to wb_mdl1, we can test whether we should include the IV of ‘social_int’.
You can use KableExtra to present your model comparison results in a well formatted table.
Look at the amount of variation in wellbeing scores explained by models “wb_mdl1” and “wb_mdl2”.
From this, can we answer the second research question of whether weekly outdoor time explains a significant amount of variance in wellbeing scores over and above social interactions?
Provide justification/rationale for your answer.
You will need to review the R-Squared and Adjusted R-Squared values.
Does weekly outdoor time explain a significant amount of variance in wellbeing scores over and above social interactions?
To address RQ2, you need to statistically compare “wb_mdl1” and “wb_mdl2”.
You can use KableExtra to present your model comparison results in a well formatted table.
Compare the two following models, each looking at the associations of Wellbeing scores and different predictor variables.
\(\text{Wellbeing} = \beta_0 + \beta_1 \cdot \text{Social~Interactions} + \beta_2 \cdot \text{Age} + \epsilon\)
\(\text{Wellbeing} = \beta_0 + \beta_1 \cdot \text{Outdoor~Time} + \epsilon\)
Report which model you think best fits the data, and justify your answer.
The code below fits 6 different models based on our mwdata:
model1 <- lm(wellbeing ~ social_int, data = mwdata)
model2 <- lm(wellbeing ~ social_int + outdoor_time, data = mwdata)
model3 <- lm(wellbeing ~ social_int + age, data = mwdata)
model4 <- lm(wellbeing ~ social_int + outdoor_time + age, data = mwdata)
model5 <- lm(wellbeing ~ social_int + outdoor_time + age + steps_k, data = mwdata)
model6 <- lm(wellbeing ~ social_int + outdoor_time, data = wb_data)For each of the below pairs of models, what methods are/are not available for us to use for comparison and why?
-
model1vsmodel2 -
model2vsmodel3 -
model1vsmodel4 -
model3vsmodel5 -
model2vsmodel6
This flowchart might help you to reach your decision:
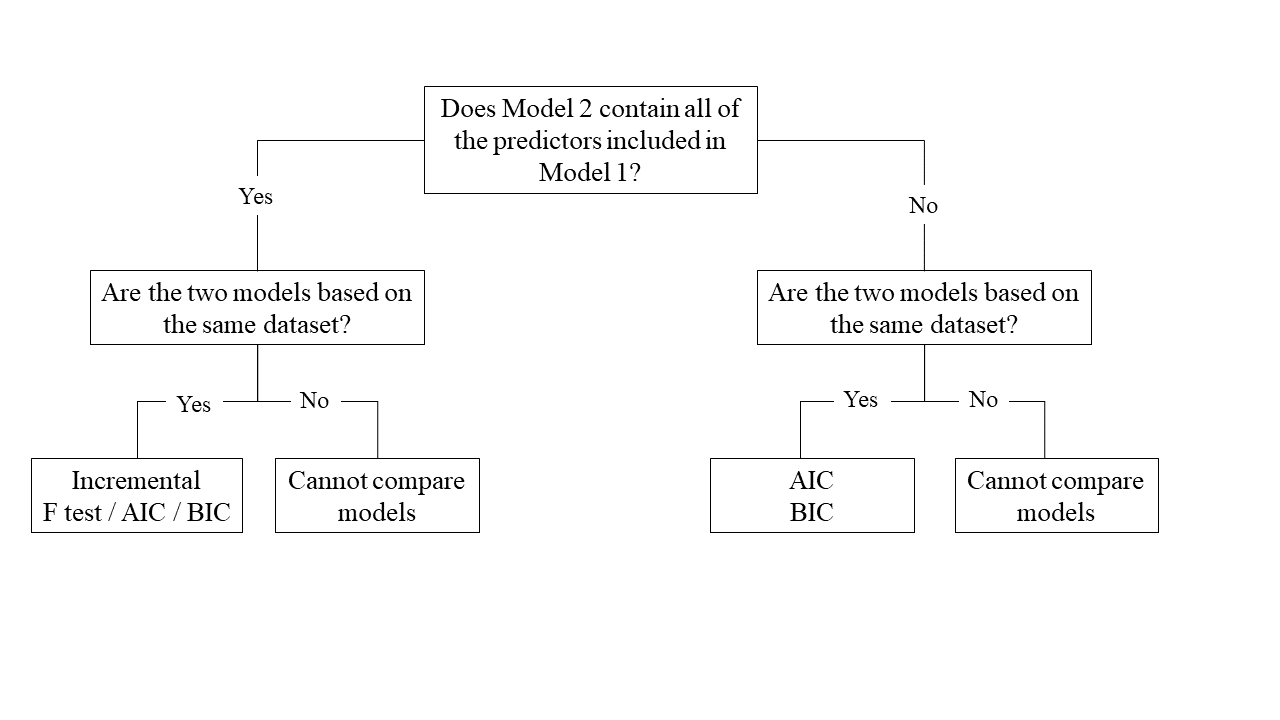
You may need to examine the dataset, and check for accuracy (e.g., are there any impossible / out of range values?) and completeness (e.g., are there any missing values?).
Compile Report
Knit your report to PDF, and check over your work. To do so, you should make sure:
- Only the output you want your reader to see is visible (e.g., do you want to hide your code?)
- Check that the tinytex package is installed
- Ensure that the ‘yaml’ (bit at the very top of your document) looks something like this:
---
title: "this is my report title"
author: "B1234506"
date: "07/09/2024"
output: bookdown::pdf_document2
---If you are having issues knitting directly to PDF, try the following:
- Knit to HTML file
- Open your HTML in a web-browser (e.g. Chrome, Firefox)
- Print to PDF (Ctrl+P, then choose to save to PDF)
- Open file to check formatting
To not show the code of an R code chunk, and only show the output, write:
```{r, echo=FALSE}
# code goes here
```To show the code of an R code chunk, but hide the output, write:
```{r, results='hide'}
# code goes here
```To hide both code and output of an R code chunk, write:
```{r, include=FALSE}
# code goes here
```You must make sure you have tinytex installed in R so that you can “Knit” your Rmd document to a PDF file:
install.packages("tinytex")
tinytex::install_tinytex()