Connecting hypothesis testing and confidence intervals

1 Hypothesis testing

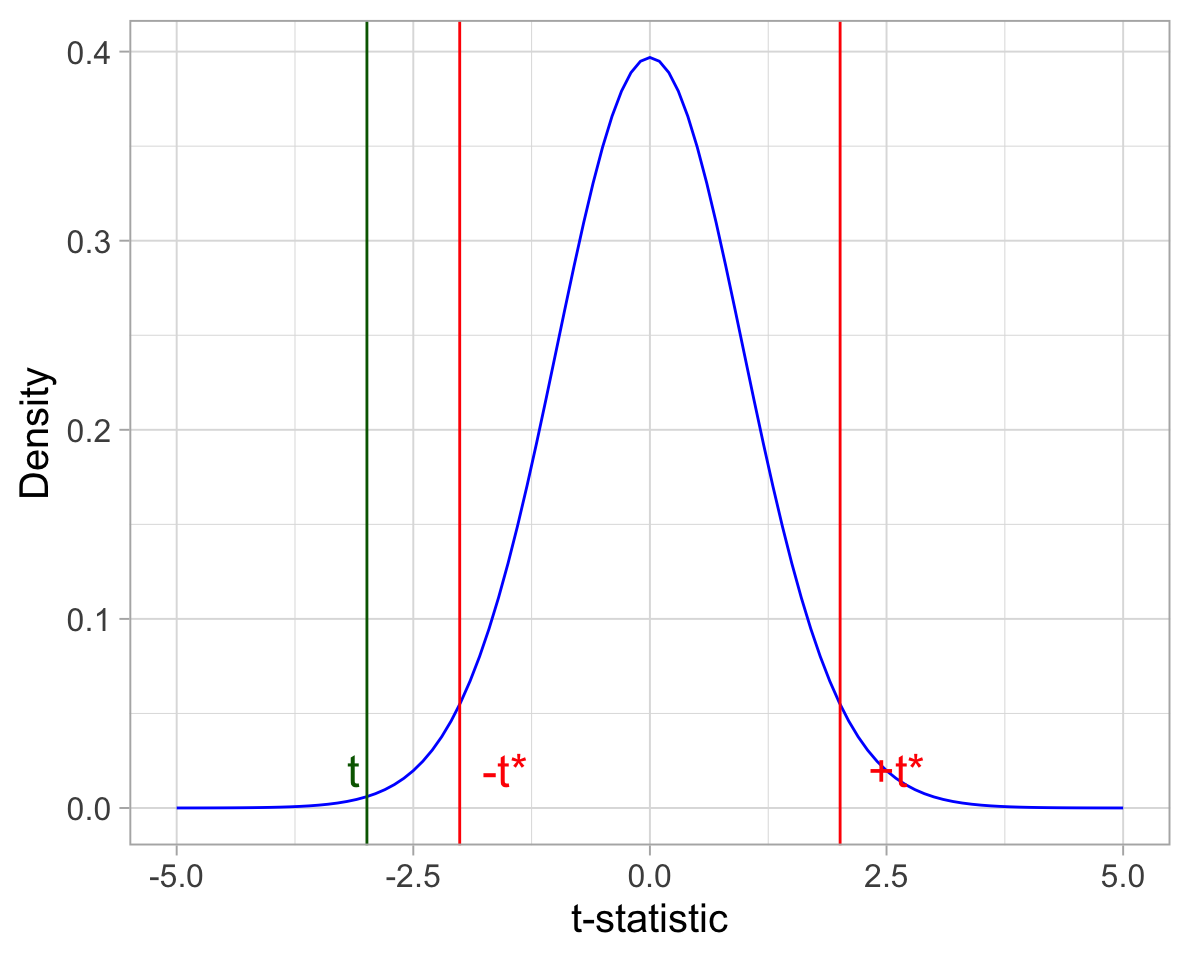
Consider the two-sided hypothesis testing case

$$H_0:\mu ={\mu }_0$$ $$H_1:\mu \ne {\mu }_0$$

Where the test statistic used in order to test the above claim is:

$$t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}}$$

At the 5% significance level:

• we reject the null hypothesis $H_0$ whenever the observed t-statistic lies beyond the critical values:

$$t\le -t^{\ast }\text{or}t\ge +t^{\ast }$$

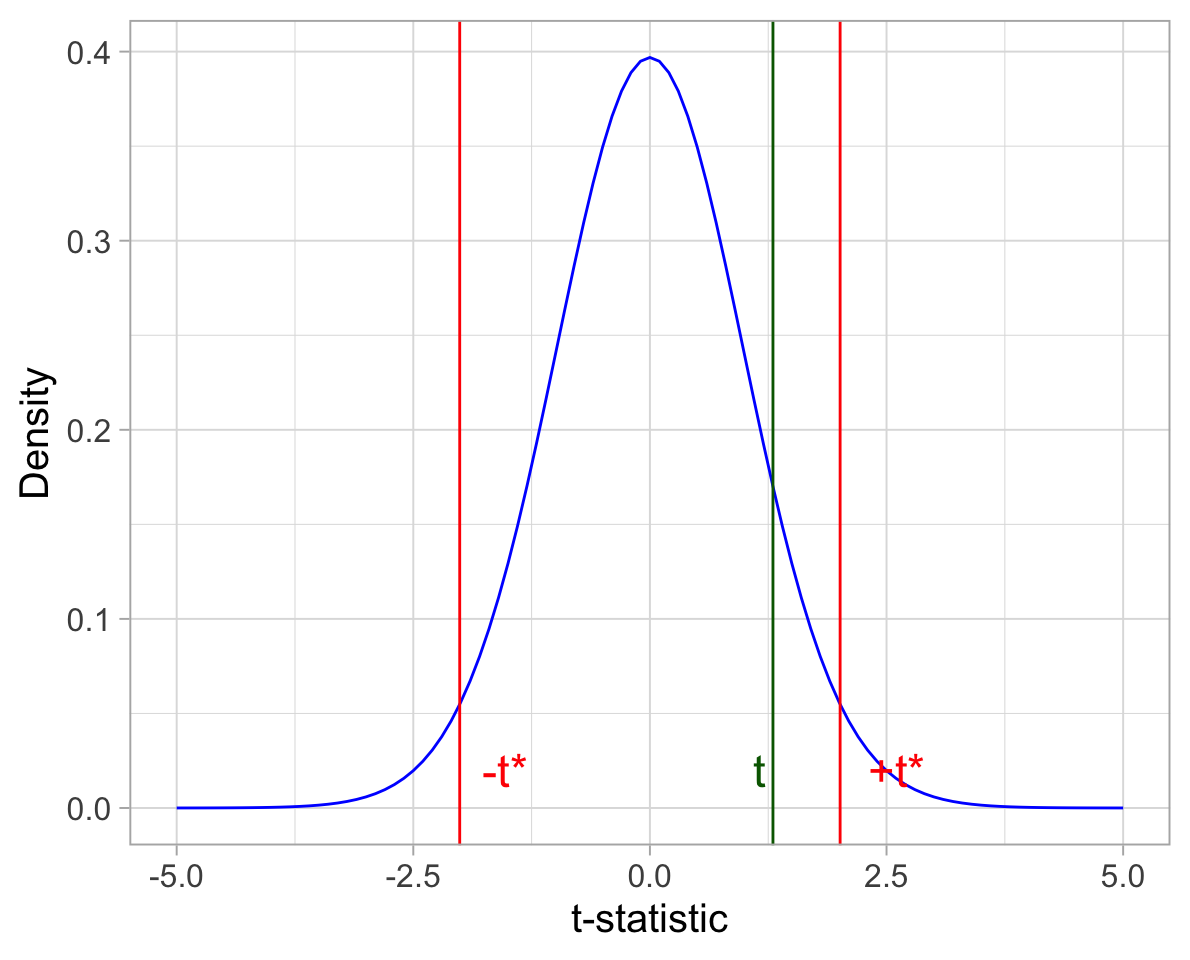
• we do not reject the null hypothesis $H_0$ whenever the observed t-statistic lies within the critical values:

$$-t^{\ast }<t<+t^{\ast }$$

2 Confidence interval

A 95% confidence interval for the population mean is given by

$$[\overline{x}-t^{\ast }\times \frac{s}{\sqrt{n}},\overline{x}+t^{\ast }\times \frac{s}{\sqrt{n}}]$$

This is often written as

$$\overline{x}\pm t^{\ast }\times \frac{s}{\sqrt{n}}$$

where $\pm t^{\ast }$ are the quantiles of a t-distribution jointly cutting an overall probability of $\alpha$ in the tails.

3 From HT to CI

In the hypothesis test, we do not reject the null hypothesis at the 5% significance level whenever ${\mu }_0$ lies inside of the 95% CI:

$$\begin{array}{r}\mathbf{\text{Do not reject }}{H}_0:\mu ={\mu }_0\mathbf{\text{ if}}\\ \\ -t^{\ast }& <t<+t^{\ast }\\ -t^{\ast }& <\frac{\overline{x}-{\mu }_0}{\frac{s}{\sqrt{n}}}<+t^{\ast }\\ -t^{\ast }\times \frac{s}{\sqrt{n}}& <\overline{x}-{\mu }_0<+t^{\ast }\times \frac{s}{\sqrt{n}}\\ -\overline{x}-t^{\ast }\times \frac{s}{\sqrt{n}}& <-{\mu }_0<-\overline{x}+t^{\ast }\times \frac{s}{\sqrt{n}}\\ \overline{x}+t^{\ast }\times \frac{s}{\sqrt{n}}& >{\mu }_0>\overline{x}-t^{\ast }\times \frac{s}{\sqrt{n}}\\ \overline{x}-t^{\ast }\times \frac{s}{\sqrt{n}}& <{\mu }_0<\overline{x}+t^{\ast }\times \frac{s}{\sqrt{n}}\\ {\mu }_0\text{ inside of }& [\overline{x}-t^{\ast }\times \frac{s}{\sqrt{n}},\overline{x}+t^{\ast }\times \frac{s}{\sqrt{n}}]\\ {\mu }_0\text{ inside of }& \text{95\% CI}\end{array}$$