Random Variables (Continuous)

Semester 1 - Week 10

1 Formative Report B

Instructions and data were released in week 7.

Next week: Submission of Formative report B

Your group must submit one PDF file for formative report B by 12 noon on Friday the 1st of December 2023 (next week).

To submit go to the course Learn page, click “Assessment”, then click “Submit Formative Report B (PDF file only)”.

No extensions. As mentioned in the Assessment Information page, no extensions are possible for group-based reports.

1.1 Tasks

For formative report B, you will be asked to perform the following tasks, each related to a week of teaching in this course.
This week’s task is highlighted in bold below. Please only focus on completing that task this week. In the next section, you will also find the guided sub-steps that you need to consider to complete this week’s task.

B1) Create a new categorical variable, Rating, taking the value ‘Good’ if the audience score is > 50, and ‘Bad’ otherwise. Inspect and describe the joint probability distribution of movie genre and rating.
B2) Investigate if a movie receiving a good rating is independent of the genre.
B3) Computing and plotting probabilities with a binomial distribution.
B4) Computing and plotting probabilities with a normal distribution.
B5) Plot standard error of the mean, and finish the report write-up (i.e., knit to PDF, and submit the PDF for formative feedback).

2 B4 sub-tasks

This week you will only focus on task B4. Below there are sub-steps you need to consider to complete task B4.

Tip

To see the hints, hover your cursor on the superscript numbers.

Focus on completing all of the lab tasks, and leave non-essential things like changing colors for later.

If, after looking at the hint, you still have no clue on how to answer a question, check the worked example below!

Context

As detailed last week, a new movie theatre is opening in Texas soon. The management team are thinking of innovative launch events, and they’d like to host a movie trivia night where viewers can compete to win free cinema tickets for the year! They want to make sure however that their questions aren’t too easy, or too difficult, so gave viewers an IQ test so that they could see where to pitch their questions.

According to a recent survey, the average IQ in Texas is 97.4. The management team decided they are satisfied with their questions’ level of difficulty if the probability of movie viewers’ having an IQ score above 97.4 is between 50% and 60%. Otherwise, they will adjust the difficulty of the questions by making them easier (if the probability is <50%) or harder (>60%).

In this lab, you will need to consider the variables IQ1 to IQ50 (i.e. the IQ score of each of the 50 audience raters for each movie) from the Hollywood movies dataset when answering the questions below.

Reopen last week’s Rmd file, and continue building on last week’s work. Make sure you are still using the movies dataset filtered to only include the top 3 genres.¹

Consider the IQ1-IQ50 variables, are they discrete or continuous?²

README: Wide vs long data

Currently the IQ data are in wide format, i.e. each movie has multiple columns providing the IQ scores of the 50 audience raters. However, later on we will want to plot the IQ scores of all raters across all movies. To do so, ggplot wants a single column of IQ scores into aes().

Consider this fictitious dataset in wide form:

df <- tibble(
    movie = c('x1', 'x2', 'x3'),
    IQ1   = c(91, 92, 93),
    IQ2   = c(101, 102, 103)
)
df

# A tibble: 3 × 3
  movie   IQ1   IQ2
  <chr> <dbl> <dbl>
1 x1       91   101
2 x2       92   102
3 x3       93   103

To go from two columns of IQ scores to a single one, we can get the data in long form as follows:

df_long <- df %>%
    pivot_longer(IQ1:IQ2, names_to = "IQ_ID", values_to = "IQ_Scores")
df_long

# A tibble: 6 × 3
  movie IQ_ID IQ_Scores
  <chr> <chr>     <dbl>
1 x1    IQ1          91
2 x1    IQ2         101
3 x2    IQ1          92
4 x2    IQ2         102
5 x3    IQ1          93
6 x3    IQ2         103

The function pivot_longer takes the range of columns you want to compress (IQ1 to IQ2 in this case), and the names of 2 new columns to create:

names_to: where the names of the columns to compress will go into - in this case, “IQ_ID”
values_to: where the values of the columns to compress will go into - in this case, “IQ_Scores”

You can also go from long data back to wide data. To do so, use the pivot_wider function:

df_long

# A tibble: 6 × 3
  movie IQ_ID IQ_Scores
  <chr> <chr>     <dbl>
1 x1    IQ1          91
2 x1    IQ2         101
3 x2    IQ1          92
4 x2    IQ2         102
5 x3    IQ1          93
6 x3    IQ2         103

df_long %>% 
    pivot_wider(names_from = "IQ_ID", values_from = "IQ_Scores")

# A tibble: 3 × 3
  movie   IQ1   IQ2
  <chr> <dbl> <dbl>
1 x1       91   101
2 x2       92   102
3 x3       93   103

Using the pivot_longer() function, pivot the data so that it is in long format. Ensure the column names go into a new column called “IQ_ID”, and the values go into a column called “IQ_Scores”.³

README: Independence

As each movie was rated by a different pool of 50 audience raters, the variable IQ_Scores can be considered an independent sample of IQ scores.

This is because a single audience rater didn’t appear in more than one movie. Even if the column IQ_ID says “IQ1” for multiple movies, the rater with id “IQ1” for movie “American Reunion”, say, won’t be the same rater with id “IQ1” for movie “Battleship”.

Plot the sample distribution of the IQ_Scores variable either using a histogram or density plot.⁴

What kind of distribution does your plot follow? Estimate the parameters of your distribution from the sample data.⁵

Plot the fitted normal distribution on top of the sample distribution. Is the normal distribution a good fit?⁶

Calculate the following:⁷
- The probability of a movie viewer having an IQ score <97.4, i.e. less than the Texas average.
- The probability of a movie viewer having an IQ score >97.4, i.e. more than the Texas average.

Calculate the following:⁸
- The value of IQ that 25% of movie watchers have scores equal to or less than
- The value of IQ that 50% of movie watchers have scores equal to or less than
- The value of IQ that 75% of movie watchers have scores equal to or less than
- The interval comprising the middle 95% of the people’s IQ scores in the sample

How do the normal quartiles computed above compare to those obtained from the summary() function? If they are similar, this will provide further evidence that the normal distribution is a good model for IQ scores.
Based on the probabilities you have reported above, do you think that the new movie theatre should simplify the questions for their trivia night, make them harder, or make no changes? Justify your answer.
In the analysis section of your report, write up a summary of what you have reported above, using proper rounding to 2 decimal places and avoiding any reference to R code or functions.

3 Worked Example

The dataset available at https://uoepsy.github.io/data/RestaurantTips2.csv was collected by the owner of a US bistro, and contains 99 observations on 10 variables. It is a subset of the RestaurantTips.csv data presented in the past weeks, focusing only on parties of 2 people.⁹

Following from the bistro owner’s interest in whether they should consider introducing a 2 for 1 coffee deal or a loyalty scheme, they are also considering running a weekly quiz night in the bistro. The quiz is only open to pairs of individuals, and given that the bistro is located in a student area, the owner wants to make the quiz very demanding, and therefore wants the questions to be at a level where someone with a ‘superior’ or ‘well above average’ IQ (i.e., scores 120+) would be challenged. We need to advise the bistro owner whether the questions that they have generated are at their desired level of difficulty.

Variable Name	Description
Bill	Size of the bill (in dollars)
Tip	Size of the tip (in dollars)
Credit	Paid with a credit card? n or y
Guests	Number of people in the group
Day	Day of the week: m=Monday, t=Tuesday, w=Wednesday, th=Thursday, or f=Friday
Server	Code for specific waiter/waitress: A, B, or C
PctTip	Tip as a percentage of the bill
HadCoffee	Number of guests in the group who had coffee
IQ1	Score on IQ test for guest 1
IQ2	Score on IQ test for guest 2

library(tidyverse)
tips2 <- read_csv("https://uoepsy.github.io/data/RestaurantTips2.csv")
head(tips2)

# A tibble: 6 × 10
   Bill   Tip Credit Guests Day   Server PctTip HadCoffee   IQ1   IQ2
  <dbl> <dbl> <chr>   <dbl> <chr> <chr>   <dbl>     <dbl> <dbl> <dbl>
1  23.7 10    n           2 f     A        42.2         2    93   100
2  32.0  5.01 y           2 f     A        15.7         2    96    98
3  17.4  3.61 y           2 f     B        20.8         2    94    99
4  15.4  3    n           2 f     B        19.5         2    99   108
5  18.6  2.5  n           2 f     A        13.4         2   129   106
6  21.6  3.44 n           2 f     B        16           2    82   118

If we were asked to describe what kind of variables IQ1 and IQ2 were, and to comment on the kind of probability distribution it may follow, we could say:

IQ1 and IQ2 represent the IQ scores of each individual within a group of two. These are both continuous variables that could be modeled by a normal distribution.

We could transform the tips2 dataset from wide to long format using the following command:

tips2_long <- tips2 %>%
    pivot_longer(IQ1:IQ2, names_to = "ID", values_to = "IQ_Scores")
tips2_long

# A tibble: 198 × 10
    Bill   Tip Credit Guests Day   Server PctTip HadCoffee ID    IQ_Scores
   <dbl> <dbl> <chr>   <dbl> <chr> <chr>   <dbl>     <dbl> <chr>     <dbl>
 1  23.7 10    n           2 f     A        42.2         2 IQ1          93
 2  23.7 10    n           2 f     A        42.2         2 IQ2         100
 3  32.0  5.01 y           2 f     A        15.7         2 IQ1          96
 4  32.0  5.01 y           2 f     A        15.7         2 IQ2          98
 5  17.4  3.61 y           2 f     B        20.8         2 IQ1          94
 6  17.4  3.61 y           2 f     B        20.8         2 IQ2          99
 7  15.4  3    n           2 f     B        19.5         2 IQ1          99
 8  15.4  3    n           2 f     B        19.5         2 IQ2         108
 9  18.6  2.5  n           2 f     A        13.4         2 IQ1         129
10  18.6  2.5  n           2 f     A        13.4         2 IQ2         106
# ℹ 188 more rows

pivot_longer()

Pivot longer takes “wide” data and transforms them to “long” form. An example is given below:

toy_data <- tibble(
    a = c(1, 2, 3),
    x1 = c(11, 12, 13),
    x2 = c(21, 22, 23)
)
toy_data

# A tibble: 3 × 3
      a    x1    x2
  <dbl> <dbl> <dbl>
1     1    11    21
2     2    12    22
3     3    13    23

long_toy_data <- toy_data %>%
    pivot_longer(x1:x2, names_to = "x", values_to = "score")
long_toy_data

# A tibble: 6 × 3
      a x     score
  <dbl> <chr> <dbl>
1     1 x1       11
2     1 x2       21
3     2 x1       12
4     2 x2       22
5     3 x1       13
6     3 x2       23

We can plot the sample distribution of the IQ_Scores variable either using a histogram or a density plot.

Let’s plot both the histogram and density plot for instructional purposes only, in a report you would only report one of the two as they show similar information. We plot both now for instructional purposes and, in particular, we ask you to focus on the differences in the y axes.

library(patchwork)
plt_hist <- ggplot(tips2_long, aes(x = IQ_Scores)) + 
    geom_histogram(colour = 'white') +
    labs(x = "IQ scores")

plt_dens <- ggplot(tips2_long, aes(x = IQ_Scores)) + 
    geom_density() + 
    labs(x = "IQ scores")

plt_hist | plt_dens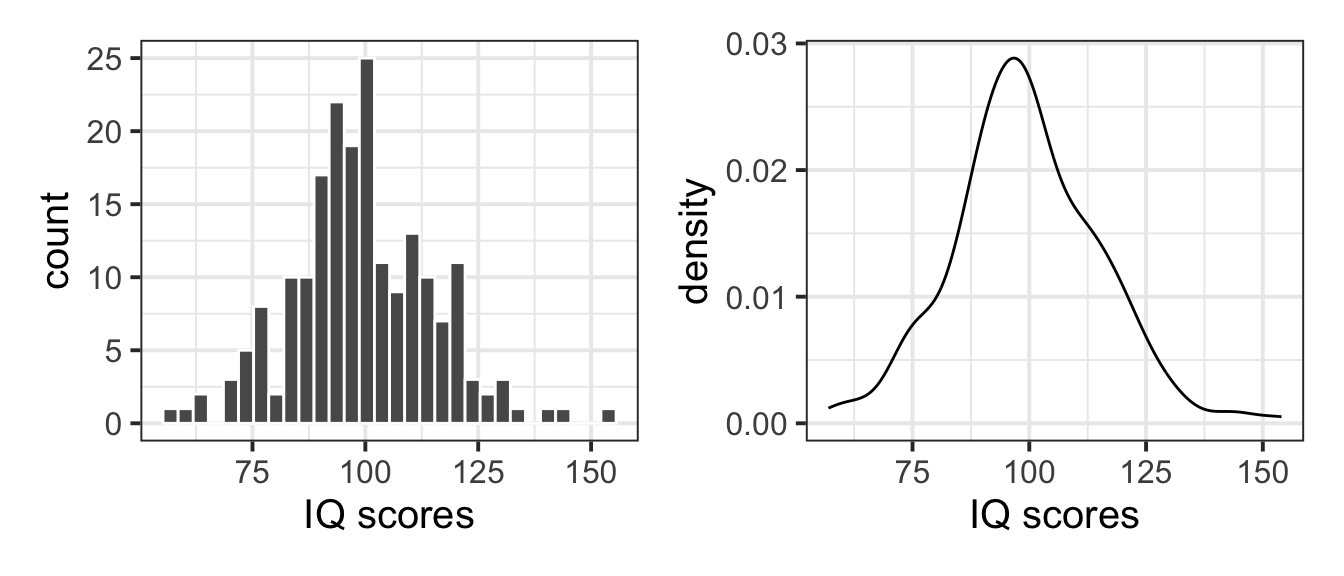

As you will notice, the plot on the left panel shows counts on the y axis, i.e. the absolute frequency of each bin interval. The plot on the right panel, instead, shows the density on the y axis. If we wanted to plot on top of the histogram a normal curve, we would need to change the y axis of the histogram to be a comparable measure, i.e. also a density rather than a count.

You can do so by adding y = after_stat(density) in the aes() specification, and you can now see that both y axes agree:

plt_hist <- ggplot(tips2_long, aes(x = IQ_Scores, y = after_stat(density))) + 
    geom_histogram(colour = 'white') +
    labs(x = "IQ scores")

plt_dens <- ggplot(tips2_long, aes(x = IQ_Scores)) + 
    geom_density() + 
    labs(x = "IQ scores")

plt_hist | plt_dens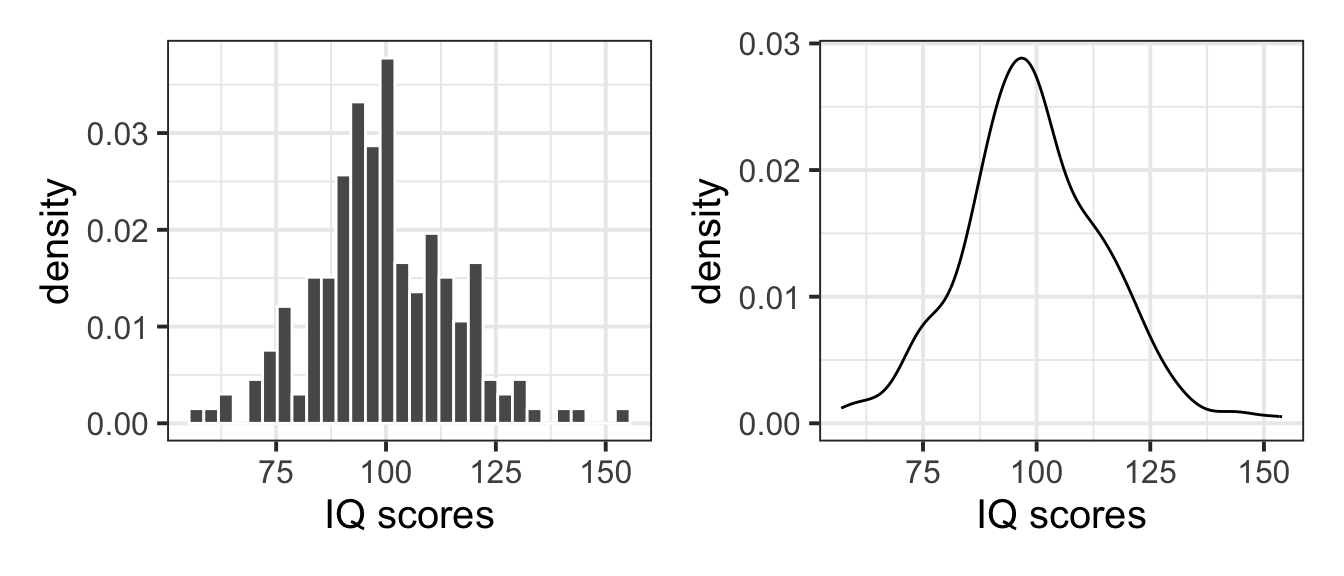

Fitting a distribution

Fitting a normal distribution to data involves estimating the parameters of the distribution from the data. In other words, we want to find values for $\mu$ and $\sigma$ from the variable IQ_Scores in the our data, and we denote the estimated parameters with $\hat{\mu}$ and $\hat{\sigma}$. You create those symbols, you can type in the Rmd file $\hat{\mu}$ and $\hat{\sigma}$ .

We can now fit a normal distribution to the variable. To do so, we need to start by estimating the parameters of the normal distribution:
- $\hat{\mu}$, the mean IQ score in the sample
- $\hat{\sigma}$, the estimated standard deviation in the sample

# The mean of the sample of IQ scores
tips_mu_hat <- mean(tips2_long$IQ_Scores) 
tips_mu_hat

[1] 99.33333

# The standard deviation of the sample of IQ scores
tips_sigma_hat <- sd(tips2_long$IQ_Scores)
tips_sigma_hat

[1] 15.7025

We can then compare the sample distribution to the normal distribution, and comment on whether the normal fit is good:

First we will create a tibble with the normal distribution at a grid of x values.

M $\pm$ 4 * SD vs M $\pm$ 3 * SD
Typically, the interval M $\pm$ 3 * SD includes roughly all of the distribution values (99.7%). However, in this case a few IQ scores escape the interval (as they are so widespread). As such, we extended the plotting interval to M $\pm$ 4 * SD.
Feel free to try with a grid of x values between M $\pm$ 3 * SD, and you will see that some scores exceed the plot range.

normal_distr <- tibble(
    x_grid = seq(tips_mu_hat - 4 * tips_sigma_hat, 
                 tips_mu_hat + 4 * tips_sigma_hat, 
                 by = 0.1),
    y_grid = dnorm(x_grid, mean = tips_mu_hat, sd = tips_sigma_hat)
)

We can plot the sample distribution and put the fitted normal distribution on top:

bistro_iq <- ggplot() + 
    geom_histogram(data = tips2_long, aes(x = IQ_Scores, y = after_stat(density)), 
                   color = 'white') +
    geom_line(data = normal_distr, aes(x = x_grid, y = y_grid),
              color = 'red') +
    labs(x = "IQ scores")
bistro_iq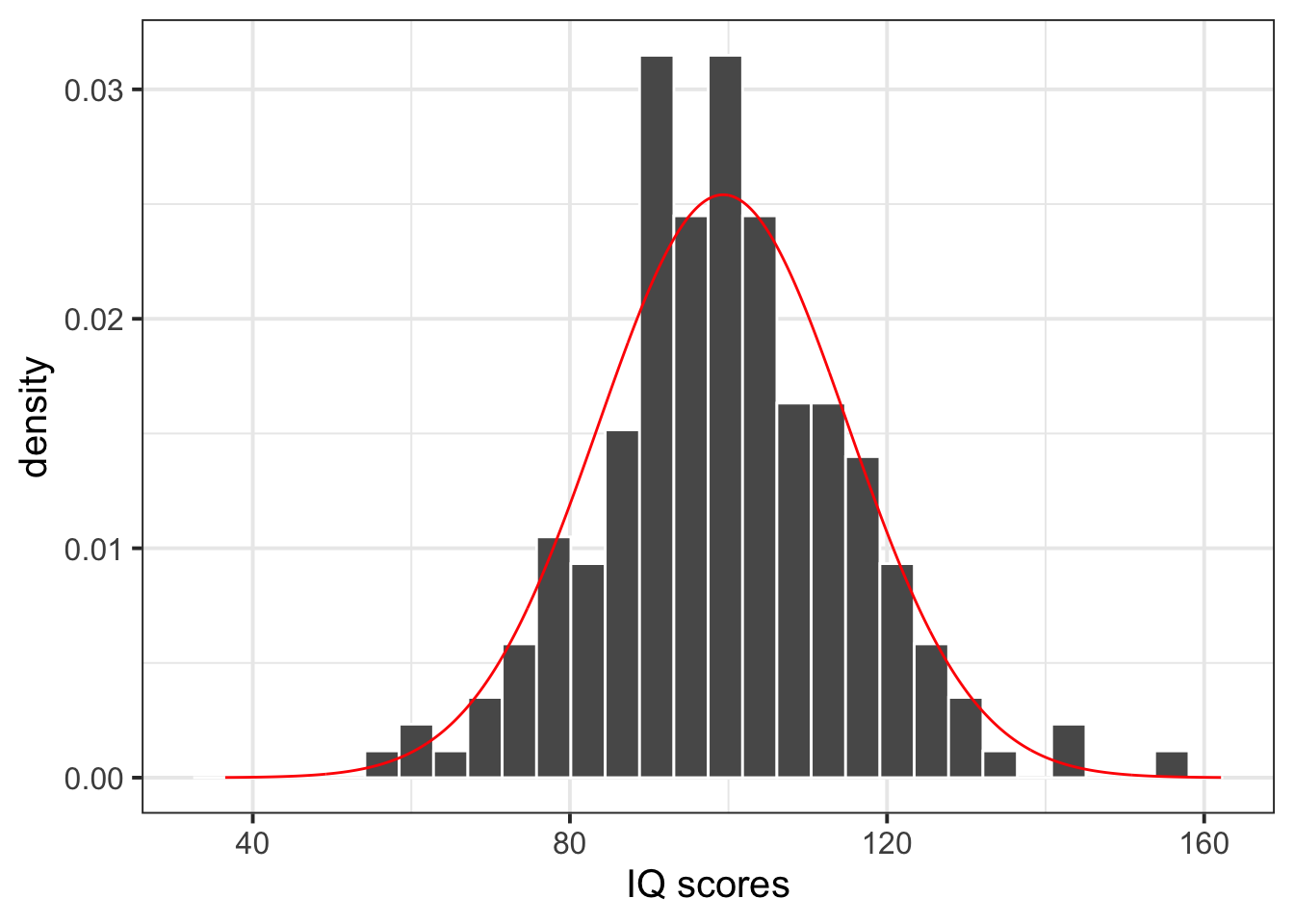

Figure 1: Distribution of Bistro Customer IQ Scores.

The normal distribution seems to be a good fit for the sample distribution, as the shape of the histogram tends to agree with the normal distribution across all possible values. The histogram appears to be symmetric around the mean and follows the normal bell-shaped curve.

We can use the fitted normal distribution to calculate the probabilities, for example:

To calculate the probability that a bistro customer has an IQ below 120, we can compute the following:

pnorm(120, tips_mu_hat, tips_sigma_hat)

[1] 0.9059362

To calculate the probability that a bistro customer has an IQ above 120, we can compute the following:

# P(X > 120)
pnorm(120, tips_mu_hat, tips_sigma_hat, lower.tail = FALSE)

[1] 0.09406377

or alternatively

# 1 - P(X < 120)
1 - pnorm(120, tips_mu_hat, tips_sigma_hat)

[1] 0.09406377

To calculate the probability that a bistro customer has an IQ above 100, we can compute the following:

# P(X > 100)
pnorm(100, tips_mu_hat, tips_sigma_hat, lower.tail = FALSE)

[1] 0.4830676

or alternatively

# 1 - P(X < 100)
1 - pnorm(100, tips_mu_hat, tips_sigma_hat)

[1] 0.4830676

To calculate the probability that a bistro customer has an IQ between 100 and 130, we can compute the following:

P(a < X < b) = P(X < b) - P(X < a) when a = 100 and b = 130 so that P(100 < X < 130) = P(X < 130) - P(X < 100)

# P(100 < X < 130) = 
# P(X < 130) - P(X < 100)
pnorm(130, tips_mu_hat, tips_sigma_hat) - pnorm(100, tips_mu_hat, tips_sigma_hat)

[1] 0.4576566

We can calculate the value of IQ that a specific percentage of bistro customers have scores equal to or less than, for example:

s.t. means such that

To calculate the value of IQ that 25% of bistro customers have scores equal to or less than, we can compute the following:

qnorm(p = 0.25, mean = tips_mu_hat, sd = tips_sigma_hat)

[1] 88.74216

To calculate the value of IQ that 50% of bistro customers have scores equal to or less than, we can compute the following:

qnorm(0.5, tips_mu_hat, tips_sigma_hat)

[1] 99.33333

To calculate the value of IQ that 75% of bistro customers have scores equal to or less than, we can compute the following:

qnorm(0.75, tips_mu_hat, tips_sigma_hat)

[1] 109.9245

We can also comment on how these normal quartiles values compare to those from the summary() output:

summary(tips2_long$IQ_Scores)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  57.00   90.25   98.00   99.33  109.75  154.00

The estimated quartiles are very similar to those from the summary output, providing further indication that the sample of IQ scores follows a normal distribution.

To summarise the IQ scores of the bistro customers, we could compute the interval comprising the middle 95% of the customers IQ scores:

If we want 0.95 probability in the middle, we need to split the leftover 0.05 probability equally between the two tails: 0.025 in the left, and 0.025 in the right. However, qnorm() wants the probability to the left, so we will give 0.025 and 0.975 = 1 - 0.025 as values.

qnorm(c(0.025, 0.975), mean = tips_mu_hat, sd = tips_sigma_hat)

[1]  68.5570 130.1097

95% of the bistro customers had IQ scores between 69 and 130.

Alternatively

Alternatively, to specify that one probability is on the left tail and the other is on the upper tail, you have to run two separate statements:

qnorm(0.025, mean = tips_mu_hat, sd = tips_sigma_hat)

[1] 68.557

qnorm(0.025, mean = tips_mu_hat, sd = tips_sigma_hat, lower.tail = FALSE)

[1] 130.1097

For a classification of IQ scores, see the Wechsler Intelligence Scales classification table.

Example writeup

Figure 1 displays the distribution of IQ scores, with a normal distribution superimposed as a red histogram. Most of the bistro customers (95%) have IQ scores between 69 and 130. Based on our analysis above, 48% of bistro customers are likely to have IQ scores above 100, though there is less than a 10% chance that customers have superior IQ scores (i.e., above 120). Therefore the bistro owner has set the questions to his quiz at the desired level of difficulty - the vast majority of his customers should find the questions extremely challenging. However, if the Bistro owner did want to make some changes, they should only consider making the quiz more difficult.

4 Student Glossary

To conclude the lab, add the new functions to the glossary of R functions.

Function	Use and package
`dnorm()`	?
`pnorm()`	?
`pivot_longer()`	?
`seq()`	?
`geom_histogram()`	?
`geom_density()`	?
`geom_line()`	?
`after_stat()`	?

References

Lock, Robin H, Patti Frazer Lock, Kari Lock Morgan, Eric F Lock, and Dennis F Lock. 2020. Statistics: Unlocking the Power of Data. John Wiley & Sons.

Footnotes

Hint: Ask last week’s driver for the Rmd file, they should share it with the group via the group discussion space or email. To download the file from the server, go to the RStudio Files pane, tick the box next to the Rmd file, and select More > Export.↩︎
Hint: Technically, the values you see in the data are discrete. In Psychology, however, IQ is assumed to be a continuous variable and it’s only discrete due to a limitation of our measuring ability.
In other words, if we were able to measure it more accurately, there would be no reason why this couldn’t be continuous and we could imagine getting an IQ of 126.4374325677…
To summarise, IQ is an example of a variable that is considered as coming from a continuous scale, but it can only be measured with discrete precision.↩︎
Hint: When the data is wide, we can make it long using pivot_longer(). When we make data longer, we’re essentially making lots of columns into 2 longer columns. Below, in the animation, the wide variable x, y and z go into a new longer column called "name" (specified by the argument names_to = "name") that specifies which (x/y/z) it came from, and the values get put into the "val" column (specified by the argument values_to = "val").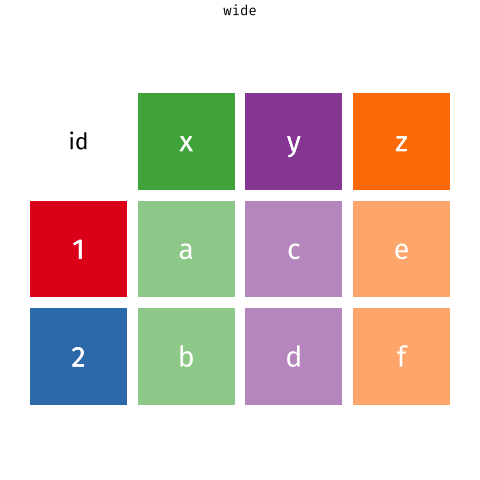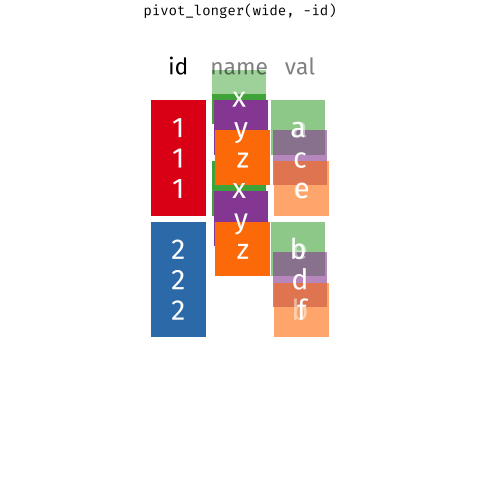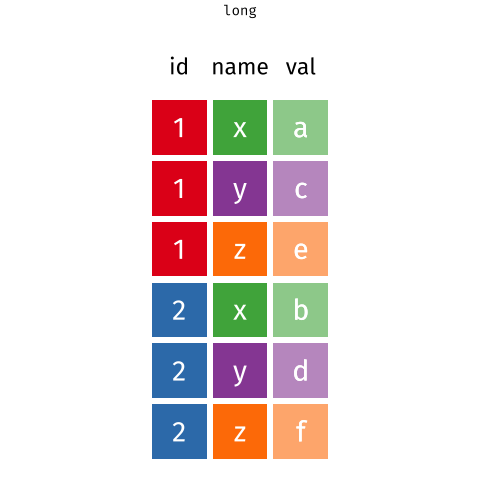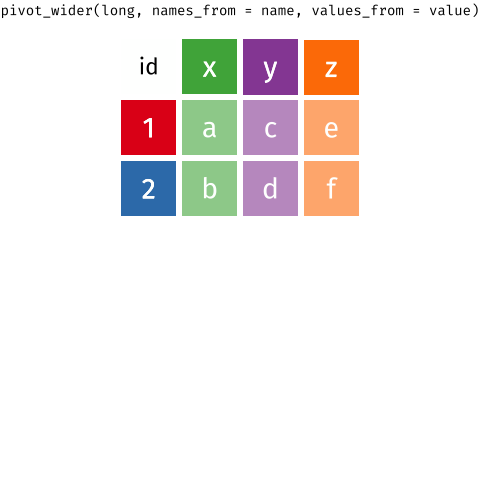

Source: https://fromthebottomoftheheap.net/2019/10/25/pivoting-tidily/

↩︎
Hint: Here you will need to specify geom_histogram() or geom_density().

To save space, if you wish to plot this next to another plot, recall that you can use the patchwork package to arrange plots either adjacent to one another (via |) or stacked (via /).↩︎
Hint: A normal distribution has two parameters, the mean ($\mu$) and the standard deviation ($\sigma$).↩︎
Hint: Here you will need to consider using dnorm(), as you are interested in the normal distribution at values of x.

First, you will need to create a tibble with two columns:
- The first column will contain a sequence of x-values (a grid) for which you want to compute the normal distribution curve at
- The second column will contain the y-values: the normal distribution at that sequence of x-values.
This way, you will have the x-values and the heights (normal distribution) at those x-values.
When specifying your x-axis sequence, consider how many standard deviations above and below the mean to give. This can either be 2, 3, or 4. Alternative you can go from the minimum of your data to the maximum.
For the y-values, use the dnorm() function with inputs being the x-axis grid, the sample mean, and sample standard deviation.
Plot this on top of the histogram/density using geom_line(data = ?, aes(x = ?, y = ?)). If you are using a histogram, make sure the y-axis are comparable: counts vs density isn’t appropriate!↩︎
Hint: Here you are being asked to calculate:
- P(X <= x) = P(X < x)
- P(X >= x) = P(X > x)
↩︎
Hint:

For the first three questions, you are being asked to calculate the quantile x such that P(X <= x) is 0.25, 0.50, and 0.75 respectively. That is, you are asked to find the first, second, and third quartiles respectively.

For the final question, you are looking for those values that comprise the middle 0.95 of the distribution, i.e. cutting an area of 0.05 outside.
The 0.05 probability needs to be equally divided between the left (0.025) and the right (0.025) tails. Also note that a probability of 0.025 to the right is equivalent to a probability of 0.975 to the left (= 1 - 0.025). In symbols, you are asked to calculate P(a < X < b) where a is the 2.5th percentile and b is the 97.5th percentile.↩︎
Data adapted from Lock et al. (2020).↩︎