Preliminaries

  1. Open Rstudio, create a new R script or RMarkdown document (whichever you prefer working with) and give it a title for this week.

  2. Load any of the packages you think you might be using today.
    By now you may have started get into a sort of routine with R, and you might know what functions you like, and which you don’t. Because there are so many alternatives for doing the same thing, the packages and functions you use are very much up to you.
    If I’m planning on doing some multilevel modelling, I will tend to load these by default at the top:

    library(tidyverse) # for everything
library(lme4) # for fitting models
library(broom.mixed) # for tidying model output

Exercises

lmer() >> glmer()

Remember how we simply used glm() and could specify the family = "binomial" in order to fit a logistic regression? Well it’s much the same thing for multi-level models!

  • Gaussian model:
    • lmer(y ~ x1 + x2 + (1 | g), data = data)
  • Binomial model:
    • glmer(y ~ x1 + x2 + (1 | g), data = data, family = binomial(link='logit'))
      or
    • glmer(y ~ x1 + x2 + (1 | g), data = data, family = "binomial")
      or
    • glmer(y ~ x1 + x2 + (1 | g), data = data, family = binomial)

For more on Binary vs Binomial, see this in depth section.

Novel Word Learning: Data Codebook

load(url("https://uoepsy.github.io/msmr/data/nwl.RData"))

In the nwl data set (accessed using the code above), participants with aphasia are separated into two groups based on the general location of their brain lesion: anterior vs. posterior. There is data on the numbers of correct and incorrect responses participants gave in each of a series of experimental blocks. There were 7 learning blocks, immediately followed by a test. Finally, participants also completed a follow-up test.
Data were also collect from healthy controls.
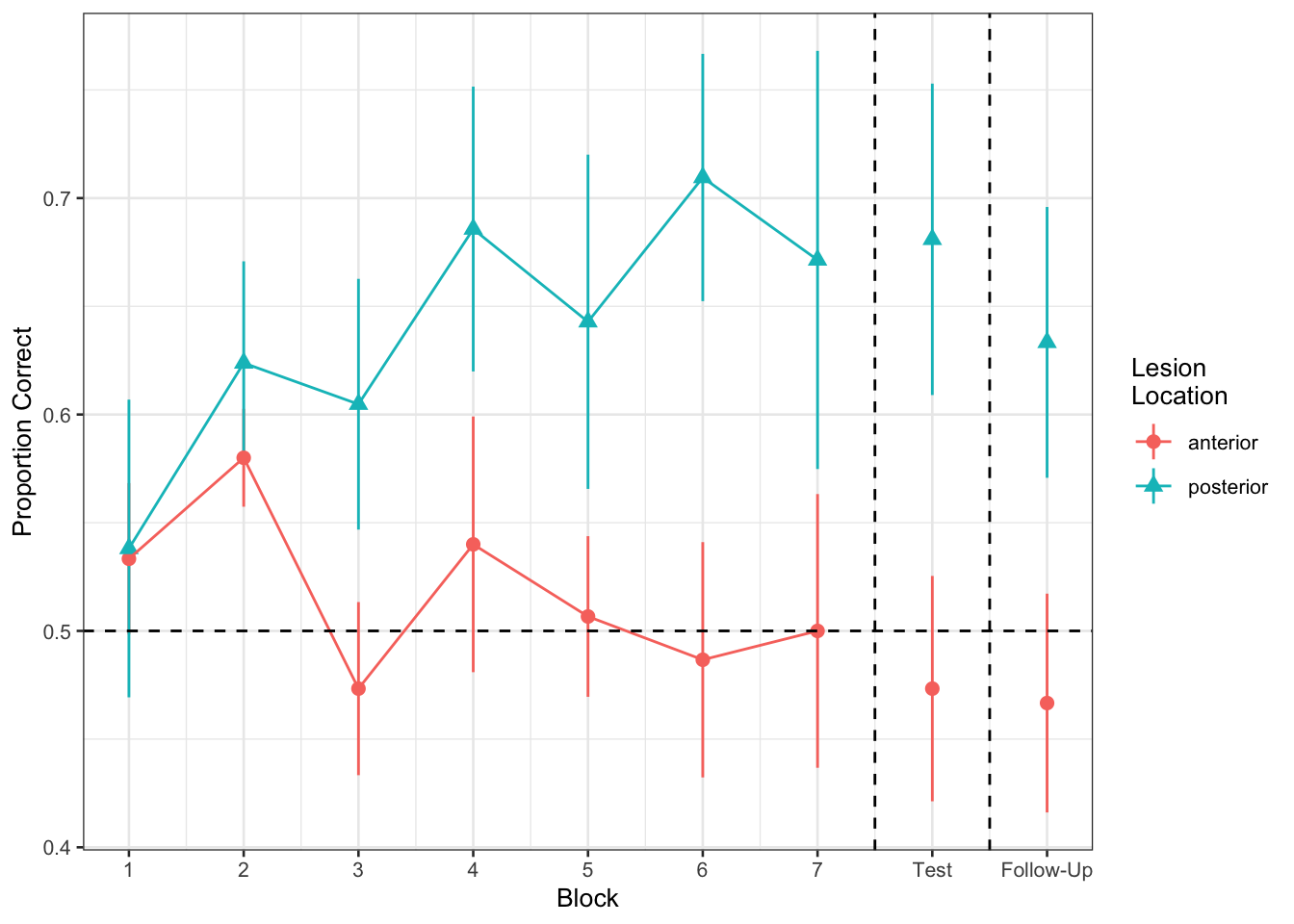
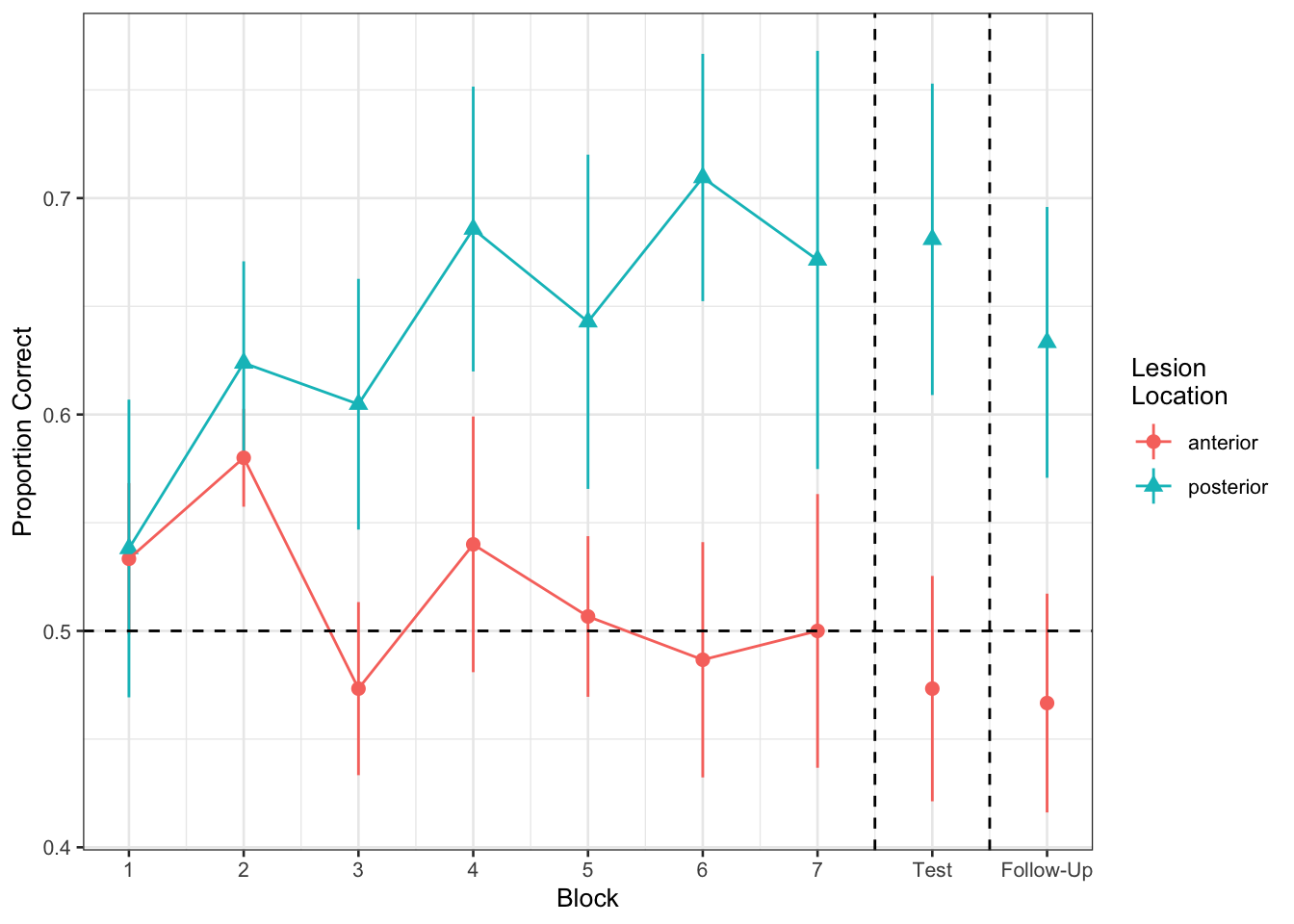
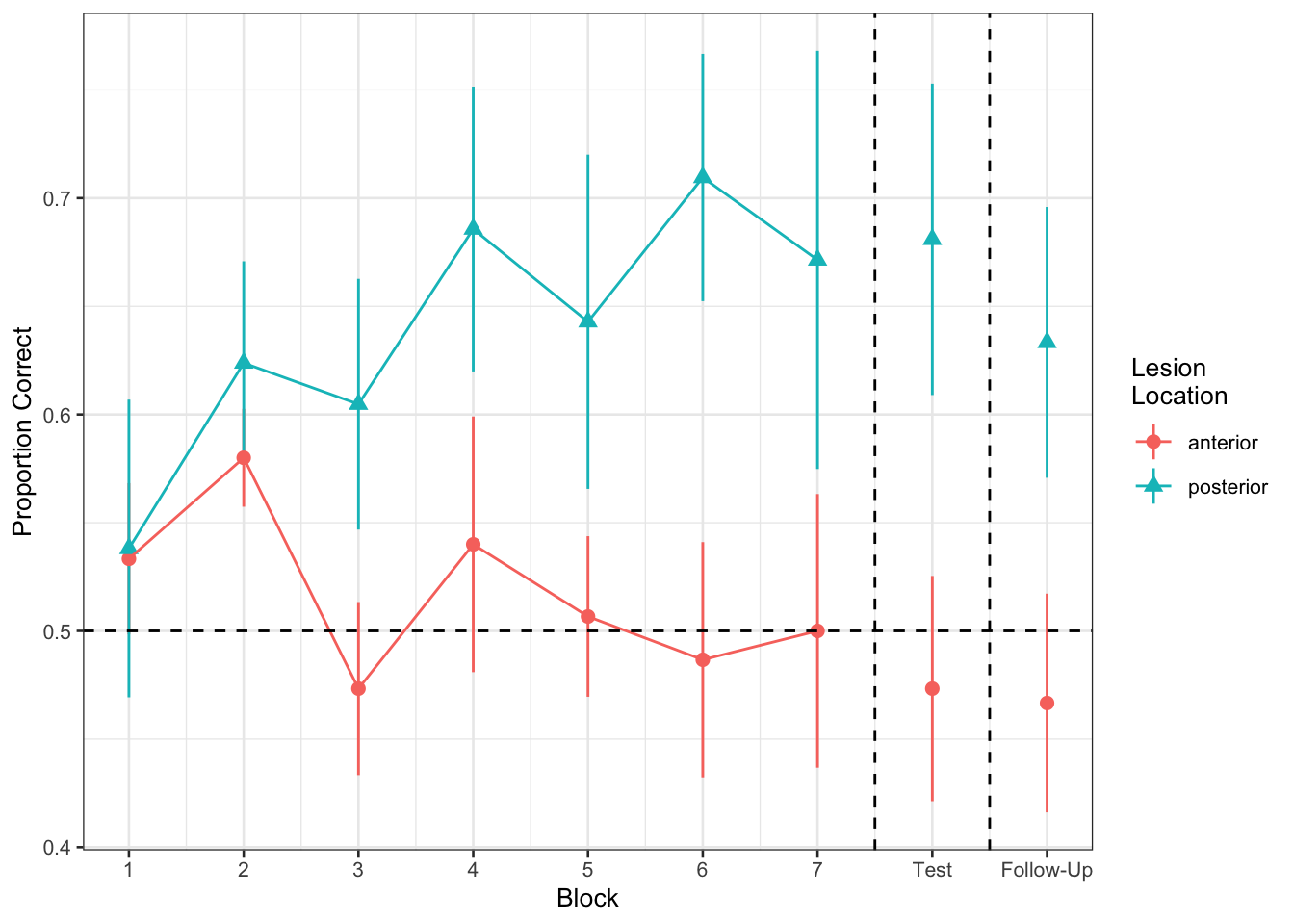
Figure 1 shows the differences between lesion location groups in the average proportion of correct responses at each point in time (i.e., each block, test, and follow-up)

Differences between groups in the average proportion of correct responses at each block

Figure 1: Differences between groups in the average proportion of correct responses at each block

variable description
group Whether participant is a stroke patient (‘patient’) or a healthy control (‘control’)
lesion_location Location of brain lesion: anterior vs posterior
block Experimental block (1-9). Blocks 1-7 were learning blocks, immediately followed by a test in block 8. Block 9 was a follow-up test at a later point
PropCorrect Proportion of 30 responses in a given block that the participant got correct
NumCorrect Number of responses (out of 30) in a given block that the participant got correct
NumError Number of responses (out of 30) in a given block that the participant got incorrect
ID Participant Identifier
Phase Experimental phase, corresponding to experimental block(s): ‘Learning’, ‘Immediate’,‘Follow-up’
Question A1

Load the data. Take a look around. Any missing values? Can you think of why?

Solution

Question A2

Our broader research aim today is to compare the two lesion location groups (those with anterior vs. posterior lesions) with respect to their accuracy of responses over the course of the study.

  • What is the outcome variable?

Hint: Think carefully: there might be several variables which either fully or partly express the information we are considering the “outcome” here.

Solution

Question A3

Research Question 1:
Is the learning rate (training blocks) different between the two lesion location groups?

Hints:

  • Do we want cbind(num_successes, num_failures)?

  • Ensure you are running models on only the data we are actually interested in.

    • Are the healthy controls included in the research question under investigation?
    • Are the testing blocks included in the research question, or only the learning blocks?

  • We could use model comparison via likelihood ratio tests (using anova(model1, model2, model3, ...). For this question, we could compare:

    • A model with just the change over the sequence of blocks
    • A model with the change over the sequence of blocks and an overall difference between groups
    • A model with groups differing with respect to their change over the sequence of blocks

  • What about the random effects part?

    1. What are our observations grouped by?
    2. What variables can vary within these groups?
    3. What do you want your model to allow to vary within these groups?

Suggested answers to the hints if you don’t know where to start

Solution

Question A4

Research Question 2
In the testing phase, does performance on the immediate test differ between lesion location groups, and does the retention from immediate to follow-up test differ between the two lesion location groups?

Let’s try a different approach to this. Instead of fitting various models and comparing them via likelihood ratio tests, just fit the one model which could answer both parts of the question above.

Hints:

  • This might required a bit more data-wrangling before hand. Think about the order of your factor levels (alphabetically speaking, “Follow-up” comes before “Immediate”)!

Solution

Interpreting coefficients in logistic regression
Take some time to remind yourself from USMR of the interpretation of logistic regression coefficients.

The interpretation of the fixed effects of a logistic multilevel model is not very different.
We can obtain the fixed effects from our model by using:

  • fixef(model)
  • summary(model)$coefficients
  • coef(summary(model))
  • tidy(model) from the broom.mixed package
  • (there are probably more ways, but I can’t think of them right now!)

It’s just that for multilevel models, we can model by-cluster random variation around these effects.

Question A5
  1. In family = binomial(link='logit'). What function is used to relate the linear predictors in the model to the expected value of the response variable?
  2. How do we convert this into something more interpretable?

Solution

Question A6

Make sure you pay attention to trying to interpret each fixed effect from your models.
These can be difficult, especially when it’s logistic, and especially when there are interactions.

  • What is the increase in the odds of answering correctly in the immediate test for someone with a posterior legion compared to someone with an anterior legion?

Solution

OPTIONAL: A7

Recreate the visualisation in Figure 2.

Differences between groups in the average proportion of correct responses at each block

Figure 2: Differences between groups in the average proportion of correct responses at each block

Solution

Coding Schemes for Categorical Predictors

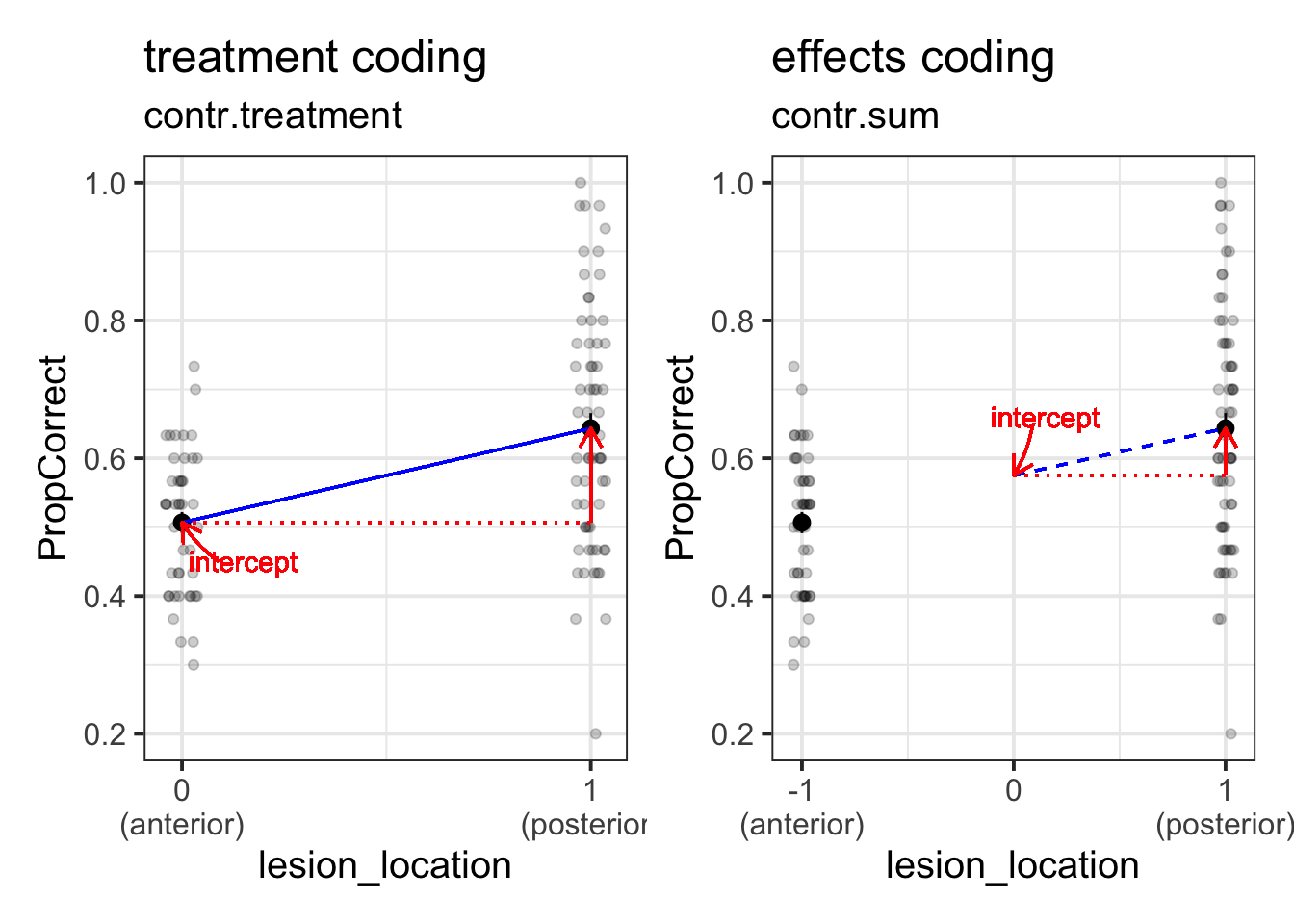
Remember that categorical predictors get inputted into our model as a series of variables which are 0s and 1s? Previously the variable in our model for lesion location was actually being coded with 0 representing one level, and 1 representing the other. This is known as “treatment coding”.

There are lots of other ways we might encode our categorical predictors. One common approach is to use “effects coding”. In the case where we have a binary predictor, this makes zero the mid-point between the two - i.e., the overall mean (this is a bit like mean-centering a continuous predictor).

If we recall that the intercept is “when all predictors are zero”, and that when we have an interaction Y~A+B+A*B in our model, the individual coefficients for A and B are estimated “when the other variable is zero”, then we can start to understand how these different ways of encoding our categorical predictors can change what we are getting out of our model. (Note, they don’t actually change anything about the model fit, but they change what information we are estimating from the model).

If you want to understand this a little more, take a look at this in depth section.

Question A8

This code is that we used to answer question A4 above, only we have edited it to change lesion location to be fitted with “effects coding”.

nwl_test <- filter(nwl, block > 7, !is.na(lesion_location)) %>%
    mutate(
        Phase = factor(Phase),
        Phase = fct_relevel(Phase, "Immediate")
    )

m.recall.loc.effcoding <- 
    glmer(cbind(NumCorrect, NumError) ~ Phase * lesion_location + (1 | ID), 
          contrasts = list(lesion_location = "contr.sum"),
          data = nwl_test, family="binomial")

The interpretation of this is going to get pretty tricky - we have a logistic regression, and we have different coding scheme for our categorical predictor, and we have an interaction.. 🤯

Can you work out the interpretation of the fixed effects estimates?

Solution

Hang on.. p-values are back?!

We noted at the end of last week that we don’t have p-values for lmer()1, but you might notice that we do now have them when we’ve fitted a model with glmer()?

The reason is partly just one of convention. There is a standard practice for determining the statistical significance of parameters in the generalised linear model, relying on asymptotic Wald tests which evaluate differences in log-likelihood.

Reading: Inference in MLM

In USMR, we fitted various simple linear models using lm(), and we could get out either a table of coefficients (for example, Table 1) or a table of the reduction in sums of squared residuals (for example, Table 2). In both of these cases we had a nice set of p-values for us to look at (in R, we often find the p-values in the column named something like Pr(>F)).

A quick reminder: a p-value is the probability of observing results as or more extreme than the obtained ones, if the data were really generated by the hypothesised model or process).

Table 1: t-tests for slope coefficients for predictors in a linear model

Term

Estimate

Std. Error

t value

Pr(>|t|)

(Intercept)

5.37

4.32

1.24

.224

outdoor_time

0.59

0.17

3.51

.001

social_int

1.80

0.27

6.70

< .001


Table 2: F-tests for predictors in a linear model

Term

df

Sum Sq

Mean Sq

F value

Pr(>F)

outdoor_time

1

1,427.94

1,427.94

37.77

< .001

social_int

1

1,697.82

1,697.82

44.91

< .001

Residuals

29

1,096.24

37.80


We could get p-values for these models because we know what the distribution of test statistics of interest (e.g. \(F\)-statistics and \(t\)-statistics), will look like if the null hypothesis were true (i.e., we can describe what they look like in terms of \(F\) and \(t\) distributions with specific degrees of freedom (look back to the USMR materials for a formula).

Unfortunately, the same is not true of multilevel models. For the multilevel model, we can think of it as having residuals at multiple levels: we have the random variation of clusters around the fixed effects, and then random variation of observations around the cluster-level effects (more on this in Week 4).
In the rare occasion that you have a perfectly balanced experimental design, then ratios of sums of squares for multi-level models follow an \(F\)-distribution, in which we know the numerator and denominator degrees of freedom (this means we can work out the degrees of freedom for the \(t\)-test of our fixed effect parameters). Unfortunately, in the real world where things are not often perfectly balanced, determining the denominator degrees of freedom becomes unclear.

Last week, we mentioned a couple of approaches that we might take for drawing inferences, finding ways to compute p-values or confidence intervals.2 We’re going to now extend this to include a few more, and discuss the strengths and limitations of the different approaches.

For these examples…

For the following examples, we’re going to return to our dataset of various toys, and we are going to be concerned with whether practice (the hrs_week variable) is associated with changes in reading ages (R_AGE variable).
To accommodate for the clustered nature of the data, we are going to fit a model with both intercepts and slopes varying by toy-type.

toys_read <- read_csv("https://uoepsy.github.io/data/toyexample.csv")
full_model <- lmer(R_AGE ~ hrs_week + (1 + hrs_week | toy_type), data = toys_read)
summary(full_model)
## Linear mixed model fit by REML ['lmerMod']
## Formula: R_AGE ~ hrs_week + (1 + hrs_week | toy_type)
##    Data: toys_read
## 
## REML criterion at convergence: 637.8
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.51393 -0.58005 -0.00348  0.64053  2.38403 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  toy_type (Intercept) 2.0349   1.4265       
##           hrs_week    0.7834   0.8851   0.63
##  Residual             4.3702   2.0905       
## Number of obs: 132, groups:  toy_type, 20
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   1.7559     0.9610   1.827
## hrs_week      1.1435     0.2957   3.867
## 
## Correlation of Fixed Effects:
##          (Intr)
## hrs_week -0.547
Use a normal approximation (not advisable)

Satterthwaite df approximation

Kenward Rogers df approximations

Likelihood Ratio Test (LRT)

Optional: Parametric Bootstrap LRT

Optional: Parametric Bootstrap Confidence Intervals

Optional: Case-based Bootstrap Confidence Intervals

If you want more information (not required reading for this course), then Julian Faraway has a page here with links to some worked examples, and Ben Bolker has a wealth of information on his GLMM FAQ pages.

  1. We also didn’t get \(R^2\). Check out http://bbolker.github.io/mixedmodels-misc/glmmFAQ.html#how-do-i-compute-a-coefficient-of-determination-r2-or-an-analogue-for-glmms↩︎

  2. It’s always important to note that aiming for a p-value or confidence interval to make a dichotomous decision is only one approach to doing statistics. If you continue to develop your learning of statistics after this course (which we hope you will!), then you will find that there are other schools of thought that bring different benefits.↩︎