Why the need for SEM?

We’ve been mentioning Structural Equation Modelling (SEM) for a few weeks now, but we haven’t been very clear on what exactly it is. Is it CFA? Is it Path Analysis? In fact it is both - it is the overarching framework of which CFA and Path Analysis are just parts.

The beauty comes in when we put these two approaches together.
Path analysis, as we saw last week, offers a way of specifying and evaluating a structural model, in which variables relate to one another in various ways, via different (sometimes indirect) paths. Common models like our old friend multiple regression can be expressed in a Path Analysis framework.
Factor Analysis, on the other hand, brings something absolutely crucial to the table - it allows us to mitigate some of the problems which are associated with measurement error by specifying the existence of some latent variable.

Combine them and we can reap the rewards of having both a structural model and a measurement model. The measurement model is our specification between the items we directly observed, and the latent variables of which we consider these items to be manifestations. The structural model is our specified model of the relationships between the latent variables.

Measurement Error

You will often find research that foregoes the measurement model by taking a scale score (i.e., the sum or mean of a set of likert-type questions). This is what we did in the example in last week’s exercises, e.g.:

  • Intention to vaccinate (scored on a range of 0-100.
  • Health Locus of Control (HLC) score (average score on a set of items relating to perceived control over ones own health).
  • Religiosity (average score on a set of items relating to an individual’s religiosity).

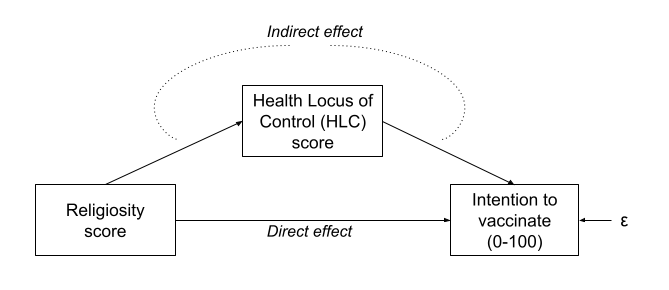
In doing so, we make the assumption that these variables provide measurements of the underlying latent construct without error. Furthermore, when taking the average score, we also make the assumption that each item is equally representative of our construct.

One option would be to conduct a factor analysis, extract the factor scores, and then conduct a path analysis with those scores. This avoids the problem of equally weighting of items to construct, but does not solve our issue of the fact that these variables are imperfect measures of the latent construct.

Scale Scores

If you think about it, taking the mean of a set of items still has the sense of being a ‘factor structure’ in that we think of the items as being , but it constrains all our item variances to be equal, and all our factor loadings to be equal. So it doesn’t really have the benefits of a factor model.

Let’s demonstrate this, using a dataset from the CFA week exercises. It doesn’t matter what it is for this example, so I’m just going to keep the first 4 items (it will save me typing out all the others!)

df <- read_csv("https://uoepsy.github.io/data/conduct_problems_2.csv")[,1:4]
head(df)
## # A tibble: 6 x 4
##    item1  item2   item3  item4
##    <dbl>  <dbl>   <dbl>  <dbl>
## 1 -0.968 -0.686 -0.342   0.600
## 2  0.275 -0.327 -0.0166 -1.08 
## 3  0.255  0.826 -0.308  -1.15 
## 4  1.73   1.67  -0.381   1.13 
## 5 -0.464 -0.584 -0.507  -1.34 
## 6 -0.501 -1.11  -0.310  -1.39

Now suppose that we are just going to take the mean of each persons score on the items, and use that as our measure of “conduct problems.”
We can achieve this easily with rowMeans()

# column bind the data with a column of the row means. 
# only print the head of the data for now
cbind(df, mean = rowMeans(df)) %>% head
##        item1      item2       item3      item4        mean
## 1 -0.9675984 -0.6855043 -0.34177376  0.6001866 -0.34867246
## 2  0.2745735 -0.3273500 -0.01657507 -1.0766079 -0.28648988
## 3  0.2551321  0.8264966 -0.30772456 -1.1498056 -0.09397535
## 4  1.7250373  1.6668358 -0.38103462  1.1259439  1.03419559
## 5 -0.4644687 -0.5836654 -0.50720784 -1.3393316 -0.72366836
## 6 -0.5006721 -1.1075611 -0.30969029 -1.3871634 -0.82627171

Expressed as a factor model, what we are specifying is the below. Notice how we make it so that certain paths are identical by using a label i (for all factor loadings) and j (for all item variances).

mean_model <- '
    CP =~ i*item1 + i*item2 + i*item3 + i*item4
    item1 ~~ j*item1
    item2 ~~ j*item2
    item3 ~~ j*item3
    item4 ~~ j*item4
'
fitmean <- sem(mean_model, data = df)

We can obtain our factor scores using predict(). Let’s put them side-by-side with our rowMeans(), and we need to standardise them to get them in the same units:

factor_scores = scale(predict(fitmean))
rowmeans = scale(rowMeans(df))
cbind(factor_scores, rowmeans) %>% head
##               CP            
## [1,] -0.37898601 -0.37898601
## [2,] -0.30348243 -0.30348243
## [3,] -0.06972665 -0.06972665
## [4,]  1.30012568  1.30012568
## [5,] -0.83431508 -0.83431508
## [6,] -0.95889854 -0.95889854

Reliability

The accuracy and inconsistency with which an observed variable reflects the underlying construct that we consider it to be measuring is termed the reliability.

A silly example

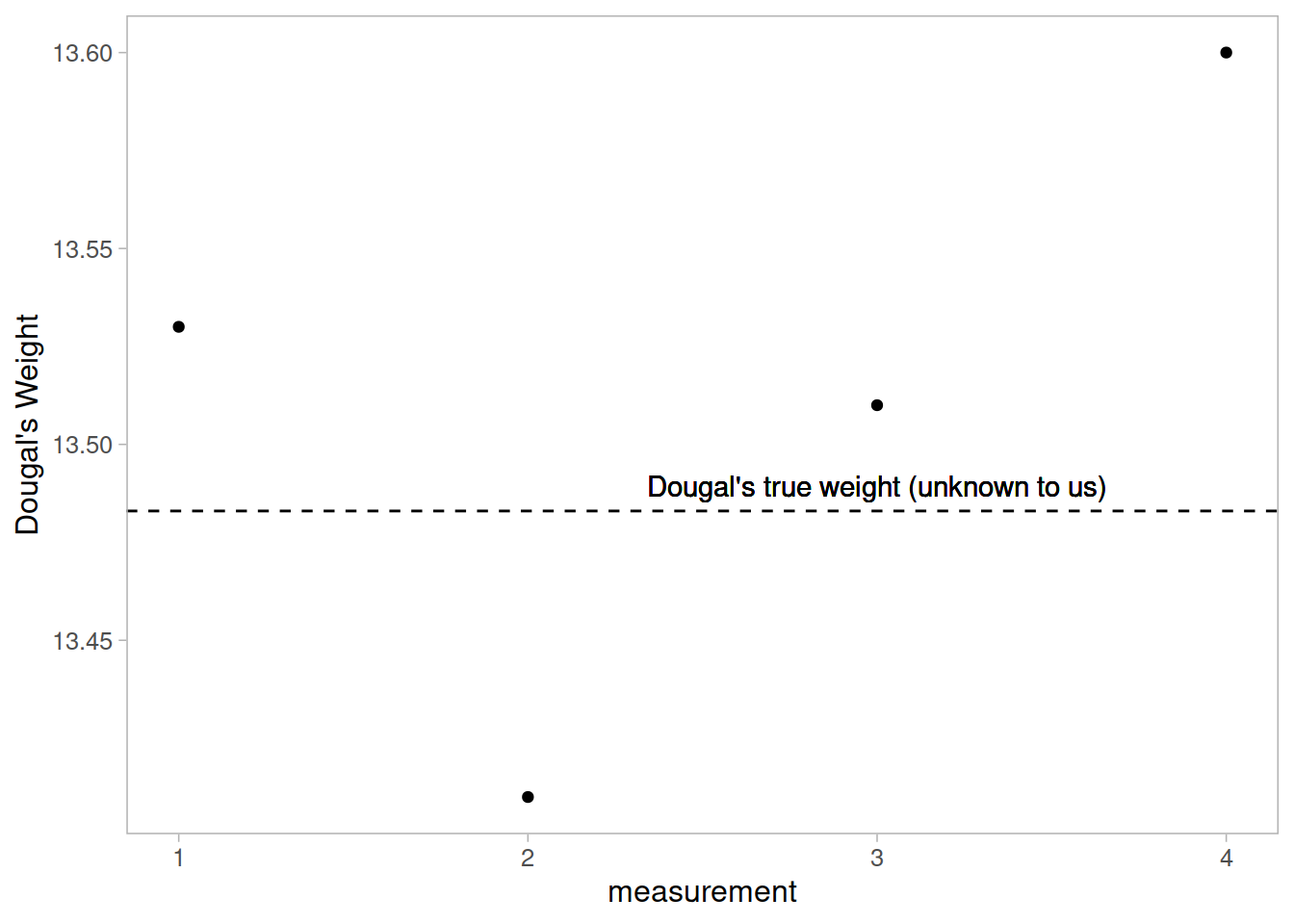
Suppose I’m trying to weigh my dog. I have a set of scales, and I put him on the scales. He weighs in at 13.53kg. I immediately do it again, and the scales this time say 13.41kg. I do it again. 13.51kg, and again, 13.60kg. What is happening? Is Dougal’s weight (Dougal is the dog, by the way) randomly fluctuating by 100g? Or are my scales just a bit inconsistent, and my observations contain measurement error?

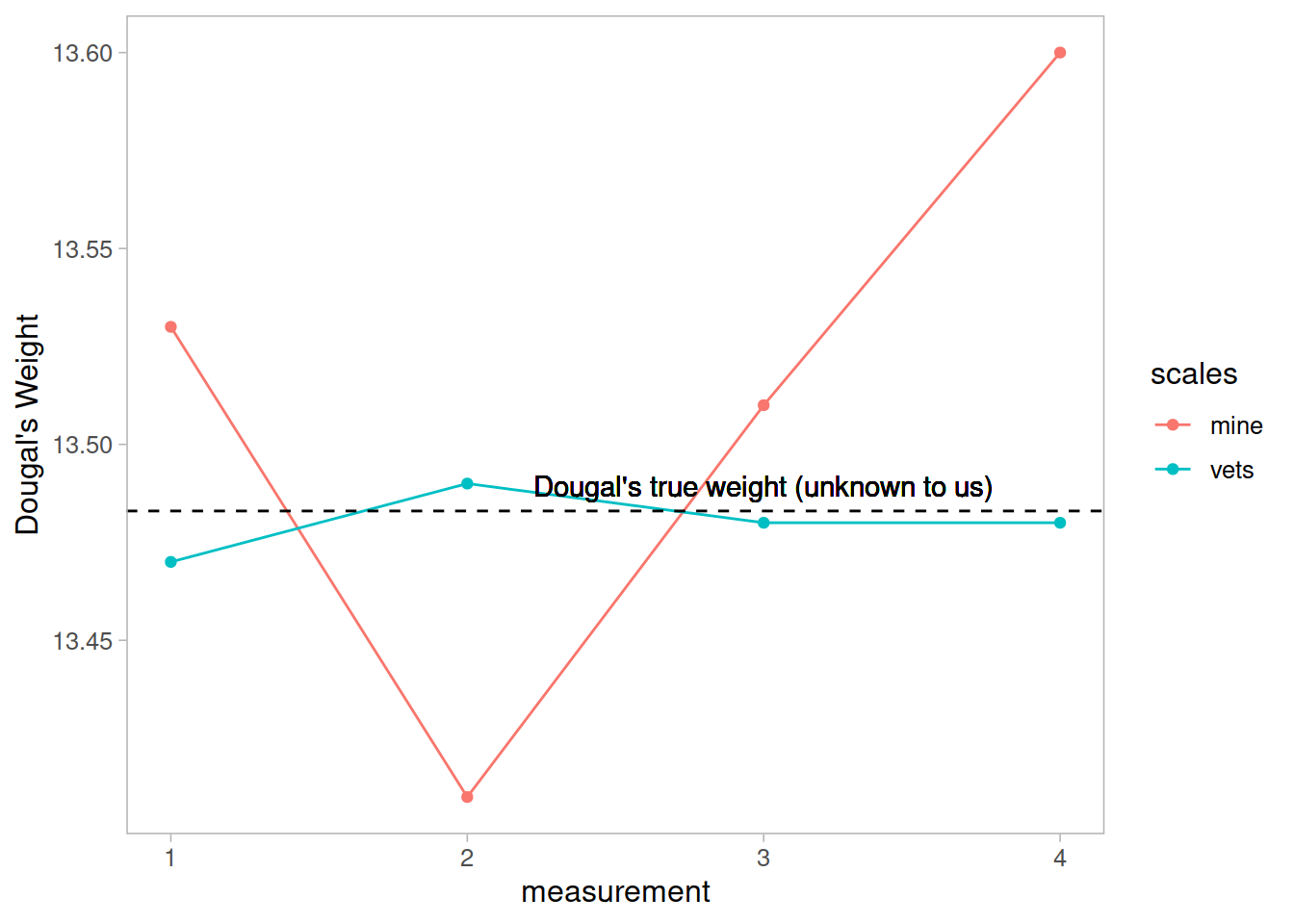
I take him to the vets, where they have a much better set of weighing scales, and I do the same thing (measure him 4 times). The weights are 13.47, 13.49, 13.48, 13.48.
The scales at the vets are clearly more reliable. We still don’t know Dougal’s true weight, but we are better informed to estimate it if we go on the measurements from the scales at the vet.1

Another way to think about reliability is to take the view that \(\text{observations = truth + error}\).
More error = less reliable.

There are different types of reliability:

  • test re-test reliability: correlation between values over repeated measurements.
  • alternate-form reliability: correlation between scores on different forms/versions of a test (we might want different versions to avoid practice effects).
  • Inter-rater reliability: correlation between values obtained from different raters.

The form of reliability we are going to be most concerned with here is known as Internal Consistency. This is the extent to which items within a scale are correlated with one another. There are two main measures of this:

alpha and omega

\[ \begin{align} & \text{Cronbach's }\alpha = \frac{n \cdot \overline{cov(ij)}}{\overline{\sigma^2_i} + (n-1) \cdot \overline{cov(ij)}} & \\ & \text{Where:} \\ & n = \text{number of items} \\ & \overline{cov(ij)} = \text{average covariance between item-pairs} \\ & \overline{\sigma^2_i} = \text{average item variance} \\ \end{align} \] Ranges from 0 to 1 (higher is better).
You can get this using the alpha() function from the psych package.

McDonald’s Omega \(\omega\) is substantially more complicated, but avoids the limitation that Cronbach’s alpha which assumes that all items are equally related to the construct. You can get it using the omega() function from the psych package. If you want more info about it then the help docs (?omega()) are a good place to start.

You can’t test the structural model if the measurement model is bad

if you test the relationships between a set of latent factors, and they are not reliably measured by the observed items, then this error propagates up to influence the fit of the model.
To test the measurement model, it is typical to saturate the structural model (i.e., allow all the latent variables to correlate with one another). This way any misfit is due to the measurement model.

Fit indices

After spending much of our time in the regression framework, the move to SEM can feel mind-boggling. Give two researchers the same whiteboard on which your variables are drawn, and they may connect them in completely different ways. This flexibility can at first make SEM feel like a free-for-all (i.e., just do whatever you like, get a p-value out of it, and off we go!). However, to some people this is one of the main benefits: it forces you to be explicit in specifying your theory, and allows you to test your theory and examine how well it fits with the data you observed.

We have actually already go to grips with the starting point of how structural equation models work in the previous weeks. We begin with an observed covariance matrix, we fit our theoretical model to the data, and our estimation method (e.g. maximum likelihood) provides us with the set of parameter estimates for our model which best reproduce the observed covariance matrix. Of course, they will not perfectly reproduce the covariance matrix, but our parameter estimates will give us a model implied covariance matrix. We can compare this to the observed covariance matrix in order to assess the fit of our theoretical model.

Global fit

\(\chi^2\)

For structural equation models, a chi-square value can be obtained which reflects the discrepancy between the model-implied covariance matrix and the observed covariance matrix. We can then calculate a p-value for this chi-square statistic by using the chi-square distribution with the degrees of freedom equivalent to that of the model.

If we denote the population covariance matrix as \(\Sigma\) and the model-implied covariance matrix as \(\Sigma(\Theta)\), then we can think of the null hypothesis here as \(H_0: \Sigma - \Sigma(\Theta) = 0\). In this way our null hypothesis is that our theoretical model is correct (and can therefore perfectly reproduce the covariance matrix).

It is very sensitive to departures from normality, as well as small sample sizes, and can often lead to rejecting otherwise adequate models.

Parsimonious fit

RMSEA

Based on the \(\chi^2/df\) ratio, this measure of fit is intended to take into account for the fact the model might hold approximately (rather than exactly) in the population.

Typical cut-offs:
\(<0.05\) : Close fit
\(>0.1\) : Poor fit

AIC, BIC and SSBIC

We have already been introduced to AIC and BIC in the regression world, but we now add to that the sample size adjusted BIC (SSBIC). These indices are only meaningful when making comparisons, meaning that two different models must be estimated. Lower values indicate better fit. comparing mode The AIC is a comparative measure of fit and so it is meaningful only when two different models are estimated. Lower values indicate a better fit and so the model with the lowest AIC is the best fitting model. There are somewhat different formulas given for the AIC in the literature, but those differences are not really meaningful as it is the difference in AIC that really matters:

Absolute fit

SRMR

Standardised root mean square residual (SRMR) summarises the average covariance residuals (discrepancies between observed and model-implied covariance matrices). Smaller SRMR equates to better fit.

Typical cut-off:
\(<0.08\) : Good fit

Incremental fit

TLI and CFI

These fit indices compare the fit of the model to the that of a baseline model. In most cases, this is the null model, in which there are no relationships between latent variables (i.e., covariances among latent variables are all assumed to be zero). TLI is somewhat sensitive to the average size of correlations in the data.

Common cut-offs: TLI
\(<0.9\) : Poor fit
\(1\) : Very good fit
\(>1\) : Possible overfitting

CFI
\(\sim 1\) : Good fit

Local fit

In addition to the overall fit of our model, we can look at specific parameters, the inclusion of which may improve model fit. These are known as modification indices, and you can get them from passing a SEM object to modindices() or modificationindices(). They provide the estimated value for each additional parameter, and the improvement in the \(\chi^2\) value that would be obtained with its addition to the model. Note that it will be tempting to look at modification indices and start adding to your model to improve fit, but this should be strongly guided by whether the additional paths make theoretical sense. Additionally, once a path is added, and modification indices are computed on the new model, you may find some completely different paths are suggested as possibly modification indices!

Exercises

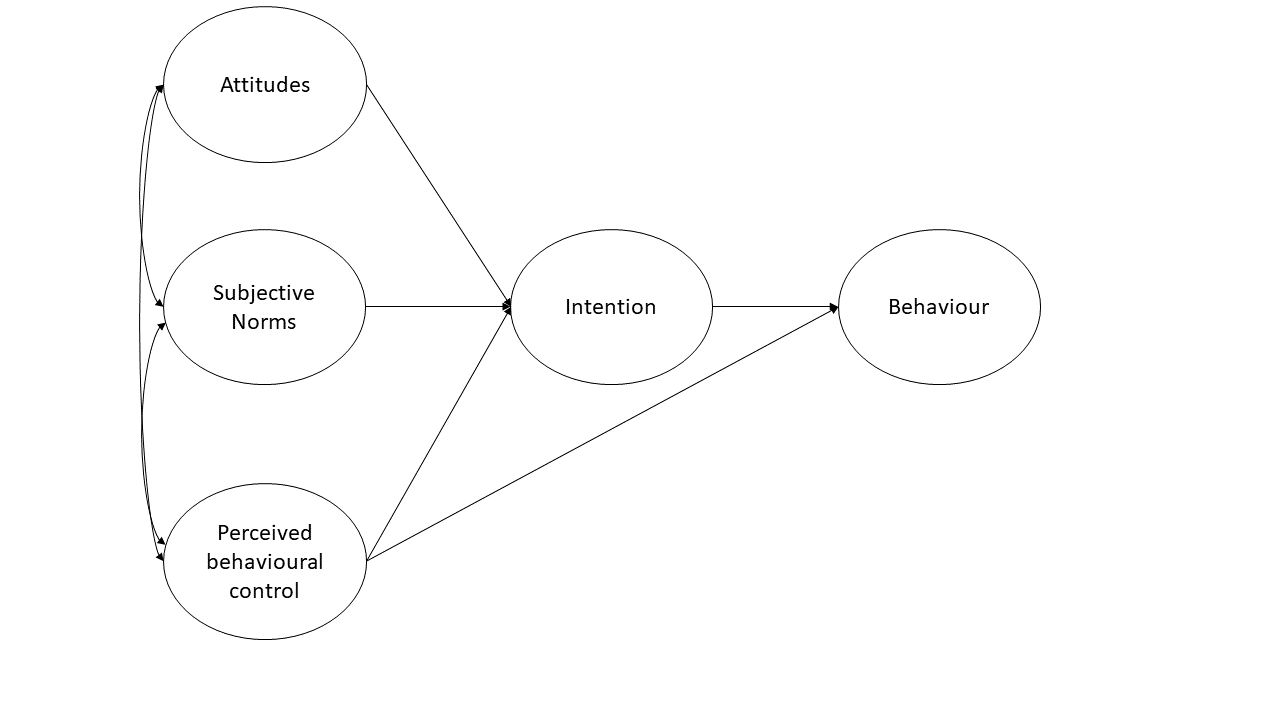
A researcher wants to apply the theory of planned behaviour to understand engagement in physical activity. The theory of planned behaviour is summarised in Figure 1 (only the latent variables and not the items are shown). Attitudes refer to the extent to which a person had a favourable view of exercising; subjective norms refer to whether they believe others whose opinions they care about believe exercise to be a good thing; and perceived behavioural control refers to the extent to which they believe exercising is under their control. Intentions refer to whether a person intends to exercise and ‘behaviour’ is a measure of the extent to which they exercised. Each construct is measured using four items.

Theory of planned behaviour (latent variables only)

Figure 1: Theory of planned behaviour (latent variables only)

The data is available either:

Question A1

Did you do the final exercise (writing up your results) from last week? Our example write-up is now visible (see last week) against which you can compare yours.

Please note: Writing-up is an important skill, and attempting these questions yourself (rather than simply reading through the example write-ups) will help a lot when it comes to writing your assessment.

Question A2

Read in the data using the appropriate function. We’ve given you .csv files for a long time now, but it’s good to be prepared to encounter all sorts of weird filetypes.

Can you successfully read in from both types of data?

Solution

Question A3

Test separate one-factor models for each construct.
Are the measurement models satisfactory? (check their fit measures).

Solution

Question A4

Using lavaan syntax, specify a structural equation model that corresponds to the model in Figure 1. For each construct use a latent variable measured by the corresponding items in the dataset.

Solution

Question A5

Estimate the model from Question A4 and evaluate the model

  • Does the model fit well?
  • Are the hypothesised paths significant?

Solution

Question A6

Examine the modification indices and expected parameter changes - are there any additional parameters you would consider including?

Solution

Question A7

Test the indirect effect of attitudes, subjective norms, and perceived behavioural control on behaviour via intentions.

Remember, when you fit the model with sem(), use se='bootstrap' to get boostrapped standard errors (it may take a few minutes). When you inspect the model using summary(), get the 95% confidence intervals for parameters with ci = TRUE.

Solution

Question A8

Write up your analysis as if you were presenting the work in academic paper, with brief separate ‘Method’ and ‘Results’ sections

Solution

  1. Of course this all assuming that the scales aren’t completely miscalibrated↩︎