Introducing Mixed Effects Models

Some background reading

• Winter, 2013
  
• Brauer & Curtin, 2018, (pdf)
  
• Luke, 2017
  

Preliminaries

1. Open Rstudio, and create a new project for this course!!
2. Create a new RMarkdown document (giving it a title for this week).

A Note on terminology

The methods we’re going to learn about in the first five weeks of this course are known by lots of different names: “multilevel models”; “hierarchical linear models”; “mixed-effect models”; “mixed models”; “nested data models”; “random coefficient models”; “random-effects models”; “random parameter models”… and so on).

What the idea boils down to is that model parameters vary at more than one level. This week, we’re going to explore what that means.

New Toys!

New package time!

These are the main packages we’re going to use in this block. It might make sense to install them now if you do not have them already (note, the rstudio.ppls.ed.ac.uk server already has lme4 installed for you).

• tidyverse
  
• lme4
  
• effects
  
• broom
• broom.mixed

New data time!

Recall the example from last semesters’ USMR course, where the lectures explored linear regression with a toy dataset of how practice influences the reading age of Playmobil characters:

Figure 1: USMR Week 8 Lecture

Let us know broaden our scope to the investigation of how practice affects reading age for all toys, (not just Playmobil characters).
You can find a dataset at https://uoepsy.github.io/data/toyexample.csv

toys_read <- read_csv("https://uoepsy.github.io/data/toyexample.csv")

The datasets contains information on 132 different toy figures. This time, however, they come from a selection of different families/types of toy. You can see the variables in the table below¹.

variable	description
toy_type	Type of Toy
toy	Character
hrs_week	Hours of practice per week
age	Age (in years)
R_AGE	Reading Age

Linear model refresh

Recall that in the course last semester we learned all about the linear regression model:

\[ \begin{align}\\ & \text{for observation }i \\ & \color{red}{Y_i} = \color{blue}{\beta_0 \cdot{} 1 + \beta_1 \cdot{} X_{1i} \ + \ ... \ + \ \beta_p \cdot{} X_{pi}} + \varepsilon_i \\ \end{align} \]

And if we wanted to write this more simply, we can express \(X_1\) to \(X_p\) as an \(n \times p\) matrix (samplesize \(\times\) parameters), and \(\beta_0\) to \(\beta_p\) as a vector of coefficients:

\[ \mathbf{y} = \boldsymbol{X\beta} + \boldsymbol{\varepsilon} \quad \\ \text{where} \quad \varepsilon \sim N(0, \sigma) \text{ independently} \]

Question A1

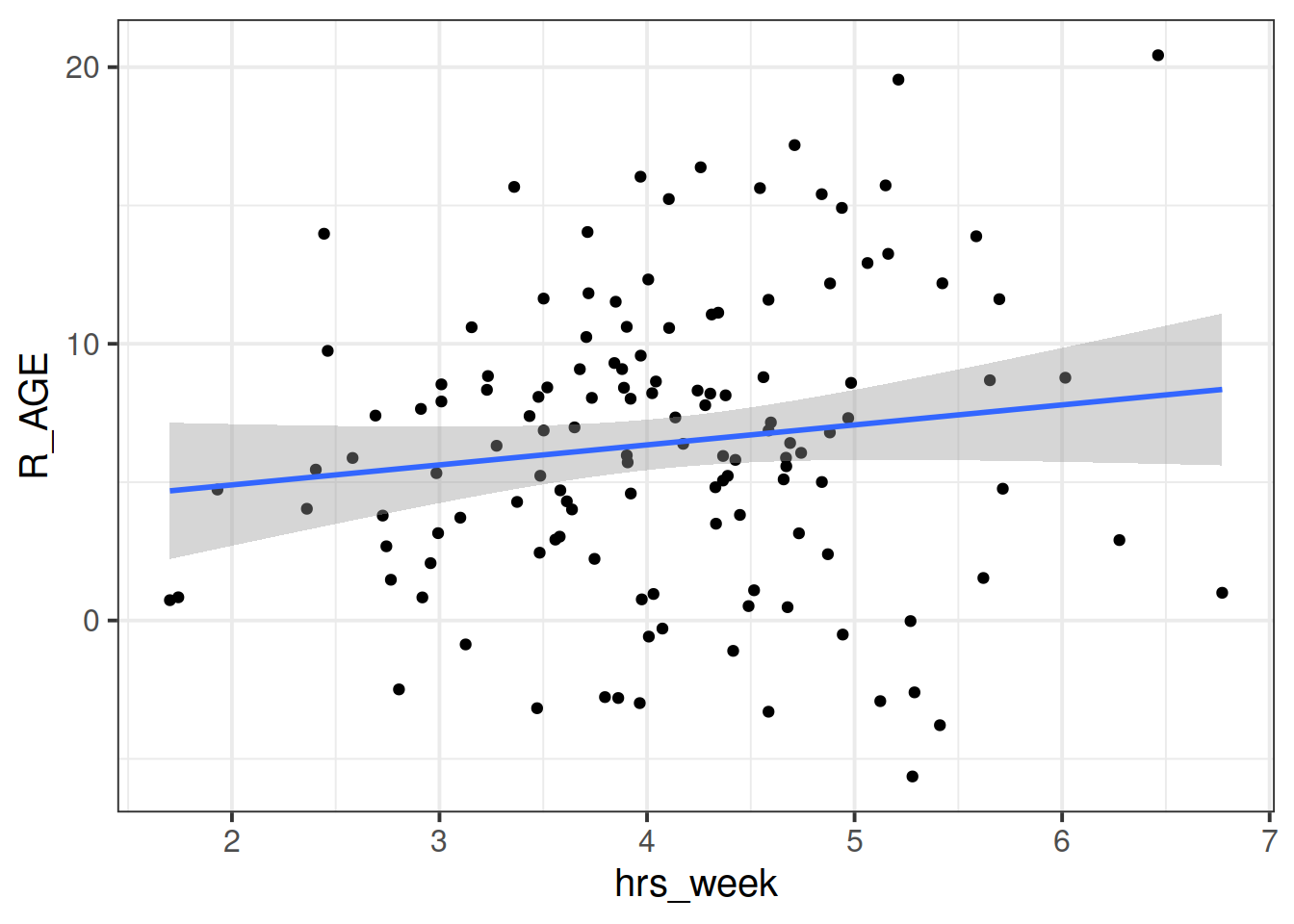
Plot the bivariate relationship between Reading Age and Hrs per Week practice, and then fit the simple linear model: \[ \text{Reading Age} \sim \beta_0 + \beta_1 \cdot \text{Hours per week practice} + \varepsilon \]

Solution

ggplot(data = toys_read, aes(x=hrs_week, y=R_AGE))+
  geom_point()+
  geom_smooth(method = "lm")

simplemod <- lm(R_AGE~hrs_week, data=toys_read)
summary(simplemod)

## 
## Call:
## lm(formula = R_AGE ~ hrs_week, data = toys_read)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -12.9086  -3.2084   0.0047   3.0493  12.3262 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)   3.4554     2.0379   1.696   0.0924 .
## hrs_week      0.7229     0.4866   1.486   0.1398  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.276 on 130 degrees of freedom
## Multiple R-squared:  0.01669,    Adjusted R-squared:  0.009131 
## F-statistic: 2.207 on 1 and 130 DF,  p-value: 0.1398

Question A2

Thinking about the assumption we make about our model: \[ \text{where} \quad \varepsilon \sim N(0, \sigma) \text{ independently} \] Have we satisfied this assumption (specifically, the assumption of independence of errors)? Our model from the previous question will assume that the residuals for all toys are independent of one another. But is this an assumption we can make? Might we not think that the Playmobil characters could be generally better at reading than the Power Rangers? Or even that ScoobyDoo figurines might be more receptive to practice than the Sock Puppets are?
The natural grouping of the toys introduces a level of dependence, which we would be best to account for.

Try running the code below.

ggplot(data = toys_read, aes(x=hrs_week, y=R_AGE))+
  geom_point()+
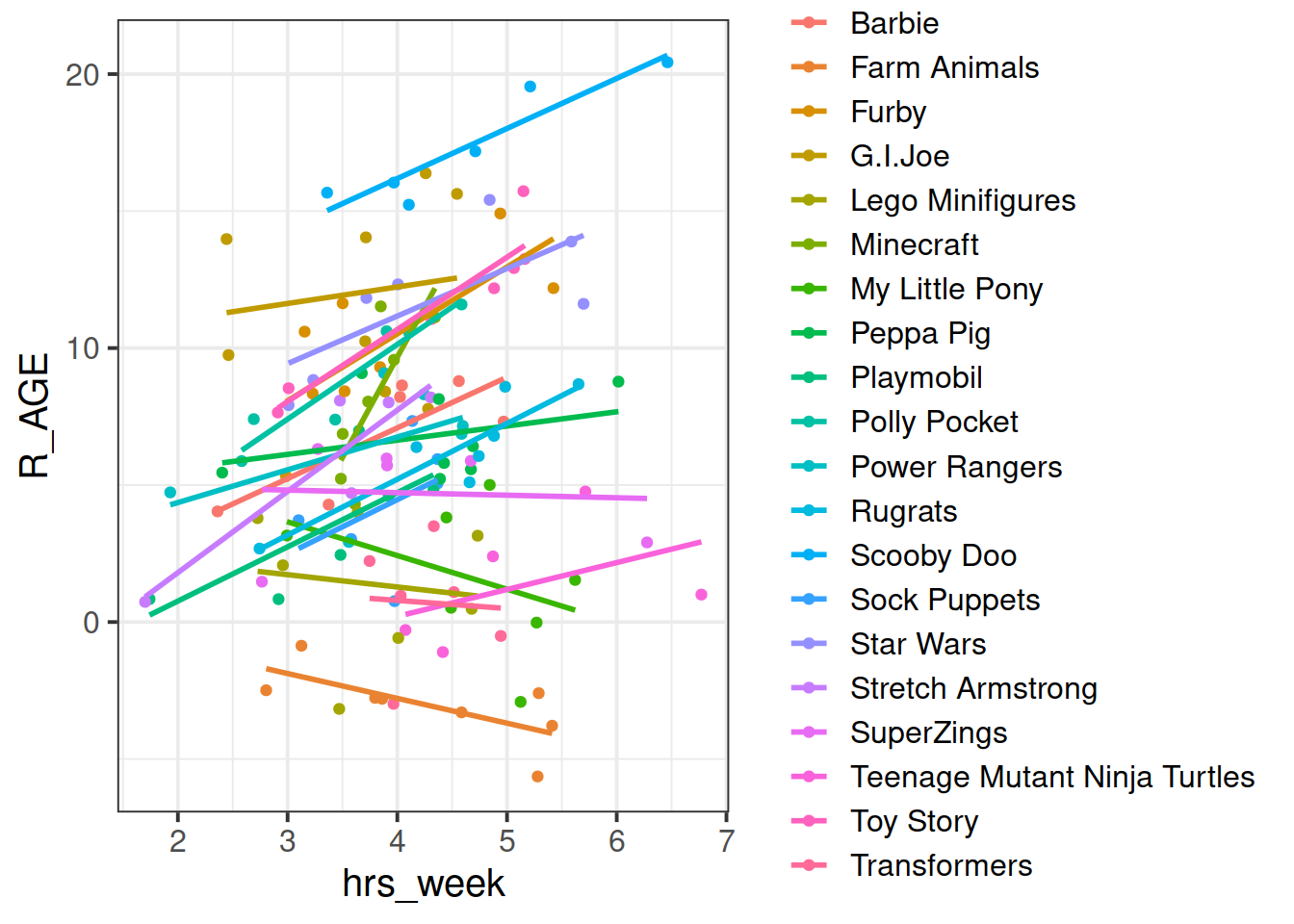
  geom_smooth(method="lm",se=FALSE)

Then try editing the code to include an aesthetic mapping from the type of toy to the color in the plot.
How do your thoughts about the relationship between Reading Age and Practice change?

Solution

ggplot(data = toys_read, aes(x=hrs_week, y=R_AGE))+
  geom_point()+
  geom_smooth(method="lm",se=FALSE)

ggplot(data = toys_read, aes(x=hrs_week, y=R_AGE, col=toy_type))+
  geom_point()+
  geom_smooth(method="lm",se=FALSE)

From the second plot, we see a lot of the toy types appear to have a positive relationship (practice increases reading age). There seem to be differences between toy types in both the general reading level (Scooby Doo characters can read very well), and in how practice influences reading age (for instance, the Farm Animals don’t seem to improve at all with practice!).

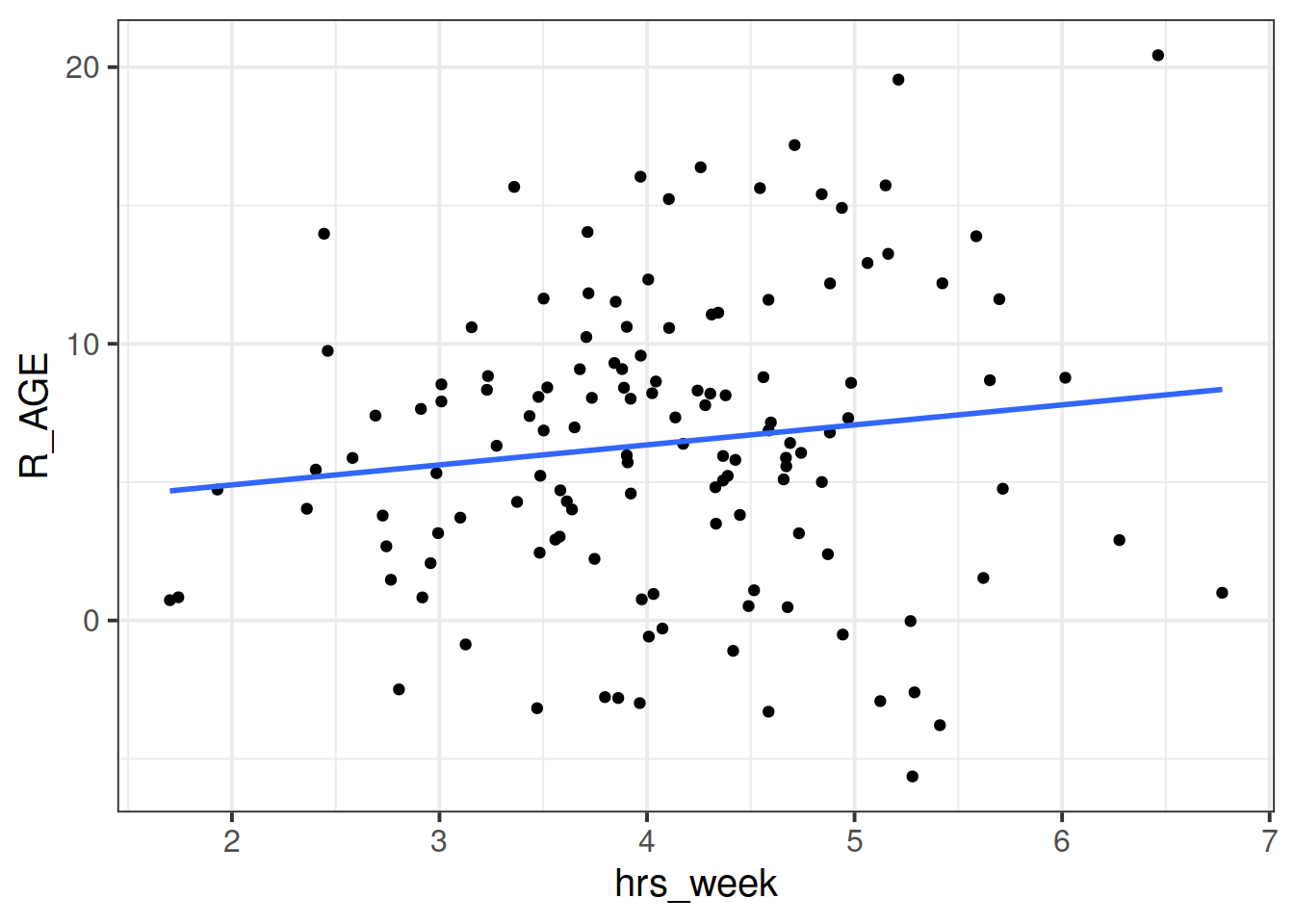
We can consider the simple regression model (lm(R_AGE ~ hrs_week, data = toys_read)) to “pool” the information from all observations together.
We’ll call this Complete Pooling.
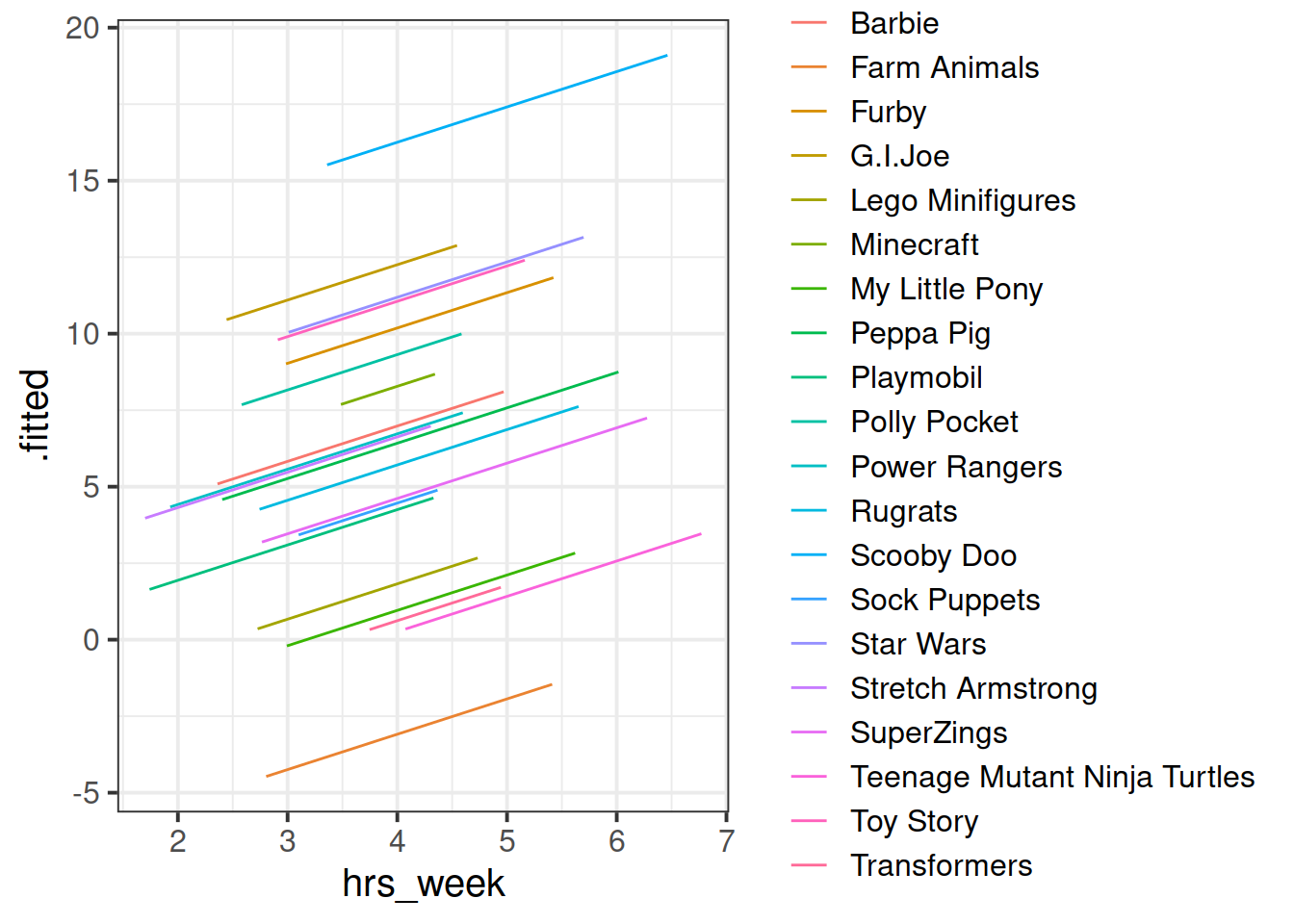
In the ‘Complete Pooling’ approach, we simply ignore the natural clustering of the toys, as if we were unaware of it. The problem is that this assumes the same regression line for all toy types, which might not be that appropriate:

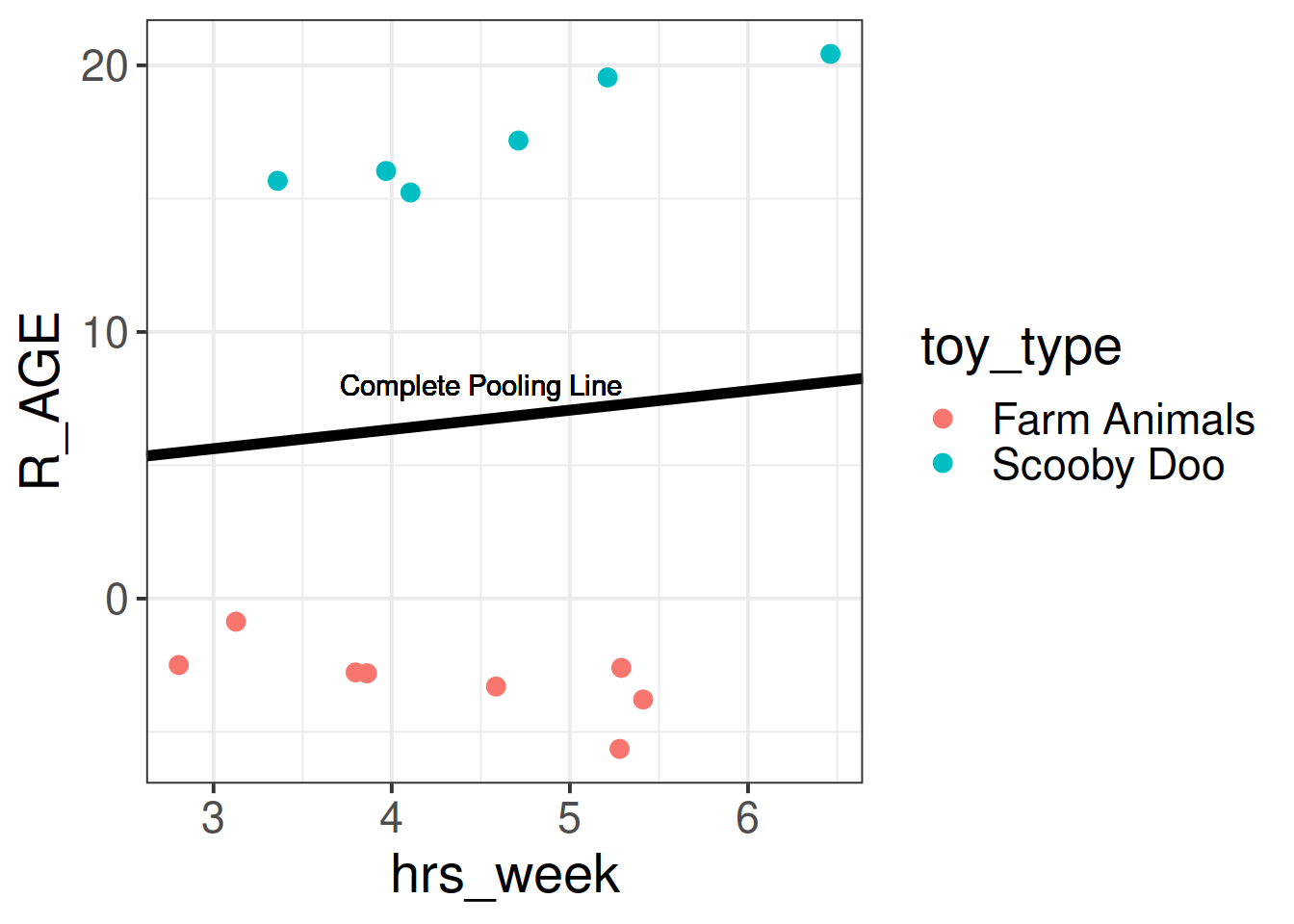
Figure 2: Complete pooling can lead to bad fit for certain groups

There are various ways we could attempt to deal with the problem that our data are in groups (or “clusters”).² With the tools you have learned in the USMR course last semester, you may be tempted to try including toy type in the model as another predictor, to allow for some toy types being generally better than others:

lm(R_AGE ~ hrs_week + toy_type, data = toys_read)

Or even to include an interaction to allow for toy types to respond differently to practice:

lm(R_AGE ~ hrs_week * toy_type, data = toys_read)

We might call this approach the No Pooling method, because the information from each cluster contributes only to an estimated parameter for that cluster, and there is no pooling of information across clusters. This is a good start, but it means that a) we are estimating a lot of parameters, and b) we are not necessarily estimating the parameter of interest (the overall effect of practice on reading age). Furthermore, we’ll probably end up having high variance in the estimates at each group.

So what if we could do something in between?… “Partial Pooling” perhaps?

Introducing MLM

Multilevel models take the approach of allowing the groups/clusters to vary around our \(\beta\) estimates.

In the lectures, we saw this as:

\[ \begin{align} & \text{for observation }j\text{ in group }i \\ \quad \\ & \text{Level 1:} \\ & \color{red}{Y_{ij}} = \color{blue}{\beta_{0i} \cdot 1 + \beta_{1i} \cdot X_{ij}} + \varepsilon_{ij} \\ & \text{Level 2:} \\ & \color{blue}{\beta_{0i}} = \gamma_{00} + \color{orange}{\zeta_{0i}} \\ & \color{blue}{\beta_{1i}} = \gamma_{10} + \color{orange}{\zeta_{1i}} \\ \quad \\ & \text{Where:} \\ & \gamma_{00}\text{ is the population intercept, and }\color{orange}{\zeta_{0i}}\text{ is the deviation of group }i\text{ from }\gamma_{00} \\ & \gamma_{10}\text{ is the population slope, and }\color{orange}{\zeta_{1i}}\text{ is the deviation of group }i\text{ from }\gamma_{10} \\ \end{align} \]

We are now assuming \(\color{orange}{\zeta_0}\), \(\color{orange}{\zeta_1}\), and \(\varepsilon\) to be normally distributed with a mean of 0, and we denote their variances as \(\sigma_{\color{orange}{\zeta_0}}^2\), \(\sigma_{\color{orange}{\zeta_1}}^2\), \(\sigma_\varepsilon^2\) respectively.

The \(\color{orange}{\zeta}\) components also get termed the “random effects” part of the model, Hence names like “random effects model,” etc.

Optional Alternative notation

Many people use the symbol \(u\) in place of \(\zeta\).
In various resources, you are likely to see \(\alpha\) used to denote the intercept instead of \(\beta_0\).

Sometimes, you will see the levels collapsed into one equation, as it might make for more intuitive reading:

\[ \color{red}{Y_{ij}} = (\color{blue}{\beta_0} + \color{orange}{\zeta_{0i}}) \cdot 1 + ( \color{blue}{\beta_{1}} + \color{orange}{\zeta_{1i}} ) \cdot X_{ij} + \varepsilon_{ij} \\ \]

And then we also have the condensed matrix form of the model, in which the Z matrix represents the grouping structure, and the \(u\) (or \(\zeta\)) are the estimated random deviations. \[ \mathbf{y} = \boldsymbol{X\beta} + \boldsymbol{Zu} + \boldsymbol{\varepsilon} \]

Fitting MLMs

Introducing lme4

We’re going to use the lme4 package, and specifically the functions lmer() and glmer().
“(g)lmer” here stands for “(generalised) linear mixed effects regression.”

You will have seen some use of these functions in the lectures. The broad syntax is:

lmer(formula, REML = logical, data = dataframe)

We write the first bit of our formula just the same as our old friend the normal linear model y ~ 1 + x + x2 + ..., where y is the name of our outcome variable, 1 is the intercept (which we don’t have to explicitly state as it will be included anyway) and x, x2 etc are the names of our explanatory variables.

But let us suppose that we wish to model our intercept not as a fixed constant, but as varying randomly according to some grouping around a fixed center. This would fit the model: \[ \begin{align} & \text{Level 1:} \\ & \color{red}{Y_{ij}} = \color{blue}{\beta_{0i} \cdot 1 + \beta_{1} \cdot X_{ij}} + \varepsilon_{ij} \\ & \text{Level 2:} \\ & \color{blue}{\beta_{0i}} = \gamma_{00} + \color{orange}{\zeta_{0i}} \\ \end{align} \] With lme4, we now have the addition of these such random effect terms, specified in parenthesis with the | operator (the vertical line | is often found to the left of the z key on QWERTY keyboards).

We use the | operator to separate the parameters (intercept, slope etc.) on the LHS, from the grouping variable(s) on the RHS, by which we would like to model these parameters as varying.

We can fit the model above by allowing the intercept to vary by our grouping variable (g below)

Random intercept model: y ~ 1 + x + (1|g)

And by extension we can also allow the effect y~x to vary between groups:

Random intercept & slope model: y ~ 1 + x + (1 + x|g)

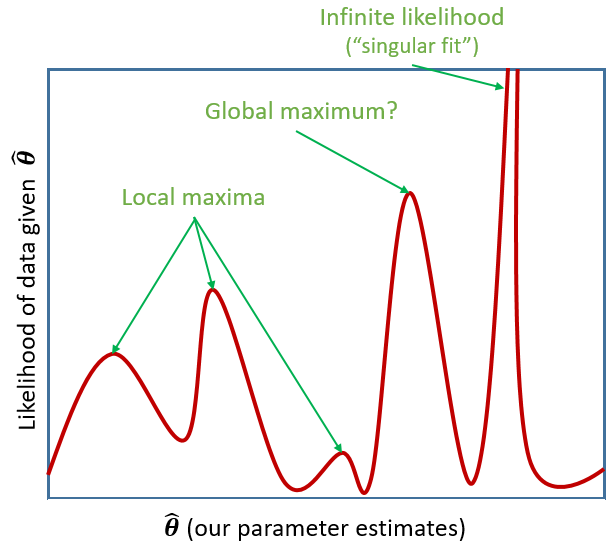
Estimation problems

For large datasets and/or complex models (lots of random-effects terms), it is quite common to get a convergence warning. There are lots of different ways to deal with these (to try to rule out hypotheses about what is causing them).

For now, if lmer() gives you convergence errors, you could try changing the optimizer. Bobyqa is a good one: add control = lmerControl(optimizer = "bobyqa") when you run your model.

What is a convergence warning??

Remember back to Week 10 of USMR, when we introduced the generalised linear model (GLM) we briefly discussed Maximum likelihood in an explanation of how models are fitted.

The key idea of maximum likelihood estimation (MLE) is that we (well, the computer) iteratively finds the set of estimates for our model which it considers to best reproduce our observed data. Recall our simple linear regression model of how practice (hrs per week) affects reading age: \[ \color{red}{ReadingAge_i} = \color{blue}{\beta_0 \cdot{} 1 + \beta_1 \cdot{} Practice_{1i}} + \varepsilon_i \] There are values of \(\beta_0\) and \(\beta_1\) and which maximise the likelihood of observing our data. For linear regression, these we obtained these same values a different way, via minimising the sums of squares. And we saw that this is not possible for more complex models (e.g., logistic), which is where we turn to MLE.

In a one-dimensional world, we could imagine the process of maximum likelihood estimation as simply finding the top of the curve:

Figure 3: MLE

However, our typical models estimate a whole bunch of parameters, and our multi-level models have yet more! So what we (our computers) need to do is find the maximum, but avoid local maxima and singularities.

Figure 4: MLE for complex models

There are different technques for doing this, which we apply by using different ‘optimisers.’ Technical problems to do with model convergence and ‘singular fit’ come into play when the optimiser we are using either can’t find a suitable maximum, or gets stuck in a singularity (think of it like a black hole of likelihood, which signifies that there is not enough variation in our data to construct such a complex model).

Fitting some models

Question A3

Using lmer() from the lme4 package, fit a model of practice (hrs_week) predicting Reading age (R_AGE), with by-toytype random intercepts. Pass the model to summary() to see the output.

Solution

library(lme4)
rmodel1 <- lmer(R_AGE ~ hrs_week + (1 | toy_type), data = toys_read)
summary(rmodel1)

## Linear mixed model fit by REML ['lmerMod']
## Formula: R_AGE ~ hrs_week + (1 | toy_type)
##    Data: toys_read
## 
## REML criterion at convergence: 653.1
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.31139 -0.62361  0.05812  0.63477  1.71073 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  toy_type (Intercept) 23.188   4.815   
##  Residual              5.006   2.237   
## Number of obs: 132, groups:  toy_type, 20
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   1.6274     1.4462   1.125
## hrs_week      1.1547     0.2317   4.983
## 
## Correlation of Fixed Effects:
##          (Intr)
## hrs_week -0.654

Question A4

Sometimes the easiest way to start understanding your model is to visualise it.

Load the package broom.mixed. Along with some handy functions tidy() and glance() which give us the information we see in summary(), there is a handy function called augment() which returns us the data in the model plus the fitted values, residuals, hat values, Cook’s D etc..

library(broom.mixed)
rmodel1 <- lmer(R_AGE ~ hrs_week + (1 | toy_type), data = toys_read)
augment(rmodel1)

## # A tibble: 132 x 14
##    R_AGE hrs_week toy_type   .fitted  .resid  .hat .cooksd .fixed    .mu .offset
##    <dbl>    <dbl> <fct>        <dbl>   <dbl> <dbl>   <dbl>  <dbl>  <dbl>   <dbl>
##  1  9.31     3.84 Furby       10.0   -0.701  0.122 7.75e-3   6.06 10.0         0
##  2 12.2      4.88 Toy Story   12.1    0.105  0.142 2.14e-4   7.26 12.1         0
##  3  8.08     3.48 Stretch A…   6.02   2.06   0.192 1.25e-1   5.64  6.02        0
##  4  9.08     3.68 Peppa Pig    6.05   3.03   0.126 1.52e-1   5.87  6.05        0
##  5  2.07     2.96 Lego Mini…   0.621  1.45   0.146 4.20e-2   5.04  0.621       0
##  6 10.2      3.71 G.I.Joe     11.9   -1.67   0.122 4.41e-2   5.91 11.9         0
##  7  8.05     3.73 Minecraft    7.97   0.0730 0.139 9.96e-5   5.94  7.97        0
##  8 11.6      4.59 Polly Poc…   9.99   1.60   0.172 6.42e-2   6.92  9.99        0
##  9 12.3      4.01 Star Wars   11.2    1.13   0.140 2.40e-2   6.25 11.2         0
## 10  5.06     4.37 Sock Pupp…   4.89   0.171  0.163 6.78e-4   6.67  4.89        0
## # … with 122 more rows, and 4 more variables: .sqrtXwt <dbl>, .sqrtrwt <dbl>,
## #   .weights <dbl>, .wtres <dbl>

Add to the code below to plot the model fitted values, and color them according to toy type.
(you may need to edit rmodel1 to be whatever name you assigned to your model).

augment(rmodel1) %>%
  ggplot(aes(x = hrs_week, y = ...... 

Solution

augment(rmodel1) %>%
  ggplot(aes(x = hrs_week, y = .fitted, col = toy_type)) + 
  geom_line()

Question A5

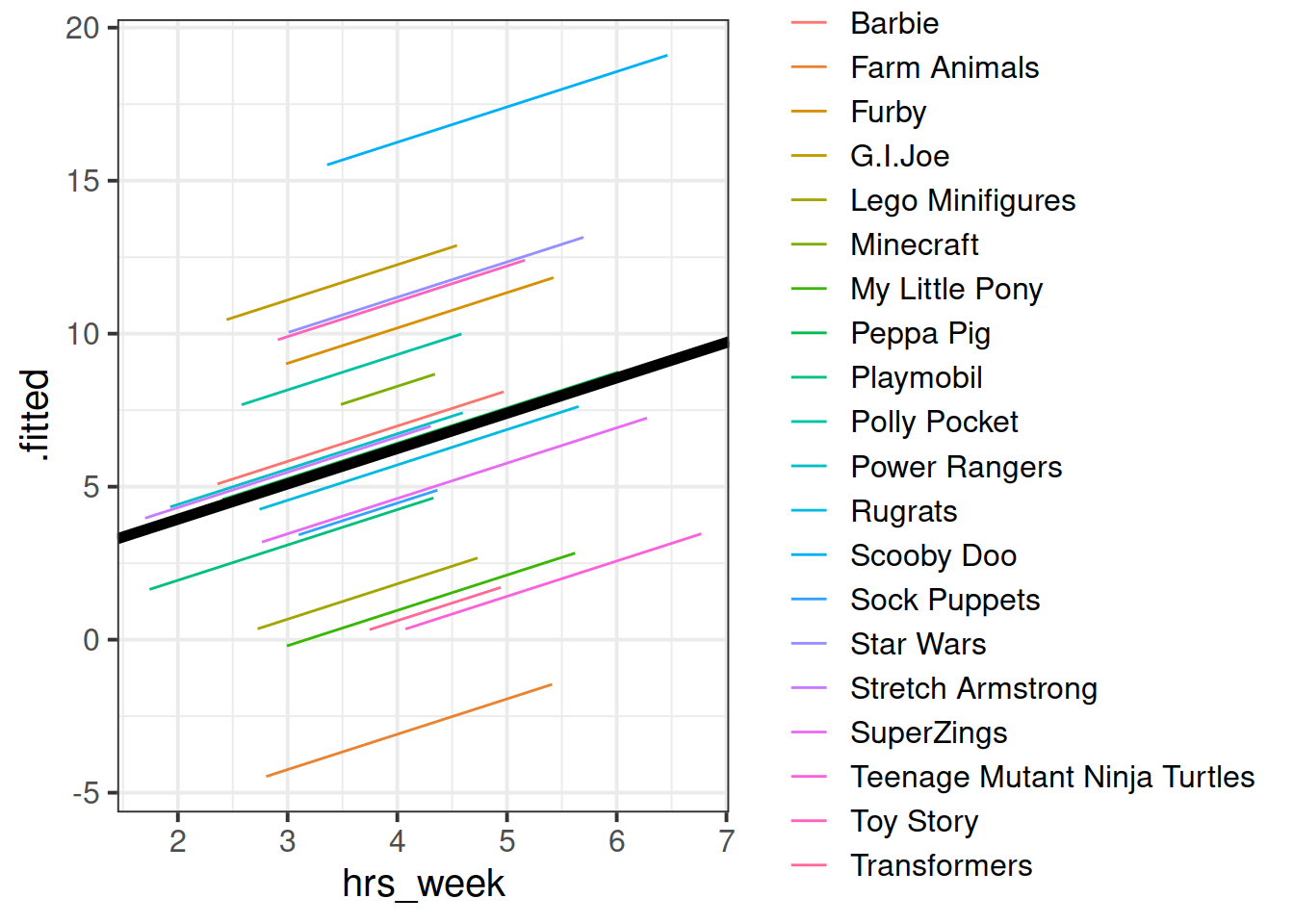
For our \(\beta\) estimates from a multilevel model, we can use fixef().

fixef(rmodel1)

## (Intercept)    hrs_week 
##    1.627422    1.154725

Can you add to the plot in the previous question, a thick black line with the intercept and slope given by fixef()?

Hint: geom_abline()

Solution

augment(rmodel1) %>%
  ggplot(aes(x = hrs_week, y = .fitted, col = toy_type)) + 
  geom_line() + 
  geom_abline(intercept = fixef(rmodel1)[1], slope = fixef(rmodel1)[2], lwd = 2)

Question A6

By now, you should have a plot which looks more or less like the below. We have added on the raw data too (the points). 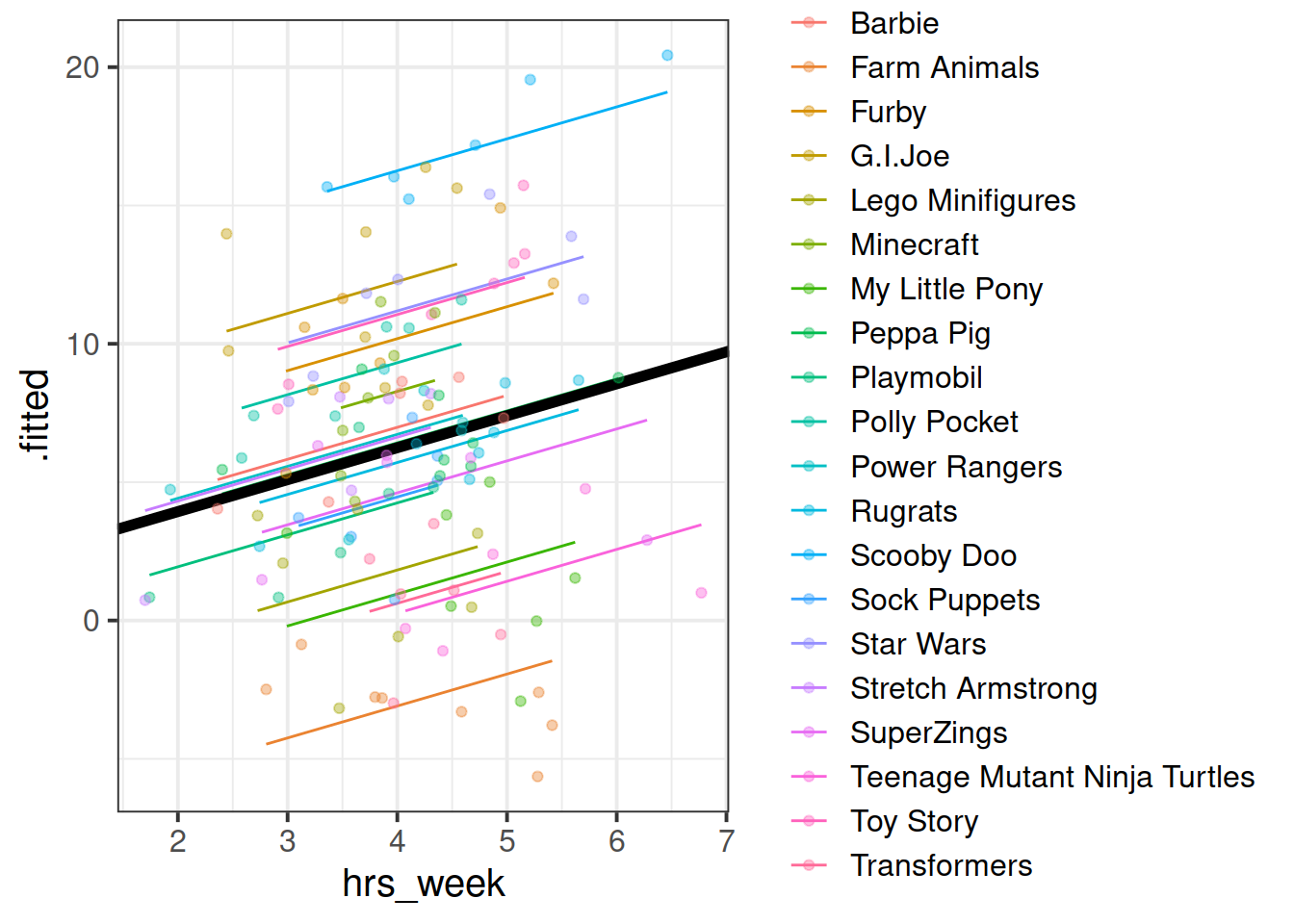Let’s try to map the parts of the plot to the summary() output of the model.
Match the coloured sections in the image below to the descriptions A through D.

1. where the black line cuts the y axis
   
2. the standard deviation of the distances from all the individual toy types lines to the black line.
   
3. the slope of the black line
   
4. the standard deviation of the distances from all the individual observations to the line for the toy type to which it belongs.

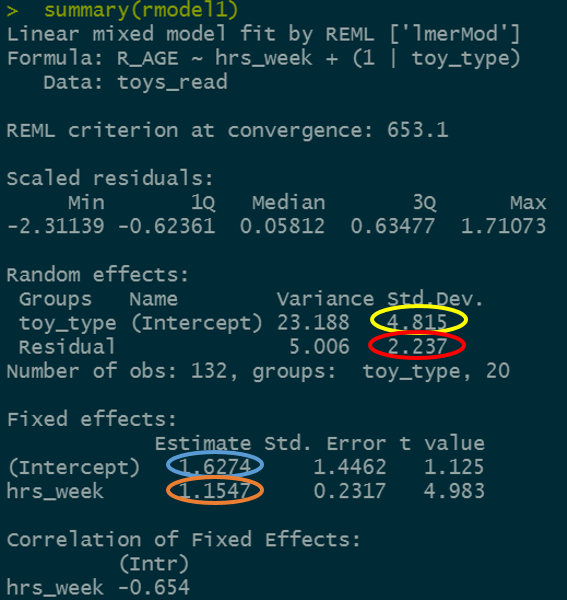
Figure 5: Summary model output, lmer(R_AGE~hrs_week + (1|toy_type), data = toys_read)

Solution

• Yellow = B
  
• Red = D
  
• Blue = A
  
• Orange = C

Question A7 - Harder

Can you know map those same coloured sections in Figure 5 to the mathematical terms in the model equation:

\[ \begin{align} & \text{Level 1:} \\ & \color{red}{ReadingAge_{ij}} = \color{blue}{\beta_{0i} \cdot 1 + \beta_{1} \cdot Practice_{ij}} + \varepsilon_{ij} \\ & \text{Level 2:} \\ & \color{blue}{\beta_{0i}} = \gamma_{00} + \color{orange}{\zeta_{0i}} \\ \quad \\ & \text{where} \\ & \color{orange}{\zeta_0} \sim N(0, \sigma_{\color{orange}{\zeta_{0}}}) \text{ independently} \\ & \varepsilon \sim N(0, \sigma_{\varepsilon}) \text{ independently} \\ \end{align} \]

Solution

• Yellow = \(\sigma_{\color{orange}{\zeta_{0}}}\)
  
• Red = \(\sigma_{\varepsilon}\)
  
• Blue = \(\gamma_{00}\)
  
• Orange = \(\beta_{1}\)

Question A8

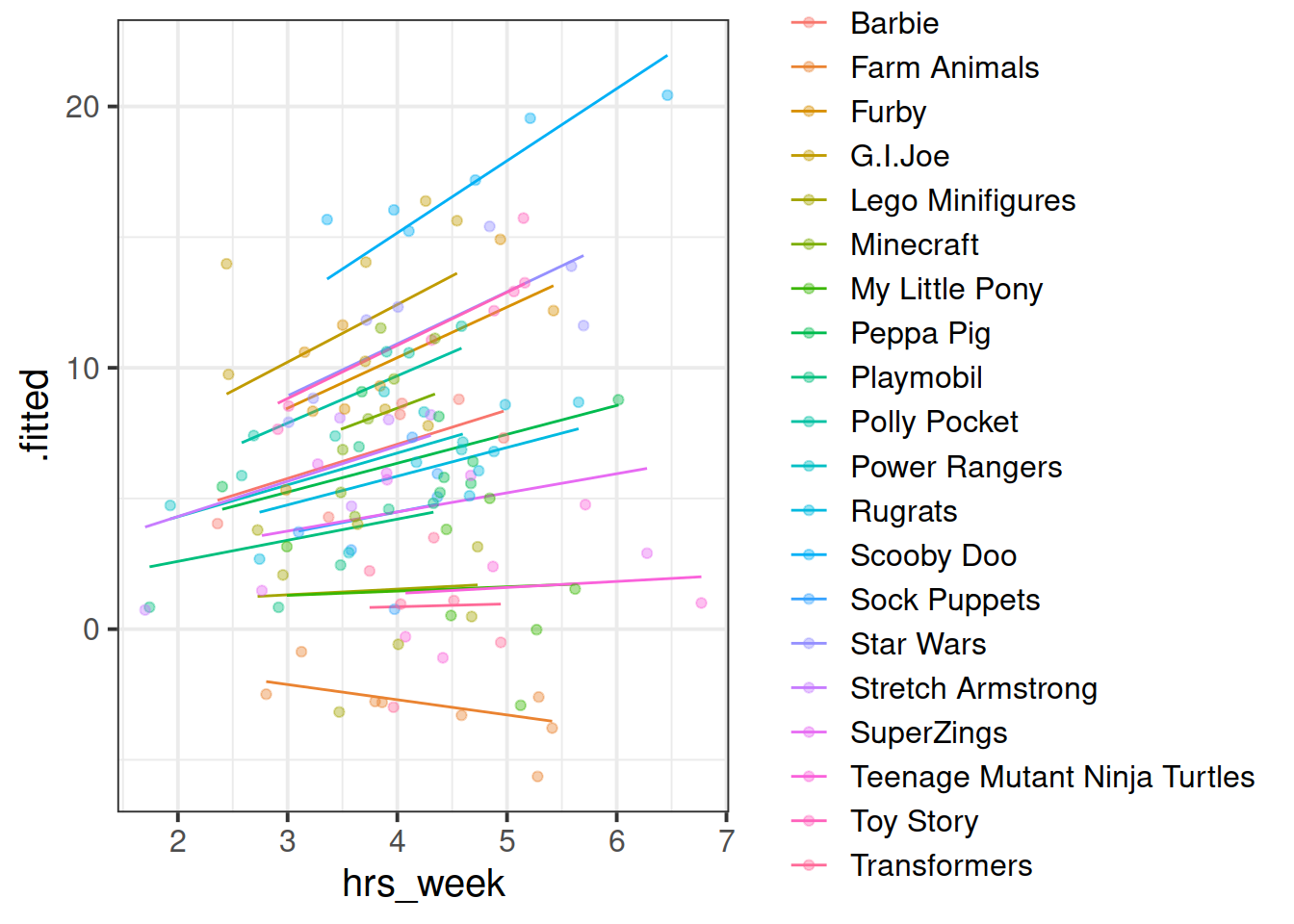
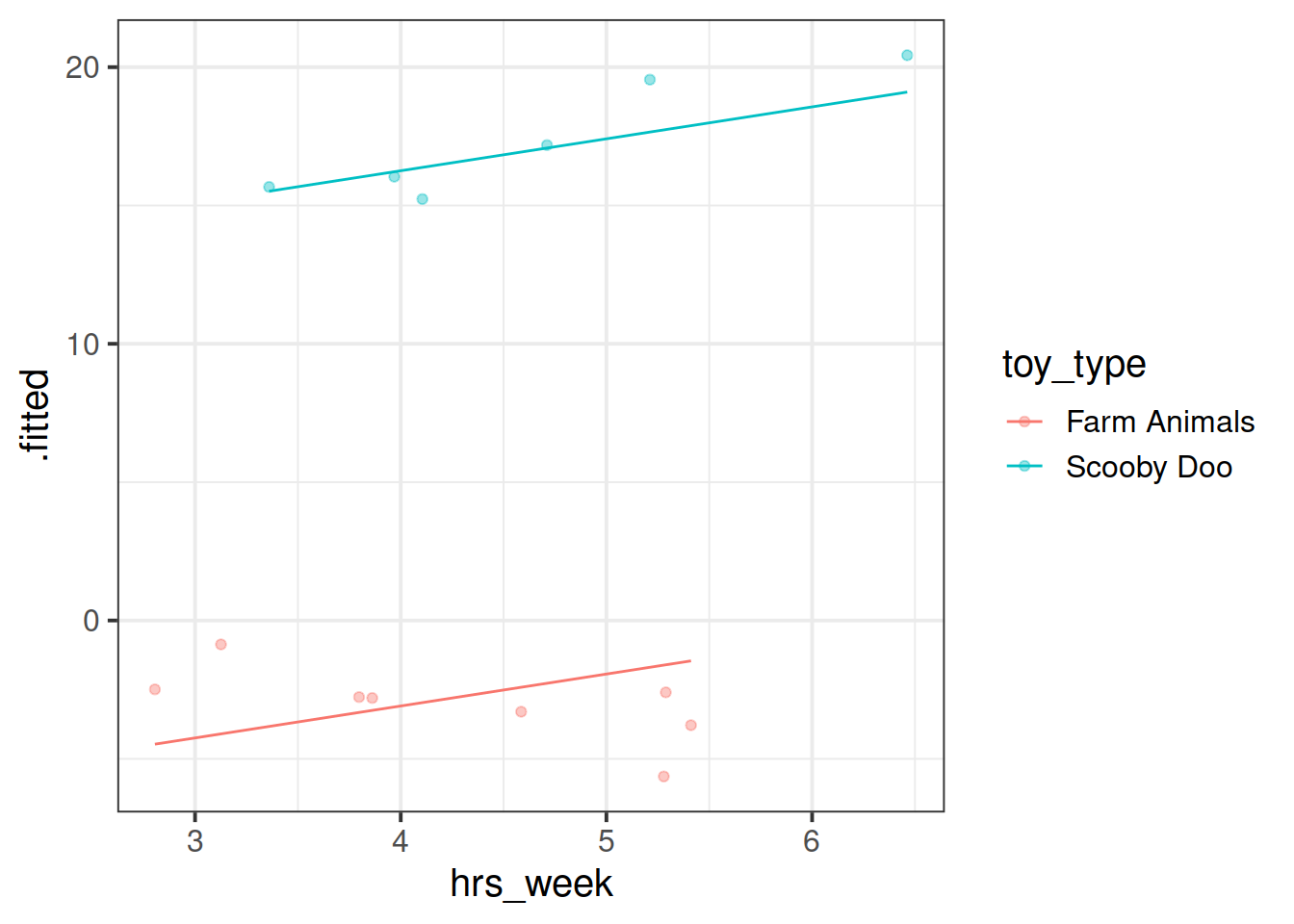
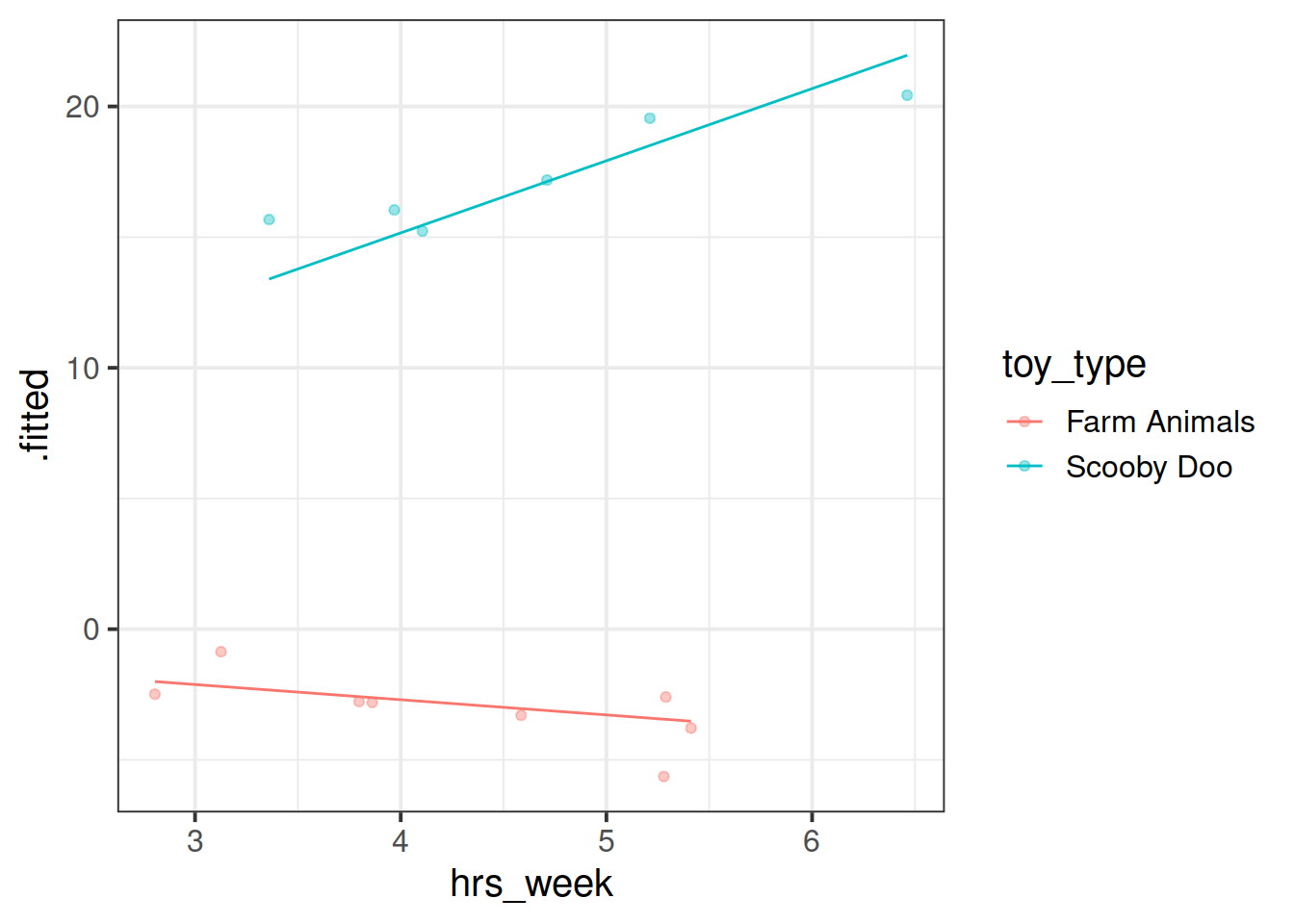
Fit a model which allows also (along with the intercept) the effect of practice (hrs_week) to vary by-toytype.
Then, using augment() again, plot the model fitted values. What do you think you will see?

Solution

rmodel2 <- lmer(R_AGE ~ 1 + hrs_week + (1 + hrs_week | toy_type), data = toys_read)
augment(rmodel2) %>%
  ggplot(aes(x = hrs_week, y = .fitted, col = toy_type)) + 
  geom_line() + 
  geom_point(aes(y=R_AGE), alpha=.4)

Question A9

Plot the model fitted values but only for the Farm Animals and the Scooby Doo toys, and add the observed reading ages too.
Do this for both the model with the random intercept only, and the model with both the random intercept and slope.

Solution

augment(rmodel1) %>%
  filter(str_detect(toy_type, "Scooby|Farm")) %>%
  ggplot(aes(x = hrs_week, y = .fitted, col = toy_type)) + 
  geom_line() + 
  geom_point(aes(y=R_AGE), alpha=.4)

augment(rmodel2) %>%
  filter(str_detect(toy_type, "Scooby|Farm")) %>%
  ggplot(aes(x = hrs_week, y = .fitted, col = toy_type)) + 
  geom_line() + 
  geom_point(aes(y=R_AGE), alpha=.4)

Some Less Guided Exercises

While the toy example considers the groupings or ‘clusters’ of different types of toy, a much more common grouping in psychological research is that of several observations belonging to the same individual. One obvious benefit of this is that we can collect many more observations with fewer participants, and account for the resulting dependency of observations. Another very crucial advantage is that we can use the same methods to study how people change over time.

WeightMaintain Data Codebook

The weight maintenance data (WeightMaintain3), a made-up data set based on Lowe et al. (2014, Obesity, 22, 94-100), contains information on overweight participants who completed a 12-week weight loss program, and were then randomly assigned to one of three weight maintenance conditions:

• None (Control)
  
• MR (meal replacements): use MR to replace one meal and snack per day
  
• ED (energy density intervention): book and educational materials on purchasing and preparing foods lower in ED (reducing fat content and/or increasing water content of foods)

Weight was assessed at baseline (start of maintenance), 12 months post, 24 months post, and 36 months post.

It is available, in .rda format, at https://uoepsy.github.io/data/WeightMaintain3.rda

Question B1

Load the data, and take a look at what is in there. Hopefully it should match the description above.

Solution

load(url("https://uoepsy.github.io/data/WeightMaintain3.rda"))
summary(WeightMaintain3)

##        ID      Condition    Assessment    WeightChange    
##  101    :  4   None:240   Min.   :0.00   Min.   :-8.3781  
##  102    :  4   ED  :240   1st Qu.:0.75   1st Qu.:-0.5024  
##  103    :  4   MR  :240   Median :1.50   Median : 0.7050  
##  104    :  4              Mean   :1.50   Mean   : 1.4438  
##  105    :  4              3rd Qu.:2.25   3rd Qu.: 2.8806  
##  106    :  4              Max.   :3.00   Max.   :14.9449  
##  (Other):696

head(WeightMaintain3)

##    ID Condition Assessment WeightChange
## 1 101      None          0 -0.116138529
## 2 101      None          1  0.333508907
## 3 101      None          2  1.678653492
## 4 101      None          3  2.756023400
## 5 102      None          0 -0.004420188
## 6 102      None          1  1.746725487

Question B2

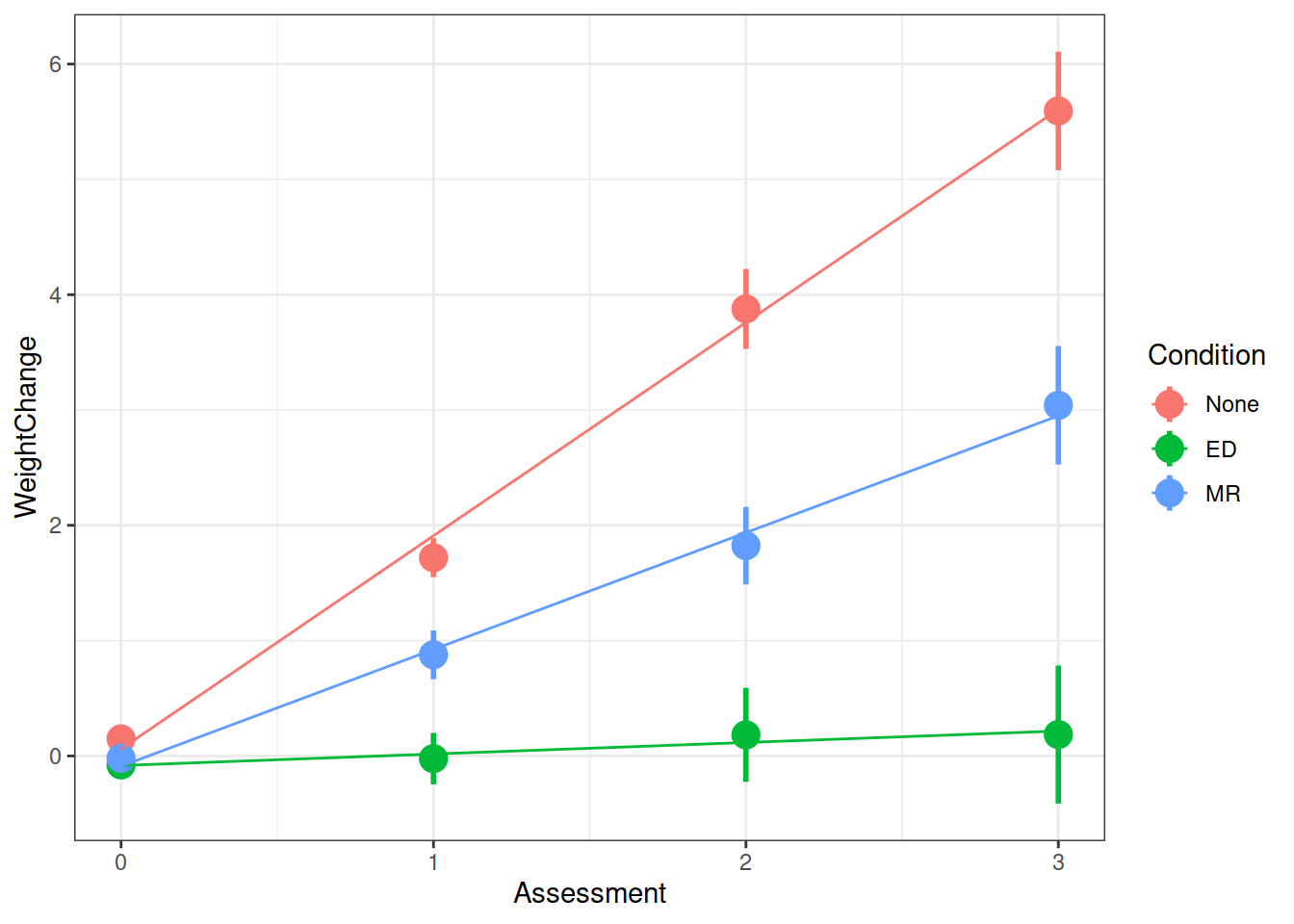
Q: Overall, did the participants maintain their weight loss or did their weights change?

Each of our participants have measurements at 4 assessments. We need to think about what this means for our random effect structure. Would we like our models to accommodate individuals to vary in their starting weight change, to vary in their weight change over the course of the assessment period, or both?

To investigate whether weights changed over the course of the assessments, or whether they stayed the same, we can fit and compare 2 models:

1. The “null” or “intercept-only” model.
2. A model with weight change predicted by assessment.

Hint: You can compare two lmer() models the same way you would compare two lm() models in R. However, note that the output will not give you an F-ratio, but a Chisq. This is because instead of comparing the residual sums of squares, we are comparing the model deviance (or \(-2 \times \text{LogLikelihood}\) of our model). This is what is known as a likelihood ratio test (LRT).

Solution

m.null <- lmer(WeightChange ~ 1 + (1 + Assessment | ID), data=WeightMaintain3)
m.base <- lmer(WeightChange ~ Assessment + (1 + Assessment | ID), data=WeightMaintain3)

anova(m.null, m.base)

## Data: WeightMaintain3
## Models:
## m.null: WeightChange ~ 1 + (1 + Assessment | ID)
## m.base: WeightChange ~ Assessment + (1 + Assessment | ID)
##        npar    AIC    BIC  logLik deviance Chisq Df Pr(>Chisq)    
## m.null    5 2638.0 2660.9 -1314.0   2628.0                        
## m.base    6 2579.4 2606.8 -1283.7   2567.4 60.66  1  6.782e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Likelihood ratio test found that the inclusion of Assessment significantly improved model fit over the null model ( \(\chi^2(1)\) = 60.66, \(p < .001\)), suggesting that participants’ weights changed over course of 36 month assessment period.

Question B3

Q: Did the experimental condition groups differ in overall weight change and rate of weight change (non-maintenance)?

Hint: It helps to break it down. There are two questions here:

1. do groups differ overall?
   
2. do groups differ over time?

We can begin to see that we’re asking two questions about the Condition variable here: “is there an effect of Condition?” and “Is there an interaction between Assessment and Condition?”

Try fitting two more models which incrementally build these levels of complexity, and compare them (perhaps to one another, perhaps to models from the previous question - think about what each comparison is testing!)

Solution

m.int <- lmer(WeightChange ~ Assessment + Condition + (Assessment | ID), 
              data=WeightMaintain3)
m.full <- lmer(WeightChange ~ Assessment*Condition + (Assessment | ID), 
               data=WeightMaintain3)

We’re going to compare all our models so far, in order. This will compare each one to the previous one, so is equivalent to:

anova(m.null, m.base)
anova(m.int, m.base)
anova(m.full, m.int)

anova(m.null, m.base, m.int, m.full)

## Data: WeightMaintain3
## Models:
## m.null: WeightChange ~ 1 + (1 + Assessment | ID)
## m.base: WeightChange ~ Assessment + (1 + Assessment | ID)
## m.int: WeightChange ~ Assessment + Condition + (Assessment | ID)
## m.full: WeightChange ~ Assessment * Condition + (Assessment | ID)
##        npar    AIC    BIC  logLik deviance   Chisq Df Pr(>Chisq)    
## m.null    5 2638.0 2660.9 -1314.0   2628.0                          
## m.base    6 2579.4 2606.8 -1283.7   2567.4 60.6605  1  6.782e-15 ***
## m.int     8 2573.9 2610.6 -1279.0   2557.9  9.4418  2   0.008907 ** 
## m.full   10 2537.5 2583.3 -1258.8   2517.5 40.3814  2  1.703e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Conditions differed overall in weight change \(\chi^2(2)=9.4, p < .01\)
Conditions differed in change over assessment period \(\chi^2(2)=40.4, p < .001\)

Question B4

We saw that we can get the coefficients using fixef(model). We can also use tidy(model), and similar to last semester, we can pull out the bit of the summary() using:

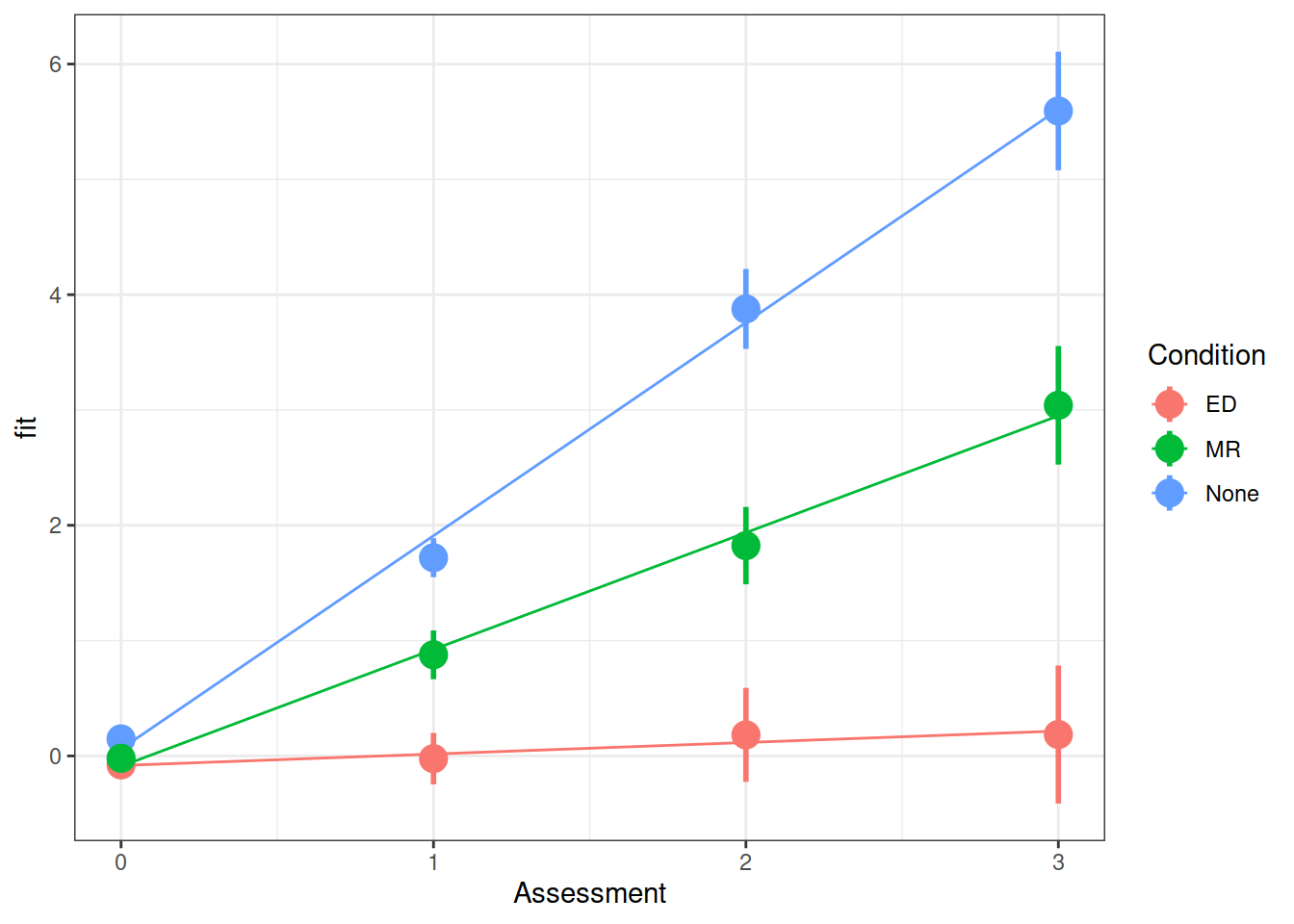
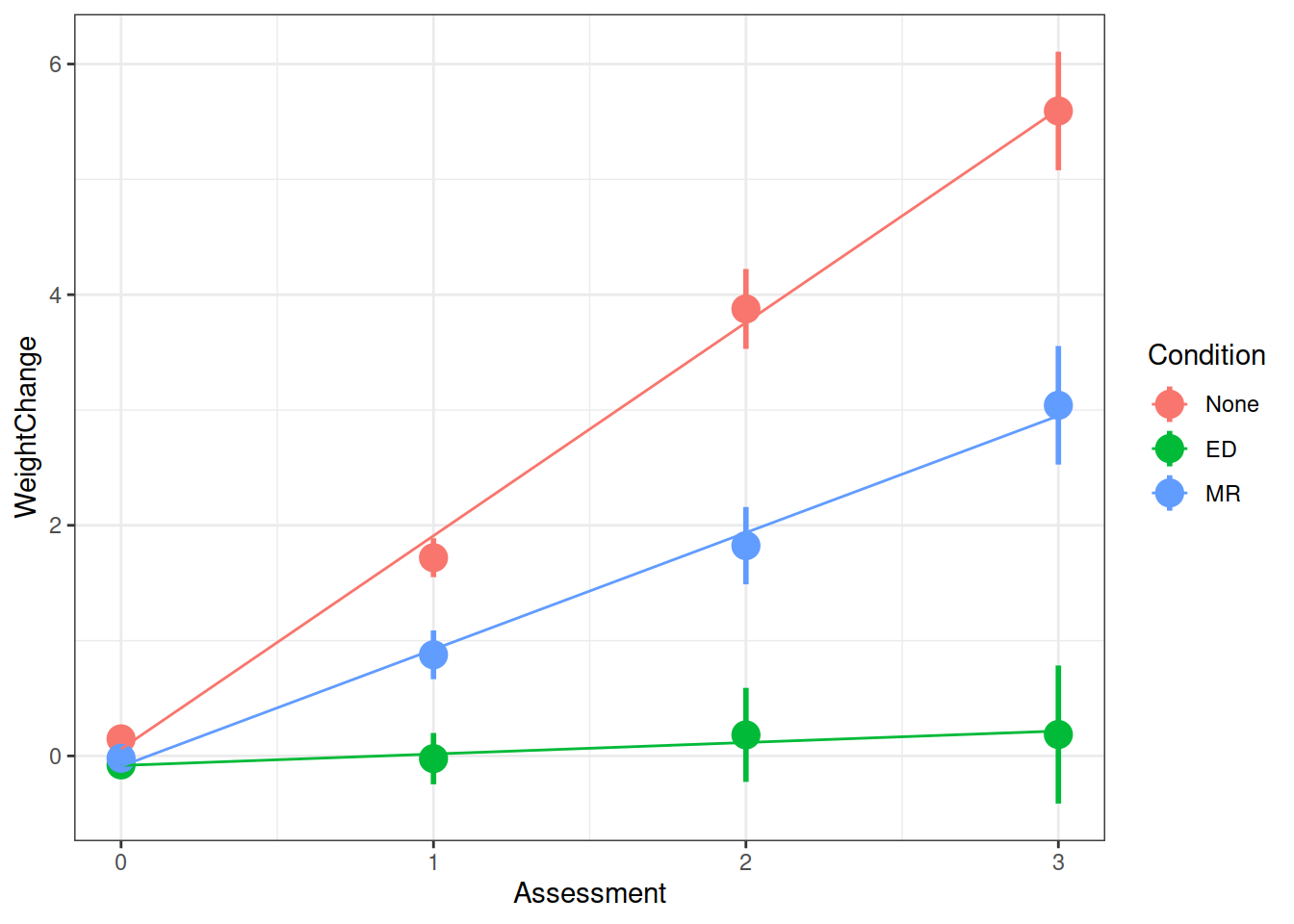
summary(model)$coefficients

From your model from the previous question which investigates whether conditions differed over in their rate of weight change, can you state how the conditions differed?

Solution

summary(m.full)$coefficients

##                           Estimate Std. Error    t value
## (Intercept)             0.06038642 0.09835879  0.6139402
## Assessment              1.84917936 0.18544623  9.9715123
## ConditionED            -0.14303302 0.13910033 -1.0282723
## ConditionMR            -0.14944649 0.13910033 -1.0743792
## Assessment:ConditionED -1.74949968 0.26226057 -6.6708452
## Assessment:ConditionMR -0.83624053 0.26226057 -3.1885865

Compared to no intervention, weight (re)gain was 1.75 lbs/year slower for the ED intervention and 0.84 lbs/year slower for the MR intervention.

Question B5

Make a graph of the model fit and the observed data.

Hint: There are lots of ways you can do this, try a couple:

1. Using the effects package, does this help? as.data.frame(effect("Assessment:Condition", model))
   
2. Using fitted(model)
3. Using augment() from the broom.mixed package.

Solution

1. Using the effect() function (and then adding the means and SEs from the original data):

ef <- as.data.frame(effect("Assessment:Condition", m.full))

ggplot(ef, aes(Assessment, fit, color=Condition)) + 
  geom_line() +
  stat_summary(data=WeightMaintain3, aes(y=WeightChange), 
               fun.data=mean_se, geom="pointrange", size=1) +
  theme_bw()

2. Using the fitted() function to extract and plot fitted values from the model:

ggplot(WeightMaintain3, aes(Assessment, WeightChange, color=Condition)) + 
  stat_summary(fun.data=mean_se, geom="pointrange", size=1) + 
  stat_summary(aes(y=fitted(m.full)), fun=mean, geom="line") + 
  theme_bw()

3. Or using augment():

augment(m.full) %>%
ggplot(., aes(Assessment, WeightChange, color=Condition)) + 
  stat_summary(fun.data=mean_se, geom="pointrange", size=1) + 
  stat_summary(aes(y=.fitted), fun=mean, geom="line") + 
  theme_bw()

Question B6

Examine the parameter estimates and interpret them (i.e., what does each parameter represent?)

m.full <- lmer(WeightChange ~ Assessment*Condition + (Assessment | ID), 
               data=WeightMaintain3)
summary(m.full)

Solution

round(coef(summary(m.full)), 3)

##                        Estimate Std. Error t value
## (Intercept)               0.060      0.098   0.614
## Assessment                1.849      0.185   9.972
## ConditionED              -0.143      0.139  -1.028
## ConditionMR              -0.149      0.139  -1.074
## Assessment:ConditionED   -1.749      0.262  -6.671
## Assessment:ConditionMR   -0.836      0.262  -3.189

• (Intercept) ==> weight change at baseline in None group
• Assessment ==> slope of weight change in None group
• ConditionED ==> baseline weight change in ED group relative to None group
• ConditionMR ==> baseline weight change in MR group relative to None group
• Assessment:ConditionED ==> slope of weight change in ED group relative to None group
• Assessment:ConditionMR ==> slope of weight change in MR groups relative to None group

---

1. Image sources:
   http://tophatsasquatch.com/2012-tmnt-classics-action-figures/
   https://www.dezeen.com/2016/02/01/barbie-dolls-fashionista-collection-mattel-new-body-types/
   https://www.wish.com/product/5da9bc544ab36314cfa7f70c
   https://www.worldwideshoppingmall.co.uk/toys/jumbo-farm-animals.asp
   https://www.overstock.com/Sports-Toys/NJ-Croce-Scooby-Doo-5pc.-Bendable-Figure-Set-with-Scooby-Doo-Shaggy-Daphne-Velma-and-Fred/28534567/product.html
   https://tvtropes.org/pmwiki/pmwiki.php/Toys/Furby
   https://www.fun.com/toy-story-4-figure-4-pack.html
   https://www.johnlewis.com/lego-minifigures-71027-series-20-pack/p5079461↩︎

2. An approach more common in Econometrics is to use “cluster robust variance estimates” but this is much less common in psychology, and not without their problems, so we will not discuss these in this course↩︎