Preliminaries

  1. Open Rstudio, and create a new RMarkdown document (giving it a title for this week).

Last week we began to cover the idea of longitudinal mixed models (or ‘multi-level models’ - whatever we’re calling them!) in our exercises on Weight Change. The lectures this week have also introduced the idea of ‘change over time’ by looking at some data from Public Health England.

In the exercises this week, we’re going to concentrate on this in combination with the other topic this week, Logistic multi-level models. Then we’re going to look at contrasts (they’re a confusing topic, and can be pretty unintuitive, but we’re going to have to do it sometime!), and talk a little bit about making inferences.

Logistic MLM

Don’t forget to look back at other materials!

Back in USMR, we introduced logistic regression in week 10. The lectures followed the example of some singing aliens that either survived or were splatted, and the exercises used some simulated data based on a hypothetical study about inattentional blindness. That content will provide a lot of the groundwork for this week, so we recommend revisiting it if you feel like it might be useful.

lmer() >> glmer()

Remember how we simply used glm() and could specify the family = "binomial" in order to fit a logistic regression? Well it’s much the same thing for multi-level models!

  • Gaussian model: lmer(y ~ x1 + x2 + (1 | g), data = data)
  • Binomial model: glmer(y ~ x1 + x2 + (1 | g), data = data, family = binomial(link='logit'))
    • or just glmer(y ~ x1 + x2 + (1 | g), data = data, family = "binomial")
    • or glmer(y ~ x1 + x2 + (1 | g), data = data, family = binomial)

Binary? Binomial? Huh?

Very briefly in the USMR materials we made the distinction between binary and binomial. This wasn’t hugely relevant at the time just because we only looked at binary outcomes.

For binary regression, all the data in our outcome variable has to be a 0 or a 1.
For example, the correct variable below:

participant question correct
1 1 1
1 2 0
1 3 1
... ... ...

But we can re-express this information in a different way, when we know the total number of questions asked.

participant questions_correct questions_incorrect
1 2 1
2 1 2
3 3 0
... ... ...

To model data when it is in this form, we can express our outcome as cbind(questions_correct, questions_incorrect)

Question A1

Load any of the packages you think you might be using today.

By now you may have started get into a sort of routine with R, and you might know what functions you like, and which you don’t. Because there are so many alternatives for doing the same thing, the packages and functions you use are very much up to you.

If I’m planning on doing some multi-level modelling, I will tend to load these by default at the top:

library(tidyverse) # for everything
library(lme4) # for fitting models
library(broom.mixed) # for tidying model output

Novel Word Learning: Data Codebook

Question A2

Load the data. Take a look around. Any missing values? Can you think of why?

Solution

Research Aims
Compare the two groups (those with anterior vs. posterior lesions) with respect to their accuracy of responses over the course of the study

Question A3: Initial thoughts
  1. What is our outcome?
  2. Is it longitudinal? (simply, is there a temporal sequence to observations within a participant?)

Hint: Think carefully about question 1. There might be several variables which either fully or partly express the information we are considering the “outcome” here.

Solution

Question A4

Research Question 1:
Is the learning rate (training blocks) different between these two groups?

Hints:

  • Do we want cbind(num_successes, num_failures)?

  • Make sure we’re running models on only the data we are actually interested in.

  • Think back to what we did in last week’s exercises using model comparison via likelihood ratio tests (using anova(model1, model2, model3, ...). We could use this approach for this question, to compare:

    • A model with just the change over the sequence of blocks
    • A model with the change over the sequence of blocks and an overall difference between groups
    • A model with groups differing with respect to their change over the sequence of blocks

  • What about the random effects part?

    1. What are our observations grouped by?
    2. What variables can vary within these groups?
    3. What do you want your model to allow to vary within these groups?
Suggested answers to the hints if you don’t know where to start

Solution

Question A5

Research Question 2
In the testing phase, does performance on the immediate test differ between lesion location groups, and does their retention from immediate to follow-up test differ?

Let’s try a different approach to this. Instead of fitting various models and comparing them via likelihood ratio tests, just fit the one model which could answer both parts of the question above.

Hints:

  • This might required a bit more data-wrangling before hand. Think about the order of your factor levels (alphabetically speaking, “Follow-up” comes before “Immediate”)!

Solution

Interpreting fixed effects

Take some time to remind yourself from USMR of the interpretation of logistic regression coefficients.

The interpretation of the fixed effects of a logistic multi-level model are no different.
We can obtain them using:

  • fixef(model)
  • summary(model)$coefficients
  • tidy(model) from broom.mixed
  • (there are probably more ways, but I can’t think of them right now!)

It’s just that for multi-level models, we can model by-cluster andom variation around these effects.

Question A6
  1. In family = binomial(link='logit'). What function is used to relate the linear predictors in the model to the expected value of the response variable?
  2. How do we convert this into something more interpretable?

Solution

Question A7

Make sure you pay attention to trying to interpret each fixed effect from your models.
These can be difficult, especially when it’s logistic, and especially when there are interactions.

  • What is the increase in the odds of answering correctly in the immediate test for someone with a posterior legion compared to someone with an anterior legion?
Optional help: Our Solution to A5

Solution

Optional extra exercise

Question A8: Extra

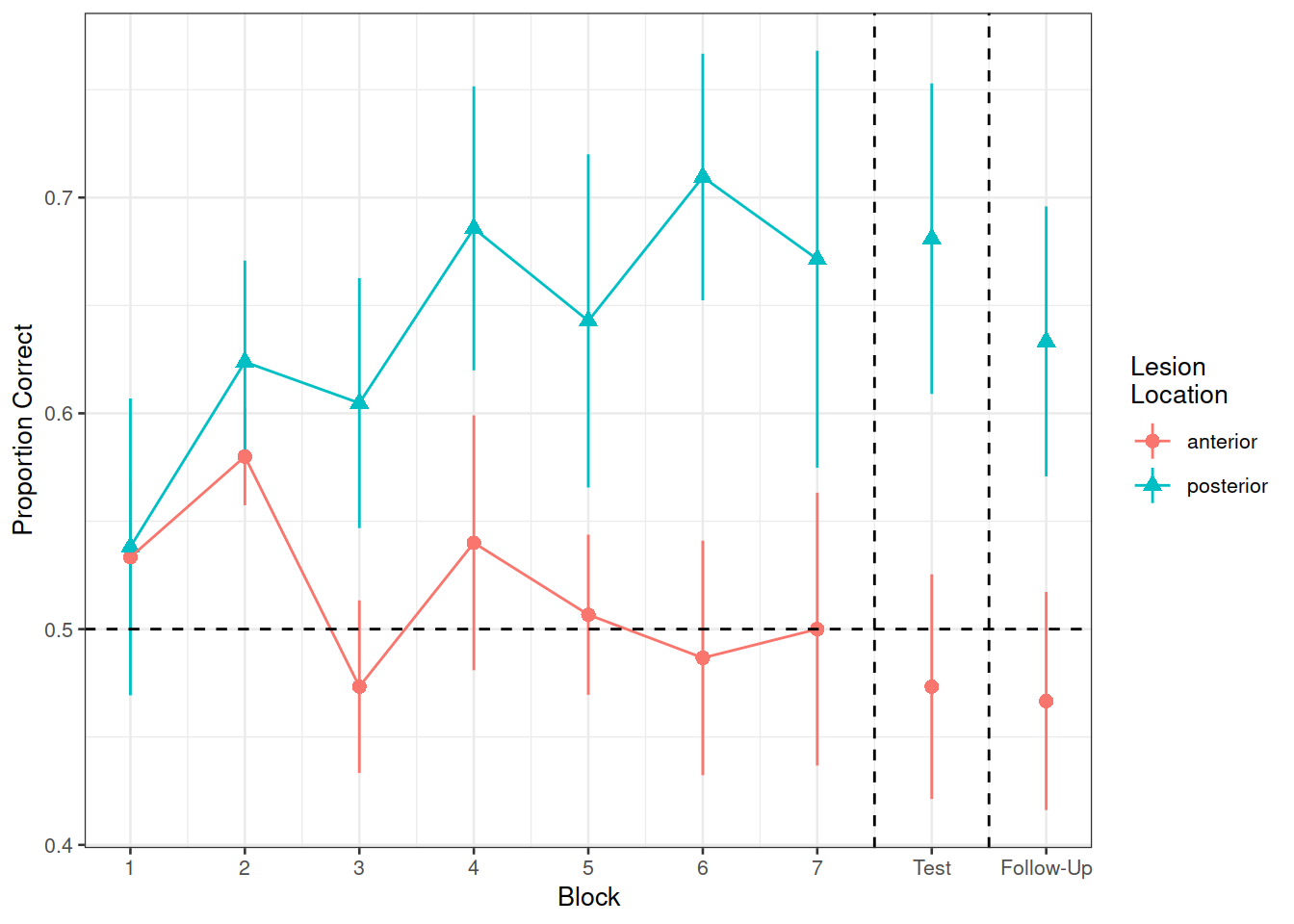
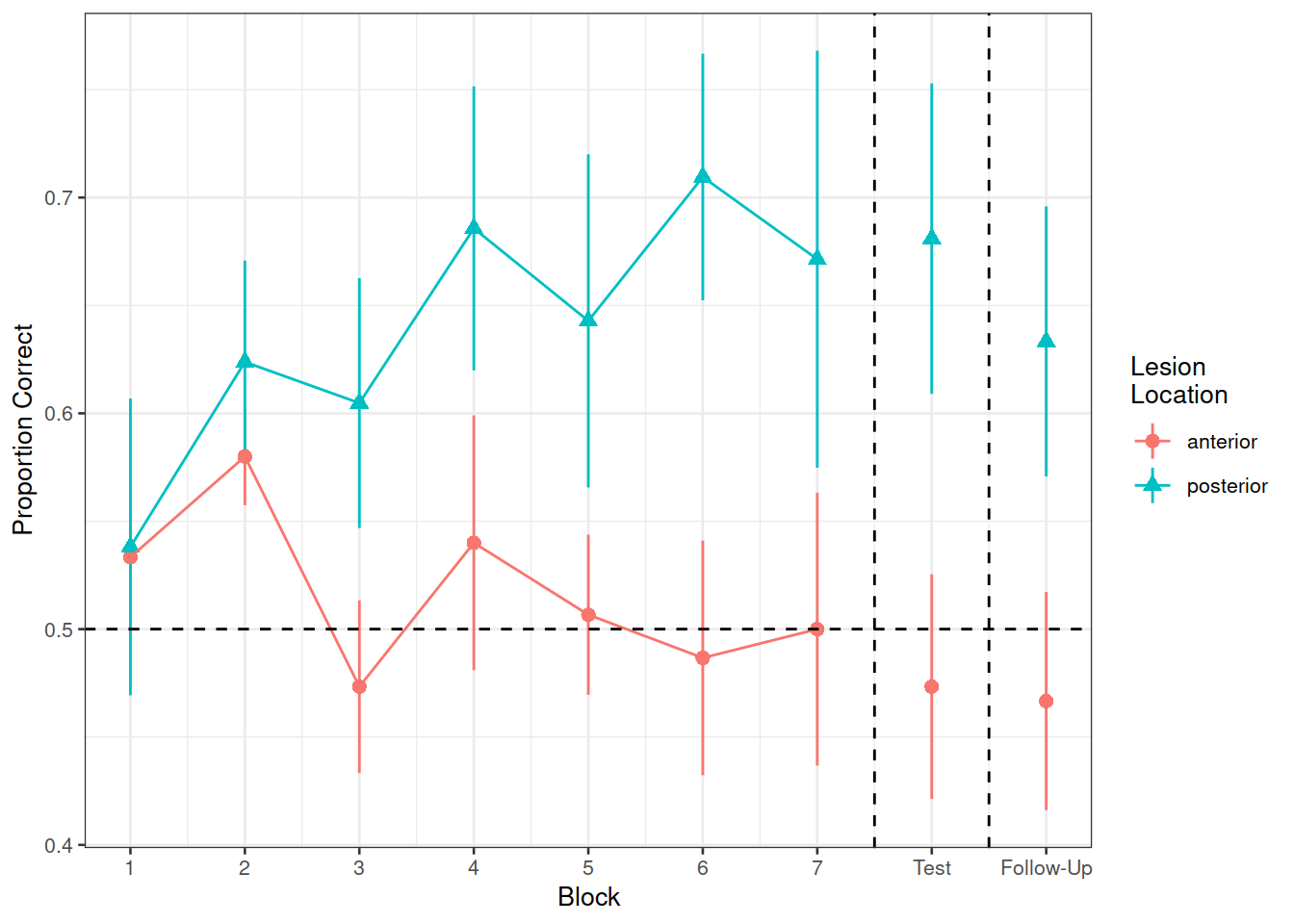
Recreate the visualisation in Figure 2.

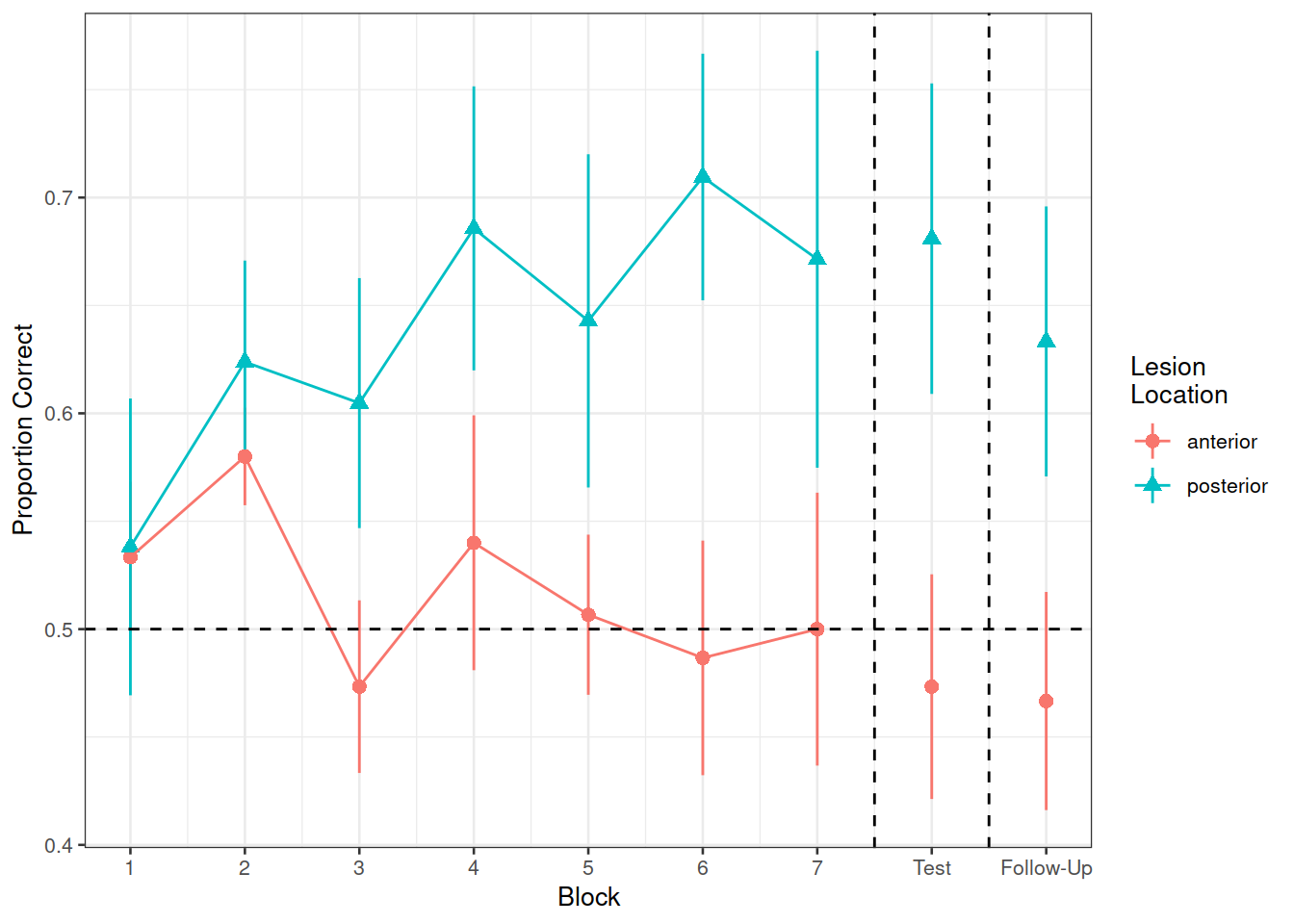
Differences between groups in the average proportion of correct responses at each block

Figure 2: Differences between groups in the average proportion of correct responses at each block

Solution

Optional Readings: Inference in MLM

What, no p-values?

Hang on, we have p-values for these models? You might have noticed that we didn’t get p-values last week1 for lmer(), but we do now for glmer()?

The reason is partly just one of convention. There is a standard practice for determining the statistical significance of parameters in the generalised linear model, relying on asymptotic Wald tests which evaluate differences in log-likelihood.

When we are in the Gaussian (“normal”) world, we’re back in the world of sums of squares. In the rare occasion that you have a perfectly balanced experimental design, then it has been shown that ratios of sums of squares for multi-level models follow an \(F\)-distribution, in which we know the numerator and denominator degrees of freedom (this means we can work out the degrees of freedom for the \(t\)-test of our fixed effect parameters). Unfortunately, in the real world where things are not often perfectly balanced, determining the denominator degrees of freedom becomes unclear.

What can we do??

So far, we have been taking the approach of model comparison. This can be good because there are lots of different criteria for comparing models. Then when it comes to the specific effects of interest, we can then talk about the effect size (i.e., the \(\beta\)), and about whether it improves model fit according to our criterion. Unfortunately, the reliability of the likelihood ratio tests which we have been using is dependent on the degrees of freedom issue above.

There are some alternatives:

  1. Kenward-Rogers adjustment:

    library(pbkrtest)
KRmodcomp(model1, model2)

  2. Satterthwaite approximation: (this will just add a column for p-values to your summary(model) output)

    library(lmerTest)
model <- lmer(......
summary(model)

  3. Parametric bootstraps

    library(pbkrtest)
PBmodcomp(full_model, restricted_model)

If you want more information (not required reading for this course), then Julian Faraway has a page here with links to some worked examples, and Ben Bolker has a wealth of information on his GLMM FAQ pages.

Contrasts

We largely avoided the discussion of cotrasts in USMR because they can be quite incomprehensible at first, and we wanted to focus on really consolidating our learning of the linear model basics.

What are contrasts and when are they relevant?

Recall when we have a categorical predictors? To continue the example in USMR, Martin’s lectures considered the utility of different types of toys (Playmo, SuperZings, and Lego).
[USMR Week 9 Lecture](https://uoepsy.github.io/usmr/lectures/lecture_8.html#36) utility of different toy_types

Figure 3: USMR Week 9 Lecture utility of different toy_types

When we put a categorical variable into our model as a predictor, we are always relying on contrasts, which are essentially just combinations of 0s & 1s which we use to define the differences which we wish to test.

The default, treatment coding, treats one level as a reference group, and results in coefficients which compare each group to that reference.
When a variable is defined as a factor in R, there will always be an attached “attribute” defining the contrasts:

#read the data
toy_utils <- read_csv("https://uoepsy.github.io/msmr/data/toyutility.csv")

#make type a factor
toy_utils <- toy_utils %>%
  mutate(
    type = factor(type)
  )
# look at the contrasts
contrasts(toy_utils$type)
##        playmo zing
## lego        0    0
## playmo      1    0
## zing        0    1

Currently, the resulting coefficients from the contrasts above will correspond to:

  • Intercept = estimated mean utility for Lego (reference group)
  • typeplaymo = estimated difference in mean utility Playmo vs Lego
  • typezing = estimated different in mean utility Zing vs Lego
Question B1

Read in the toy utility data from https://uoepsy.github.io/msmr/data/toyutility.csv.
We’re going to switch back to the normal lm() world here for a bit, so no multi-level stuff while we learn more about contrasts.

  1. Fit the model below

    model_treatment <- lm(UTILITY ~ type, data = toy_utils)

  2. Calculate the means for each group, and the differences between them, to match them to the coefficients from the model above

Solution

How can we change the way contrasts are coded?

In our regression model we are fitting an intercept plus a coefficient for each explanatory variable, and any categorical predictors are coded as 0s and 1s.

We can add constraints to our the way our contrasts are coded. In fact, with the default treatment coding, we already have applied one - we constrained them such that the intercept (\(\beta_0\)) = the mean of one of the groups.

Optional: Why constraints?

The other common constraint that is used is the sum-to-zero constraint. Under this constraint the interpretation of the coefficients becomes:

  • \(\beta_0\) represents the global mean (sometimes referred to as the “grand mean”).
  • \(\beta_1\) the effect due to group \(i\) — that is, the mean response in group \(i\) minus the global mean.

Changing contrasts in R
There are two main ways to change the contrasts in R.

  1. Change them in your data object.

    contrasts(toy_utils$type) <- "contr.sum"

  2. Change them only in the fit of your model (don’t change them in the data object)

    model_sum <- lm(UTILITY ~ type, contrasts = list(type = "contr.sum"), data = toy_utils)
Question B2
  1. Using sum-to-zero contrasts, refit the same model of utility by toy-type.
  2. Then calculate the global mean, and the differences from each mean to the global mean, to match them to the coefficients

Solution

Question B3

This code is what we used to answer question A5 above, only we have edited it to change lesion location to be fitted with sum-to-zero contrasts.

The interpretation of this is going to get pretty tricky - we have a logistic regression, and we have sum-to-zero contrasts, and we have an interaction.. 🤯

Can you work out the interpretation of the fixed effects estimates?

nwl_test <- filter(nwl, block > 7, !is.na(lesion_location)) %>%
  mutate(
    Phase = fct_relevel(factor(Phase),"Immediate")
  )

m.recall.loc.sum <- glmer(cbind(NumCorrect, NumError) ~ Phase * lesion_location + (Phase | ID), 
                      contrasts = list(lesion_location = "contr.sum"),
                  nwl_test, family="binomial")
rbind(summary(m.recall.loc.sum)$coefficients,
      summary(m.recall.loc)$coefficients)
##                                            Estimate Std. Error     z value
## (Intercept)                              0.38584493  0.2341574  1.64780173
## PhaseFollow-up                          -0.15170188  0.1688879 -0.89823996
## lesion_location1                        -0.49958816  0.2343374 -2.13191788
## PhaseFollow-up:lesion_location1          0.12717977  0.1695166  0.75024946
## (Intercept)                             -0.11375074  0.3512760 -0.32382152
## PhaseFollow-up                          -0.02452279  0.2463421 -0.09954771
## lesion_locationposterior                 0.99918109  0.4686765  2.13192071
## PhaseFollow-up:lesion_locationposterior -0.25437229  0.3390375 -0.75027786
##                                           Pr(>|z|)
## (Intercept)                             0.09939336
## PhaseFollow-up                          0.36905763
## lesion_location1                        0.03301360
## PhaseFollow-up:lesion_location1         0.45310448
## (Intercept)                             0.74607317
## PhaseFollow-up                          0.92070341
## lesion_locationposterior                0.03301337
## PhaseFollow-up:lesion_locationposterior 0.45308737

Solution

Question B4

Try playing around with the Toy Utility dataset again, fitting sum-to-zero contrasts.
Can you re-level the factor first? What happens when you do?

Tip: You can always revert easily to the treatment coding scheme, either by reading in the data again, or using

contrasts(toy_utils$type) <- NULL
contrasts(toy_utils$type)
##        playmo zing
## lego        0    0
## playmo      1    0
## zing        0    1

Solution

  1. We also didn’t get \(R^2\). Check out http://bbolker.github.io/mixedmodels-misc/glmmFAQ.html#how-do-i-compute-a-coefficient-of-determination-r2-or-an-analogue-for-glmms↩︎