Linear Regression

This lab is a long one! It takes us quite slowly through simple and multiple regression, but the broader ideas being introduced are actually quite simple - we are just drawing a straight line through some datapoints!
Try to take regular breaks during these exercises. This will help (a bit) with not getting overwhelmed - these things (both the statistics side and the programming side) take time - and repeated practice - to sink in.

Simple regression

Data: riverview.csv

Let’s imagine a study into income disparity for workers in a local authority. We might carry out interviews and find that there is a link between the level of education and an employee’s income. Those with more formal education seem to be better paid. Now we wouldn’t have time to interview everyone who works for the local authority so we would have to interview a sample, say 10%.

In this next set of exercises we will use the riverview data, which come from Lewis-Beck, 2015 and contain five attributes collected from a random sample of \(n=32\) employees working for the city of Riverview, a hypothetical midwestern city in the US. The attributes include:

• education: Years of formal education
• income: Annual income (in thousands of U.S. dollars)
• seniority: Years of seniority
• gender: Employee’s gender
• male: Dummy coded gender variable (0 = Female, 1 = Male)
• party: Political party affiliation

Preview

The first six rows of the data are:

education	income	seniority	gender	male	party
8	37.449	7	male	1	Democrat
8	26.430	9	female	0	Independent
10	47.034	14	male	1	Democrat
10	34.182	16	female	0	Independent
10	25.479	1	female	0	Republican
12	46.488	11	female	0	Democrat

The data is available at https://uoepsy.github.io/data/riverview.csv.

Question A1

Load the required libraries (probably just tidyverse for now), and read in the riverview data to your R session.
I’m going to name it riverview in my environment.

Solution

library(tidyverse)

riverview <- read_csv("https://uoepsy.github.io/data/riverview.csv")
head(riverview)

## # A tibble: 6 x 6
##   education income seniority gender  male party      
##       <dbl>  <dbl>     <dbl> <chr>  <dbl> <chr>      
## 1         8   37.4         7 male       1 Democrat   
## 2         8   26.4         9 female     0 Independent
## 3        10   47.0        14 male       1 Democrat   
## 4        10   34.2        16 female     0 Independent
## 5        10   25.5         1 female     0 Republican 
## 6        12   46.5        11 female     0 Democrat

Exploring the data

Probably the first port of call for almost any statistical analysis is to just explore the data and make sure that things look as you would expect them to look. We can do this visually, or numerically, using the skills we saw in weeks 1 and 2.

Question A2

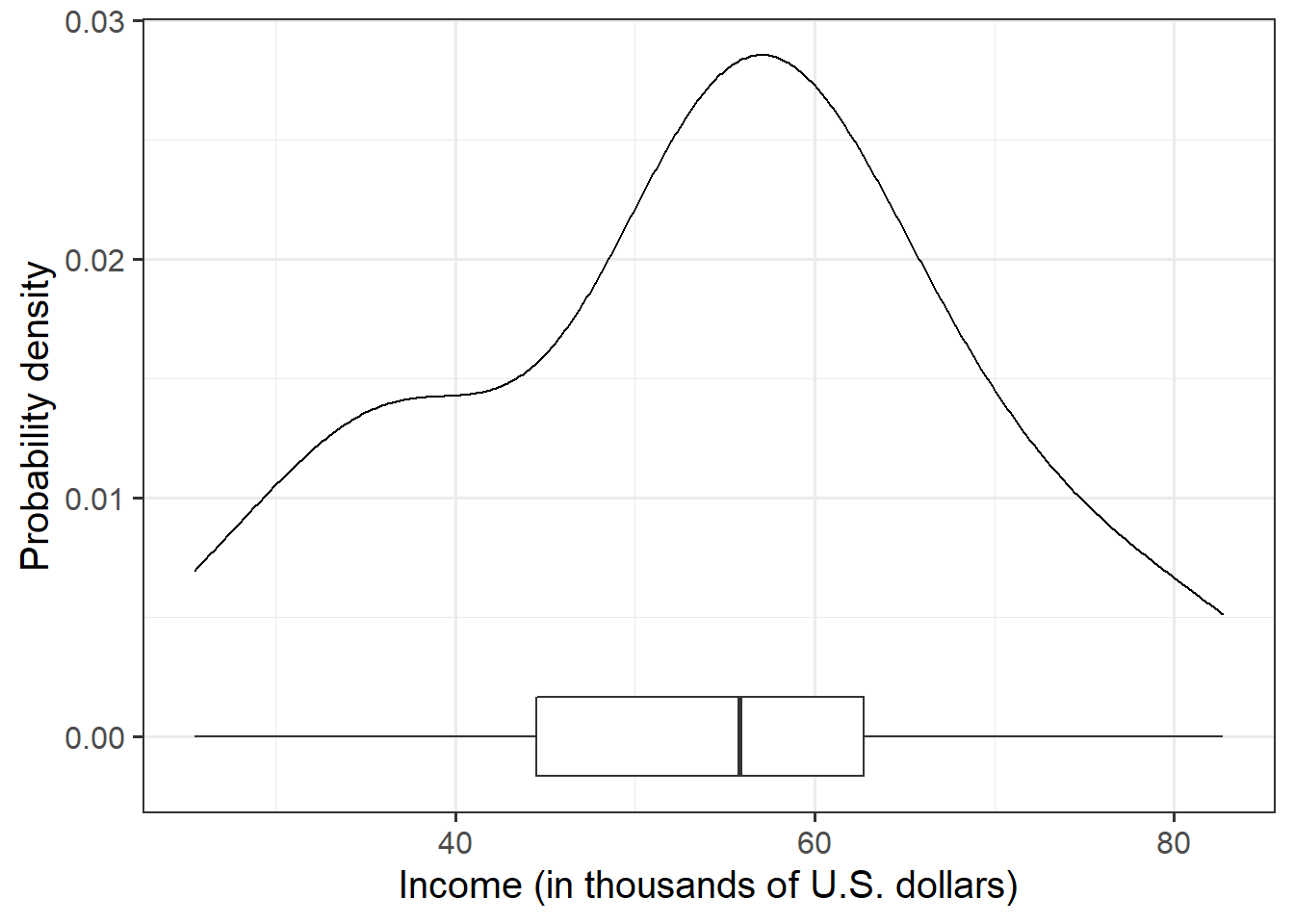
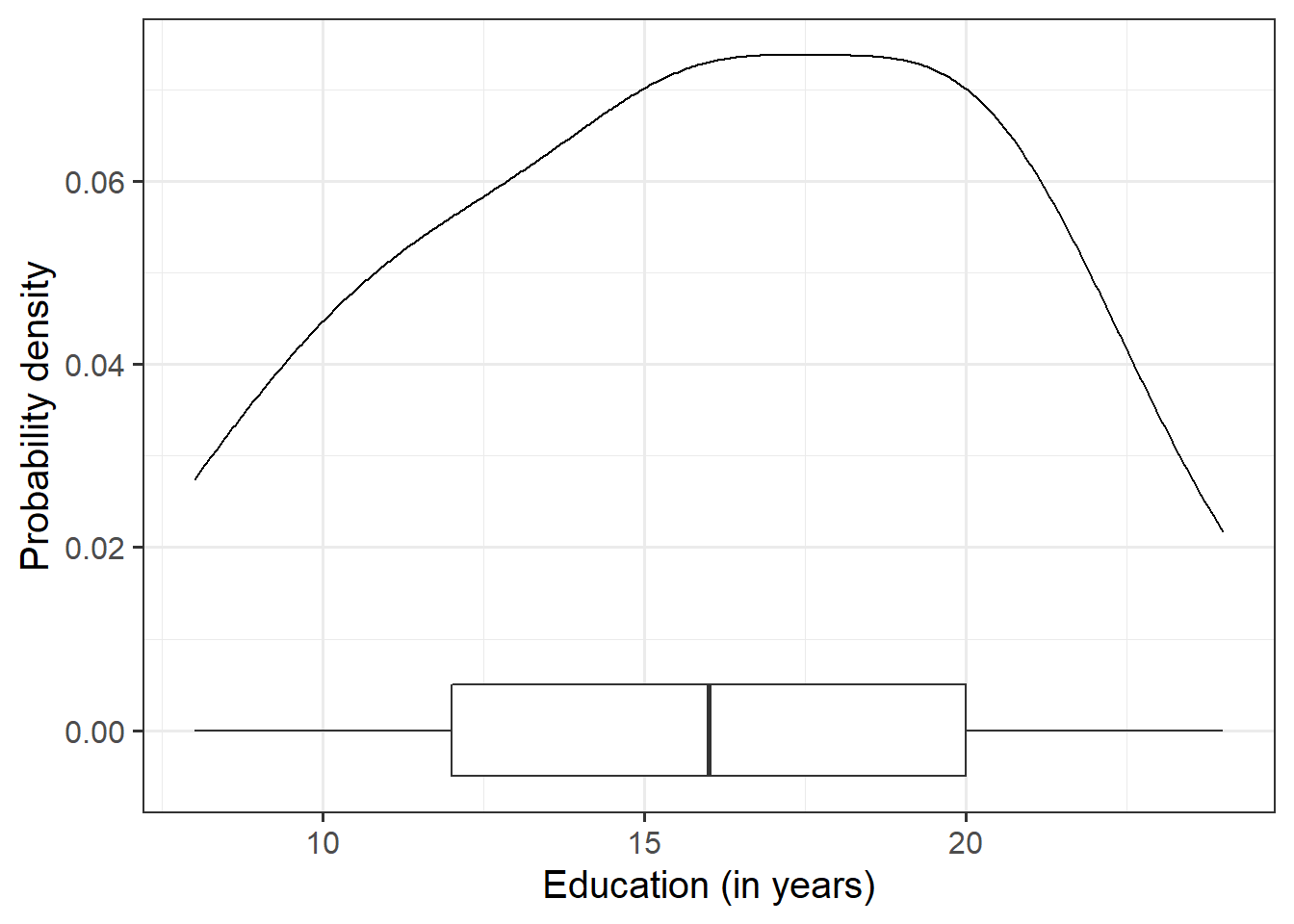
Let us first visualise and describe the marginal distributions of those variables which are of interest to us. These are the distribution of each variable (employee incomes and education levels) without reference to the values of the other variables.

• You could use, for example, geom_density() for a density plot or geom_histogram() for a histogram.
• Look at the shape, center and spread of the distribution. Is it symmetric or skewed? Is it unimodal or bimodal?
• Do you notice any extreme observations?

Solution

We can plot the marginal distribution of employee incomes as a density curve, and add a boxplot underneath to check for the presence of outliers.

The width of the geom_boxplot() is always quite wide, so I want to make it narrower so that we can see it at the same time as the density plot. Deciding on the exact value for the width here is just trial and error.

ggplot(data = riverview, aes(x = income)) +
  geom_density() +
  geom_boxplot(width = 1/300) +
  labs(x = "Income (in thousands of U.S. dollars)", 
       y = "Probability density")

Figure 1: Density plot and boxplot of employee incomes.

The plot suggests that the distribution of employee incomes is unimodal and most of the incomes are between roughly $45,000 and $70,000. The smallest income in the sample is about $25,000 and the largest income is over $80,000. (We could find the exact values using the summary() function). This suggests there is a fair amount of variation in the data. Furthermore, the boxplot does not highlight any outliers in the data.

ggplot(data = riverview, aes(x = education)) +
  geom_density() +
  geom_boxplot(width = 1/100) +
  labs(x = "Education (in years)", 
       y = "Probability density")

Figure 2: Density plot and boxplot of employee education levels.

To further summarize a distribution, it is typical to compute and report numerical summary statistics such as the mean and standard deviation. One way to compute these values is to use the summarise()/summarize() function from the tidyverse library:

riverview %>% 
  summarize(
    e = mean(income), 
    sd_income = sd(income),
    mean_edu = mean(education),
    sd_edu = sd(education)
    )

## # A tibble: 1 x 4
##       e sd_income mean_edu sd_edu
##   <dbl>     <dbl>    <dbl>  <dbl>
## 1  53.7      14.6       16   4.36

The marginal distribution of income is unimodal with a mean of approximately $53,700. There is variation in employees’ salaries (SD = $14,553).
The marginal distribution of education is unimodal with a mean of 16 years. There is variation in employees’ level of education (SD = 4.4 years).

Question A3

After we’ve looked at the marginal distributions of the variables of interest in the analysis, we typically move on to examining relationships between the variables.

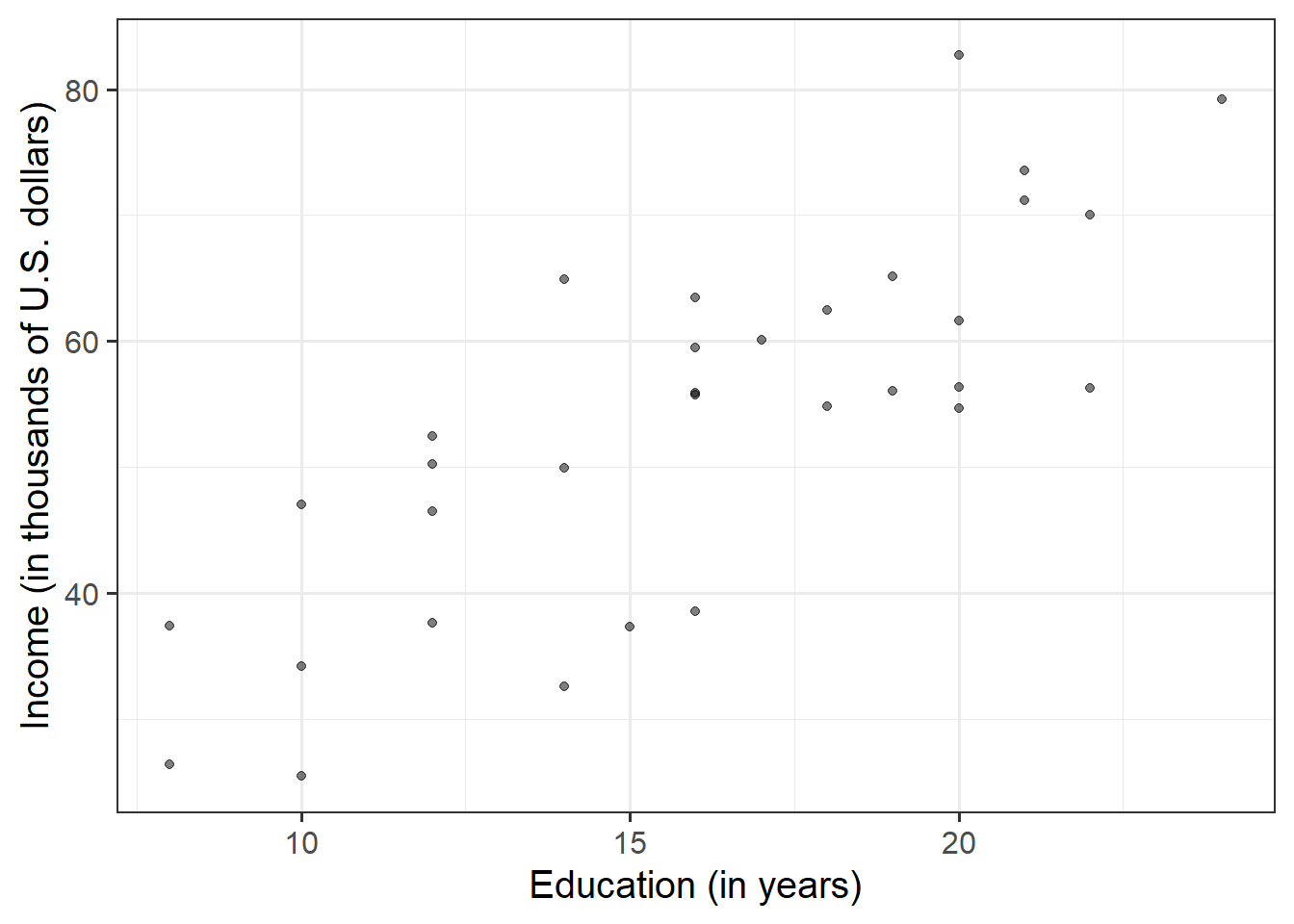
Visualise and describe (just in words) the relationship between income and level of education among the employees in the sample.

Think about:

• Direction of association
• Form of association (can it be summarised well with a straight line?)
  
• Strength of association (how closely do points fall to a recognizable pattern such as a line?)
• Unusual observations that do not fit the pattern of the rest of the observations and which are worth examining in more detail.

Solution

We are trying to investigate how income varies when varying years of formal education. Hence income is the dependent variable (on the y-axis), and education is the independent variable (on the x-axis).

ggplot(data = riverview, aes(x = education, y = income)) +
  geom_point(alpha = 0.5) +
  labs(x = "Education (in years)", 
       y = "Income (in thousands of U.S. dollars)")

Figure 3: The relationship between employees’ education level and income.

We might write:

There is a strong positive linear relationship between education level and income for the employees in the sample. High incomes tend to be observed, on average, with more years of formal education. The scatterplot does not highlight any outliers.

To comment numerically on the strength of the linear association we might compute the correlation coefficient that we were introduced to in Week 5:

riverview %>%
  select(education, income) %>%
  cor()

##           education    income
## education 1.0000000 0.7947847
## income    0.7947847 1.0000000

that is, \[ r_{\text{education, income}} = 0.79 \]

Fitting a Linear Model

The plot created in the previous question highlights a linear relationship, where the data points are scattered around an underlying linear pattern with a roughly-constant spread as x varies.

We will try to fit a simple (one explanatory variable only) linear regression model:

\[ Income = b_0 + b_1 \ Education + \epsilon \quad \\ \text{where} \quad \epsilon \sim N(0, \sigma) \text{ independently} \]

where “\(\epsilon \sim N(0, \sigma) \text{ independently}\)” means that the errors around the line have mean zero and constant spread as x varies (we’ll read more about what this means later in this lab in the section on Making Valid Inferences).

To fit linear models, we use the lm() function.
The syntax of the lm() function is:

[model name] <- lm([response variable] ~ 1 + [explanatory variable], data = [dataframe])

Why ~1?

The fitted model can be written as \[ \hat y = \hat b_0 + \hat b_1 (x) \] The predicted values for the outcome are equal to our intercept, \(\hat b_0\), plus our slope \(\hat b_1\) multiplied by the value on our explanatory variable \(x\).
The intercept is a constant. That is, we could write it as multiplied by 1: \[ \hat y = \color{blue}{\hat b_0}(\color{green}{1})\color{blue}{ + \hat b_1 }(\color{green}{x}) \]

When we specify the linear model in R, we include after the tilde sign ~ all the things which appear to the right of each of the \(\hat b\)s (the bits in green in the equartion above). That’s why the 1 is included. It is just saying “we want the intercept, \(b_0\), to be estimated.”

Question A4

Using the lm() function, fit a linear model to the sample data, in which employee income is explained by education level. Assign it to a name to store it in your environment.

Solution

As the variables are in the riverview dataframe, we would write:

model1 <- lm(income ~ 1 + education, data = riverview)

Interpreting coefficients

Question A5

Interpret the estimated intercept and slope in the context of the question of interest.

Let’s suppose we assigned our linear model object to the name “model1” in R. To obtain the estimated regression coefficients we can use it’s name in various ways and with various functions.

• type model1, i.e. simply invoke the name of the fitted model;
• type model1$coefficients;
• use the coef(model1) function;
• use the coefficients(model1) function;
• use the summary(model1) function and look under the “Estimate” column.

The estimated parameters returned by the above methods are all equivalent. However, summary() returns more information and you need to look under the column “Estimate.”

Solution

coef(model1)

## (Intercept)   education 
##   11.321379    2.651297

The fitted line is: \[ \widehat{Income} = 11.32 + 2.65 \ Education \\ \]

We can interpret the estimated intercept as follows,

The estimated average income associated with zero years of formal education is $11,321.

For the estimated slope we might write,

The estimated increase in average income associated with a one year increase in education is $2,651.

Interpreting \(\sigma\)

The parameter estimates from our simple linear regression model take the form of a line, representing the systematic part of our model \(b_0 + b_1 \ x\), which in our case is \(11.32 + 2.65 \ Education\). Deviations from the line are determined by the random error component \(\hat \epsilon\), or “residuals” (the red lines in Figure 4 below).

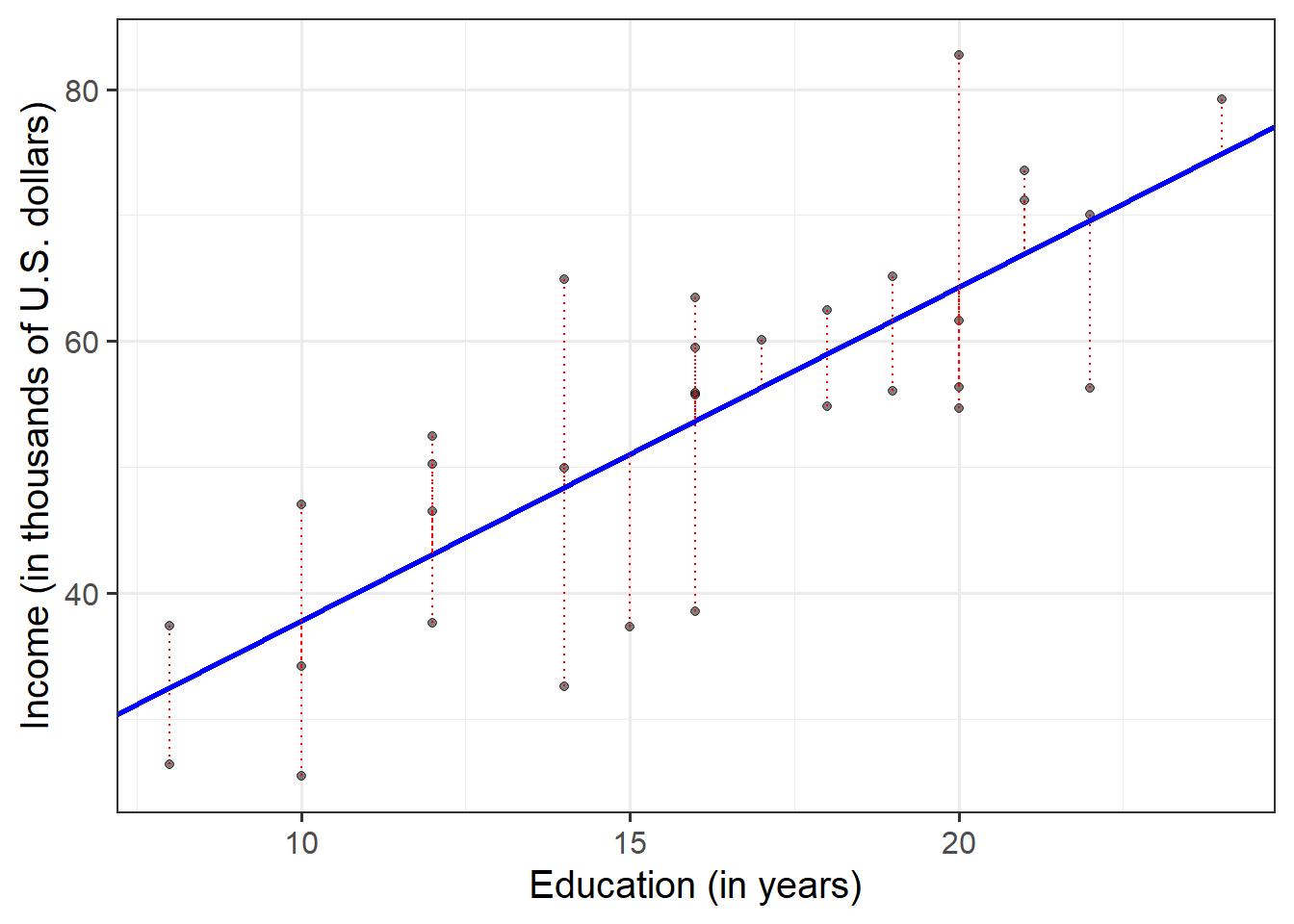
Figure 4: Simple linear regression model, with systematic part of the model in blue and residuals in red

We use \(\sigma\) to denote the standard deviation of all the residuals

Question A6

Consider the following:

1. In fitting a linear regression model, we make the assumption that the errors around the line are normally distributed around zero (this is the \(\epsilon \sim N(0, \sigma)\) bit.)
   
2. About 95% of values from a normal distribution fall within two standard deviations of the centre.

We can obtain the estimated standard deviation of the errors (\(\hat \sigma\)) from the fitted model using sigma() and giving it the name of our model.
What does this tell us?

Huh? What is \(\sigma\)?

The standard deviation of the errors, denoted by \(\sigma\) is an important quantity to estimate because it measures how much individual data points tend to deviate above and below the regression line.

A small \(\sigma\) indicates that the points hug the line closely and we should expect fairly accurate predictions, while a large \(\sigma\) suggests that, even if we estimate the line perfectly, we can expect individual values to deviate from it by substantial amounts.

When we actually estimate this quantity, we might put a hat on it, and write \(\hat \sigma\). It is equal to \[ \hat \sigma = \sqrt{\frac{SS_{Residual}}{n - 2}} \\ \begin{align} & \text{where} \\ & SS_{Residual} = \textrm{Sum of Squared Residuals} = \sum_{i=1}^n{(\epsilon_i)^2} \end{align} \]

Solution

The estimated standard deviation of the errors can be equivalently obtained by:

• typing sigma(model1);
• looking at the “Residual standard error” entry of the summary(model1) output.

Note: The term “Residual standard error” is a misnomer, as the help page for sigma says (check ?sigma). However, it’s hard to get rid of this bad name as it has been used in too many books showing R output.

sigma(model1)

## [1] 8.978116

For any particular level of education, employee incomes should be distributed above and below the regression line with standard deviation estimated to be \(\hat \sigma = 8.98\). Since \(2 \hat \sigma = 2 (8.98) = 17.96\), we expect most (about 95%) of the employee incomes to be within about $18,000 from the regression line.

Fitted and predicted values

To compute the model-predicted values for the data in the sample we can use various functions. Again, if our model object is named “model1” in our environment, we can use:

• predict(model1)
• fitted(model1)
• fitted.values(model1)
• model1$fitted.values

For example, this will give us the estimated income (point on our regression line) for each observed value of education level.

predict(model1)

##        1        2        3        4        5        6        7        8 
## 32.53175 32.53175 37.83435 37.83435 37.83435 43.13694 43.13694 43.13694 
##        9       10       11       12       13       14       15       16 
## 43.13694 48.43953 48.43953 48.43953 51.09083 53.74212 53.74212 53.74212 
##       17       18       19       20       21       22       23       24 
## 53.74212 53.74212 56.39342 59.04472 59.04472 61.69601 61.69601 64.34731 
##       25       26       27       28       29       30       31       32 
## 64.34731 64.34731 64.34731 66.99861 66.99861 69.64990 69.64990 74.95250

We can also compute model-predicted values for other (unobserved) data:

# make a tibble/dataframe with values for the predictor:
education_query <- tibble(education = c(11, 18, 50))
# model predicted values of income, for the values of education
# inside the "education_query" data
predict(model1, newdata = education_query)

##         1         2         3 
##  40.48564  59.04472 143.88621

Question A7

Compute the model-predicted income for someone with 1 year of education.

Solution

education_query <- tibble(education = c(1))
predict(model1, newdata = education_query)

##        1 
## 13.97268

Question A8

Given that our fitted model takes the form:

\[ Income = 11.32 + 2.65\cdot Education \] How can we get to this same answer manually?

Solution

We are asking what the predicted income is for someone with 1 year of education. So we can substitute in “1” for the Education variable: \[ \begin{align} Income &= 11.32 + 2.65\cdot Education \\ Income &= 11.32 + 2.65\cdot 1 \\ Income &= 11.32 + 2.65\\ Income &= 13.97 \\ \end{align} \]

Inference for regression coefficients

We have fitted a linear model, and we now know how we interpret our coefficients. But this is only part of the story.

Figure 5: Estimates without inference

To quantify the amount of uncertainty in each estimated coefficient that is due to sampling variability, we use the standard error (SE) of the coefficient. Recall that a standard error gives a numerical answer to the question of how variable a statistic will be because of random sampling.

The standard errors are found in the column “Std. Error” of the summary() of a model:

##              Estimate Std. Error  t value     Pr(>|t|)
## (Intercept) 11.321379  6.1232350 1.848921 7.434602e-02
## education    2.651297  0.3696232 7.172972 5.562116e-08

In this example the slope, 2.651, has a standard error of 0.37. One way to envision this is as a distribution. Our best guess (mean) for the slope parameter is 2.651. The standard deviation of this distribution is 0.37, which indicates the precision (uncertainty) of our estimate.

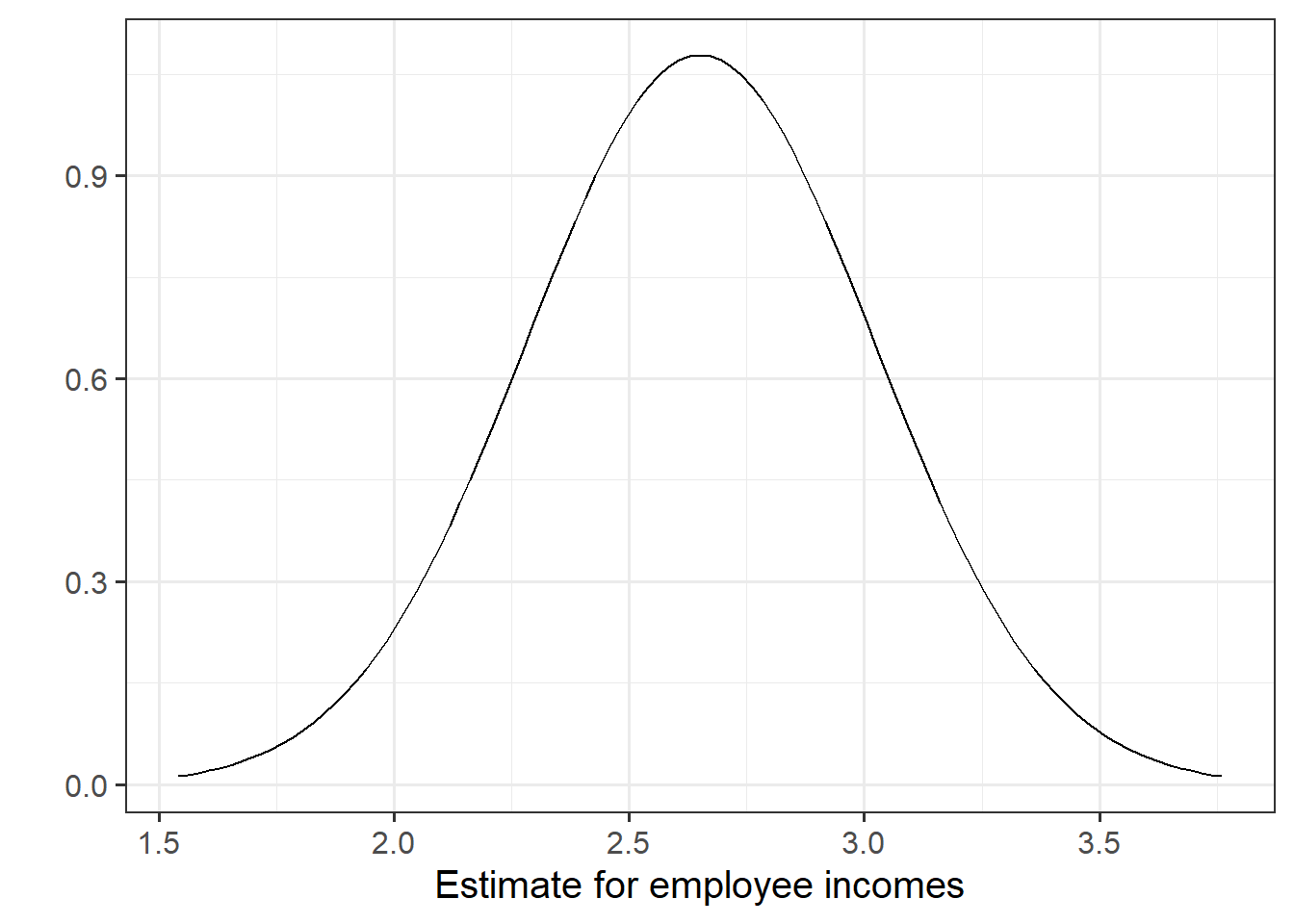
Figure 6: Sampling distribution of the slope coefficient. The distribution is approximately bell-shaped with a mean of 2.651 and a standard error of 0.37.

We can perform a test against the null hypothesis that the estimate is zero. Our test statistic: The reference distribution in this case is a t-distribution with \(n-2\) degrees of freedom, where \(n\) is the sample size, and our test statistic is:
\[ t = \frac{\hat b_1 - 0}{SE(\hat b_1)} \]

Question A9

Test the hypothesis that the population slope is zero — that is, that there is no linear association between income and education level in the population.

(Hint: you don’t need to do anything for this, you can find all the necessary information in summary() of your model)

Solution

The information is already contained in the row corresponding to the variable “education” in the output of summary(), which reports the t-statistic under t value and the p-value under Pr(>|t|):

summary(model1)

## 
## Call:
## lm(formula = income ~ 1 + education, data = riverview)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -15.809  -5.783   2.088   5.127  18.379 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  11.3214     6.1232   1.849   0.0743 .  
## education     2.6513     0.3696   7.173 5.56e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.978 on 30 degrees of freedom
## Multiple R-squared:  0.6317, Adjusted R-squared:  0.6194 
## F-statistic: 51.45 on 1 and 30 DF,  p-value: 5.562e-08

Before we interpret the results, recall that the p-value 5.56e-08 in the Pr(>|t|) column simply means \(5.56 \times 10^{-8}\). This is a very small value, hence we will report it as <.001 following the APA guidelines.

We performed a t-test against the null hypothesis that education is not a significant predictor of income: \(t(30) = 7.173,\ p < .001\), two-sided. The large t-statistic leads to a very small p-value, meaning that we have strong evidence against the null hypothesis.

Figure 7: conversations with statisticians

Model evaluation

Partitioning variation: \(R^2\)

We might ask ourselves if the model is useful. To quantify and assess model utility, we split the total variability of the response into two terms: the variability explained by the model plus the variability left unexplained in the residuals.

\[ \text{total variability in response = variability explained by model + unexplained variability in residuals} \]

Each term is quantified by a sum of squares:

\[ \begin{aligned} SS_{Total} &= SS_{Model} + SS_{Residual} \\ \sum_{i=1}^n (y_i - \bar y)^2 &= \sum_{i=1}^n (\hat y_i - \bar y)^2 + \sum_{i=1}^n (y_i - \hat y_i)^2 \\ \quad \\ \text{Where:} \\ y_i = \text{observed value} \\ \bar{y} = \text{mean} \\ \hat{y}_i = \text{model predicted value} \\ \end{aligned} \]

The R-squared coefficient is defined as the proportion of the total variability in the outcome variable which is explained by our model:
\[ R^2 = \frac{SS_{Model}}{SS_{Total}} = 1 - \frac{SS_{Residual}}{SS_{Total}} \]

Question A10

What is the proportion of the total variability in incomes explained by the linear relationship with education level?

Hint: The question asks to compute the value of \(R^2\), but you might be able to find it already computed somewhere (so much stuff is already in summary() of the model.

Solution

summary(model1)

## 
## Call:
## lm(formula = income ~ 1 + education, data = riverview)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -15.809  -5.783   2.088   5.127  18.379 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  11.3214     6.1232   1.849   0.0743 .  
## education     2.6513     0.3696   7.173 5.56e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.978 on 30 degrees of freedom
## Multiple R-squared:  0.6317, Adjusted R-squared:  0.6194 
## F-statistic: 51.45 on 1 and 30 DF,  p-value: 5.562e-08

The output of summary() displays the R-squared value in the following line:

Multiple R-squared:  0.6317

For the moment, ignore “Adjusted R-squared.” We will come back to this later on.

Optional - Manual calculation of R-Squared

riverview_fitted <- riverview %>%
  mutate(
    income_hat = predict(model1),
    resid = income - income_hat
  )
head(riverview_fitted)

## # A tibble: 6 x 8
##   education income seniority gender  male party       income_hat  resid
##       <dbl>  <dbl>     <dbl> <chr>  <dbl> <chr>            <dbl>  <dbl>
## 1         8   37.4         7 male       1 Democrat          32.5   4.92
## 2         8   26.4         9 female     0 Independent       32.5  -6.10
## 3        10   47.0        14 male       1 Democrat          37.8   9.20
## 4        10   34.2        16 female     0 Independent       37.8  -3.65
## 5        10   25.5         1 female     0 Republican        37.8 -12.4 
## 6        12   46.5        11 female     0 Democrat          43.1   3.35

riverview_fitted %>%
  summarise(
    SSModel = sum( (income_hat - mean(income))^2 ),
    SSTotal = sum( (income - mean(income))^2 )
  ) %>%
  summarise(
    RSquared = SSModel / SSTotal
  )

## # A tibble: 1 x 1
##   RSquared
##      <dbl>
## 1    0.632

Approximately 63% of the total variability in employee incomes is explained by the linear association with education level.

Testing Model Utility: \(F\) Statistic

To test if the model is useful — that is, if the explanatory variable is a useful predictor of the response — we test the following hypotheses:

\[ \begin{aligned} H_0 &: \text{the model is ineffective, } b_1 = 0 \\ H_1 &: \text{the model is effective, } b_1 \neq 0 \end{aligned} \] The relevant test-statistic is the F-statistic:

\[ \begin{split} F = \frac{MS_{Model}}{MS_{Residual}} = \frac{SS_{Model} / 1}{SS_{Residual} / (n-2)} \end{split} \]

which compares the amount of variation in the response explained by the model to the amount of variation left unexplained in the residuals.

The sample F-statistic is compared to an F-distribution with \(df_{1} = 1\) and \(df_{2} = n - 2\) degrees of freedom.¹

Optional: Another formula for the F-test.

With some algebra we can also show that: \[ F = \frac{R^2 / 1}{(1 - R^2) / (n - 2) } = \frac{R^2 / df_{Model}}{(1 - R^2) / df_{Residual} } \]

Proof:

\[ \begin{aligned} F = \frac{SS_{Model} / 1}{SS_{Residual} / (n - 2)} = \frac{\frac{SS_{Model}}{SS_{Total}}}{\frac{SS_{Residual}}{SS_{Total}} \cdot \frac{1}{(n - 2)}} = \frac{R^2 / 1}{(1 - R^2) / (n - 2)} \end{aligned} \]

Question A11

Look at the output of summary() of your model. Identify the relevant information to conduct an F-test against the null hypothesis that the model is ineffective at predicting income using education level.

Solution

summary(model1)

## 
## Call:
## lm(formula = income ~ 1 + education, data = riverview)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -15.809  -5.783   2.088   5.127  18.379 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  11.3214     6.1232   1.849   0.0743 .  
## education     2.6513     0.3696   7.173 5.56e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.978 on 30 degrees of freedom
## Multiple R-squared:  0.6317, Adjusted R-squared:  0.6194 
## F-statistic: 51.45 on 1 and 30 DF,  p-value: 5.562e-08

The relevant row is the following:

F-statistic: 51.45 on 1 and 30 DF,  p-value: 5.562e-08

We might interpret this as:

We performed an F-test for the overall significance of the regression, \(F(1, 30) = 51.45, p < .001\), indicating very strong evidence against the null hypothesis that the model is ineffective.

In other words, the data provide strong evidence that education is an effective predictor of income.

Optional: Equivalence of t-test for the slope and model utility F-test in simple regression.

In simple linear regression only, the F-statistic for overall model significance is equal to the square of the t-statistic for \(H_0: b_1 = 0\).

You can check that the squared t-statistic is equal, up to rounding error, to the F-statistic:

summary(model1)$fstatistic['value']

##    value 
## 51.45152

summary(model1)$coefficients['education','t value']

## [1] 7.172972

\[ t^2 = F \\ 7.173^2 = 51.452 \]

Here we will show the equivalence of the F-test for model effectiveness and t-test for the slope.

Recall the formula of the sum of squares due to the model. We will rewrite it in an equivalent form below: \[ \begin{aligned} SS_{Model} &= \sum_i (\hat y_i - \bar y)^2 \\ &= \sum_i (\hat b_0 + \hat b_1 x_i - \bar y)^2 \\ &= \sum_i (\bar y - \hat b_1 \bar x + \hat b_1 x_i - \bar y)^2 \\ &= \sum_i (\hat b_1 (x_i - \bar x))^2 \\ &= \hat b_1^2 \sum_i (x_i - \bar x)^2 \end{aligned} \]

The F-statistic is given by: \[ \begin{aligned} F = \frac{SS_{Model} / 1}{SS_{Residual} / (n - 2)} = \frac{\hat b_1^2 \sum_i (x_i - \bar x)^2}{\hat \sigma^2} = \frac{\hat b_1^2 }{\hat \sigma^2 / \sum_i (x_i - \bar x)^2} \end{aligned} \]

Now recall the formula of the t-statistic, \[ t = \frac{\hat b_1}{SE(\hat b_1)} = \frac{\hat b_1}{\hat \sigma / \sqrt{\sum_i (x_i - \bar x)^2}} \]

It is evident that the latter is obtained as the square root of the former.

Binary predictors

Let’s suppose that instead of having measured education in years, we had data instead on “Obtained College Degree: Yes/No.” Our explanatory variable would be binary categorical (think back to our discussion of types of data).

Let us pretend that everyone with >18 years of education has a college degree:

riverview <- 
  riverview %>%
    mutate(
      degree = ifelse(education > 18, "Yes", "No")
    )

We may then plot our relationship as a boxplot. If you want to see the individual points, you could always “jitter” them (right-hand plot below)

ggplot(riverview, aes(x = degree, y = income)) + 
  geom_boxplot() +
ggplot(riverview, aes(x = degree, y = income)) + 
  geom_jitter(height=0, width=.05)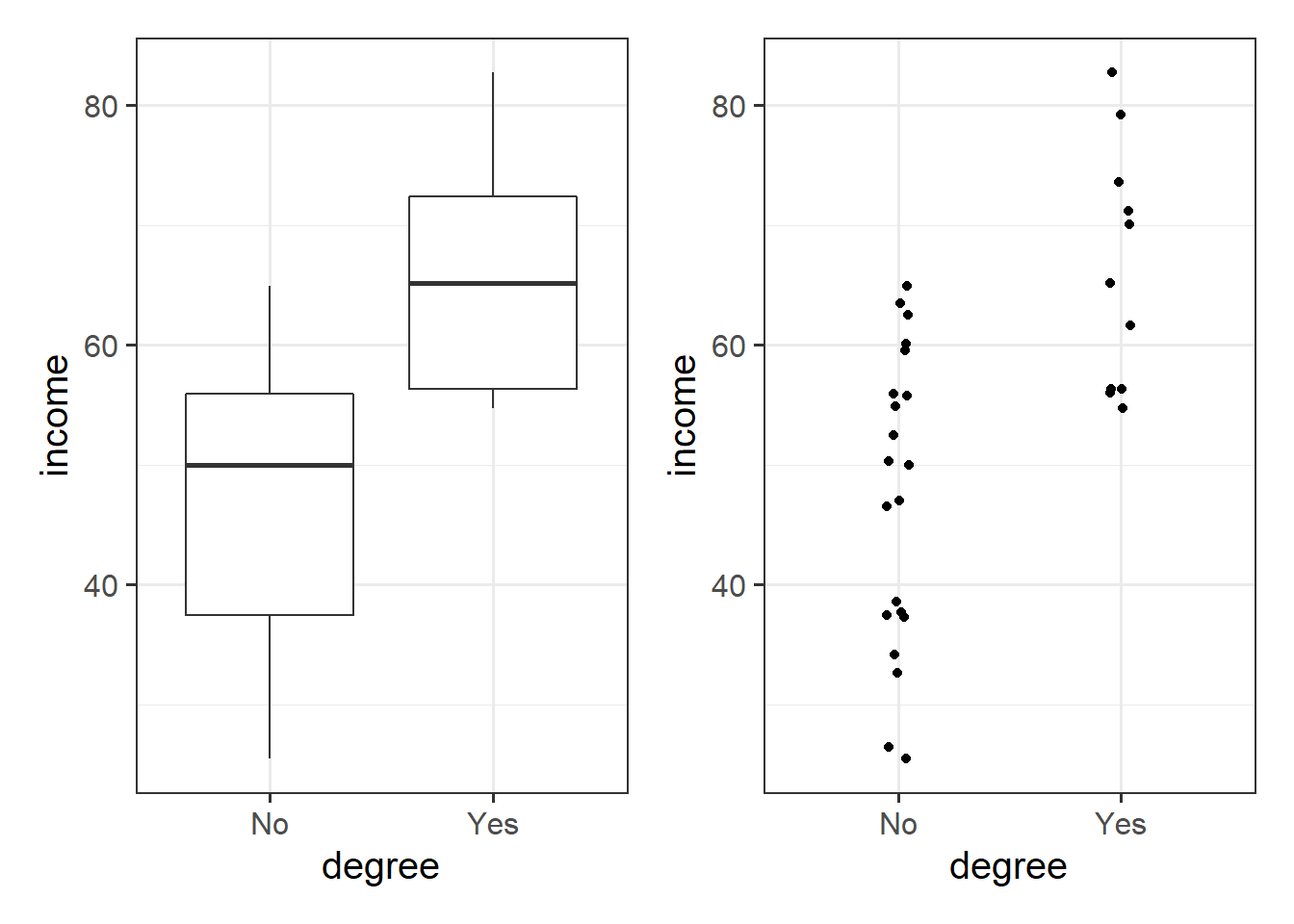

Binary predictors in linear regression

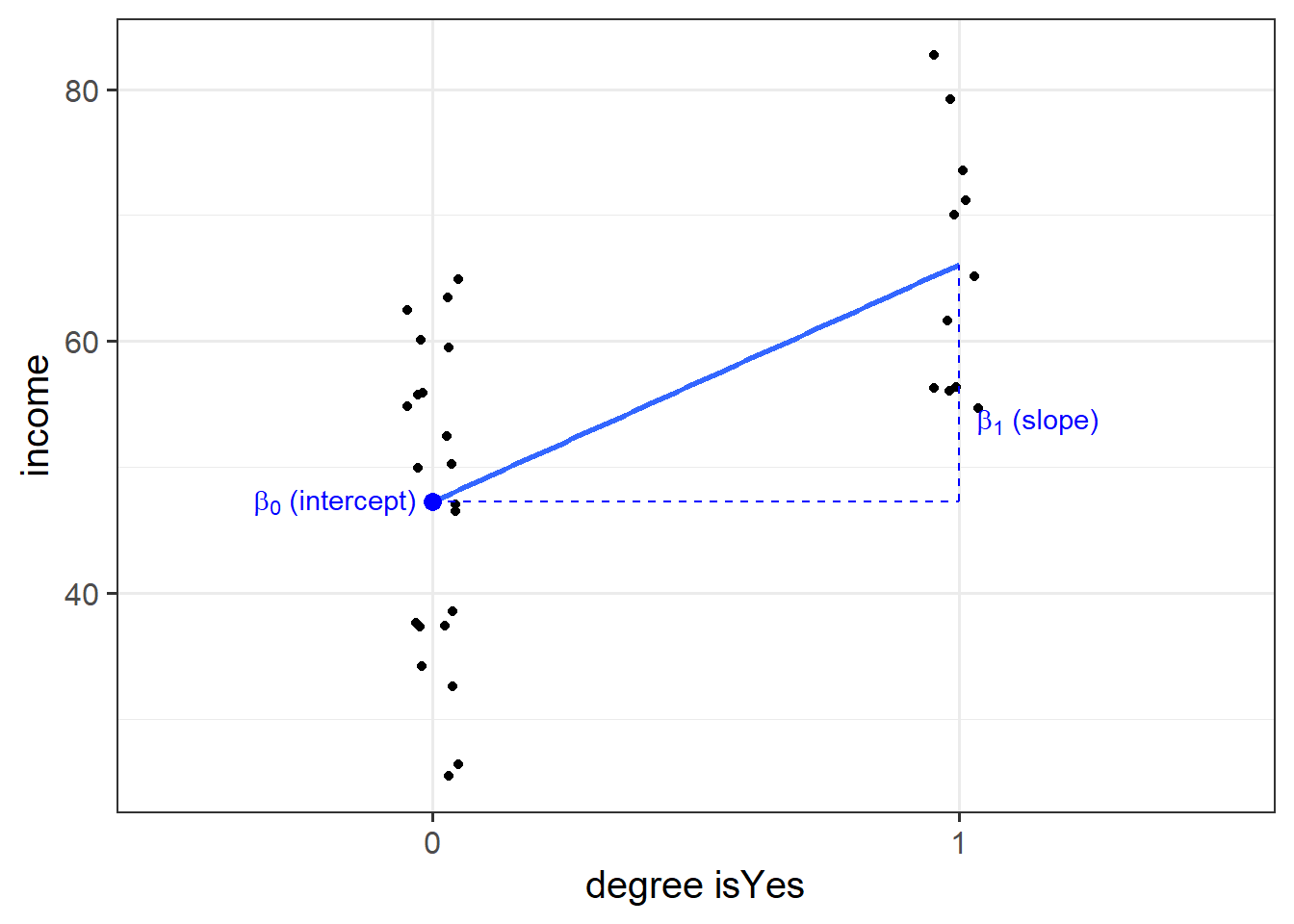
We can include categorical predictors in a linear regression, but the interpretation of the coefficients is very specific. Whereas we talked about coefficients being interpreted as “the change in \(y\) associated with a 1-unit increase in \(x\),” for categorical explanatory variables, coefficients can be considered to examine differences in group means. However, they are actually doing exactly the same thing - the model is simply translating the levels (like “Yes”/“No”) in to 0s and 1s!

So while we may have in our dataframe a categorical predictor like the middle column “degree,” below, what is inputted into our model is more like the third column, “isYes.”

## # A tibble: 32 x 3
##    income degree isYes
##     <dbl> <chr>  <dbl>
##  1   50.3 No         0
##  2   32.6 No         0
##  3   65.1 Yes        1
##  4   54.7 Yes        1
##  5   56.0 Yes        1
##  6   38.6 No         0
##  7   60.1 No         0
##  8   61.6 Yes        1
##  9   34.2 No         0
## 10   70.0 Yes        1
## # ... with 22 more rows

Our coefficients are just the same as before. The intercept is where our predictor equals zero, and the slope is the change in our outcome variable associated with a 1-unit change in our predictor.
However, “zero” for this predictor variable now corresponds to a whole level. This is known as the “reference level.” Accordingly, the 1-unit change in our predictor (the move from “zero” to “one”) corresponds to the difference between the two levels.

Multiple Regression

In this next block of exercises, we move from the simple linear regression model (one outcome variable, one explanatory variable) to the multiple regression model (one outcome variable, multiple explanatory variables).
Everything we just learned about simple linear regression can be extended (with minor modification) to the multiple regression model. The key conceptual difference is that for simple linear regression we think of the distribution of errors at some fixed value of the explanatory variable, and for multiple linear regression, we think about the distribution of errors at fixed set of values for all our explanatory variables.

Model formula

For multiple linear regression, the model formula is an extension of the one predictor (“simple”) regression model, to include any number of predictors:
\[ y = b_0 \ + \ b_1 x_1 \ + \ b_2 x_2 \ + \ ... \ + b_k x_k \ + \ \epsilon \\ \quad \\ \text{where} \quad \epsilon \sim N(0, \sigma) \text{ independently} \]

In the model specified above,

• \(\mu_{y|x_1, x_2, ..., x_k} = b_0 + b_1 x + b_2 x_2 + ... b_k x_k\) represents the systematic part of the model giving the mean of \(y\) at each combination of values of variables \(x_1\)-\(x_k\);
• \(\epsilon\) represents the error (deviation) from that mean, and the errors are independent from one another.

Visual

Note that for simple linear regression we talked about our model as a line in 2 dimensions: the systematic part \(b_0 + b_1 x\) defined a line for \(\mu_y\) across the possible values of \(x\), with \(\epsilon\) as the random deviations from that line. But in multiple regression we have more than two variables making up our model.

In this particular case of three variables (one outcome + two explanatory), we can think of our model as a regression surface (See Figure 8). The systematic part of our model defines the surface across a range of possible values of both \(x_1\) and \(x_2\). Deviations from the surface are determined by the random error component, \(\hat \epsilon\).

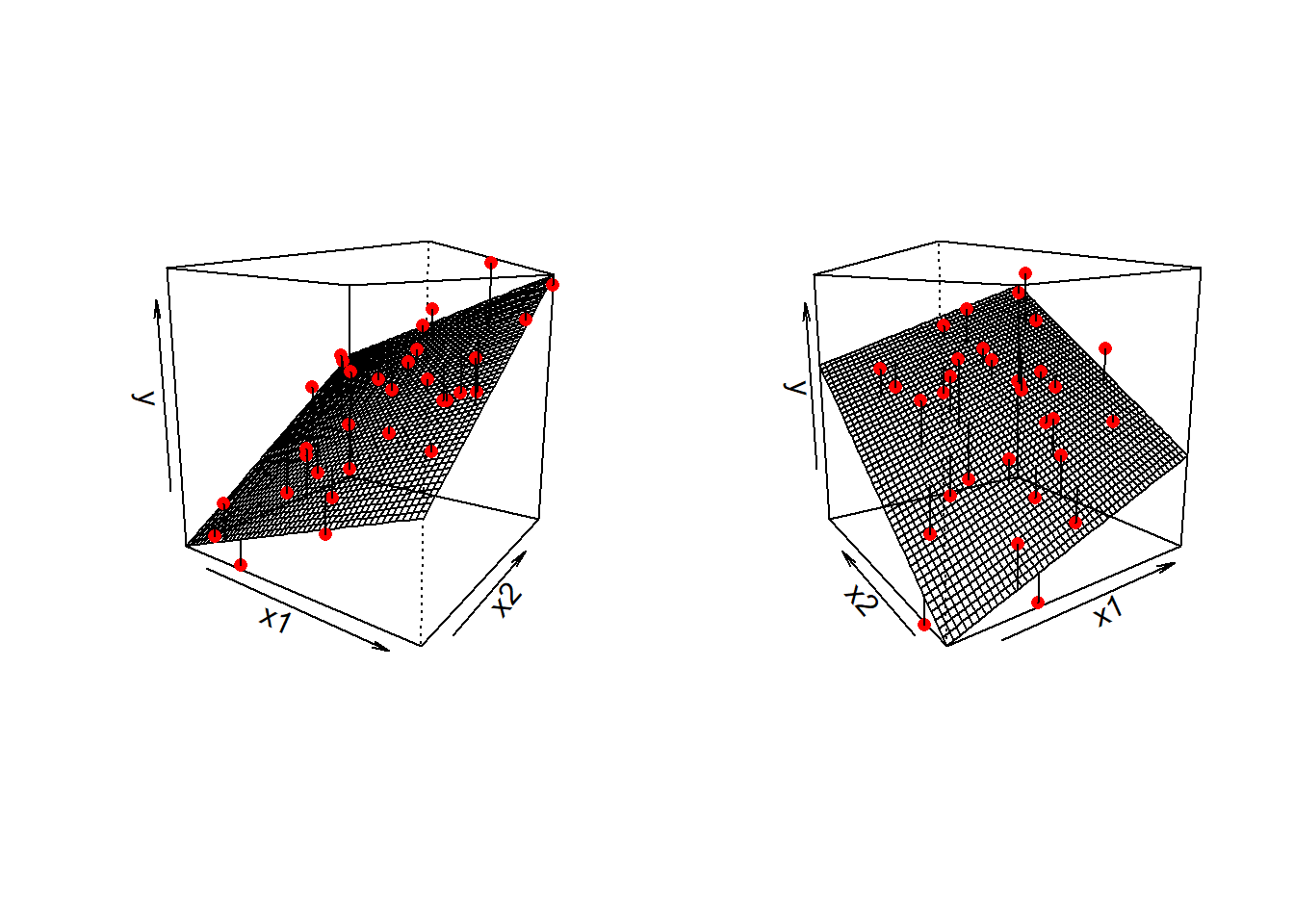
Figure 8: Regression surface for wellbeing ~ outdoor_time + social_int, from two different angles

Don’t worry about trying to figure out how to visualise it if we had any more explanatory variables! We can only concieve of 3 spatial dimensions. One could imagine this surface changing over time, which would bring in a 4th dimension, but beyond that, it’s not worth trying!.

Question B1

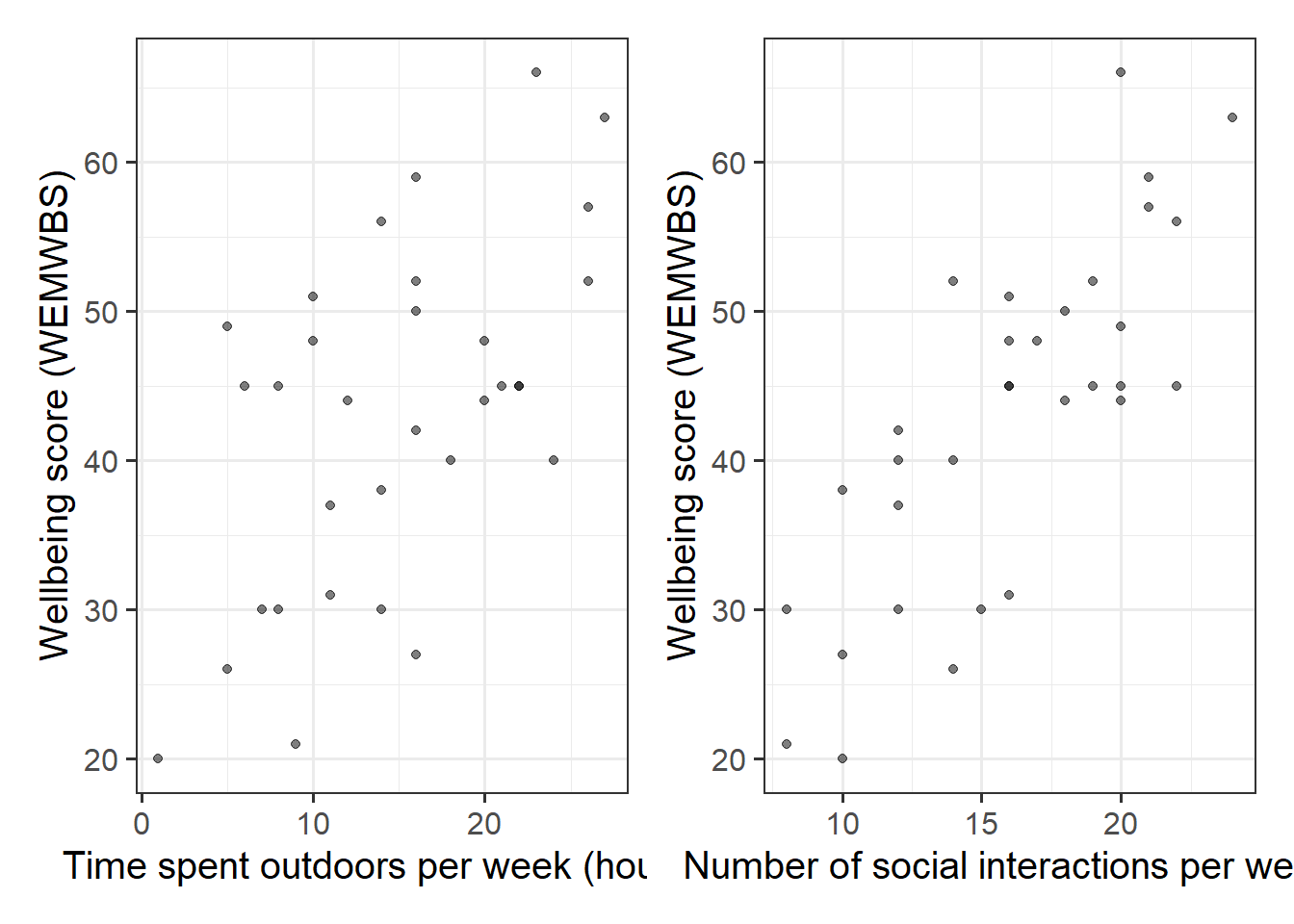
Let’s imagine that some reseachers are interested in the relationship between psychological wellbeing and time spent outdoors. They know that other aspects of peoples’ lifestyles such as how much social interaction they have can influence their mental well-being. They would like to study whether there is a relationship between well-being and time spent outdoors after taking into account the relationship between well-being and social interactions.

To evaluate this hypothesis, we are going to fit the following model:

\[ Wellbeing = b_0 \ + \ b_1 \cdot Outdoor Time \ + \ b_2 \cdot Social Interactions \ + \ \epsilon \]

First, create a new section heading in your R script or RMarkdown document (whichever you are using) for the multiple regression exercises.
Import the wellbeing data (detailed below) into R. We’ll give them the name mwdata.

Solution

library(tidyverse)
# Read in data
mwdata = read_csv(file = "https://uoepsy.github.io/data/wellbeing.csv")

Data: Wellbeing

The data is available at https://uoepsy.github.io/data/wellbeing.csv.

Description

Researchers interviewed 32 participants, selected at random from the population of residents of Edinburgh & Lothians. They used the Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70.
The researchers also asked participants to estimate the average number of hours they spend outdoors each week, the average number of social interactions they have each week (whether on-line or in-person), and whether they believe that they stick to a routine throughout the week (Yes/No).

The data in wellbeing.csv contain five attributes collected from a random sample of \(n=32\) hypothetical residents over Edinburgh & Lothians, and include:

• wellbeing: Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70.
  
• outdoor_time: Self report estimated number of hours per week spent outdoors
  
• social_int: Self report estimated number of social interactions per week (both online and in-person)
• routine: Binary Yes/No response to the question “Do you follow a daily routine throughout the week?”
• location: Location of primary residence (City, Suburb, Rural)

Preview

The first six rows of the data are:

wellbeing	outdoor_time	social_int	location	routine
30	7	8	Suburb	Routine
21	9	8	City	No Routine
38	14	10	Suburb	Routine
27	16	10	City	No Routine
20	1	10	Rural	No Routine
37	11	12	Suburb	No Routine

Question B2

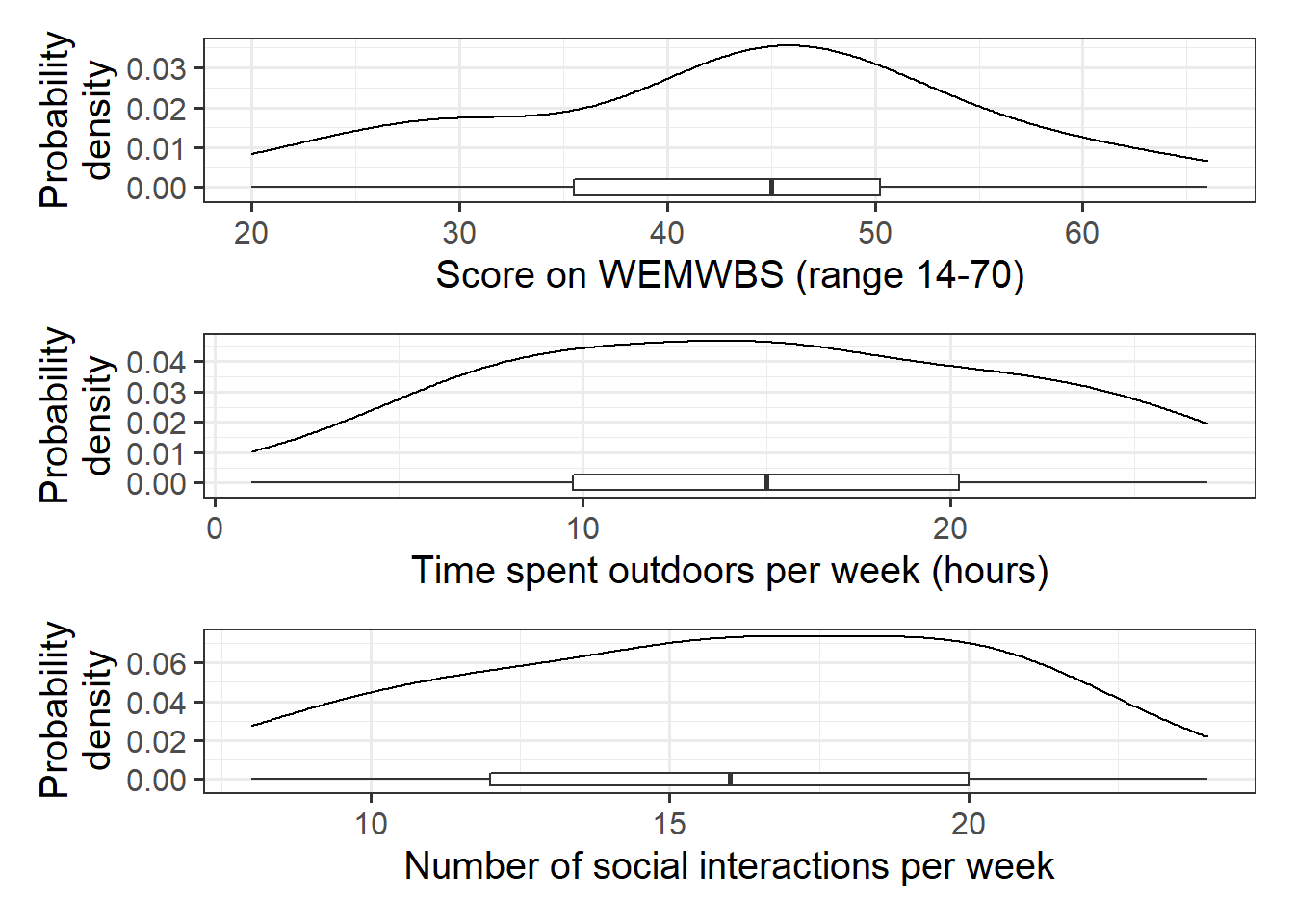
Explore and describe the relevant variables and relationships.

Hints

• Produce plots of the marginal distributions (the distributions of each variable in the analysis without reference to the other variables) of the wellbeing, outdoor_time, and social_int variables.
• Produce plots of the marginal relationships between the outcome variable (wellbeing) and each of the explanatory variables.
  
• Produce a correlation matrix of the variables which are to be used in the analysis, and write a short paragraph describing the relationships.

Correlation matrix

A table showing the correlation coefficients - \(r_{(x,y)}=\frac{\mathrm{cov}(x,y)}{s_xs_y}\) - between variables. Each cell in the table shows the relationship between two variables. The diagonals show the correlation of a variable with itself (and are therefore always equal to 1).

We can create a correlation matrix easily by giving the cor() function a dataframe. However, we only want to give it 3 columns here. Think about how we select specific columns, either using select(), or giving the column numbers inside [].

Solution

We should be familiar now with how to visualise a marginal distribution. You might choose histograms, density curves, or boxplots, or a combination:

library(patchwork) #used to arrange plots

wellbeing_plot <- 
  ggplot(data = mwdata, aes(x = wellbeing)) +
  geom_density() +
  geom_boxplot(width = 1/250) +
  labs(x = "Score on WEMWBS (range 14-70)", y = "Probability\ndensity")

outdoortime_plot <- 
  ggplot(data = mwdata, aes(x = outdoor_time)) +
  geom_density() +
  geom_boxplot(width = 1/200) +
  labs(x = "Time spent outdoors per week (hours)", y = "Probability\ndensity")

social_plot <- 
  ggplot(data = mwdata, aes(x = social_int)) +
  geom_density() +
  geom_boxplot(width = 1/150) +
  labs(x = "Number of social interactions per week", y = "Probability\ndensity")

# the "patchwork" library allows us to arrange multiple plots
wellbeing_plot / outdoortime_plot / social_plot

Figure 9: Marginal distribution plots of wellbeing sores, weekly hours spent outdoors, and social interactions

• The marginal distribution of scores on the WEMWBS is unimodal with a mean of approximately 43. There is variation in scores (SD = 11.7).
  
• The marginal distribution of weekly hours spend outdoors is unimodal with a mean of approximately 14.8 hours. There is variation in outdoor time (SD = 6.9 hours).
  
• The marginal distribution of numbers of social interactions per week is unimodal with a mean of approximately 16. There is variation in in numbers of social interactions per week (SD = 4.4).

wellbeing_outdoor <- 
  ggplot(data = mwdata, aes(x = outdoor_time, y = wellbeing)) +
  geom_point(alpha = 0.5) +
  labs(x = "Time spent outdoors per week (hours)", y = "Wellbeing score (WEMWBS)")

wellbeing_social <- 
  ggplot(data = mwdata, aes(x = social_int, y = wellbeing)) +
  geom_point(alpha = 0.5) +
  labs(x = "Number of social interactions per week", y = "Wellbeing score (WEMWBS)")

wellbeing_outdoor | wellbeing_social

Figure 10: Scatterplots displaying the relationships between scores on the WEMWBS and a) weekly outdoor time (hours), and b) weekly number of social interactions

We can either use:

# correlation matrix of the first 3 columns
cor(mwdata[,1:3])

or:

# select only the columns we want by name, and pass this to cor()
mwdata %>% 
  select(wellbeing, outdoor_time, social_int) %>%
  cor()

##              wellbeing outdoor_time social_int
## wellbeing    1.0000000    0.5815613  0.7939003
## outdoor_time 0.5815613    1.0000000  0.3394469
## social_int   0.7939003    0.3394469  1.0000000

There is a moderate, positive, linear relationship between weekly outdoor time and WEMWBS scores for the participants in the sample. Participants’ wellbeing scores tend to increase, on average, with the number of hours spent outdoors each week.
There is a moderate, positive, linear relationship between the weekly number of social interactions and WEMWBS scores for the participants in the sample. Participants’ wellbeing scores tend to increase, on average, with the weekly number of social interactions. There is also a weak positive correlation between weekly outdoor time and the weekly number of social interactions.

Note that there is a weak correlation between our two explanatory variables (outdoor_time and social_int). We will return to how this might affect our model when later on we look at the assumptions of multiple regression.

Question B3

In R, using lm(), fit the linear model specified by the formula below, assigning the output to a name to store it in your environment.

\[ Wellbeing = b_0 \ + \ b_1 \cdot Outdoor Time \ + \ b_2 \cdot Social Interactions \ + \ \epsilon \]

Tip: As we did for simple linear regression, we can fit our multiple regression model using the lm() function. We can add as many explanatory variables as we like, separating them with a +.

[model name] <- lm([response variable] ~ 1 + [explanatory variable 1] + [explanatory variable 2] + ... , data = [dataframe])

Solution

wbmodel <- lm(wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)

Interpretation of Muliple Regression Coefficients

The parameters of a multiple regression model are:

• \(b_0\) (The intercept);
• \(b_1\) (The slope across values of \(x_1\));
• …
  
• …
• \(b_k\) (The slope across values of \(x_k\));
• \(\sigma\) (The standard deviation of the errors).

You’ll hear a lot of different ways that people explain multiple regression coefficients.
For the model \(y = b_0 + b_1 x_1 + b_2 x_2 + \epsilon\), the estimate \(\hat b_1\) will often be reported as:

the increase in \(y\) for a one unit increase in \(x_1\) when…

• holding the effect of \(x_2\) constant.
• controlling for differences in \(x_2\).
• partialling out the effects of \(x_2\).
• holding \(x_2\) equal.
• accounting for effects of \(x_2\).

##               Estimate Std. Error  t value     Pr(>|t|)
## (Intercept)  5.3703775  4.3205141 1.242995 2.238259e-01
## outdoor_time 0.5923673  0.1689445 3.506284 1.499467e-03
## social_int   1.8034489  0.2690982 6.701825 2.369845e-07

The coefficient 0.59 of weekly outdoor time for predicting wellbeing score says that among those with the same number of social interactions per week, those who have one additional hour of outdoor time tend to, on average, score 0.59 higher on the WEMWBS wellbeing scale. The multiple regression coefficient measures that average conditional relationship.

Question B4

• Extract and interpret the parameter estimates (the “coefficients”) from your model (summary(), coef(), $coefficients etc will be useful here).
  
• Within what distance from the model predicted values (the regression surface) would we expect 95% of WEMWBS wellbeing scores to be? (Either sigma() or part of the output from summary() will help you for this)

Solution

coef(wbmodel)

##  (Intercept) outdoor_time   social_int 
##    5.3703775    0.5923673    1.8034489

• \(\hat \beta_0\) = 5.37, the estimated average wellbeing score associated with zero hours of outdoor time and zero social interactions per week.
  
• \(\hat \beta_1\) = 0.59, the estimated increase in average wellbeing score associated with one hour increase in weekly outdoor time, holding the number of social interactions constant (i.e., when the remaining explanatory variables are held at the same value or are fixed).
• \(\hat \beta_2\) = 1.8, the estimated increase in average wellbeing score associated with an additional social interaction per week (an increase of one), holding weekly outdoor time constant.

sigma(wbmodel)

## [1] 6.148276

The estimated standard deviation of the errors is \(\hat \sigma\) = 6.15. We would expect 95% of wellbeing scores to be within about 12.3 (\(2 \hat \sigma\)) from the model fit.

Question B5

We can obtain confidence intervals for our estimates. These provide a means of quantifying the uncertainty (or precision) of our estimates.

Think of a confidence interval like a ring-toss.
The population parameter is some value, but we only have a sample, with which we use to estimate the value in the population. 95% Confidence Intervals are a way of saying “95% of the times I might throw this ring, it will land on the stake.” (see (EpiEllie?) https://twitter.com/epiellie/status/1073385427317465089 )

Look up the function confint() and obtain some 95% Confidence Intervals for the coefficients.

Solution

confint(wbmodel, level = 0.95)

##                   2.5 %     97.5 %
## (Intercept)  -3.4660660 14.2068209
## outdoor_time  0.2468371  0.9378975
## social_int    1.2530813  2.3538164

• The average wellbeing score for all those with zero hours of outdoor time and zero social interactions per week is between -3.47 and 14.21.
  
• When holding the number of social interactions per week constant, each one hour increase in weekly outdoor time is associated with a difference in wellbeing scores between 0.25 and 0.94, on average.
  
• When holding weekly outdoor time constant, each increase of one social interaction per week is associated with a difference in wellbeing scores between 1.25 and 2.35, on average.

More Model Evaluation

Adjusted \(R^2\)

We know from our work on simple linear regression that the R-squared can be obtained as: \[ R^2 = \frac{SS_{Model}}{SS_{Total}} = 1 - \frac{SS_{Residual}}{SS_{Total}} \]

However, when we add more and more predictors into a multiple regression model, \(SS_{Residual}\) cannot increase, and may decrease by pure chance alone, even if the predictors are unrelated to the outcome variable. Because \(SS_{Total}\) is constant, the calculation \(1-\frac{SS_{Residual}}{SS_{Total}}\) will increase by chance alone.

An alternative, the Adjusted-\(R^2\), does not necessarily increase with the addition of more explanatory variables, by including a penalty according to the number of explanatory variables in the model. It is not by itself meaningful, but can be useful in determining what predictors to include in a model. \[ Adjusted{-}R^2=1-\frac{(1-R^2)(n-1)}{n-k-1} \\ \quad \\ \begin{align} & \text{Where:} \\ & n = \text{sample size} \\ & k = \text{number of explanatory variables} \\ \end{align} \]

---

In R, you can view the mutiple and adjusted \(R^2\) at the bottom of the output of summary(<modelname>):

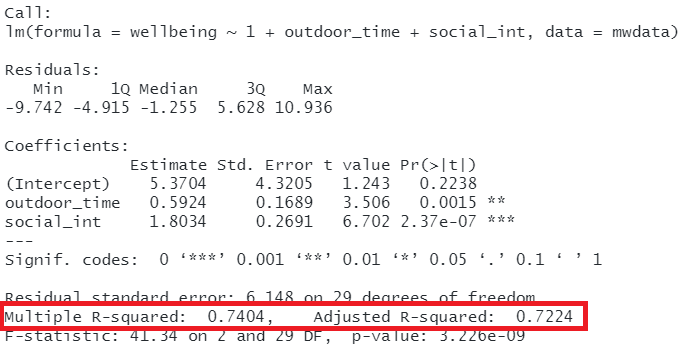
Figure 11: Multiple regression output in R, summary.lm(). R-squared highlighted

F-ratio

As in simple linear regression, the F-ratio is used to test the null hypothesis that all regression slopes are zero (it is just that now that we have multiple predictors, “all” is more than 1).

It is called the F-ratio because it is the ratio of the how much of the variation is explained by the model (per parameter) versus how much of the variation is unexplained (per remaining degrees of freedom).

\[ F_{df_{model},df_{residual}} = \frac{MS_{Model}}{MS_{Residual}} = \frac{SS_{Model}/df_{Model}}{SS_{Residual}/df_{Residual}} \\ \quad \\ \begin{align} & \text{Where:} \\ & df_{model} = k \\ & df_{error} = n-k-1 \\ & n = \text{sample size} \\ & k = \text{number of explanatory variables} \\ \end{align} \]

---

In R, at the bottom of the output of summary(<modelname>), you can view the F ratio, along with an hypothesis test against the alternative hypothesis that the at least one of the coefficients \(\neq 0\) (under the null hypothesis that all coefficients = 0, the ratio of explained:unexplained variance should be approximately 1):

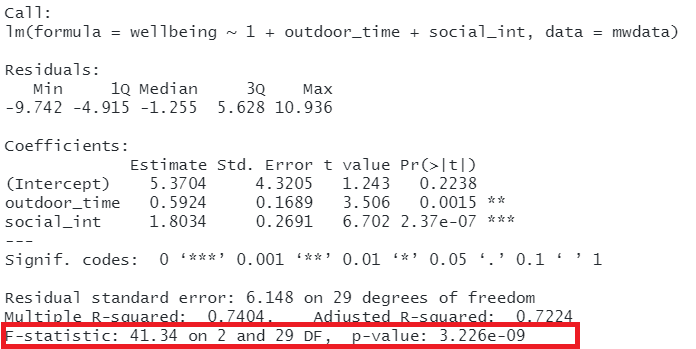
Figure 12: Multiple regression output in R, summary.lm(). F statistic highlighted

Question C1

\[ Wellbeing = \beta_0 \ + \ \beta_1 \cdot Outdoor Time \ + \ \beta_2 \cdot Social Interactions \ + \ \epsilon \]

Does our model (above) provide a better fit to the data than a model with no explanatory variables? (i.e., test against the alternative hypothesis that at least one of the explanatory variables significantly predicts wellbeing scores).

Solution

summary(wbmodel)

## 
## Call:
## lm(formula = wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -9.742 -4.915 -1.255  5.628 10.936 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    5.3704     4.3205   1.243   0.2238    
## outdoor_time   0.5924     0.1689   3.506   0.0015 ** 
## social_int     1.8034     0.2691   6.702 2.37e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.148 on 29 degrees of freedom
## Multiple R-squared:  0.7404, Adjusted R-squared:  0.7224 
## F-statistic: 41.34 on 2 and 29 DF,  p-value: 3.226e-09

Weekly social interactions and outdoor time explained 72.2% of the variance (adjusted \(R^2\) =0.722, \(F\)(2,29)=41.3, p<.001)

Model Comparison

Incremental F-test

The F-ratio we see at the bottom of summary(model) is actually a comparison between two models: our model (with some explanatory variables in predicting \(y\)) and the null model. In regression, the null model can be thought of as the model in which all explanatory variables have zero regression coefficients. It is also referred to as the intercept-only model, because if all predictor variable coefficients are zero, then the only we are only estimating \(y\) via an intercept (which will be the mean: \(\bar y\)).

But we don’t always have to comare our model to the null model. We can compare it to all the intermediate models which vary in the complexity, from the null model to our full model.

If (and only if) two models are nested (one model contains all the predictors of the other and is fitted to the same data), we can compare them using an incremental F-test.

This is a formal test of whether the additional predictors provide a better fitting model.
Formally this is the test of:

• \(H_0:\) coefficients for the added/ommitted variables are all zero.
• \(H_1:\) at least one of the added/ommitted variables has a coefficient that is not zero.

In R, we can conduct an incremental F-test by constructing two models, and passing them to the anova() function: anova(model1, model2).

Optional: F-ratio written for model comparison

The F-ratio for comparing the residual sums of squares between two models can be written as:

\[ F_{(df_R-df_F),df_F} = \frac{(SSR_R-SSR_F)/(df_R-df_F)}{SSR_F / df_F} \\ \quad \\ \begin{align} & \text{Where:} \\ & SSR_R = \text{residual sums of squares for the restricted model} \\ & SSR_F = \text{residual sums of squares for the full model} \\ & df_R = \text{residual degrees of freedom from the restricted model} \\ & df_F = \text{residual degrees of freedom from the full model} \\ \end{align} \]

Question C2

Use the code below to fit the null model.
Then, use the anova() function to perform a model comparison between our earlier model and the null model.
Check that the F statistic is the same as that which is given at the bottom of the summary() output of our model.

null_model <- lm(wellbeing ~ 1, data = mwdata)

Solution

# fit the null model
null_model <- lm(wellbeing ~ 1, data = mwdata)

# model comparison null vs wb_mdl1
anova(null_model, wbmodel)

## Analysis of Variance Table
## 
## Model 1: wellbeing ~ 1
## Model 2: wellbeing ~ 1 + outdoor_time + social_int
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1     31 4222.0                                  
## 2     29 1096.2  2    3125.8 41.345 3.226e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# extract f statistic from summary of wb_mdl1
summary(wbmodel)$fstatistic

##    value    numdf    dendf 
## 41.34465  2.00000 29.00000

# we can retrieve the p-value:
fstat = summary(wbmodel)$fstatistic[1]
df_1 = summary(wbmodel)$fstatistic[2]
df_2 = summary(wbmodel)$fstatistic[3]
pf(fstat, df_1, df_2, lower.tail = FALSE)

##        value 
## 3.225549e-09

Question C3

We can also see quickly all the F-ratios at the addition of each explanatory variable incrementally, by just using anova(model).

Fit these models:

null_model <- lm(wellbeing ~ 1, data = mwdata)
model1 <- lm(wellbeing ~ 1 + outdoor_time, data = mwdata)
model2 <- lm(wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)

And compare the different outputs from each of these lines of code:

anova(null_model, model1, model2)
anova(model2)

Using either of the outputs from the above two lines of code, does weekly outdoor time explain a significant amount of variance in wellbeing scores over and above weekly social interactions?

Solution

null_model <- lm(wellbeing ~ 1, data = mwdata)
model1 <- lm(wellbeing ~ 1 + outdoor_time, data = mwdata)
model2 <- lm(wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)
summary(model1)$adj.r.sq

## [1] 0.316154

summary(model2)$adj.r.sq

## [1] 0.7224443

The model with weekly the weekly number of social interactions as a predictor explains 72% of the variance, and the model without explains 32%.

anova(model1, model2)

## Analysis of Variance Table
## 
## Model 1: wellbeing ~ 1 + outdoor_time
## Model 2: wellbeing ~ 1 + outdoor_time + social_int
##   Res.Df    RSS Df Sum of Sq      F   Pr(>F)    
## 1     30 2794.1                                 
## 2     29 1096.2  1    1697.8 44.914 2.37e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Numbers of social interactions was found to explain a significant amount of variance in wellbeing scores over and above weekly outdoor time
\(F\)(1,29)=44.91, p<.001.

Question C4

Play around with changing the order of the explanatory variables in our model. This will not change the summary() output, but it will change the anova(model) output.

model2 <- lm(wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)
model2a <- lm(wellbeing ~ 1 + social_int + outdoor_time, data = mwdata)
summary(model2)
summary(model2a)
anova(model2)
anova(model2a)

Solution

The summary() output for these two models will be the same numbers, but just in a different order.

model2 <- lm(wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)
model2a <- lm(wellbeing ~ 1 + social_int + outdoor_time, data = mwdata)
summary(model2)$coefficients

##               Estimate Std. Error  t value     Pr(>|t|)
## (Intercept)  5.3703775  4.3205141 1.242995 2.238259e-01
## outdoor_time 0.5923673  0.1689445 3.506284 1.499467e-03
## social_int   1.8034489  0.2690982 6.701825 2.369845e-07

summary(model2a)$coefficients

##               Estimate Std. Error  t value     Pr(>|t|)
## (Intercept)  5.3703775  4.3205141 1.242995 2.238259e-01
## social_int   1.8034489  0.2690982 6.701825 2.369845e-07
## outdoor_time 0.5923673  0.1689445 3.506284 1.499467e-03

The anova() output will be different for these two models, because it tests the incremental addition of each explanatory variable in the order in which they are inputted into the model.

anova(model2)

## Analysis of Variance Table
## 
## Response: wellbeing
##              Df Sum Sq Mean Sq F value    Pr(>F)    
## outdoor_time  1 1427.9  1427.9  37.775 1.068e-06 ***
## social_int    1 1697.8  1697.8  44.914 2.370e-07 ***
## Residuals    29 1096.2    37.8                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

anova(model2a)

## Analysis of Variance Table
## 
## Response: wellbeing
##              Df  Sum Sq Mean Sq F value    Pr(>F)    
## social_int    1 2661.03 2661.03  70.395 3.015e-09 ***
## outdoor_time  1  464.73  464.73  12.294  0.001499 ** 
## Residuals    29 1096.24   37.80                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We should be careful when we conduct research and take the time to think about what exactly we are measuring, and how.

The notion of performing the “incremental tests” that we have just seen provides a good example of when we can fall foul of “measurement error.”
If you’re interested, we have written up a fun little example on incremental validity, which you can find here.

Question C5

Does the addition of routine provide significant improvement to model fit, after accounting for the effects of outdoor time and social interactions?

Solution

We can do this with one:

model3 <- lm(wellbeing ~ 1 + outdoor_time + social_int + routine, data = mwdata)
anova(model3)

Or the same thing with two models:

model2 <- lm(wellbeing ~ 1 + outdoor_time + social_int, data = mwdata)
model3 <- lm(wellbeing ~ 1 + outdoor_time + social_int + routine, data = mwdata)
anova(model2, model3)

Making Valid Inferences

So far, we have been fitting and interpreting our regression models. In each case, we first specified the model, then visually explored the marginal distributions and relationships of variables which would be used in the analysis. Then, once we fitted the model, we began to examine the fit by studying what the various parameter estimates represented, and the spread of the residuals. We saw these in the output of summary() of a model - they were shown in the parts of the output inside the red boxes in Figure 13).

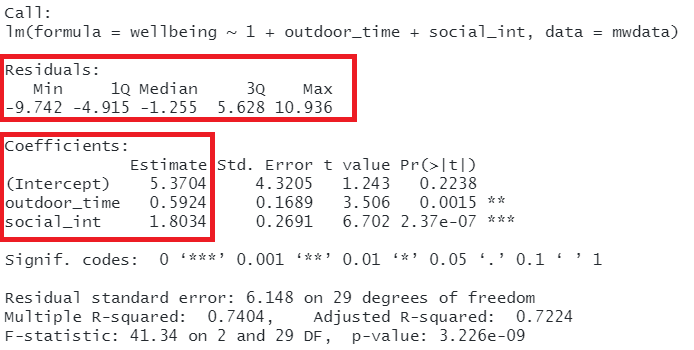
Figure 13: Multiple regression output in R, summary.lm(). Residuals and Coefficients highlighted

We also discussed drawing inferences using our model estimates, as well as using a model to make predictions. However, we should really not have done this prior to being satisfied that our model meets a certain set of assumptions. All of the estimates, intervals and hypothesis tests (see Figure 14) resulting from a regression analysis assume a certain set of conditions have been met. Meeting these conditions is what allows us to generalise our findings beyond our sample (i.e., to the population).

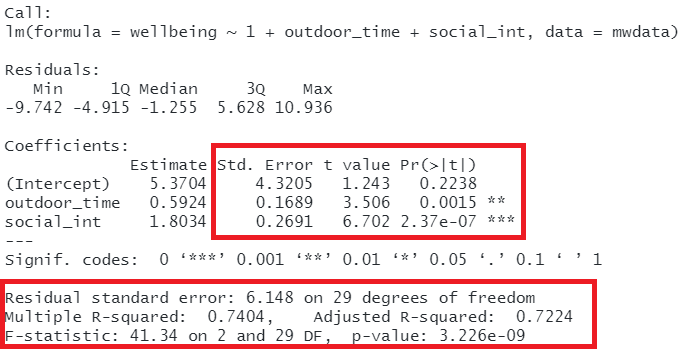
Figure 14: Multiple regression output in R, summary.lm(). Hypothesis tests highlighted

Assumptions

Assumptions: The broad idea

All our work here is in aim of making models of the world.

• Models are models. They are simplifications. They are therefore wrong.
  
• Our residuals ( \(y - \hat{y}\) ) reflect everything that we don’t account for in our model.
  
• In an ideal world, our model accounts for all the systematic relationships. The leftovers (our residuals) are just random noise.
  
• If our model is mis-specified, or we don’t measure some systematic relationship, then our residuals will reflect this.
  We check by examining how much “like randomness” the residuals appear to be (zero mean, normally distributed, constant variance, i.i.d (“independent and identically distributed”). These ideas tend to get referred to as our “assumptions.”
  
• While we will never know whether our residuals contain only randomness (we can never observe everything), our ability to generalise from the model we fit on sample data to the wider population relies on these assumptions.

---

Assumptions in a nutshell

In using linear regression, we have assumptions about our model in that we assume that modelling the outcome variable as a linear combination of the explanatory variables is an appropriate thing to do.
We also make certain assumptions about what we have left out of our model - the errors component.

Specifically, we assume that our errors have “zero mean and constant variance”.

• mean of the residuals = zero across the predicted values on the linear predictor.
  
• spread of residuals is normally distributed and constant across the predicted values on the linear predictor.

What does it look like?

What does it not look like?

Things look a bit wrong (like there is something systematic that we haven’t accounted for), when our residuals do not have mean zero:

Or do not have constant variance:

Assumptions in R

We can get a lot of plots for this kind of thing by using plot(model)

Here’s what it looks like for a nice neat model:

plot(my_model)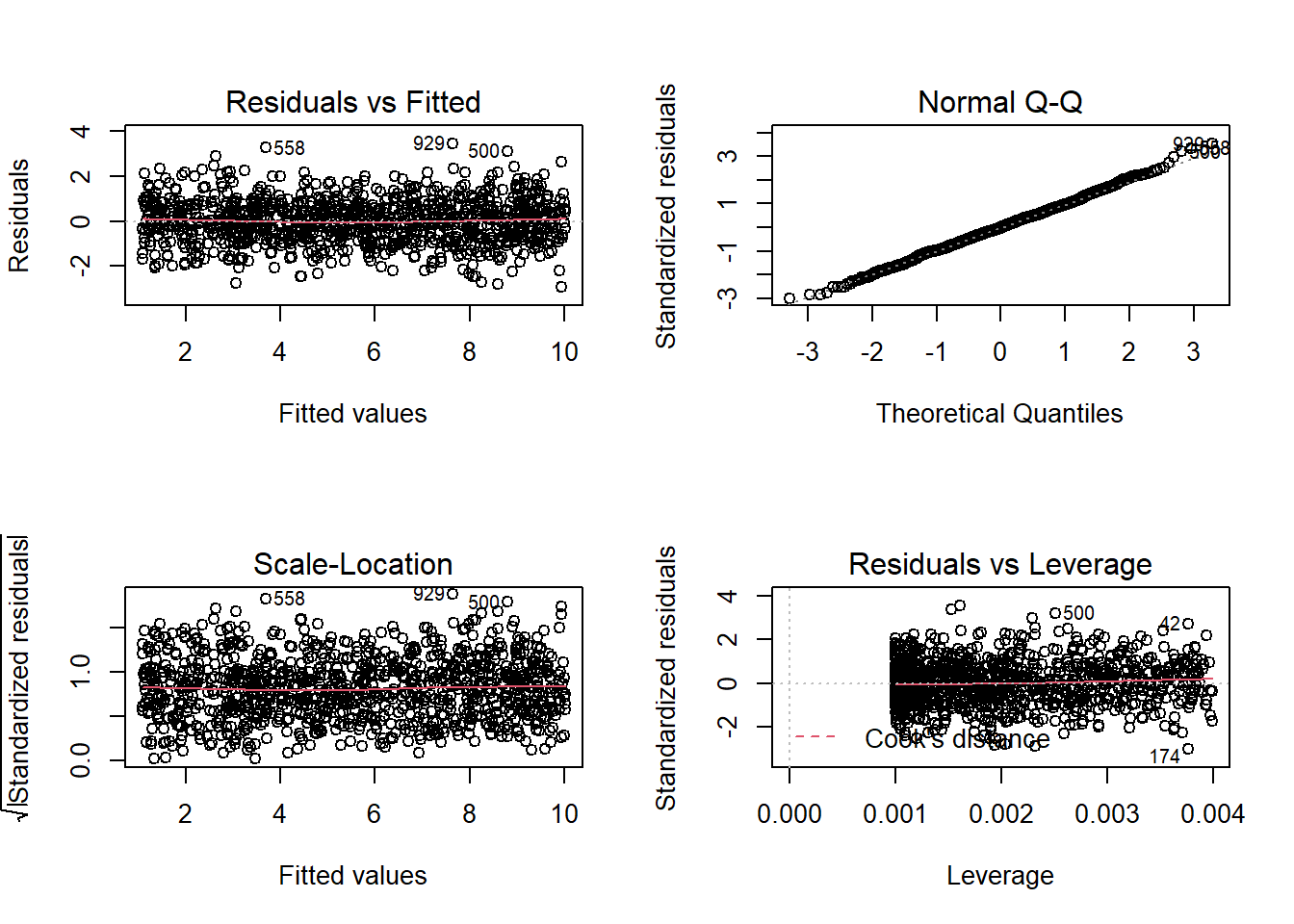

---

Some people don’t like the higher-level/broad picture approach to thinking about assumptions of our analysis, and prefer a step-by-step list of things to make sure they tick off. For those of you who would like this, you can find our page on “assumptions & diagnostics: the recipe book way”.

Recall our last model (from Question C5), in which we fitted a model assessing how we might explain wellbeing by the combination of social interactions, routine, and outdoor time.
The code for this model is given below.
Let’s take a look at the diagnostic plots given by passing the model to the plot() function.

mwdata = read_csv(file = "https://uoepsy.github.io/data/wellbeing.csv")
wbmodel2 <- lm(wellbeing ~ social_int + routine + outdoor_time, data=mwdata)
plot(wbmodel2)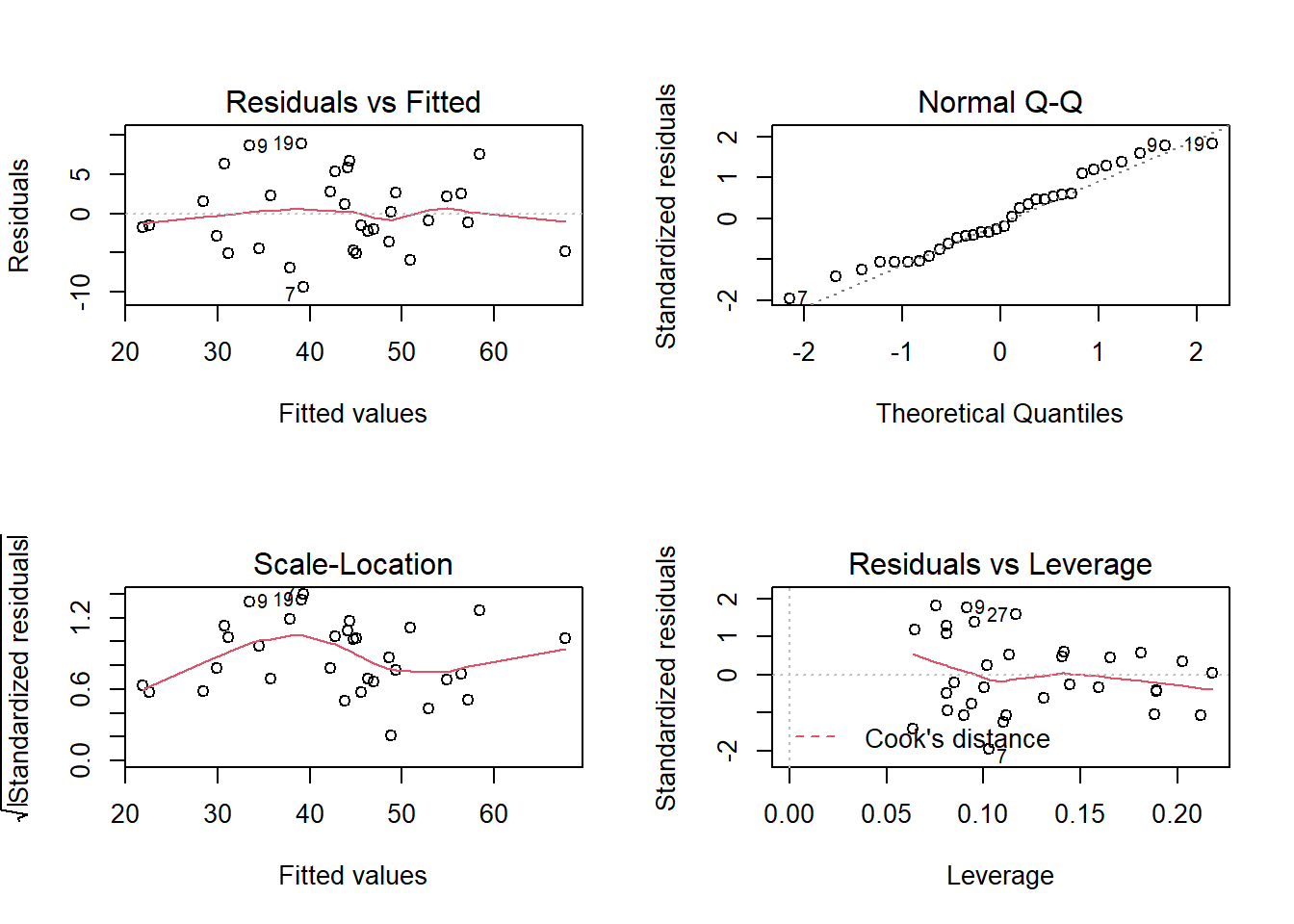

The model doesn’t look too bad.

• The top left plot (residuals vs fitted) shows a reasonably straight red line, which indicates that the mean of the residuals is close to zero across the fitted values.
  
• The top right plot (QQplot of residuals) shows that the residuals are fairly close to the dotted line, indicating they follow close to a normal distribution (QQplots plot the values against the associated percentiles of the normal distribution. So if we had ten values, it would order them lowest to highest, then plot them on the y against the 10th, 20th, 30th.. and so on percentiles of the standard normal distribution (mean 0, SD 1)).
  
• The bottom left plot (scale location plot) shows the square-root of the absolute value of the standardised residuals. This allows us to examine the extent to which the variance of the residuals changes accross the fitted values. A straight red line indicates reasonably constant variance. It’s a bit wiggly here!
  
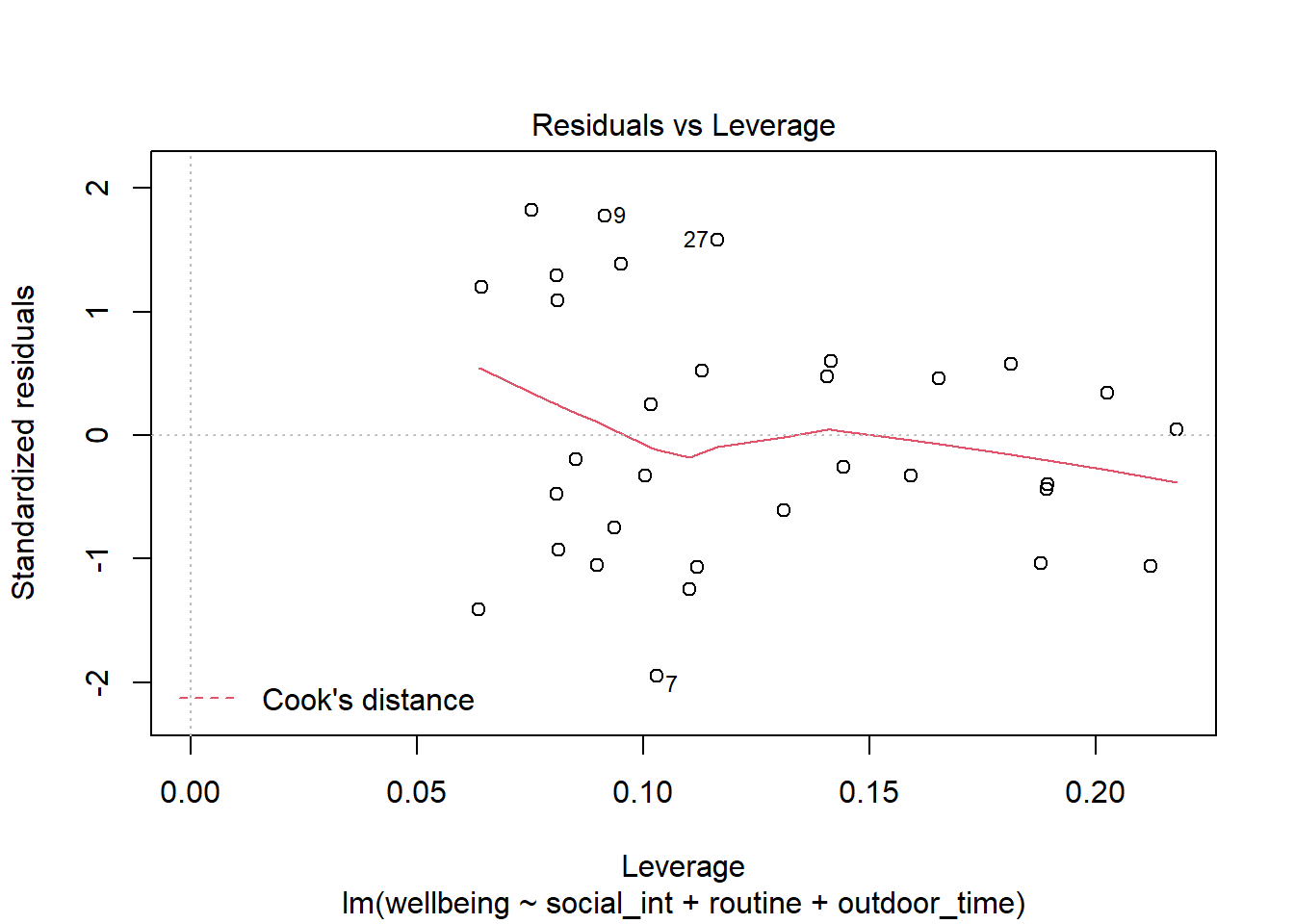
• The bottom right plot (residuals vs leverage plot) shows the extent to which datapoints that have higher residuals (are far away from our regression line) have the potential to unduly influence our line. We’ll look at this idea of influence later on.

Question Optional: D1

We can perform tests to examine how (un)likely we would be to see some residuals like those we have got, if they were sampled from a normally distribution.

The Shapiro-Wilk test is a test against the alternative hypothesis that the residuals were not sampled from a normally distributed population. We can perform this test quickly in R using shapiro.test(residuals(modelname)).
Conduct this test now on the model we just plotted above. What do you conclude?

Solution

shapiro.test(residuals(wbmodel2))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(wbmodel2)
## W = 0.96791, p-value = 0.4439

A Shapiro-Wilk test failed to reject the null hypothesis that the residuals were drawn from a normally distributed population (\(W = 0.97\), \(p = .44\))

Question Optional: D2

The ncvTest(model) function (from the car package) performs a test against the alternative hypothesis that the error variance changes with the level of the fitted value (also known as the “Breusch-Pagan test”). \(p >.05\) indicates that we do not have evidence that the assumption has been violated.
Try conducting this test now, on the same model as the previous question.

Solution

library(car)
ncvTest(wbmodel2)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.1018826, Df = 1, p = 0.74958

Visual inspection of suggested little sign of non-constant variance, with the Breusch-Pagan test failing to reject the null that error variance does not change across the fitted values (\(\chi^2(1)=0.102\), \(p = .75\))

Multicollinearity

For the linear model with multiple explanatory variables, we need to also think about multicollinearity - this is when two (or more) of the predictors in our regression model are moderately or highly correlated.
Recall our interpretation of multiple regression coefficients as
“the effect of \(x_1\) on \(y\) when holding the values of \(x_2\), \(x_3\), … \(x_k\) constant”

This interpretation falls down if predictors are highly correlated because if, e.g., predictors \(x_1\) and \(x_2\) are highly correlated, then changing the value of \(x_1\) necessarily entails a change the value of \(x_2\) meaning that it no longer makes sense to talk about holding \(x_2\) constant.

We can assess multicollinearity using the variance inflation factor (VIF), which for a given predictor \(x_j\) is calculated as:
\[ VIF_j = \frac{1}{1-R_j^2} \\ \] Where \(R_j^2\) is the coefficient of determination (the R-squared) resulting from a regression of \(x_j\) on to all the other predictors in the model (\(x_j = x_1 + ... x_k + \epsilon\)).
The more highly correlated \(x_j\) is with other predictors, the bigger \(R_j^2\) becomes, and thus the bigger \(VIF_j\) becomes.

The square root of VIF indicates how much the SE of the coefficient has been inflated due to multicollinearity. For example, if the VIF of a predictor variable were 4.6 (\(\sqrt{4.6} = 2.1\)), then the standard error of the coefficient of that predictor is 2.1 times larger than if the predictor had zero correlation with the other predictor variables. Suggested cut-offs for VIF are varied. Some suggest 10, others 5. Define what you will consider an acceptable value prior to calculating it.

In R, the vif() function from the car package will provide VIF values for each predictor in your model.

Question Optional: D3

Calculate the variance inflation factor (VIF) for the predictors in the model.

Write a sentence summarising whether or not you consider multicollinearity to be a problem here.

Solution

vif(wbmodel2)

##   social_int      routine outdoor_time 
##     1.130708     1.014136     1.142259

VIF values <5 indicate that multicollinearity is not adversely affecting model estimates.

Individual Case Diagnostics

In linear regression, individual cases in our data can influence our model more than others. There are a variety of measures we can use to evaluate the amount of misfit and influence that single observations have on our model and our model estimates.

THERE ARE NO HARD RULES FOR WHAT COUNTS AS “INFLUENTIAL” AND HOW WE SHOULD DEAL WITH THESE CASES

There are many ways to make a cake. recipes can be useful, but you really need to think about what ingredients you actually have (what data you have).

You don’t have to exclude influential observations. Try to avoid blindly following cut-offs, and try to think carefully about outliers and influential points and whether you want to exclude them, and whether there might be some other model specification that captures this in some estimable way. Do these observations change the conclusions you make (you can try running models with and without certain cases).

There are various measures of outlyngness and influence. Here are a few. You do not need to remember all of these!

Regression outliers:
A large residual \(\hat \epsilon_i\) - i.e., a big discrepancy between their predicted y-value and their observed y-value.

• Standardised residuals: For residual \(\hat \epsilon_i\), divide by the estimate of the standard deviation of the residuals. In R, the rstandard() function will give you these
• Studentised residuals: For residual \(\hat \epsilon_i\), divide by the estimate of the standard deviation of the residuals excluding case \(i\). In R, the rstudent() function will give you these. Values \(>|2|\) (greater in magnitude than two) are considered potential outliers.

High leverage cases:
These are cases which have considerable potential to influence the regression model (e.g., cases with an unusual combination of predictor values).

• Hat values: are used to assess leverage. In R, The hatvalues() function will retrieve these.
  Hat values of more than \(2 \bar{h}\) (2 times the average hat value) are often worth looking at. \(\bar{h}\) is calculated as \(\frac{k + 1}{n}\), where \(k\) is the number of predictors, and \(n\) is the sample size.

High influence cases:
When a case has high leverage and is an outlier, it will have a large influence on the regression model.

• Cook’s Distance: combines leverage (hatvalues) with outlying-ness to capture influence. In R, the cooks.distance() function will provide these.
  There are many suggested Cook’s Distance cut-offs.
• DFFit: the change in the predicted value at the \(i^{th}\) observation with and without the \(i^{th}\) observation is included in the regression.
  
• DFbeta: the change in a specific coefficient with and without the \(i^{th}\) observation is included in the regression.
  
• DFbetas: the change in a specific coefficient divided by the standard error, with and without the \(i^{th}\) observation is included in the regression.
  
• COVRATIO: measures the effect of an observation on the covariance matrix of the parameter estimates. In simpler terms, it captures an observation’s influence on standard errors. Values which are \(>1+\frac{3(k+1)}{n}\) or \(<1-\frac{3(k+1)}{n}\) are sometimes considered as having strong influence.

You can get a whole bucket-load of these measures with the influence.measures() function.

• influence.measures(my_model) will give you out a dataframe of the various measures.
  
• summary(influence.measures(my_model)) will provide a nice summary of what R deems to be the influential points.

Question Optional: D4

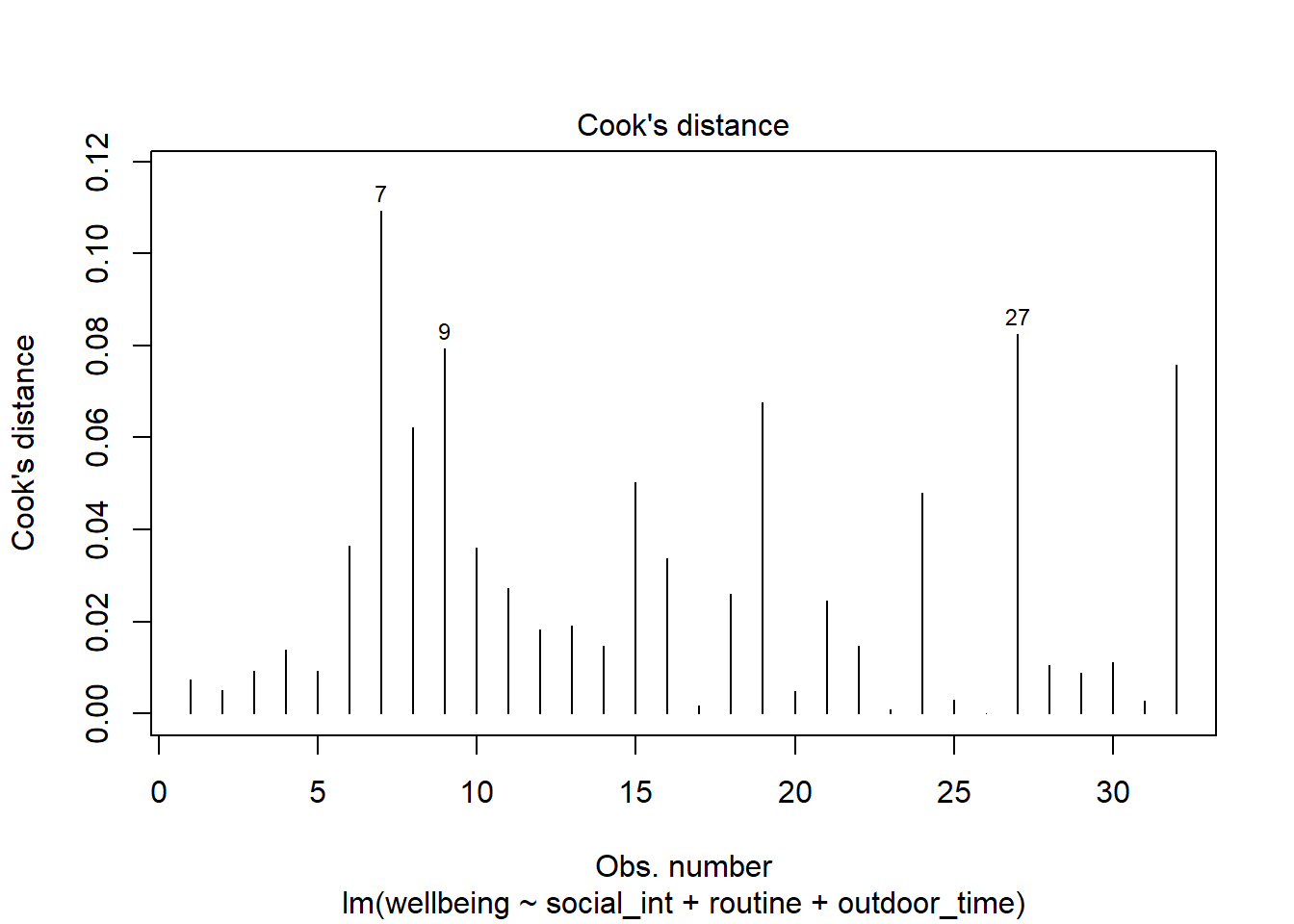
Plot the Cook’s Distance values, does it look like there may be any highly influential points?
(You can use plot(model, which = 4) and plot(model, which = 5)).

Solution

These don’t look too bad to me - there aren’t a small number of cases which have exceptionally high values (relative to the others) for Cook’s D.

plot(wbmodel2, which = 4)

plot(wbmodel2, which = 5)

---

1. \(SS_{Total}\) has \(n - 1\) degrees of freedom as one degree of freedom is lost in estimating the population mean with the sample mean \(\bar{y}\). \(SS_{Residual}\) has \(n - 2\) degrees of freedom. There are \(n\) residuals, but two degrees of freedom are lost in estimating the intercept and slope of the line used to obtain the \(\hat y_i\)s. Hence, by difference, \(SS_{Model}\) has \(n - 1 - (n - 2) = 1\) degree of freedom.↩︎

---

This workbook was written by Josiah King, Umberto Noe, and Martin Corley, and is licensed under a Creative Commons Attribution 4.0 International License.