Week 7 Exercises: PCA & EFA

New packages

We’re going to be needing some different packages this week (no more lme4!).
Make sure you have these packages installed:

• psych
  
• GPArotation
  
• car

PCA & EFA

Overview

Both Principal Component Analysis (PCA) and Exploratory Factor Analysis (EFA) are methods of “dimension reduction” — i.e. we start with lots of correlated variables and we reduce down to a smaller set of dimensions which capture how people vary in those original variables. PCA & EFA are quite similar, and many use them interchangeably, but the theoretical assumptions underpinning them are quite different.

	Principal Component Analysis	Factor Analysis
what it does	take a set of correlated variables, reduce to orthogonal dimensions that capture variability	take a set of correlated variables, ask what set of dimensions (not necessarily orthogonal!) explain variability
what the dimensions are	dimensions are referred to as “components” - they are simply “composites” and do not necessarily exist	dimensions are referred to as “factors”. They are assumed to be underlying latent variables that are the cause of why people have different scores on the observed variables
example	Socioeconomic status (SES) might be a composite measure of family income, parental education, etc. If my SES increases, that doesn’t mean my parents suddenly get more education (it’s the other way around)	Anxiety (the unmeasurable construct) is a latent factor. My underlying anxiety is what causes me to respond “strongly agree” to “I am often on edge”

A Note: In Psychology, the distinction between the two can sometimes become blurred, and people will interpret and give meaning to the components of a PCA

In Diagrams

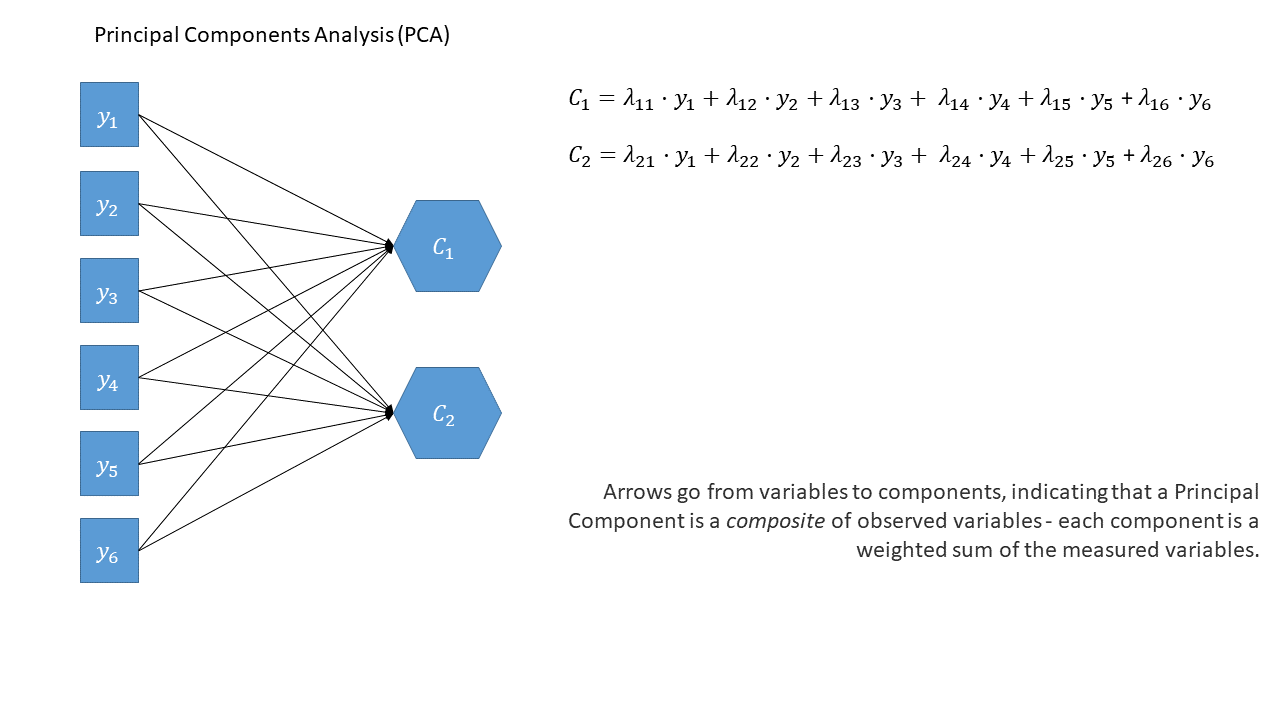
One way to think about this is to draw the two approaches in diagrammatic form, mapping the relationships between variables. There are conventions for these sort of diagrams:

• squares = variables we observe
• circles = variables we don’t observe
• single-headed arrows = regression paths (pointed at outcome)
• double-headed arrows = correlation

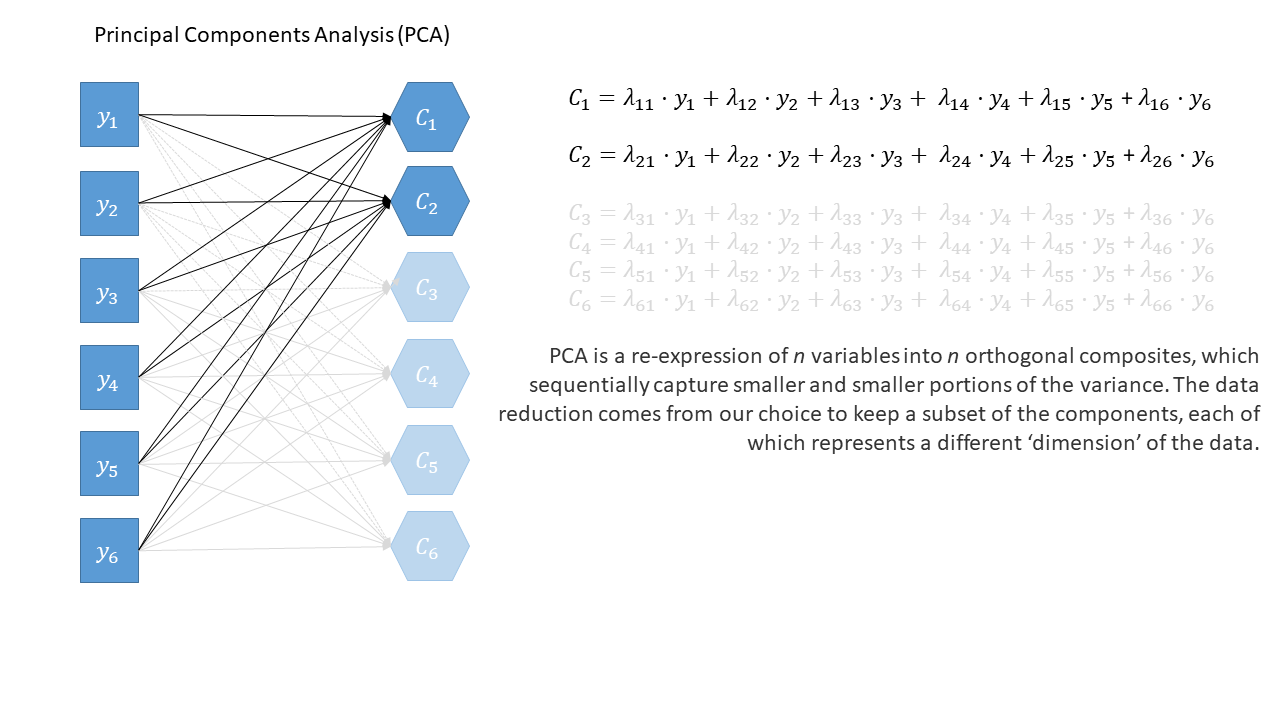
In the diagrams below, note how the directions of the arrows are different between PCA and FA - in PCA, each component \(C_i\) is the weighted combination of the observed variables \(y_1, ...,y_n\), whereas in FA, each measured variable \(y_i\) is seen as generated by some latent factor(s) \(F_i\) plus some unexplained variance \(u_i\).

PCA as a diagram

Note that the idea of a ‘composite’ requires us to use a special shape (the hexagon), but many people would just use a square.

optional: PCA in full

Principal components sequentially capture the orthogonal (i.e., perpendicular) dimensions of the dataset with the most variance. The data reduction comes when we retain fewer components than we have dimensions in our original data. So if we were being pedantic, the diagram for PCA would look something like the diagram below.

EFA as a diagram

Exploratory Factor Analysis as a diagram has arrows going from the factors to the observed variables. Unlike PCA, we also have ‘uniqueness’ factors for each variable, representing the various stray causes that are specific to each variable. Sometimes, these uniqueness are represented by an arrow only, but they are technically themselves latent variables, and so can be drawn as circles.

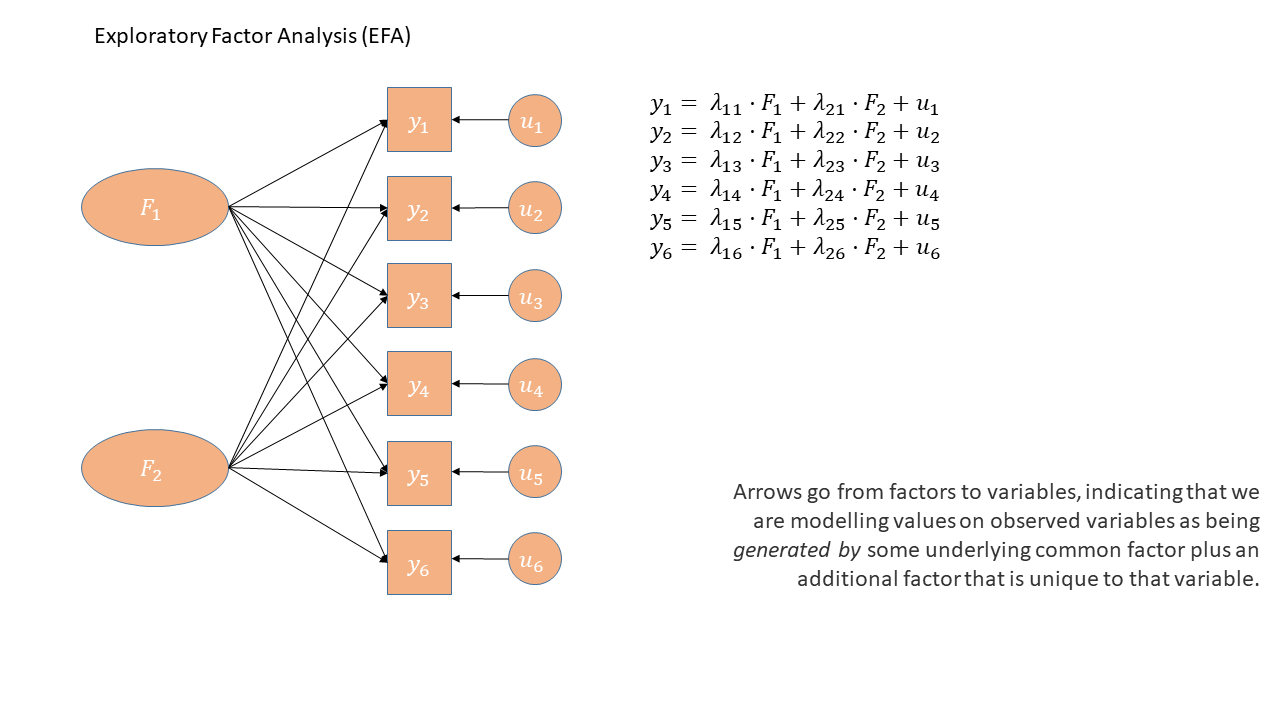
It might help to read the \(\lambda\)s as beta-weights like in regression (\(b\), or \(\beta\)), because that’s all they really are. The equation \(y_i = \lambda_{1i} F_1 + \lambda_{2i} F_2 + u_i\) is just our way of saying that the variable \(y_i\) is the manifestation of some amount (\(\lambda_{1i}\)) of an underlying factor \(F_1\), some amount (\(\lambda_{2i}\)) of some other underlying factor \(F_2\), and some error (\(u_i\)). It’s just a set of regressions!

Reducing the dimensionality of job performance

Data: jobperfbonus.csv

A company has asked line managers to fill out a questionnaire that asks them to rate the performance of each employee. The dataset we are providing contains each employee’s rating on 15 different aspects of their performance.

The company doesn’t know what to do with so much data, and wants us to reduce it to a smaller number of distinct variables.

It can be downloaded at https://uoepsy.github.io/data/jobperfbonus.csv

Table 1: data dictionary for jobperfbonus.csv

variable	question
name	employee name
q1	How effectively do they prioritize tasks to ensure project deadlines are met?
q2	Rate their ability to create and maintain project schedules and timelines.
q3	How well do they allocate resources to ensure efficient project execution?
q4	Rate their proficiency in identifying and mitigating project risks.
q5	How effectively do they communicate project progress and updates to stakeholders?
q6	How well do they collaborate with team members to achieve common goals?
q7	Rate their ability to actively listen to and consider the ideas and opinions of others.
q8	How effectively do they contribute to a positive team environment?
q9	Rate their willingness to provide support and assistance to team members when needed.
q10	How well do they resolve conflicts and disagreements within the team?
q11	How proficient are they in applying technical concepts and principles relevant to their role?
q12	Rate their ability to stay updated with the latest developments and trends in their field.
q13	How effectively do they troubleshoot technical issues and find innovative solutions?
q14	Rate their skill in translating complex technical information into understandable terms for non-technical stakeholders.
q15	How well do they leverage technical expertise for problem-solving?

Question 1

Load the data, and take a look at it.

We’re going to want to reduce these 15 variables (or “items”) down into a smaller set. Should we use PCA or EFA?

Solution 1.

jobperf <- read_csv("https://uoepsy.github.io/data/jobperfbonus.csv")
head(jobperf)

# A tibble: 6 × 16
  name      q1    q2    q3    q4    q5    q6    q7    q8    q9   q10   q11   q12
  <chr>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Kang,…     1     2     2     1     2     3     2     3     2     2     3     4
2 Zouni…     5     4     3     4     5     4     3     4     5     4     2     5
3 el-Sy…     4     3     3     4     4     4     3     4     2     3     2     2
4 Thomp…     2     3     1     3     2     3     2     4     4     2     5     4
5 Wahl,…     4     4     2     3     4     3     3     4     2     3     3     5
6 al-Ko…     1     2     1     1     1     5     3     4     3     3     3     3
# ℹ 3 more variables: q13 <dbl>, q14 <dbl>, q15 <dbl>

Probably going to want to use PCA, because we’re less interested in thinking about underlying latent dimensions of ‘job performance’ - i.e. we want to get a ‘composite’ rather than an underlying factor.

Question 2

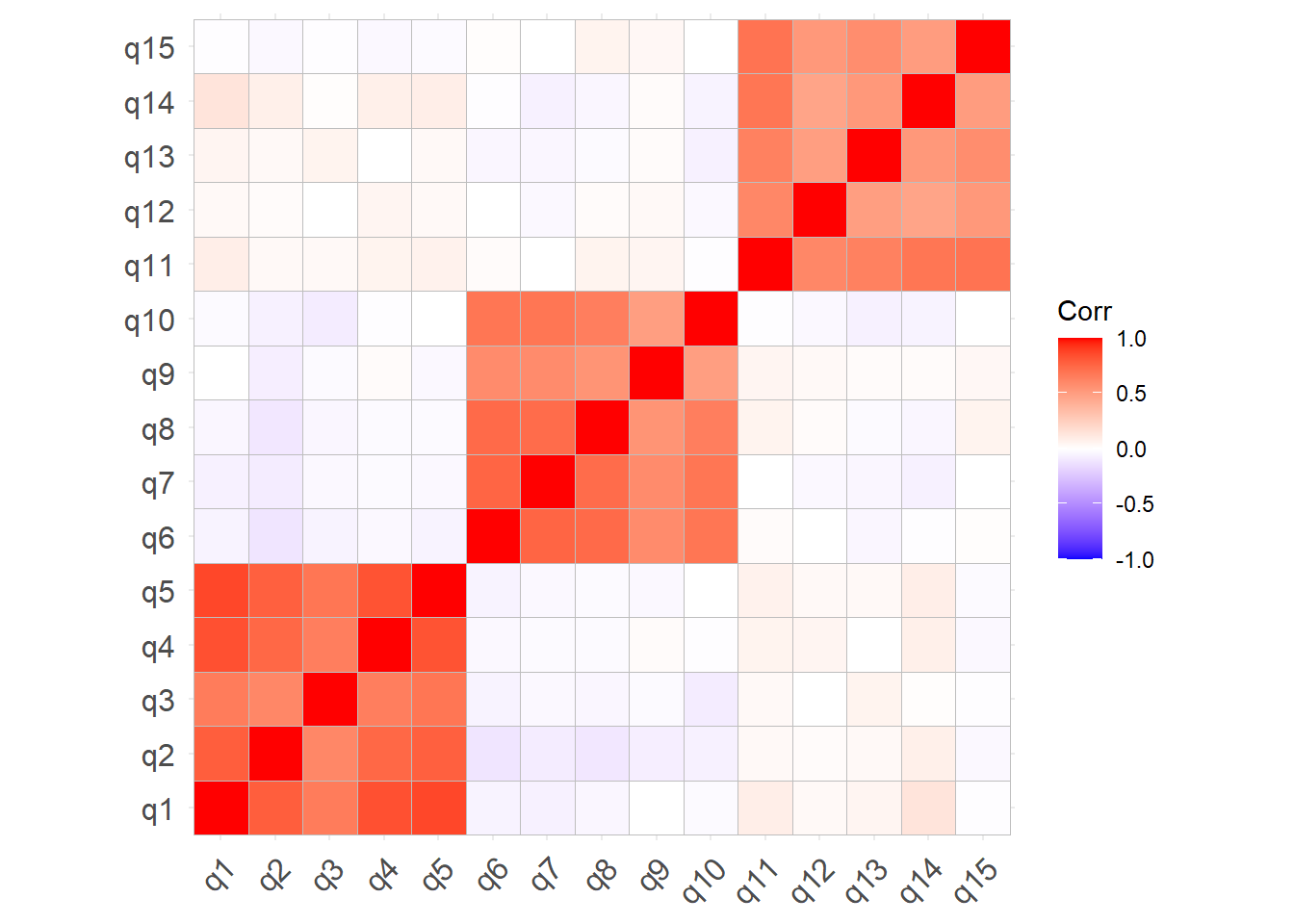
Explore the relationships between variables in the data. Below are various ways to do this.

You’re probably going to want to subset out just the relevant variables (q1 to q15).

Correlation Matrix

You can give the cor() function a dataset and it will show you the correlations between all pairs of variables.
It returns a ‘correlation matrix’ - which has a row for each variable and a column for each variable. Correlation matrices are square (same number of rows as columns), and symmetric (rotate it 90 degrees and it looks the same). The diagonals of the correlation matrix are all 1, because every variable is perfectly correlated with itself.

cor(eg_data) |>
  round(2)

       item_1 item_2 item_3 item_4 item_5
item_1   1.00   0.74   0.56  -0.61  -0.67
item_2   0.74   1.00   0.44  -0.53  -0.55
item_3   0.56   0.44   1.00  -0.35  -0.42
item_4  -0.61  -0.53  -0.35   1.00   0.46
item_5  -0.67  -0.55  -0.42   0.46   1.00

Correlation matrices can get big! For \(k\) variables, the correlation matrix contains \(\frac{k(k+1)}{2}\) unique numbers. Sometimes you can get more from visualising the correlation matrix.

library(ggcorrplot)
ggcorrplot(cor(eg_data))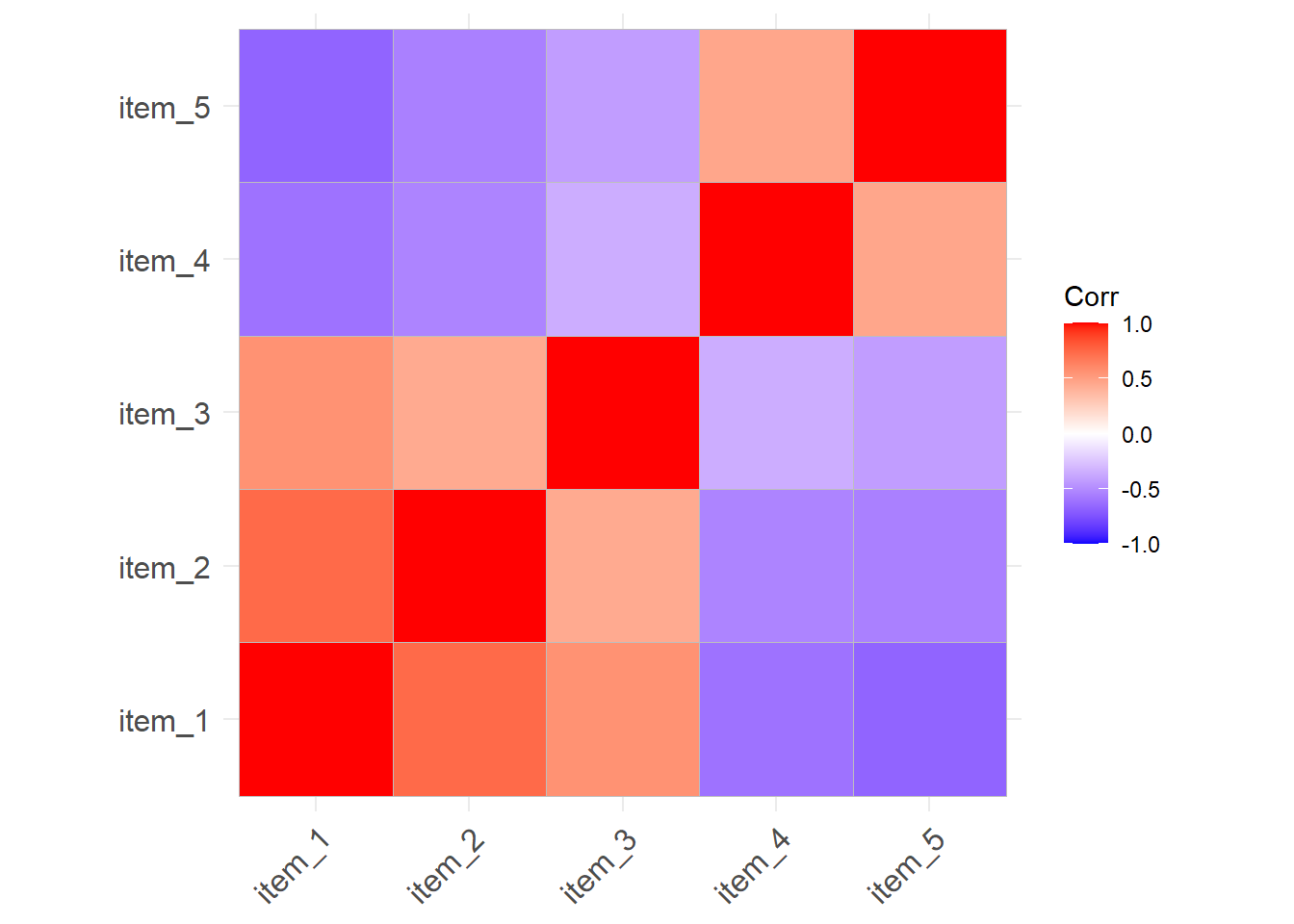

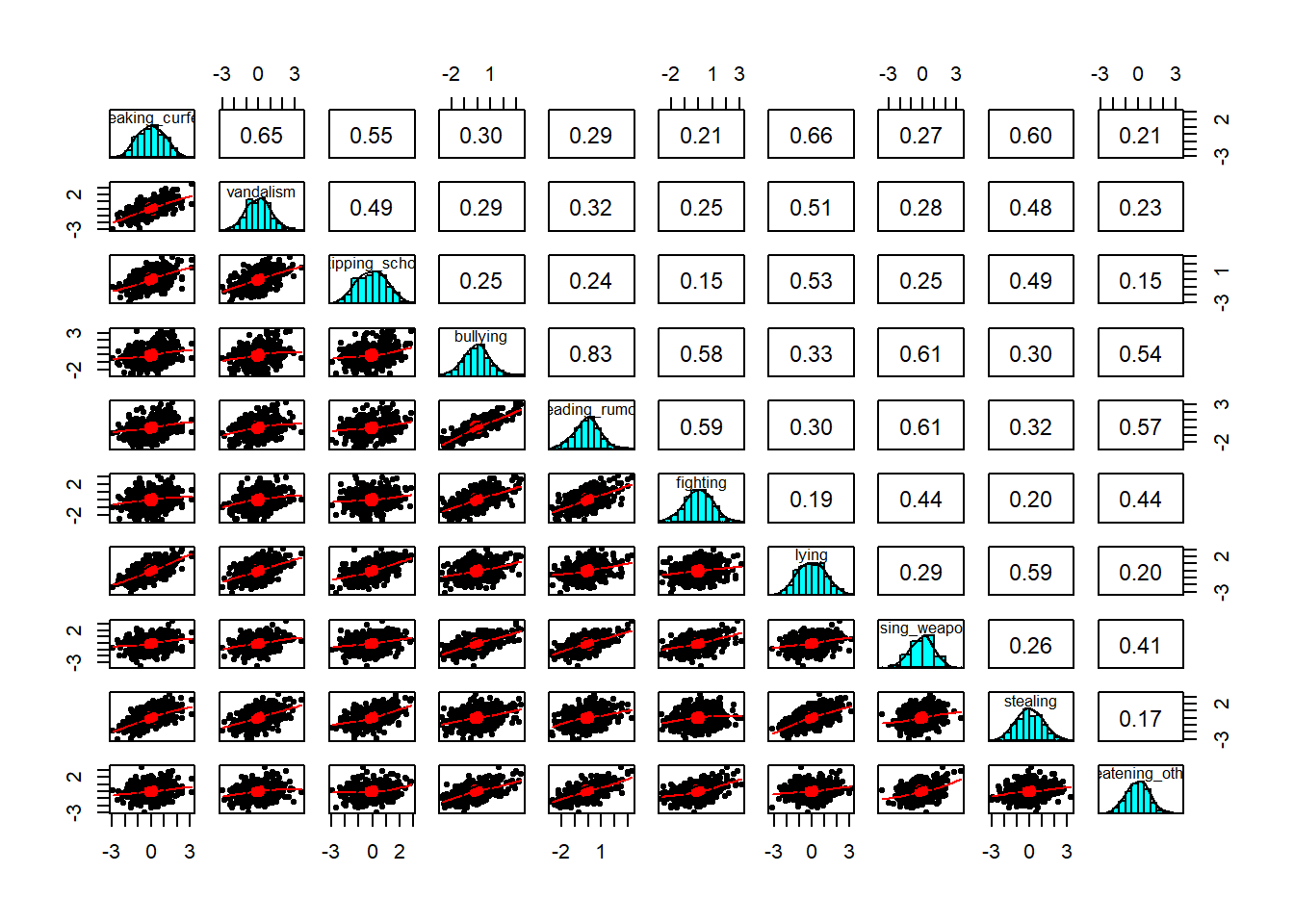
Scatterplot Matrix

A Scatterplot Matrix is basically the same idea as a correlation matrix, but instead of the numeric correlation coefficient between each pair, we have a scatterplot between each pair.

It’s a good way to check for linearity of relationships prior to data reduction. These methods of data reduction are all based on correlations, which assume the relations we are capturing are linear.

We can check linearity of relations using pairs() and also pairs.panels(data) (from the psych package), and you can view the histograms on the diagonals, allowing you to check univariate normality (which is usually a good enough proxy for multivariate normality).

• pairs(data) - make a scatterplot matrix
• from psych, pairs.panels(data) - make a scatterplot matrix with correlations on the upper triangle
• from car, scatterplotMatrix(data)

Additionally, also from psych, the multi.hist(data) function will give us the individual histograms for each variable

Solution 2. Let’s keep the full data with the names, but make a new object that is just the performance data:

qperf <- jobperf |> select(-name)

It looks like we’ve got some very strong groups of questions there - q1 to q5 are all highly related to one another, as are q6 to q10, and q11 to q15. Furthermore, the relations between those sets are very weak, suggesting 3 groups that are fairly distinct.

library(ggcorrplot)
ggcorrplot(cor(qperf))

You’ll probably have to zoom in when you do this yourself, as there are a lot of little plots there!

library(psych)
pairs.panels(qperf)

Question 3

How much variance in the data will be captured by 15 principal components?

Hints

We can figure this out without having to do anything - it’s a theoretical question!

Solution 3. All of it!
The right hand entry of the “Cumulative Var” row is 1 - it explains everything.

principal(qperf, nfactors = 15, rotate = "none")

Principal Components Analysis
Call: principal(r = qperf, nfactors = 15, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
      PC1  PC2   PC3   PC4   PC5   PC6   PC7   PC8   PC9  PC10  PC11  PC12
q1   0.86 0.30 -0.20 -0.10  0.03 -0.03 -0.01 -0.08 -0.05 -0.07 -0.06  0.06
q2   0.83 0.21 -0.22 -0.06 -0.04  0.01  0.05 -0.17 -0.08  0.27  0.28 -0.04
q3   0.73 0.23 -0.21  0.36  0.07  0.17  0.00  0.37  0.24 -0.02  0.07 -0.03
q4   0.83 0.31 -0.23 -0.04 -0.02 -0.11 -0.05 -0.07 -0.06 -0.08 -0.21  0.06
q5   0.86 0.30 -0.23 -0.06 -0.06  0.00 -0.01 -0.03 -0.03 -0.08 -0.07 -0.03
q6  -0.37 0.81 -0.11 -0.04 -0.04  0.03  0.03  0.14 -0.04  0.11 -0.08  0.35
q7  -0.36 0.80 -0.14  0.02 -0.03  0.09  0.05  0.06 -0.05  0.28 -0.20 -0.25
q8  -0.34 0.80 -0.09  0.03 -0.13  0.08 -0.07  0.13 -0.31 -0.20  0.21 -0.04
q9  -0.27 0.70 -0.05  0.18  0.51 -0.34 -0.08 -0.15  0.05 -0.04  0.06 -0.03
q10 -0.33 0.75 -0.15 -0.18 -0.22  0.10  0.11 -0.21  0.36 -0.14  0.06 -0.04
q11  0.21 0.24  0.84 -0.08  0.01  0.03 -0.12  0.06 -0.05 -0.12 -0.09 -0.18
q12  0.17 0.17  0.72  0.20 -0.36 -0.48  0.14  0.06  0.03  0.04  0.02  0.01
q13  0.19 0.15  0.76  0.20  0.17  0.28  0.42 -0.16 -0.09 -0.04 -0.03  0.05
q14  0.25 0.17  0.73 -0.49  0.22 -0.04  0.03  0.23  0.08  0.06  0.08  0.03
q15  0.11 0.19  0.79  0.16 -0.08  0.20 -0.42 -0.18  0.06  0.10  0.01  0.10
     PC13  PC14  PC15 h2       u2 com
q1   0.02 -0.13 -0.27  1 -2.2e-16 1.7
q2  -0.13  0.07  0.02  1  0.0e+00 2.0
q3   0.00  0.03 -0.02  1  7.8e-16 3.0
q4   0.08  0.28  0.06  1  0.0e+00 2.0
q5   0.03 -0.25  0.21  1  3.3e-16 1.8
q6  -0.17 -0.03  0.02  1 -8.9e-16 2.2
q7   0.09 -0.02 -0.03  1 -1.6e-15 2.3
q8   0.11  0.03  0.00  1 -4.4e-16 2.3
q9  -0.01 -0.02  0.02  1  2.2e-16 3.1
q10 -0.01  0.03  0.00  1 -1.1e-15 2.8
q11 -0.32  0.03 -0.01  1  2.7e-15 1.9
q12  0.05 -0.03 -0.02  1  2.8e-15 3.0
q13  0.05  0.01  0.01  1  1.6e-15 2.7
q14  0.15  0.01  0.02  1  1.0e-15 2.9
q15  0.11 -0.02  0.00  1  2.2e-15 2.3

                       PC1  PC2  PC3  PC4  PC5  PC6  PC7  PC8  PC9 PC10 PC11
SS loadings           4.13 3.54 3.27 0.56 0.55 0.53 0.42 0.41 0.32 0.27 0.25
Proportion Var        0.28 0.24 0.22 0.04 0.04 0.04 0.03 0.03 0.02 0.02 0.02
Cumulative Var        0.28 0.51 0.73 0.77 0.80 0.84 0.87 0.89 0.92 0.93 0.95
Proportion Explained  0.28 0.24 0.22 0.04 0.04 0.04 0.03 0.03 0.02 0.02 0.02
Cumulative Proportion 0.28 0.51 0.73 0.77 0.80 0.84 0.87 0.89 0.92 0.93 0.95
                      PC12 PC13 PC14 PC15
SS loadings           0.24 0.21 0.17 0.12
Proportion Var        0.02 0.01 0.01 0.01
Cumulative Var        0.97 0.98 0.99 1.00
Proportion Explained  0.02 0.01 0.01 0.01
Cumulative Proportion 0.97 0.98 0.99 1.00

Mean item complexity =  2.4
Test of the hypothesis that 15 components are sufficient.

The root mean square of the residuals (RMSR) is  0 
 with the empirical chi square  0  with prob <  NA 

Fit based upon off diagonal values = 1

Question 4

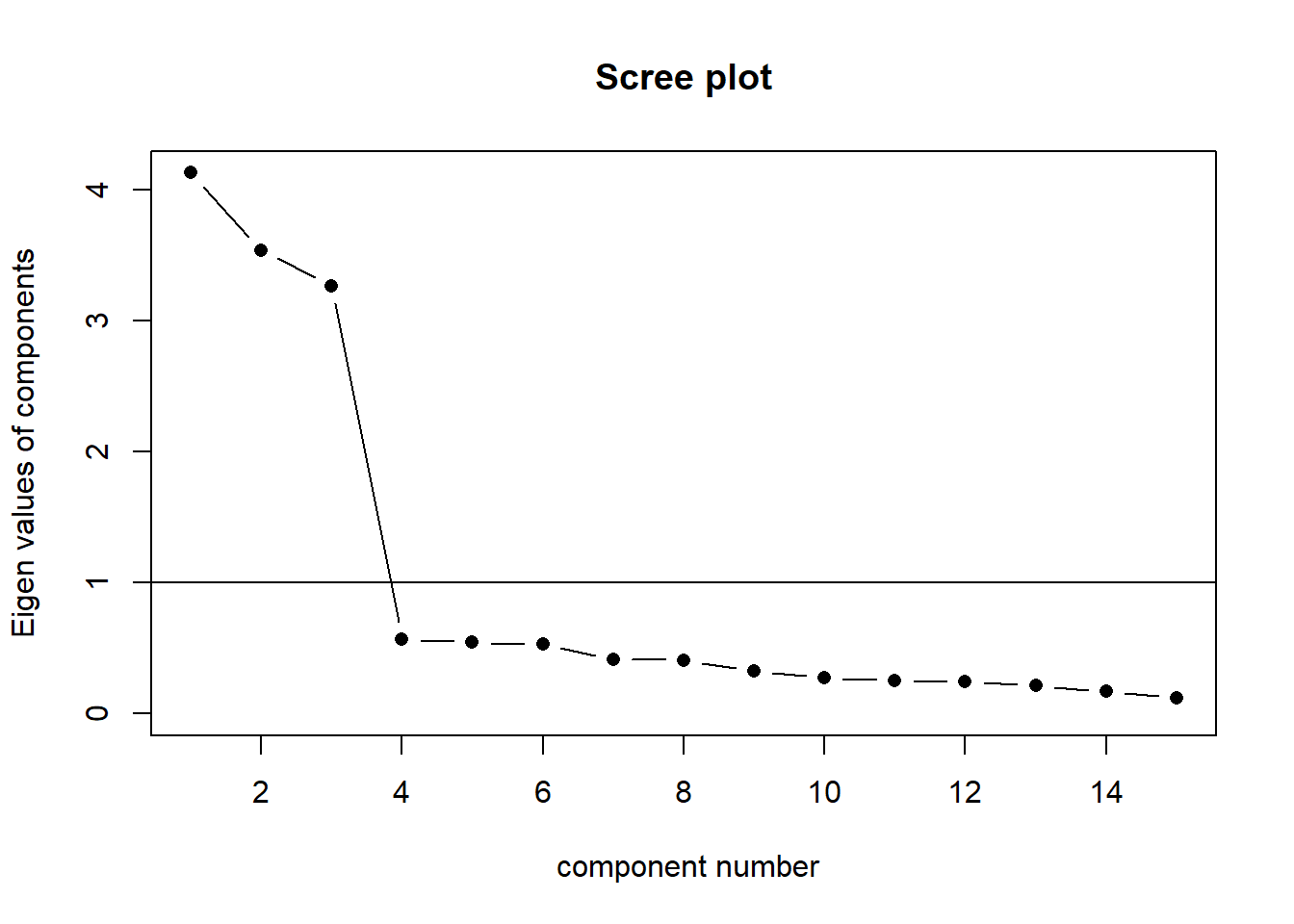
How many components should we keep? Below are some reminders of the various criteria we can use to help us come to a decision.

Kaiser’s rule

According to Kaiser’s rule, we should keep the principal components having variance larger than 1.

The variances of each PC are shown in the row of the output named SS loadings and also in the $values from the object created by principal().

Standardized variables have a variance equal 1, and if we have \(k\) standardised variables, then the total variance in the data is \(k\). An eigenvalue of <1 represents that it is accounting for less variance than any individual original variable.

NOTE: Kaiser’s Rule will very often lead to over-extracting (keeping too many components)

The scree plot

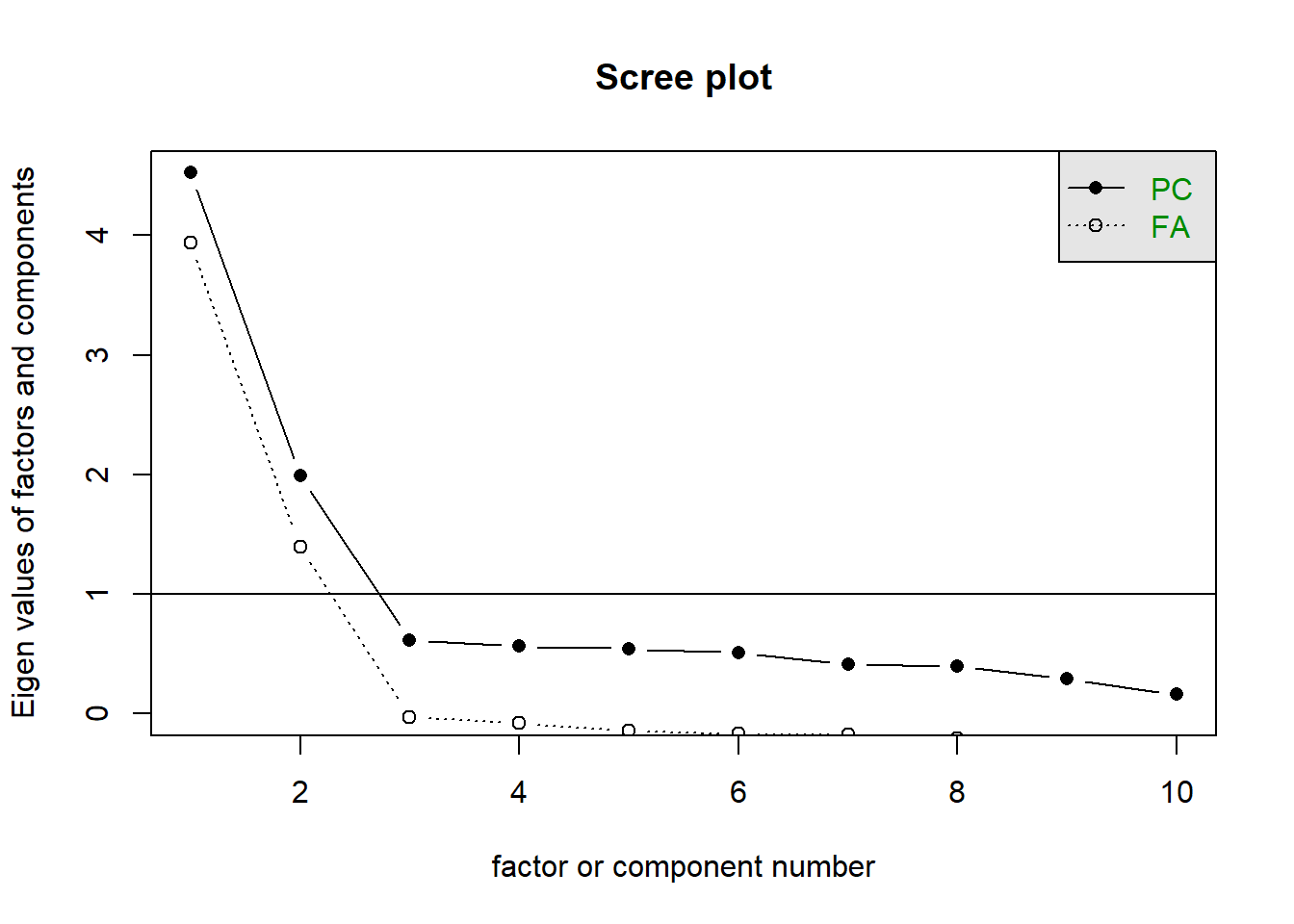
The scree plot is a graphical criterion which involves plotting the variance for each principal component. This can be easily done by calling plot on the variances, which are stored in $values of the object created by principal(), or by using the scree() function from the psych package.

When conducting an EFA as opposed to a PCA, you can remove the factors = FALSE bit.

library(psych)
scree(eg_data, factors = FALSE)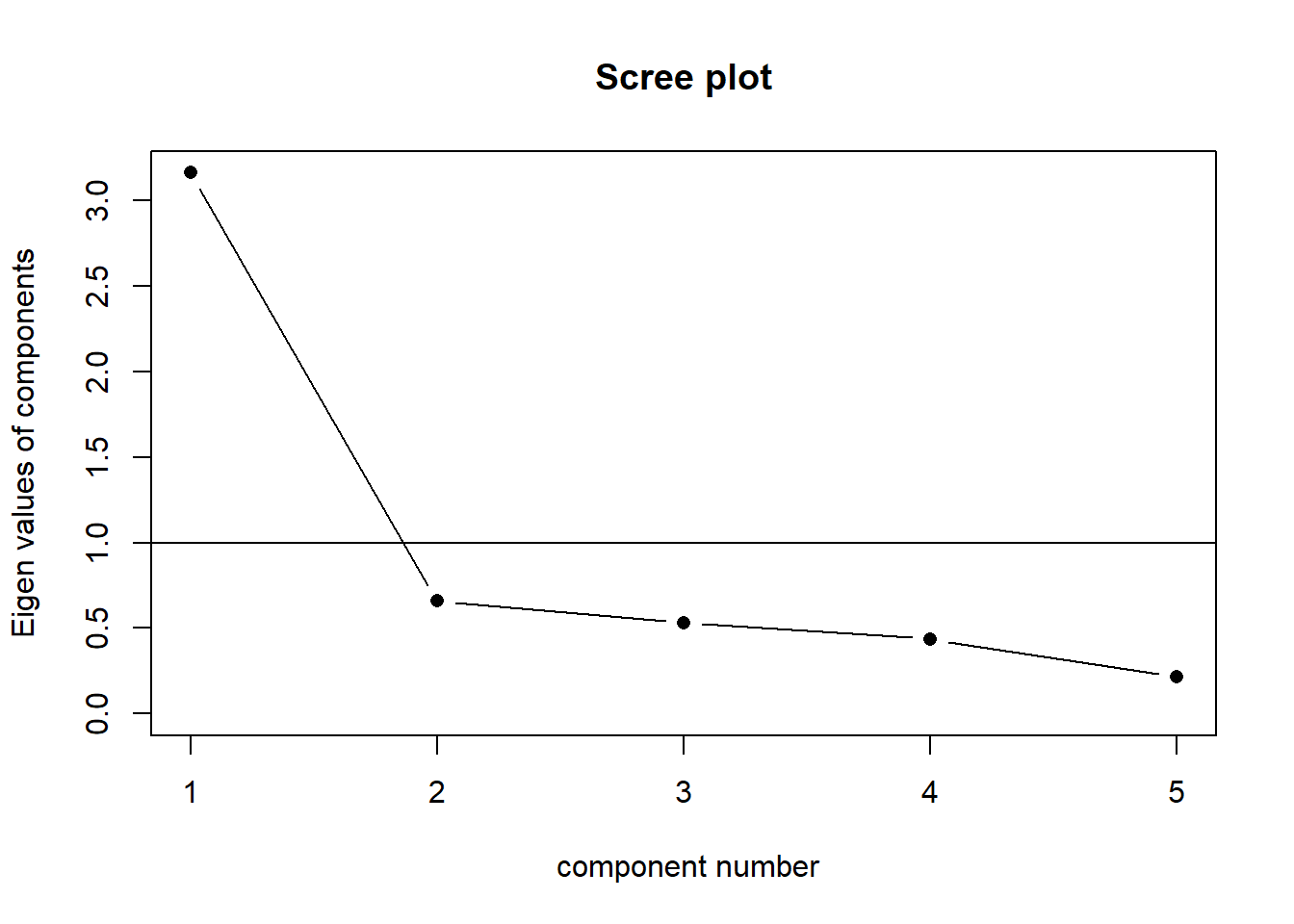

A typical scree plot features higher variances for the initial components and quickly drops to small variances where the curve is almost flat. The flat part of the curve represents the noise components, which are not able to capture the main sources of variability in the system.

According to the scree plot criterion, we should keep as many principal components up to where the “elbow” in the plot occurs. So in the above plot, the elbow occurs at 2, so we would keep 1.

NOTE: Scree plots are subjective and may have multiple or no obvious kinks/elbows, making them hard to interpret

Velicer’s Minimum Average Partial (MAP) method

The Minimum Average Partial (MAP) test computes the partial correlation matrix (removing and adjusting for a component from the correlation matrix), sequentially partialling out each component. At each step, the partial correlations are squared and their average is computed.
At first, the components which are removed will be those that are most representative of the shared variance between 2+ variables, meaning that the “average squared partial correlation” will decrease. At some point in the process, the components being removed will begin represent variance that is specific to individual variables, meaning that the average squared partial correlation will increase.
The MAP method is to keep the number of components for which the average squared partial correlation is at the minimum.

We can conduct MAP in R using the VSS() function.
When conducting an EFA as opposed to a PCA, you can set fm and rotate to the factor extraction method and rotation of your choosing.

library(psych)
VSS(eg_data, rotate = "none", 
    plot = FALSE, fm="pc", n = ncol(eg_data))

Very Simple Structure
Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm, 
    n.obs = n.obs, plot = plot, title = title, use = use, cor = cor)
VSS complexity 1 achieves a maximimum of 0.91  with  1  factors
VSS complexity 2 achieves a maximimum of 0.95  with  2  factors

The Velicer MAP achieves a minimum of 0.06  with  1  factors 

BIC achieves a minimum of  Inf  with    factors

Sample Size adjusted BIC achieves a minimum of  Inf  with    factors

Statistics by number of factors 
  vss1 vss2   map dof chisq prob sqresid  fit RMSEA BIC SABIC complex eChisq
1 0.91 0.00 0.065   0    NA   NA 9.5e-01 0.91    NA  NA    NA      NA     NA
2 0.78 0.95 0.225   0    NA   NA 5.2e-01 0.95    NA  NA    NA      NA     NA
3 0.61 0.90 0.523   0    NA   NA 2.4e-01 0.98    NA  NA    NA      NA     NA
4 0.51 0.81 1.000   0    NA   NA 4.5e-02 1.00    NA  NA    NA      NA     NA
5 0.43 0.69    NA   0    NA   NA 1.6e-29 1.00    NA  NA    NA      NA     NA
  SRMR eCRMS eBIC
1   NA    NA   NA
2   NA    NA   NA
3   NA    NA   NA
4   NA    NA   NA
5   NA    NA   NA

(be aware there is a lot of other information in this output too! For now just focus on the map column), and the part of the output that says “The Velicer MAP achieves a minimum of 0.06 with ?? factors”.

NOTE: The MAP method will sometimes tend to under-extract (suggest too few components)

Parallel analysis

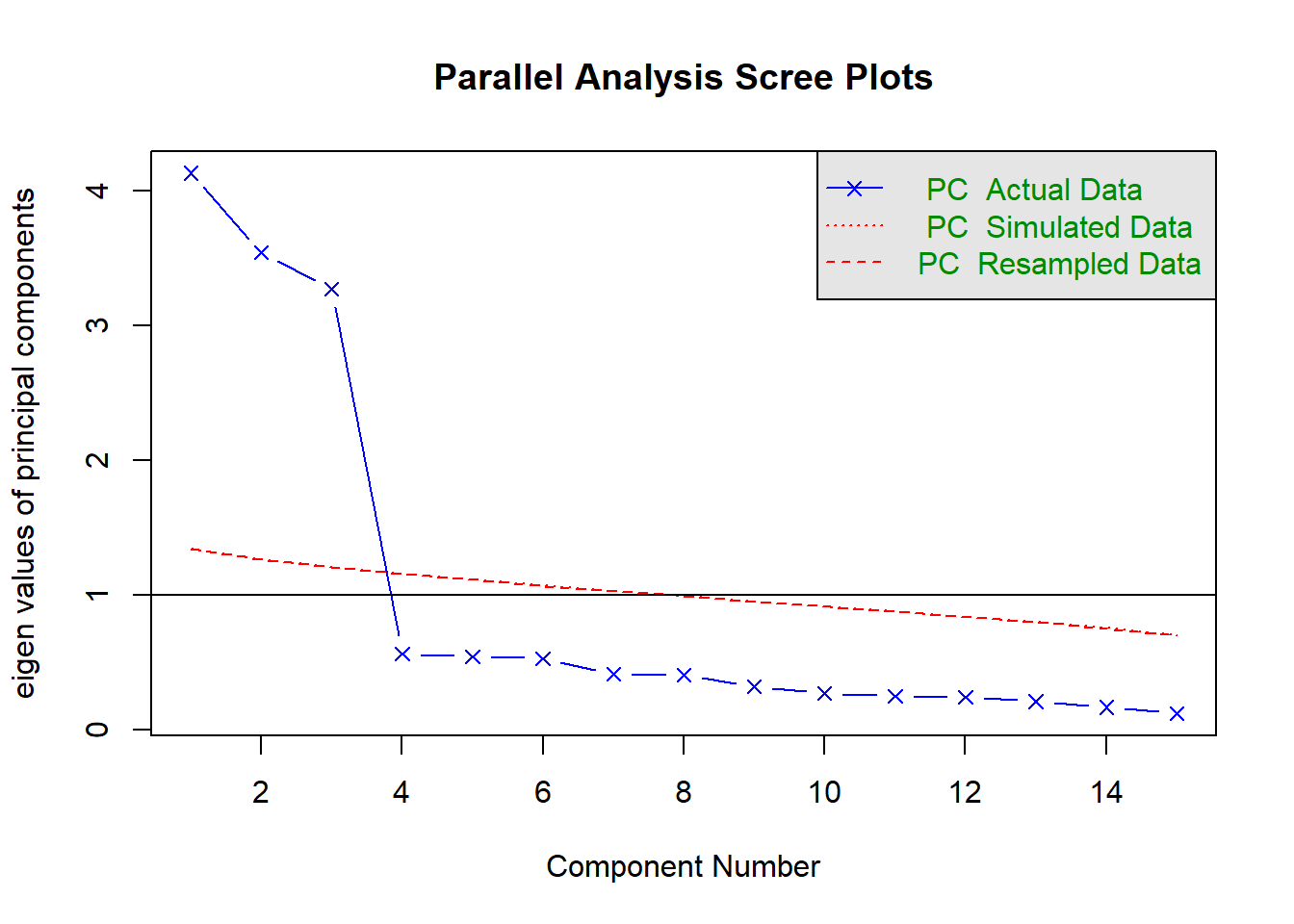
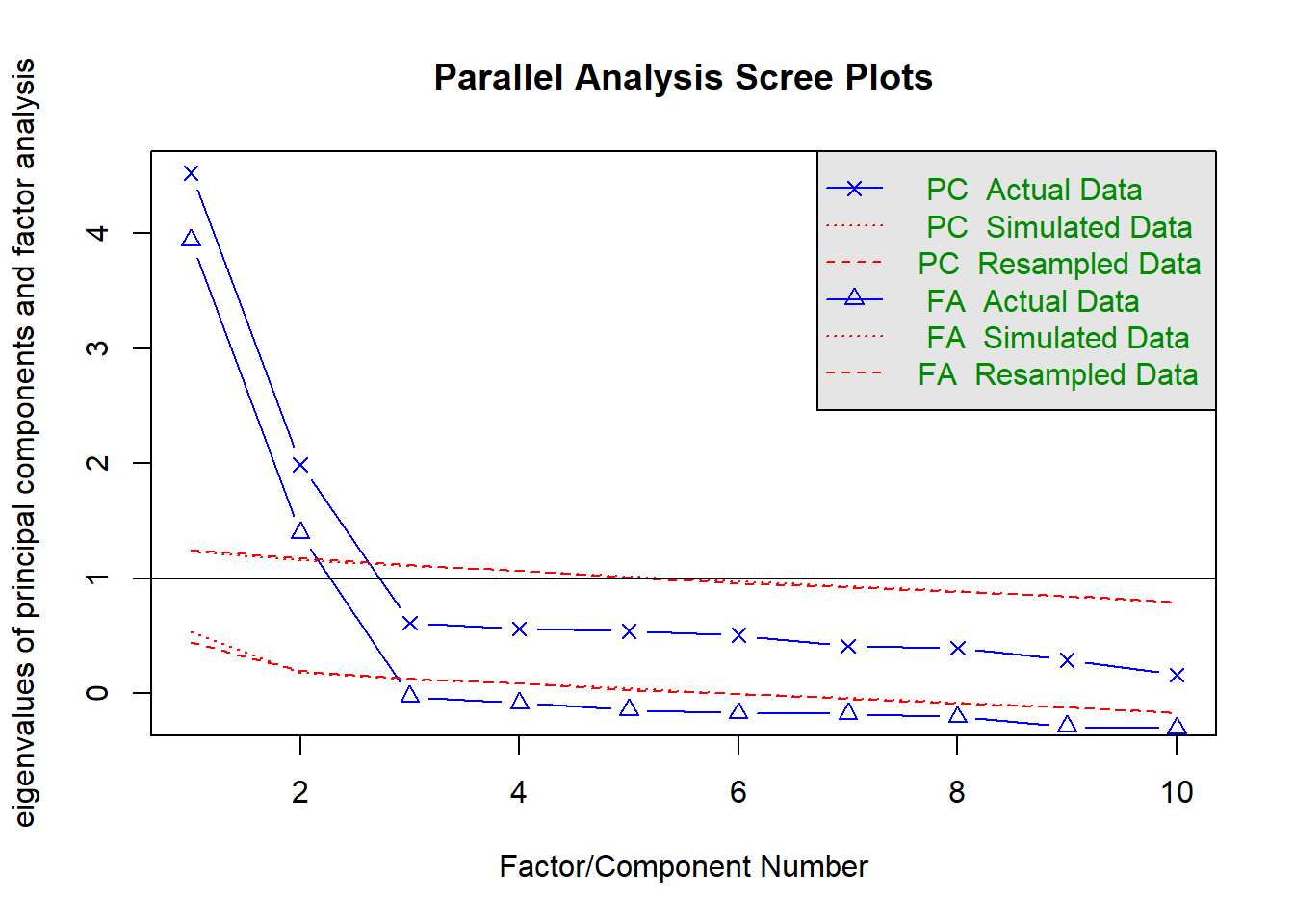
Parallel analysis involves simulating lots of datasets of the same dimension but in which the variables are uncorrelated. For each of these simulations, a PCA is conducted on its correlation matrix, and the eigenvalues are extracted. We can then compare our eigenvalues from the PCA on our actual data to the average eigenvalues across these simulations. In theory, for uncorrelated variables, no components should explain more variance than any others, and eigenvalues should be equal to 1. In reality, variables are rarely truly uncorrelated, and so there will be slight variation in the magnitude of eigenvalues simply due to chance. The parallel analysis method suggests keeping those components for which the eigenvalues are greater than those from the simulations.

It can be conducted in R using the fa.parallel() function.
When conducting an EFA as opposed to a PCA, you can set fa = "both" to do this for both factor extraction and principal components.

library(psych)
fa.parallel(eg_data, fa="pc", n.iter = 500)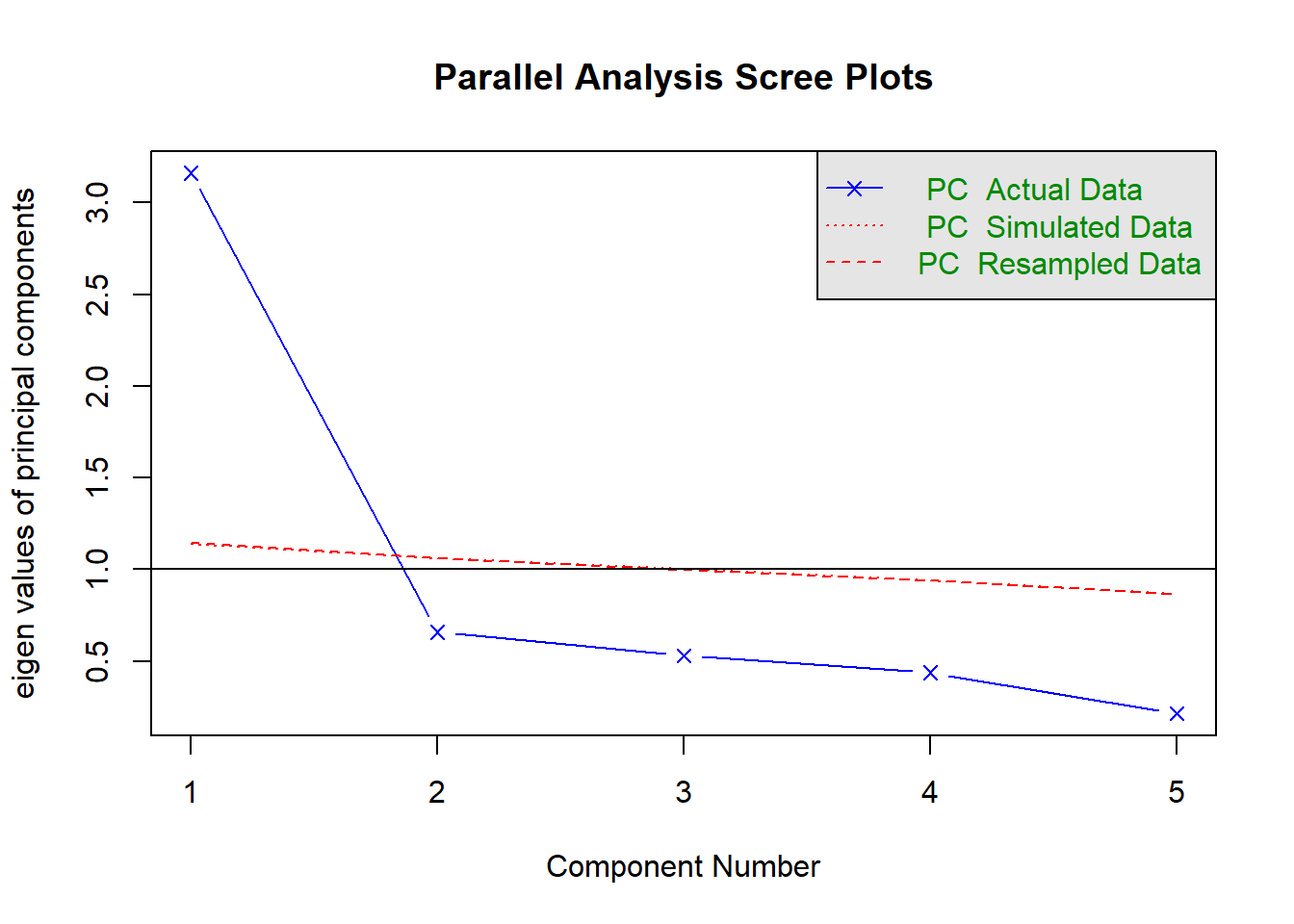

Parallel analysis suggests that the number of factors =  NA  and the number of components =  1 

NOTE: Parallel analysis will sometimes tend to over-extract (suggest too many components)

Solution 4. According to Kaiser’s rule, we should keep 3 components

principal(qperf, nfactors = 15, rotate = "none")$values

 [1] 4.1317854 3.5401412 3.2705885 0.5647474 0.5450217 0.5294260 0.4169243
 [8] 0.4073109 0.3236653 0.2736555 0.2514002 0.2446895 0.2113519 0.1685639
[15] 0.1207284

Solution 5. According to the Scree plot, I would suggest keeping 3 components

scree(qperf, factors = FALSE)

Solution 6. According to the MAP, we should keep 3 components

VSS(qperf, n = ncol(qperf), 
    rotate = "none", fm = "pc", plot = FALSE)

Very Simple Structure
Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm, 
    n.obs = n.obs, plot = plot, title = title, use = use, cor = cor)
VSS complexity 1 achieves a maximimum of 0.95  with  3  factors
VSS complexity 2 achieves a maximimum of 0.97  with  6  factors

The Velicer MAP achieves a minimum of 0.02  with  3  factors 

BIC achieves a minimum of  Inf  with    factors

Sample Size adjusted BIC achieves a minimum of  Inf  with    factors

Statistics by number of factors 
   vss1 vss2   map dof chisq prob sqresid  fit RMSEA BIC SABIC complex eChisq
1  0.41 0.00 0.137   0    NA   NA 2.5e+01 0.41    NA  NA    NA      NA     NA
2  0.70 0.71 0.079   0    NA   NA 1.2e+01 0.71    NA  NA    NA      NA     NA
3  0.95 0.96 0.021   0    NA   NA 1.6e+00 0.96    NA  NA    NA      NA     NA
4  0.95 0.96 0.031   0    NA   NA 1.3e+00 0.97    NA  NA    NA      NA     NA
5  0.83 0.97 0.046   0    NA   NA 1.0e+00 0.98    NA  NA    NA      NA     NA
6  0.84 0.97 0.070   0    NA   NA 7.3e-01 0.98    NA  NA    NA      NA     NA
7  0.77 0.95 0.100   0    NA   NA 5.6e-01 0.99    NA  NA    NA      NA     NA
8  0.76 0.93 0.123   0    NA   NA 3.9e-01 0.99    NA  NA    NA      NA     NA
9  0.68 0.93 0.149   0    NA   NA 2.9e-01 0.99    NA  NA    NA      NA     NA
10 0.68 0.93 0.204   0    NA   NA 2.1e-01 0.99    NA  NA    NA      NA     NA
11 0.68 0.93 0.258   0    NA   NA 1.5e-01 1.00    NA  NA    NA      NA     NA
12 0.61 0.92 0.386   0    NA   NA 8.8e-02 1.00    NA  NA    NA      NA     NA
13 0.60 0.87 0.540   0    NA   NA 4.3e-02 1.00    NA  NA    NA      NA     NA
14 0.60 0.87 1.000   0    NA   NA 1.5e-02 1.00    NA  NA    NA      NA     NA
15 0.60 0.87    NA   0    NA   NA 1.3e-27 1.00    NA  NA    NA      NA     NA
   SRMR eCRMS eBIC
1    NA    NA   NA
2    NA    NA   NA
3    NA    NA   NA
4    NA    NA   NA
5    NA    NA   NA
6    NA    NA   NA
7    NA    NA   NA
8    NA    NA   NA
9    NA    NA   NA
10   NA    NA   NA
11   NA    NA   NA
12   NA    NA   NA
13   NA    NA   NA
14   NA    NA   NA
15   NA    NA   NA

Solution 7. According to the parallel analysis, we should keep 3 components

fa.parallel(qperf, fa="pc", n.iter = 500)

Parallel analysis suggests that the number of factors =  NA  and the number of components =  3 

Solution 8. In this case, everything agrees that we should retain 3 components:

guides	suggestion
Kaiser	3
Scree	3
MAP	3
Parallel Analysis	3

Question 5

Conduct a principal components analysis extracting the number of components you decided on from the previous question.

Be sure to set rotate = "none" (a conventional PCA does not use rotations - it is simply about data reduction. The line is a bit blurred here, but once we start introducing rotations, we are moving more towards a form of EFA).

Examine the loadings for the components. By thinking in relation to the questions that were asked (refer back to Table 1), what do you think each component is capturing?

Solution 9. It’s rarely as neat as this, but we can see the patterns of higher loadings for the groups of 5 questions on each component.

• PC1 has higher loadings for q1 to q5
• PC2 has higher loadings for q6 to q10
• PC3 has higher loadings for q11 to q15

Looking back at the questions in Table 1, questions 1 to 5 were all about stuff related to ‘project management’. Questions 6 to 10 were all about collaboration with team members, and questions 11 to 15 were all about technical skill.

principal(qperf, nfactors = 3, rotate = "none")

Principal Components Analysis
Call: principal(r = qperf, nfactors = 3, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
      PC1  PC2   PC3   h2   u2 com
q1   0.86 0.30 -0.20 0.88 0.12 1.4
q2   0.83 0.21 -0.22 0.78 0.22 1.3
q3   0.73 0.23 -0.21 0.63 0.37 1.4
q4   0.83 0.31 -0.23 0.83 0.17 1.4
q5   0.86 0.30 -0.23 0.87 0.13 1.4
q6  -0.37 0.81 -0.11 0.80 0.20 1.4
q7  -0.36 0.80 -0.14 0.79 0.21 1.5
q8  -0.34 0.80 -0.09 0.76 0.24 1.4
q9  -0.27 0.70 -0.05 0.56 0.44 1.3
q10 -0.33 0.75 -0.15 0.70 0.30 1.5
q11  0.21 0.24  0.84 0.82 0.18 1.3
q12  0.17 0.17  0.72 0.57 0.43 1.2
q13  0.19 0.15  0.76 0.64 0.36 1.2
q14  0.25 0.17  0.73 0.62 0.38 1.3
q15  0.11 0.19  0.79 0.68 0.32 1.2

                       PC1  PC2  PC3
SS loadings           4.13 3.54 3.27
Proportion Var        0.28 0.24 0.22
Cumulative Var        0.28 0.51 0.73
Proportion Explained  0.38 0.32 0.30
Cumulative Proportion 0.38 0.70 1.00

Mean item complexity =  1.3
Test of the hypothesis that 3 components are sufficient.

The root mean square of the residuals (RMSR) is  0.04 
 with the empirical chi square  146.87  with prob <  1.2e-08 

Fit based upon off diagonal values = 0.99

Question 6

Extract the scores on the principal components.
The company wants to reward teamwork. Pick 10 people they should give a bonus to.

Hints

As seen in the reading, we can extract scores (a score on each component for each row of our original dataset) using the $scores from the object fitted with principal().

This will contain as many sets of scores as there are components. One of these (given the previous question) might be of use here.

You’ll likely want to join them back to the column of names. So we can figure out who gets the bonus. cbind() or bind_cols() might help here.

Solution 10. The second component seems to capture a lot of ‘teamwork’ related questions. So if we extract scores on that second component, we could then pick the 10 people for whom they are highest on that component.

This will extract the scores:

principal(qperf, nfactors = 3, rotate = "none")$scores

Let’s combine them with the original data that contains the employee names, so we can figure out who to give bonuses to.
We could do this with cbind(), or bind_cols(),

# first we bind the columns of the scores, back to 
# the original data which contains the names
jobperf <- 
  bind_cols(
    principal(qperf, nfactors = 3, rotate = "none")$scores,
    jobperf
  ) 

# we can then choose just the 10 people 
# who have the highest scores on PC2 (the teamwork component)
jobperf |> select(name, PC2) |>
  arrange(desc(PC2))

# A tibble: 400 × 2
   name                 PC2
   <chr>              <dbl>
 1 Robinson, Shayla    2.88
 2 Hunt, Maliek        2.56
 3 Kearns, Sarah       2.50
 4 Phillips, Nashelle  2.42
 5 al-Masih, Sawada    2.34
 6 Uren, Bethany       2.29
 7 Dhanoa, Eunice      2.23
 8 Billings, Justin    2.22
 9 Brown, Jameela      2.14
10 Guire, Lucas        2.13
# ℹ 390 more rows

Conduct Problems

Data: Conduct Problems

A researcher is developing a new brief measure of Conduct Problems. She has collected data from n=450 adolescents on 10 items, which cover the following behaviours:

1. Breaking curfew
2. Vandalism
3. Skipping school
4. Bullying
5. Spreading malicious rumours
6. Fighting
7. Lying
8. Using a weapon
9. Stealing
10. Threatening others

Our task is to use the dimension reduction techniques we learned about in the lecture to help inform how to organise the items she has developed into subscales.

The data can be found at https://uoepsy.github.io/data/conduct_probs_scale.csv

Question 7

Read in the dataset.
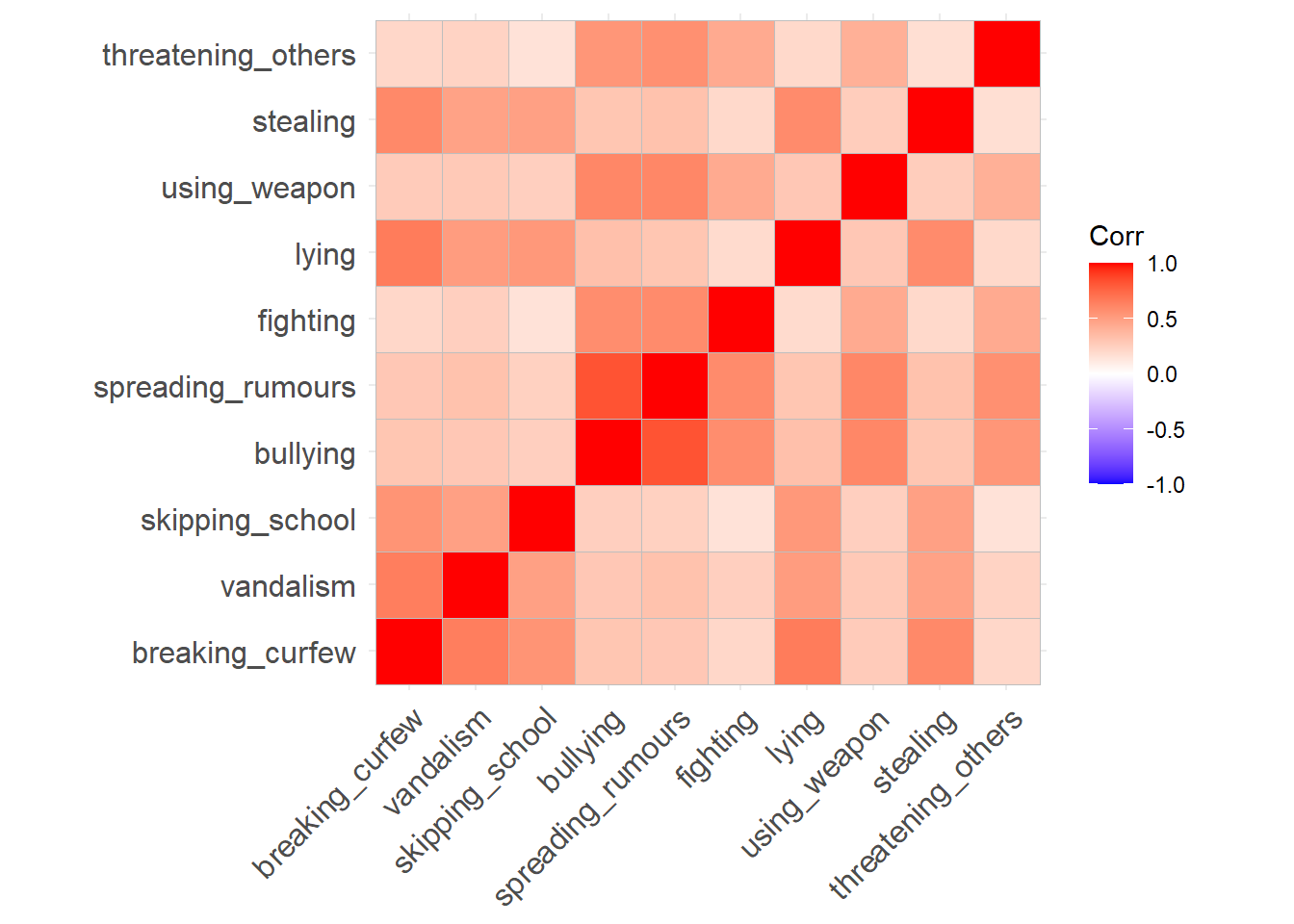
Create a correlation matrix for the items, and inspect the items to check their suitability for exploratory factor analysis (below are a couple of ways we can do this).

Bartlett’s Test

The function cortest.bartlett(cor(data), n = nrow(data)) conducts “Bartlett’s test”. This tests against the null that the correlation matrix is proportional to the identity matrix (a matrix of all 0s except for 1s on the diagonal).

• Null hypothesis: observed correlation matrix is equivalent to the identity matrix
  
• Alternative hypothesis: observed correlation matrix is not equivalent to the identity matrix.

What is the identity matrix?

The “Identity matrix” is a matrix of all 0s except for 1s on the diagonal.
e.g. for a 3x3 matrix:
\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \] If a correlation matrix looks like this, then it means there is no shared variance between the items, so it is not suitable for factor analysis

Kaiser, Meyer, Olkin Measure of Sampling Adequacy

You can check the “factorability” of the correlation matrix using KMO(data) (also from psych!).

• Rules of thumb:
  • \(0.8 < MSA < 1\): the sampling is adequate
  • \(MSA <0.6\): sampling is not adequate
  • \(MSA \sim 0\): large partial correlations compared to the sum of correlations. Not good for FA

Kaiser’s suggested cuts

These are Kaiser’s corresponding adjectives suggested for each level of the KMO:

• 0.00 to 0.49 “unacceptable”
  
• 0.50 to 0.59 “miserable”
  
• 0.60 to 0.69 “mediocre”
  
• 0.70 to 0.79 “middling”
  
• 0.80 to 0.89 “meritorious”
  
• 0.90 to 1.00 “marvelous”

Solution 11.

cpdata <- read.csv("https://uoepsy.github.io/data/conduct_probs_scale.csv")
# discard the first column
cpdata <- cpdata[,-1]

Here’s a correlation matrix. There’s no obvious blocks of items here, but we can see that there are some fairly high correlations, as well as some weaker ones. All are positive.

ggcorrplot(cor(cpdata))

The Bartlett’s test comes out with a p-value of 0 (which isn’t possible, but it’s been rounded for some reason). This suggests that we reject the null of this test (that our correlation matrix is proportional to the identity matrix). This is good. It basically means “we have some non-zero correlations”!

cortest.bartlett(cor(cpdata), n=450)

$chisq
[1] 2237.533

$p.value
[1] 0

$df
[1] 45

The overall sampling adequacy is 0.87, which is pretty good! (or rather, which is ‘meritorious’!). MSA for all items is >.8

KMO(cpdata)  

Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = cpdata)
Overall MSA =  0.87
MSA for each item = 
   breaking_curfew          vandalism    skipping_school           bullying 
              0.84               0.88               0.92               0.82 
 spreading_rumours           fighting              lying       using_weapon 
              0.81               0.94               0.88               0.95 
          stealing threatening_others 
              0.90               0.94 

Finally, all the relationships here look fairly linear:

pairs.panels(cpdata)

Question 8

How many dimensions should be retained?

This question can be answered in the same way as we did above for PCA - use a scree plot, parallel analysis, and MAP test to guide you.

You can use fa.parallel(data, fa = "both") to conduct both parallel analysis and view the scree plot!

Solution 12. The scree plot shows a kink at 3, which suggests retaining 2 components.

scree(cpdata)

Solution 13. The MAP suggests retaining 2 factors. I’m just extracting the actuall map values here to save having to show all the other output. We can see that the 2nd entry is the smallest:

VSS(cpdata, plot = FALSE, n = ncol(cpdata))$map

 [1] 0.10575332 0.03377130 0.05762202 0.10352974 0.14935664 0.25195168
 [7] 0.39743503 0.45518643 1.00000000         NA

Solution 14. Parallel analysis suggests 2 factors as well:

fa.parallel(cpdata, fa = "both")

Parallel analysis suggests that the number of factors =  2  and the number of components =  2 

Solution 15. Again, a quite clear picture that 2 factors is preferred:

guides	suggestion
Scree	2
MAP	2
Parallel Analysis	2

Question 9

Use the function fa() from the psych package to conduct and EFA to extract 2 factors (this is what we suggest based on the various tests above, but you might feel differently - the ideal number of factors is subjective!). Use a suitable rotation (rotate = ?) and extraction method (fm = ?).

myfa <- fa(data, nfactors = ?, rotate = ?, fm = ?)

Hints

Would you expect factors to be correlated? If so, you’ll want an oblique rotation.

Rotations

When we apply a rotation to an EFA, we make it so that some loadings are smaller and some are higher - essentially creating a ‘simple structure’ (where each variable loads strongly on only one factor and weakly on all other factors). This structure simplifies the interpretation of factors, making them more distinct and easily understandable.

There are two types of rotations - “orthogonal” and “oblique”. Orthogonal rotations preserve the orthogonality of the factors (i.e. ensure they are uncorrelated, and therefore capturing completely distinct things). Oblique rotations allow the factors to be correlated and estimates that correlation (as indicated by the double headed arrow between them in the diagram below)

It’s pretty hard to find an intuition for “rotations” because they are a mathematical transformation applied to a matrix (and none of that is really ‘intuitive’). At the broadest level, think of a rotation as allowing the dimensions to no longer be perpendicular when viewed in the space of our observed variables.

Factor Extraction Methods

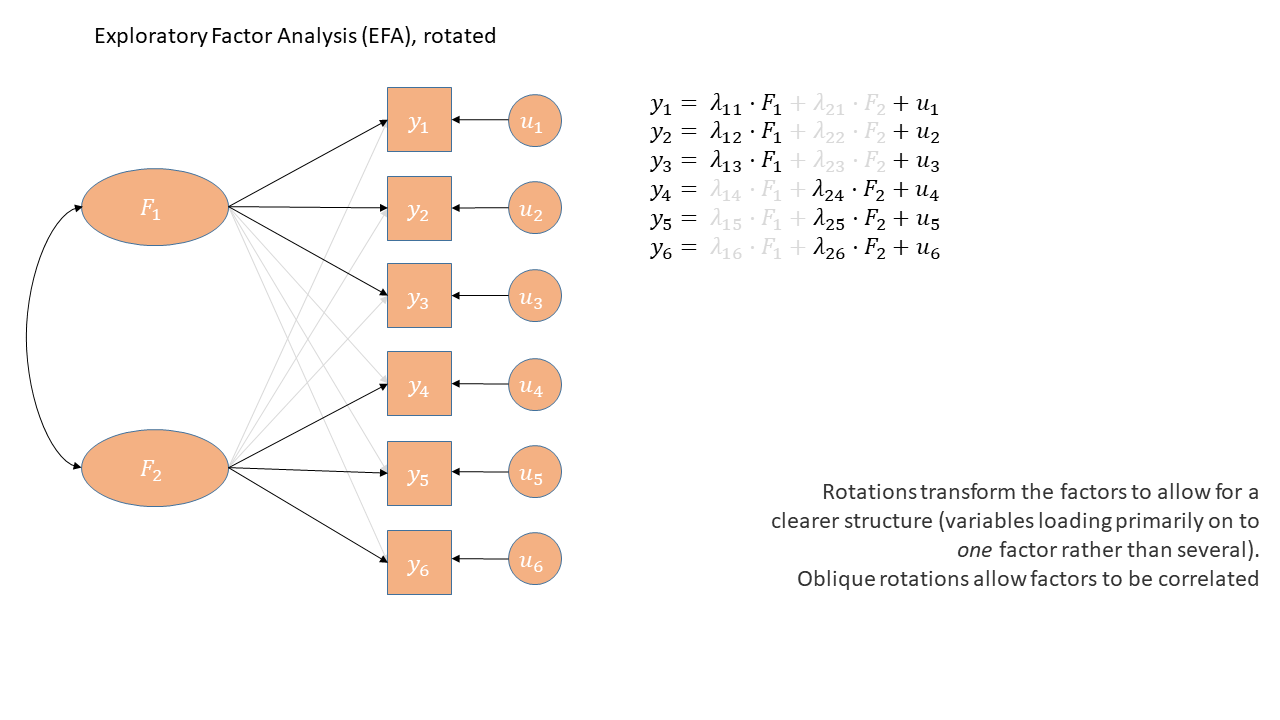
PCA (using eigendecomposition) is itself a method of extracting the different dimensions from our data. However, there are lots more available for factor analysis.

You can find a lot of discussion about different methods both in the help documentation for the fa() function from the psych package, and there are lots of discussions both in papers and on forums.

As you can see, this is a complicated issue, but when you have a large sample size, a large number of variables, for which you have similar communalities, then the extraction methods tend to agree. For now, don’t fret too much about the factor extraction method.¹

The main contenders are Maximum Likelihood (ml), Minimum Residuals (minres) and Principal Axis Factoring (paf).

Maximum Likelihood has the benefit of providing standard errors and fit indices that are useful for model testing, but the disadvantage is that it is sensitive to violations of normality, and can sometimes fail to converge, or produce solutions with impossible values such as factor loadings >1 (known as “Heywood cases”), or factor correlations >1.
Minimum Residuals (minres) and Principal Axis Factoring (paf) will both work even when maximum likelihood fails to converge, and are slightly less susceptible to deviations from normality. They are a bit more sensitive to the extent to which the items share variance with one another.

Solution 16. For example, you could choose an oblimin rotation to allow factors to correlate and use ml as the extraction method.

conduct_efa <- fa(cpdata, nfactors=2, rotate='oblimin', fm="ml")

Question 10

Inspect your solution. Make sure to look at and think about the loadings, the variance accounted for, and the factor correlations (if estimated).

Hints

Just printing an fa object:

myfa <- fa(data, ..... )
myfa

Will give you lots and lots of information.
You can extract individual parts using:

• myfa$loadings for the loadings
• myfa$Vaccounted for the variance accounted for by each factor
• myfa$Phi for the factor correlation matrix

You can find a quick guide to reading the fa output here: efa_output.pdf.

Solution 17. Things look pretty good here. Each item has a clear primary loading on to one of the factors, and the complexity for all items is 1 (meaning they’re clearly link to just one of the factors). The h2 column is showing that the 2 factor solution is explaining 38%+ of the variance in each item. Both factors are well determined, having at least 3 salient loadings.

The 2 factors together explain 57% of the variance in the data - both factors explain a similar amount (29% for factor 1, 28% for factor 2).

We can also see that there is a moderate correlation between the two factors. Use of an oblique rotation was appropriate - if the correlation had been very weak, then it might not have differed much from if we used an orthogonal rotation.

conduct_efa

Factor Analysis using method =  ml
Call: fa(r = cpdata, nfactors = 2, rotate = "oblimin", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                     ML1   ML2   h2   u2 com
breaking_curfew    -0.05  0.88 0.74 0.26   1
vandalism           0.05  0.69 0.51 0.49   1
skipping_school    -0.01  0.67 0.44 0.56   1
bullying            0.90  0.00 0.81 0.19   1
spreading_rumours   0.93 -0.02 0.85 0.15   1
fighting            0.65 -0.02 0.42 0.58   1
lying               0.02  0.77 0.60 0.40   1
using_weapon        0.63  0.09 0.45 0.55   1
stealing            0.04  0.70 0.51 0.49   1
threatening_others  0.62 -0.01 0.38 0.62   1

                       ML1  ML2
SS loadings           2.91 2.80
Proportion Var        0.29 0.28
Cumulative Var        0.29 0.57
Proportion Explained  0.51 0.49
Cumulative Proportion 0.51 1.00

 With factor correlations of 
     ML1  ML2
ML1 1.00 0.43
ML2 0.43 1.00

Mean item complexity =  1

Question 11

Look back to the description of the items, and suggest a name for your factors based on the patterns of loadings.

Hints

To sort the loadings, you can use

print(myfa$loadings, sort = TRUE)

Solution 18. You can inspect the loadings using:

print(conduct_efa$loadings, sort=TRUE)

Loadings:
                   ML1    ML2   
bullying            0.899       
spreading_rumours   0.931       
fighting            0.653       
using_weapon        0.629       
threatening_others  0.621       
breaking_curfew            0.878
vandalism                  0.694
skipping_school            0.671
lying                      0.767
stealing                   0.696

                 ML1   ML2
SS loadings    2.890 2.782
Proportion Var 0.289 0.278
Cumulative Var 0.289 0.567

We can see that, ordered like this, we have five items that have high loadings for one factor and another five items that have high loadings for the other.

The five items for factor 1 all have in common that they are non-aggressive forms of conduct problems. The five items for factor 2 are all more aggressive behaviours. We could, therefore, label our factors: ‘non-aggressive’ and ‘aggressive’ conduct problems.

Question 12

Compare your three different solutions:

1. your current solution from the previous questions
2. one where you fit 1 more factor
3. one where you fit 1 fewer factors

Which one looks best?

Hints

We’re looking here to assess:

• how much variance is accounted for by each solution
• do all factors load on 3+ items at a salient level?
  
• do all items have at least one loading at a salient level?
• are there any “Heywood cases” (communalities or standardised loadings that are >1)?
• should we perhaps remove some of the more complex items?
• is the factor structure (items that load on to each factor) coherent, and does it make theoretical sense?

Solution 19. The 1-factor model explains 37% of the variance (as opposed to the 57% explained by the 2 factor solution), and all items load fairly high on the factor. The downside here is that we’re not discerning between different types of conduct problems that we did in the 2 factor solution.

conduct_1 <- fa(cpdata, nfactors=1, fm="ml")
conduct_1

Factor Analysis using method =  ml
Call: fa(r = cpdata, nfactors = 1, fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                    ML1   h2   u2 com
breaking_curfew    0.42 0.18 0.82   1
vandalism          0.42 0.18 0.82   1
skipping_school    0.35 0.13 0.87   1
bullying           0.89 0.79 0.21   1
spreading_rumours  0.90 0.81 0.19   1
fighting           0.64 0.41 0.59   1
lying              0.43 0.18 0.82   1
using_weapon       0.68 0.46 0.54   1
stealing           0.42 0.17 0.83   1
threatening_others 0.61 0.38 0.62   1

                ML1
SS loadings    3.69
Proportion Var 0.37

Mean item complexity =  1
Test of the hypothesis that 1 factor is sufficient.

df null model =  45  with the objective function =  5.03 with Chi Square =  2237.53
df of  the model are 35  and the objective function was  1.78 

The root mean square of the residuals (RMSR) is  0.19 
The df corrected root mean square of the residuals is  0.22 

The harmonic n.obs is  450 with the empirical chi square  1464.73  with prob <  1.9e-285 
The total n.obs was  450  with Likelihood Chi Square =  789.3  with prob <  3.4e-143 

Tucker Lewis Index of factoring reliability =  0.557
RMSEA index =  0.219  and the 90 % confidence intervals are  0.206 0.232
BIC =  575.48
Fit based upon off diagonal values = 0.8
Measures of factor score adequacy             
                                                   ML1
Correlation of (regression) scores with factors   0.96
Multiple R square of scores with factors          0.92
Minimum correlation of possible factor scores     0.84

The 3-factor model explains 60% of the variance (only 3% more than the 2-factor model). Notably, the third factor is not very clearly defined - it only has 1 salient loading (possibly 2 if we consider the 0.31 to be salient, but that item is primarily loaded on the 2nd factor).

conduct_3 <- fa(cpdata, nfactors=3, rotate='oblimin', fm="ml")
conduct_3

Factor Analysis using method =  ml
Call: fa(r = cpdata, nfactors = 3, rotate = "oblimin", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                     ML1   ML2   ML3   h2   u2 com
breaking_curfew    -0.02  0.61  0.31 0.71 0.29 1.5
vandalism           0.06  0.12  0.74 0.72 0.28 1.1
skipping_school     0.00  0.56  0.14 0.44 0.56 1.1
bullying            0.90  0.09 -0.10 0.82 0.18 1.0
spreading_rumours   0.92 -0.02  0.03 0.85 0.15 1.0
fighting            0.65 -0.13  0.14 0.43 0.57 1.2
lying               0.02  0.85 -0.06 0.67 0.33 1.0
using_weapon        0.63  0.08  0.02 0.45 0.55 1.0
stealing            0.06  0.69  0.02 0.53 0.47 1.0
threatening_others  0.62 -0.08  0.09 0.39 0.61 1.1

                       ML1  ML2  ML3
SS loadings           2.93 2.14 0.94
Proportion Var        0.29 0.21 0.09
Cumulative Var        0.29 0.51 0.60
Proportion Explained  0.49 0.36 0.16
Cumulative Proportion 0.49 0.84 1.00

 With factor correlations of 
     ML1  ML2  ML3
ML1 1.00 0.39 0.32
ML2 0.39 1.00 0.68
ML3 0.32 0.68 1.00

Mean item complexity =  1.1
Test of the hypothesis that 3 factors are sufficient.

df null model =  45  with the objective function =  5.03 with Chi Square =  2237.53
df of  the model are 18  and the objective function was  0.02 

The root mean square of the residuals (RMSR) is  0.01 
The df corrected root mean square of the residuals is  0.02 

The harmonic n.obs is  450 with the empirical chi square  3.98  with prob <  1 
The total n.obs was  450  with Likelihood Chi Square =  10.51  with prob <  0.91 

Tucker Lewis Index of factoring reliability =  1.009
RMSEA index =  0  and the 90 % confidence intervals are  0 0.016
BIC =  -99.46
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   ML1  ML2  ML3
Correlation of (regression) scores with factors   0.96 0.93 0.88
Multiple R square of scores with factors          0.93 0.86 0.77
Minimum correlation of possible factor scores     0.85 0.72 0.53

Question 13

Drawing on your previous answers and conducting any additional analyses you believe would be necessary to identify an optimal factor structure for the 10 conduct problems, write a brief text that summarises your method and the results from your chosen optimal model.

Hints

Write about the process that led you to the number of factors. Discuss the patterns of loadings and provide definitions of the factors.

Solution 20. The main principles governing the reporting of statistical results are transparency and reproducibility (i.e., someone should be able to reproduce your analysis based on your description).

An example summary would be:

First, the data were checked for their suitability for factor analysis. Normality was checked using visual inspection of histograms, linearity was checked through the inspection of the linear and lowess lines for the pairwise relations of the variables, and factorability was confirmed using a KMO test, which yielded an overall KMO of \(.87\) with no variable KMOs \(<.50\). An exploratory factor analysis was conducted to inform the structure of a new conduct problems test. Inspection of a scree plot alongside parallel analysis (using principal components analysis; PA-PCA) and the MAP test were used to guide the number of factors to retain. All three methods suggested retaining two factors; however, a one-factor and three-factor solution were inspected to confirm that the two-factor solution was optimal from a substantive and practical perspective, e.g., that it neither blurred important factor distinctions nor included a minor factor that would be better combined with the other in a one-factor solution. These factor analyses were conducted using maximum likelihood estimation and (for the two- and three-factor solutions) an oblimin rotation, because it was expected that the factors would correlate. Inspection of the factor loadings and correlations reinforced that the two-factor solution was optimal: both factors were well-determined, including 5 loadings \(>|0.3|\) and the one-factor model blurred the distinction between different forms of conduct problems. The factor loadings are provided in Table 2². Based on the pattern of factor loadings, the two factors were labelled ‘aggressive conduct problems’ and ‘non-aggressive conduct problems’. These factors had a correlation of \(r=.43\). Overall, they accounted for 57% of the variance in the items, suggesting that a two-factor solution effectively summarised the variation in the items.

Table 2: Factor Loadings

	ML1	ML2
spreading_rumours	0.93
bullying	0.90
fighting	0.65
using_weapon	0.63
threatening_others	0.62
vandalism		0.88
stealing		0.77
lying		0.70
skipping_school		0.69
breaking_curfew		0.67

Footnotes

1. (It’s a bit like the optimiser issue in the multi-level model block)

2. You should provide the table of factor loadings. It is conventional to omit factor loadings \(<|0.3|\); however, be sure to ensure that you mention this in a table note.