Week 4 Exercises: Nested and Crossed

Psychoeducation Treatment Effects

Data: gadeduc.csv

This is synthetic data from a randomised controlled trial, in which 30 therapists randomly assigned patients (each therapist saw between 2 and 28 patients) to a control or treatment group, and monitored their scores over time on a measure of generalised anxiety disorder (GAD7 - a 7 item questionnaire with 5 point likert scales).

The control group of patients received standard sessions offered by the therapists. For the treatment group, 10 mins of each sessions was replaced with a specific psychoeducational component, and patients were given relevant tasks to complete between each session. All patients had monthly therapy sessions. Generalised Anxiety Disorder was assessed at baseline and then every visit over 4 months of sessions (5 assessments in total).

The data are available at https://uoepsy.github.io/data/lmm_gadeduc.csv

You can find a data dictionary below:

Table 1: Data Dictionary: lmm_gadeduc.csv

variable	description
patient	A patient code in which the labels take the form <Therapist initials>_<group>_<patient number>.
visit_0	Score on the GAD7 at baseline
visit_1	GAD7 at 1 month assessment
visit_2	GAD7 at 2 month assessment
visit_3	GAD7 at 3 month assessment
visit_4	GAD7 at 4 month assessment

Question 1

Uh-oh… these data aren’t in the same shape as the other datasets we’ve been giving you..

Can you get it into a format that is ready for modelling?

Hints

• It’s wide, and we want it long.
  
• Once it’s long. “visit_0”, “visit_1”,.. needs to become the numbers 0, 1, …
• One variable (patient) contains lots of information that we want to separate out. There’s a handy function in the tidyverse called separate(), check out the help docs!

Solution 1. Here’s the data. We have one row per patient, but we have multiple observations for each patient across the columns..

geduc = read_csv("https://uoepsy.github.io/data/lmm_gadeduc.csv")
head(geduc)

# A tibble: 6 × 6
  patient      visit_0 visit_1 visit_2 visit_3 visit_4
  <chr>          <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
1 VC_Control_1      24      24      26      29      28
2 VC_Control_2      24      26      28      29      30
3 VC_Control_3      25      29      27      29      30
4 VC_Control_4      24      25      25      26      26
5 VC_Control_5      28      28      27      29      28
6 VC_Control_6      26      28      25      27      28

We can make it long by taking the all the columns from visit_0 to visit_4 and shoving their values into one variable, and keeping the name of the column they come from as another variable:

geduc |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD")

# A tibble: 2,410 × 3
   patient      visit     GAD
   <chr>        <chr>   <dbl>
 1 VC_Control_1 visit_0    24
 2 VC_Control_1 visit_1    24
 3 VC_Control_1 visit_2    26
 4 VC_Control_1 visit_3    29
 5 VC_Control_1 visit_4    28
 6 VC_Control_2 visit_0    24
 7 VC_Control_2 visit_1    26
 8 VC_Control_2 visit_2    28
 9 VC_Control_2 visit_3    29
10 VC_Control_2 visit_4    30
# ℹ 2,400 more rows

Solution 2. Now we know how to get our data long, we need to sort out our time variable (visit) and make it into numbers.
We can replace all occurrences of the string "visit_" with nothingness "", and then convert them to numeric.

geduc |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD") |>
  mutate(
    visit = as.numeric(gsub("visit_","",visit))
  ) 

# A tibble: 2,410 × 3
   patient      visit   GAD
   <chr>        <dbl> <dbl>
 1 VC_Control_1     0    24
 2 VC_Control_1     1    24
 3 VC_Control_1     2    26
 4 VC_Control_1     3    29
 5 VC_Control_1     4    28
 6 VC_Control_2     0    24
 7 VC_Control_2     1    26
 8 VC_Control_2     2    28
 9 VC_Control_2     3    29
10 VC_Control_2     4    30
# ℹ 2,400 more rows

Solution 3. Finally, we need to sort out the patient variable. It contains 3 bits of information that we will want to have separated out. It has the therapist (their initials), then the group (treatment or control), and then the patient number. These are all separated by an underscore “_“.

The separate() function takes a column and separates it into several things (as many things as we give it), splitting them by some user defined separator such as an underscore:

geduc_long <- geduc |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD") |>
  mutate(
    visit = as.numeric(gsub("visit_","",visit))
  ) |>
  separate(patient, into=c("therapist","group","patient"), sep="_")

And we’re ready to go!

geduc_long

# A tibble: 2,410 × 5
   therapist group   patient visit   GAD
   <chr>     <chr>   <chr>   <dbl> <dbl>
 1 VC        Control 1           0    24
 2 VC        Control 1           1    24
 3 VC        Control 1           2    26
 4 VC        Control 1           3    29
 5 VC        Control 1           4    28
 6 VC        Control 2           0    24
 7 VC        Control 2           1    26
 8 VC        Control 2           2    28
 9 VC        Control 2           3    29
10 VC        Control 2           4    30
# ℹ 2,400 more rows

Question 2

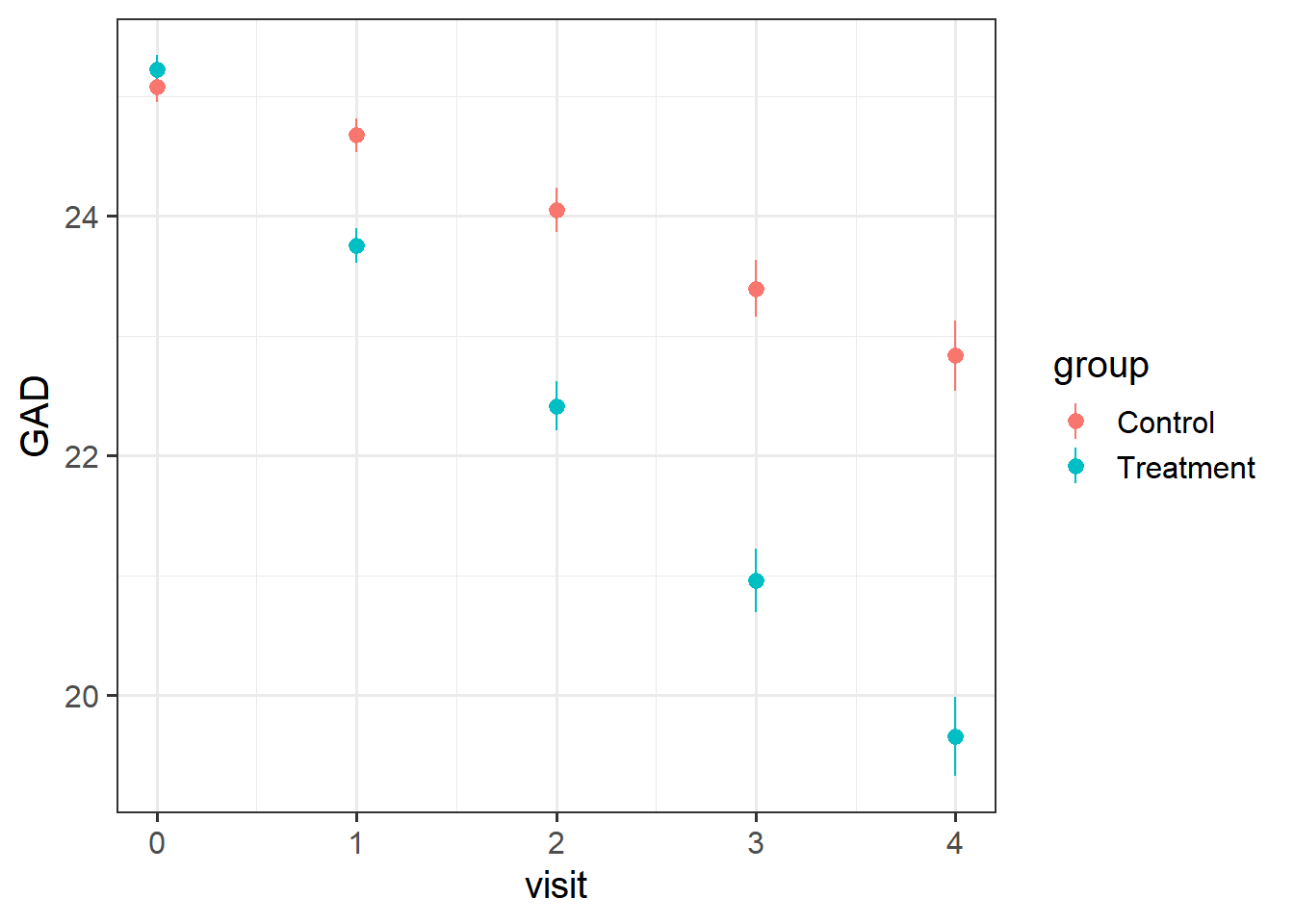
Visualise the data. Does it look like the treatment had an effect?
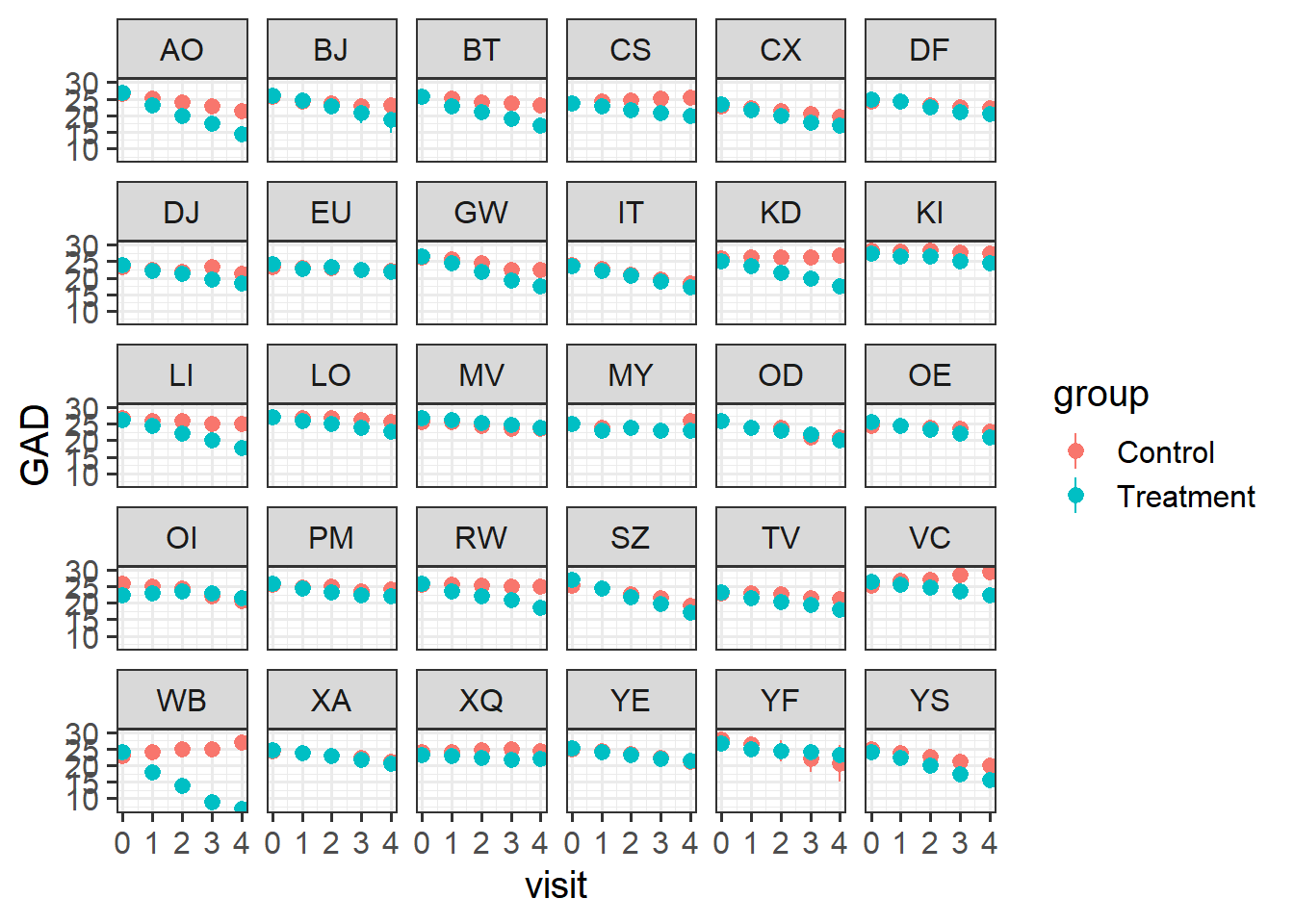
Does it look like it worked for every therapist?

Hints

• remember, stat_summary() is very useful for aggregating data inside a plot.

Solution 4. Here’s the overall picture. The average score on the GAD7 at each visit gets more and more different between the two groups. The treatment looks effective..

ggplot(geduc_long, aes(x = visit, y = GAD, col = group)) +
  stat_summary(geom="pointrange")

Let’s split this up by therapist, so we can see the averages across each therapist’s set of patients.
There’s clear variability between therapists in how well the treatment worked. For instance, the therapists EU and OD don’t seem to have much difference between their groups of patients.

ggplot(geduc_long, aes(x = visit, y = GAD, col = group)) +
  stat_summary(geom="pointrange") +
  facet_wrap(~therapist)

Question 3

Fit a model to test if the psychoeducational treatment is associated with greater improvement in anxiety over time.

Solution 5. We want to know if how anxiety (GAD) changes over time (visit) is different between treatment and control (group).

Hopefully this should hopefully come as no surprise¹ - it’s an interaction!

lmer(GAD ~ visit * group + ...
       ...
     data = geduc_long)

Solution 6. We have multiple observations for each of the 482 patients, and those patients are nested within 30 therapists.

Note that in our data, the patient variable does not uniquely specify the individual patients. i.e. patient “1” from therapist “AO” is a different person from patient “1” from therapist “BJ”. To correctly group the observations into different patients (and not ‘patient numbers’), we need to have therapist:patient.

So we capture therapist-level differences in ( ... | therapist) and the patients-within-therapist-level differences in ( ... | therapist:patient):

lmer(GAD ~ visit * group + ...
       ( ... | therapist) + 
       ( ... | therapist:patient),
     data = geduc_long)

Solution 7. Note that each patient can change differently in their anxiety levels over time - i.e. the slope of visit could vary by participant.

Likewise, some therapists could have patients who change differently from patients from another therapist, so visit|therapist can be included.

Each patient is in one of the two groups - they’re either treatment or control. So we can’t say that “differences in anxiety due to treatment varies between patients”, because for any one patient the “difference in anxiety due to treatment” is not defined in our study design.

However, therapists see multiple different patients, some of which are in the treatment group, and some of which are in the control group. So the treatment effect could be different for different therapists!

mod1 <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist)+
               (1+visit|therapist:patient),
             geduc_long)

Question 4

For each of the models below, what is wrong with the random effect structure?

modelA <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist)+
               (1+visit|patient),
             geduc_long)

modelB <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist/patient),
             geduc_long)

Solution 8.

modelA <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist)+
               (1+visit|patient),
             geduc_long)

The patient variable doesn’t capture the different patients within therapists, so this actually fits crossed random effects and treats all data where patient==1 as from the same group (even if this includes several different patients’ worth of data from different therapists!)

modelB <- lmer(GAD ~ visit*group + 
               (1+visit*group|therapist/patient),
             geduc_long)

Using the / here means we have the same random slopes fitted for therapists and for patients-within-therapists. but the effect of group can’t vary by patient, so this doesn’t work. hence why we need to split them up into (...|therapist)+(...|therapist:patient).

Question 5

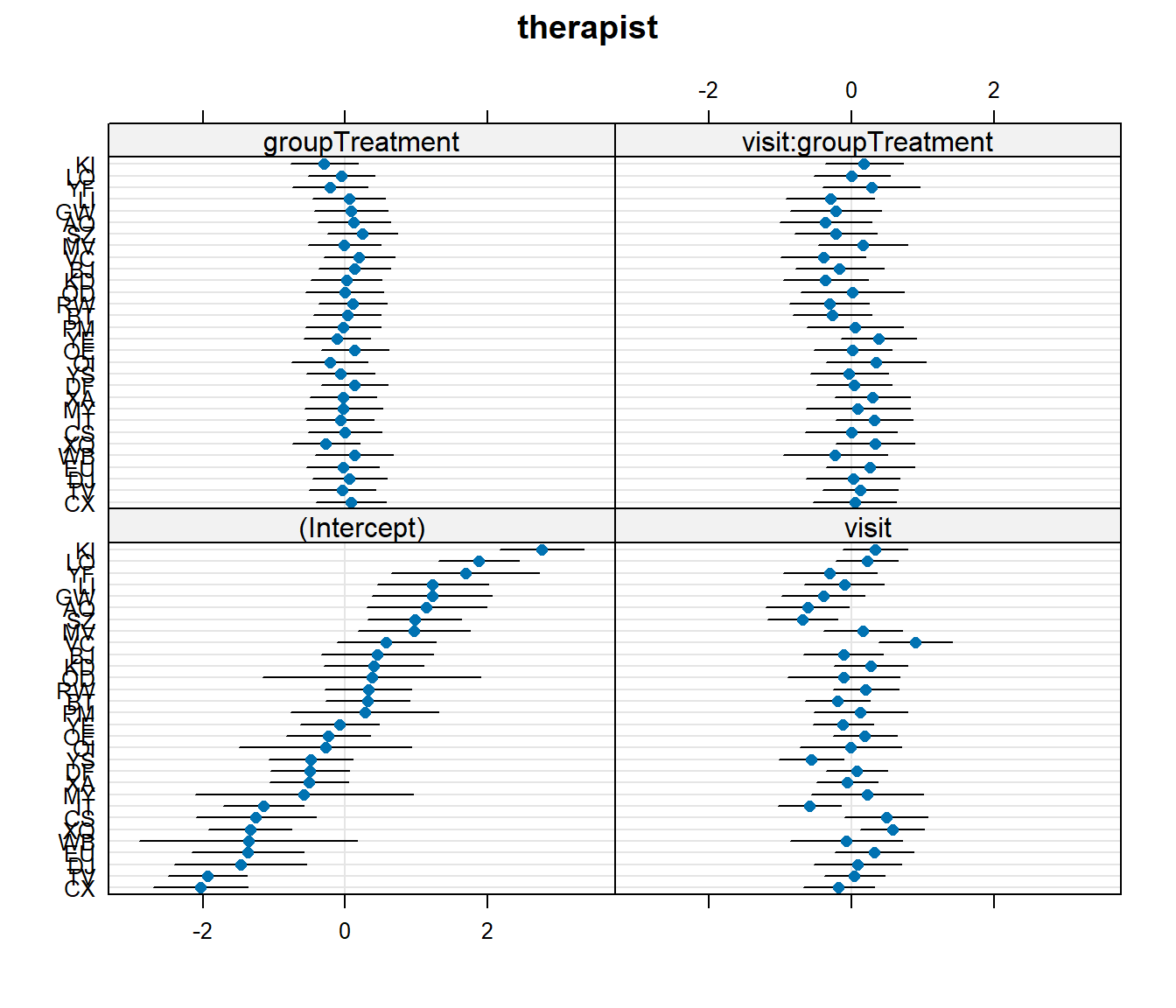
Let’s suppose that I don’t want the psychoeducation treatment, I just want the standard therapy sessions that the ‘Control’ group received. Which therapist should I go to?

Hints

dotplot.ranef.mer() might help here!
You can read about ranef in Chapter 2 #making-model-predictions.

Solution 9. It would be best to go to one of the therapists SZ, YS, or IT…

Why? These therapists all have the most negative slope of visit:

dotplot.ranef.mer(ranef(mod1))$therapist

Question 6

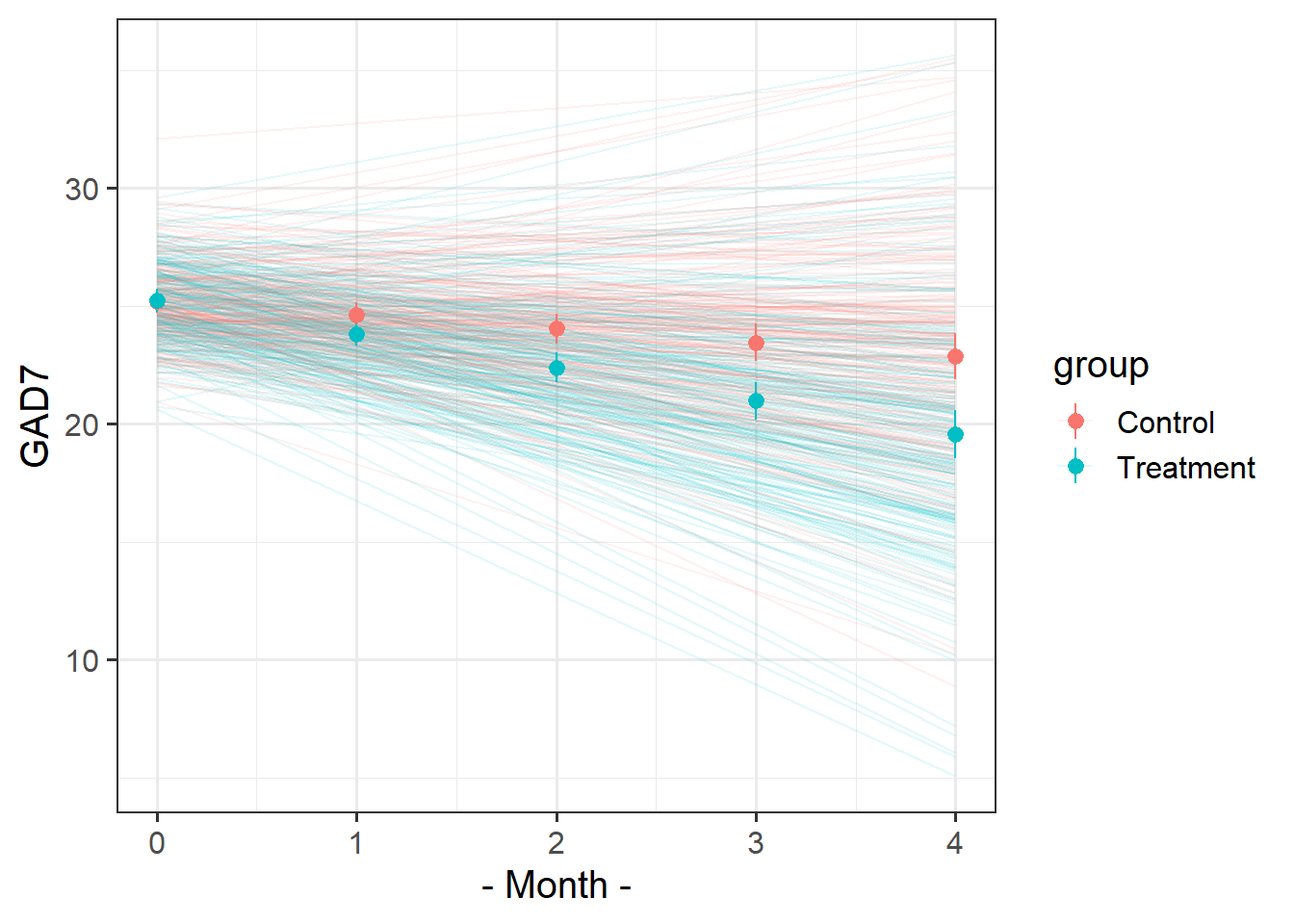
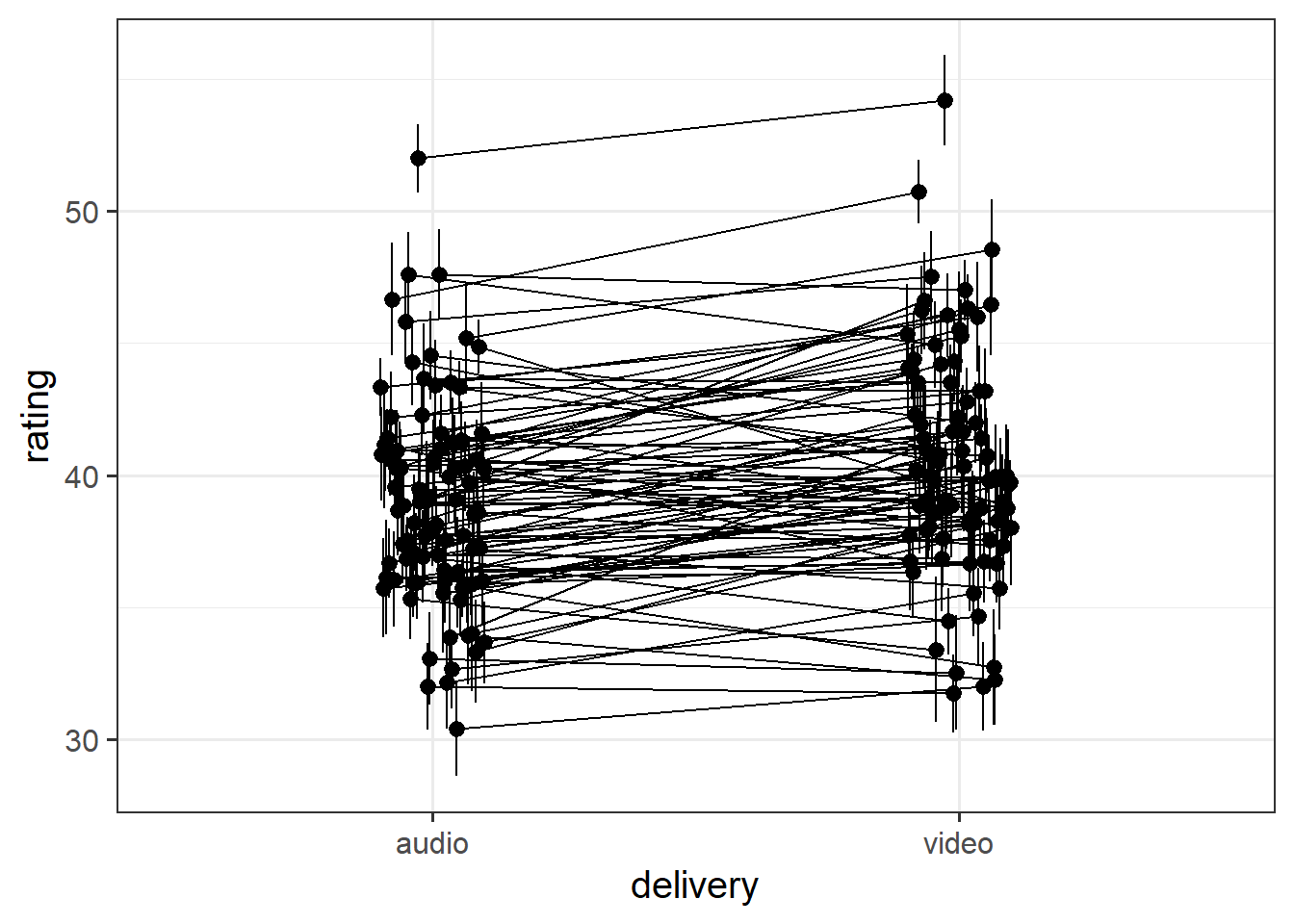
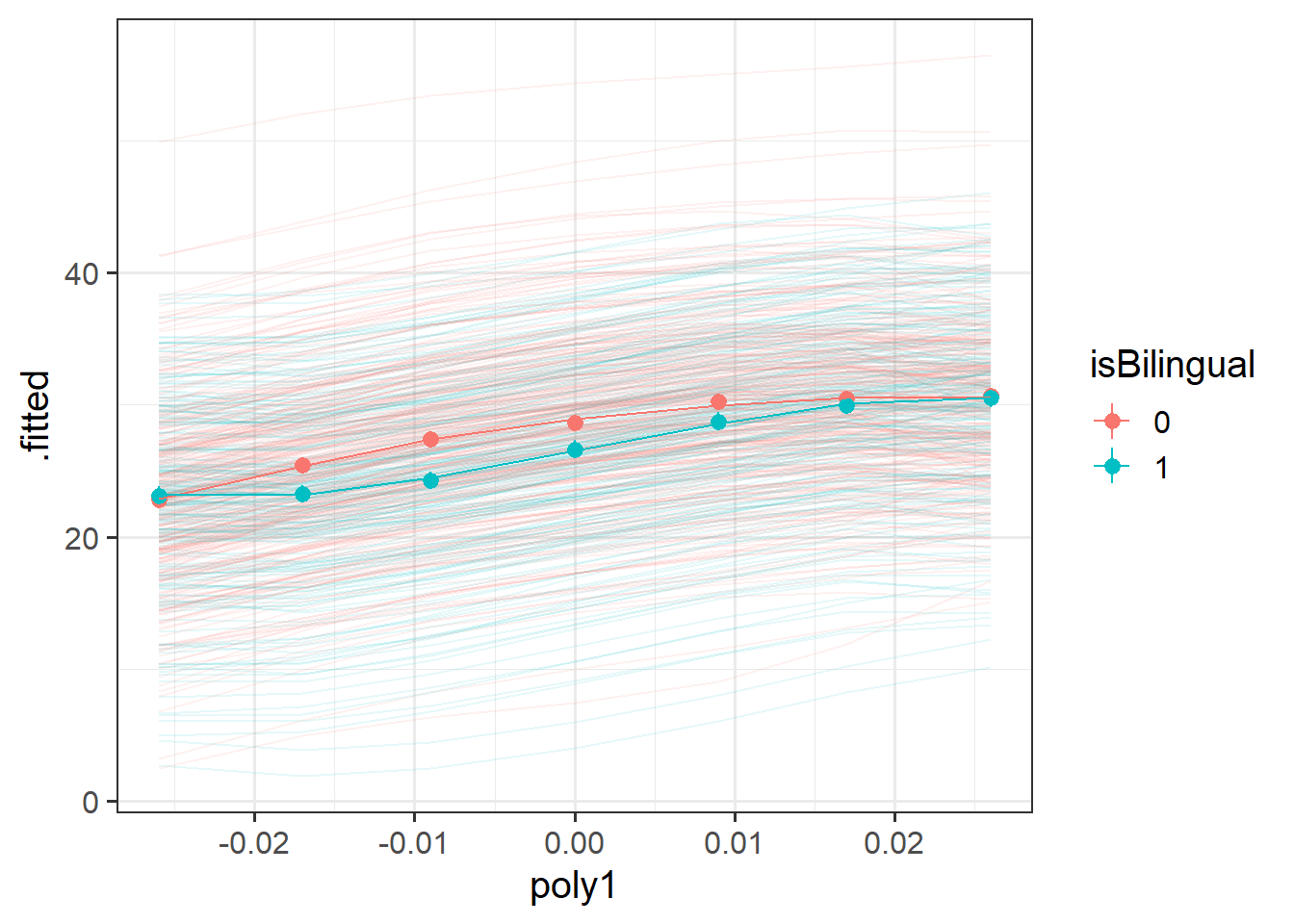
Recreate this plot.

The faint lines represent the model estimated lines for each patient. The points and ranges represent our fixed effect estimates and their uncertainty.

Hints

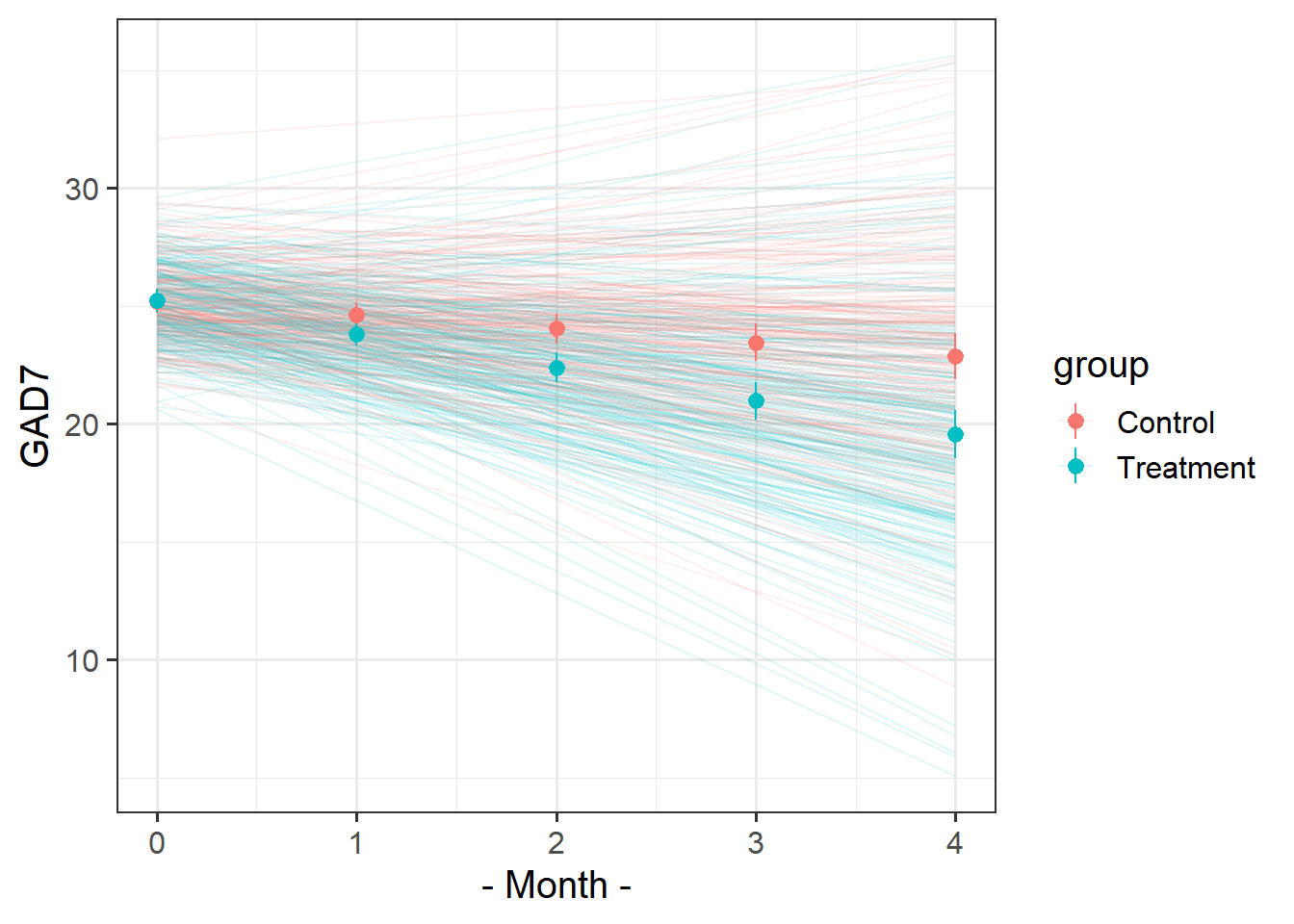
• you can get the patient-specific lines using augment() from the broom.mixed package, and the fixed effects estimates using the effects package.
• remember that the “patient” column doesn’t group observations into unique patients.
• remember you can pull multiple datasets into ggplot:

ggplot(data = dataset1, aes(x=x,y=y)) + 
  geom_point() + # points from dataset1
  geom_line(data = dataset2) # lines from dataset2

• see more in Chapter 2 #visualising-models

Solution 10. The effects package will give us the fixed effect estimates:

library(effects)
library(broom.mixed)
effplot <- effect("visit*group",mod1) |>
  as.data.frame()

We want to get the fitted values for each patient. We can get fitted values using augment(). But the patient variable doesn’t capture the unique patients, it just captures their numbers (which aren’t unique to each therapist).
So we can create a new column called upatient which pastes together the therapists initials and the patient numbers

augment(mod1) |> 
  mutate(
    upatient = paste0(therapist,patient),
    .after = patient # place the column next to the patient col
  )

# A tibble: 2,410 × 17
     GAD visit group   therapist patient upatient .fitted .resid  .hat .cooksd
   <dbl> <dbl> <fct>   <fct>     <fct>   <chr>      <dbl>  <dbl> <dbl>   <dbl>
 1    24     0 Control VC        1       VC1         24.2 -0.198 0.454 0.0210 
 2    24     1 Control VC        1       VC1         25.3 -1.28  0.239 0.239  
 3    26     2 Control VC        1       VC1         26.4 -0.360 0.186 0.0128 
 4    29     3 Control VC        1       VC1         27.4  1.56  0.294 0.508  
 5    28     4 Control VC        1       VC1         28.5 -0.522 0.563 0.284  
 6    24     0 Control VC        2       VC2         24.8 -0.843 0.454 0.383  
 7    26     1 Control VC        2       VC2         26.2 -0.171 0.239 0.00426
 8    28     2 Control VC        2       VC2         27.5  0.502 0.186 0.0250 
 9    29     3 Control VC        2       VC2         28.8  0.174 0.294 0.00633
10    30     4 Control VC        2       VC2         30.2 -0.153 0.563 0.0246 
# ℹ 2,400 more rows
# ℹ 7 more variables: .fixed <dbl>, .mu <dbl>, .offset <dbl>, .sqrtXwt <dbl>,
#   .sqrtrwt <dbl>, .weights <dbl>, .wtres <dbl>

Solution 11.

library(effects)
library(broom.mixed)
effplot <- effect("visit*group",mod1) |>
  as.data.frame()

augment(mod1) |> 
  mutate(
    upatient = paste0(therapist,patient),
    .after = patient # place the column next to the patient col
  ) |>
  ggplot(aes(x=visit,y=.fitted,col=group))+
  stat_summary(geom="line", aes(group=upatient,col=group), alpha=.1)+
  geom_pointrange(data=effplot, aes(y=fit,ymin=lower,ymax=upper,col=group))+
  labs(x="- Month -",y="GAD7")

Jokes

Data: lmm_laughs.csv

These data are simulated to imitate an experiment that investigates the effect of visual non-verbal communication (i.e. gestures, facial expressions) on joke appreciation. 90 Participants took part in the experiment, in which they each rated how funny they found a set of 30 jokes. For each participant, the order of these 30 jokes was randomly set for each run of the experiment. For each participant, the set of jokes was randomly split into two halves, with the first half being presented in audio-only, and the second half being presented in audio and video. This meant that each participant saw 15 jokes with video and 15 without, and each joke would be presented in with video roughly half of the times it was seen.

The researchers want to investigate whether the delivery (audio/audiovideo) of jokes is associated with differences in humour-ratings.

Data are available at https://uoepsy.github.io/data/lmm_laughs.csv

Table 2: Data Dictionary: lmm_laughs.csv

variable	description
ppt	Participant Identification Number
joke_label	Joke presented
joke_id	Joke Identification Number
delivery	Experimental manipulation: whether joke was presented in audio-only ('audio') or in audiovideo ('video')
rating	Humour rating chosen on a slider from 0 to 100

Question 7

Prior to getting hold of any data, we should be able to write out the structure of our ideal “maximal” model given that we have a description of the design of the study.

Can you do so?

Hints

Don’t know where to start? Try following the steps in Chapter 8 #maximal-model.

Solution 12. We want to estimate the effect of delivery on humour rating of jokes:
rating ~ delivery

We have 30 observations for each participant. Participants are just another sampling unit here.
rating ~ delivery + (1 | ppt)

We have 90 observations for each joke. We’re not interested in specific jokes here, so we can think of these as a random set of experimental items that we might choose differently next time we conduct an experiment to assess delivery~rating: rating ~ delivery + (1 | ppt) + (1 | joke_id)

Participants each see 15 jokes without video, and 15 with. The delivery variable is “within” participant. Some participants might respond differently when there is video (vs without) whereas some might not rate jokes any differently. The effect of delivery on rating might be vary by participant:
rating ~ delivery + (1 + delivery | ppt) + (1 | joke_id)

Each joke is presented both with and without the video. Some jokes might really benefit from gestures and facial expressions, whereas some might not. The effect of delivery on rating might be vary by joke:
rating ~ delivery + (1 + delivery | ppt) + (1 + delivery | joke_id)

Question 8

Read in and clean the data (if necessary).

Create some plots showing:

1. the average rating for audio vs audio+video for each joke
2. the average rating for audio vs audio+video for each participant

Hints

• you could use facet_wrap, or even stat_summary!
  
• you might want to use joke_id, rather than joke_label (the labels are very long!)

Solution 13. Here is one using facet_wrap:

ggplot(laughs, aes(x = delivery, y = rating)) +
  geom_boxplot()+
  facet_wrap(~joke_id)

And one using stat_summary() for participants:

ggplot(laughs, aes(x = delivery, y = rating)) +
  stat_summary(geom="pointrange", aes(group = ppt),
               position = position_dodge(width=.2))+
  stat_summary(geom="line", aes(group = ppt),
               position = position_dodge(width=.2))

Question 9

Fit an appropriate model to address the research aims of the study.

Hints

This should be the one you came up with a couple of questions ago!

Solution 14.

mod <- lmer(rating ~ delivery + 
              (1 + delivery | joke_id) +
              (1 + delivery| ppt), data = laughs)

Question 10

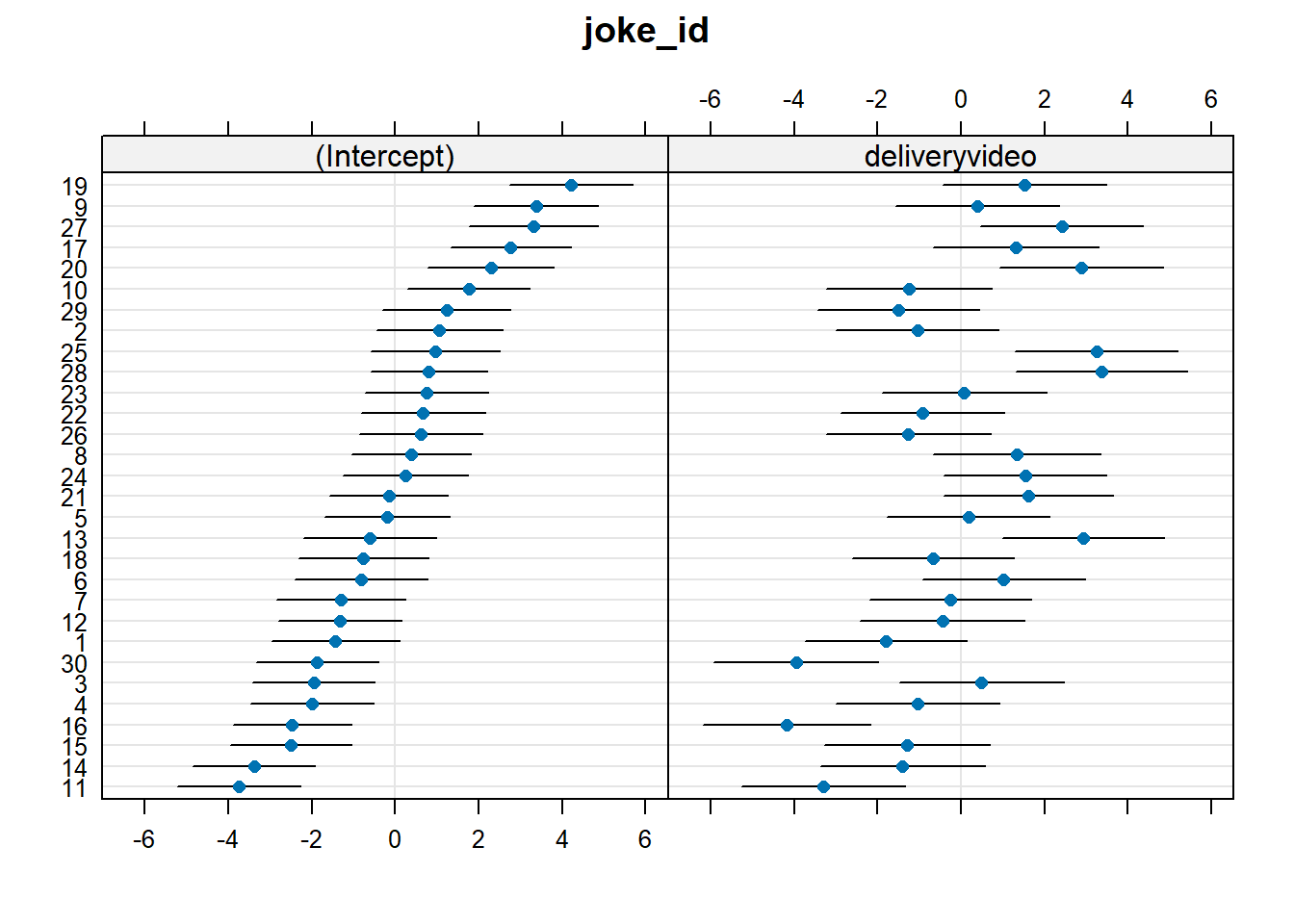
Which joke is funniest when presented just in audio? For which joke does the video make the most difference to ratings?

Hints

These can all be answered by examining the random effects with ranef().
See Chapter 2 #making-model-predictions.

If you’re using joke_id, can you find out the actual joke that these correspond to?

Solution 15.

dotplot.ranef.mer(ranef(mod))$joke_id

Joke 19 is the funniest apparently! (not sure I agree)

Lots of ways to find what the joke actually is. Here is one way:

laughs |> count(joke_id, joke_label) |>
  filter(joke_id==19) |>
  pull(joke_label)

[1] "How many psychiatrists does it take to change a lightbulb? Just one, but the lightbulb really has to want to change."

And from the plot above, Joke 28 has the most benefit of video. We can quickly check this with something like:

ranef(mod)$joke_id |>
  filter(deliveryvideo == max(deliveryvideo))

   (Intercept) deliveryvideo
28   0.8070427      3.373723

The joke itself is a bit weird.. maybe the video really helped!

laughs |> count(joke_id, joke_label) |>
  filter(joke_id==28) |>
  pull(joke_label)

[1] "An Alsatian went to a telegram office, took out a blank form and wrote:\n\"Woof. Woof. Woof. Woof. Woof. Woof. Woof. Woof. Woof.\"\nThe clerk examined the paper and politely told the dog: \"There are only nine\nwords here. You could send another \x91Woof' for the same price.\"\n\"But,\" the dog replied, \"that would make no sense at all.\""

Question 11

Do jokes that are rated funnier when presented in audio-only tend to also benefit more from the addition of video?

Hints

Think careful about this question. The random effects show us that jokes vary in their intercepts (ratings in audio-only) and in their effects of delivery (the random slopes). We want to know if these are related..

Solution 16.

VarCorr(mod)

 Groups   Name          Std.Dev. Corr  
 ppt      (Intercept)   3.5095         
          deliveryvideo 1.7828   -0.002
 joke_id  (Intercept)   2.1479         
          deliveryvideo 2.2420   0.390 
 Residual               5.8336         

It’s the correlation here that tell us - jokes rated higher in the audio-only tend to have a bigger effect of the video.

We can see this in a plot if we like. Here every dot is a joke, and the x-axis shows whether it is above or below the average rating for audio-only (the intercept). The y-axis shows whether it is above or below the average effect of video.

plot(ranef(mod)$joke)

Question 12

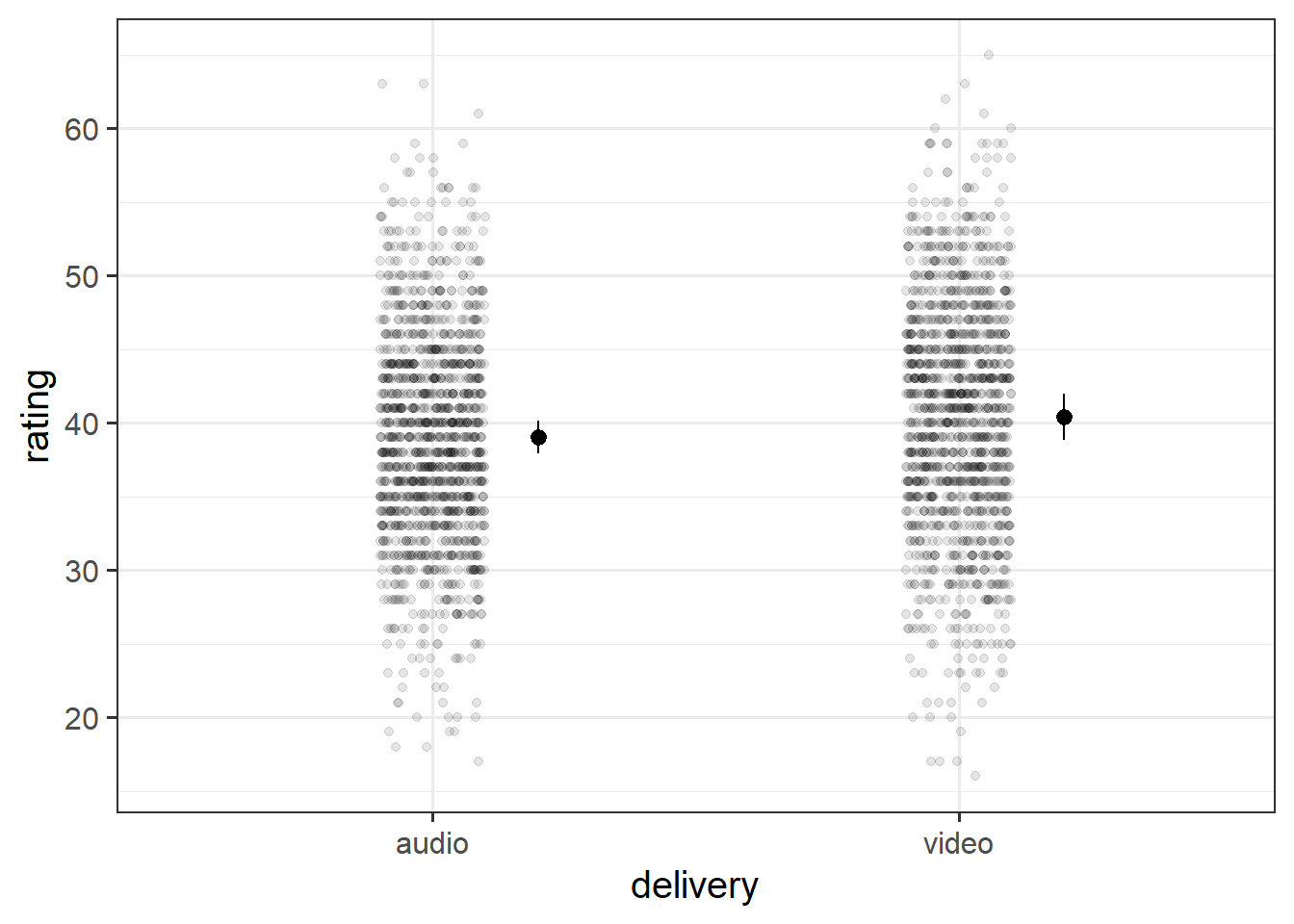
Create a plot of the estimated effect of video on humour-ratings. Try to plot not only the fixed effects, but the raw data too.

Hints

See e.g. Chapter 2 #visualising-models

Solution 17.

library(effects)

plotdatf <- effect("delivery",mod) |>
  as.data.frame()

ggplot(data = laughs, aes(x = delivery)) +
  geom_jitter(aes(y = rating), width = .1, height = 0, alpha = .1) +
  geom_pointrange(data = plotdatf,
                  aes(y = fit, ymin = lower, ymax = upper),
                  position=position_nudge(x=.2))

Optional Extra: Vocab Development

Data: pvt_bilingual.csv

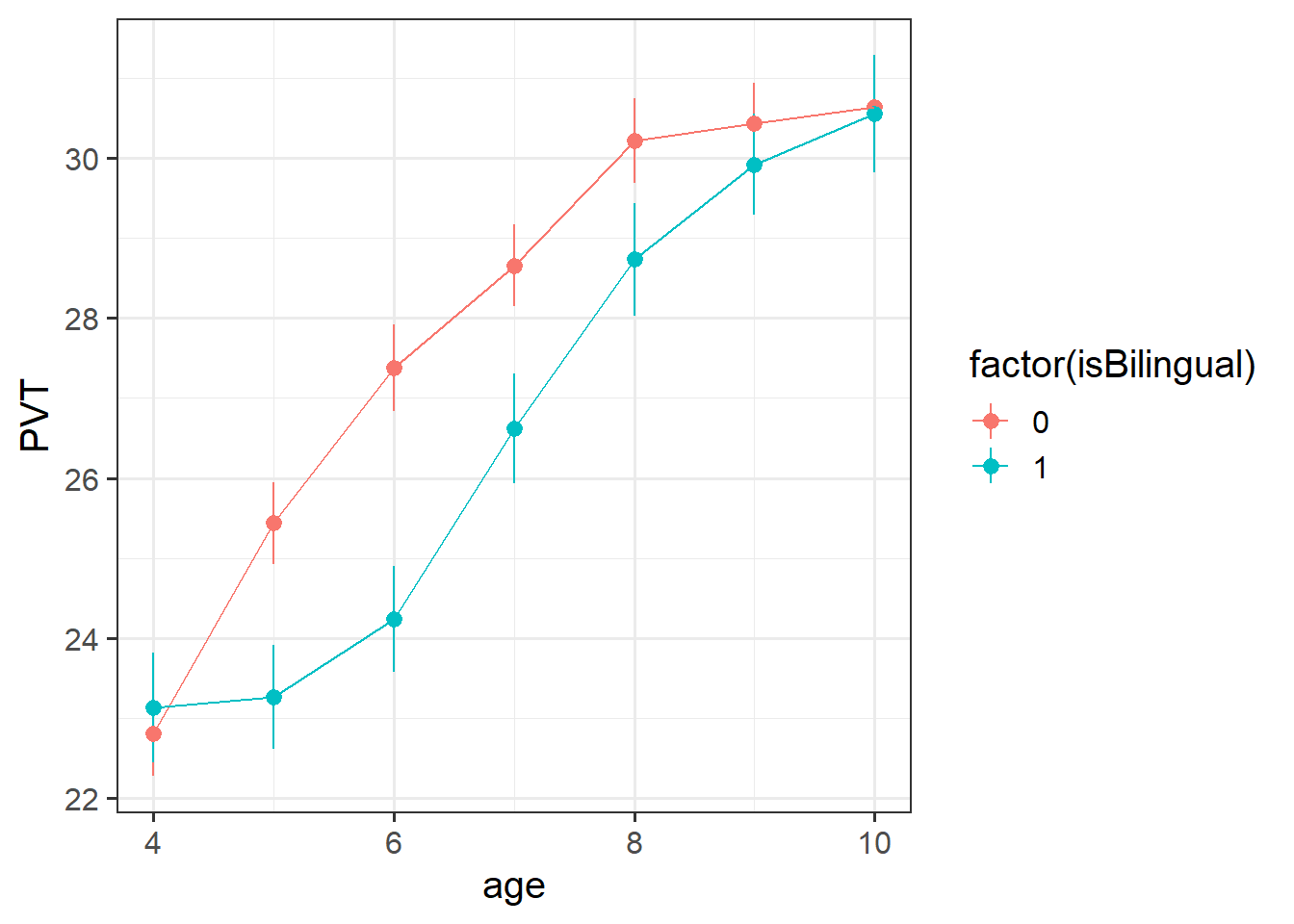
494 children from 30 schools were included in the study. Children were assessed on a yearly basis for 7 years throughout primary school on a measure of vocabulary administered in English, the Picture Vocab Test (PVT). 301 were monolingual English speakers, and 193 were bilingual (english + another language).

Previous research conducted on monolingual children has suggested that that scores on the PVT increase steadily up until the age of approximately 7 or 8 at which point they begin to plateau. The aim of the present study is to investigate differences in the development of vocabulary between monolingual and bilingual children.

The data are available at https://uoepsy.github.io/data/pvt_bilingual.csv.

Table 3: Data Dictionary: pvt_bilingual.csv

variable	description
child	Child's name
school	School Identifier
isBilingual	Binary variable indicating whether the child is monolingual (0) or bilingual (1)
age	Age (years)
PVT	Score on the Picture Vocab Test (PVT). Scores range 0 to 60

Question 13 - Less Guided

Conduct an analysis to estimate the differences in trajectories of vocabulary development between monolingual and bilingual children over the course of primary school.

If you can, try writing up your results!

Hints

1. always plot your data!
2. read the study background: “increase steadily … before beginning to plateau” describes a curve!
   
3. plotting the data can give an initial sense of the possible need for higher order polynomials.
   
4. multiple observations for each child. multiple children in each school..

Solution 18. Let’s read in the data:

pvt <- read_csv("https://uoepsy.github.io/data/pvt_bilingual.csv")
head(pvt)

# A tibble: 6 × 5
  child   school   isBilingual   age   PVT
  <chr>   <chr>          <dbl> <dbl> <dbl>
1 Gabriel School 1           0     4    20
2 Gabriel School 1           0     5    21
3 Gabriel School 1           0     6    22
4 Gabriel School 1           0     7    24
5 Gabriel School 1           0     8    38
6 Gabriel School 1           0     9    39

First, we’re going to want isBilingual to be a factor, because the 1s and 0s are categories, not numbers.

pvt <- pvt |> mutate(isBilingual = factor(isBilingual))

We have 30 distinct schools:

n_distinct(pvt$school)

[1] 30

And 418 distinct children. Is that right?

n_distinct(pvt$child)

[1] 418

Given that the pvt$child variable is just the first name of the child, it’s entirely likely that there will be, for instance more than one “Martin”.

This says that there are 487!

pvt |> count(school, child) |> nrow()

[1] 487

But wait… we could still have issues. What if there were 2 “Martin”s at the same school??

pvt |> 
  # count the school-children groups
  count(school, child) |> 
  # arrange the output so that the highest 
  # values of the 'n' column are at the top
  arrange(desc(n))

# A tibble: 487 × 3
   school    child        n
   <chr>     <chr>    <int>
 1 School 14 James       14
 2 School 14 Michelle    14
 3 School 15 Michael     14
 4 School 21 Daniel      14
 5 School 3  Jackson     14
 6 School 5  Raven       14
 7 School 9  Kaamil      14
 8 School 1  Allyssa      7
 9 School 1  Armon        7
10 School 1  Dakota       7
# ℹ 477 more rows

Aha! There are 7 cases where schools have two children of the same name. Remember that each child was measured at 7 timepoints. We shouldn’t have people with 14!

If we actually look at the data, we’ll see that it is very neatly organised, with each child’s data together. This means that we could feasibly make an educated guess that, e.g., the “Jackson” from “School 3” in rows 155-161 is different from the “Jackson” from “School 3” at rows 190-196.

Because of the ordering of our data, we can do something like this:

pvt <- 
  pvt |>
  # group by the school and child
  group_by(school, child) |>
  mutate(
    # make a new variable which counts from 1 to 
    # the number of rows for each school-child
    n_obs = 1:n()
  ) |>
  # ungroup the data
  ungroup() |>
  mutate(
    # change it so that if the n_obs is >7, the 
    # child becomes "[name] 2", to indicate they're the second
    # child with that name
    child = ifelse(n_obs>7, paste0(child," 2"), child)
  )

Now we have 494!

pvt |> count(school, child) |> nrow()

[1] 494

And nobody has anything other than 7 observations!

pvt |> count(school, child) |>
  filter(n != 7)

# A tibble: 0 × 3
# ℹ 3 variables: school <chr>, child <chr>, n <int>

Phew!

Solution 19. How many bilingual children?

pvt |> group_by(isBilingual) |>
  summarise(nchild = n_distinct(child))

# A tibble: 2 × 2
  isBilingual nchild
  <fct>        <int>
1 0              272
2 1              178

How many children (mono/bilingual) in each school?

pvt |> group_by(school, isBilingual) |>
  summarise(nchild = n_distinct(child)) |>
  ggplot(aes(y=school,x=nchild,fill=isBilingual))+
  geom_col()

Okay, let’s just fit an intercept-only model:

pvt_null <- lmer(PVT ~ 1 + 
                   (1 | school) +
                   (1 | school:child), data = pvt)
summary(pvt_null)

Linear mixed model fit by REML ['lmerMod']
Formula: PVT ~ 1 + (1 | school) + (1 | school:child)
   Data: pvt

REML criterion at convergence: 23844.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.7768 -0.5984  0.0068  0.5744  4.1806 

Random effects:
 Groups       Name        Variance Std.Dev.
 school:child (Intercept) 33.48    5.786   
 school       (Intercept) 19.76    4.445   
 Residual                 43.59    6.602   
Number of obs: 3458, groups:  school:child, 494; school, 30

Fixed effects:
            Estimate Std. Error t value
(Intercept)  27.5263     0.8667   31.76

As we can see from summary(pvt_null), the random intercept variances are 33.48 for child-level, 19.76 for school-level, and the residual variance is 43.59.

So child level differences account for \(\frac{33.48}{33.48 + 19.76 + 43.59} = 0.35\) of the variance in PVT scores, and child & school differences together account for \(\frac{33.48 + 19.76}{33.48 + 19.76 + 43.59} = 0.55\) of the variance.

Here’s an initial plot too:

ggplot(pvt, aes(x=age,y=PVT,col=factor(isBilingual)))+
  stat_summary(geom="pointrange")+
  stat_summary(geom="line")

Solution 20. I feel like either raw or orthogonal polynomials would be fine here - there’s nothing explicit from the study background about stuff “at baseline”. There’s the stuff about the plateau at 7 or 8, but we can get that from the model plots. Orthogonal will allow us to compare the trajectories overall (their linear trend, the ‘curviness’ and ‘wiggliness’).

An additional benefit of orthogonal polynomials is that we are less likely to get singular fits when we include polynomial terms in our random effects. Remember, raw polynomials are correlated, so often the by-participant variances in raw poly terms are highly correlated.

I’ve gone for 3 degrees of polynomials here because the plot above shows a bit of an S-shape for the bilinguals.

pvt <- pvt |> mutate(
  poly1 = poly(age, 3)[,1],
  poly2 = poly(age, 3)[,2],
  poly3 = poly(age, 3)[,3],
)

These models do not converge.
I’ve tried to preserve the by-child random effects of time, because while I think Schools probably do vary, all the schools teach the same curriculum, whereas there’s a lot of varied things that can influence a child’s vocabulary, both in and out of school.

mod1 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + (poly1 + poly2 + poly3)*isBilingual | school) + 
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod2 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual * (poly1 + poly2) + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod3 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual * poly1 + poly2 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod4 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual + poly1 + poly2 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod5 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
# relative to the variance in time slopes, there's v little by-school variance in bilingual differences in vocab

mod6 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly2 +  poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
# looks like curvature doesn't vary between schools much as linear and wiggliness 

this one converges!

mod7 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

Solution 21. Let’s plot the predictions:

library(broom.mixed)
augment(mod7) |> 
  mutate(
    poly1 = round(poly1, 3) # because of rounding errors that make plot weird
  ) |>
  ggplot(aes(x=poly1,col=isBilingual))+
  stat_summary(geom="pointrange",aes(y=PVT))+
  stat_summary(geom="line", aes(y=.fitted))

Remember that these are just the average of all model fitted values. Because everyone has complete data here, we can use these to visualise our model estimates without worrying about them being distorted by missing data. Just like the fixed effects themselves though, all this is focussed on “the average child from the average school”. The plot hides a lot of the variability that we have actually modelled. For instance, consider how our view changes when we add in the individual lines for each child (below). The lines for the average child are just the same as above, but we can now see just how much children vary.

augment(mod7) |> 
  mutate(
    poly1 = round(poly1, 3) 
  ) |>
  ggplot(aes(x=poly1,col=isBilingual))+
  # make a line for each "school-child" group: 
  geom_line(aes(group=interaction(school,child),
                y=.fitted),alpha=.1)+
  stat_summary(geom="pointrange",aes(y=PVT))+
  stat_summary(geom="line", aes(y=.fitted))

Let’s refit our model with lmerTest:

mod7 <- lmerTest::lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

summary(mod7)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + (1 + poly1 +  
    poly3 | school) + (1 + (poly1 + poly2 + poly3) | school:child)
   Data: pvt

REML criterion at convergence: 23076.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.4457 -0.5499 -0.0004  0.5261  4.4194 

Random effects:
 Groups       Name        Variance Std.Dev. Corr             
 school:child (Intercept)   34.86   5.904                    
              poly1       1842.60  42.926    0.01            
              poly2       3945.86  62.816   -0.08  0.23      
              poly3        684.38  26.161    0.19  0.61  0.87
 school       (Intercept)   19.97   4.468                    
              poly1        928.32  30.468   -0.40            
              poly3        335.59  18.319   -0.52 -0.12      
 Residual                   31.93   5.651                    
Number of obs: 3458, groups:  school:child, 494; school, 30

Fixed effects:
                    Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)          27.9464     0.8987   31.1128  31.098  < 2e-16 ***
poly1               157.0421     9.5750   39.5964  16.401  < 2e-16 ***
poly2               -48.9606     8.0944  517.6541  -6.049 2.80e-09 ***
poly3                -1.2793     8.1739   61.5750  -0.157  0.87614    
isBilingual1         -1.2113     0.5863  465.7927  -2.066  0.03939 *  
poly1:isBilingual1   16.6104    12.3121  501.9133   1.349  0.17791    
poly2:isBilingual1   56.2609    12.9500  517.6541   4.344 1.68e-05 ***
poly3:isBilingual1  -34.3286    11.8629 1217.8366  -2.894  0.00387 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) poly1  poly2  poly3  isBln1 pl1:B1 pl2:B1
poly1       -0.215                                          
poly2       -0.013  0.026                                   
poly3       -0.184 -0.003  0.072                            
isBilingul1 -0.250 -0.001  0.020 -0.020                     
ply1:sBlng1  0.000 -0.500 -0.020 -0.022 -0.001              
ply2:sBlng1  0.008 -0.016 -0.625 -0.045 -0.033  0.033       
ply3:sBlng1 -0.009 -0.020 -0.050 -0.566  0.034  0.038  0.079

Solution 22. The exact value of the coefficients here don’t really give us anything meaningful. Note that in our plots above, the x-axis is “poly1”, which is some weirdly re-scaled version of “age”, so these coefficients represent things like the estimated change in PVT when “moving up 1 in poly1”. But these units are not remotely useful to us. Even if we wanted to try and scale back to get out something we could interpret in terms of years of age, the whole point of non-linear change is that we can’t just say “PVT increases by \(b\) with every extra year of age”, because we need to consider the higher order polynomial terms.

The long and the short of it is that while the numbers don’t really matter here, the sign (+ or -) and the significance does tell us stuff:

term	est	p	interpretation
(Intercept)	27.95	*	average vocab score at the mean age (for monolingual)
poly1	157.04	*	vocab increases over time (for monolingual children)
poly2	-48.96	*	the increase in vocab becomes more gradual (for monolingual children)
poly3	-1.28		no significant wiggliness to vocab trajectory of the average monolingual child
isBilingual1	-1.21	*	average vocab score at mean age is lower for bilingual vs monolingual children
poly1:isBilingual1	16.61		no significant difference in linear trend of vocab for bilingual vs monolingual
poly2:isBilingual1	56.26	*	curvature for vocab trajectory of bilingual children significantly differs from that of monolinguals
poly3:isBilingual1	-34.33	*	wiggliness for vocab trajectory of bilingual children significantly differs from that of monolinguals

From the random effects, we get even more information! All this stuff is kind of “added context” for the conclusions (which will come from our fixed effects).

VarCorr(mod7)

 Groups       Name        Std.Dev. Corr                
 school:child (Intercept)  5.9043                      
              poly1       42.9256   0.005              
              poly2       62.8161  -0.078  0.227       
              poly3       26.1606   0.191  0.609  0.871
 school       (Intercept)  4.4683                      
              poly1       30.4683  -0.403              
              poly3       18.3190  -0.524 -0.116       
 Residual                  5.6510                      

School’s vary in the average child vocab score at mean age with an SD of 4.5. Schools with higher vocab scores at the mean age tend to have lower linear increase. Within schools, children vary in the vocab scores at mean age with an SD of 5.9. Children with steeper linear increase in vocab tend to have less curvature.

Optional Extra: Test Enhanced Learning

Data: Test-enhanced learning

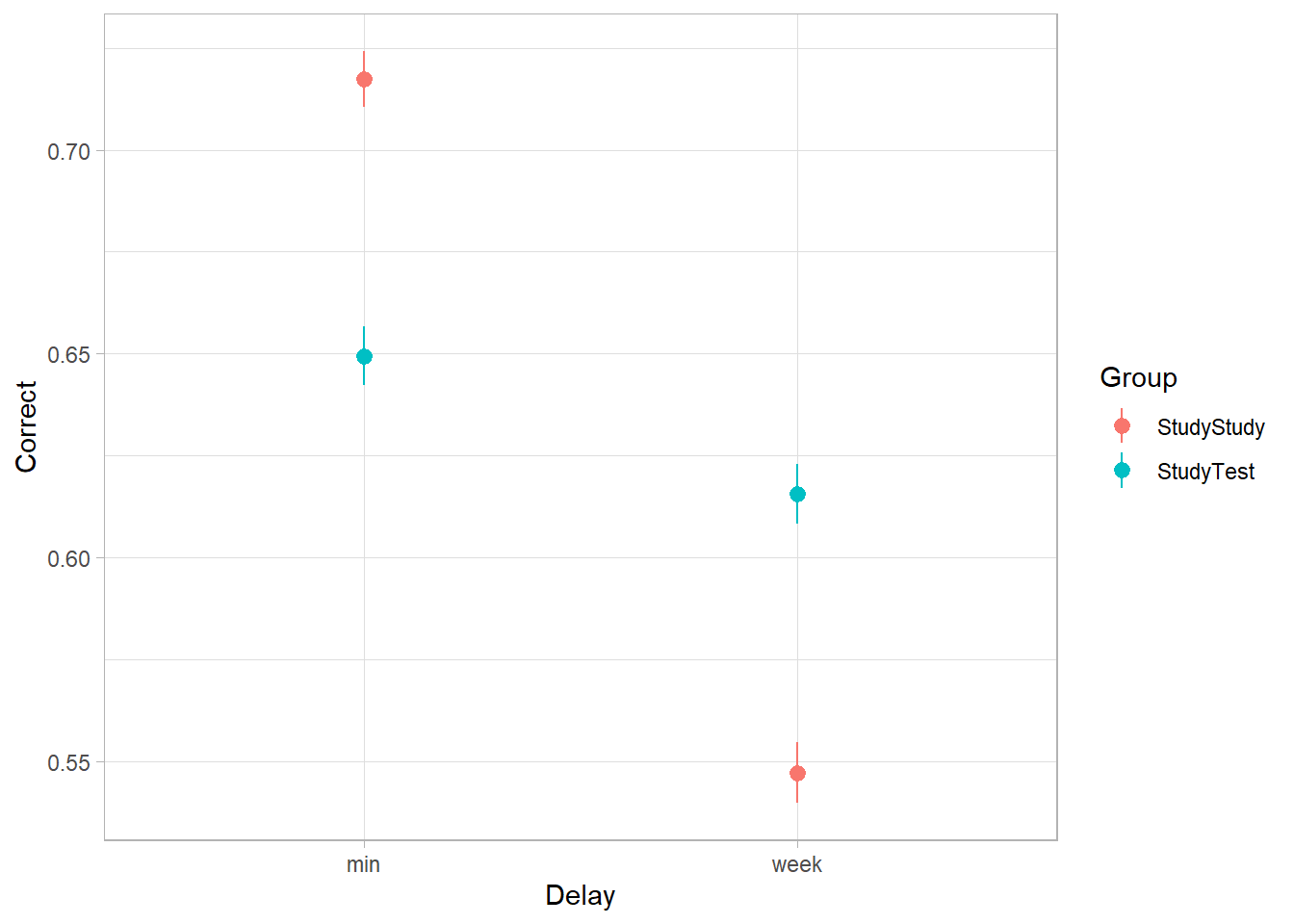
An experiment was run to conceptually replicate “test-enhanced learning” (Roediger & Karpicke, 2006): two groups of 25 participants were presented with material to learn. One group studied the material twice (StudyStudy), the other group studied the material once then did a test (StudyTest). Recall was tested immediately (one minute) after the learning session and one week later. The recall tests were composed of 175 items identified by a keyword (Test_word).

The critical (replication) prediction is that the StudyStudy group recall more items on the immediate test, but the StudyTest group will retain the material better and thus perform better on the 1-week follow-up test.

The following code loads the data into your R environment by creating a variable called tel:

load(url("https://uoepsy.github.io/data/testenhancedlearning.RData"))

Table 4: Data Dictionary: testenhancedlearning.Rdata

variable	description
Subject_ID	Unique Participant Identifier
Group	Group denoting whether the participant studied the material twice (StudyStudy), or studied it once then did a test (StudyTest)
Delay	Time of recall test ('min' = Immediate, 'week' = One week later)
Test_word	Word being recalled (175 different test words)
Correct	Whether or not the word was correctly recalled
Rtime	Time to recall word (milliseconds)

Question 14

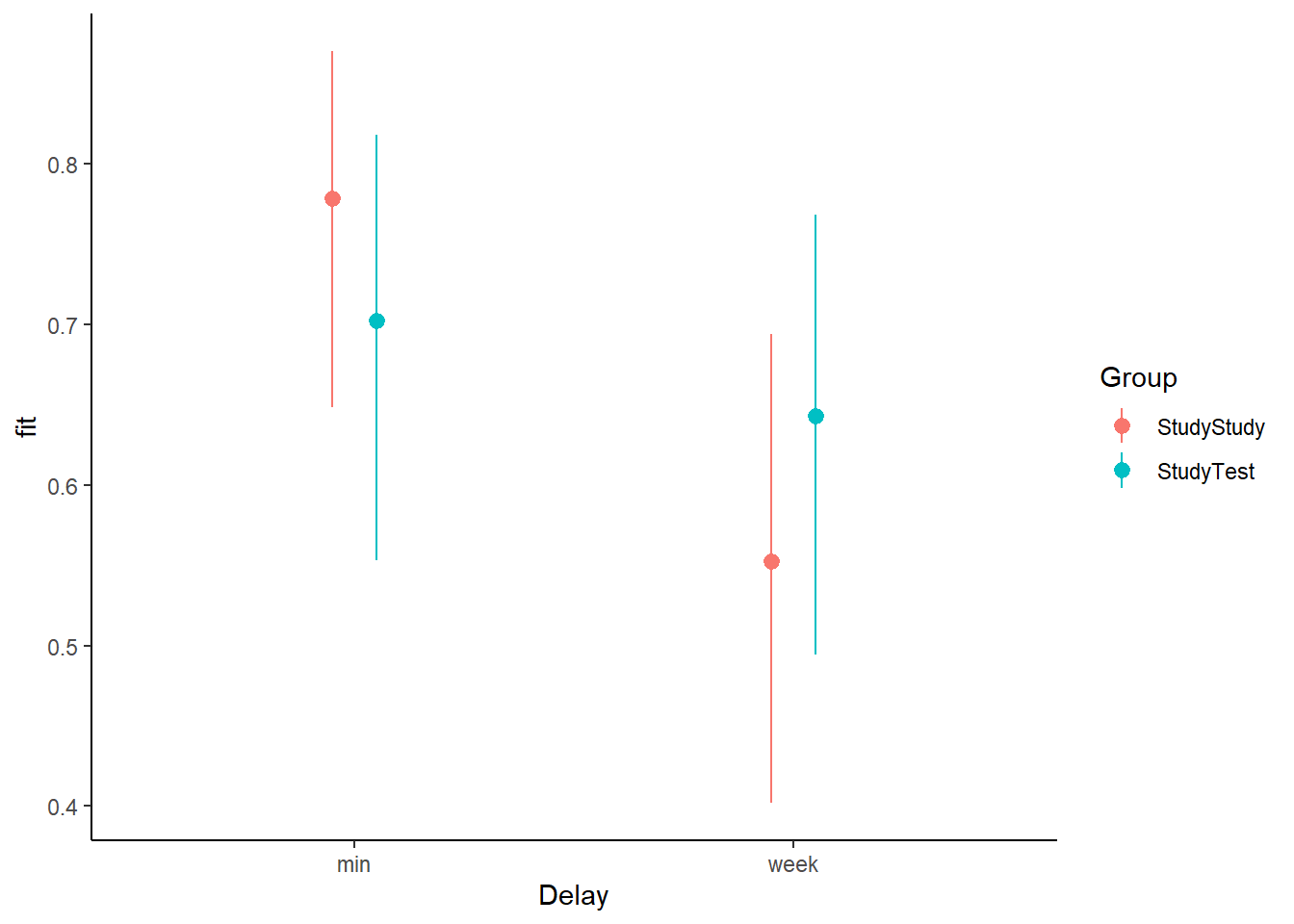
Load and plot the data. Does it look like the effect was replicated?

The critical (replication) prediction is that the StudyStudy group recall more items on the immediate test, but the StudyTest group will retain the material better and thus perform better on the 1-week follow-up test.

Hints

We can actually look at this from a couple of different angles. The most obvious option is to take successful learning as “correctly recalling” an item. This means we take the Correct variable as our outcome.

Note we also have Rtime - the “time-to-recall” of an item. This could also work as an outcome, but note that it also includes the time it took participants to provide an incorrect response too. If this was your own project, you may well want to provide analyses of Correct, and then also of the time-taken, but on the subset of correctly recalled items.

Solution 23.

load(url("https://uoepsy.github.io/data/testenhancedlearning.RData"))

ggplot(tel, aes(Delay, Correct, col=Group)) + 
  stat_summary(fun.data=mean_se, geom="pointrange")+
  theme_light()

That looks like test-enhanced learning to me!

Question 15

Test the critical hypothesis using a mixed-effects model.

Fit the maximal random effect structure supported by the experimental design. Simplify the random effect structure until you reach a model that converges.

Note: Some of the models you attempt here might take time to fit. This is normal, and you can cancel the estimation at any time by pressing the escape key.
I suggest that you write your initial model, set it running, and then look at the first solution to see if it converged for me. You can assume that if it didn’t work for me, it also won’t work for you. I’ve shown the random effects for each model, in case it helps in deciding your next step.

Hints

What we’re aiming to do here is to follow Barr et al.’s advice of defining our maximal model and then removing only the terms to allow a non-singular fit.

• What kind of model will you use? What is our outcome? is it binary, or continuous?
• We can expect variability across subjects (some people are better at learning than others) and across items (some of the recall items are harder than others). How should this be represented in the random effects?

Solution 24. We have a crossed random effect structure here. Each participant was tested on every word, and each word was seen by every participant.

Subjects were tested at both the min and week, so Delay|Subject_ID can be included (some people might retain the items better than others).
Likewise the words were seen at both min and week, and some words might be more easy to retain than others (Delay|Test_word).

The participants are in either one group or another, so we can’t have Group|Subject_ID. However, the words were seen by people in both groups, so we can have Group|Test_word.

This one took my computer about 6 minutes.

mod1 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 + Delay * Group | Test_word),
             family=binomial, data=tel)

Warning message:
In checkConv(attr(opt, “derivs”), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0184773 (tol = 0.002, component 1)

VarCorr(mod1)

 Groups     Name                     Std.Dev. Corr                
 Test_word  (Intercept)              1.057208                     
            Delayweek                0.059611 -0.341              
            GroupStudyTest           0.067625 -0.835  0.802       
            Delayweek:GroupStudyTest 0.115439 -0.783  0.852  0.996
 Subject_ID (Intercept)              1.594518                     
            Delayweek                0.210026 -0.623              

Solution 25. Lets remove the interaction in the by-word random effects.
This one took about 5 minutes…

mod2 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 + Delay + Group | Test_word),
             family=binomial, data=tel)

Warning message:
In checkConv(attr(opt, “derivs”), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.00887744 (tol = 0.002, component 1)

VarCorr(mod2)

 Groups     Name           Std.Dev. Corr         
 Test_word  (Intercept)    1.076941              
            Delayweek      0.074697 -0.801       
            GroupStudyTest 0.109342 -0.928  0.966
 Subject_ID (Intercept)    1.589794              
            Delayweek      0.210633 -0.601       

Solution 26. We still have a singular fit here. Thinking about the study, if we are going to remove one of the by-testword random effects (Delay or Group), which one do we consider to be more theoretically justified? Is the effect of Delay likely to vary by test-words? More so than the effect of group is likely to vary by test-words?
Quite possibly - it’s reasonable to think that some words will be more easily retained over a week than others, but I can’t come up with a reason to think why StudyTest vs StudyStudy would have a different effect for some words than others.

Let’s remove the by-testword random effect of group.

mod3 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 + Delay | Test_word),
             family=binomial, data=tel)

This one converges! But we still have a correlation of -1.
Why did we not get a warning message?

VarCorr(mod3)

 Groups     Name        Std.Dev. Corr  
 Test_word  (Intercept) 1.027514       
            Delayweek   0.055424 -1.000
 Subject_ID (Intercept) 1.598967       
            Delayweek   0.208732 -0.599

The isSingular() function allows us to check for when a model is close to singularity (i.e. on the boundary of the feasible parameter space):

isSingular(mod3)

[1] FALSE

This suggests that we’re fine! However, note that this function has a tolerance, which is by default set to 1e-4, or 0.0001. Change this to 1e-3, and it indicates a problem.

isSingular(mod3, tol=1e-3)

[1] TRUE

So we’re kind of in a grey area that suggests we are close to overfitting here, so it might be worth continuing to simplify.

Solution 27.

mod4 <- glmer(Correct ~ Delay*Group +
             (1 + Delay | Subject_ID) +
             (1 | Test_word),
             family=binomial, data=tel)

Even when we raise the tolerance here, we’re still fine:

isSingular(mod4, tol=1e-3)

[1] FALSE

And here’s our random effects:

VarCorr(mod4)

 Groups     Name        Std.Dev. Corr  
 Test_word  (Intercept) 0.99805        
 Subject_ID (Intercept) 1.58653        
            Delayweek   0.19670  -0.521

Solution 28. In the process of getting to our final model, we’ve just fitted quite a few models that didn’t converge. We definitely don’t want to do anything with these models (i.e. we shouldn’t report them or use them in model comparisons etc).

However, it can sometimes be useful to just check how estimates of fixed effects and their standard errors differ across these models. More often than not, this simply provides us with reassurance that the removal of random effects hasn’t actually had too much of an impact on anything we’re going to conduct inferences on.

For instance, in all these models, the fixed effects estimates are all pretty similar, suggesting that they’ve all found similar estimates of these parameters which have been largely invariant to our refinement of the random effects.

term	mod1	mod2	mod3	mod4
(Intercept)	1.275 (0.332)	1.283 (0.331)	1.267 (0.332)	1.257 (0.329)
Delayweek	-1.065 (0.071)	-1.071 (0.071)	-1.057 (0.07)	-1.047 (0.068)
GroupStudyTest	-0.415 (0.456)	-0.429 (0.454)	-0.401 (0.457)	-0.398 (0.453)
Delayweek:GroupStudyTest	0.781 (0.103)	0.795 (0.102)	0.776 (0.101)	0.776 (0.099)

Question 16

Create a plot of the predicted probabilities and uncertainty for each of the Delay * Group combinations.

Solution 29.

library(effects)
effplot <- effect("Delay:Group", mod4) |>
  as.data.frame()

ggplot(effplot, aes(Delay, fit, color=Group)) + 
  geom_pointrange(aes(ymax=upper, ymin=lower), 
                  position=position_dodge(width = 0.2))+
  theme_classic() # just for a change :)

Question 17

Here are odds ratios for our model:

# cbind combines columns
cbind(
  # the odds ratios:
  OR = exp(fixef(mod4)), 
  # the CIs:
  exp(confint(mod4, method="Wald", parm="beta_"))
)

                                OR     2.5 %    97.5 %
(Intercept)              3.5155077 1.8444914 6.7003803
Delayweek                0.3510452 0.3075298 0.4007181
GroupStudyTest           0.6715269 0.2761216 1.6331515
Delayweek:GroupStudyTest 2.1734992 1.7894502 2.6399723

What should we do with this information? How should we apply test-enhanced learning to learning R and statistics?

Solution 30. We’ll get the benefits of test-enhanced learning if we try these exercises before looking at any of the solutions that are visible! If we don’t test ourselves, we’re more likely to forget it in the long run.

Footnotes

1. if it does, head back to where we learned about interactions in the single level regressions lm(). It’s just the same here.