Hypothesis testing & Confidence intervals

1. Interpret a confidence interval as the plausible values of a parameter that would not be rejected in a two-sided hypothesis test.

2. Determine the decision for a two-sided hypothesis test from an appropriately constructed confidence interval.

3. Be able to explain the difference between a significant result and an important result.

Hypothesis testing

Consider the two-sided hypothesis testing case

\[ H_0 : \mu = \mu_0 \\ H_1 : \mu \neq \mu_0 \]

Where the test statistic used in order to test the above claim is:

\[ t = \frac{\bar x - \mu_0}{s / \sqrt{n}} \]

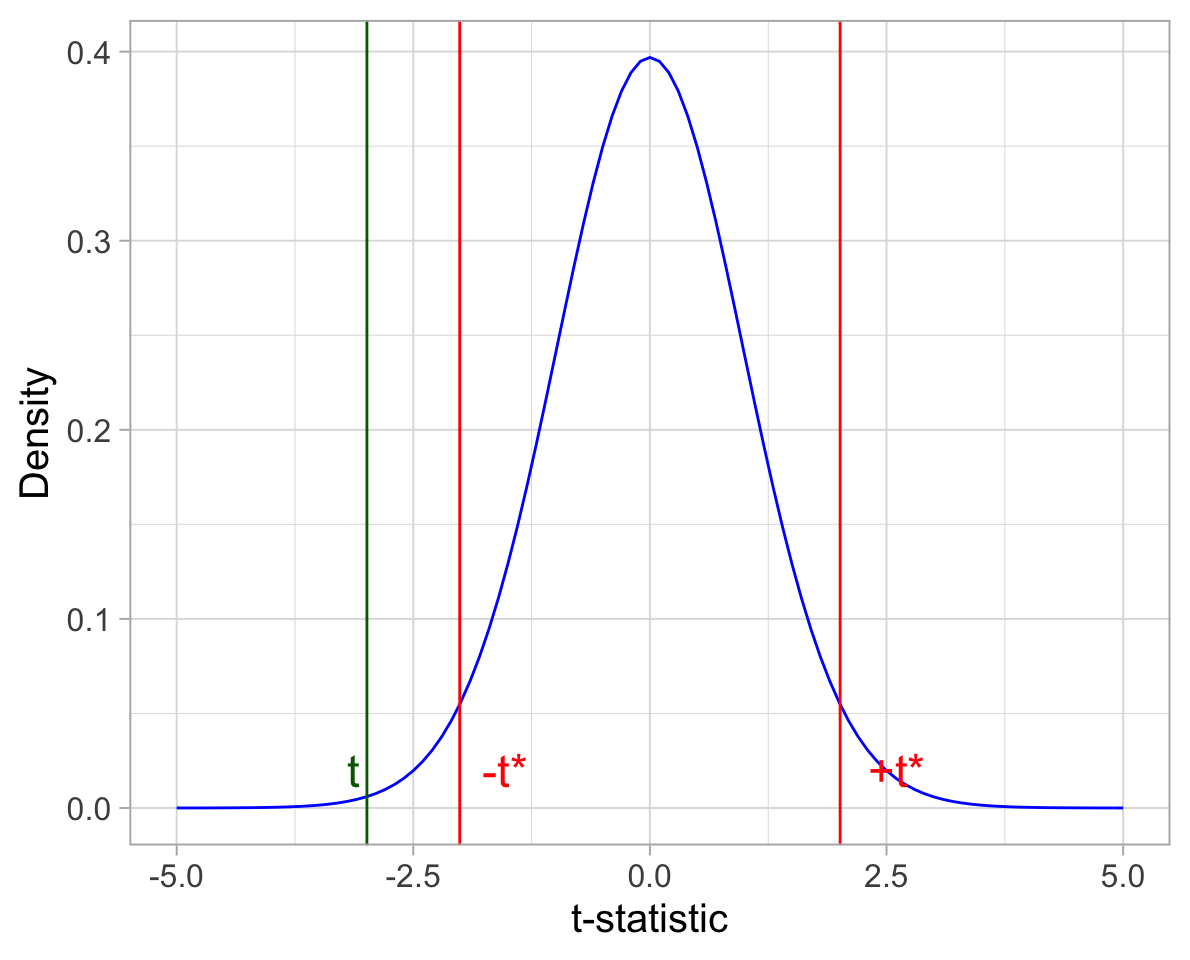
At the 5% significance level:

• we reject the null hypothesis \(H_0\) whenever the observed t-statistic lies beyond the critical values:

\[t \leq -t^* \qquad \text{or} \qquad t \geq +t^*\]

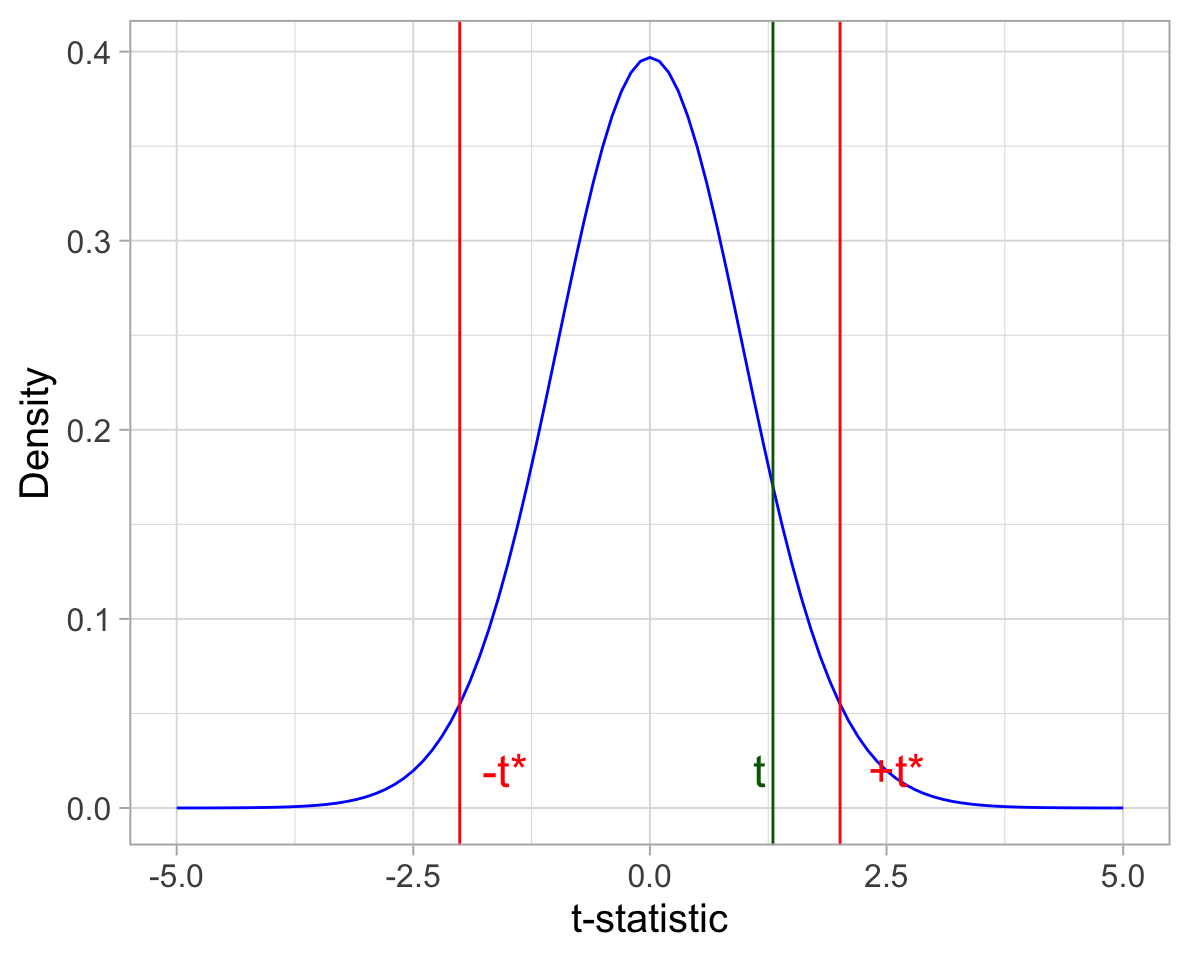
• we do not reject the null hypothesis \(H_0\) whenever the observed t-statistic lies within the critical values:

\[-t^* < t < +t^*\]

Confidence interval

A 95% confidence interval for the population mean is given by

\[\left[ \bar x - t^* \cdot \frac{s}{\sqrt n}, \ \ \bar x + t^* \cdot \frac{s}{\sqrt n} \right]\]

From HT to CI

In the hypothesis test, we do not reject the null hypothesis at the 5% significance level whenever \(\mu_0\) lies inside of the 95% CI:

\[ \textbf{Do not reject } H_0 : \mu = \mu_0 \textbf{ if} \\ \quad \\ -t^* < t < +t^* \\ -t^* < \frac{\bar x - \mu_0}{\frac{s}{\sqrt n}} < +t^* \\ -t^* \cdot \frac{s}{\sqrt n}< \bar x - \mu_0 < +t^* \cdot \frac{s}{\sqrt n} \\ -\bar x -t^* \cdot \frac{s}{\sqrt n}< - \mu_0 < -\bar x +t^* \cdot \frac{s}{\sqrt n} \\ \bar x + t^* \cdot \frac{s}{\sqrt n} > \mu_0 > \bar x - t^* \cdot \frac{s}{\sqrt n} \\ \bar x - t^* \cdot \frac{s}{\sqrt n} < \mu_0 < \bar x + t^* \cdot \frac{s}{\sqrt n} \\ \mu_0 \text{ inside of } \left[ \bar x - t^* \cdot \frac{s}{\sqrt n}, \ \ \bar x + t^* \cdot \frac{s}{\sqrt n} \right] \\ \mu_0 \text{ inside of 95% CI} \]

Exercises: Story Spoilers

In this week’s exercises we will consider ratings for stories with and without spoilers. At the 5% significance level, we will test the following claim:

Research question
Does having a story spoiled lead, on average, to a different rating?

A recent study by Leavitt et al.¹ investigated whether a story spoiler that gives away the ending early diminishes suspense and hurts enjoyment. For twelve different short stories, the study’s authors created a second version in which a spoiler paragraph at the beginning discussed the story and revealed the outcome. Each version of the twelve stories was read by at least 30 people and rated on a 1 to 10 scale to create an overall rating for the story, with higher ratings indicating greater enjoyment of the story. Stories 1 to 4 were ironic twist stories, stories 5 to 8 were mysteries, and stories 9 to 12 were literary stories.

Data Codebook

Download link
https://uoepsy.github.io/data/StorySpoilers.csv

Preview
The top six rows of the data are:

Story	Spoiler	Original
1	4.7	3.8
2	5.1	4.9
3	7.9	7.4
4	7.0	7.1
5	7.1	6.2
6	7.2	6.1

Codebook

• Story: ID for story

• Spoiler: Average (0-10) rating for spoiler version

• Original: Average (0-10) rating for original version

Source

Leavitt, J. and Christenfeld, N., “Story Spoilers Don’t Spoil Stories,” Psychological Science, August 12, 2011.

Question 1

Read the data into R.

Solution

library(tidyverse)
stories <- read_csv("https://uoepsy.github.io/data/StorySpoilers.csv")
head(stories)

## # A tibble: 6 × 3
##   Story Spoiler Original
##   <dbl>   <dbl>    <dbl>
## 1     1     4.7      3.8
## 2     2     5.1      4.9
## 3     3     7.9      7.4
## 4     4     7        7.1
## 5     5     7.1      6.2
## 6     6     7.2      6.1

Question 2

In the lectures you saw how to perform a test on the mean of a single variable.

• How could you measure whether or not having a story spoiled leads to a different rating, on average, by using a single variable?

• What feature do this data have that makes it possible to go from two variables to a single variable?

Solution

The alternative hypothesis is the one directly related to the research claim. Recall the question: “Does having a story spoiled lead, on average, to a different rating?”

The data are an example of paired data. Each row corresponds to a single entity, i.e. a single story. So the two ratings under the Spoiler and Original columns refer to the same story.

The data correspond to measurements of the same entities (the stories) “Before” and “After” something (adding or not a spoiler).

We can go from two variables to a single one by taking the difference, as the two variables refer to the same stories (units).

We compute the column “Diff” as the difference in ratings between original stories and spoiler stories.

• When Diff is less than 0, the original story rating is lower than the spoiler story rating.

  • Diff = Original - Spoiler. If Original - Spoiler < 0, then we have that Original < Spoiler.

• When Diff is larger than 0, the original story rating is higher than the spoiler story rating.

  • Diff = Original - Spoiler. If Original - Spoiler > 0, then we have that Original > Spoiler.

• When Diff is equal to 0, the original story rating is the same as the spoiler story rating.

  • Diff = Original - Spoiler. If Original - Spoiler = 0, then we have that Original = Spoiler.

Question 3

Compute a new variable, called Diff, representing the difference in ratings between the original and spoiler stories.

Solution

stories <- stories %>%
    mutate(Diff = Original - Spoiler)
stories

## # A tibble: 12 × 4
##    Story Spoiler Original   Diff
##    <dbl>   <dbl>    <dbl>  <dbl>
##  1     1     4.7      3.8 -0.9  
##  2     2     5.1      4.9 -0.200
##  3     3     7.9      7.4 -0.5  
##  4     4     7        7.1  0.100
##  5     5     7.1      6.2 -0.900
##  6     6     7.2      6.1 -1.10 
##  7     7     7.1      6.7 -0.400
##  8     8     7.2      7   -0.200
##  9     9     4.8      4.3 -0.5  
## 10    10     5.2      5   -0.200
## 11    11     4.6      4.1 -0.5  
## 12    12     6.7      6.1 -0.600

Question 4

State the null and alternative hypothesis.

Solution

\[ H_0 : \mu_{\text{Diff}} = 0 \\ H_1 : \mu_{\text{Diff}} \neq 0 \]

Question 5

Compute a 95% confidence interval for the difference in ratings.

Solution

n <- nrow(stories)
xbar <- mean(stories$Diff)
s <- sd(stories$Diff)
se <- s / sqrt(n)

tstar <- qt(c(0.025, 0.975), df = n - 1)
tstar

## [1] -2.200985  2.200985

Confidence interval:

ci <- xbar + tstar * se
ci

## [1] -0.7125281 -0.2708052

Since tstar stores two values inside,

tstar

## [1] -2.200985  2.200985

when you do xbar + tstar * se, the first value will be the sample mean (xbar) plus the first value within tstar (that is, -2.200985) times the SE. As you can see, when you do +tstar, if the value within tstar has a minus sign, it’s the same as doing - because +- becomes -. The second value will be the sample mean (xbar) plus the second value within tstar (that is, +2.200985) times the SE.

Question 6

Using the 95% confidence interval, make a decision on whether or not to reject the null hypothesis.

Solution

The confidence interval is [-0.71, -0.27].

The claimed value for the population mean difference in ratings is 0.

As the 95% CI doesn’t include the value 0, at the 5% significance level we reject the null hypothesis that the population mean difference in ratings between original and spoiler stories is 0.

Question 7

Verify whether you would reach to the same conclusion if you perform a hypothesis test via the p-value method.

Solution

mu0 <- 0
tobs <- (xbar - mu0) / se
tobs

## [1] -4.899683

pvalue <- 2 * pt(abs(tobs), df = n - 1, lower.tail = FALSE)
pvalue

## [1] 0.0004718576

As \(p \leq 0.05\), we reject \(H_0\).

Question 8

Write up your results.

Solution

We tested whether spoiling stories leads to, on average, different ratings. At the 5% significance level, the sample results provide very strong evidence against the null hypothesis and in favour of the alternative one that the average difference in rating between original and spoiler stories is not 0; \(t(11) = -4.90, p < .001\), two-sided.

We are 95% confident that original stories have a rating between 0.27 and 0.71 lower, on average, than spoiler stories.

References

---

1. Leavitt, J. and Christenfeld, N., “Story Spoilers Don’t Spoil Stories,” Psychological Science, August 12, 2011.↩︎