3. Assumptions and Diagnostics | Centering

Exercises: Assumptions & Diagnostics

Data: Wellbeing Across Scotland

For these next set of exercises we continue with our recurring study in which researchers want to look at the relationship between time spent outdoors and mental wellbeing, across all of Scotland. Data is collected from 20 of the Local Authority Areas and is accessible at https://uoepsy.github.io/data/LAAwellbeing.csv.

variable description
ppt Participant ID
name Participant Name
laa Local Authority Area
outdoor_time Self report estimated number of hours per week spent outdoors
wellbeing Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being. The scale is scored by summing responses to each item, with items answered on a 1 to 5 Likert scale. The minimum scale score is 14 and the maximum is 70.
density LAA Population Density (people per square km)
Question 1

The code below will read in the data and fit the model with by-LAA random intercepts and slopes of outdoor time.

library(tidyverse)
library(lme4)
scotmw <- read_csv("https://uoepsy.github.io/data/LAAwellbeing.csv")
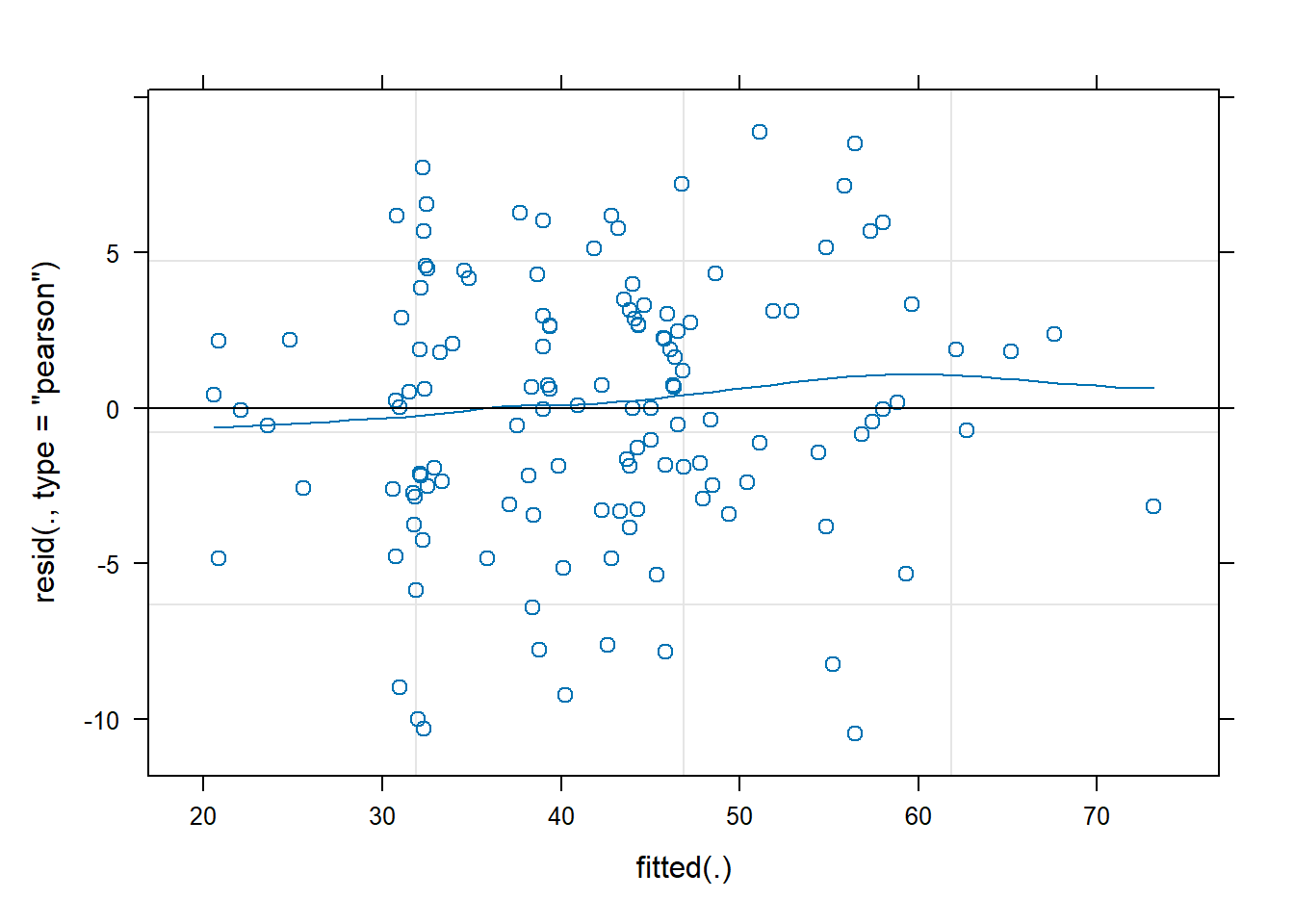
rs_model <- lmer(wellbeing ~ 1 + outdoor_time + (1 + outdoor_time | laa), data = scotmw)
  1. Plot the residuals vs fitted values, and assess the extend to which the assumption holds that the residuals are zero mean.
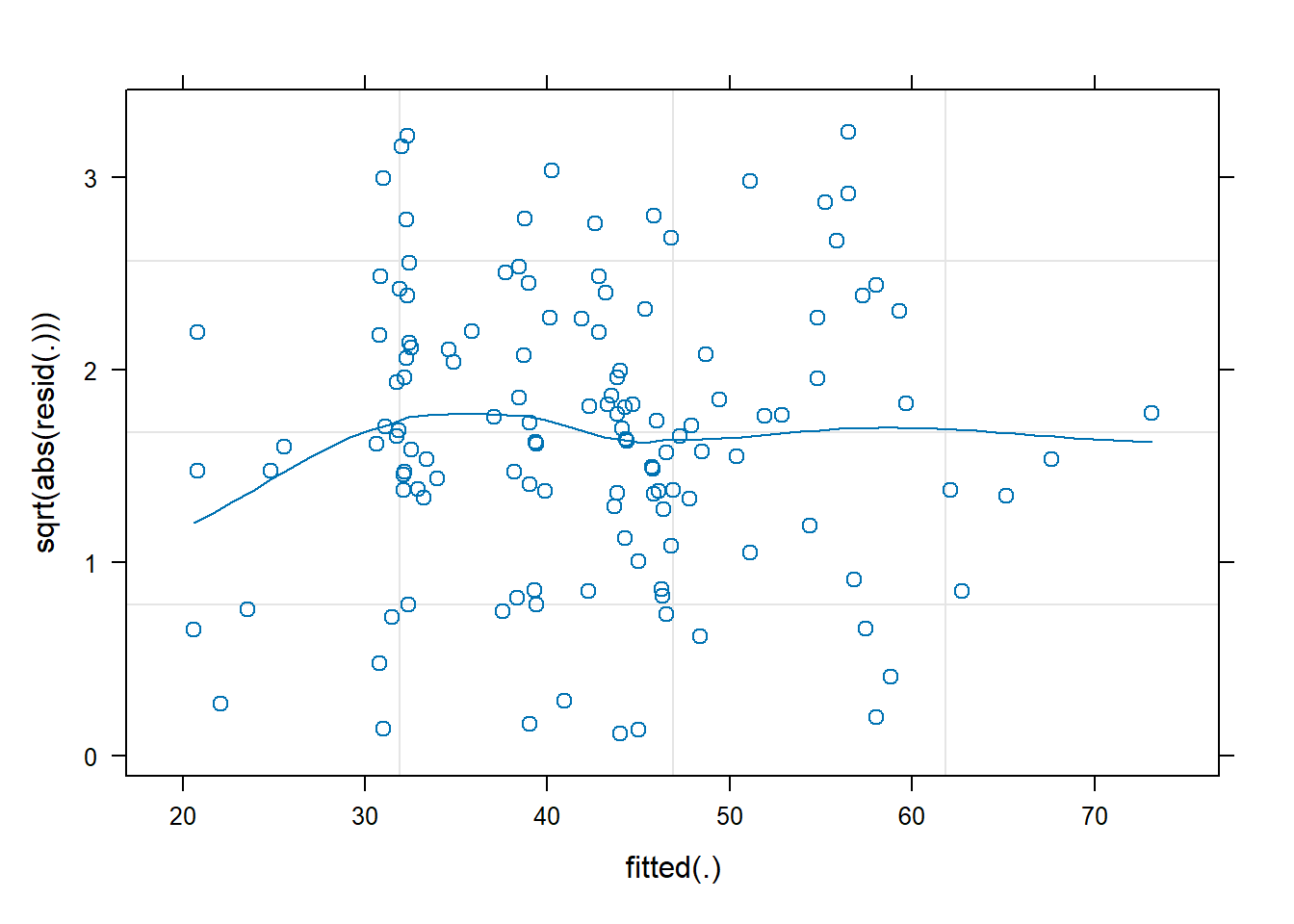
  2. Construct a scale-location plot. This is where the square-root of the absolute value of the standardised residuals is plotted against the fitted values, and allows you to more easily assess the assumption of constant variance.
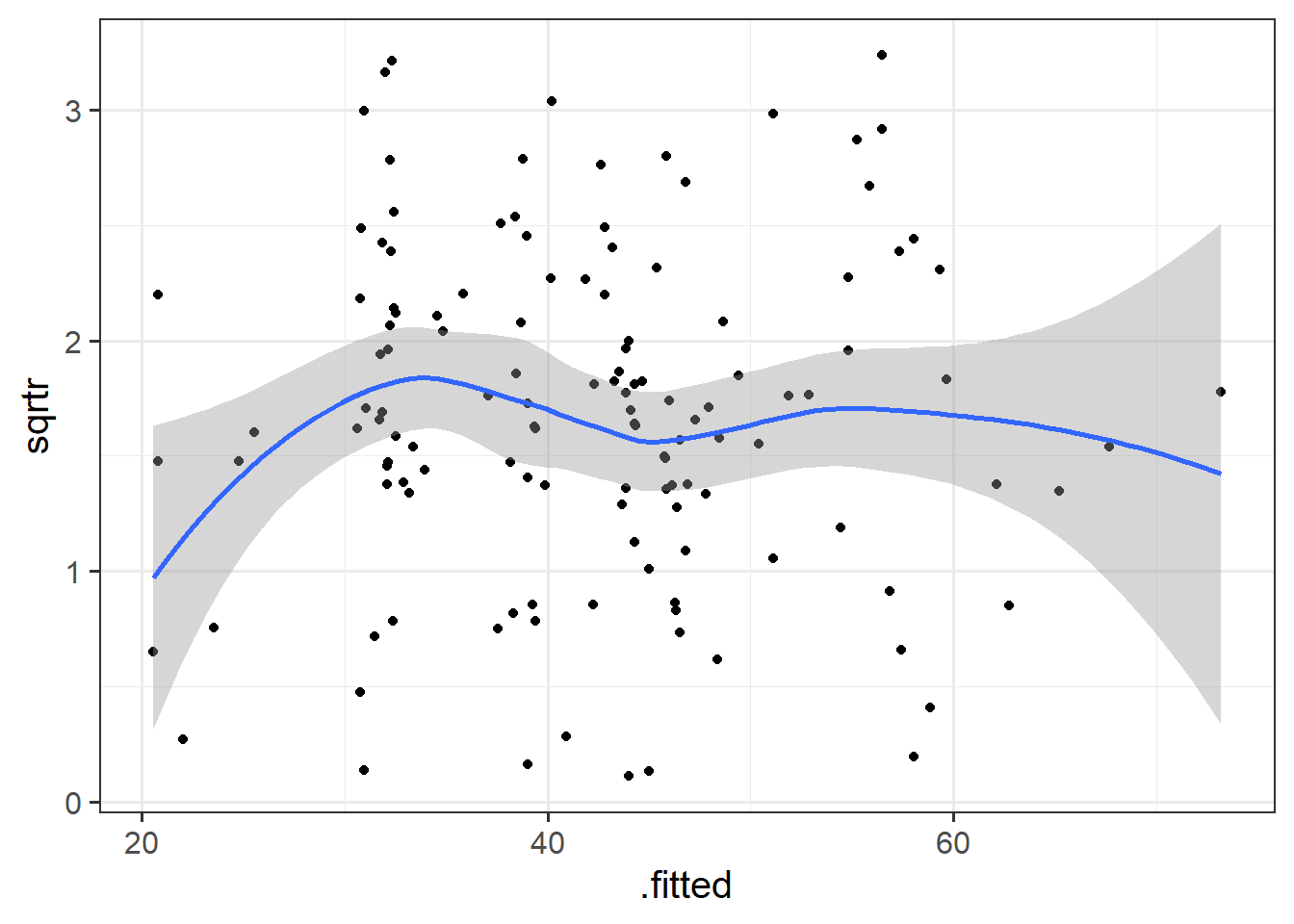
  • Optional: can you create the same plot using ggplot, starting with the augment() function from the broom.mixed package?

plot(model) will give you this plot, but you might want to play with the type = c(......) argument to get the smoothing line

Question 2

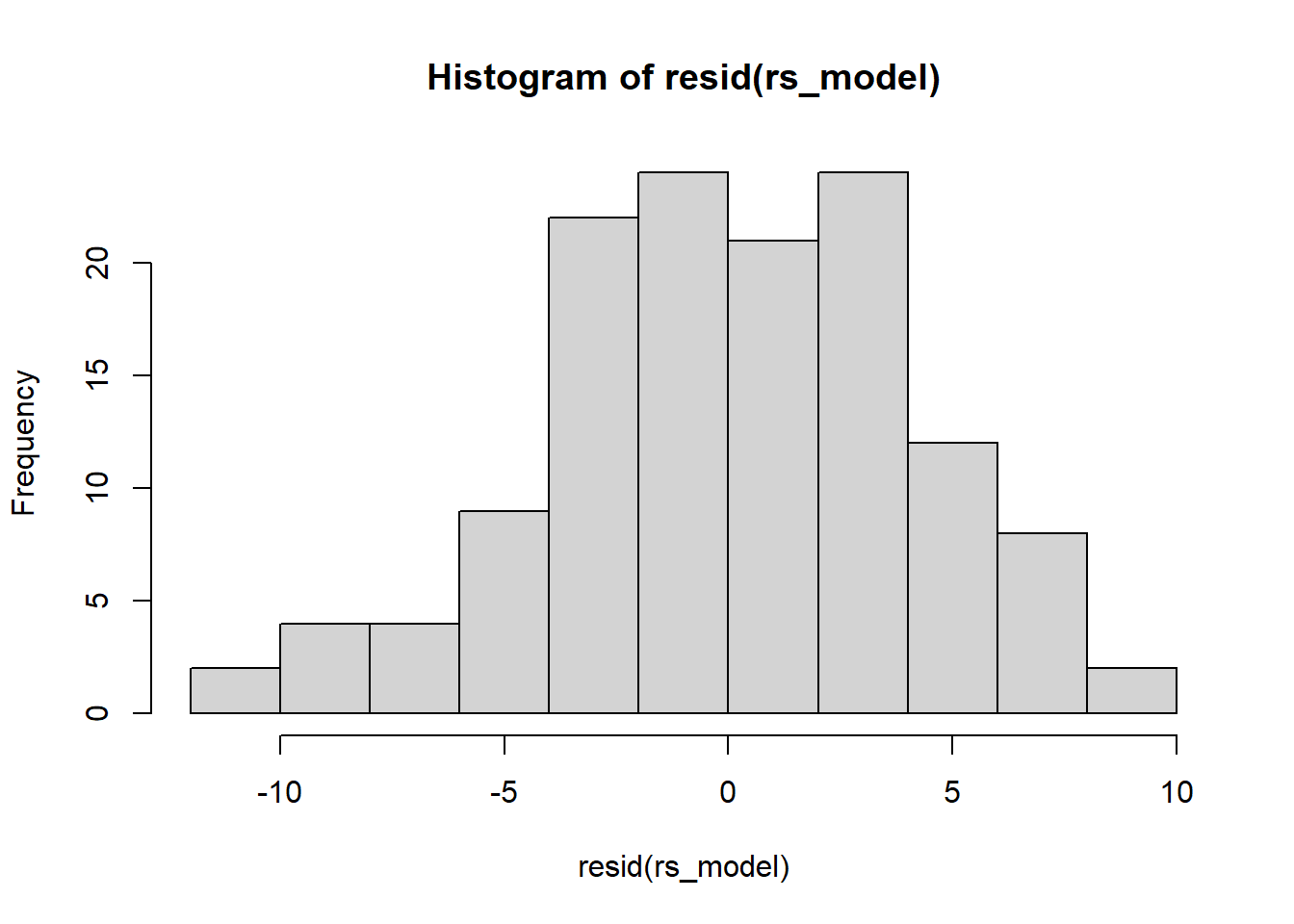
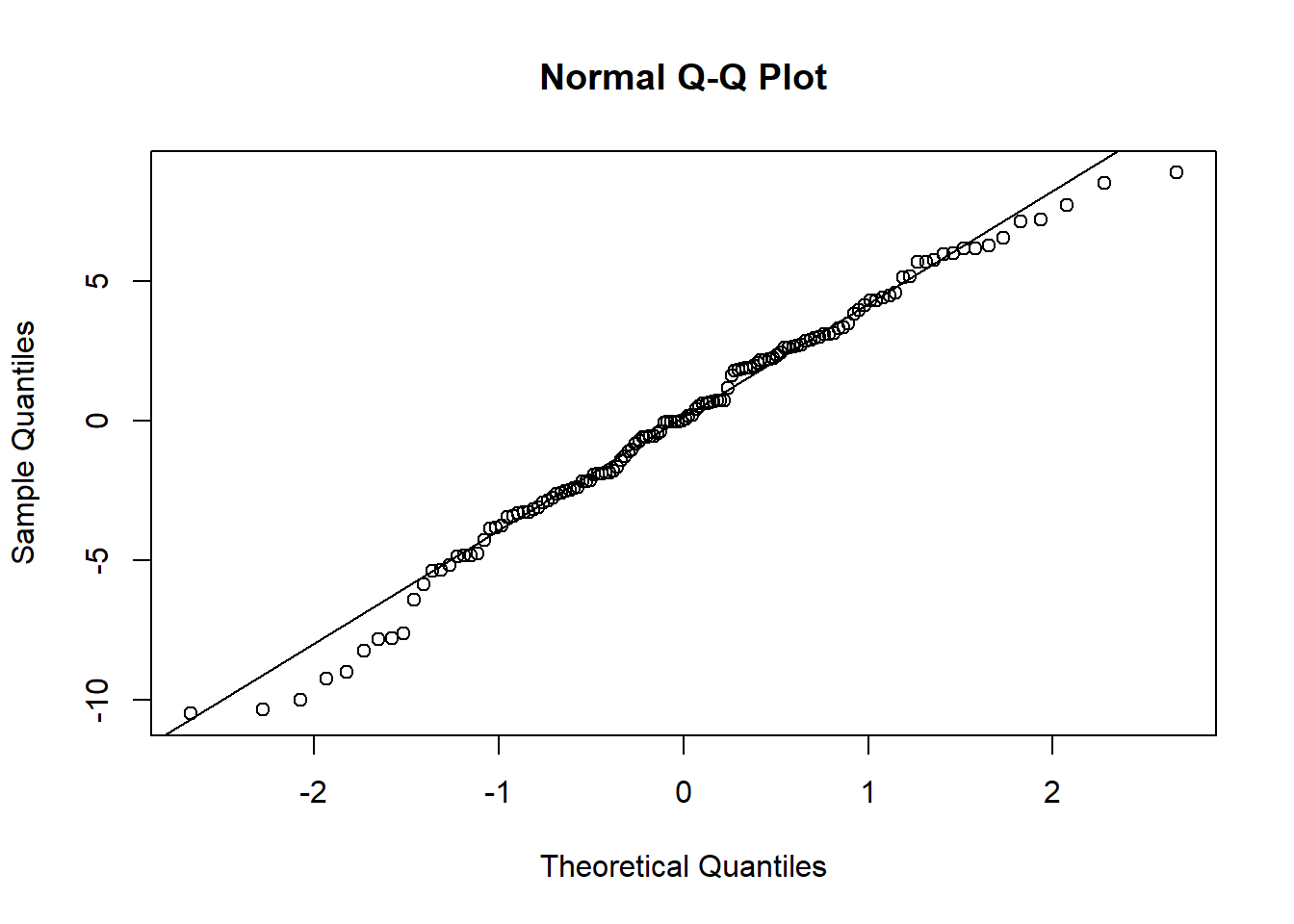
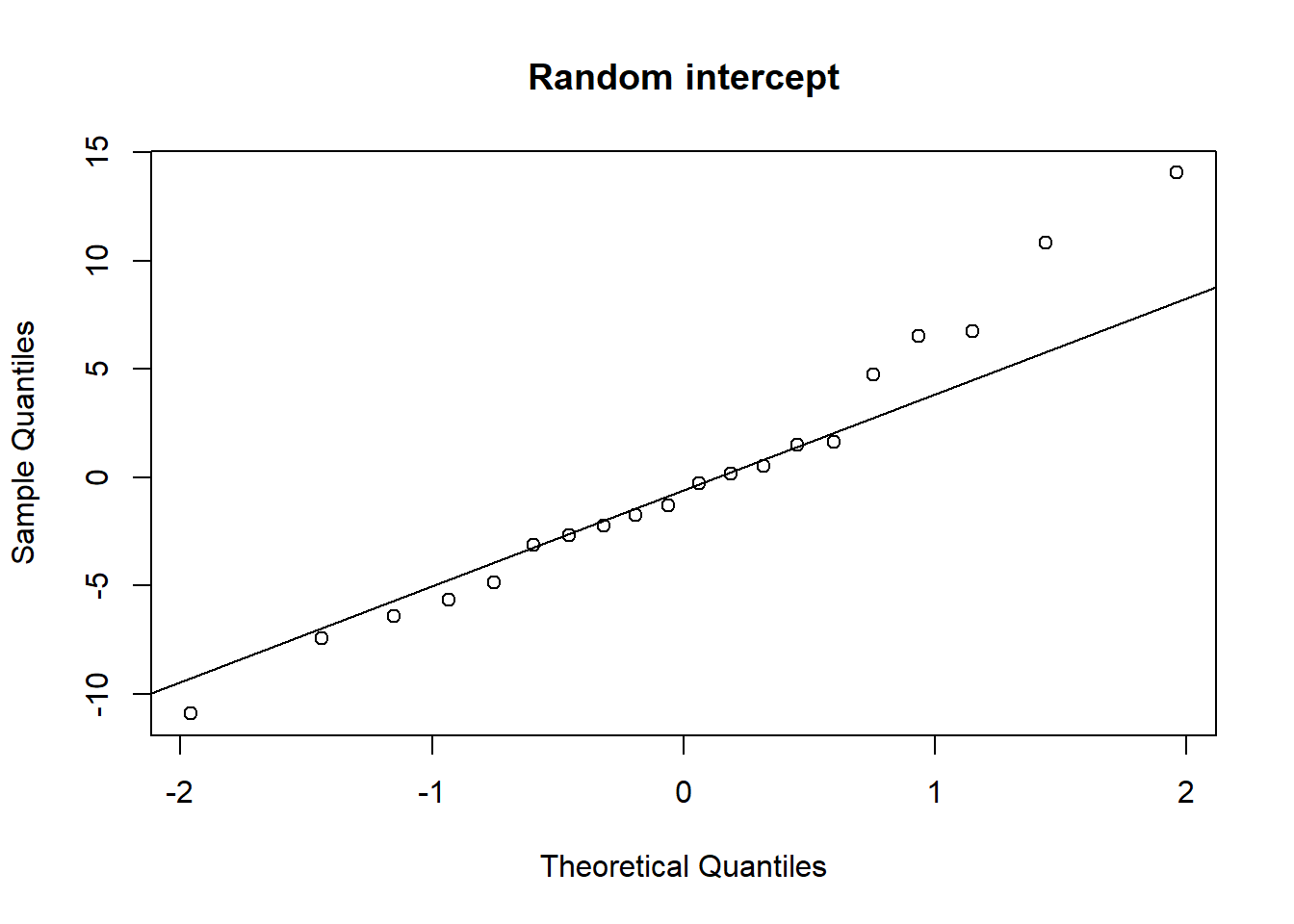
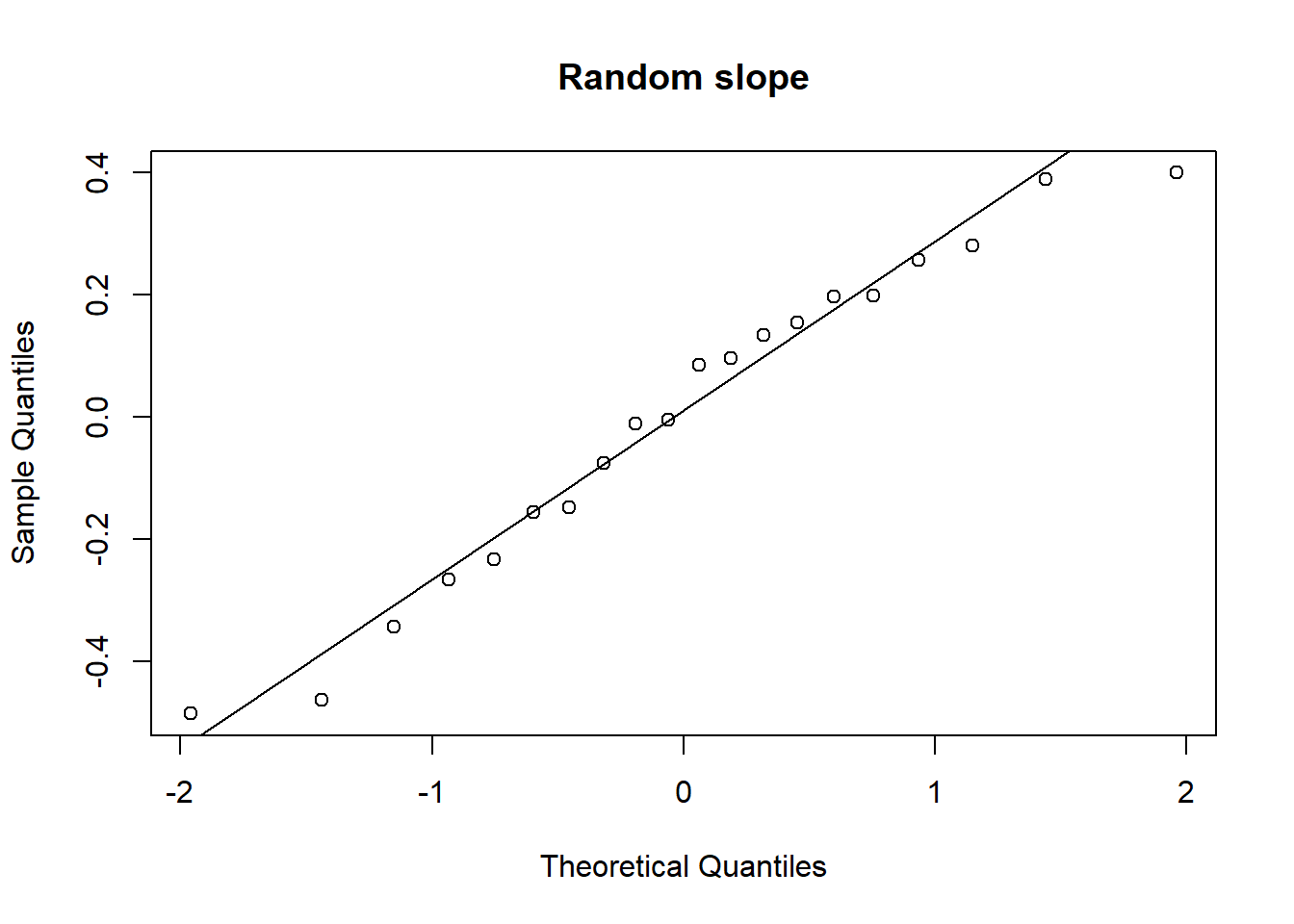
Examine the normality of both the level 1 and level 2 residuals.

  • Use hist() if you like, or qqnorm(residuals) followed by qqline(residuals)
  • Extracting the level 2 residuals (the random effects) can be difficult. ranef(model) will get you some of the way.

Question 3
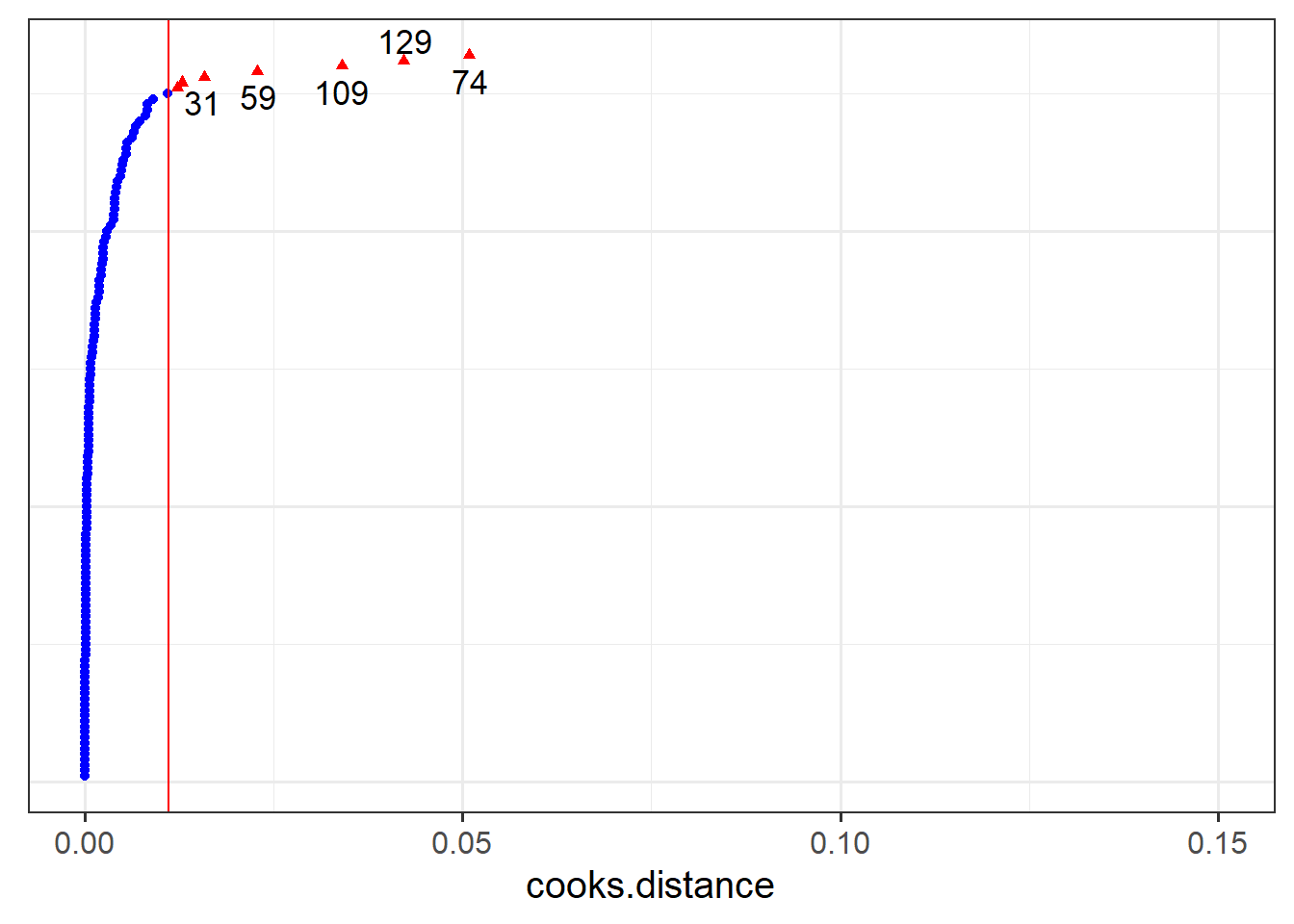
  1. Which person in the dataset has the greatest influence on our model?
  2. For which person is the model fit the worst (i.e., who has the highest residual?)
  3. Which LAA has the greatest influence on our model?
  • as well as hlm_influence() in the HLMdiag package there is another nice function, hlm_augment()
  • we can often end up in confusion because the \(i^{th}\) observation inputted to our model (and therefore the \(i^{th}\) observation of hlm_influence() output) might not be the \(i^{th}\) observation in our original dataset - there may be missing data! (Luckily, we have no missing data in this dataset).

Question 4
  1. Looking at the random effects, which LAA shows the least benefit to wellbeing as outdoor time increases, and which shows the greatest benefit?
  2. What is the estimated wellbeing for people from City of Edinburgh with zero hours of outdoor time per week, and what is their associated increases in wellbeing for every hour per week increase in outdoor time?


Exercises: Centering in the MLM

We have some data from a study investigating how perceived persuasiveness of a speaker is influenced by the rate at which they speak.

dap2 <- read_csv("https://uoepsy.github.io/data/dapr2_2122_report1.csv")

We can fit a simple linear regression (one predictor) to evaluate how speech rate (variable sp_rate in the dataset) influences perceived persuasiveness (variable persuasive in the dataset). There are various ways in which we can transform the predictor variable sp_rate, which in turn can alter the interpretation of some of our estimates:

Raw X

m1 <- lm(persuasive ~ sp_rate, data = dap2)
summary(m1)$coefficients
             Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 55.532060  6.4016670  8.674625 6.848945e-15
sp_rate     -0.190987  0.4497113 -0.424688 6.716809e-01

The intercept and the coefficient for speech rate are interpreted as:

  • (Intercept): A audio clip of someone speaking at zero phones per second is estimated as having an average persuasive rating of 55.53.
  • sp_rate: For every increase of one phone per second, perceived persuasiveness is estimated to decrease by -0.19.

Mean-Centered X

We can mean center our predictor and fit the model again:

dap2 <- dap2 %>% mutate(sp_rate_mc = sp_rate - mean(sp_rate))
m2 <- lm(persuasive ~ sp_rate_mc, data = dap2)
summary(m2)$coefficients
             Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 52.874667  1.3519418 39.110165 6.429541e-80
sp_rate_mc  -0.190987  0.4497113 -0.424688 6.716809e-01
  • (Intercept): A audio clip of someone speaking at the mean phones per second is estimated as having an average persuasive rating of 52.87.
  • sp_rate_mc: For every increase of one phone per second, perceived persuasiveness is estimated to decrease by -0.19.

Standardised X

We can standardise our predictor and fit the model yet again:

dap2 <- dap2 %>% mutate(sp_rate_z = scale(sp_rate))
m3 <- lm(persuasive ~ sp_rate_z, data = dap2)
summary(m3)$coefficients
             Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 52.874667   1.351942 39.110165 6.429541e-80
sp_rate_z   -0.576077   1.356471 -0.424688 6.716809e-01
  • (Intercept): A audio clip of someone speaking at the mean phones per second is estimated as having an average persuasive rating of 52.87.
  • sp_rate_z: For every increase of one standard deviation in phones per second, perceived persuasiveness is estimated to decrease by -0.58.

Remember that the scale(sp_rate) is subtracting the mean from each value, then dividing those by the standard deviation. The standard deviation of dap2$sp_rate is:

sd(dap2$sp_rate)
[1] 3.016315

so in our variable dap2$sp_rate_z, a change of 3.02 gets scaled to be a change of 1 (because we are dividing by sd(dap2$sp_rate)).

coef(m1)[2] * sd(dap2$sp_rate)
  sp_rate 
-0.576077 
coef(m3)[2]
sp_rate_z 
-0.576077

Note that these models are identical. When we conduct a model comparison between the 3 models, the residual sums of squares is identical for all models:

anova(m1,m2,m3)
Analysis of Variance Table

Model 1: persuasive ~ sp_rate
Model 2: persuasive ~ sp_rate_mc
Model 3: persuasive ~ sp_rate_z
  Res.Df   RSS Df Sum of Sq F Pr(>F)
1    148 40576                      
2    148 40576  0         0         
3    148 40576  0         0

What changes when you center or scale a predictor in a standard regression model (one fitted with lm())?

  • The variance explained by the predictor remains exactly the same
  • The intercept will change to be the estimated mean outcome where that predictor is “0”. Scaling and centering changes what “0” represents, thereby changing this estimate (the significance test will therefore also change because the intercept now has a different meaning)
  • The slope of the predictor will change according to any scaling (e.g. if you divide your predictor by 10, the slope will multiply by 10).
  • The test of the slope of the predictor remains exactly the same.

Data: Hangry

The study is interested in evaluating whether hunger influences peoples’ levels of irritability (i.e., “the hangry hypothesis”), and whether this is different for people following a diet that includes fasting. 81 participants were recruited into the study. Once a week for 5 consecutive weeks, participants were asked to complete two questionnaires, one assessing their level of hunger, and one assessing their level of irritability. The time and day at which participants were assessed was at a randomly chosen hour between 7am and 7pm each week. 46 of the participants were following a five-two diet (five days of normal eating, 2 days of fasting), and the remaining 35 were following no specific diet.

The data are available at: https://uoepsy.github.io/data/hangry.csv.

variable description
q_irritability Score on irritability questionnaire (0:100)
q_hunger Score on hunger questionnaire (0:100)
ppt Participant
fivetwo Whether the participant follows the five-two diet
Question 1

Read carefully the description of the study above, and try to write out (in lmer syntax) an appropriate model to test the research aims.
e.g.:

outcome ~ explanatory variables + (???? | grouping)

Try to think about the maximal random effect structure (i.e. everything that can vary by-grouping is estimated as doing so).

To help you think through the steps to get from a description of a research study to a model specification, think about your answers to the following questions.

Q: What is our outcome variable?
Q: What are our explanatory variables?
Q: Is there any grouping (or “clustering”) of our data that we consider to be a random sample? If so, what are the groups?

  • The research is looking at how hunger influences irritability, and whether this is different for people on the fivetwo diet.
  • We can split our data in to groups of each participant. We can also split it into groups of each diet. Which of these groups have we randomly sampled? Do we have a random sample of participants? Do we have a random sample of diets? Another way to think of this is “if i repeated the experiment, what these groups be different?”

Recall our research aim:

… whether hunger influences peoples’ levels of irritability (i.e., “the hangry hypothesis”), and whether this is different for people following a diet that includes fasting.

Forgetting about any differences due to diet, let’s just think about the relationship between irritability and hunger. How should we interpret this research aim?
Was it:

  1. “Are people more irritable if they are, on average, more hungry than other people?”
  2. “Are people more irritable if they are, for them, more hungry than they usually are?”
  3. Some combination of both a. and b.

This is just one demonstration of how the statistical methods we use can constitute an integral part of our development of a research project, and part of the reason that data analysis for scientific cannot be so easily outsourced after designing the study and collecting the data.

As our data currently is currently stored, the relationship between irritability and the raw scores on the hunger questionnaire q_hunger represents some ‘total effect’ of hunger on irritability. This is a bit like interpretation c. above - it’s a composite of both the ‘within’ ( b. ) and ‘between’ ( a. ) effects. The problem with this is that the ‘total effect’ isn’t necessarily all that meaningful. It may tell us that ‘being higher on the hunger questionnaire is associated with being more irritable’, but how can we apply this information? It is not specifically about the comparison between hungry people and less hungry people, and nor is it about how person i changes when they are more hungry than usual. It is both these things smushed together.

To disaggregate the ‘within’ and ‘between’ effects of hunger on irritability, we can group-mean center. For ‘between’, we are interested in how irritability is related to the average hunger levels of a participant, and for ‘within’, we are asking how irritability is related to a participants’ relative levels of hunger (i.e., how far above/below their average hunger level they are.).

Question 2

Add to the data these two columns:

  1. a column which contains the average hungriness score for each participant.
  2. a column which contains the deviation from each person’s hunger score to that person’s average hunger score.

You’ll find group_by() %>% mutate() very useful here.

Question 3

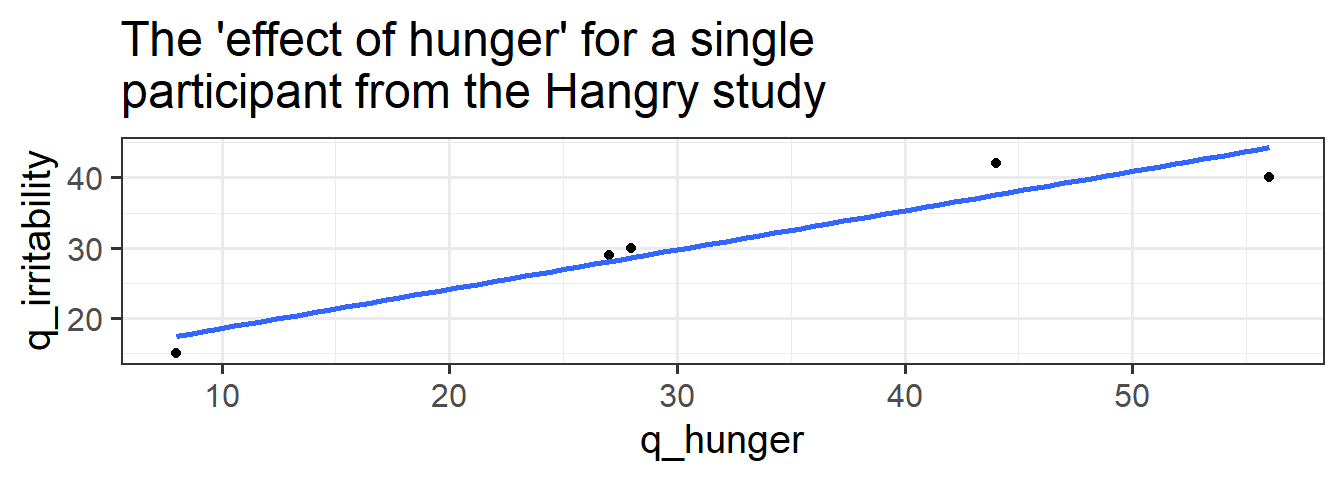
For each of the new variables you just added, plot the irritability scores against those variables.

  • Does it look like hungry people are more irritable than less hungry people?
  • Does it look like when people are more hungry than normal, they are more irritable?

Question 4

We have taken the raw hunger scores and separated them into two parts (raw hunger scores = participants’ average hunger score + observation level deviations from those averages), that represent two different aspects of the relationship between hunger and irritability.

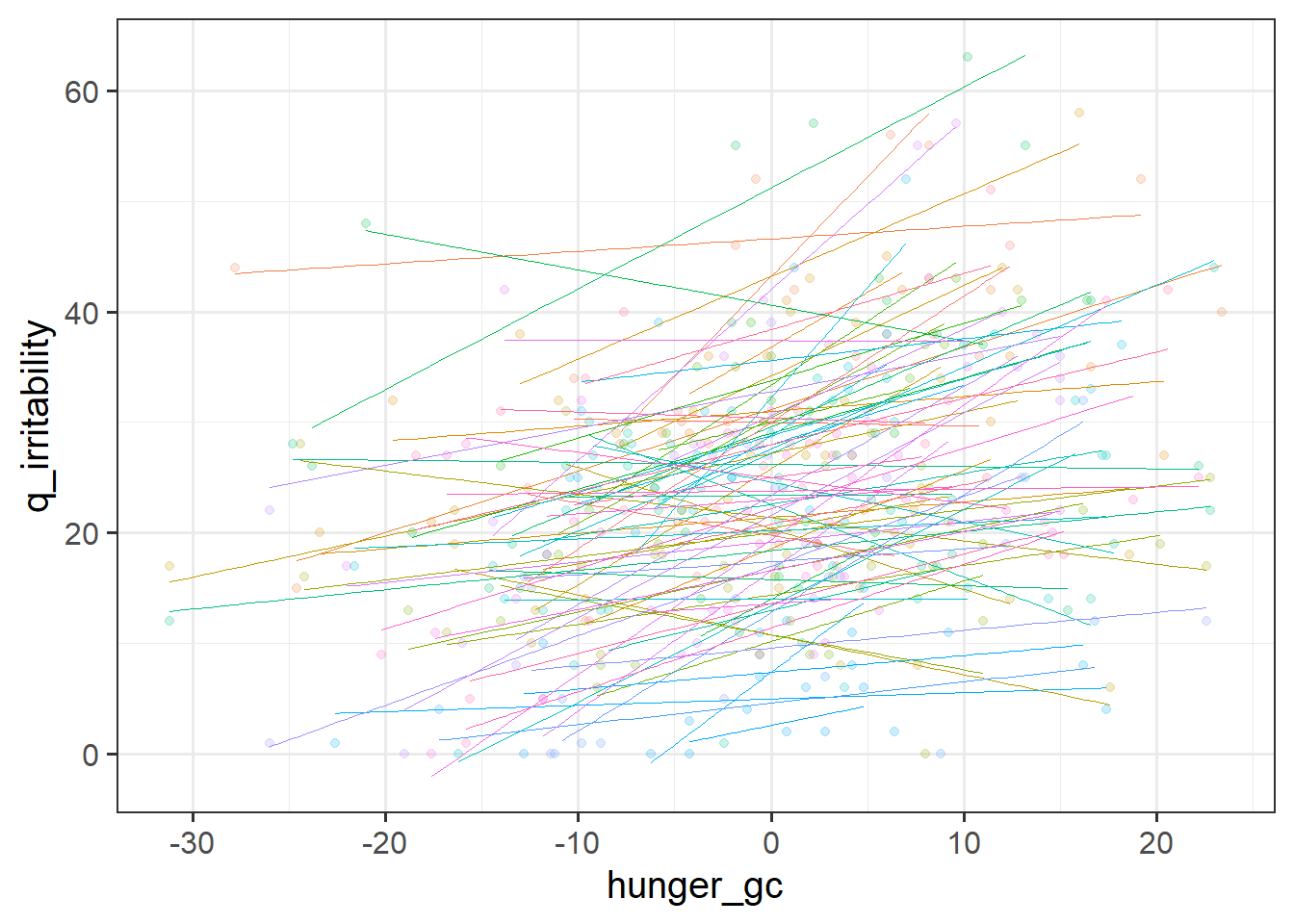
Adjust your model specification to include these two separate variables as predictors, instead of the raw hunger scores.

  • hunger * diet could be replaced by (hunger1 + hunger2) * diet, thereby allowing each aspect of hunger to interact with diet.
  • We can only put one of these variables in the random effects (1 + hunger | participant). Recall that above we discussed how we cannot have (diet | participant), because “an effect of diet” makes no sense for a single participant (they are either on the diet or they are not, so there is no ‘effect’). Similarly, each participant has only one value for their average hungriness.

Question 5

Hopefully, you have fitted a model similar to the below:

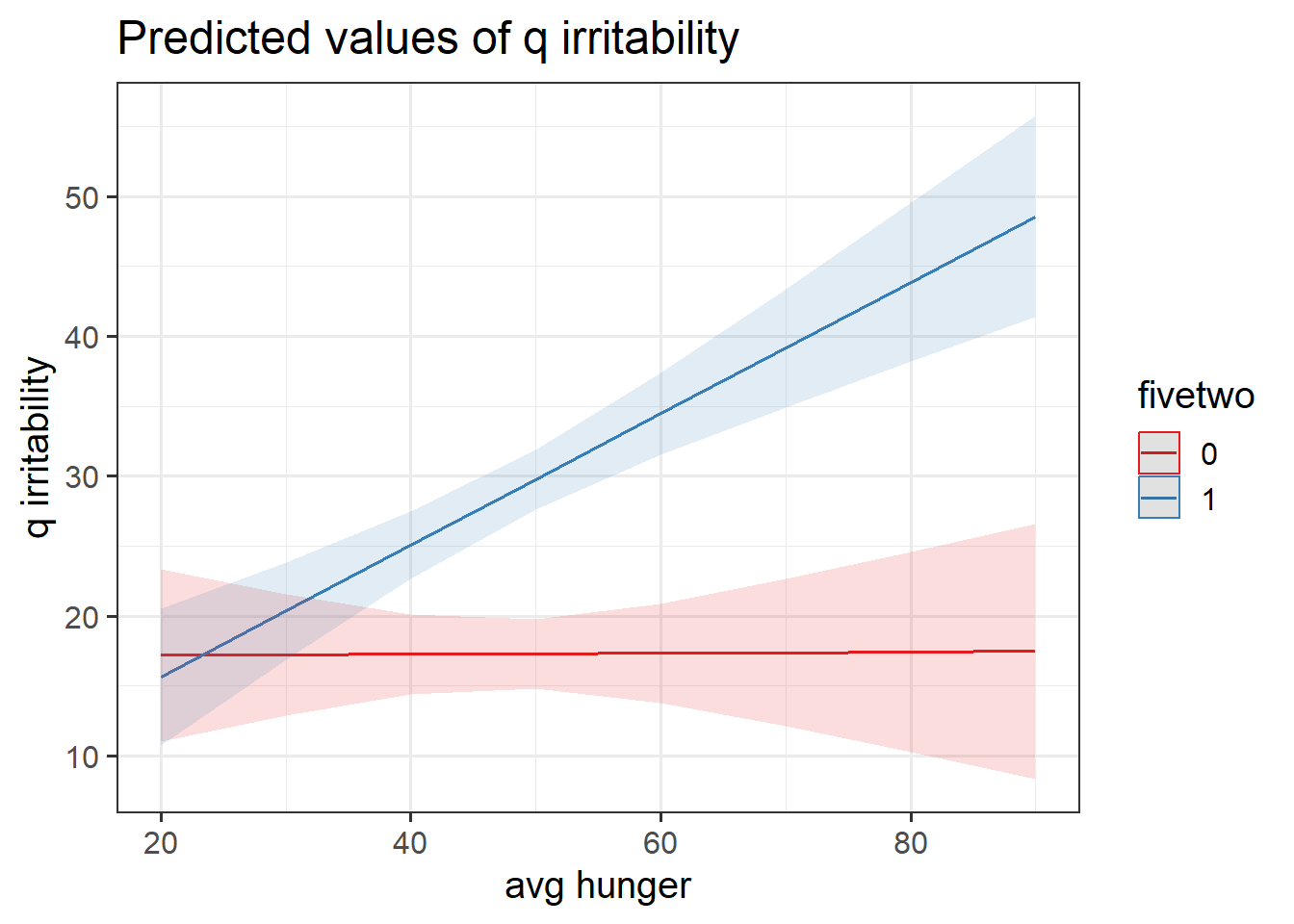
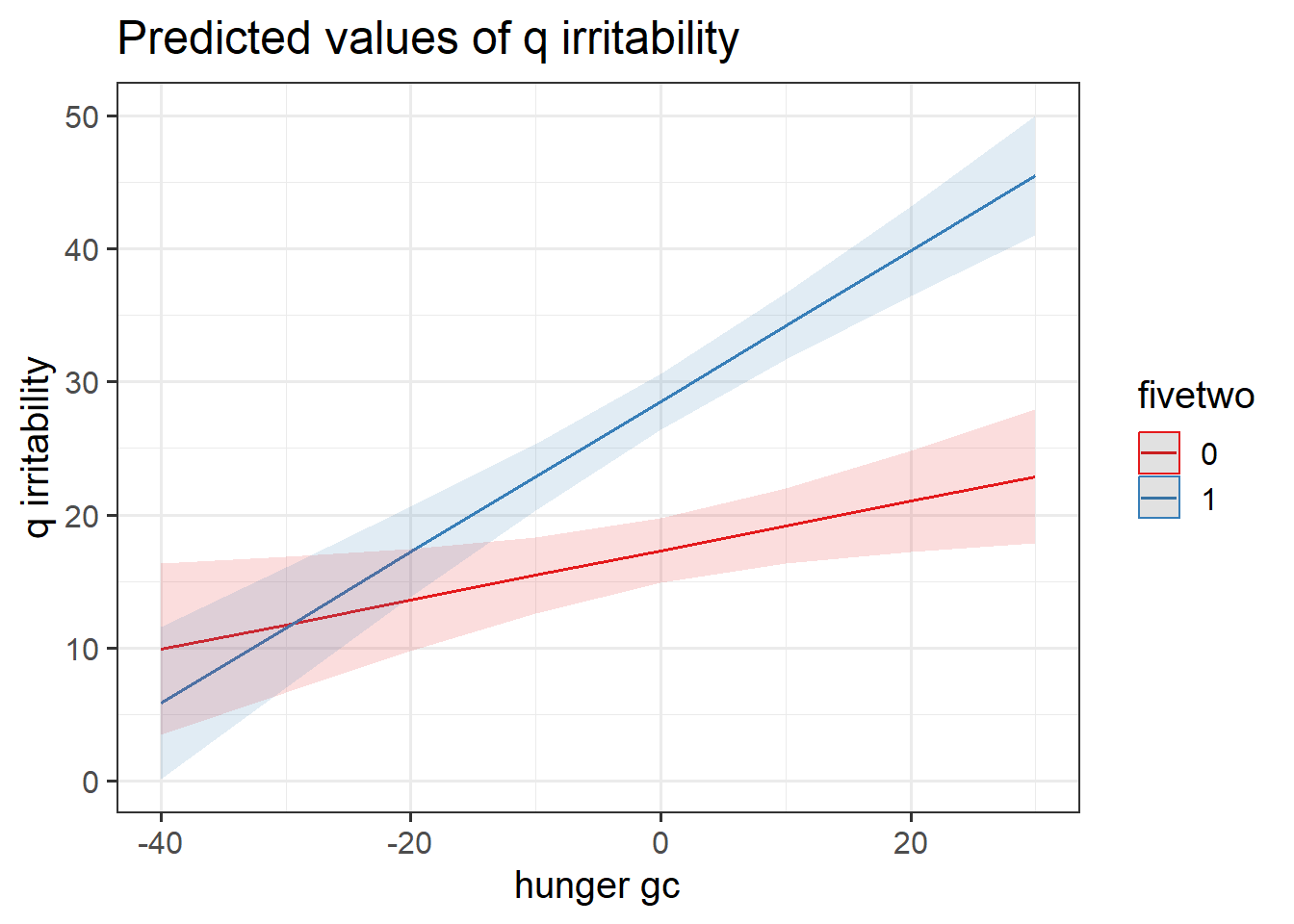
hangrywb <- lmer(q_irritability ~ (avg_hunger + hunger_gc) * fivetwo + 
                (1 + hunger_gc | ppt), data = hangry,
            control = lmerControl(optimizer="bobyqa"))

Below, we have obtained p-values using the Kenward Rogers Approximation of \(df\) for the test of whether the fixed effects are zero, so we can see the significance of each estimate.

Provide an answer for each of these questions:

  1. For those following no diet, is there evidence to suggest that people who are on average more hungry are more irritable?
  2. Is there evidence to suggest that this is different for those following the five-two diet? In what way?
  3. Do people following no diet tend to be more irritable when they are more hungry than they usually are?
  4. Is there evidence to suggest that this is different for those following the five-two diet? In what way?
  5. (Trickier:) What does the fivetwo coefficient represent?
Model Summary
Parameter Coefficient SE 95% CI t df p
Fixed Effects
(Intercept) 17.13 5.21 (6.75, 27.51) 3.29 77.00 0.002
avg hunger 3.86e-03 0.11 (-0.21, 0.22) 0.04 77.00 0.971
hunger gc 0.19 0.08 (0.03, 0.34) 2.45 70.40 0.017
fivetwo (1) -10.85 6.62 (-24.03, 2.32) -1.64 77.00 0.105
avg hunger × fivetwo (1) 0.47 0.14 (0.20, 0.74) 3.44 77.00 < .001
hunger gc × fivetwo (1) 0.38 0.10 (0.18, 0.58) 3.75 73.64 < .001
Random Effects
SD (Intercept: ppt) 6.93
SD (hunger_gc: ppt) 0.38
Cor (Intercept~hunger_gc: ppt) -0.01
SD (Residual) 4.83

Question 6

Construct two plots showing the two model estimated interactions. Think about your answers to the previous question, and check that they match with what you are seeing in the plots (do not underestimate the utility of this activity for helping understanding!).

This isn’t as difficult as it sounds. the sjPlot package can do it in one line of code!

Question 7

Provide tests or confidence intervals for the parameters of interest, and write-up the results.

df approximations likelihood-based
tests or CIs for model parameters library(parameters)
model_parameters(model, ci_method="kr")		 confint(model, type="profile")
model comparison
(different fixed effects, same random effects)		 library(pbkrtest)
KRmodcomp(model1,model0)		 anova(model0,model)
fit models with REML=TRUE.
good option for small samples		 fit models with REML=FALSE.
needs large N at both levels (40+)

Other within-group transformations

As well as within-group mean centering a predictor (like we have done above), we can within-group standardise a predictor. This would disagregate within and between effects, but interpretation would of the within effect would be the estimated change in \(y\) associated with being 1 standard deviation higher in \(x\) for that group.