Information about solutions

Solutions for these exercises are available immediately below each question.
We would like to emphasise that much evidence suggests that testing enhances learning, and we strongly encourage you to make a concerted attempt at answering each question before looking at the solutions. Immediately looking at the solutions and then copying the code into your work will lead to poorer learning.
We would also like to note that there are always many different ways to achieve the same thing in R, and the solutions provided are simply one approach.

Relevant packages

  • psych

Where PCA aims to summarise a set of measured variables into a set of orthogonal (uncorrelated) components as linear combinations (a weighted average) of the measured variables, Factor Analysis (FA) assumes that the relationships between a set of measured variables can be explained by a number of underlying latent factors.

Note how the directions of the arrows in Figure 1 are different between PCA and FA - in PCA, each component \(C_i\) is the weighted combination of the observed variables \(y_1, ...,y_n\), whereas in FA, each measured variable \(y_i\) is seen as generated by some latent factor(s) \(F_i\) plus some unexplained variance \(u_i\).

It might help to read the \(\lambda\)s as beta-weights (\(b\), or \(\beta\)), because that’s all they really are. The equation \(y_i = \lambda_{1i} F_1 + \lambda_{2i} F_2 + u_i\) is just our way of saying that the variable \(y_i\) is the manifestation of some amount (\(\lambda_{1i}\)) of an underlying factor \(F_1\), some amount (\(\lambda_{2i}\)) of some other underlying factor \(F_2\), and some error (\(u_i\)).

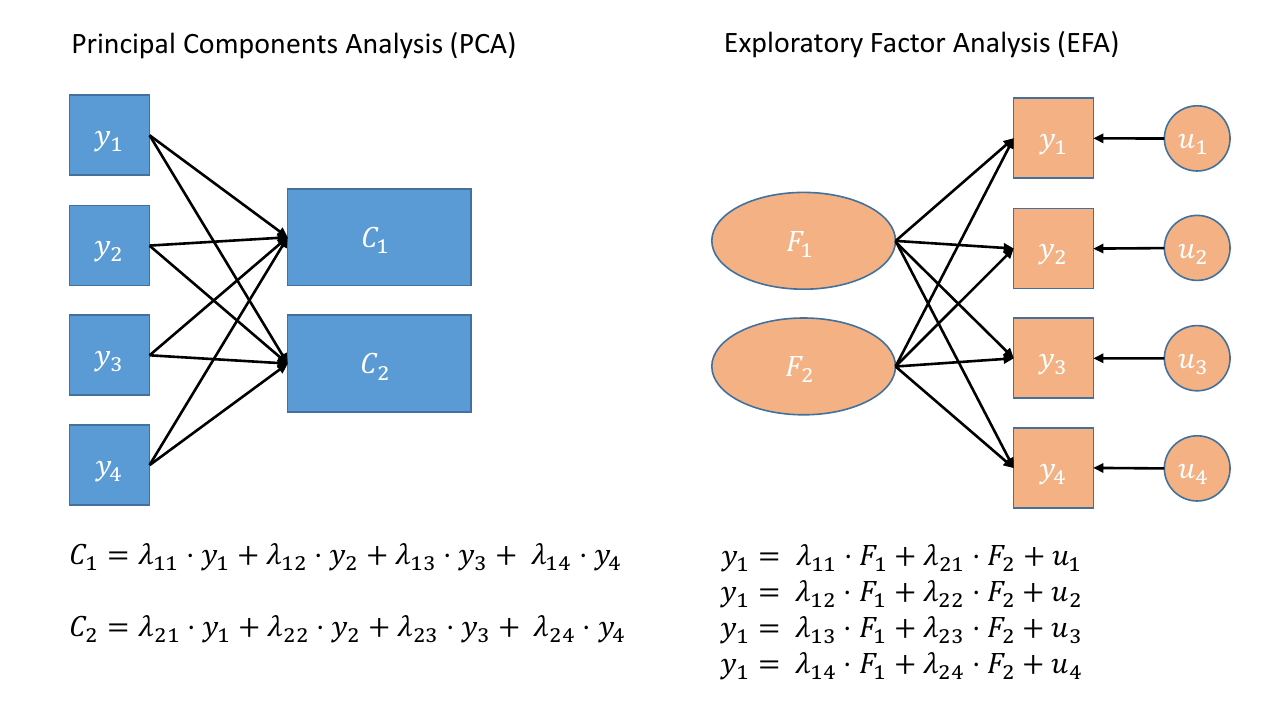
Path diagrams for PCA and FA

Figure 1: Path diagrams for PCA and FA

In Exploratory Factor Analysis (EFA), we are starting with no hypothesis about either the number of latent factors or about the specific relationships between latent factors and measured variables (known as the factor structure). Typically, all variables will load on all factors, and a transformation method such as a rotation (we’ll cover this in more detail below) is used to help make the results more easily interpretable.1

Data: Conduct Problems

A researcher is developing a new brief measure of Conduct Problems. She has collected data from n=450 adolescents on 10 items, which cover the following behaviours:

  1. Stealing
  2. Lying
  3. Skipping school
  4. Vandalism
  5. Breaking curfew
  6. Threatening others
  7. Bullying
  8. Spreading malicious rumours
  9. Using a weapon
  10. Fighting

Your task is to use the dimension reduction techniques you learned about in the lecture to help inform how to organise the items she has developed into subscales.

The data can be found at https://uoepsy.github.io/data/conduct_probs.csv

Preliminaries

Question A1

Read in the dataset from https://uoepsy.github.io/data/conduct_probs.csv.
The first column is clearly an ID column, and it is easiest just to discard this when we are doing factor analysis.

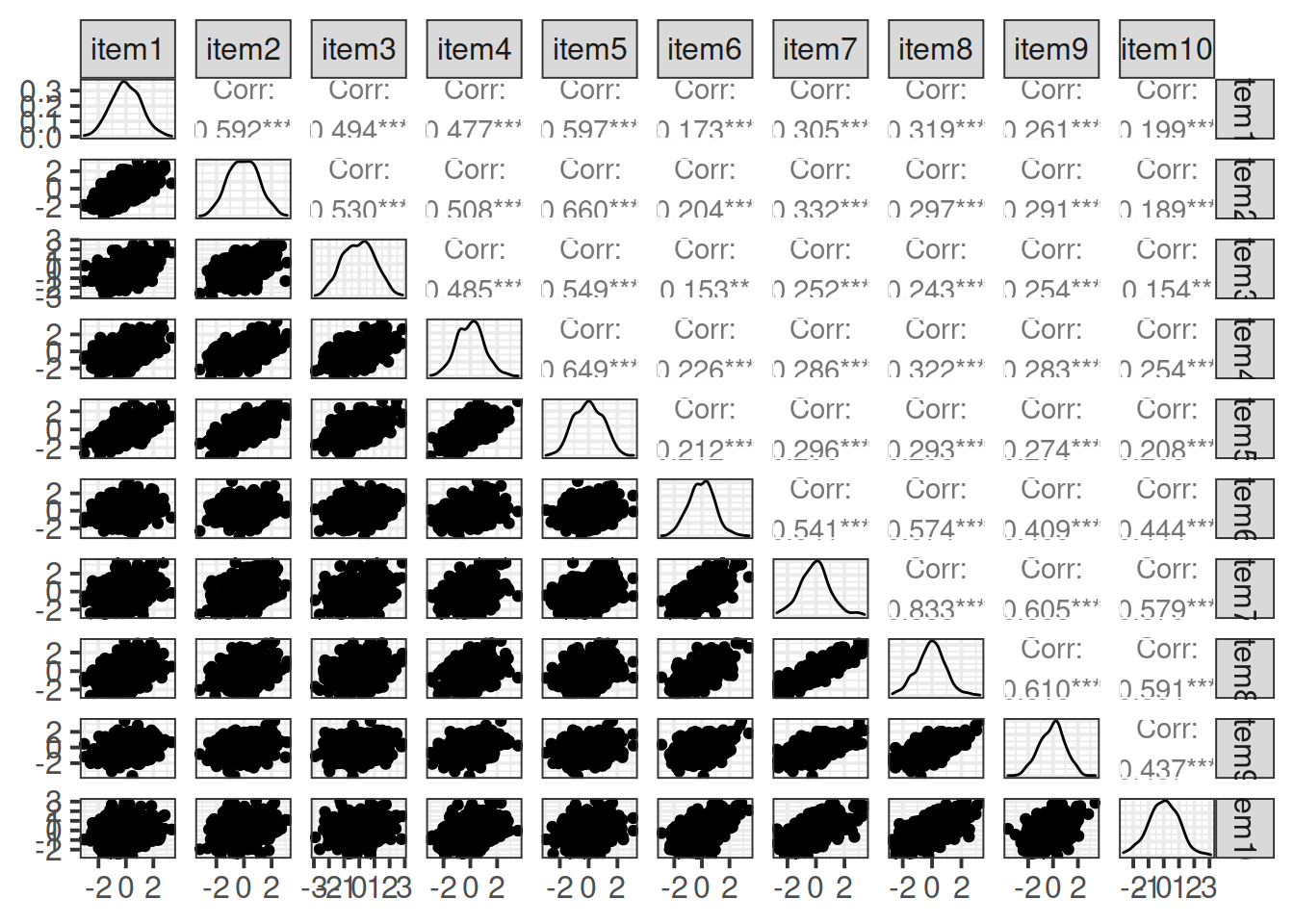
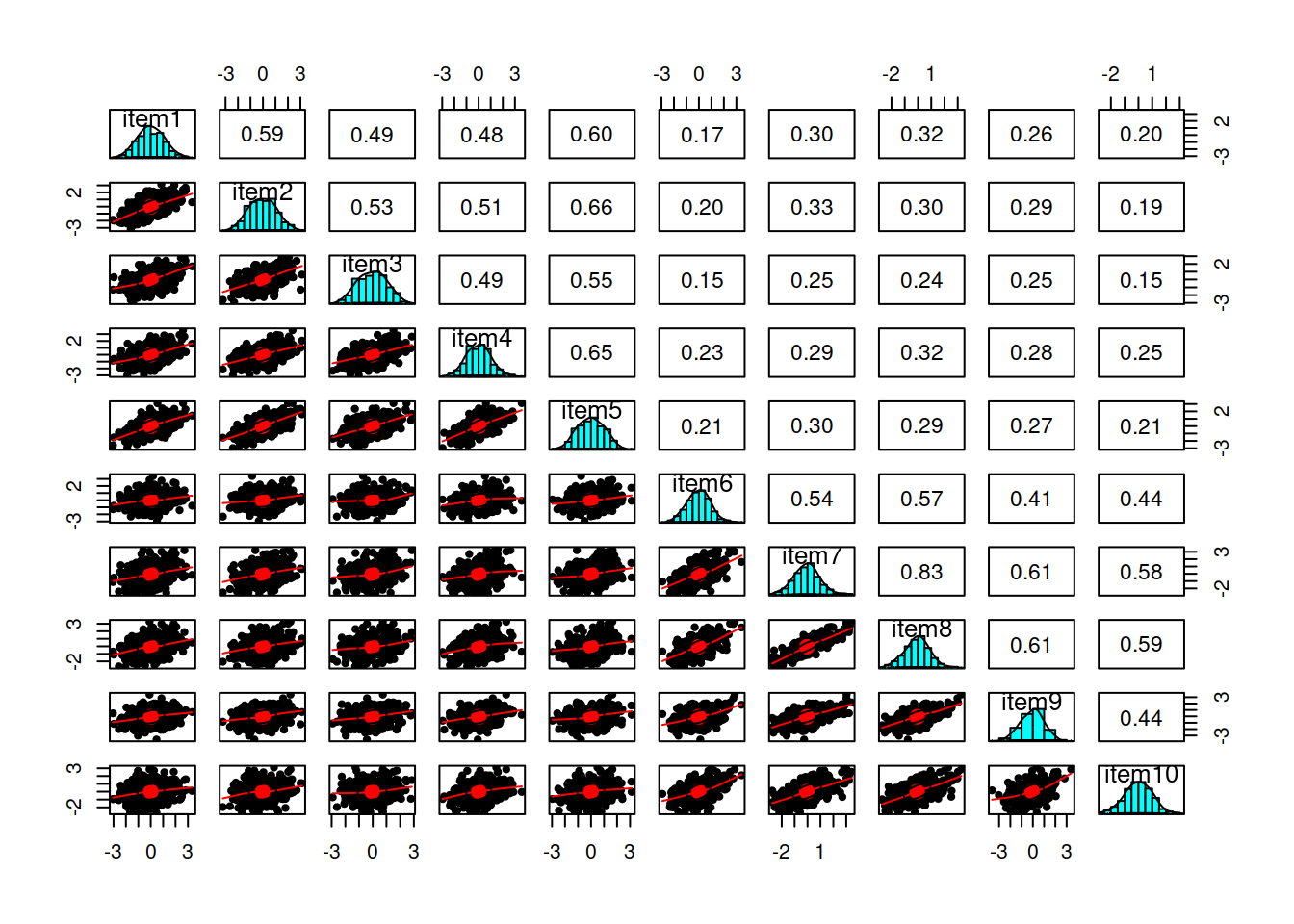
Create a correlation matrix for the items.
Inspect the items to check their suitability for exploratory factor analysis.

  • You can use a function such as cor or corr.test(data) (from the psych package) to create the correlation matrix.
  • The function cortest.bartlett(cor(data), n = nrow(data)) conducts Bartlett’s test that the correlation matrix is proportional to the identity matrix (a matrix of all 0s except for 1s on the diagonal).
  • You can check linearity of relations using pairs.panels(data) (also from psych), and you can view the histograms on the diagonals, allowing you to check univariate normality (which is usually a good enough proxy for multivariate normality).
  • You can check the “factorability” of the correlation matrix using KMO(data) (also from psych!).
    • Rules of thumb:
      • \(0.8 < MSA < 1\): the sampling is adequate
      • \(MSA <0.6\): sampling is not adequate
      • \(MSA \sim 0\): large partial correlations compared to the sum of correlations. Not good for FA
Optional Kaiser’s suggested cuts

Solution

How many factors?

Question A2

How many dimensions should be retained? This question can be answered in the same way as we did above for PCA.

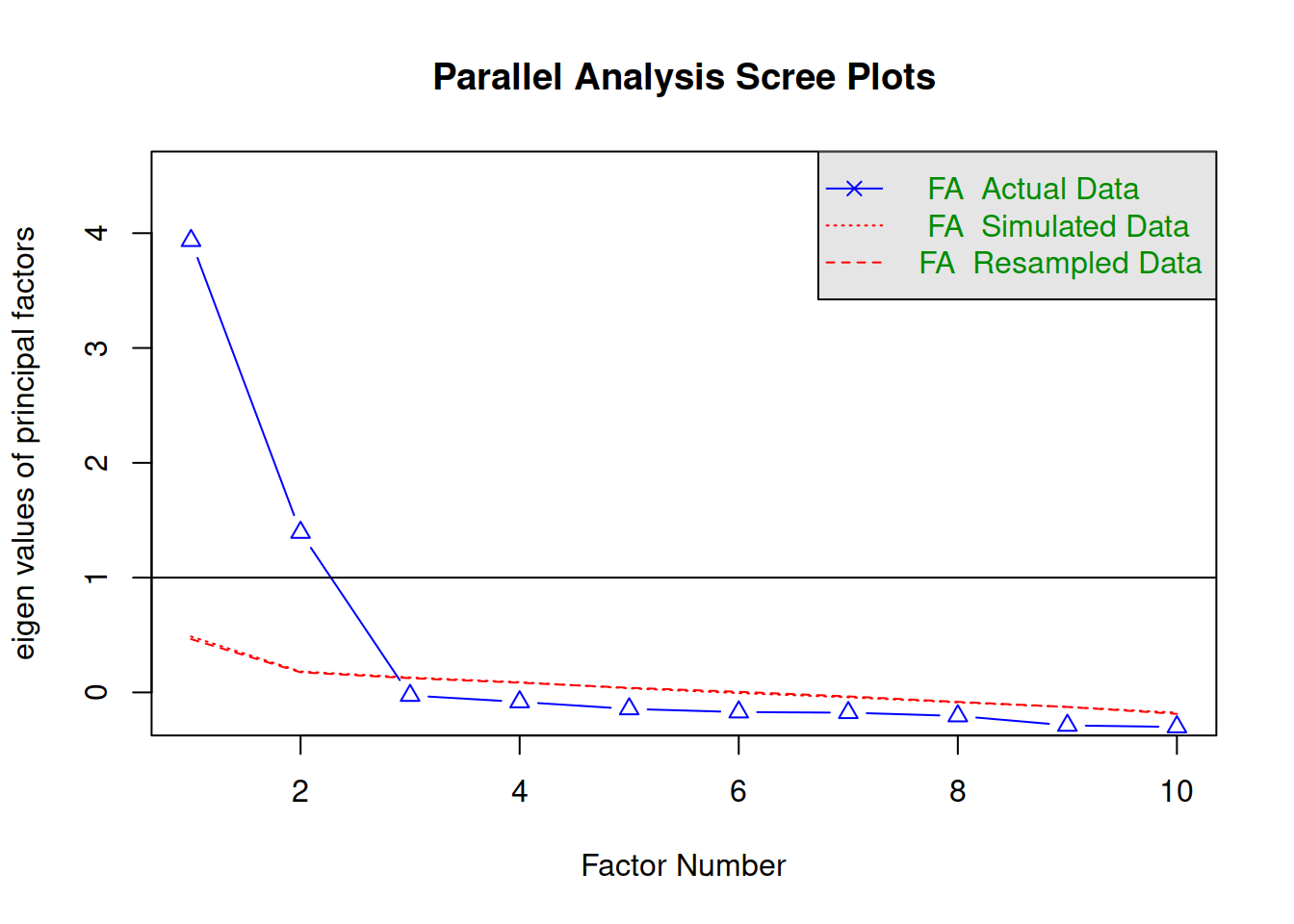
Use a scree plot, parallel analysis, and MAP test to guide you.
You can use fa.parallel(data, fm = "fa") to conduct both parallel analysis and view the scree plot!

Solution

Perform EFA

Now we need to perform the factor analysis. But there are two further things we need to consider, and they are:

  1. whether we want to apply a rotation to our factor loadings, in order to make them easier to interpret, and
  2. how do we want to extract our factors (it turns out there are loads of different approaches!).

Rotations?

Rotations are so called because they transform our loadings matrix in such a way that it can make it more easy to interpret. You can think of it as a transformation applied to our loadings in order to optimise interpretability, by maximising the loading of each item onto one factor, while minimising its loadings to others. We can do this by simple rotations, but maintaining our axes (the factors) as perpendicular (i.e., uncorrelated) as in Figure 3, or we can allow them to be transformed beyond a rotation to allow the factors to correlate (Figure 4).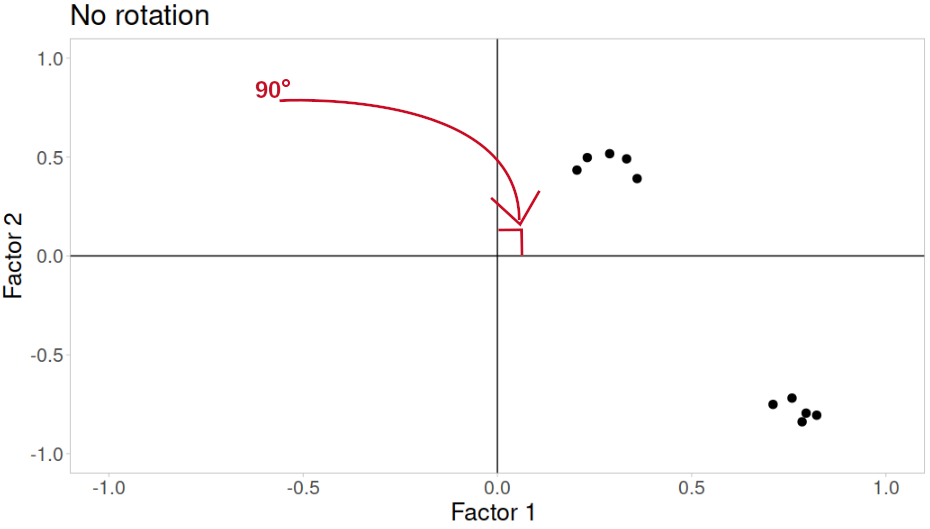
No rotation

Figure 2: No rotation

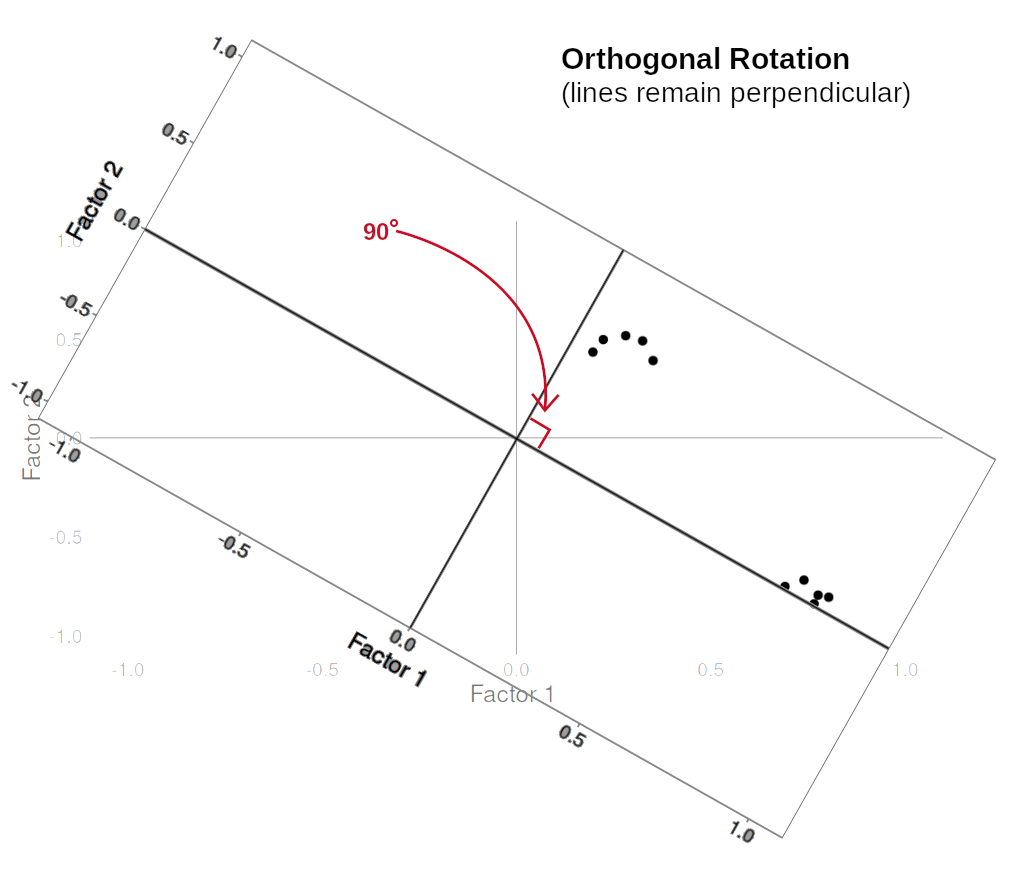
Orthogonal rotation

Figure 3: Orthogonal rotation

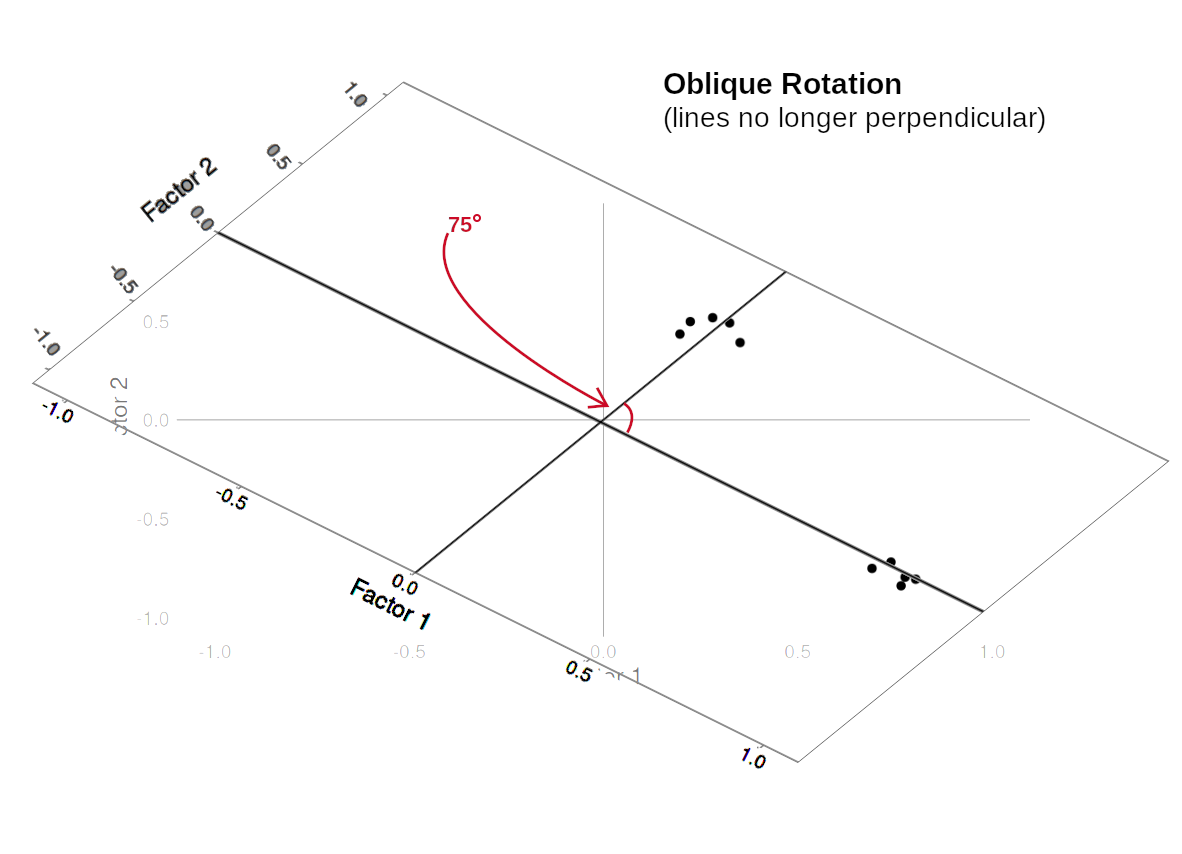
Oblique rotation

Figure 4: Oblique rotation

In our path diagram of the model (Figure 5), all the factor loadings remain present, but some of them become negligible. We can also introduce the possible correlation between our factors, as indicated by the curved arrow between \(F_1\) and \(F_2\).

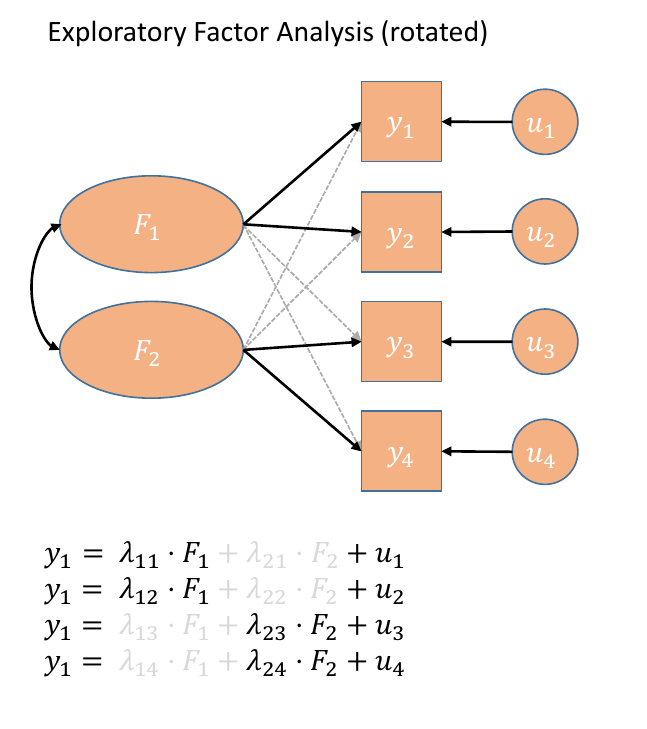
Path diagrams for EFA with rotation

Figure 5: Path diagrams for EFA with rotation

Factor Extraction

PCA (using eigendecomposition) is itself a method of extracting the different dimensions from our data. However, there are lots more available for factor analysis.

You can find a lot of discussion about different methods both in the help documentation for the fa() function from the psych package:

Factoring method fm=“minres” will do a minimum residual as will fm=“uls.” Both of these use a first derivative. fm=“ols” differs very slightly from “minres” in that it minimizes the entire residual matrix using an OLS procedure but uses the empirical first derivative. This will be slower. fm=“wls” will do a weighted least squares (WLS) solution, fm=“gls” does a generalized weighted least squares (GLS), fm=“pa” will do the principal factor solution, fm=“ml” will do a maximum likelihood factor analysis. fm=“minchi” will minimize the sample size weighted chi square when treating pairwise correlations with different number of subjects per pair. fm =“minrank” will do a minimum rank factor analysis. “old.min” will do minimal residual the way it was done prior to April, 2017 (see discussion below). fm=“alpha” will do alpha factor analysis as described in Kaiser and Coffey (1965)

And there are lots of discussions both in papers and on forums.

As you can see, this is a complicated issue, but when you have a large sample size, a large number of variables, for which you have similar communalities, then the extraction methods tend to agree. For now, don’t fret too much about the factor extraction method.2

Question A3

Use the function fa() from the psych package to conduct and EFA to extract 2 factors (this is what we suggest based on the various tests above, but you might feel differently - the ideal number of factors is subjective!). Use a suitable rotation and extraction method (fm).

conduct_efa <- fa(data, nfactors = ?, rotate = ?, fm = ?)

Solution

Inspect

Question A4

Inspect the loadings (conduct_efa$loadings) and give the factors you extracted labels based on the patterns of loadings.

Look back to the description of the items, and suggest a name for your factors

Solution

Question A5

How correlated are your factors?

We can inspect the factor correlations (if we used an oblique rotation) using:

conduct_efa$Phi

Solution

Write-up

Question A6

Drawing on your previous answers and conducting any additional analyses you believe would be necessary to identify an optimal factor structure for the 10 conduct problems, write a brief text that summarises your method and the results from your chosen optimal model.

Solution

PCA & EFA Comparison Exercise

Question A7

Using the same data, conduct a PCA using the principal() function.

What differences do you notice compared to your EFA?

Do you think a PCA or an EFA is more appropriate in this particular case?

Solution

  1. When we have some clear hypothesis about relationships between measured variables and latent factors, we might want to impose a specific factor structure on the data (e.g., items 1 to 10 all measure social anxiety, items 11 to 15 measure health anxiety, and so on). When we impose a specific factor structure, we are doing Confirmatory Factor Analysis (CFA). This is not covered in this course, but it’s important to note that in practice EFA is not wholly “exploratory” (your theory will influence the decisions you make) nor is CFA wholly “confirmatory” (in which you will inevitably get tempted to explore how changing your factor structure might improve fit).↩︎

  2. (It’s a bit like the optimiser issue in the multi-level model block)↩︎

  3. You should provide the table of factor loadings. It is conventional to omit factor loadings \(<|0.3|\); however, be sure to ensure that you mention this in a table note.↩︎