Assumptions, Diagnostics, and Random Effect Structures
Information about solutions
Solutions for these exercises are available immediately below each question.
We would like to emphasise that much evidence suggests that testing enhances learning, and we strongly encourage you to make a concerted attempt at answering each question before looking at the solutions. Immediately looking at the solutions and then copying the code into your work will lead to poorer learning.
We would also like to note that there are always many different ways to achieve the same thing in R, and the solutions provided are simply one approach.
Preliminaries
- Create a new RMarkdown document or R script (whichever you like) for this week.
Assumptions
Toy data
Recall our toy example data in which we fitted a multilevel model to model how practice (in hours per week) influences the reading age of toy figurines which are grouped by toy-type (Playmobil, Powerrangers, Farm Animals etc).

toys_read <- read_csv("https://uoepsy.github.io/data/toyexample.csv")Run the code below to fit the model with by-toy-type random intercepts and slopes of practice.
library(tidyverse)
library(lme4)
toys_read <- read_csv("https://uoepsy.github.io/data/toyexample.csv")
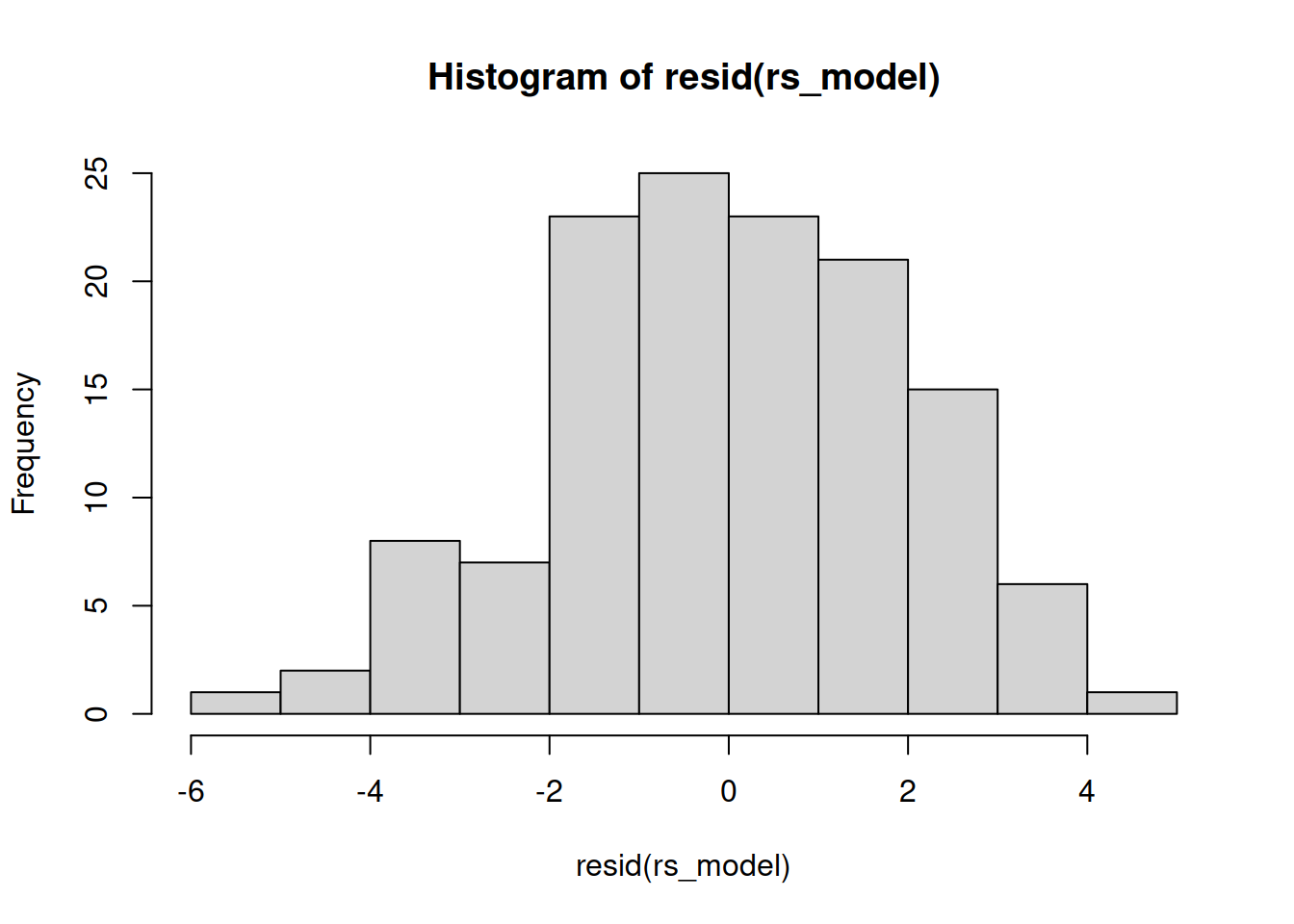
rs_model <- lmer(R_AGE ~ 1 + hrs_week + (1 + hrs_week | toy_type), data = toys_read)Plot the residuals vs fitted model, and assess the extend to which the assumption holds that the residuals are zero mean.
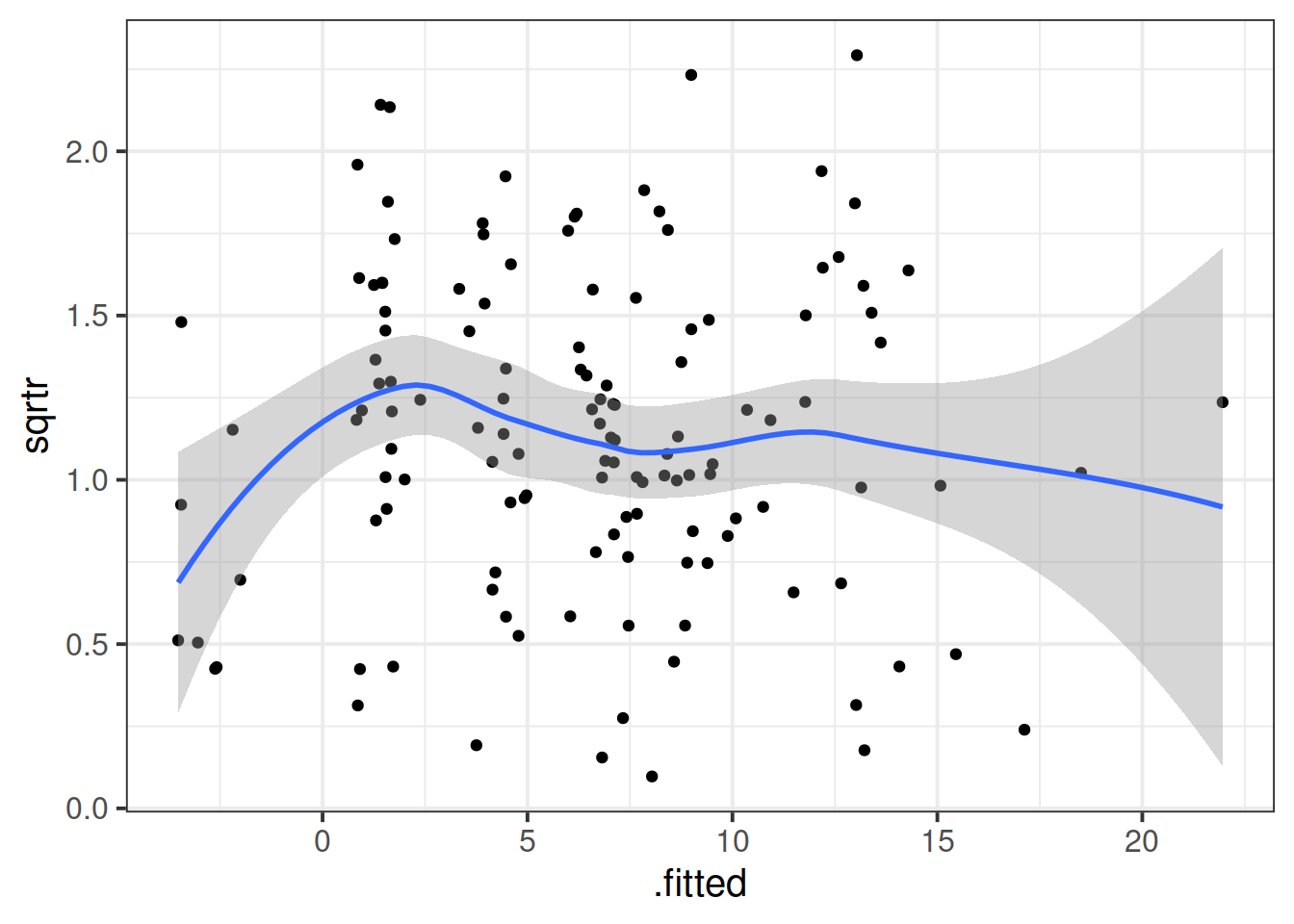
Construct a scale-location plot. This is where the square-root of the absolute value of the standardised residuals is plotted against the fitted values, and allows you to more easily assess the assumption of constant variance.
Using the augment() function from the broom.mixed package, construct the same plot using ggplot.
(constructing plots like this manually is a really useful way to help understand what exactly is being plotted)
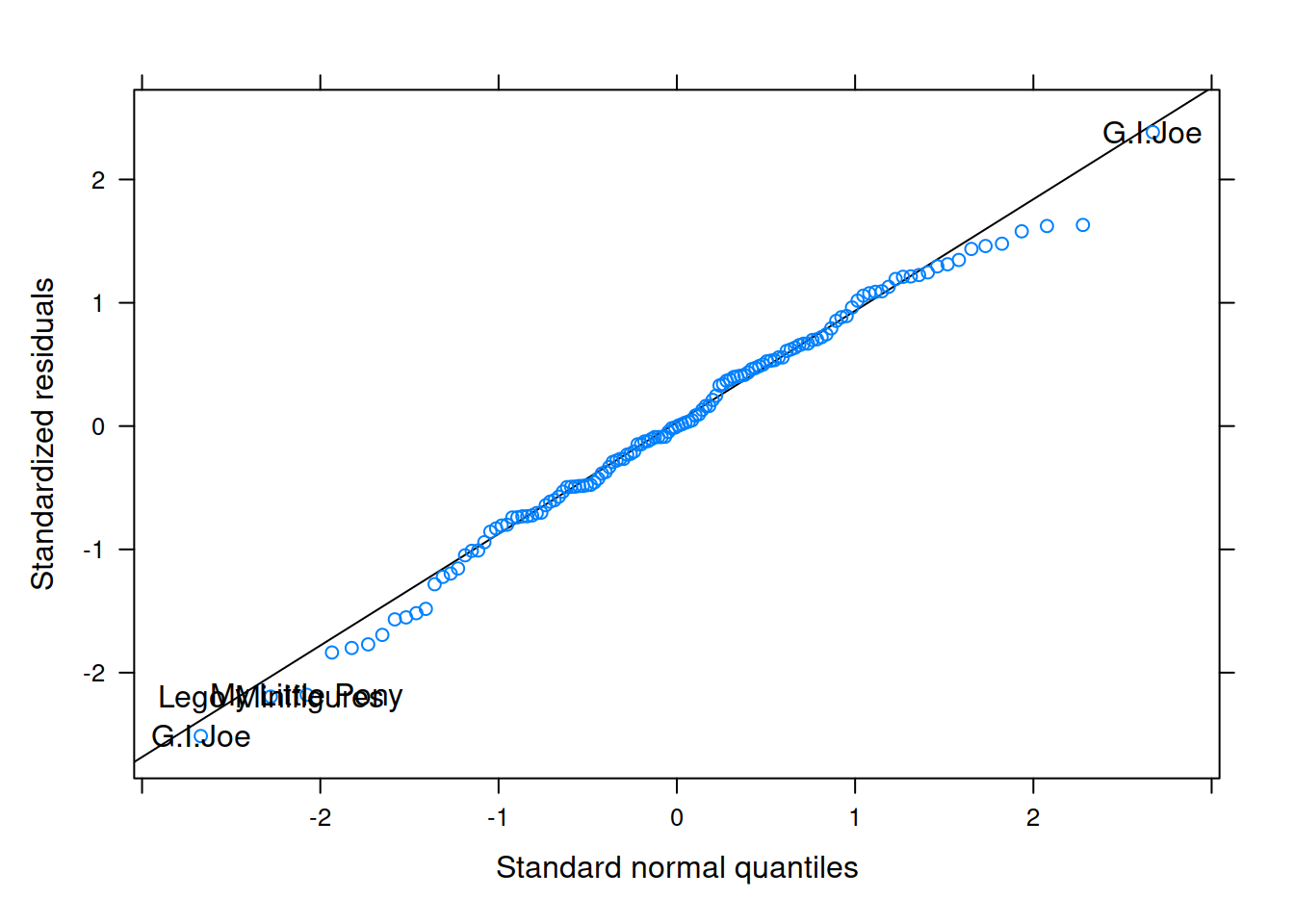
Examine the normality of both the level 1 and level 2 residuals.
Diagnostics
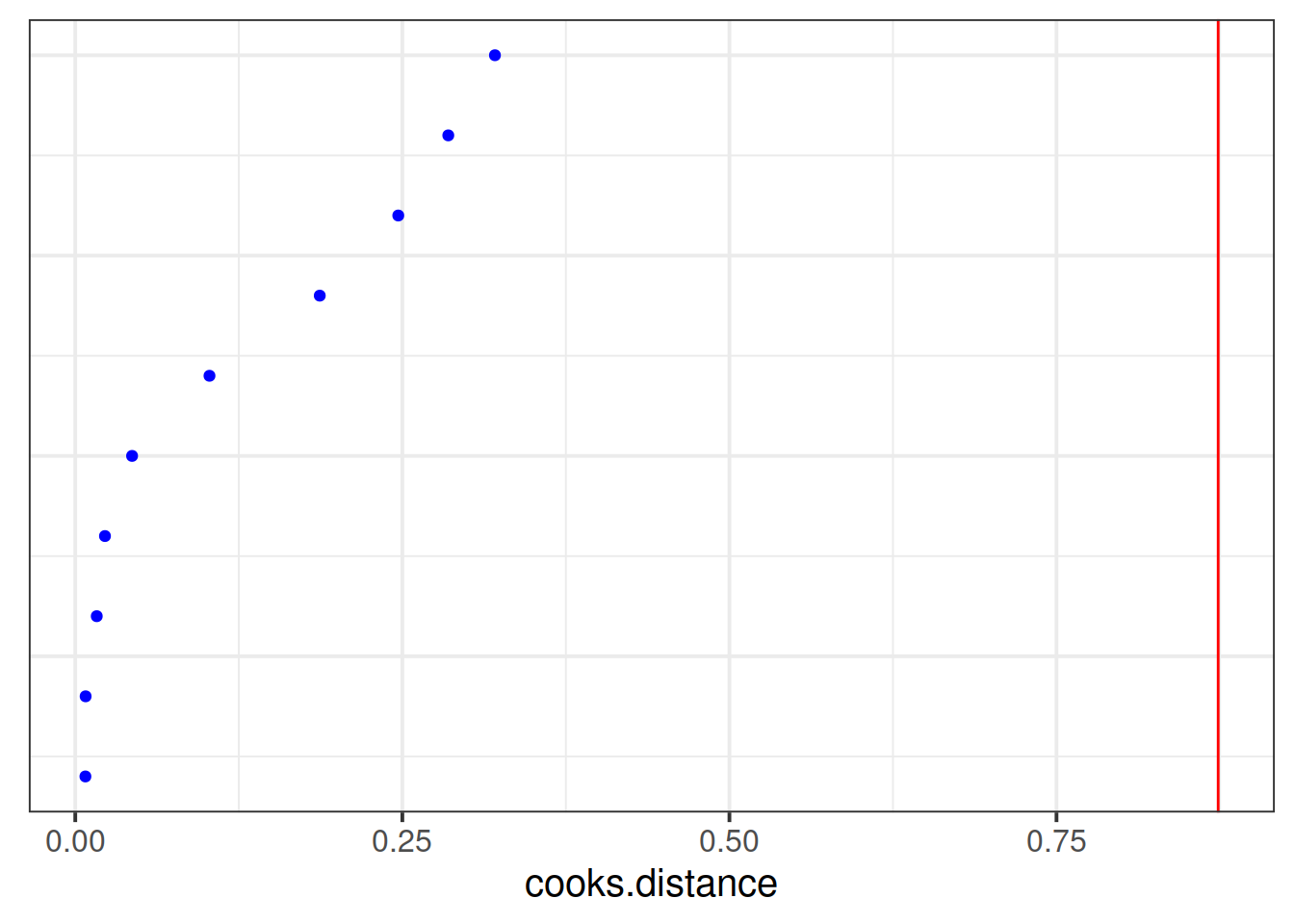
Which toy in the dataset has the greatest influence on our model?
Hint: as well as hlm_influence() in the HLMdiag package there is another nice function, hlm_augment()
We can often end up in confusion because the \(i^{th}\) observation inputted to our model (and therefore the \(i^{th}\) observation of hlm_influence() output) might not be the \(i^{th}\) observation in our original dataset - there may be missing data!
(Luckily, we have no missing data in the Toy dataset).
For which toy is the model fit the worst (i.e., who has the highest residual?)
Which type of toy has the greatest influence on our model?
Looking at the random effects, which toy type shows the least improvement in reading age as practice increases, and which shows the greatest improvement?
What is the estimated reading age for sock puppets with zero hours of practice per week, and what is their estimated change in reading age for every hour per week increase in practice?
Convergence Issues
Singular fits
You may have noticed that a lot of our models over the last few weeks have been giving a warning: boundary (singular) fit: see ?isSingular.
Up to now, we’ve been largely ignoring these warnings. However, this week we’re going to look at how to deal with this issue.
The warning is telling us that our model has resulted in a ‘singular fit.’ Singular fits often indicate that the model is ‘overfitted’ - that is, the random effects structure which we have specified is too complex to be supported by the data.
Perhaps the most intuitive advice would be remove the most complex part of the random effects structure (i.e. random slopes). This leads to a simpler model that is not over-fitted. In other words, start simplying from the top (where the most complexity is) to the bottom (where the lowest complexity is). Additionally, when variance estimates are very low for a specific random effect term, this indicates that the model is not estimating this parameter to differ much between the levels of your grouping variable. It might, in some experimental designs, be perfectly acceptable to remove this or simply include it as a fixed effect.
A key point here is that when fitting a mixed model, we should think about how the data are generated. Asking yourself questions such as “do we have good reason to assume subjects might vary over time, or to assume that they will have different starting points (i.e., different intercepts)?” can help you in specifying your random effect structure
You can read in depth about what this means by reading the help documentation for ?isSingular. For our purposes, a relevant section is copied below:
… intercept-only models, or 2-dimensional random effects such as intercept + slope models, singularity is relatively easy to detect because it leads to random-effect variance estimates of (nearly) zero, or estimates of correlations that are (almost) exactly -1 or 1.
Convergence warnings
Issues of non-convergence can be caused by many things. If you’re model doesn’t converge, it does not necessarily mean the fit is incorrect, however it is is cause for concern, and should be addressed, else you may end up reporting inferences which do not hold.
There are lots of different things which you could do which might help your model to converge. A select few are detailed below:
double-check the model specification and the data
adjust stopping (convergence) tolerances for the nonlinear optimizer, using the optCtrl argument to [g]lmerControl. (see
?convergencefor convergence controls).- What is “tolerance?” Remember that our optimizer is the the method by which the computer finds the best fitting model, by iteratively assessing and trying to maximise the likelihood (or minimise the loss).
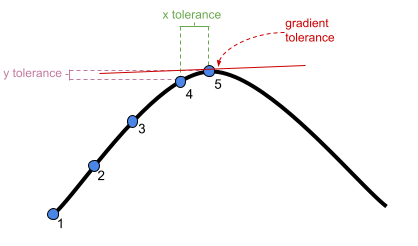
Figure 1: An optimizer will stop after a certain number of iterations, or when it meets a tolerance threshold
- What is “tolerance?” Remember that our optimizer is the the method by which the computer finds the best fitting model, by iteratively assessing and trying to maximise the likelihood (or minimise the loss).
center and scale continuous predictor variables (e.g. with
scale)Change the optimization method (for example, here we change it to
bobyqa):lmer(..., control = lmerControl(optimizer="bobyqa"))
glmer(..., control = glmerControl(optimizer="bobyqa"))Increase the number of optimization steps:
lmer(..., control = lmerControl(optimizer="bobyqa", optCtrl=list(maxfun=50000))
glmer(..., control = glmerControl(optimizer="bobyqa", optCtrl=list(maxfun=50000))Use
allFit()to try the fit with all available optimizers. This will of course be slow, but is considered ‘the gold standard’; “if all optimizers converge to values that are practically equivalent, then we would consider the convergence warnings to be false positives.”Consider simplifying your model, for example by removing random effects with the smallest variance (but be careful to not simplify more than necessary, and ensure that your write up details these changes)
Recall Questions C1-C6 in last week’s exercises, we used the WeightMaintain3 dataset and fitted some models:
load(url("https://uoepsy.github.io/data/WeightMaintain3.rda"))
m.base <- lmer(WeightChange ~ Assessment + (1 + Assessment | ID), data=WeightMaintain3)
m.int <- lmer(WeightChange ~ Assessment + Condition + (1 + Assessment | ID), data=WeightMaintain3)
m.full <- lmer(WeightChange ~ Assessment * Condition + (1 + Assessment | ID), data=WeightMaintain3)Many of these were singular fits, and we ignored them, e.g:
isSingular(m.base)## [1] TRUEThink carefully about how you might simplify the random effect structure for these models, and pay close attention to the study design. What do we think the baseline weight change should be? Should it be the same for everyone? If so, might we want to remove the random intercept, which we can do by setting it to 0.
Random effects
When specifying a random effects model, think about the data you have and how they fit in the following table:
| Criterion: | Repetition: If the experiment were repeated: |
Desired inference: The conclusions refer to: |
|---|---|---|
| Fixed effects | Same levels would be used | The levels used |
| Random effects | Different levels would be used | A population from which the levels used are just a (random) sample |
For example, applying the criteria to the following questions:
Do dogs learn faster with higher rewards?
FIXED: reward
RANDOM: dog
Do students read faster at higher temperatures?
FIXED: temperature
RANDOM: student
Does people speaking one language speak faster than another?
FIXED: the language
RANDOM: the people speaking that language
Sometimes, after simplifying the model, you find that there isn’t much variability in a specific random effect and, if it still leads to singular fits or convergence warnings, it is common to just model that variable as a fixed effect.
Other times, you don’t have sufficient data or levels to estimate the random effect variance, and you are forced to model it as a fixed effect. This is similar to trying to find the “best-fit” line passing through a single point… You can’t because you need two points!
Random effects in lme4
Below are a selection of different formulas for specifying different random effect structures, taken from the lme4 vignette. This might look like a lot, but over time and repeated use of multilevel models you will get used to reading these in a similar way to getting used to reading the formula structure of y ~ x1 + x2 in all our linear models.
| Formula | Alternative | Meaning |
|---|---|---|
| \(\text{(1 | g)}\) | \(\text{1 + (1 | g)}\) | Random intercept with fixed mean |
| \(\text{0 + offset(o) + (1 | g)}\) | \(\text{-1 + offset(o) + (1 | g)}\) | Random intercept with a priori means |
| \(\text{(1 | g1/g2)}\) | \(\text{(1 | g1) + (1 | g1:g2)}\) | Intercept varying among \(g1\) and \(g2\) within \(g1\) |
| \(\text{(1 | g1) + (1 | g2)}\) | \(\text{1 + (1 | g1) + (1 | g2)}\) | Intercept varying among \(g1\) and \(g2\) |
| \(\text{x + (x | g)}\) | \(\text{1 + x + (1 + x | g)}\) | Correlated random intercept and slope |
| \(\text{x + (x || g)}\) | \(\text{1 + x + (x | g) + (0 + x | g)}\) | Uncorrelated random intercept and slope |
Table 1: Examples of the right-hand-sides of mixed effects model formulas. \(g\), \(g1\), \(g2\) are grouping factors, covariates and a priori known offsets are \(x\) and \(o\).
Three-level nesting
Data: Treatment Effects
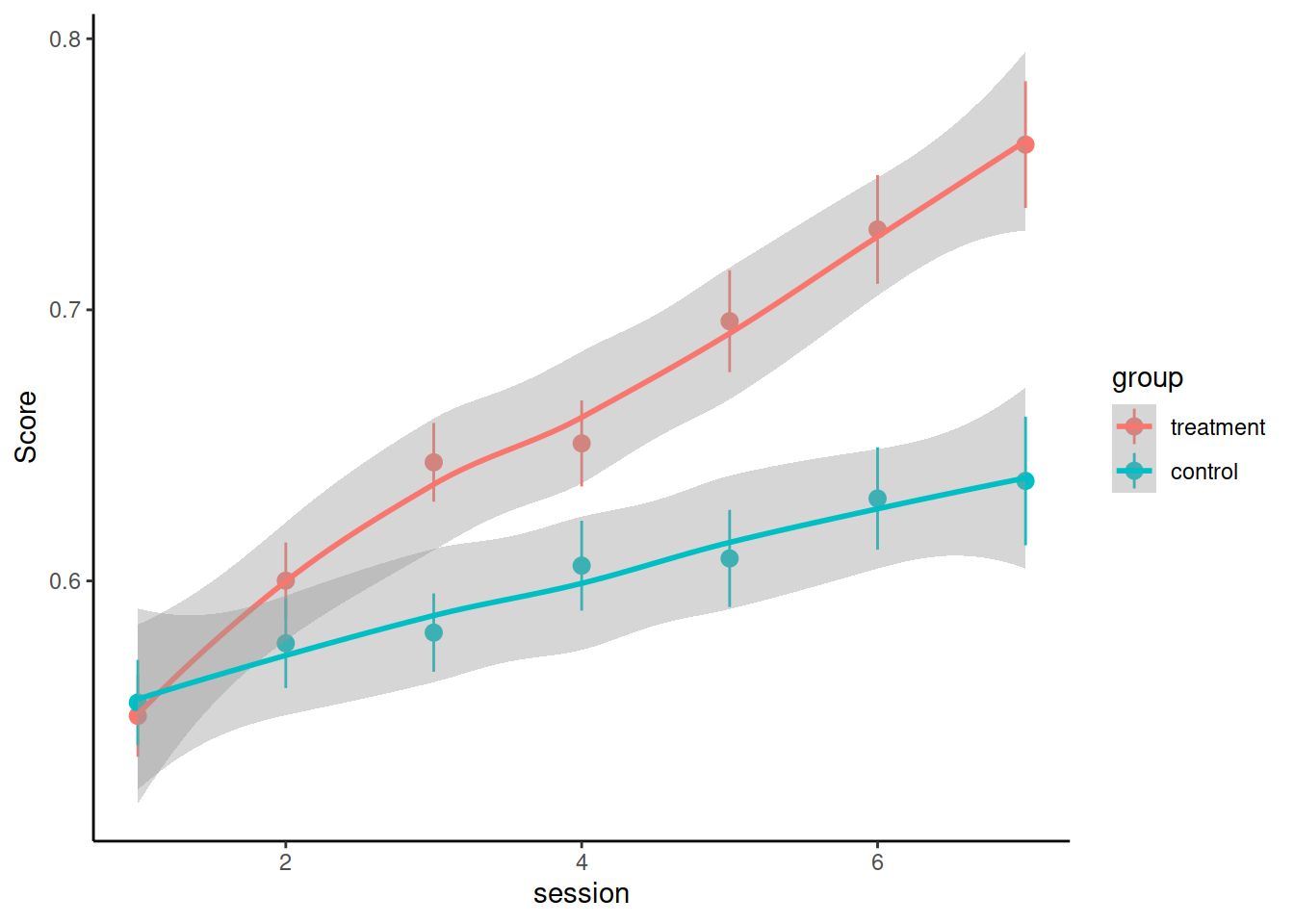
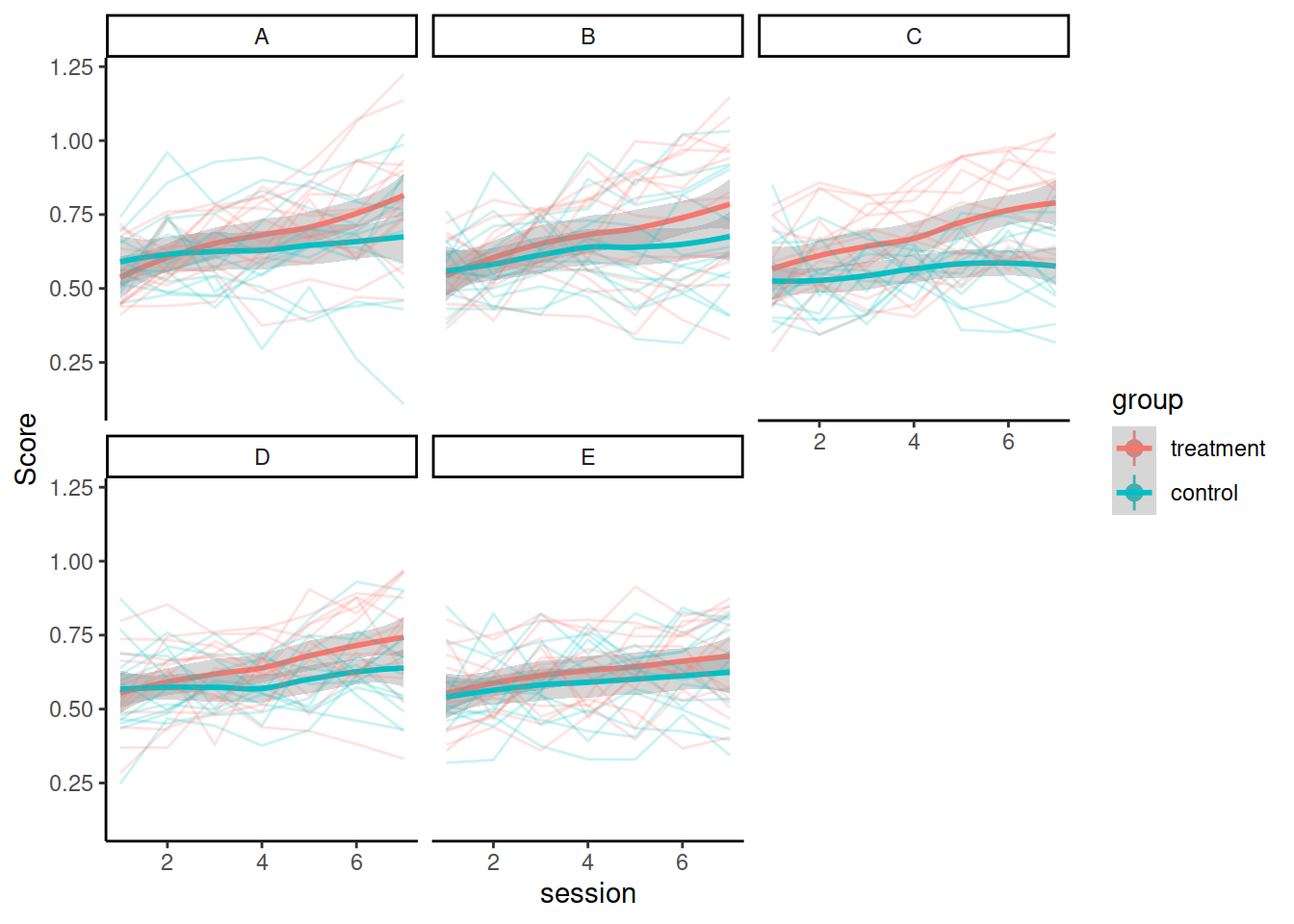
Synthetic data from a RCT treatment study: 5 therapists randomly assigned participants to control or treatment group and monitored the participants’ performance over time. There was a baseline test, then 6 weeks of treatment, with test sessions every week (7 total sessions).
The following code will load in your R session an object already called tx with the data:
load(url("https://uoepsy.github.io/msmr/data/tx.Rdata"))| group | session | therapist | Score | PID |
|---|---|---|---|---|
| control | 1 | A | 0.56 | A_control_15 |
| control | 1 | B | 0.61 | B_control_15 |
| control | 1 | C | 0.54 | C_control_15 |
| control | 1 | D | 0.45 | D_control_15 |
| control | 1 | E | 0.59 | E_control_15 |
| control | 1 | A | 0.56 | A_control_21 |
Load and visualise the data. Does it look like the treatment had an effect on the performance score?
Consider these questions when you’re designing your model(s) and use your answers to motivate your model design and interpretation of results:
- What are the levels of nesting? How should that be reflected in the random effect structure?
- What is the shape of change over time? Do you need polynomials to model this shape? If yes, what order polynomials?
Test whether the treatment had an effect using mixed-effects modelling.
Try to fit the maximal model.
Does it converge? Is it singular?
Try adjusting your model by removing random effects or correlations, examine the model again, and so on..
Try the code below to use the allFit() function to fit your final model with all the available optimizers.1
- You might need to install the
dfoptimpackage to get one of the optimizers
sumfits <- allFit(yourmodel)
summary(sumfits)
Crossed random effects
Data: Test-enhanced learning
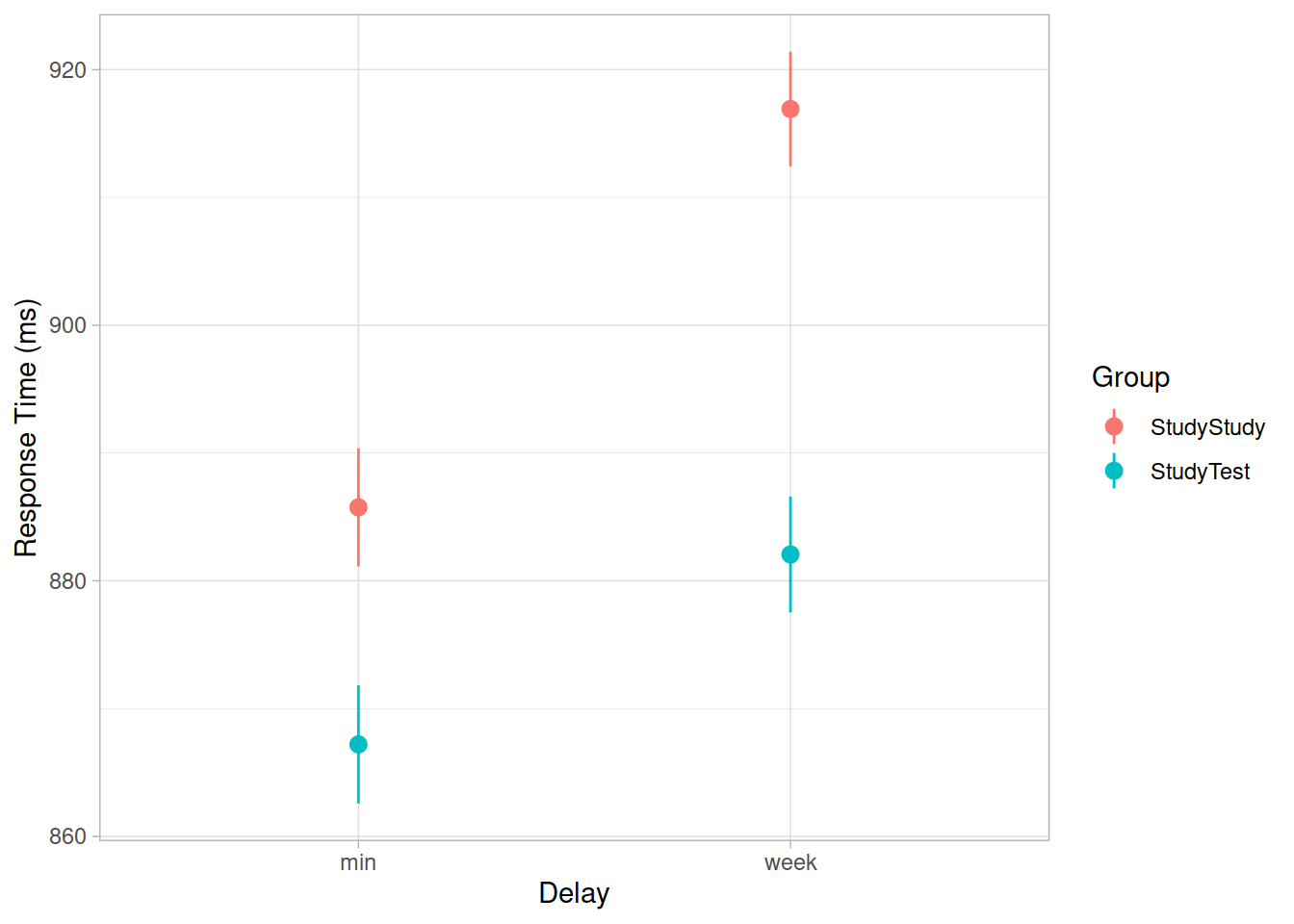
An experiment was run to conceptually replicate “test-enhanced learning” (Roediger & Karpicke, 2006): two groups of 25 participants were presented with material to learn. One group studied the material twice (StudyStudy), the other group studied the material once then did a test (StudyTest). Recall was tested immediately (one minute) after the learning session and one week later. The recall tests were composed of 175 items identified by a keyword (Test_word). One of the researchers’ questions concerned how test-enhanced learning influences time-to-recall.
The critical (replication) prediction is that the StudyStudy group should perform somewhat better on the immediate recall test, but the StudyTest group will retain the material better and thus perform better on the 1-week follow-up test.
The following code loads the data into your R environment by creating a variable called tel:
load(url("https://uoepsy.github.io/data/testenhancedlearning.RData"))| Subject_ID | Group | Delay | Test_word | Correct | Rtime |
|---|---|---|---|---|---|
| StudyTest_L | StudyTest | min | van | 1 | 456.81 |
| StudyTest_L | StudyTest | week | dinosaur | 0 | 888.13 |
| StudyTest_L | StudyTest | min | typewriter | 0 | 713.43 |
| StudyTest_L | StudyTest | min | chimney | 0 | 725.52 |
| StudyTest_L | StudyTest | week | dog | 1 | 472.69 |
| StudyTest_L | StudyTest | min | turkey | 1 | 574.30 |
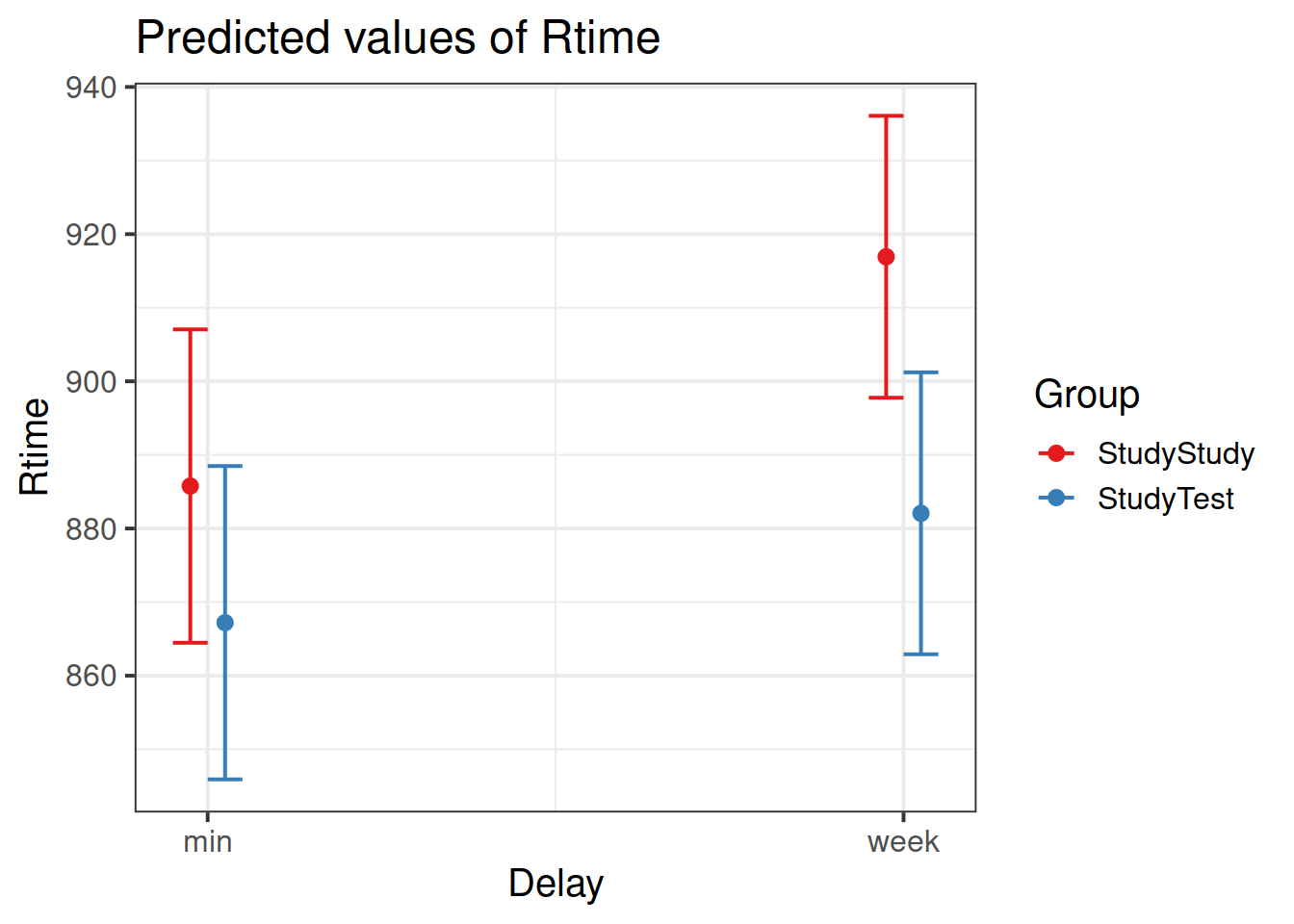
Load and plot the data. Does it look like the effect was replicated?
Test the critical hypothesis using a mixed-effects model. Fit the maximal random effect structure supported by the experimental design.
Some questions to consider:
Item accuracy is a binary variable. What kind of model will you use?
We can expect variability across subjects (some people are better at learning than others) and across items (some of the recall items are harder than others). How should this be represented in the random effects?
If a model takes ages to fit, you might want to cancel it by pressing the escape key. It is normal for complex models to take time, but for the purposes of this task, give up after a couple of minutes, and try simplifying your model.
The model with maximal random effects will probably not converge, or will obtain a singular fit. Simplify the model until you achieve convergence.
What we’re aiming to do here is to follow Barr et al.’s advice of defining our maximal model and then removing only the terms to allow a non-singular fit.
Note: This strategy - starting with the maximal random effects structure and removing terms until obtaining model convergence, is just one approach, and there are drawbacks (see Matuschek et al., 2017). There is no consensus on what approach is best (see ?isSingular).
Tip: you can look at the variance estimates and correlations easily by using the VarCorr() function. What jumps out?
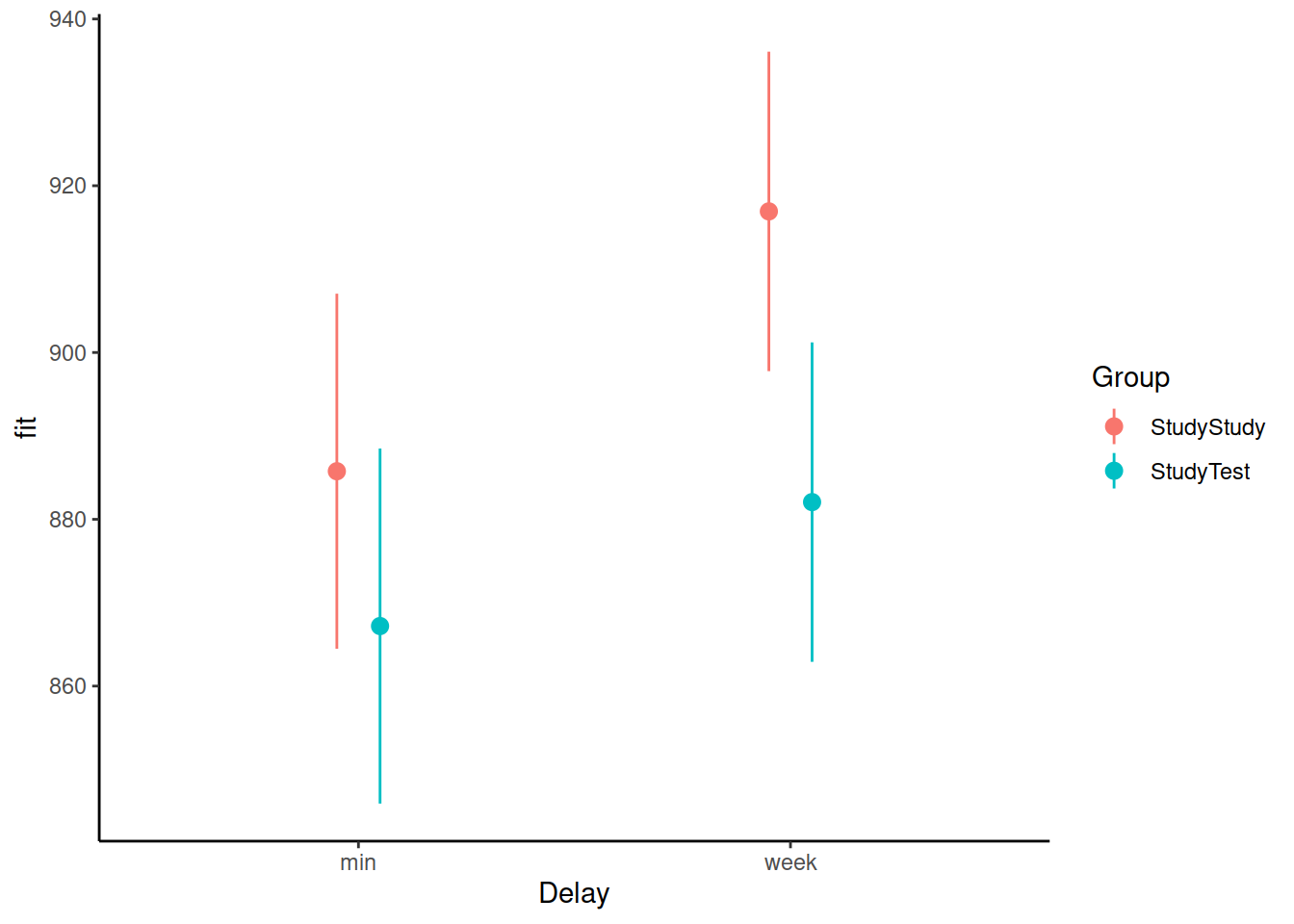
Load the effects package, and try running this code:
library(effects)
ef <- as.data.frame(effect("Delay:Group", m2))What is ef? and how can you use it to plot the model-estimated condition means and variability?
Can we get a similar plot using plot_model() from the sjPlot package?
What should we do with this information? How can we apply test-enhanced learning to learning R and statistics?
Less-Guided Exercises
Data: Naming
72 children from 10 schools were administered the full Boston Naming Test (BNT-60) on a yearly basis for 5 years to examine development of word retrieval. Five of the schools taught lessons in a bilingual setting with English as one of the languages, and the remaining five schools taught in monolingual English.
The data is available at https://uoepsy.github.io/data/bntmono.csv.
| variable | description |
|---|---|
| child_id | unique child identifier |
| school_id | unique school identifier |
| BNT60 | score on the Boston Naming Test-60. Scores range from 0 to 60 |
| schoolyear | Year of school |
| mlhome | Mono/Bi-lingual School. 0 = Bilingual, 1 = Monolingual |
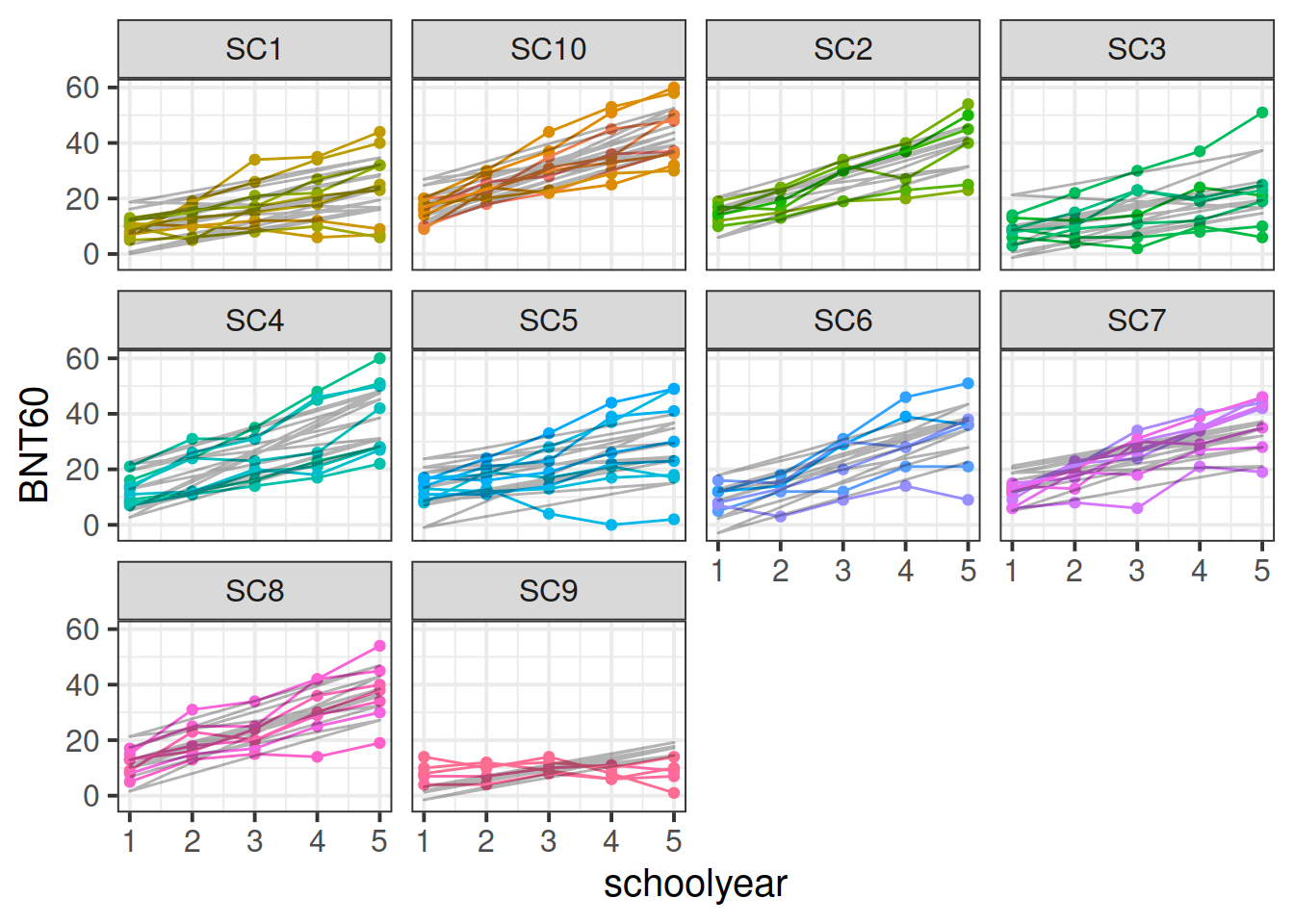
Fit a model examining the interaction between the effects of school year and mono/bilingual teaching on word retrieval, with random intercepts only for children and schools.
tip: make sure your variables are of the right type first - e.g. numeric, factor etc
Examine the fit and consider your model assumptions, and assess what might be done to improve the model in order to make better statistical inferences.
Using a method of your choosing, conduct inferences from your model and write up the results.
If you have an older version of
lme4, thenallFit()might not be directly available, and you will need to run the following:source(system.file("utils", "allFit.R", package="lme4")).↩︎
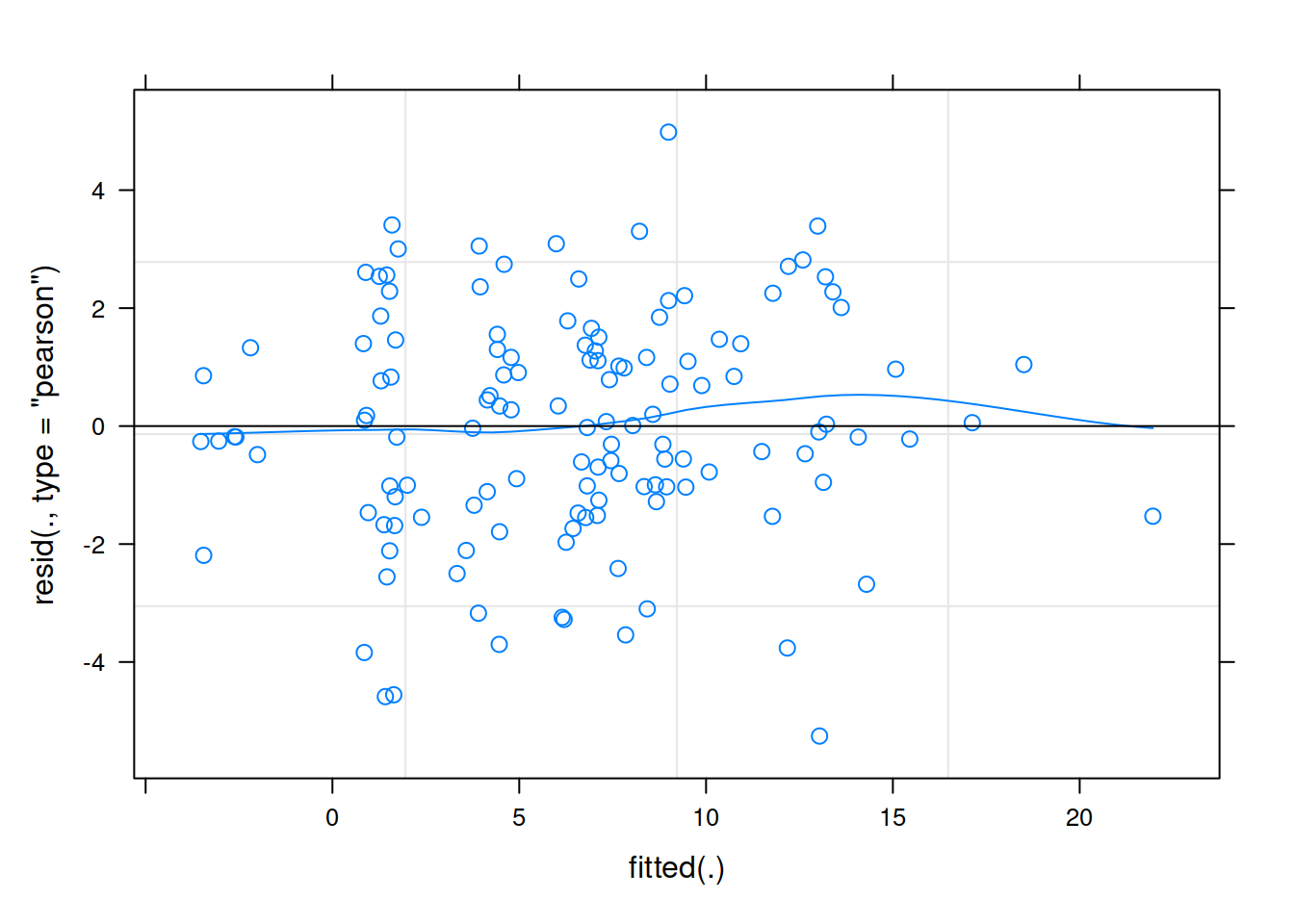
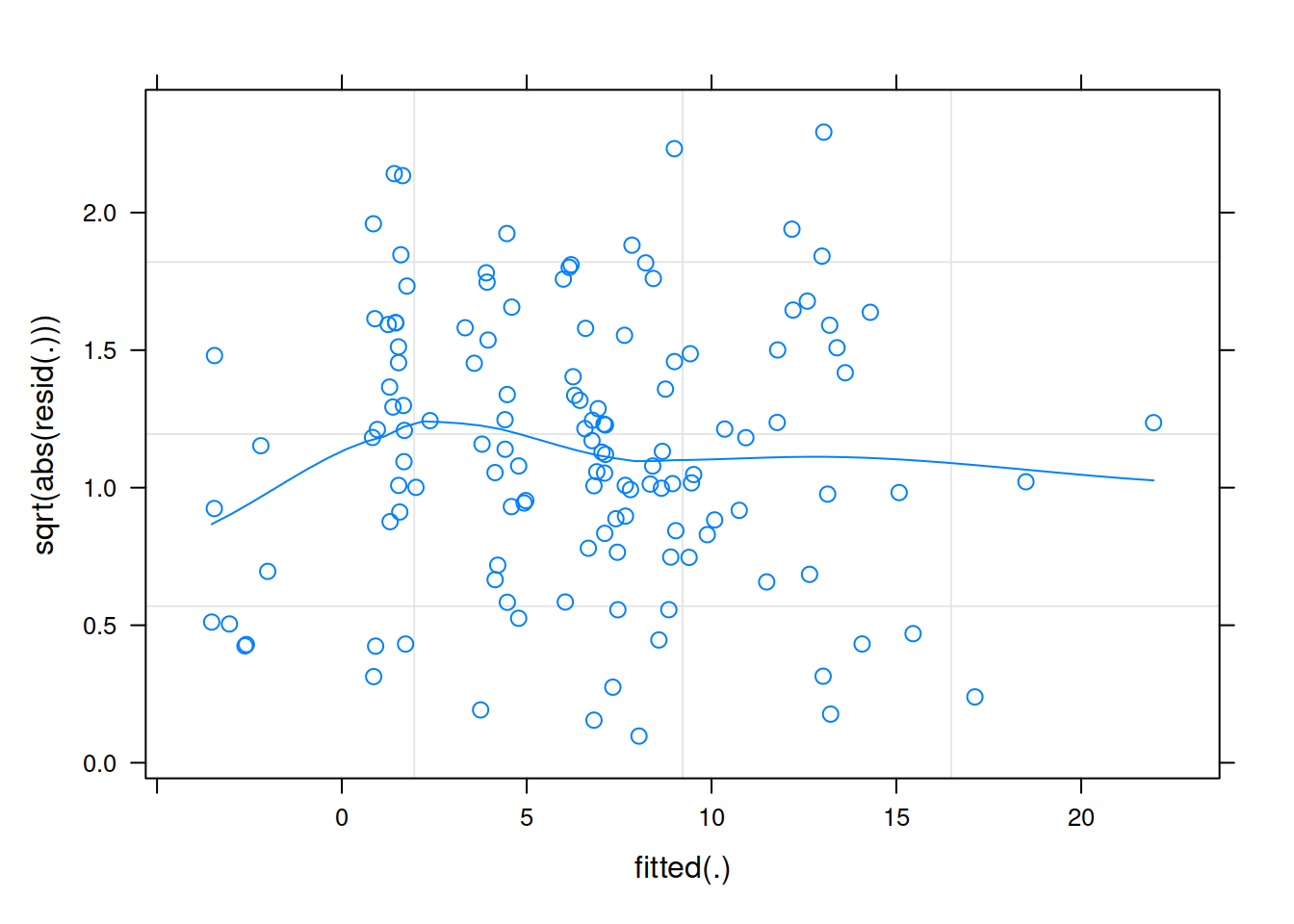
 Level 2
Level 2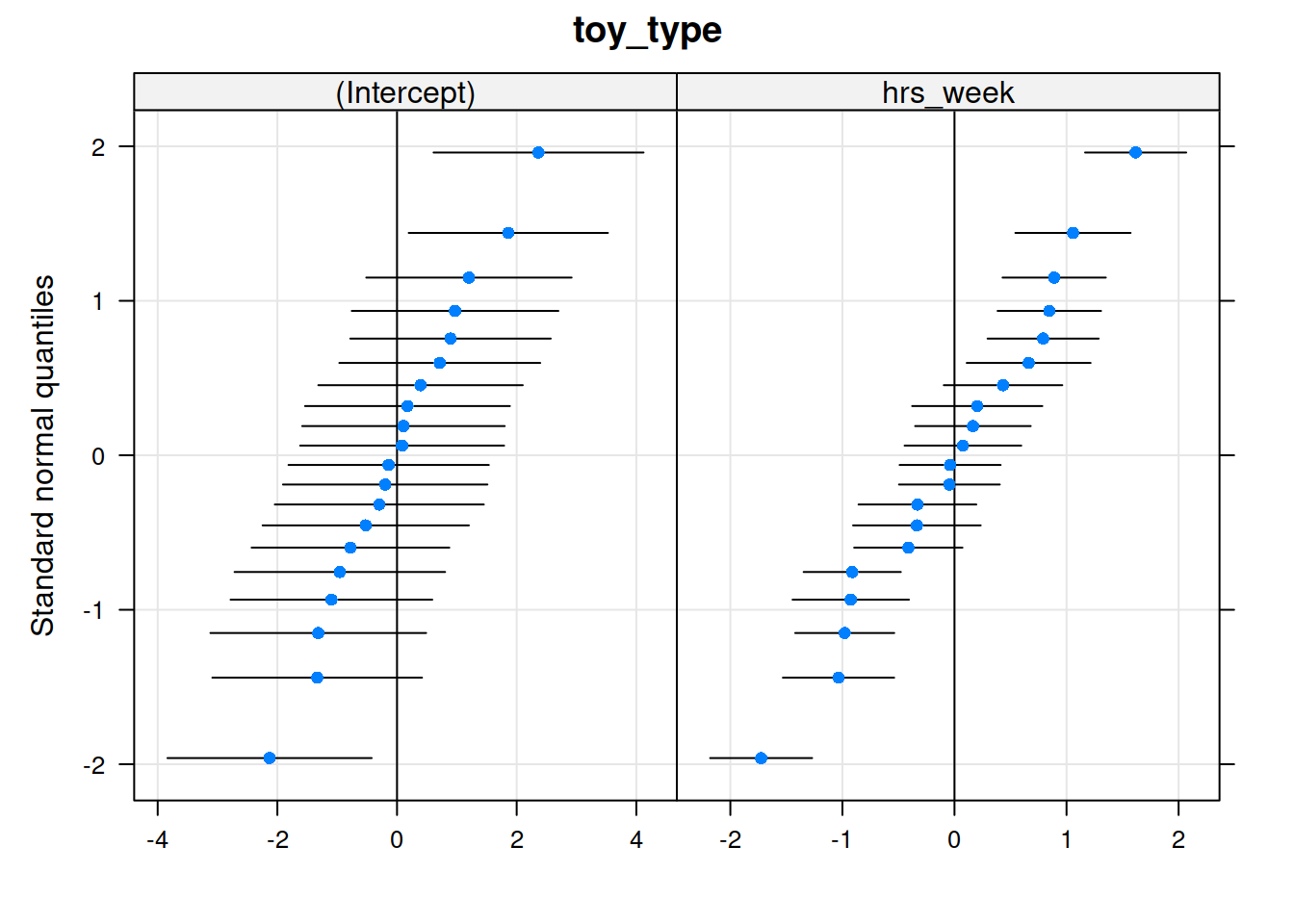
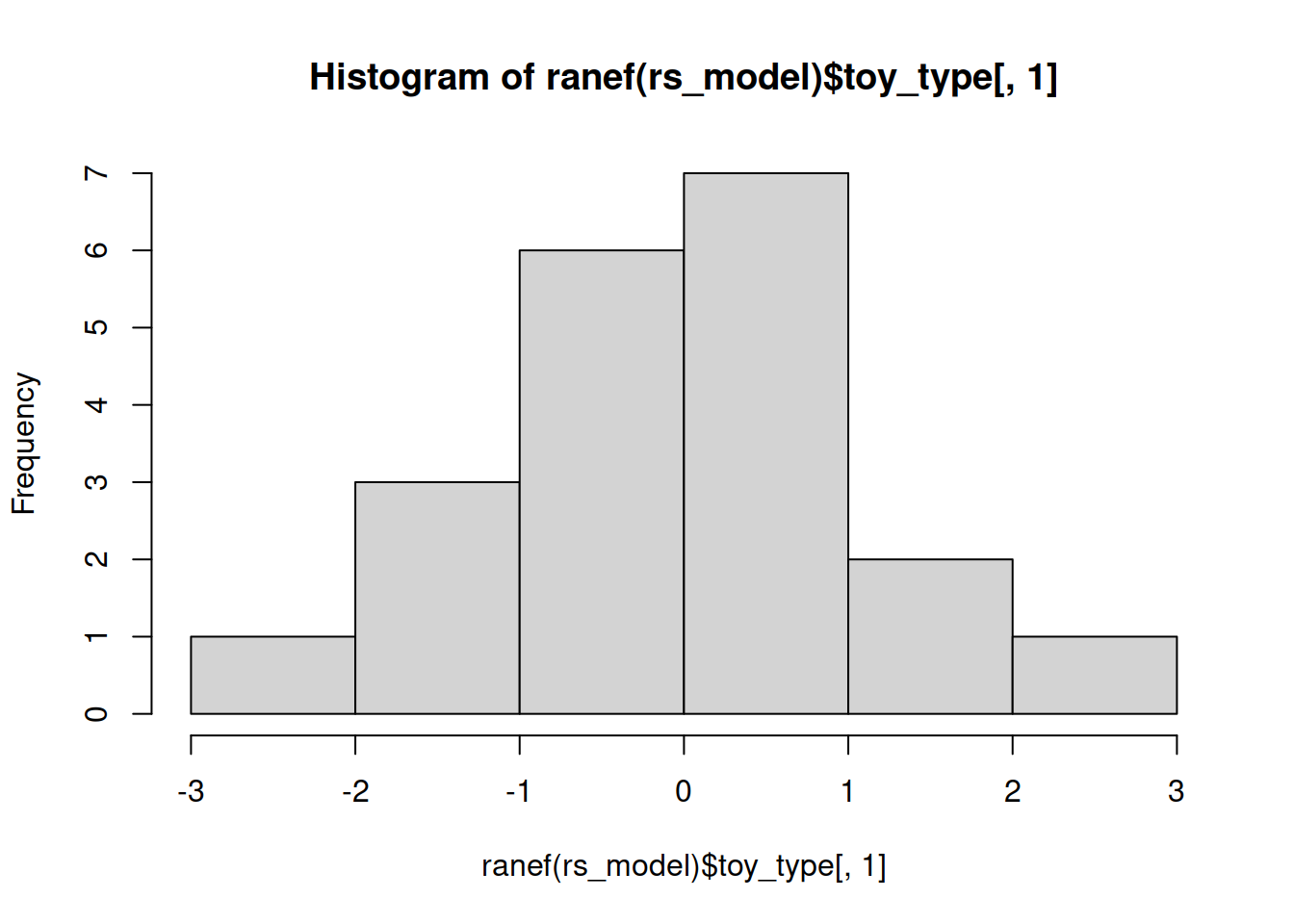
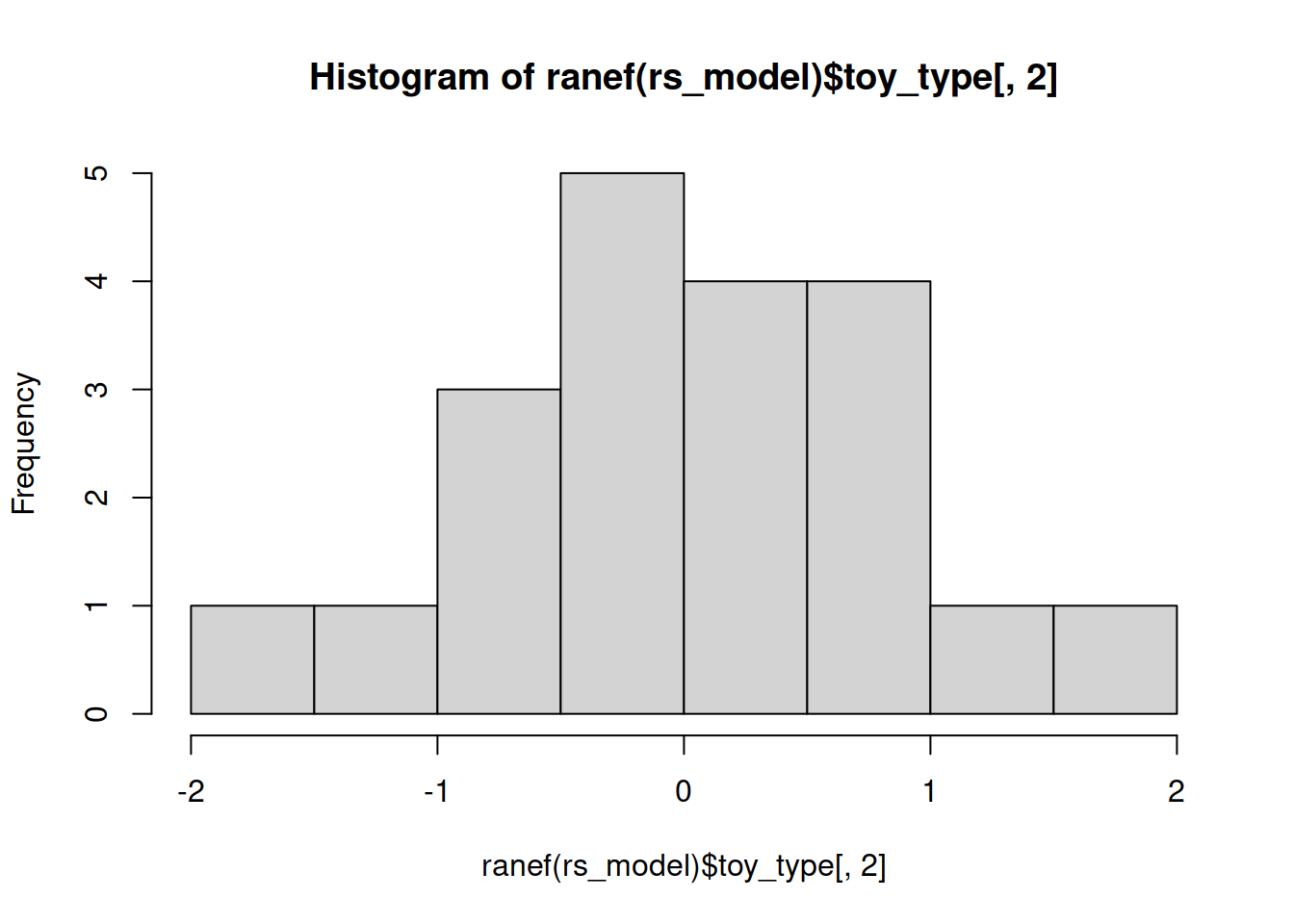
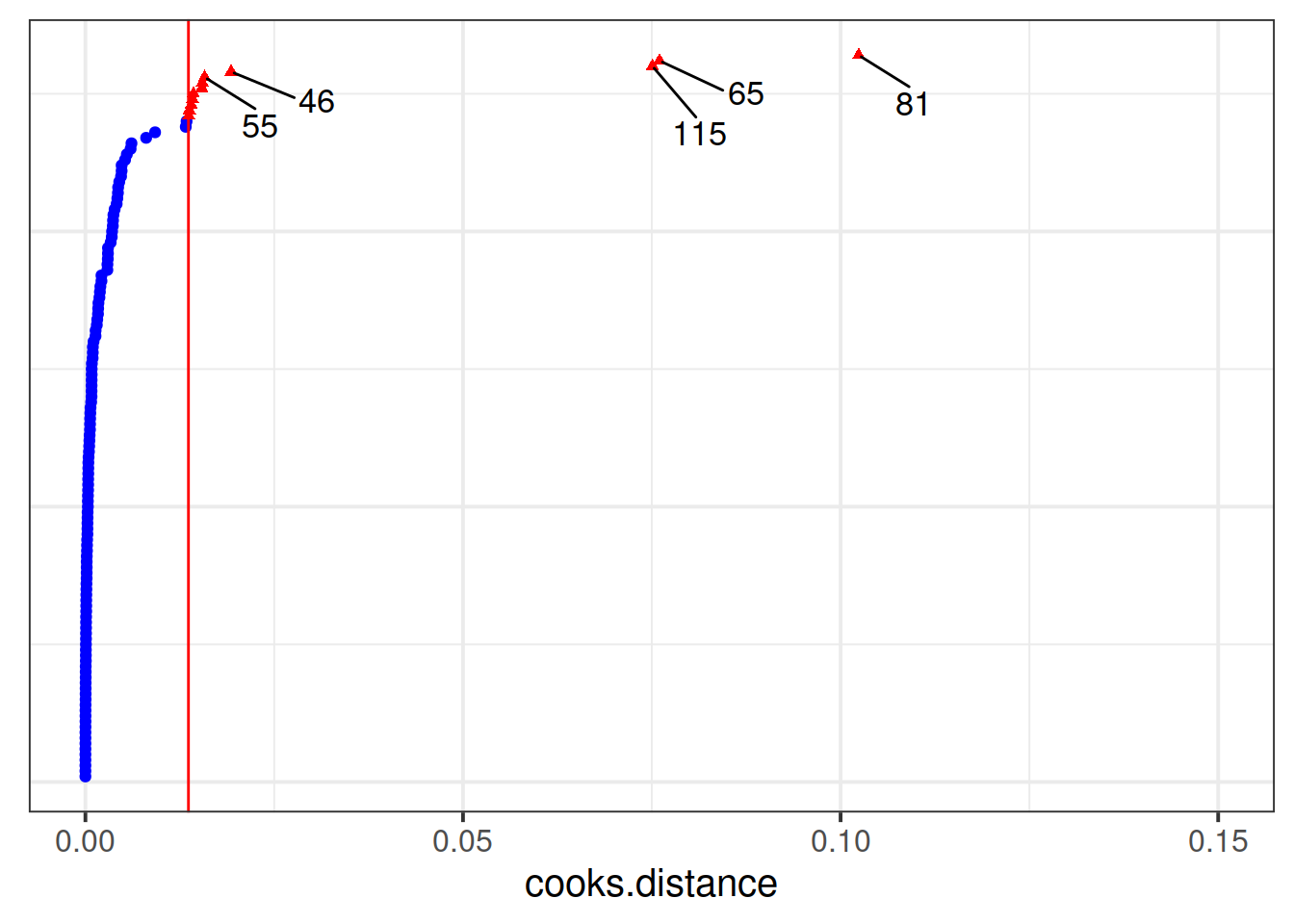


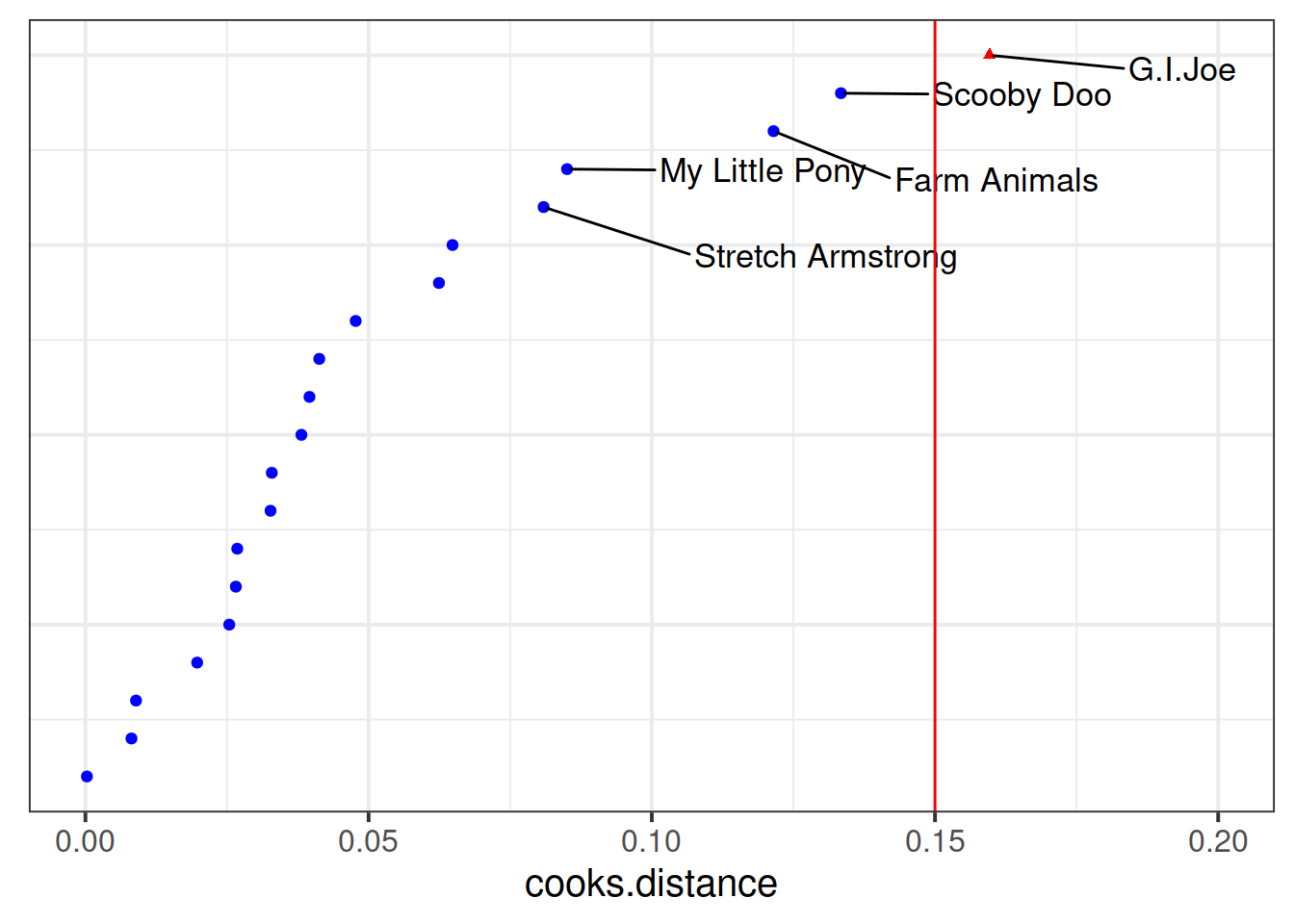

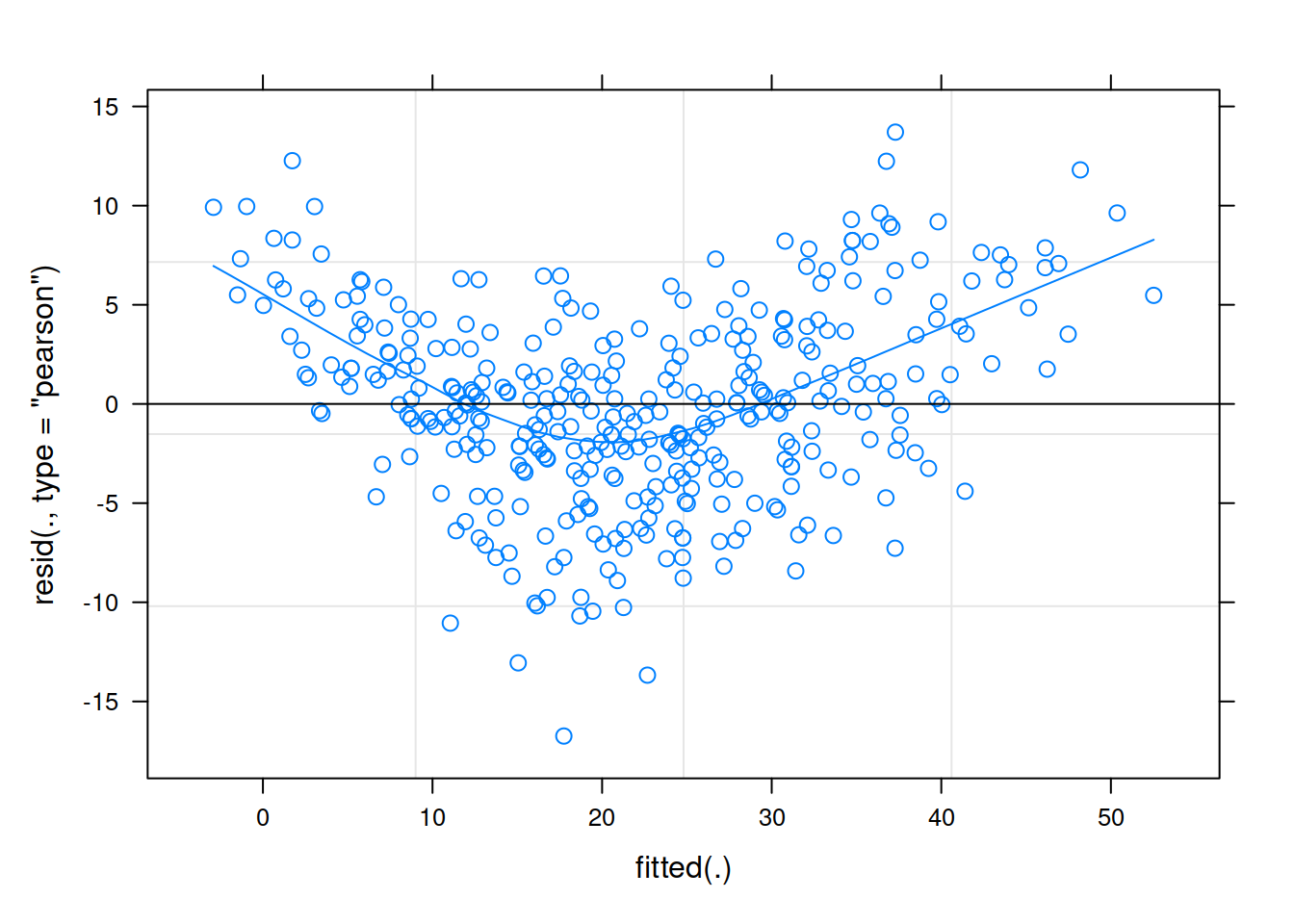
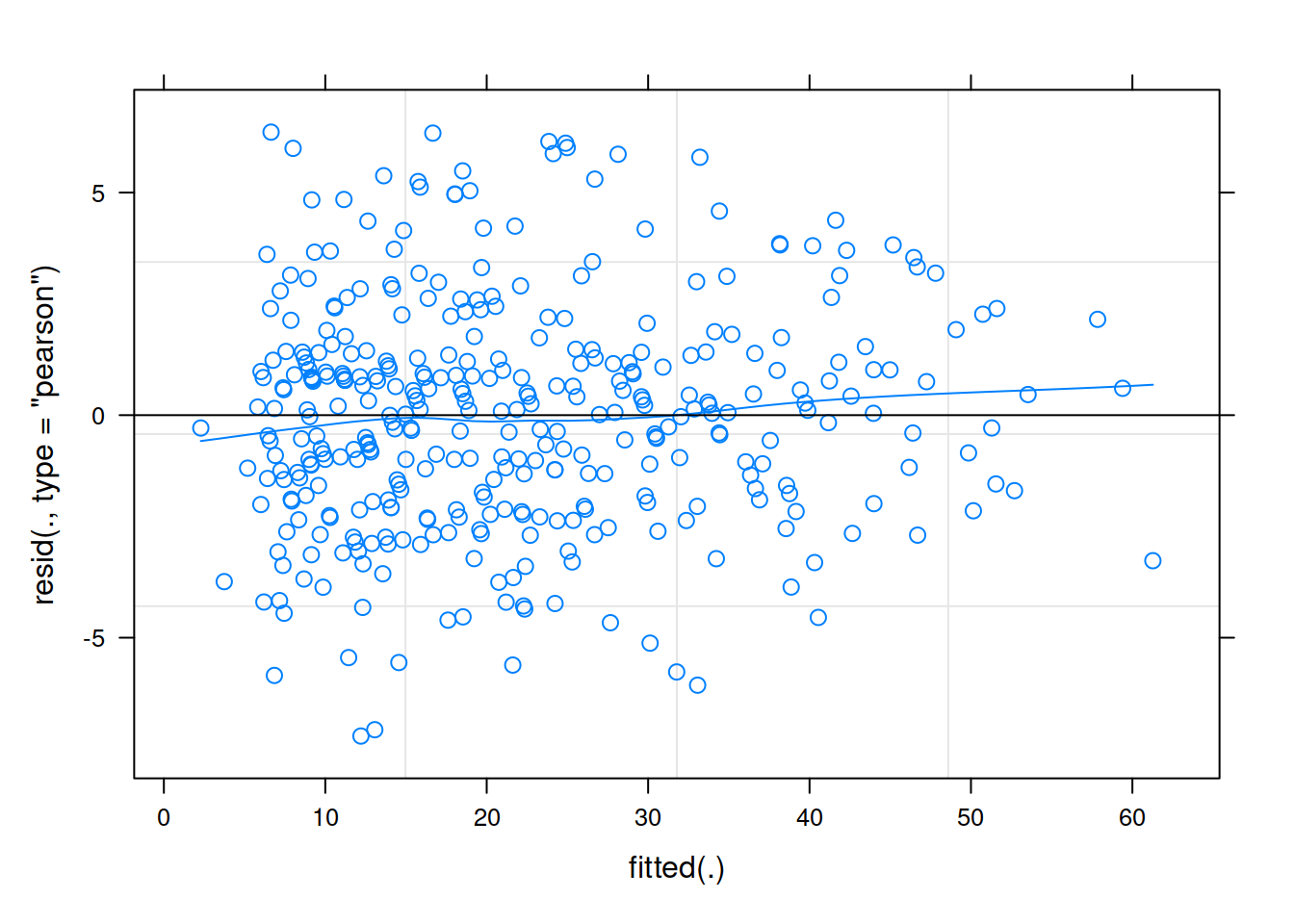 Much better!
Much better!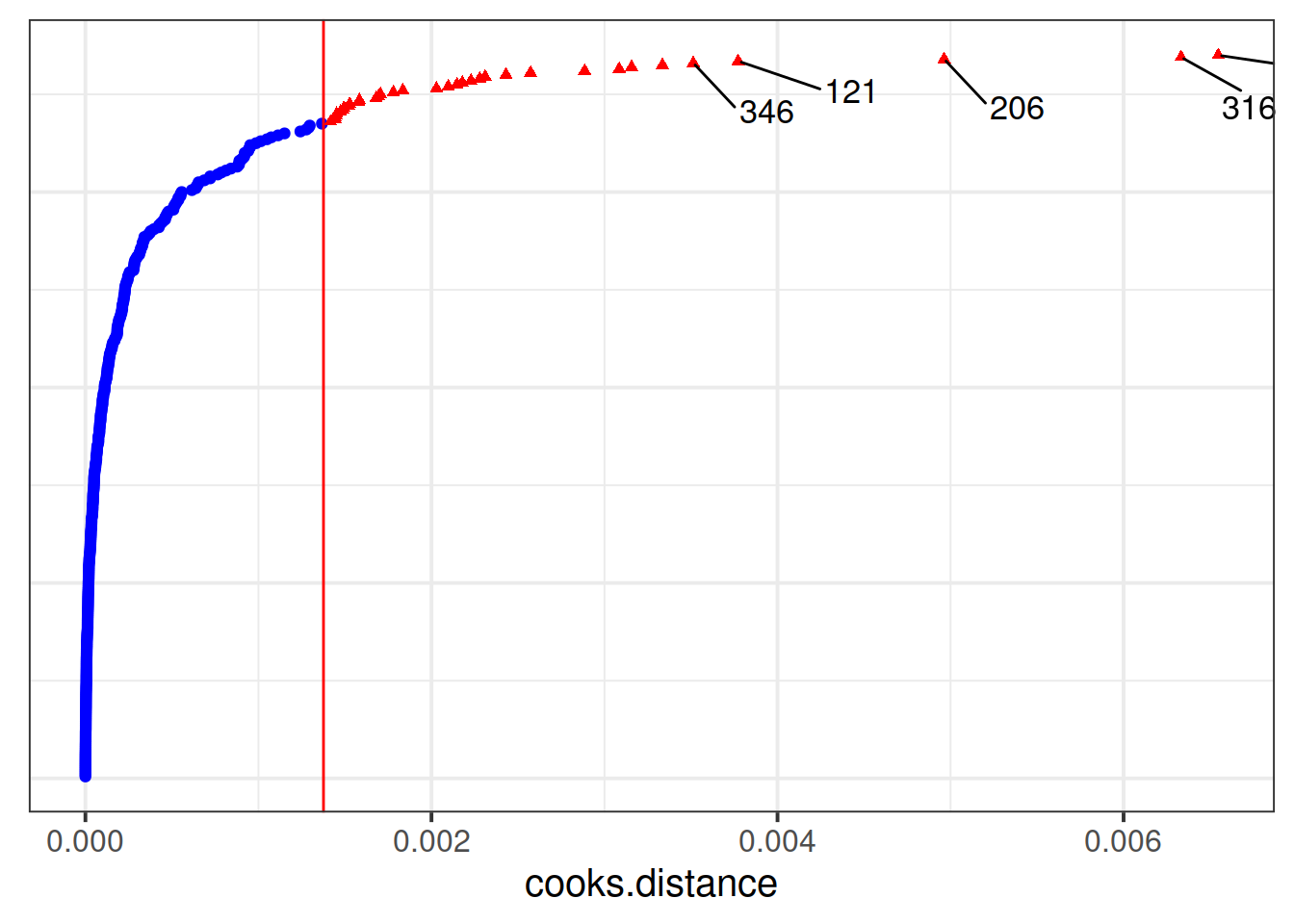
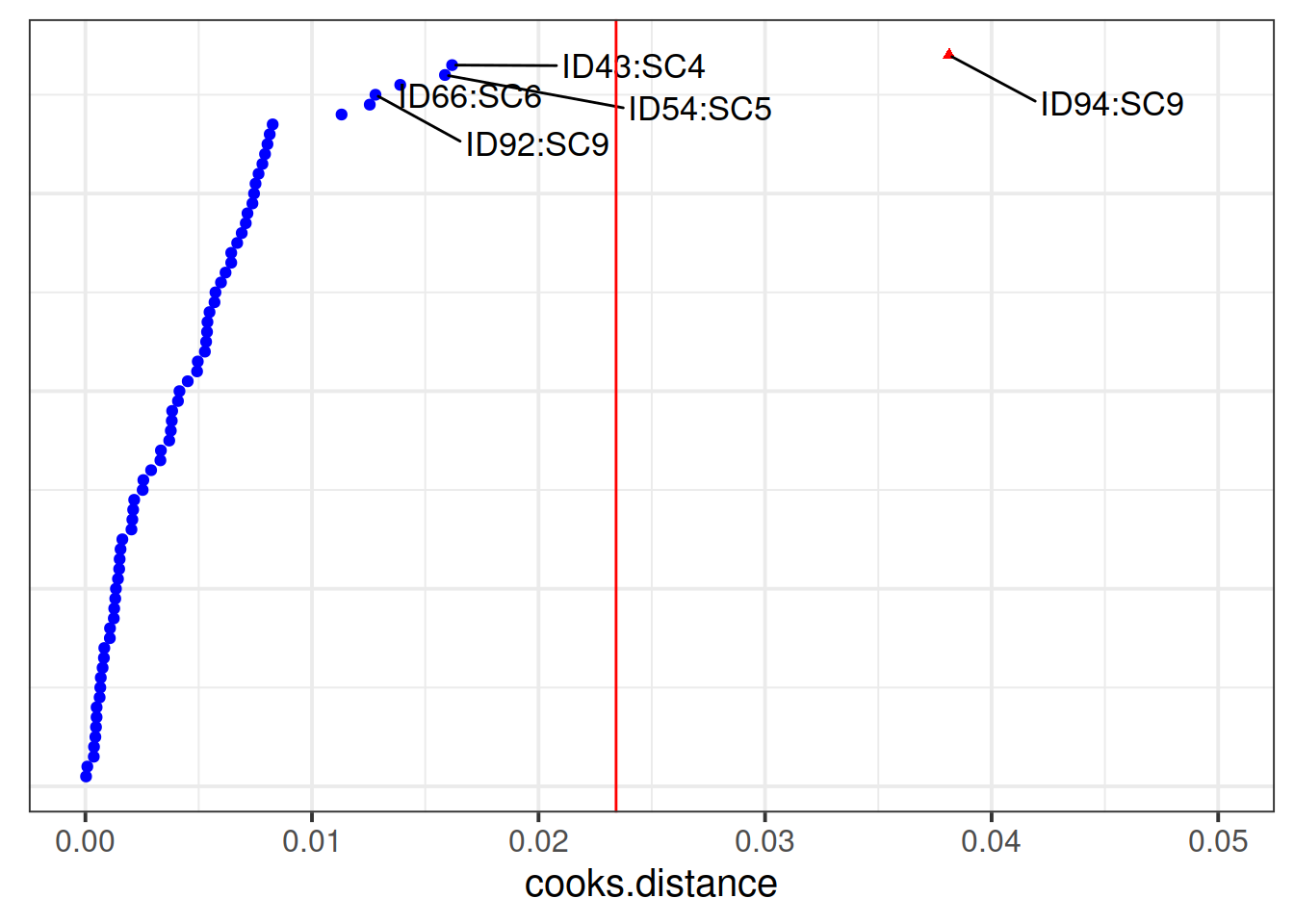 And then we can examine the effects to the fixed effects and our standard errors when we remove this child:
And then we can examine the effects to the fixed effects and our standard errors when we remove this child: