Interactions II: Cat x Cat

Learning Objectives

At the end of this lab, you will:

1. Be able to interpret a categorical \(\times\) categorical interaction.
2. Visualize and probe interactions.
3. Be able to read interaction plots.

What You Need

You will need to have completed [Lab X].

Required R Packages

Remember to load all packages within a code chunk at the start of your RMarkdown file using library(). If you do not have a package and need to install, do so within the console using install.packages(" "). For further guidance on installing/updating packages, see Section C here.

For this lab, you will need to load the following package(s):

• tidyverse
• sjPlot
• emmeans

Lab Data

You can download the data required for this lab here or read it in via this link https://uoepsy.github.io/data/cognitive_experiment_3_by_2.csv

Study Overview

Research Question

Specify specific question

A group of researchers wants to test an hypothesised theory according to which the difference in performance between explicit and implicit memory tasks will be greatest for Huntington patients in comparison to controls. On the other hand, the difference in performance between explicit and implicit memory tasks will not significantly differ between patients with amnesia in comparison to controls.

Cognitive Exp 3x2 data codebook.

Description

The researchers designed a study yielding a 3 by 2 factorial design to test this theory. The first factor, “Diagnosis”, classifies the three types of individuals:

• 1 denotes amnesic patients;
• 2 denotes Huntingtons patients; and
• 3 denotes a control group of individuals with no known neurological disorder.

The second factor, “Task”, tells us to which of two tasks each study participant was randomly assigned to:

• 1 = grammar task, which consists of classifying letter sequences as either following or not following grammatical rules; and
• 2 = recognition task, which consists of recognising particular stimuli as stimuli that have previously been presented during the task.

Keep in mind that each person has been randomly assigned to one of the two tasks, so there are five observations per cell of the design.¹

The tasks chosen by the researchers have been picked to map onto the theoretical differences between the three types of research participants. The first task (grammar) is known to reflect implicit memory processes, whereas the recognition task is known to reflect explicit memory processes. If the theory is correct, we would expect the difference in scores between the recognition and grammar tasks to be relatively similar for the control and amnesiac groups, but relatively larger for the Huntingtons group compared to controls.

Preview

The first ten rows of the data are:

Rows: 30 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (3): Diagnosis, Task, Y

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Setup

Setup

1. Create a new RMarkdown file
2. Load the required package(s)
3. Read the cognitive_experiment_3_by_2 dataset into R, assigning it to an object named cog.

Solution

#Loading the required package(s)
library(tidyverse)
library(sjPlot)

Registered S3 method overwritten by 'parameters':
  method                      from       
  plot.check_clusterstructure performance

Learn more about sjPlot with 'browseVignettes("sjPlot")'.

library(emmeans)

# Reading in data and storing to an object named 'cog'
cog <- read_csv("https://uoepsy.github.io/data/cognitive_experiment_3_by_2.csv")

Rows: 30 Columns: 3

── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (3): Diagnosis, Task, Y

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Exercises

Question 1

Examine the dataset, and perform all the appropriate data management steps:

• Convert categorical variables to factors
• Label appropriately factors to aid with your model interpretations
• If needed, provide better variable names

Solution

head(cog)

# A tibble: 6 × 3
  Diagnosis  Task     Y
      <dbl> <dbl> <dbl>
1         1     1    44
2         1     1    63
3         1     1    76
4         1     1    72
5         1     1    45
6         1     2    70

The columns Diagnosis and Task should be coded into factors with better labels (i.e., without making reference to the codebook, it is not clear what “1” and “2” represent). The function factor() can be used by specifying the current levels and what labels each level should map to.

cog <- cog %>%
    mutate(
        Diagnosis = factor(Diagnosis, 
                           levels = c(1, 2, 3),
                           labels = c('Amnesic', 'Huntingtons', 'Control')),
        Task = factor(Task, 
                      levels = c(1, 2),
                      labels = c('Grammar', 'Recognition'))
    ) %>%
    rename(
        Score = Y
    )

#Use head() function to check renaming
head(cog)

# A tibble: 6 × 3
  Diagnosis Task        Score
  <fct>     <fct>       <dbl>
1 Amnesic   Grammar        44
2 Amnesic   Grammar        63
3 Amnesic   Grammar        76
4 Amnesic   Grammar        72
5 Amnesic   Grammar        45
6 Amnesic   Recognition    70

Question 2

Choose appropriate reference levels for the factors.

Solution

The Diagnosis factor has a group coded ‘Control’ which lends itself naturally to be the reference category.

cog$Diagnosis <- relevel(cog$Diagnosis, 'Control')

levels(cog$Diagnosis)

[1] "Control"     "Amnesic"     "Huntingtons"

There is no natural reference category for the Task factor, so we will leave it unaltered. However, if you are of a different opinion, please note that there is no absolute correct answer. As long as you interpret the model correctly, you will reach to the same conclusions as someone that has chosen a different baseline category.

Question 3

Specify a multiple regression model to test the research hypothesis.

Solution

Define the dummy variables for Diagnosis:

\[ D_\text{Amnesic} = \begin{cases} 1 & \text{if Diagnosis is Amnesic} \\ 0 & \text{otherwise} \end{cases} \quad D_\text{Huntingtons} = \begin{cases} 1 & \text{if Diagnosis is Huntingtons} \\ 0 & \text{otherwise} \end{cases} \quad (\text{Control is base level}) \]

Define the dummy variable for Task:

\[ T_\text{Recognition} = \begin{cases} 1 & \text{if Task is Recognition} \\ 0 & \text{otherwise} \end{cases} \quad (\text{Grammar is base level}) \]

The model becomes

\[ \begin{aligned} Score &= \beta_0 \\ &+ \beta_1 D_\text{Amnesic} + \beta_2 D_\text{Huntingtons} \\ &+ \beta_3 T_\text{Recognition} \\ &+ \beta_4 (D_\text{Amnesic} * T_\text{Recognition}) + \beta_5 (D_\text{Huntingtons} * T_\text{Recognition}) \\ &+ \epsilon \end{aligned} \]

Question 4

Fit the specified model using lm(), and store the model in an object named mdl_int.

Note: Fortunately, R computes the dummy variables for us! Thus. each row in the summary of the model will correspond to one of the estimated \(\beta\)’s in the equation above.

Solution

mdl_int <- lm(Score ~ Diagnosis * Task, data = cog)

summary(mdl_int)

Call:
lm(formula = Score ~ Diagnosis * Task, data = cog)

Residuals:
   Min     1Q Median     3Q    Max 
-16.00 -12.25   2.00  11.75  18.00 

Coefficients:
                                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)                            80.000      5.859  13.653 8.27e-13 ***
DiagnosisAmnesic                      -20.000      8.287  -2.414  0.02379 *  
DiagnosisHuntingtons                  -40.000      8.287  -4.827 6.45e-05 ***
TaskRecognition                        15.000      8.287   1.810  0.08281 .  
DiagnosisAmnesic:TaskRecognition      -10.000     11.719  -0.853  0.40192    
DiagnosisHuntingtons:TaskRecognition   40.000     11.719   3.413  0.00228 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 13.1 on 24 degrees of freedom
Multiple R-squared:  0.7394,    Adjusted R-squared:  0.6851 
F-statistic: 13.62 on 5 and 24 DF,  p-value: 2.359e-06

Question 5

Create a table of group means, and map each coefficient to the group means.

Solution

means <- cog %>%
    group_by(Diagnosis, Task) %>% 
    summarise(M = mean(Score))

`summarise()` has grouped output by 'Diagnosis'. You can override using the
`.groups` argument.

means

# A tibble: 6 × 3
# Groups:   Diagnosis [3]
  Diagnosis   Task            M
  <fct>       <fct>       <dbl>
1 Control     Grammar        80
2 Control     Recognition    95
3 Amnesic     Grammar        60
4 Amnesic     Recognition    65
5 Huntingtons Grammar        40
6 Huntingtons Recognition    95

We can also convert it to a 3 by 2 table of means. In the table below, the ‘Control’ row represents the base level for the Diagnosis factor, while the column ‘Grammar’ represents the base level for the Task factor.

means %>%
  pivot_wider(names_from = Task, values_from = M)

# A tibble: 3 × 3
# Groups:   Diagnosis [3]
  Diagnosis   Grammar Recognition
  <fct>         <dbl>       <dbl>
1 Control          80          95
2 Amnesic          60          65
3 Huntingtons      40          95

• \(\hat{\beta}_0\) = 80
  = Mean(Control, Grammar)

• \(\hat{\beta}_1\) = -20
  = Mean(Amnesic, Grammar) - Mean(Control, Grammar)
  = 60 - 80

• \(\hat{\beta}_2\) = -40
  = Mean(Huntingtons, Grammar) - Mean(Control, Grammar)
  = 40 - 80

• \(\hat{\beta}_3\) = 15
  = Mean(Control, Recognition) - Mean(Control, Grammar)
  = 95 - 80

• \(\hat{\beta}_4\) = -10
  = [Mean(Amnesic, Recognition) - Mean(Amnesic, Grammar)] -
  [Mean(Control, Recognition) - Mean(Control, Grammar)]
  = [65 - 60] - [95 - 80] = 5 - 15 = -10

• \(\hat{\beta}_5\) = 40
  = [Mean(Huntingtons, Recognition) - Mean(Huntingtons, Grammar)] -
  [Mean(Control, Recognition) - Mean(Control, Grammar)]
  = [95 - 40] - [95 - 80] = 55 - 15 = 40

Question 6

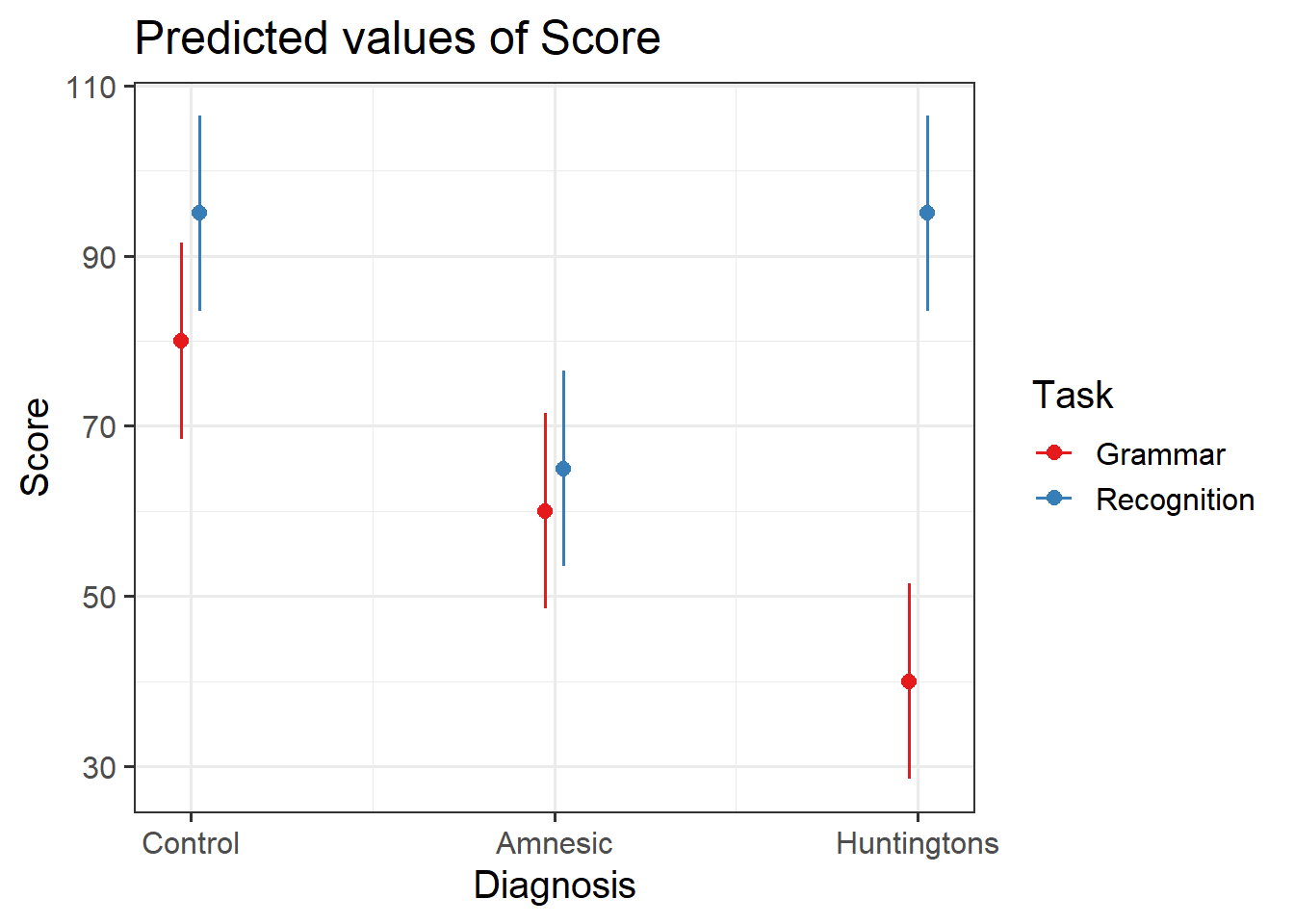
Use the function plot_model() (from the sjPlot package) to investigate the interactions.

Hint: Remember from last week that the default behaviour of plot_model() is to plot the parameter estimates and their confidence intervals. This is where type = " " will come handy.

Solution

plot_model(mdl_int, type = "int")

The red dots (‘Grammar’) represent the baseline for Task, while ‘Control’ is the baseline for Diagnosis.

If you imagine connecting the dots of the same color with a line, you can see that the two virtual lines are not parallel, suggesting the presence of an interaction. The difference in score between recognition and grammar tasks for Huntingtons patients (consider the vertical difference) is larger than the difference in score between recognition and grammar tasks for the Control patients. If those vertical differences were the same, there would be no interaction.

Question 7

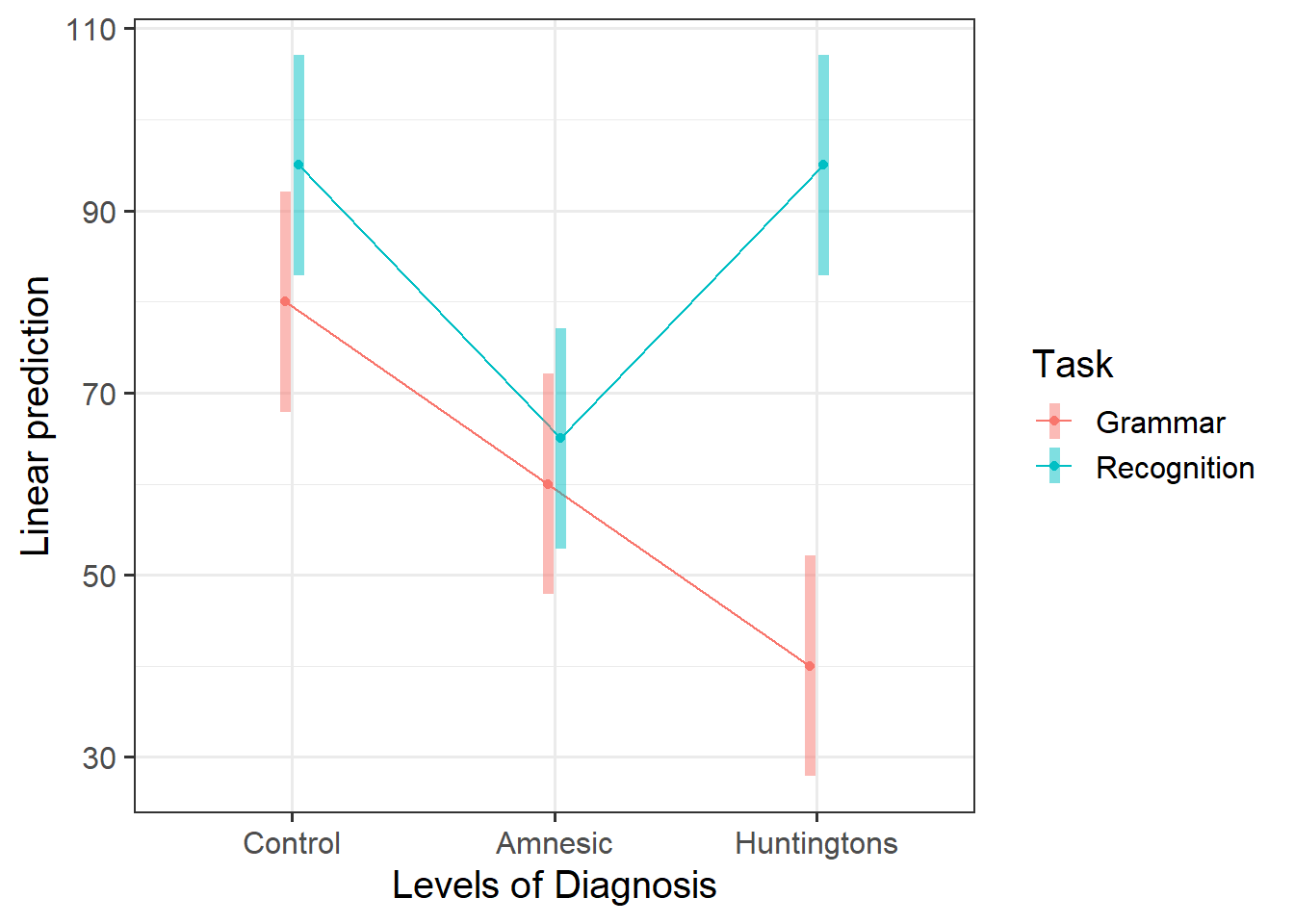
An alternative to plot_model() is the function emmip() (from the emmeans package) which stands for EMMeans Interaction Plot. Use the function emmip() to investigate the interactions.

Hint: You must provide as the first argument the fitted model, then a special formula saying what to plot on the x axis and what to use to differentiate the colors: colors ~ x, and then CIs = TRUE tells the function to display uncertainty intervals.

Solution

emmip(mdl_int, Task ~ Diagnosis, CIs = TRUE)

Visualising the interactions

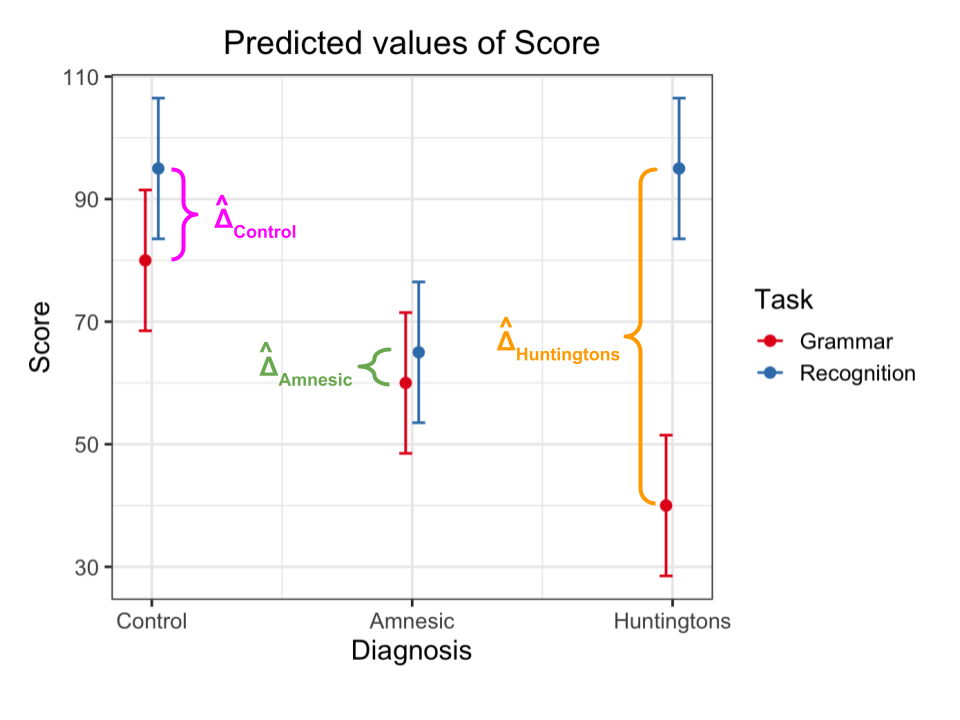
In the interaction plot above you can see three highlighted differences, where the differences are denoted with the Greek letter \(\Delta\) (“delta”) with a hat on top, \(\hat \Delta\), to denote that those are estimates for the unknown population differences based on the available sample data. The corresponding population differences are unknown as we don’t have the data for the entire population, and they are denoted with a \(\Delta\) without a hat on top.

You can see highlighted:

• The difference in the mean score between Recognition and Grammar for Control patients, \(\hat \Delta_{\text{Control}}\)
• The difference in the mean score between Recognition and Grammar for Amnesic patients, \(\hat \Delta_{\text{Amnesic}}\)
• The difference in the mean score between Recognition and Grammar for Huntingtons patients, \(\hat \Delta_{\text{Huntingtons}}\)

An interaction is present if the effect of Task (i.e. the difference in mean score between Recognition and Grammar tasks) substantially varies across the possible values for Diagnosis. That is, if the difference for Amnesic is not the same as that for Control, or if the difference for Huntingtons is not the same as that for Control, or both.

The model summary returns two rows for the interactions. Let’s focus on this row:

## DiagnosisAmnesic:TaskRecognition      -10.000     11.719  -0.853  0.40192    

It returns an estimate for the difference

\[ \hat \beta_4 = \hat \Delta_{\text{Amnesic}} - \hat \Delta_{\text{Control}} \]

and also performs a test for the hypothesis that the differences are equal in the population:

\[ H_0: \Delta_{\text{Amnesic}} = \Delta_{\text{Control}} \\ H_1: \Delta_{\text{Amnesic}} \neq \Delta_{\text{Control}} \]

or, equivalently, that:

\[ H_0: \Delta_{\text{Amnesic}} - \Delta_{\text{Control}} = 0 \\ H_1: \Delta_{\text{Amnesic}} - \Delta_{\text{Control}} \neq 0 \]

Let’s now focus on the last row:

## DiagnosisHuntingtons:TaskRecognition   40.000     11.719   3.413  0.00228 ** 

It returns an estimate for the difference

\[ \hat \beta_5 = \hat \Delta_{\text{Huntingtons}} - \hat \Delta_{\text{Control}} \]

and also performs a test for the hypothesis that the differences are equal in the population:

\[ H_0: \Delta_{\text{Huntingtons}} = \Delta_{\text{Control}} \\ H_1: \Delta_{\text{Huntingtons}} \neq \Delta_{\text{Control}} \]

or, equivalently, that:

\[ H_0: \Delta_{\text{Huntingtons}} - \Delta_{\text{Control}} = 0 \\ H_1: \Delta_{\text{Huntingtons}} - \Delta_{\text{Control}} \neq 0 \]

Question 8

Interpret the model output in the context of the research hypothesis.

Solution

Let’s recall the researchers’ hypothesis:

A group of researchers wants to test an hypothesised theory according to which the difference in performance between explicit and implicit memory tasks will be greatest for Huntington patients in comparison to controls.
On the other hand, the difference in performance between explicit and implicit memory tasks will not significantly differ between patients with amnesia in comparison to controls.

We can get a nice printout of the model summary as follows:

tab_model(mdl_int, show.stat = TRUE)

	Score
Predictors	Estimates	CI	Statistic	p
(Intercept)	80.00	67.91 – 92.09	13.65	<0.001
Diagnosis [Amnesic]	-20.00	-37.10 – -2.90	-2.41	0.024
Diagnosis [Huntingtons]	-40.00	-57.10 – -22.90	-4.83	<0.001
Task [Recognition]	15.00	-2.10 – 32.10	1.81	0.083
Diagnosis [Amnesic] * Task [Recognition]	-10.00	-34.19 – 14.19	-0.85	0.402
Diagnosis [Huntingtons] * Task [Recognition]	40.00	15.81 – 64.19	3.41	0.002
Observations	30
R2 / R2 adjusted	0.739 / 0.685

We could interpret it as follows:

The difference in scores between the recognition and grammar tasks, respectively measuring explicit and implicit memory, for Huntingtons patients in comparison to controls was significant and indicated a difference of \(\hat \beta_5 = 40\) points in explicit vs implicit memory performance: \(t(24) = 3.41, p = 0.002\).

The difference in scores between the recognition and grammar tasks, respectively measuring explicit and implicit memory, for amnesiac patients in comparison to controls was estimated to be \(\hat \beta_4 = -10\) points but it is not found to be significantly different from 0: \(t(24) = -0.85, p = 0.40\).

This indicates that the researchers’ hypothesis that the difference in performance between explicit and implicit memory tasks does not differ significantly between amnesic and control patients, while it does differ significantly between Huntington and control patients.

We can also provide an interpretation of the interaction plot:

plot_model(mdl_int, type = "int")

Compared to controls, amnesiac patients will have a significant deficit in explicit memory (as measured by the recognition task), but not on implicit memory (as measured by the grammar task).

Compared to controls, Huntingtons patients will have a significant deficit in implicit memory (as measured by the grammar task) but not in explicit memory (as measured by the recognition task).

Footnotes

1. Some researchers may point out that a design where each person was assessed on both tasks might have been more efficient. However, the task factor in such design would then be within-subjects, meaning that the scores corresponding to the same person would be correlated. To analyse such design we will need a different method which is discussed next year!