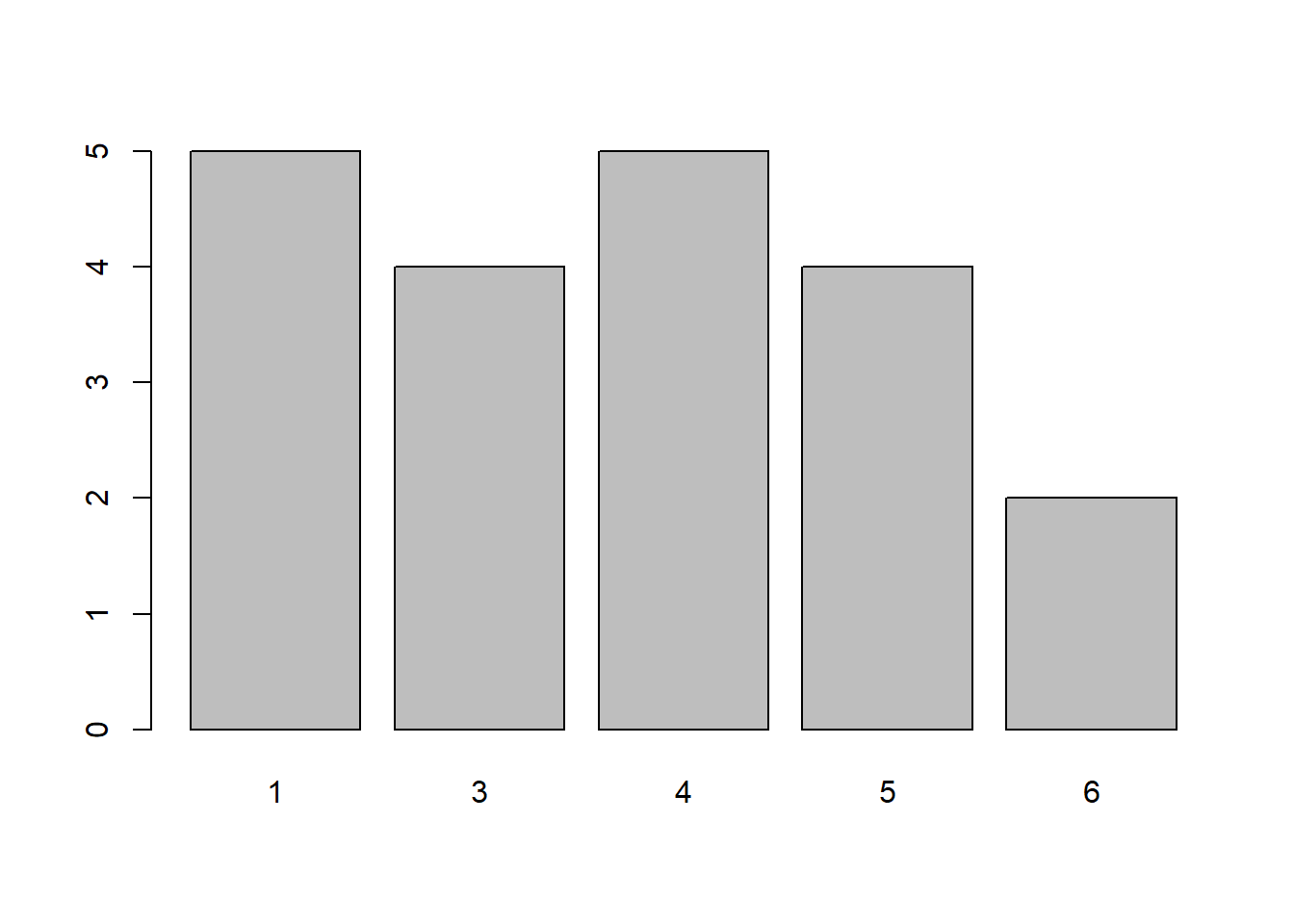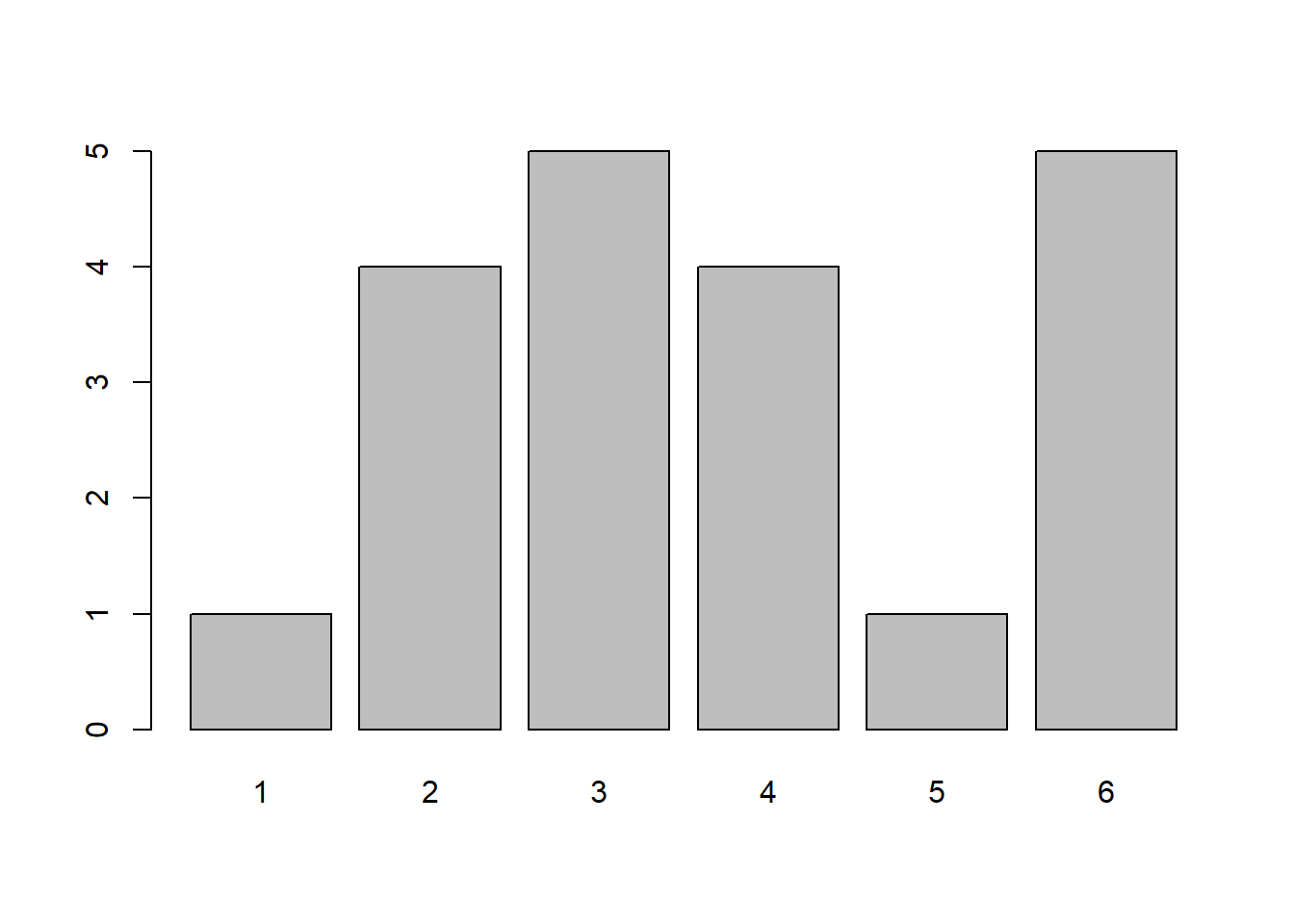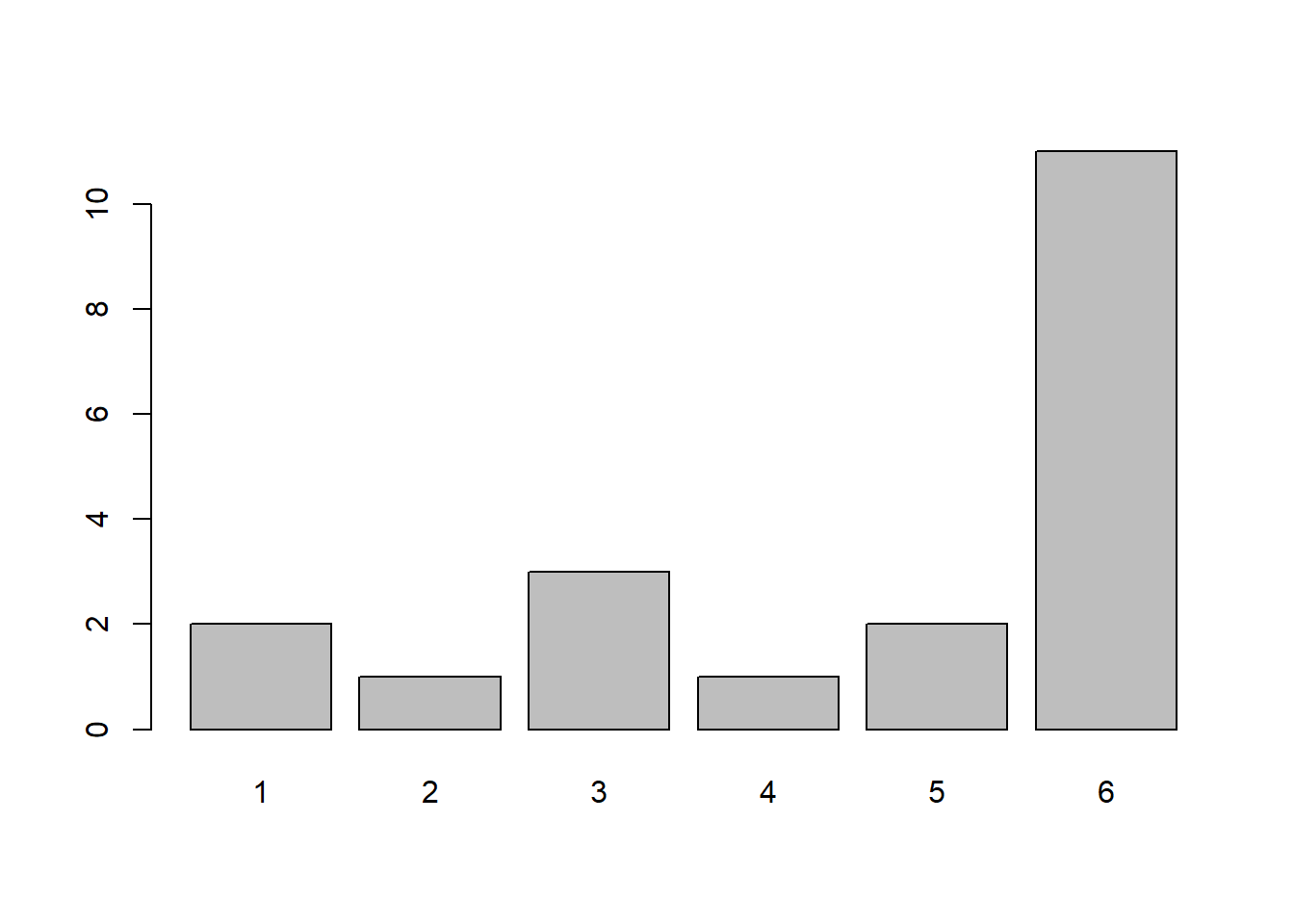Exercises: Intro R

First things

The very first things to do are to open RStudio and get a blank script ready for writing your code!

Our recommendation is that you have an R project for this course, and use a new script for each week of work. See the tip about “R projects” in Section 1A.

Pet Data

We’re going to play with some data on a sample of licensed pets from the city of Seattle, USA. It can be downloaded (or read directly into R) from https://uoepsy.github.io/data/pets_seattle.csv. It contains information on the license ID, year of issue, as well as the species, breeds and weights of each pet. You can find a data dictionary in Table 1

Table 1: Seattle Pets: Data dictionary

Variable	Description
license_year	Year in which license was issued
license_number	Unique license ID number
animals_name	Full name of pet
species	Species of pet
primary_breed	Primary breed of pet
secondary_breed	Secondary breed of pet
weight_kg	Weight in kilograms

Question 1

Write a line of code that reads in the data to your R session. Then examine the dimensions of the dataset, and take a look at the first few lines.

Hints

You’ll need the read.csv() function. Remember to assign it a name to store it in your environment.
1B #basic-data-wrangling contains an example of reading in data from a URL. You’ll then want to play with functions like dim() and head().

Solution 1. We’re going to call it petdata in our environment here. Don’t forget the quotation marks around the url (otherwise R will look for an object in your environment called https://..., which isn’t there).

petdata<-read.csv("https://uoepsy.github.io/data/pets_seattle.csv")
dim(petdata)

[1] 1956    7

We can see there are 1956 rows and 7 columns.
And we can see the first few rows here:

head(petdata)

  license_year license_number  animals_name species         primary_breed
1         2018      LNS150171        Norman     Dog                 Boxer
2         2017        LN20666         Henry     Dog          Bichon Frise
3         2018      LN8000658 Vega Williams     Dog                   Mix
4         2018       LN730940         Molly     Dog   Australian Shepherd
5         2016       LN964607         Gremy     Dog Chihuahua, Short Coat
6         2018      LNS117115        Shadow     Dog   Retriever, Labrador
  secondary_breed weight_kg
1             Mix     29.15
2        Havanese     23.70
3         Unknown     21.13
4             Mix     18.70
5         Terrier     20.36
6         Unknown     11.51

Question 2

What are the names of the 47th and the 200th animals in the dataset? (use R code to find out)

Hints

You’ll probably want to make use of the square brackets data[rows, columns].

Solution 2. There are lots of different ways to do this. We can get out the entire rows, either individually:

petdata[47,]
petdata[200,]

Or together:

petdata[c(47,200),]

    license_year license_number animals_name species       primary_breed
47          2018      LNS140233     Hooligan     Dog Retriever, Labrador
200         2017       LN584186  Maple Syrup     Cat  Domestic Shorthair
    secondary_breed weight_kg
47          Unknown     12.27
200         Unknown      4.66

Or we can extract the names only:

# These all do the same
petdata[c(47,200),"animals_name"]
petdata[c(47,200),3]
petdata$animals_name[c(47,200)]

The will all give us these names:

[1] "Hooligan"    "Maple Syrup"

In the last one, we use the $ to access the animals_name variable. In this case, we don’t need to specify [rows, columns] inside the square brackets, because it’s a single variable - there are no columns.

• dataframe[rows, columns]
  
• variable[entries]

Question 3

Subset the data to only the animals which are dogs, and store this subset as another named object in your environment.
Do the same for the cats.

Hints

You’ll want to think about how we access data via asking for those entries that meet a specific condition (see 1B #accessing-by-a-condition)

Solution 3. We can ask “which entries of species variable are equal to ‘Dog’?” by using pet$species=="Dog".
This will give us a TRUE for each dog, and a FALSE for each non-dog.
We can then use this set of TRUEs and FALSEs to access those rows for which it is TRUE in our data:

dogdata <- petdata[petdata$species=="Dog", ]
catdata <- petdata[petdata$species=="Cat", ]

Question 4

Find the name and weight of the heaviest cat, and of the lightest dog.

Hints

You could do this using the original data you read in from question 1, or use the subsets you created in question 3. You’ll again want to supply a condition within square brackets data[?==?]. That condition may well have something to do with being equal to the min() or the max() of some variable.

Solution 4. We can use min() and max() to return the minimum and maximum of a variable:

min(dogdata$weight_kg)

[1] 0.39

max(catdata$weight_kg)

[1] 5.48

We could then ask for each entry “is this cat’s weight the maximum cat’s weight?” with catdata$weight_kg == max(catdata$weight_kg) and then use that condition to access the rows in our dataset where the weight_kg variable is at its maximum:

catdata[catdata$weight_kg == max(catdata$weight_kg), ]

    license_year license_number animals_name species      primary_breed
414         2018      LNS101014       Smokey     Cat Domestic Shorthair
    secondary_breed weight_kg
414             Mix      5.48

dogdata[dogdata$weight_kg == min(dogdata$weight_kg), ]

     license_year license_number animals_name species  primary_breed
1126         2017      LNS139134       Claire     Dog Great Pyrenees
     secondary_breed weight_kg
1126         Unknown      0.39

Question 5

Does the original dataset contain only dogs and cats?

Hints

Given what you did in question 3, you might be able to answer this by just looking at your environment.

Solution 5. In the environment, we can see that the entire dataset has 1956 observations, the Dog’s data frame has 1322, and the Cat’s has 632.
So there are 2 missing!

Question 6

Extract the entries of the original dataset for which the species is neither “Dog” nor “Cat”?
What are the names and species of these animals?

Hints

This is a slightly complex one. 1B #more-complex-conditions might help you here.

Solution 6. As always, there are lots of different ways.
Here are three:

“not a dog AND not a cat”

We can ask if something is not a dog by using petdata$species != "Dog". But we want the rows where the species is not a dog and it’s not a cat. So it’s two conditions:

petdata[petdata$species != "Cat" & petdata$species != "Dog", ]

     license_year license_number     animals_name species primary_breed
1505         2018      LNS147013    Billy the Kid    Goat     Miniature
1655         2018      LNS132953 Vincent Van Goat    Goat     Miniature
     secondary_breed weight_kg
1505         Unknown    103.48
1655         Unknown     73.96

“not (dog OR cat)”

We could also do this in other ways, such as asking for all the entries which are either “Dog” or “Cat”, and then negating them:

petdata[!(petdata$species == "Cat" | petdata$species == "Dog"), ]

     license_year license_number     animals_name species primary_breed
1505         2018      LNS147013    Billy the Kid    Goat     Miniature
1655         2018      LNS132953 Vincent Van Goat    Goat     Miniature
     secondary_breed weight_kg
1505         Unknown    103.48
1655         Unknown     73.96

“not one of [Dog, Cat]”

Another clever little operator is the %in% operator, which asks whether something is in a set of things. Unfortunately, we can’t use !%in% to mean “not in”, so we need to put the ! right at the start of the condition:

petdata[!petdata$species %in% c("Cat","Dog"), ]

     license_year license_number     animals_name species primary_breed
1505         2018      LNS147013    Billy the Kid    Goat     Miniature
1655         2018      LNS132953 Vincent Van Goat    Goat     Miniature
     secondary_breed weight_kg
1505         Unknown    103.48
1655         Unknown     73.96

Question 7

Create a new variable in the data, which contains the weights of all the animals, but rounded to the nearest kg.

Hints

Try looking up the help documentation for the function round(). Try playing with it in the console, e.g. round(c(3.5, 4.257, 1.1111)). You may find it helpful to look back at 1B #adding/changing-a-variable.

• “to the nearest kg” would mean we want no decimal points. Note that round() has a digits argument. e.g. round(22.324, digits = 2) and round(22.324, digits = 1) do different things.

Solution 7. We’re wanting this variable as a new column in the data, so don’t forget the dataframe$newvariable <- ...... bit.

petdata$weight_rounded <- round(petdata$weight_kg)

Question 8

Try giving the dataset to the function summary(). You’ll get out some information on each of the variables. It is likely that you’ll get more useful information for the variables containing information on the animal’s weights than for those containing their names, breeds etc because these variables are vectors of “characters”. We’ll start to look more about different types of data next week.

Solution 8. Easy to do!

summary(petdata)

  license_year  license_number     animals_name         species         
 Min.   :2015   Length:1956        Length:1956        Length:1956       
 1st Qu.:2017   Class :character   Class :character   Class :character  
 Median :2018   Mode  :character   Mode  :character   Mode  :character  
 Mean   :2018                                                           
 3rd Qu.:2018                                                           
 Max.   :2018                                                           
 primary_breed      secondary_breed      weight_kg       weight_rounded 
 Length:1956        Length:1956        Min.   :  0.390   Min.   :  0.0  
 Class :character   Class :character   1st Qu.:  4.707   1st Qu.:  5.0  
 Mode  :character   Mode  :character   Median : 16.630   Median : 17.0  
                                       Mean   : 15.312   Mean   : 15.3  
                                       3rd Qu.: 22.500   3rd Qu.: 22.0  
                                       Max.   :103.480   Max.   :103.0  

Simulating Dice

Question 9

Copy the code from the lecture which creates a custom function called dice() (copied below).
Be sure to run the code (highlight it all with your cursor, and hit “run” in the top right, or press Ctrl/Cmd+Enter).

dice <- function(num = 1) {
  sum(sample(1:6, num, replace=TRUE))
}

What did that code do?

In a sense, this code does nothing: It won’t give you any output when you run it. What it is actually doing, though, is defining a function called dice(). If you look at your environment panel (top right), you’ll see dice appear when you run the code.

To produce some output, we have to call the function dice() (by writing it into code: dice(4), for example). dice() wants to be supplied with some information (in the argument num). If no information is supplied, num will take a default value of 1. (So writing dice() is equivalent to writing dice(1)).

What does dice() do with num? It calls another function, sample(), with 3 arguments. We didn’t write sample(): it’s a function that’s “supplied with” R. To find out more about what sample() does:

• click inside the brackets just after sample() in your R script;

• press TAB (⇥), then F1

• you should see some help appear in the bottom right-hand panel of RStudio.

You will find that “sample() takes a sample … from the elements of x …” If you compare the code in RStudio to the code under “Usage” you’ll see that where the help has x, we have 1:6. So what does 1:6 mean? One way to find out is to open the console in RStudio (bottom left) and just type stuff in. What happens when you type 1:6? What about 2:17? (What about 6:1?)

Remember: The console is the place to “try stuff out” (don’t worry, you can’t break it).

What you will discover is that 1:6 creates a vector (list of similar things, in this case numbers) of the numbers 1-6. The next bit of the sample() function is size. In the dice() function, the num passes down to the size of the sample(): Looking through the help, size is the number of items to choose. So sample(1:6, 1) would choose one number from the numbers 1-6 at random; sample(1:6, 3) would choose 3, and so on. The last argument, replace=TRUE, tells sample() what to do with a number once it’s been picked: Does it go ‘back into the bag’ to be picked again (TRUE) or not? (FALSE)?

Around the outside is sum() which simply sums the numbers on however many (num) dice you “rolled”.

Putting it all together, our dice() function “throws num dice” by sample()ing from the numbers 1-6 num times, replaceing each number when it’s been picked, and sums the numbers of all the dice.

Question 10

Use the function you just made to ‘roll a die’ a few times. Check that it works like you expect.

Hints

You just need to run dice() a few times. A single die means num = 1, which is the default.

Solution 9.

dice()

[1] 2

dice()

[1] 2

dice()

[1] 1

dice()

[1] 6

Question 11

Look up the function replicate(). We can use it to do something in R lots of times! For instance, replicate(20, 1+1) will evaluate 1+1 twenty times.

Use replicate() to simulate 20 rolls of a single die, and store the results in an object in your environment. Give it an easily identifiable name.
What does each value in this object represent?

Solution 10.

rolls20 <- replicate(20, dice(num = 1))
rolls20

 [1] 5 4 3 4 6 5 1 1 4 3 3 6 5 1 4 5 1 3 4 1

Each value in rolls20 represents the simulated roll of a single die. We roll our die, and get a 5, we roll it again and get 4, the third roll we get 3, and so on..

Question 12

Create a barplot showing the frequency with which each number was landed on in the 20 rolls.

Hints

The functions table() and barplot() were used to do this in the lecture.

Solution 11. Your plots will look slightly different to these, because all of our dice are random!

# We can get the frequency table using table()
table(rolls20)

rolls20
1 3 4 5 6 
5 4 5 4 2 

# Which we can then pass to the barplot() function:
barplot(table(rolls20))

Question 13

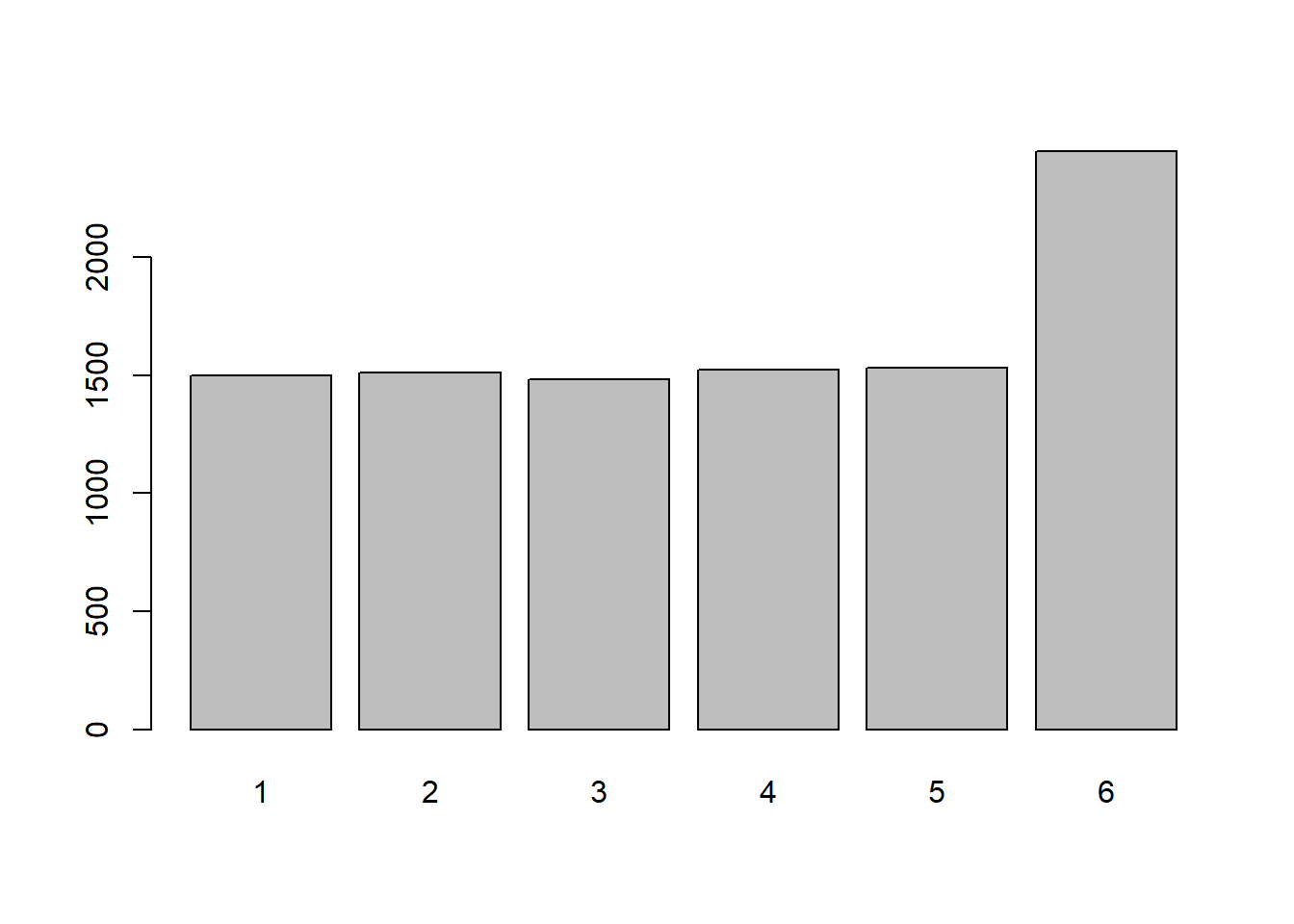
Do the same for 100 rolls, and then for 1,000. What do you notice?

Solution 12.

morerolls <- replicate(100, dice(1))
barplot(table(morerolls))

morerolls2 <- replicate(1000, dice(1))
barplot(table(morerolls2))

The more rolls we do of the dice, the flatter the graph becomes. This is because there is an equal probability of the die landing on any of the responses - there is a uniform probability.

Question 14

Copy the code below into your script and run it. It creates a new function called wdice() which simulates the rolling of num dice which are slightly weighted.

Roll a single weighted die 20 times and plot the frequency distribution. Do the same for 100 and 1,000 rolls of a single die. Does a pattern emerge? At how many rolls?

wdice <- function(num = 1){
    sum(sample(1:6, num, replace=TRUE, prob = c(0.15,0.15,0.15,0.15,0.15,0.25)))
}

Solution 13.

wdice <- function(num = 1){
    sum(sample(1:6, num, replace=TRUE, prob = c(0.15,0.15,0.15,0.15,0.15,0.25)))
}

wd <- replicate(20, wdice(1))
barplot(table(wd))

wd <- replicate(1000, wdice(1))
barplot(table(wd))

wd <- replicate(10000, wdice(1))
barplot(table(wd))

The die is clearly weighted towards landing on 6. However, is 20 rolls enough to reliably observe this? In our 20 rolls above, it landed on 3 quite a bit too (yours will be different)! The pattern becomes clearer after 1000 rolls.

Question 15

Remember, wdice() and dice() are really just relying on different functions, like sample(). Try playing around with sample() in the console again - what does the prob = c(....) bit do?

Solution 14. The prob bit is defining the probabilities of observing each outcome - i.e. there is a 25% chance of rolling a 6.

Question 16

Let’s try to modify the wdice() function. Edit the code for wdice() so that 50% of the time it lands on number 6.

Hints

• To test out your modified function, you will need to re-run the code which defines the function. When we use wdice() we use the function which is in our environment. If we want to edit the function, we need to then overwrite (or “replace”/“reassign”) the object in our environment.
  
• We need to be careful to remember that the probability of different outcomes should sum to 1 (i.e., it’s not possible to “50% of the time land on 6” as well as “70% of the time land on 5”!).

Solution 15.

wdice <- function(num = 1){
    sum(sample(1:6, num, replace=TRUE, prob = c(0.1,0.1,0.1,0.1,0.1,0.5)))
}

Question 17

Can you observe the weighting in your new die (the one which 50% of the time lands on number 6) in only 20 rolls?

Solution 16.

wd <- replicate(20, wdice(1))
barplot(table(wd))

The die is very clearly weighted to land on 6. We can see this in just 20 rolls. Presumably it will become even clearer if we increased how many times we roll it.

Question 18

Conceptually, what can we learn from this toy example?

Solution 17. The more highly weighted a die is, the less we have to roll it in order to observe that weighting.