Generalised Linear Model
Some very quick recaps
Binary!
So what do we do if we want to do a similar analysis but for an outcome variable that is not numeric?
We measure a lot of things as categories, and sometimes what our research is interested in is what variables influence the likelihood that an observation will fall into a given category.
In the lecture, we saw an example in which our participants (aliens), were either splatted or survived.

Consider the following questions:
- What features of speech influence the likelihood of an utterance being perceived as true/false?
- What lifestyle and demographic variables influence the chances that a person does/does not smoke?
- Does preference for milk vs dark chocolate depend on personality traits?
The common thread in the questions above is that they all contain a dichotomy: “splatted/not splatted”, “true/false”, “does/does not”, “milk vs dark”.
A note: This sort of binary thinking can be useful, but it is important to remember that it can in part be simply a result of measurement. For instance, we might initially consider “has blond hair” to be binary “Yes/No”, but that doesn’t mean that in the real world people either have blond hair or they don’t. We could instead choose to measure hair colour via colorimetric measures of the energy at each spectral wavelength, meaning “blondness” could become a continuum. While binary thinking can be useful, it is not difficult to think of ways in which it can be harmful.
Introducing GLM
Research Questions Is susceptibility to change blindness influenced by level of alcohol intoxication and perceptual load?
Watch the following video
Simons, D. J., & Levin, D. T. (1997). Change blindness. Trends in cognitive sciences, 1(7), 261-267.
You may well have already heard of these series of experiments, or have seen similar things on TV.
For a given participant in the ‘Door Study’, give a description of the outcome variable of interest, and ask yourself whether it is binary.
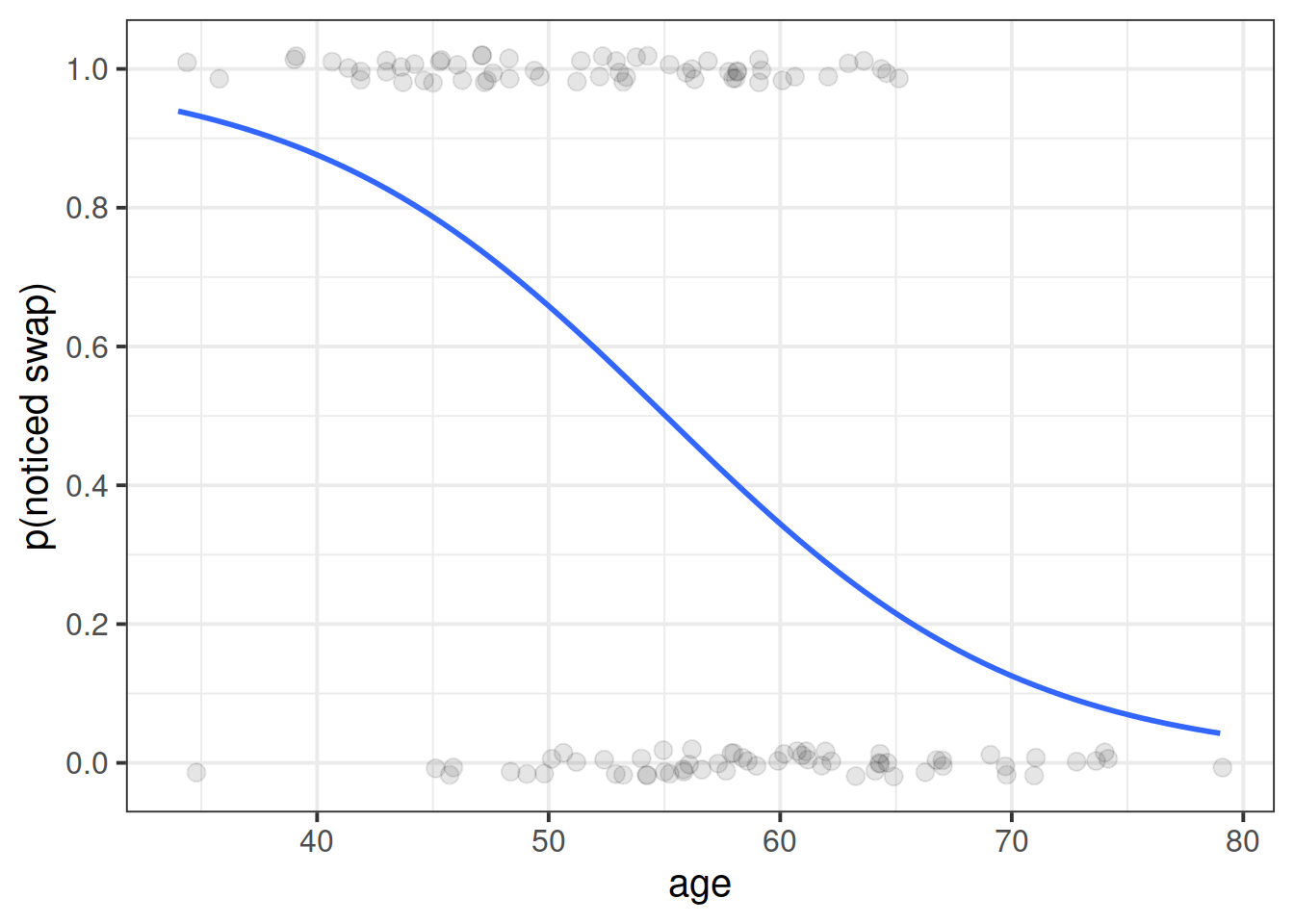
Read in the data, and plot the relationship between the age variable and the notice variable.
Use geom_point(), and add to the plot geom_smooth(method="lm"). This will plot the regression line for a simple model of lm(notice ~ age).
Just visually following the line from the plot produced in the previous question, what do you think the predicted model value would be for someone who is aged 30?
What does this value mean?
What we are interested in evaluating here is really the probability of noticing the experimenter-swap.
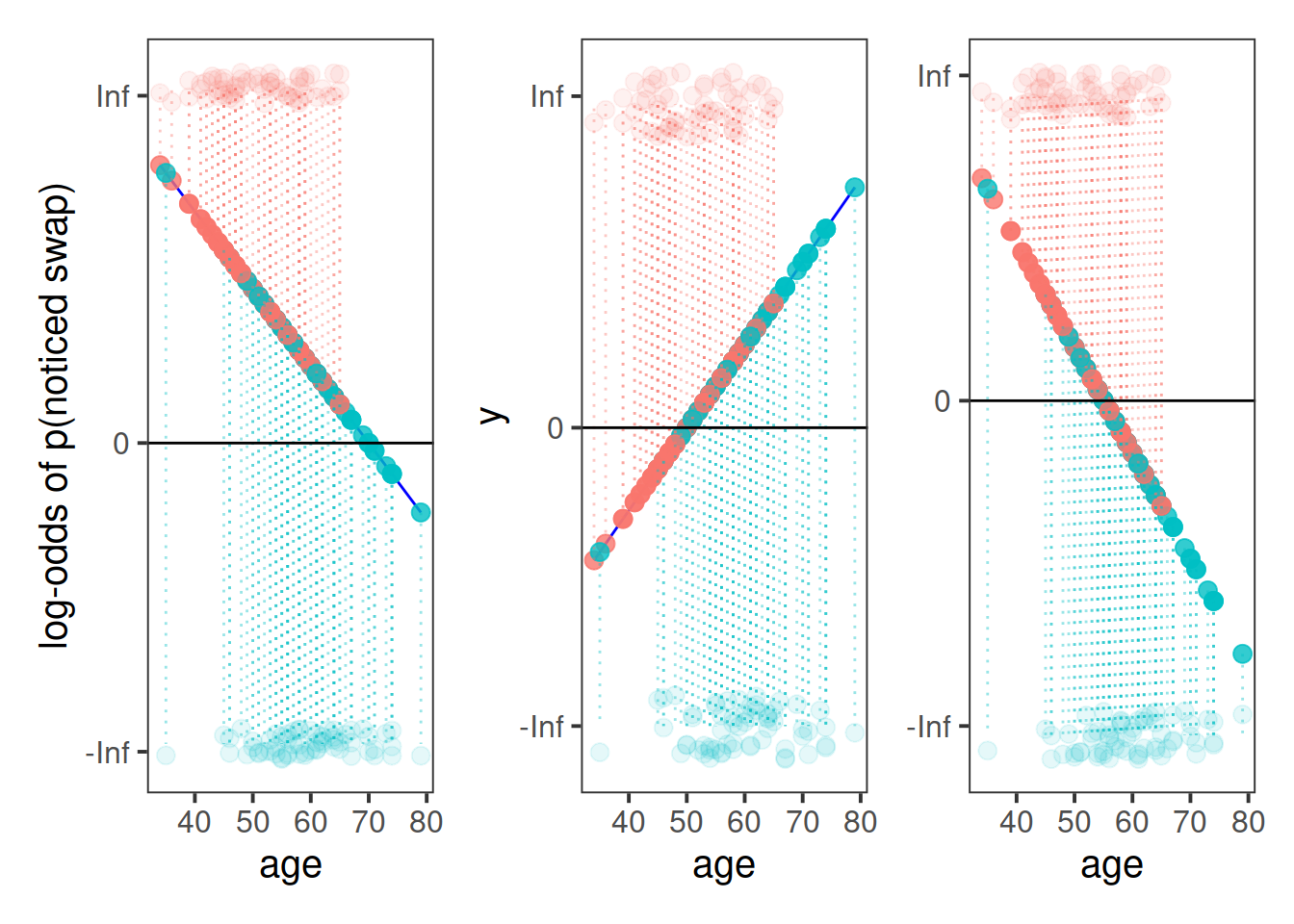
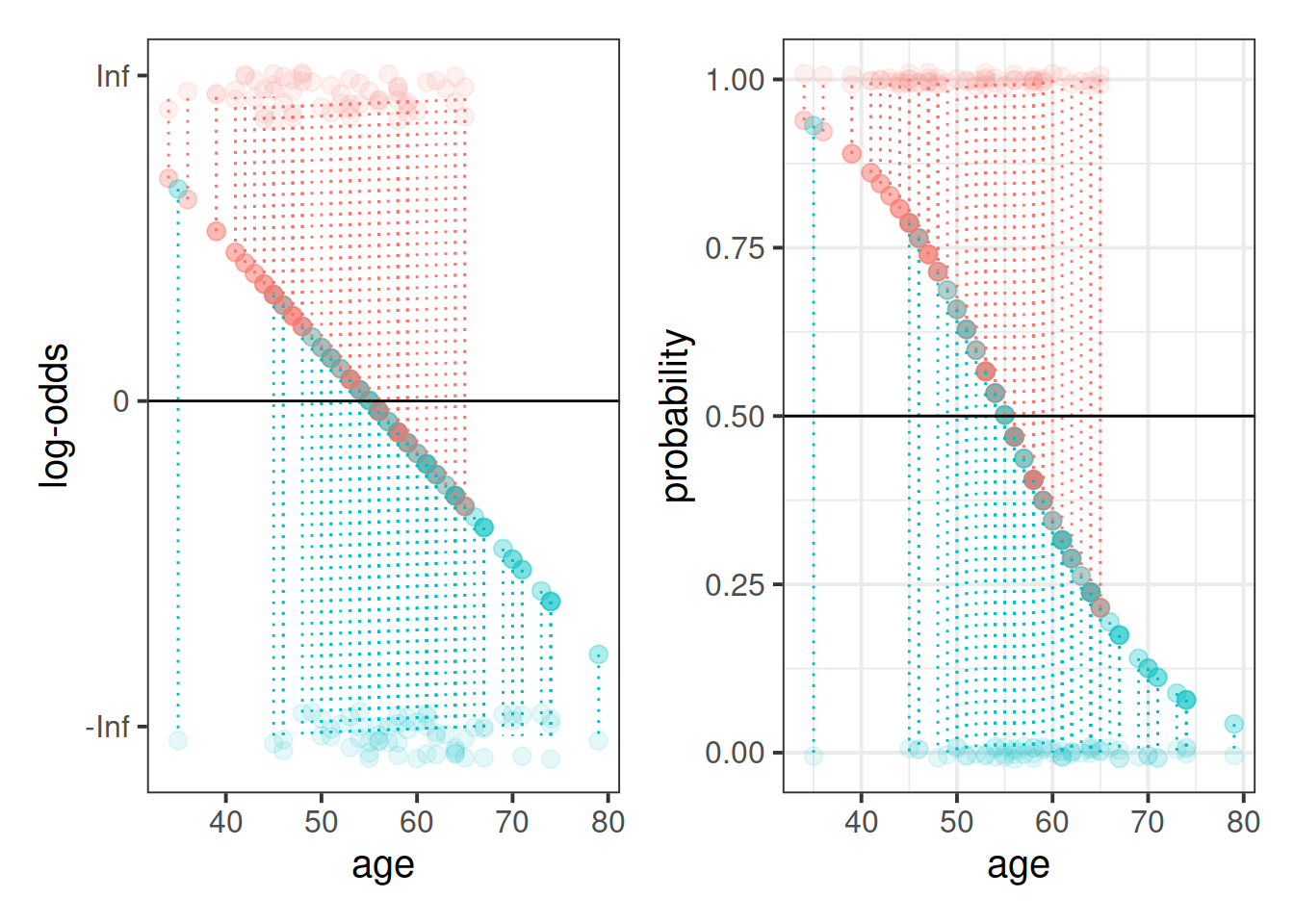
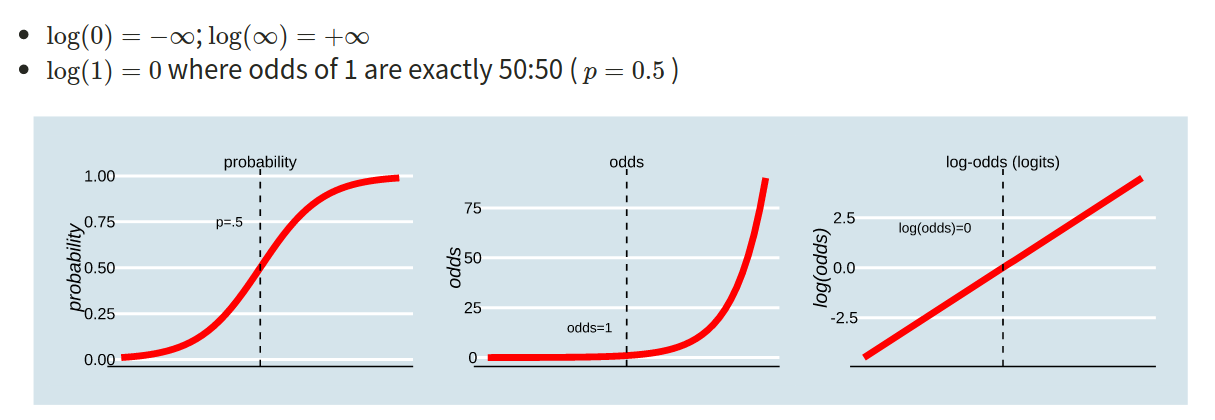
This is where the Generalised Linear Model (GLM) comes in. With a little bit of trickery, we can translate probability (restricted to between 0 and 1, and not represented by a straight line), into “log-odds”, which is both linear and unbounded (see Figure 2).
Probability, odds, log-odds
If we let \(p\) denote the probability of a given event, then:
- \(\frac{p}{(1-p)}\) are the odds of the event happening. For example, the odds of rolling a 6 with a normal die is 1/5 (sometimes this is expressed ‘1:5’, and in gambling the order is sometimes flipped and you’ll see ‘5/1’ or ‘odds of five to one’).
- \(ln(\frac{p}{(1-p)})\) are the log-odds of the event.
- The probability of a coin landing on heads if 0.5, or 50%. What are the odds, and what are the log-odds?
- This year’s Tour de France winner, Tadej Pogacar, was given odds of 11 to 4 by a popular gambling site (i.e., if we could run the race over and over again, for every 4 he won he would lose 11). Translate this into the implied probability of him winning.
How is this useful?
Recall the linear model formula we have seen a lot of over the last couple of weeks:
\[
\color{red}{Y} = \color{blue}{\beta_0 \cdot{} 1 + \beta_1 \cdot{} X_1 + ... + \beta_k \cdot{} X_k}
\]
Because we are defining a linear relationship here, we can’t directly model the probabilities (because they are bounded by 0 and 1, and they are not linear). But we can model the log-odds of the event happening.
Our model formula thus becomes:
\[
\color{red}{ln\left(\frac{p}{1-p} \right)} = \color{blue}{\beta_0 \cdot{} 1 + \beta_1 \cdot{} X_1 + ... + \beta_k \cdot{} X_k} \\
\quad \\
\text{Where} Y_i \sim Binomial(n, p_i) \text{ for a given }x_i \\
\text{and } n = 1 \text{for binary responses}
\]
To fit a logistic regression model, we need to useglm(), a slightly more general form of lm().
The syntax is pretty much the same, but we need to add in a family at the end, to tell it that we are doing a binomial1 logistic regression.
Using the drunkdoor.csv data, fit a model investigating whether participants’ age predicts the log-odds of noticing the person they are talking to be switched out mid-conversation. Look at the summary() output of your model.
lm(y ~ x1 + x2, data = data)
- is the same as:
glm(y ~ x1 + x2, data = data, family = "gaussian")
(Gaussian is another name for the normal distribution)
Interpreting coefficients from a logistic regression can be difficult at first.
Based on your model output, complete the following sentence:
“Being 1 year older decreases _________ by 0.13.”
Unfortunately, if we talk about increases/decreases in log-odds, it’s not that intuitive.
What we often do is translate this back into odds.
The opposite of the natural logarithm is the exponential (see here for more details if you are interested), and in R these functions are log() and exp():
log(2)## [1] 0.6931472exp(log(2))## [1] 2log(exp(0.6931472))## [1] 0.6931472Exponentiate the coefficients from your model in order to translate them back from log-odds, and provide an interpretation of what the resulting numbers mean.
Based on your answer to the previous question, calculate the odds of noticing the swap for a one year-old (for now, forget about the fact that this experiment wouldn’t work on a 1 year old!)
And what about for a 40 year old?
Can you translate the odds back to probabilities?
We can easily get R to extract these predicted probabilities for us.
- Calculate the predicted log-odds (probabilities on the logit scale):
predict(model, type="link")
- Calculate the predicted probabilities:
predict(model, type="response")
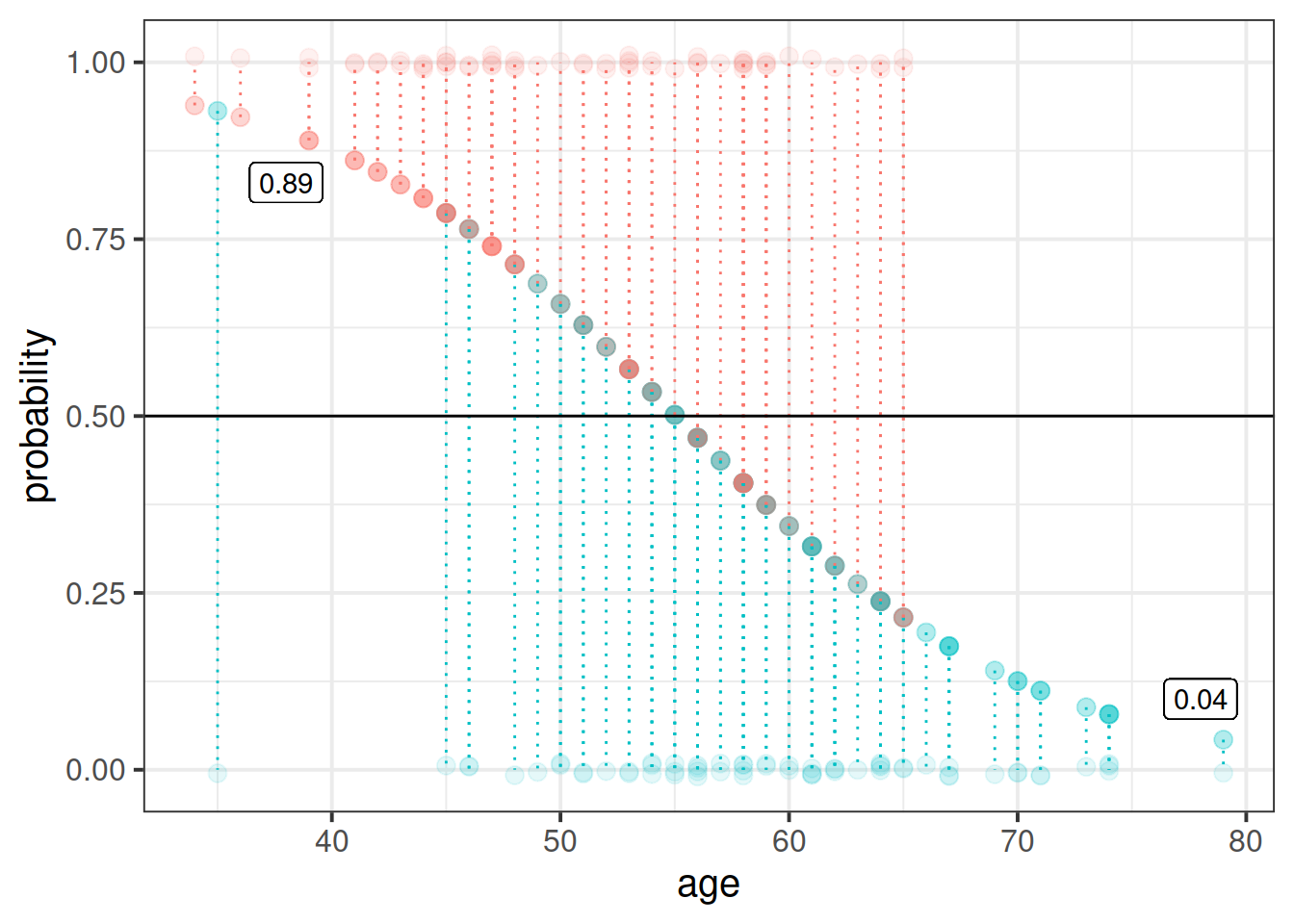
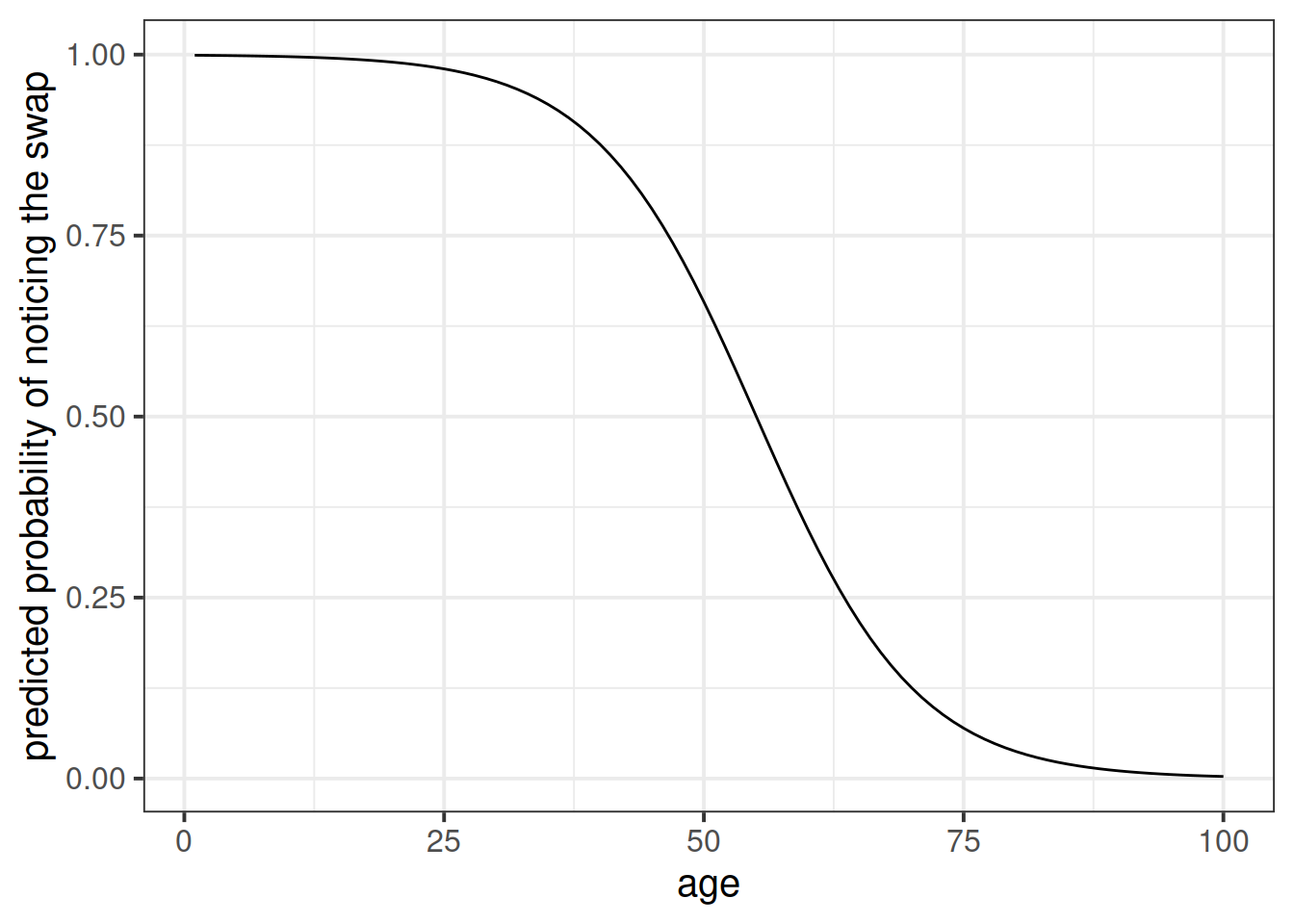
The code below creates a dataframe with the variable age in it, which has the values 1 to 100. Can you use this object in the predict() function, along with your model, to calculate the predicted probabilities of the outcome (noticing the swap) for each value of age? How about then plotting them?
ages100 <- tibble(age = 1:100)
We have the following model coefficients, in terms of log-odds:
summary(model1)$coefficients## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 7.1562479 1.57163317 4.553383 5.279002e-06
## age -0.1299931 0.02818848 -4.611569 3.996402e-06We can convert these to odds by using exp():
exp(coef(model1))## (Intercept) age
## 1282.0913563 0.8781015In order to say something along the lines of “For every year older someone is, the odds of noticing the mid-conversation swap (the outcome event happening) decreases by 0.88.”
Why can we not translate this into a straightforward statement about the change in probability of the outcome for every year older someone is?
GLM as a classifier
From the model we created in the earlier exercises:
drunkdoor <- read_csv("")
model1 <- glm(notice ~ age, data = drunkdoor, family="binomial")- Add new column to the drunkdoor dataset which contains the predicted probability of the outcome for each observation.
- Then, using
ifelse(), add another column which is these predicted probabilities translated into the predicted binary outcome (0 or 1) based on whether the probability is greater than >.5.
- Create a two-way contingency table of the predicted outcome and the observed outcome.
Hint: you don’t need the newdata argument for predict() if you want to use the original data the model was fitted on.
A table of predicted outcome vs observed outcome sometimes gets referred to as a confusion matrix, and we can think of the different cells in general terms (Figure 5).
Another way to think about how our model is fitted is that it aims to maximise (TP + TN)/n, or, put another way, to minimise (FP+FN)/n.
Which is equivalent to the good old idea of minimising sums of squares (where we minimise the extend to which the predicted values differ from the observed values).

Figure 5: Confusion Matrix
What percentage of the n = 120 observations are correctly classified by our model, when the threshold is set at 0.5?
Exercises
Approaching a research question
Recall our research question, which we will now turn to:
Research Questions Is susceptibility to change blindness influenced by level of alcohol intoxication and perceptual load?
Try and make a mental list of the different relationships between variables that this question invokes, can you identify one variable as the ‘outcome’ or ‘response’ variable? (it often helps to think about the implicit direction of the relationship in the question)
Think about our outcome variable and how it is measured. What type of data is it? Numeric? Categorical?
What type of distribution does it follow? For instance, do values vary around a central point, or fall into one of various categories, or follow the count of successes in a number of trials?
Think about our explanatory variable(s). Is there more than one? What type of variables are they? Do we want to model these together? Might they be correlated?
Are there any other variables (measured or unmeasured) which our prior knowledge or theory suggests might be relevant?
Fitting the model
- Write a sentence describing the model you will fit. It might help to also describe each variable as you introduce it.
- Fit the model.
Things to think about:
- Do you want BAC on the current scale, or could you transform it somehow?
- Is condition a factor? What is your reference level? Have you checked
contrasts(drunkdoor$condition)? (This will only work if you make it a factor first)
Compute 95% confidence intervals for the log-odds coefficients using confint(). Wrap the whole thing in exp() in order to convert all these back into odds and odds-ratios.
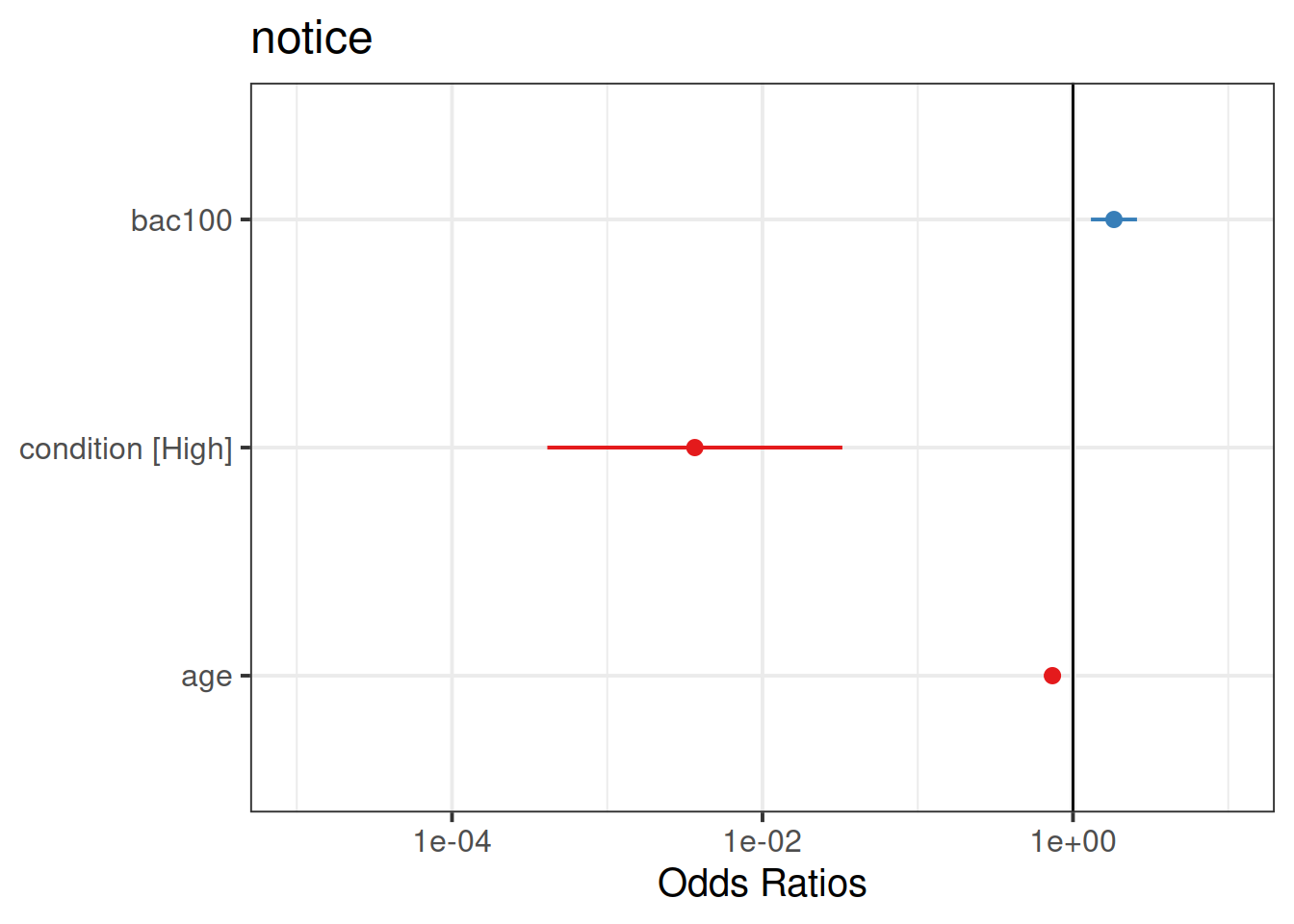
Try the sjPlot package and using plot_model() on your model. What do you get?
Tip:, for some people this plots seems to miss out plotting the BAC effect, so you might need to add:
plot_model(model) +
scale_y_log10(limits = c(1e-05,10))
Looking beyond
This week we have looked at one specific type of Generalised Linear Model, in order to fit a binary logistic regression. We can use GLM to fit all sorts of models, depending on what type of data our outcome variable is, and this is all through the family = part of the model syntax.
For instance, if we had data which was binomial but with an \(n > 1\), for instance the number of correct answers in 10 trials:
| participant | trials_correct | trials_incorrect | x1 |
|---|---|---|---|
| id1 | 1 | 9 | 114 |
| id2 | 4 | 6 | 113 |
| id3 | 7 | 3 | 83 |
| id4 | 8 | 2 | 141 |
| id5 | 3 | 7 | 115 |
| ... | ... | ... | ... |
We could model this with family = "binomial" using the two columns as the outcome:
glm(cbind(trials_correct, trials_incorrect) ~ x1, data = data, family = "binomial")
Or if we had count data, which can range from 0 to Infinity (theoretically), e.g.:
| person | n_fish_caught | age |
|---|---|---|
| id1 | 8 | 44 |
| id2 | 7 | 46 |
| id3 | 13 | 29 |
| id4 | 6 | 56 |
| id5 | 14 | 37 |
| ... | ... | ... |
We could model this using family = "poisson":
glm(n_fish_caught ~ age, data = data, family = "poisson")
If you want a really nice resource to help you in your future studies, then https://bookdown.org/roback/bookdown-BeyondMLR/ is an excellent read.
For real studies demonstrating the effects used in the example here, see:
- Simons, D. J., & Levin, D. T. (1997). Change blindness. Trends in cognitive sciences, 1(7), 261-267.
- Colflesh, G. J., & Wiley, J. (2013). Drunk, but not blind: The effects of alcohol intoxication on change blindness. Consciousness and cognition, 22(1), 231-236.
- Murphy, G., & Murphy, L. (2018). Perceptual load affects change blindness in a real‐world interaction. Applied cognitive psychology, 32(5), 655-660.
In this case it happens to be the special case of a binomial where \(n=1\), which sometimes gets referred to as ‘binary logistic regression’↩︎

This workbook was written by Josiah King, Umberto Noe, and Martin Corley, and is licensed under a Creative Commons Attribution 4.0 International License.
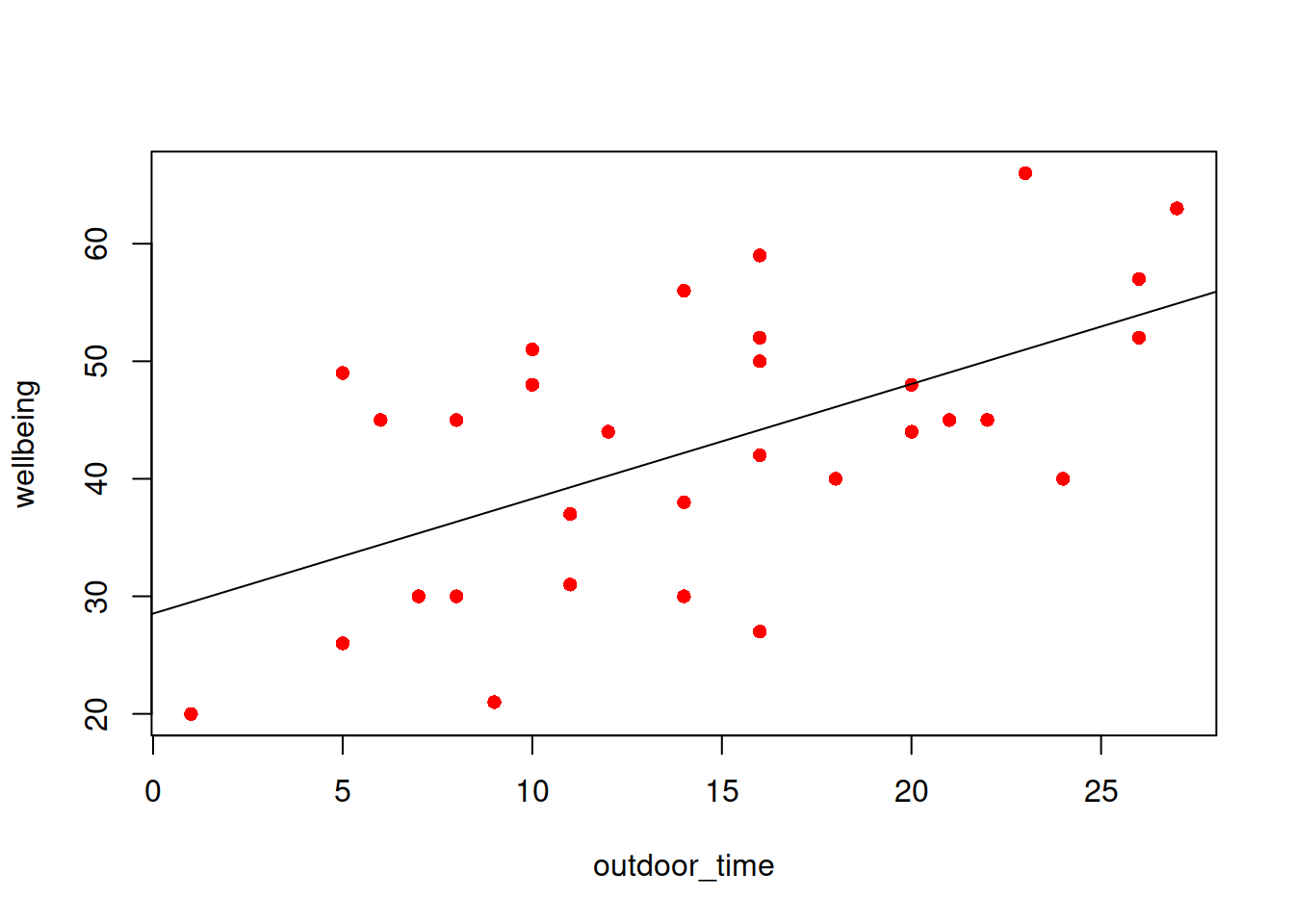
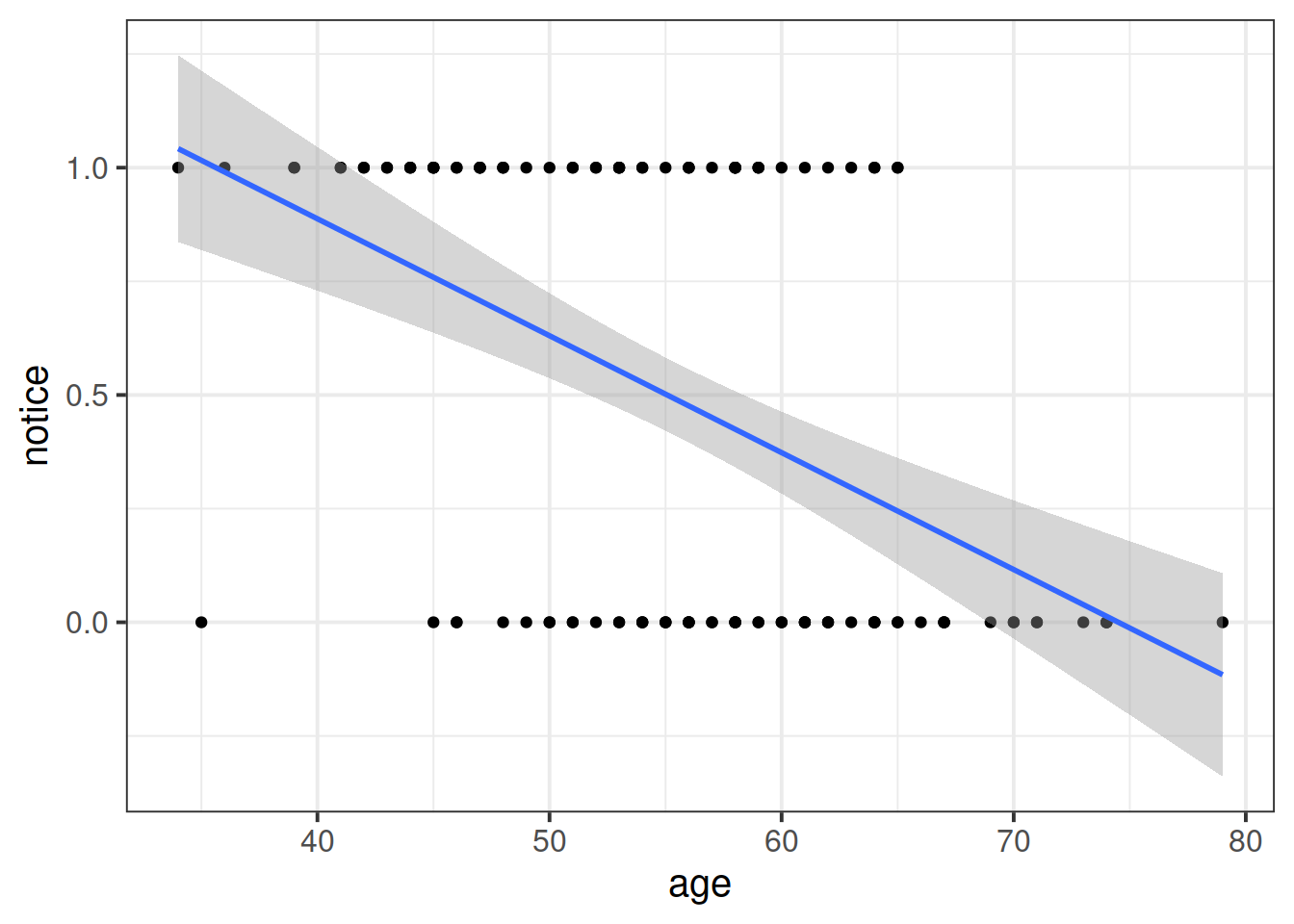
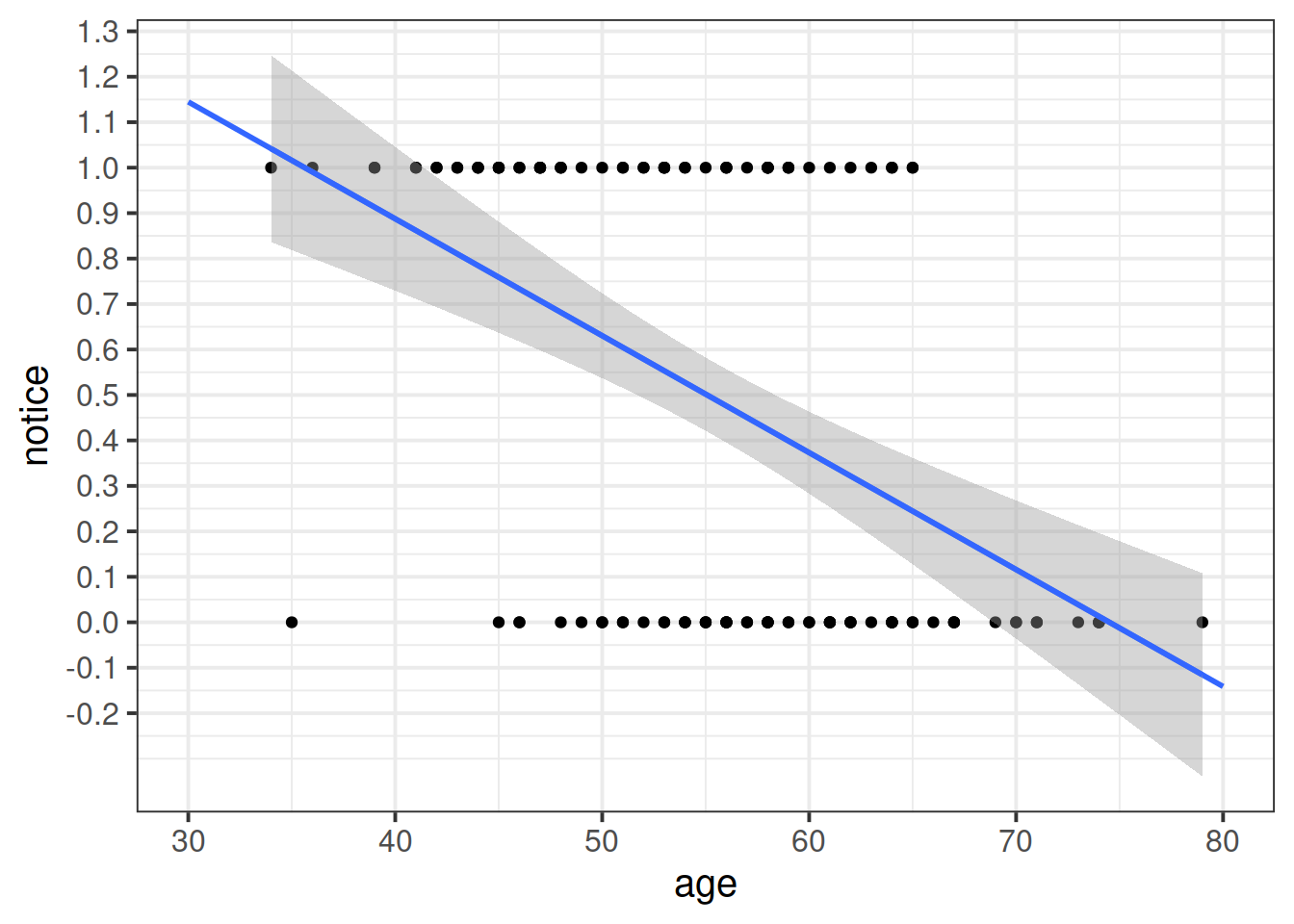
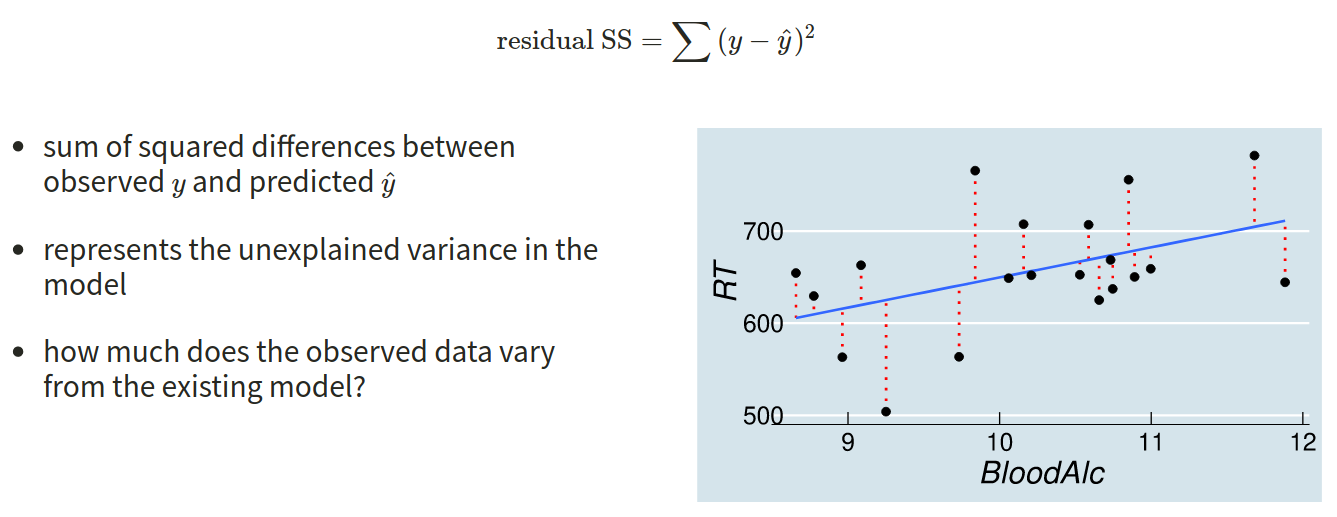
 The reason we have to do something different is because for our actual observations, the event has either happened or it hasn’t. So we can’t take the raw data as “probabilities” which we can translate into log-odds. We can try, but it doesn’t make sense, and we would just be trying to fit some line between infinity and negative infinity. This would mean the residuals would also all be infinity, and so it becomes impossible to work out anything!
The reason we have to do something different is because for our actual observations, the event has either happened or it hasn’t. So we can’t take the raw data as “probabilities” which we can translate into log-odds. We can try, but it doesn’t make sense, and we would just be trying to fit some line between infinity and negative infinity. This would mean the residuals would also all be infinity, and so it becomes impossible to work out anything!