| person | y | x | ... |
|---|---|---|---|
| 1 | ... | ... | ... |
| 1 | ... | ... | ... |
| 1 | ... | ... | ... |
| 2 | ... | ... | ... |
| 2 | ... | ... | ... |
| 2 | ... | ... | ... |
| 3 | ... | ... | ... |
| 3 | ... | ... | ... |
| 3 | ... | ... | ... |
Recap!
Data Analysis for Psychology in R 3
Psychology, PPLS
University of Edinburgh
Course Overview
This week
- Lec1: Recap of core concepts
- Lec2: Exam prep session
- Lab: Mock Exam Qs
Broad ideas
multivariate
mixed models/multi-level models
- multiple values per cluster
- each value is an observation
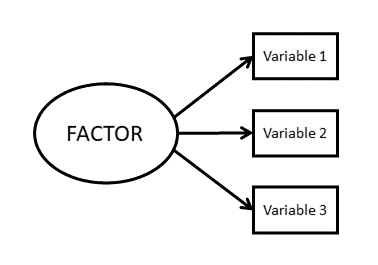
psychometrics
- multiple values (\(y1, ..., y_k\)) representing the same construct
- the set of values is “an observation” of [construct]
| person | y1 | y2 | y3 | ... |
|---|---|---|---|---|
| 1 | ... | ... | ... | ... |
| 2 | ... | ... | ... | ... |
| 3 | ... | ... | ... | ... |
| ... | ... | ... | ... | ... |
two questions
scoring
Q: To do anything with [construct \(Y\)], how do we get one number to represent an observation of \(Y\)?
- is one number enough - are \(y1,y2,...,yk\) really unidimensional?
- is it a valid and reliable measure of \(Y\)?
understanding
Q: How does [set of scores \(y1,y2,...,yk\)] get at [construct \(Y\)]?
- are the variables equally representative of \(Y\)?
- is there just one dimension to \(Y\) or are there multiple?
- what are they? are they correlated?
- how do they relate to \(y1,y2,...,yk\)?
- does a priori measurement model fit well in my sample?
- is it a valid and reliable measure of \(Y\)?
things we’ve explored…
scoring multi-item measures
scale scores
add ’em all up, you’ve got \(Y\)
- clinically ‘meaningful’?
- but only ‘meaningful’ if underlying model holds (which it almost definitely doesn’t!)
dimension reduction
identify smaller number of dimensions that capture how people co-vary across across the items.
Where people fall on those dimensions = their score on \(Y\).
PCA: reduce to set of orthogonal dimensions sequentially capturing most variability.
Scores are weighted composites of responses to items.FA: explore (EFA) or test (CFA) model of underlying dimensions (possibly correlated) that explain variability in items.
Scores are estimates of standing on latent factor(s).
understanding multi-item measures
dimension reduction
identify smaller number of dimensions that capture how people co-vary across across the items.
Where people fall on those dimensions = their score on \(Y\).
- PCA: reduce to set of orthogonal dimensions sequentially capturing most variability.
Scores are weighted composites of responses to items.
- FA: explore (EFA) or test (CFA) model of underlying dimensions (possibly correlated) that explain variability in items.
understanding multi-item measures
\[ \begin{align} \text{Outcome} &=& \text{Model} &\quad + \quad& \text{Error} \\ \quad \\ \text{observed cov/cor} &=& \text{factor loadings and} &\quad + \quad& \text{unique variance for} \\ \text{matrix of items}& &\text{factor correlations} &\quad \quad& \text{each item} \\ \end{align} \]
dimensions
the idea
cov/cor between times can reflect the extent to which items ‘measure the same thing’
Three variables measuring unrelated things:
Rate agreement on:
- Q1: I am the life and soul of the party
- Q2: I like penguins
- Q3: I enjoy studying statistics
Three variables perfectly measuring the exact same thing
Time spent looking at phone last week:
- In hours
- In days
- In weeks
Three variables measuring the same thing but differently
Rate agreement on:
- Q1: I think cake is the best food
- Q2: I feel great when I eat cake
- Q3: I often eat cake
the idea
cov/cor between times can reflect the extent to which items ‘measure the same thing’
Three variables measuring unrelated things:
Rate agreement on:
- Q1: I am the life and soul of the party
- Q2: I like penguins
- Q3: I enjoy studying statistics
Three variables perfectly measuring the exact same thing
Time spent looking at phone last week:
- In hours
- In days
- In weeks
Three variables measuring the same thing but differently
Rate agreement on:
- Q1: I think cake is the best food
- Q2: I feel great when I eat cake
- Q3: I often eat cake
the idea
cov/cor between times can reflect the extent to which items ‘measure the same thing’
Three variables measuring unrelated things:
Rate agreement on:
- Q1: I am the life and soul of the party
- Q2: I like penguins
- Q3: I enjoy studying statistics
Three variables perfectly measuring the exact same thing
Time spent looking at phone last week:
- In hours
- In days
- In weeks
Three variables measuring the same thing but differently
Rate agreement on:
- Q1: I think cake is the best food
- Q2: I feel great when I eat cake
- Q3: I enjoy studying statistics
the idea
cov/cor between times can reflect the extent to which items ‘measure the same thing’
- people vary in lots of ways over k variables
- capture the ways in which people vary.
the idea
cov/cor between times can reflect the extent to which items ‘measure the same thing’
- people vary in lots of ways over k variables
- capture the ways in which people vary.
the idea
cov/cor between times can reflect the extent to which items ‘measure the same thing’
- people vary in lots of ways over k variables
- capture the ways in which people vary.
| y3 | y1 | y2 | y4 | y5 | y6 | |
|---|---|---|---|---|---|---|
| y3 | 1.00 | 0.75 | 0.76 | 0.13 | 0.16 | 0.15 |
| y1 | 0.75 | 1.00 | 0.76 | 0.38 | 0.32 | 0.25 |
| y2 | 0.76 | 0.76 | 1.00 | 0.14 | 0.27 | 0.23 |
| y4 | 0.13 | 0.38 | 0.14 | 1.00 | 0.74 | 0.71 |
| y5 | 0.16 | 0.32 | 0.27 | 0.74 | 1.00 | 0.67 |
| y6 | 0.15 | 0.25 | 0.23 | 0.71 | 0.67 | 1.00 |
dimension reduction
what do we get out?
broadly:
relationships between observed variables and our new dimensions
amount of variance captured/explained by each dimension
loadings - PCA
Principal Components Analysis
Call: principal(r = somedata, nfactors = 6, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 PC2 PC3 PC4 PC5 PC6 h2 u2 com
y1 0.81 -0.43 -0.28 0.10 -0.16 -0.20 1 5.6e-16 2.1
y2 0.74 -0.55 0.22 -0.17 -0.23 0.16 1 4.4e-16 2.5
y3 0.69 -0.61 0.04 0.09 0.37 0.03 1 6.7e-16 2.6
y4 0.70 0.59 -0.30 0.16 -0.01 0.20 1 4.4e-16 2.7
y5 0.71 0.53 -0.03 -0.43 0.11 -0.08 1 1.1e-15 2.7
y6 0.68 0.56 0.40 0.25 -0.03 -0.09 1 1.7e-15 3.0
...loadings
cor(item, component)
loadings - orthogonal EFA
Factor Analysis using method = minres
Call: fa(r = somedata, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.84 0.25 0.78 0.22 1.2
y2 0.87 0.11 0.77 0.23 1.0
y3 0.88 0.04 0.77 0.23 1.0
y4 0.11 0.90 0.82 0.18 1.0
y5 0.16 0.81 0.69 0.31 1.1
y6 0.13 0.78 0.62 0.38 1.1
...loadings
cor(item, Factor)
lm(item ~ Factor)
(where items and Factors are standardised)
loadings\(^2\)
- variance in item explained by Factor (like \(R^2\)!)
PCA
Principal Components Analysis
Call: principal(r = somedata, nfactors = 6, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 PC2 PC3 PC4 PC5 PC6 h2 u2 com
y1 0.81 -0.43 -0.28 0.10 -0.16 -0.20 1 5.6e-16 2.1
y2 0.74 -0.55 0.22 -0.17 -0.23 0.16 1 4.4e-16 2.5
y3 0.69 -0.61 0.04 0.09 0.37 0.03 1 6.7e-16 2.6
y4 0.70 0.59 -0.30 0.16 -0.01 0.20 1 4.4e-16 2.7
y5 0.71 0.53 -0.03 -0.43 0.11 -0.08 1 1.1e-15 2.7
y6 0.68 0.56 0.40 0.25 -0.03 -0.09 1 1.7e-15 3.0
PC1 PC2 PC3 PC4 PC5 PC6
SS loadings 3.15 1.80 0.38 0.32 0.23 0.12
Proportion Var 0.52 0.30 0.06 0.05 0.04 0.02
Cumulative Var 0.52 0.83 0.89 0.94 0.98 1.00
...- Essentially a calculation
- Re-expresses \(k\) items as \(k\) orthogonal dimensions (components) the sequentially capture most variance
- We decide to keep a subset of components based on:
- how many things we ultimately want
- how much variance is captured
- Theory about what the dimensions are doesn’t really matter
conceptual shift to EFA
Factor Analysis using method = minres
Call: fa(r = somedata, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.84 0.25 0.78 0.22 1.2
y2 0.87 0.11 0.77 0.23 1.0
y3 0.88 0.04 0.77 0.23 1.0
y4 0.11 0.90 0.82 0.18 1.0
y5 0.16 0.81 0.69 0.31 1.1
y6 0.13 0.78 0.62 0.38 1.1
MR1 MR2
SS loadings 2.28 2.15
Proportion Var 0.38 0.36
Cumulative Var 0.38 0.74
Proportion Explained 0.51 0.49
Cumulative Proportion 0.51 1.00
...- Is a model (set of parameters are estimated)
“variance captured by components”- “variance explained by factors”
- We choose a model that best explains our observed relationships
- numerically (i.e. distinct factors that each capture something shared across items)
- theoretically (i.e. factors make sense)
EFA compared to PCA
Pretty much the same idea: captures relations between items and dimensions, and variance explained by dimensions
BUT - the aim is to explain, not just reduce
- best explanation becomes theory driven, and is focused on having a “simple structure” (think: clearly defined dimensions).
blurred lines
in psych, PCA is often used as a type of EFA (components are interpreted meaningfully, considered as ‘explanatory’, and sometimes rotated! In most other fields, PCA is pure reduction)
loadings - orthogonal EFA
Factor Analysis using method = minres
Call: fa(r = somedata, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.84 0.25 0.78 0.22 1.2
y2 0.87 0.11 0.77 0.23 1.0
y3 0.88 0.04 0.77 0.23 1.0
y4 0.11 0.90 0.82 0.18 1.0
y5 0.16 0.81 0.69 0.31 1.1
y6 0.13 0.78 0.62 0.38 1.1
...loadings
cor(item, Factor)
lm(item ~ Factor)
(where items and Factors are standardised)
loadings\(^2\)
- variance in item explained by Factor (like \(R^2\)!)

SSloadings & Variance Accounted for
Factor Analysis using method = minres
Call: fa(r = somedata, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.84 0.25 0.78 0.22 1.2
y2 0.87 0.11 0.77 0.23 1.0
y3 0.88 0.04 0.77 0.23 1.0
y4 0.11 0.90 0.82 0.18 1.0
y5 0.16 0.81 0.69 0.31 1.1
y6 0.13 0.78 0.62 0.38 1.1
MR1 MR2
SS loadings 2.28 2.15
...SSloadings
- “sum of squared loadings”
- \(R^2\) from
lm(item1 ~ Factor)+
\(R^2\) fromlm(item2 ~ Factor)+
\(R^2\) fromlm(item3 ~ Factor)+ ….
(where items and Factors are standardised)![]()
SSloadings & Variance Accounted for
Factor Analysis using method = minres
Call: fa(r = somedata, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.84 0.25 0.78 0.22 1.2
y2 0.87 0.11 0.77 0.23 1.0
y3 0.88 0.04 0.77 0.23 1.0
y4 0.11 0.90 0.82 0.18 1.0
y5 0.16 0.81 0.69 0.31 1.1
y6 0.13 0.78 0.62 0.38 1.1
MR1 MR2
SS loadings 2.28 2.15
Proportion Var 0.38 0.36
...“Variance Accounted For”
Total variance = number of items
\(\frac{\text{SSloadings}}{\text{nr items}}\) = variance accounteds for by each factor
SSloadings & Variance Accounted for
Principal Components Analysis
Call: principal(r = somedata, nfactors = 6, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 PC2 PC3 PC4 PC5 PC6 h2 u2 com
y1 0.81 -0.43 -0.28 0.10 -0.16 -0.20 1 5.6e-16 2.1
y2 0.74 -0.55 0.22 -0.17 -0.23 0.16 1 4.4e-16 2.5
y3 0.69 -0.61 0.04 0.09 0.37 0.03 1 6.7e-16 2.6
y4 0.70 0.59 -0.30 0.16 -0.01 0.20 1 4.4e-16 2.7
y5 0.71 0.53 -0.03 -0.43 0.11 -0.08 1 1.1e-15 2.7
y6 0.68 0.56 0.40 0.25 -0.03 -0.09 1 1.7e-15 3.0
PC1 PC2 PC3 PC4 PC5 PC6
SS loadings 3.15 1.80 0.38 0.32 0.23 0.12
Proportion Var 0.52 0.30 0.06 0.05 0.04 0.02
Cumulative Var 0.52 0.83 0.89 0.94 0.98 1.00
...h2, u2
Factor Analysis using method = minres
Call: fa(r = somedata, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
MR1 MR2 h2 u2 com
y1 0.84 0.25 0.78 0.22 1.2
y2 0.87 0.11 0.77 0.23 1.0
y3 0.88 0.04 0.77 0.23 1.0
y4 0.11 0.90 0.82 0.18 1.0
y5 0.16 0.81 0.69 0.31 1.1
y6 0.13 0.78 0.62 0.38 1.1
MR1 MR2
SS loadings 2.28 2.15
Proportion Var 0.38 0.36
...Communalities (h2) & Uniqueness (u2):
h2: Variance in an item explained by all factors
u2: Unexplained variance in an item
lm(item ~ F1 + F2 + ...)
(where items and Factors are standardised)- Communality = \(R^2\)
- Uniqueness = \(1-R^2\) from
EFA output and rotations
\[ \begin{align} \text{Outcome} &=& \text{Model} &\quad + \quad& \text{Error} \\ \quad \\ \text{observed cov/cor} &=& \text{factor loadings and} &\quad + \quad& \text{unique variance for} \\ \text{matrix of items}& &\text{factor correlations} &\quad \quad& \text{each item} \\ \end{align} \]
- think of a rotation as a transformation applied to the factor loadings that may result in a non-zero correlation between factors
- it doesn’t change the numerical ‘fit’ of the model, but it changes the interpretation
EFA output and rotations
Loadings:
ML2 ML1
y1 0.875 0.408
y2 0.877 0.203
y3 0.869 0.164
y4 0.231 0.944
y5 0.270 0.791
y6 0.232 0.760
ML2 ML1
SS loadings 2.471 2.329
Proportion Var 0.412 0.388
Cumulative Var 0.412 0.800
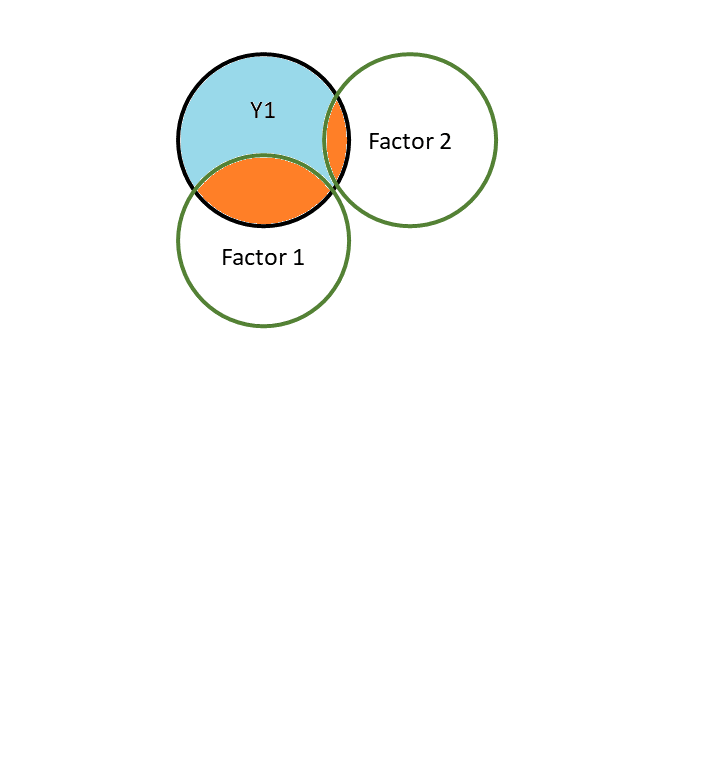
...Structure matrix
Shows
cor(item, Factor)but Factors are now correlated with one another!
EFA output and rotations
Loadings:
ML2 ML1
y1 0.826 0.178
y2 0.890 -0.045
y3 0.892 -0.084
y4 -0.035 0.953
y5 0.054 0.776
y6 0.022 0.754
ML2 ML1
SS loadings 2.275 2.120
Proportion Var 0.379 0.353
Cumulative Var 0.379 0.733
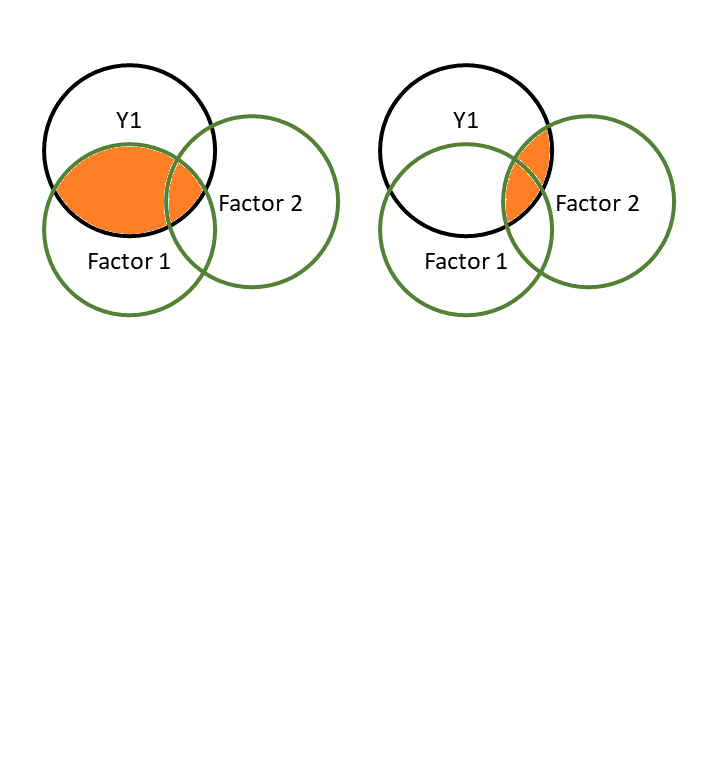
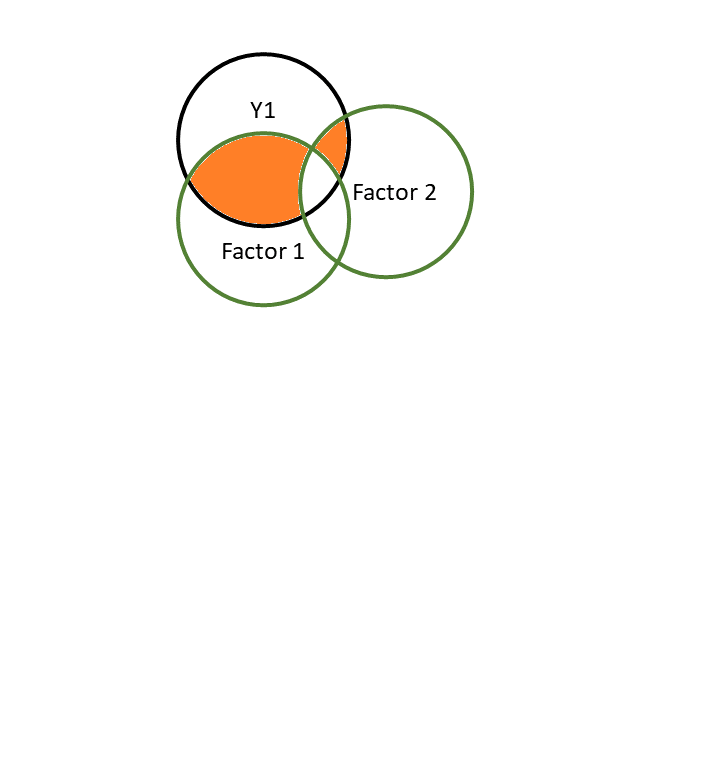
...Pattern matrix
shows variance in item uniquely explained by each Factor
like
lm(item ~ F1 + F2 + ...) |> coef()
(where items and Factors are standardised)
EFA output and rotations
Loadings:
ML2 ML1
y1 0.826 0.178
y2 0.890 -0.045
y3 0.892 -0.084
y4 -0.035 0.953
y5 0.054 0.776
y6 0.022 0.754
ML2 ML1
SS loadings 2.275 2.120
Proportion Var 0.379 0.353
Cumulative Var 0.379 0.733
... With factor correlations of ML2 ML1
ML2 1.000 0.278
ML1 0.278 1.000Factor Correlations
cor(Factor1, Factor2)
EFA output and rotations
Structure
Loadings:
ML2 ML1
y1 0.875 0.408
y2 0.877 0.203
y3 0.869 0.164
y4 0.231 0.944
y5 0.270 0.791
y6 0.232 0.760
ML2 ML1
SS loadings 2.471 2.329
Proportion Var 0.412 0.388
Cumulative Var 0.412 0.800
...Pattern
Loadings:
ML2 ML1
y1 0.826 0.178
y2 0.890 -0.045
y3 0.892 -0.084
y4 -0.035 0.953
y5 0.054 0.776
y6 0.022 0.754
ML2 ML1
SS loadings 2.275 2.120
Proportion Var 0.379 0.353
Cumulative Var 0.379 0.733
...Vaccounted
SSloadings are simply summing the squared values of the columns.
“Variance Accounted For” - slightly trickier because of factor correlations.
ML2 ML1
SS loadings 2.291 2.136
Proportion Var 0.382 0.356
Cumulative Var 0.382 0.738
...

CFA
theories of what and how a tool measures thing(s)
EFA
Goal: discovery / theory generation
- let all items load on all factors
- aim is to get a simple structure
- each item has one primary loading and its other loadings are small/negligible
CFA
Goal: theory testing
- set specific items to load on specific factors
- and do not load onto others
- and do not load onto others
- aim is to test if the model does a good job of capturing the observed relationships in the data
why do y1, …, y4 covary with one another?
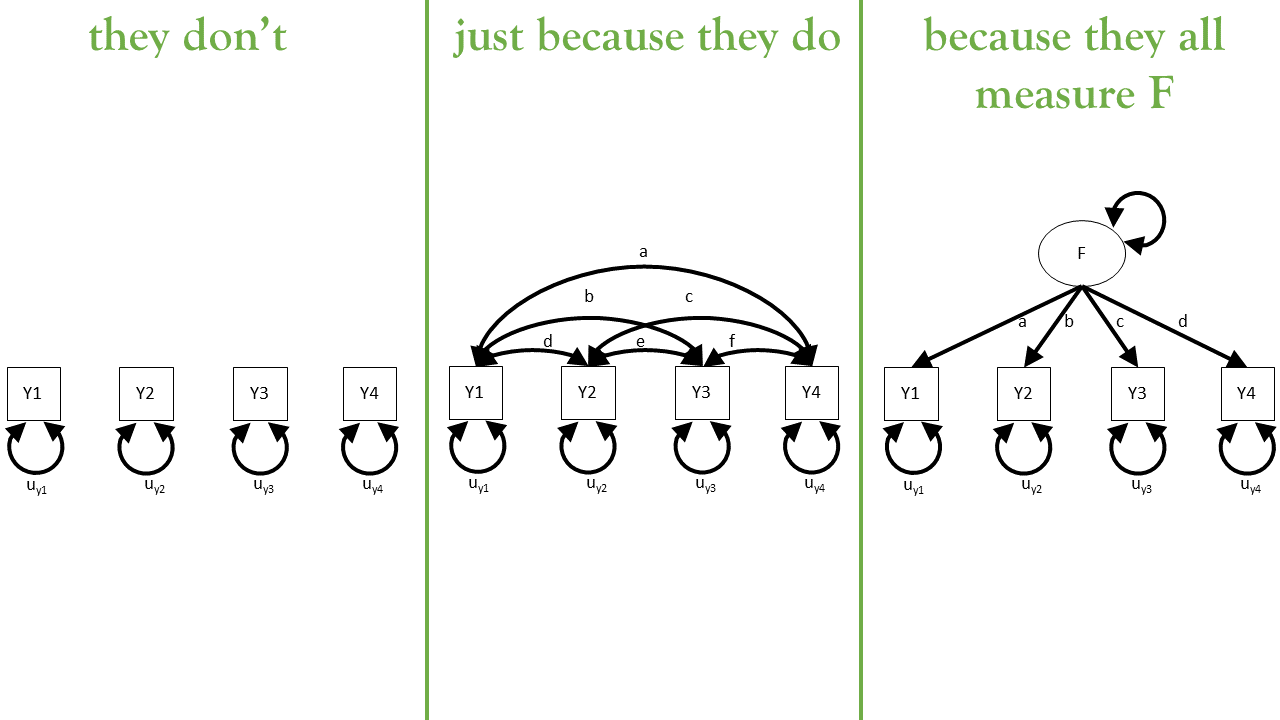
results
- does the model fit well?
- how well can it reproduce the observed covariance matrix?
- are the loadings big enough?
- and then we might focus more on the relationships between the latent factors (because these are of interest)
Underlying considerations about measurement
Q: is a measurement tool reliable?
Am I consistently actually measuring a thing?
- this is all necessary because of measurement error
- with perfect measurement we would only need one variable
- more measurement error >>> lower reliability
- sometimes i’m scored too high, sometimes too low, etc.. noise!
- Reliability is a precursor to validity; a test cannot be valid if it is not reliable.
- lots of different ways to investigate reliability
- test-retest
- parallel forms
- inter-rater
- internal consistency (i.e. within a multi-item measure)
- \(\alpha\) (assumes equal loadings)
- \(\omega\) (based on factor model)
Q: is a measurement tool valid?
Am I measuring the thing I think I’m measuring?
- Lots of different types:
- face validity
- content validity
- convergent validity
- discriminant validity
- predictive validity
- some are assessed through studying the measurement scale and how it is interpreted
- some can be assessed through expected relations with other constructs