Confirmatory Factor Analysis (CFA)
Data Analysis for Psychology in R 3
Psychology, PPLS
University of Edinburgh
Course Overview
|
multilevel modelling working with group structured data |
regression refresher |
| the multilevel model | |
| more complex groupings | |
| centering, assumptions, and diagnostics | |
| recap | |
|
factor analysis working with multi-item measures |
measurement and dimensionality |
| exploring underlying constructs (EFA) | |
| testing theoretical models (CFA) | |
| reliability and validity | |
| recap & exam prep |
Week 8 TR;DL
- PCA just takes a set of observed variables and reduces.
- we don’t really care what the components are, we don’t have a theory why variables are correlated
- EFA is a model of underlying ‘latent variables/factors’ that give rise to responses on observed variables
- we give a meaning to the underlying factors
- The aim is to explore different models (e.g., 1 factor, 2 factor) to understand what our measurement tool captures
- the “best” model here is a combination of
- variance explained
- “simple structure” (clear patterns of loadings)
- theoretical coherence
This week
- CFA vs EFA
- CFA in R (lavaan)
- Model fit
- Model modification
- the gateway to SEM
from EFA to CFA
What is your quest?
I have too many correlated variables. I just need to reduce → PCA
I want to understand the underlying structure of my set of correlated variables → EFA
I have a theoretical structure underlying a set of correlated variables. I want to test it → CFA
I need a way to get a single score for a construct → mean scores/sum scores/PCA/EFA/CFA
In diagrams: EFA
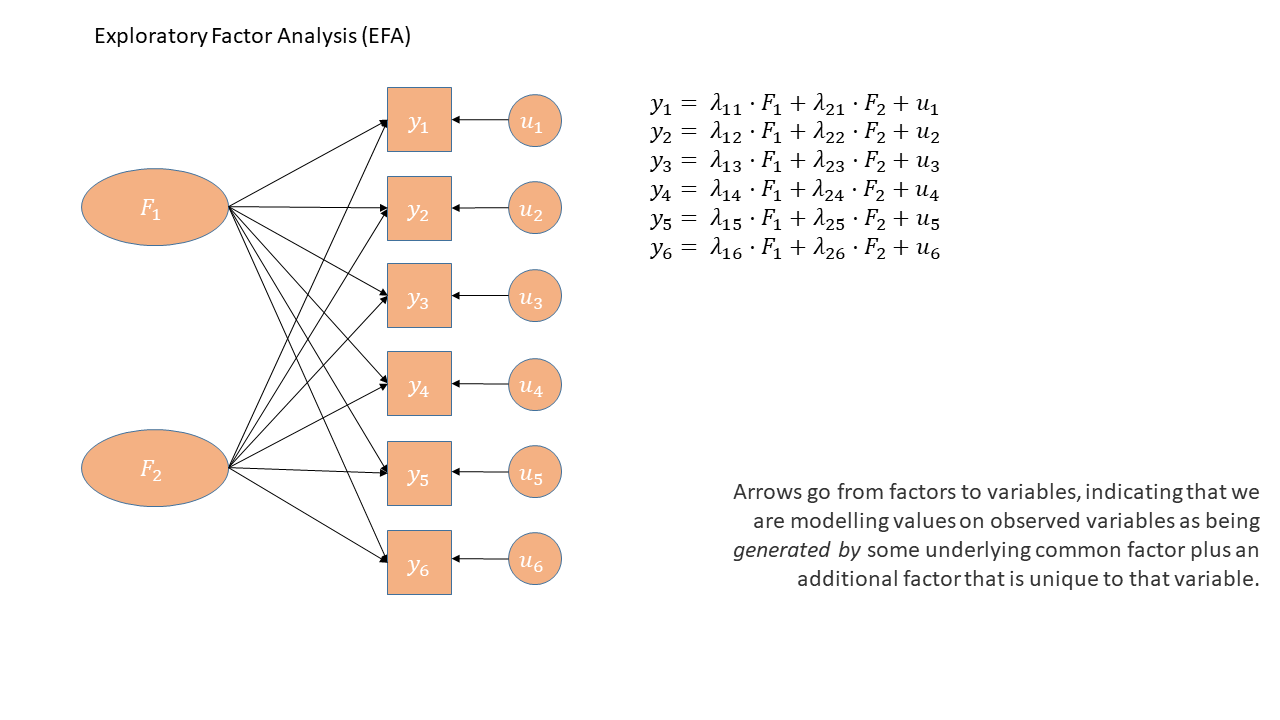
In diagrams: EFA (oblique rotation)
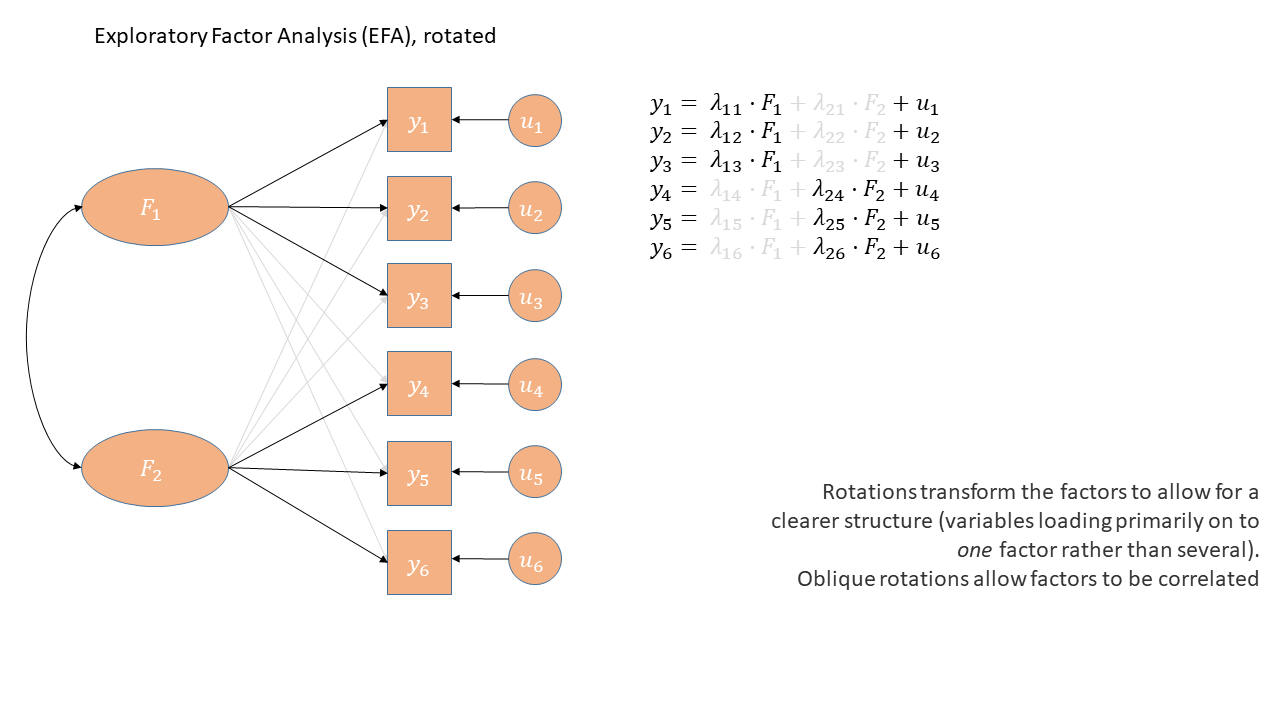
In diagrams: CFA
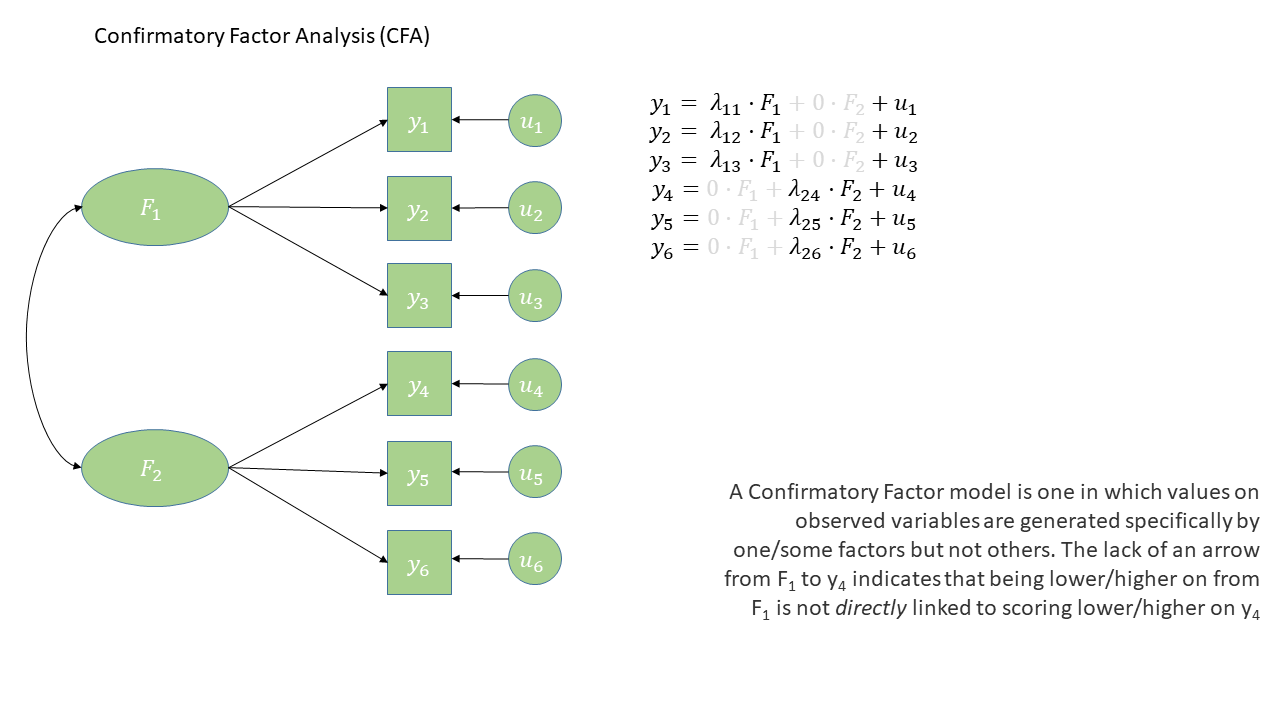
In diagrams: CFA
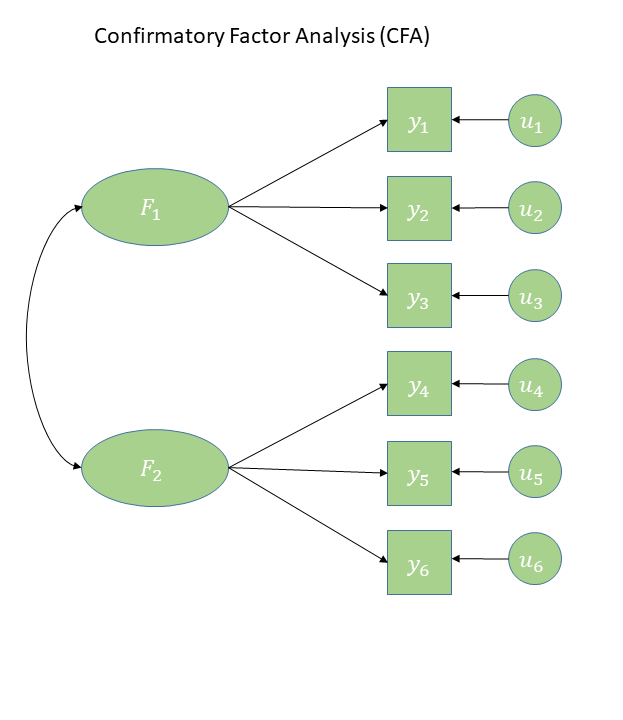
- Some arrows are absent
- This is what imposes our theory
- The reason that \(y_1\) and \(y_2\) are correlated is because:
- they both represent \(F_1\)
- they both represent \(F_1\)
- The reason that \(y_1\) and \(y_6\) are correlated is because:
- \(y_1\) is a manifestation of \(F_1\),
- \(y_6\) is a manifestation of \(F_2\),
- and \(F_1\) and \(F_2\) are correlated
In diagrams: residuals in CFA
different ways people choose to draw the same thing…
CFA in R
The steps of CFA1
- measures, assumptions, data
- specification
- identification
- estimation
- fit
- possible respecification ⚠
- interpretation
the lavaan package
“latent variable analysis”
general modelling framework that estimates models that may include latent variables
Typically done in 2 steps
Previously:
lm(formula, data = mydata)glm(formula, data = mydata)lmer(formula, data = mydata)
With {lavaan}:
Specify model formula in quotation marks:
mymod <- "................"Estimate1 formula with a fitting function such as:
mymod.est <- cfa(mymod, data = mydata)
lavaan operators
| Formula type | Operator | Mnemonic |
|---|---|---|
| latent variable definition | =~ |
“is measured by” |
| (residual) (co)variance | ~~ |
“covaries with” |

F1 =~ y1 + y2 + y3
F2 =~ y4 + y5 + y6
F1 ~~ F2example: QRI

| var | wording |
|---|---|
| s1 | To what extent could you turn to this person for advice about problems? |
| s2 | To what extent could you count on this person for help with a problem? |
| s3 | To what extent can you really count on this person to distract you from your worries when you feel under stress? |
| s4 | To what extent can you count on this person to listen to you when you are very angry at someone else? |
| c1 | How often do you have to work hard to avoid conflict with this person? |
| c2 | How much do you argue with this person? |
| c3 | How much would you like this person to change? |
| c4 | How often does this person make you feel angry? |
| d1 | How positive a role does this person play in your life? |
| d2 | How significant is this relationship in your life? |
| d3 | How close will your relationship be with this person in 10 years? |
| d4 | How much would you miss this person if the two of you could not see or talk with each other for a month? |
example: QRI
s2 d4 c3 c4 d1 c2 s1 s4 d2 c1 s3 d3
1 4 4 5 5 5 4 3 3 2 3 5 5
2 3 5 4 4 2 4 4 5 2 4 4 4
3 4 5 4 5 4 2 5 3 6 2 4 5
4 3 6 4 3 5 3 3 4 4 2 5 5
5 6 7 1 2 4 2 7 7 4 1 7 5
6 3 5 5 4 4 3 5 4 3 3 5 5example: QRI
lavaan 0.6-19 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Number of observations 374
Model Test User Model:
Test statistic 81.100
Degrees of freedom 51
P-value (Chi-square) 0.005
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
support =~
s1 0.601 0.062 9.765 0.000
s2 0.707 0.064 11.010 0.000
s3 0.642 0.074 8.676 0.000
s4 0.608 0.072 8.407 0.000
conflict =~
c1 0.860 0.077 11.102 0.000
c2 0.810 0.063 12.909 0.000
c3 0.614 0.072 8.532 0.000
c4 0.808 0.064 12.673 0.000
depth =~
d1 0.617 0.063 9.759 0.000
d2 0.770 0.069 11.175 0.000
d3 0.621 0.061 10.119 0.000
d4 0.634 0.062 10.143 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
support ~~
conflict -0.530 0.063 -8.473 0.000
depth 0.613 0.062 9.956 0.000
conflict ~~
depth -0.425 0.065 -6.551 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.s1 0.763 0.070 10.860 0.000
.s2 0.738 0.077 9.626 0.000
.s3 1.188 0.102 11.625 0.000
.s4 1.151 0.098 11.781 0.000
.c1 1.259 0.116 10.893 0.000
.c2 0.692 0.076 9.128 0.000
.c3 1.251 0.102 12.276 0.000
.c4 0.735 0.078 9.409 0.000
.d1 0.839 0.075 11.146 0.000
.d2 0.885 0.089 9.923 0.000
.d3 0.771 0.071 10.880 0.000
.d4 0.797 0.073 10.861 0.000
support 1.000
conflict 1.000
depth 1.000 example: QRI
lavaan 0.6-19 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Number of observations 374
Model Test User Model:
Test statistic 81.100
Degrees of freedom 51
P-value (Chi-square) 0.005
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
support =~
s1 0.601 0.062 9.765 0.000
s2 0.707 0.064 11.010 0.000
s3 0.642 0.074 8.676 0.000
s4 0.608 0.072 8.407 0.000
conflict =~
c1 0.860 0.077 11.102 0.000
c2 0.810 0.063 12.909 0.000
c3 0.614 0.072 8.532 0.000
c4 0.808 0.064 12.673 0.000
depth =~
d1 0.617 0.063 9.759 0.000
d2 0.770 0.069 11.175 0.000
d3 0.621 0.061 10.119 0.000
d4 0.634 0.062 10.143 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
support ~~
conflict -0.530 0.063 -8.473 0.000
depth 0.613 0.062 9.956 0.000
conflict ~~
depth -0.425 0.065 -6.551 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.s1 0.763 0.070 10.860 0.000
.s2 0.738 0.077 9.626 0.000
.s3 1.188 0.102 11.625 0.000
.s4 1.151 0.098 11.781 0.000
.c1 1.259 0.116 10.893 0.000
.c2 0.692 0.076 9.128 0.000
.c3 1.251 0.102 12.276 0.000
.c4 0.735 0.078 9.409 0.000
.d1 0.839 0.075 11.146 0.000
.d2 0.885 0.089 9.923 0.000
.d3 0.771 0.071 10.880 0.000
.d4 0.797 0.073 10.861 0.000
support 1.000
conflict 1.000
depth 1.000 latent variable scaling
the latent factor is unobserved
its scale doesn’t exist - we need to fix it to something.
We can…
fix its variance to 1 (as previous slides).
std.lv = TRUE >> latent variables are standardised
lavaan 0.6-19 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Number of observations 374
Model Test User Model:
Test statistic 81.100
Degrees of freedom 51
P-value (Chi-square) 0.005
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
support =~
s1 0.601 0.062 9.765 0.000
s2 0.707 0.064 11.010 0.000
s3 0.642 0.074 8.676 0.000
s4 0.608 0.072 8.407 0.000
conflict =~
c1 0.860 0.077 11.102 0.000
c2 0.810 0.063 12.909 0.000
c3 0.614 0.072 8.532 0.000
c4 0.808 0.064 12.673 0.000
depth =~
d1 0.617 0.063 9.759 0.000
d2 0.770 0.069 11.175 0.000
d3 0.621 0.061 10.119 0.000
d4 0.634 0.062 10.143 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
support ~~
conflict -0.530 0.063 -8.473 0.000
depth 0.613 0.062 9.956 0.000
conflict ~~
depth -0.425 0.065 -6.551 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.s1 0.763 0.070 10.860 0.000
.s2 0.738 0.077 9.626 0.000
.s3 1.188 0.102 11.625 0.000
.s4 1.151 0.098 11.781 0.000
.c1 1.259 0.116 10.893 0.000
.c2 0.692 0.076 9.128 0.000
.c3 1.251 0.102 12.276 0.000
.c4 0.735 0.078 9.409 0.000
.d1 0.839 0.075 11.146 0.000
.d2 0.885 0.089 9.923 0.000
.d3 0.771 0.071 10.880 0.000
.d4 0.797 0.073 10.861 0.000
support 1.000
conflict 1.000
depth 1.000 latent variable scaling (marker method)
the latent factor is unobserved
its scale doesn’t exist - we need to fix it to something.
We can…
fix it to having the same scale as one of the items (defaults to the first one).
the default in lavaan
lavaan 0.6-19 ended normally after 37 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Number of observations 374
Model Test User Model:
Test statistic 81.100
Degrees of freedom 51
P-value (Chi-square) 0.005
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
support =~
s1 1.000
s2 1.177 0.155 7.588 0.000
s3 1.070 0.158 6.759 0.000
s4 1.013 0.153 6.633 0.000
conflict =~
c1 1.000
c2 0.942 0.104 9.025 0.000
c3 0.714 0.100 7.150 0.000
c4 0.940 0.105 8.972 0.000
depth =~
d1 1.000
d2 1.247 0.162 7.702 0.000
d3 1.007 0.137 7.374 0.000
d4 1.027 0.139 7.383 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
support ~~
conflict -0.274 0.052 -5.293 0.000
depth 0.227 0.042 5.450 0.000
conflict ~~
depth -0.226 0.048 -4.678 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.s1 0.763 0.070 10.860 0.000
.s2 0.738 0.077 9.626 0.000
.s3 1.188 0.102 11.625 0.000
.s4 1.151 0.098 11.781 0.000
.c1 1.259 0.116 10.893 0.000
.c2 0.692 0.076 9.128 0.000
.c3 1.251 0.102 12.276 0.000
.c4 0.735 0.078 9.409 0.000
.d1 0.839 0.075 11.146 0.000
.d2 0.885 0.089 9.923 0.000
.d3 0.771 0.071 10.880 0.000
.d4 0.797 0.073 10.861 0.000
support 0.361 0.074 4.883 0.000
conflict 0.740 0.133 5.551 0.000
depth 0.381 0.078 4.880 0.000latent variable scaling (its all the same)
standardisation
- Back with EFA, we were working with correlations
- everything was already standardised
- everything was already standardised
- Now we are working with covariances
- model parameters depend on the scales of the variables
standardisation
Std.lvcolumn = latent variables are standardised, observed variables aren’t
Std.allcolumn = both latent variables and observed variables are standardised
lavaan 0.6-19 ended normally after 37 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Number of observations 374
Model Test User Model:
Test statistic 81.100
Degrees of freedom 51
P-value (Chi-square) 0.005
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
support =~
s1 1.000 0.601 0.567
s2 1.177 0.155 7.588 0.000 0.707 0.636
s3 1.070 0.158 6.759 0.000 0.642 0.508
s4 1.013 0.153 6.633 0.000 0.608 0.493
conflict =~
c1 1.000 0.860 0.608
c2 0.942 0.104 9.025 0.000 0.810 0.698
c3 0.714 0.100 7.150 0.000 0.614 0.481
c4 0.940 0.105 8.972 0.000 0.808 0.686
depth =~
d1 1.000 0.617 0.559
d2 1.247 0.162 7.702 0.000 0.770 0.633
d3 1.007 0.137 7.374 0.000 0.621 0.578
d4 1.027 0.139 7.383 0.000 0.634 0.579
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
support ~~
conflict -0.274 0.052 -5.293 0.000 -0.530 -0.530
depth 0.227 0.042 5.450 0.000 0.613 0.613
conflict ~~
depth -0.226 0.048 -4.678 0.000 -0.425 -0.425
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.s1 0.763 0.070 10.860 0.000 0.763 0.679
.s2 0.738 0.077 9.626 0.000 0.738 0.596
.s3 1.188 0.102 11.625 0.000 1.188 0.742
.s4 1.151 0.098 11.781 0.000 1.151 0.757
.c1 1.259 0.116 10.893 0.000 1.259 0.630
.c2 0.692 0.076 9.128 0.000 0.692 0.513
.c3 1.251 0.102 12.276 0.000 1.251 0.768
.c4 0.735 0.078 9.409 0.000 0.735 0.529
.d1 0.839 0.075 11.146 0.000 0.839 0.688
.d2 0.885 0.089 9.923 0.000 0.885 0.599
.d3 0.771 0.071 10.880 0.000 0.771 0.666
.d4 0.797 0.073 10.861 0.000 0.797 0.665
support 0.361 0.074 4.883 0.000 1.000 1.000
conflict 0.740 0.133 5.551 0.000 1.000 1.000
depth 0.381 0.078 4.880 0.000 1.000 1.000model fit & idenfication
The steps of CFA1
- measures, assumptions, data
- specification ✓
- identification
- estimation ✓
- fit
- possible respecification ⚠
- interpretation
what is model fit?
“how well does my model reproduce my outcome?”
Previous models (lm, lmer):
- outcome = a single variable
\[ \begin{align} \text{outcome} &= \text{model} &+ \text{error} \\ \quad \\ \text{observed variable} & = \text{coefficients and predictor variables} &+ \text{error} \\ \quad \\ \text{observed variable} & = \text{model predicted values} &+ \text{error} \\ \end{align} \]
CFA1
- outcome = a covariance matrix
\[ \begin{align} \text{outcome} &= \text{model} &+ \text{error} \\ \quad \\ \text{observed covariance matrix} & = \text{model parameters} &+ \text{error} \\ \quad \\ \text{observed covariance matrix} & = \text{model implied covariance matrix} &+ \text{error} \\ \end{align} \]
what are the model parameters?
the estimated paths on the diagram!
how does a diagram imply a covariance?
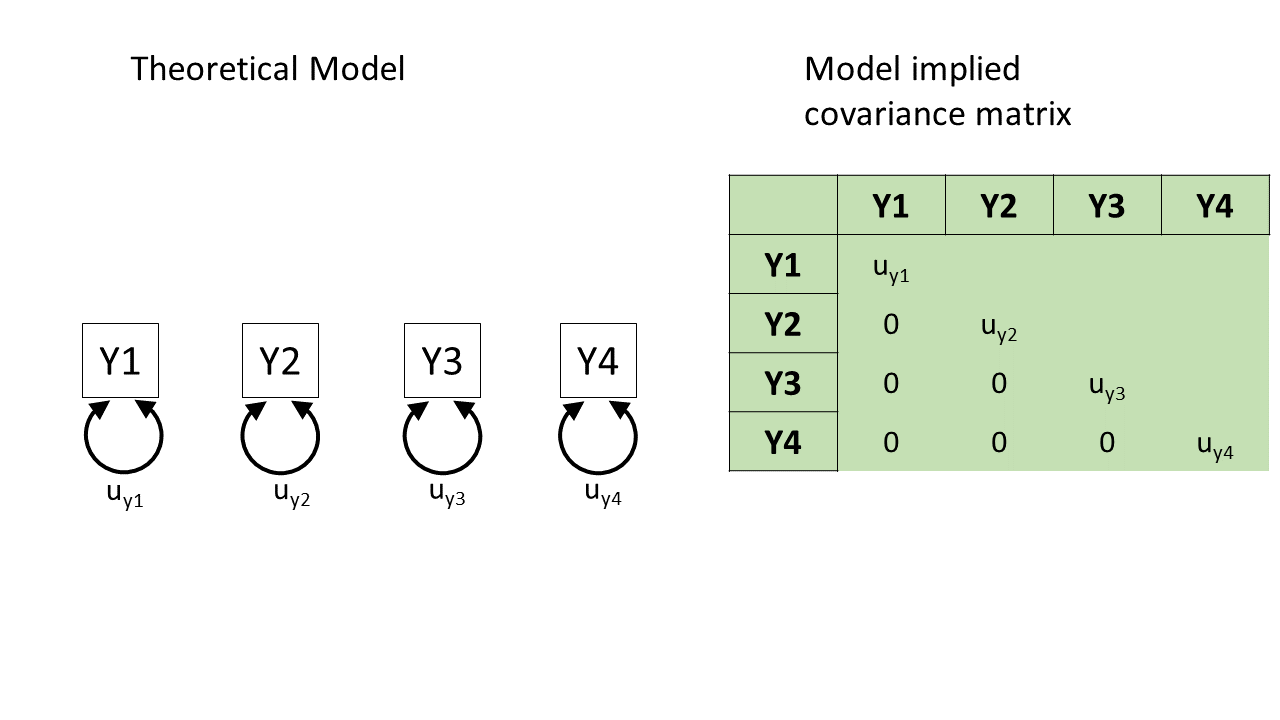
how does a diagram imply a covariance? (2)
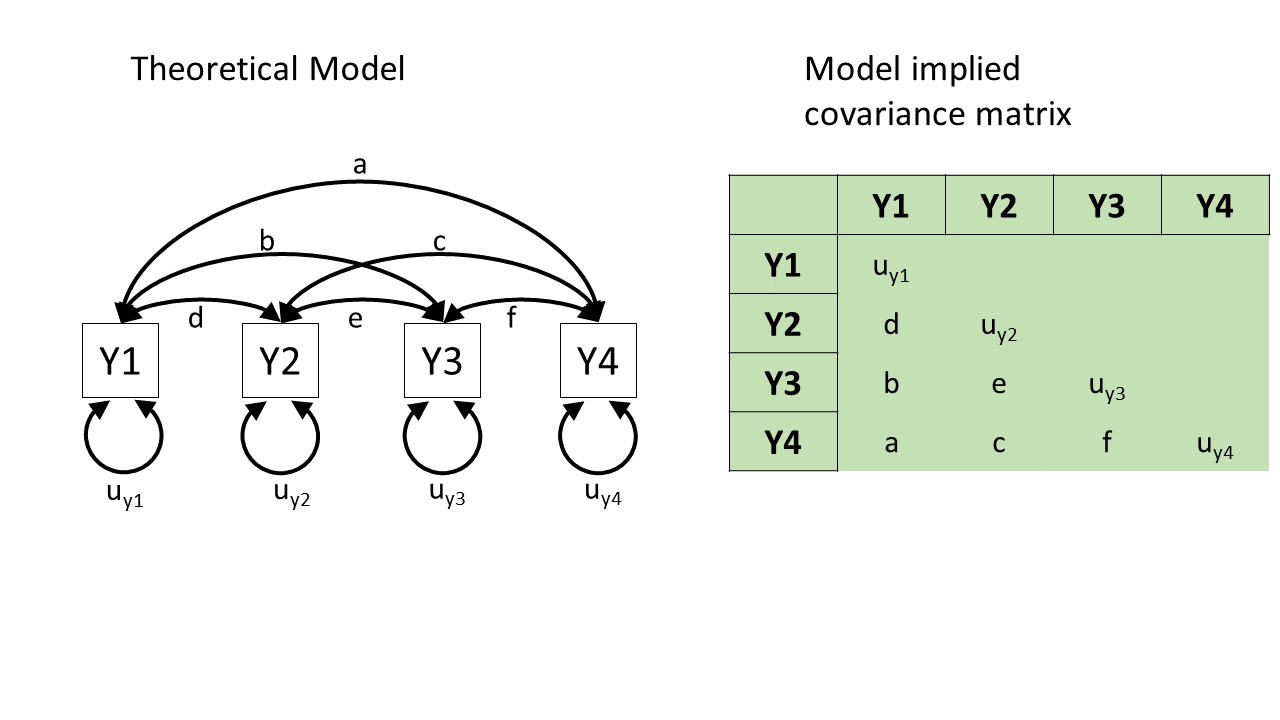
how does a diagram imply a covariance? (3)
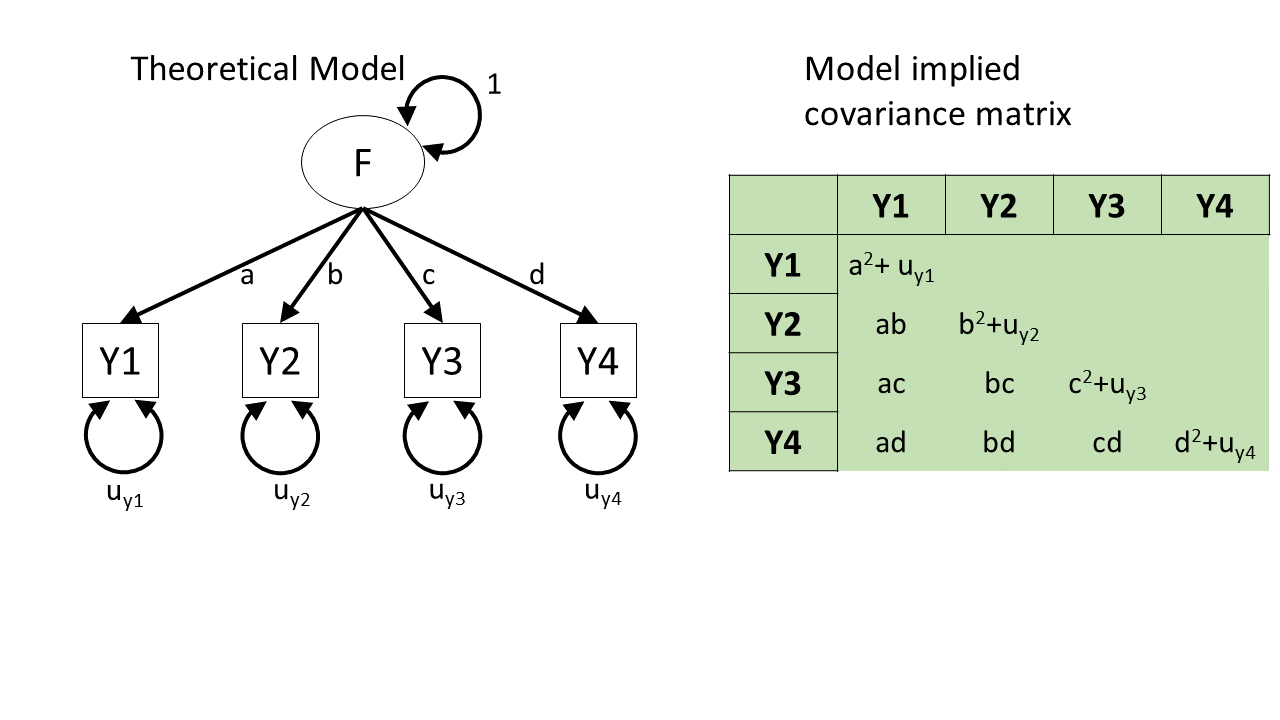
identifiability
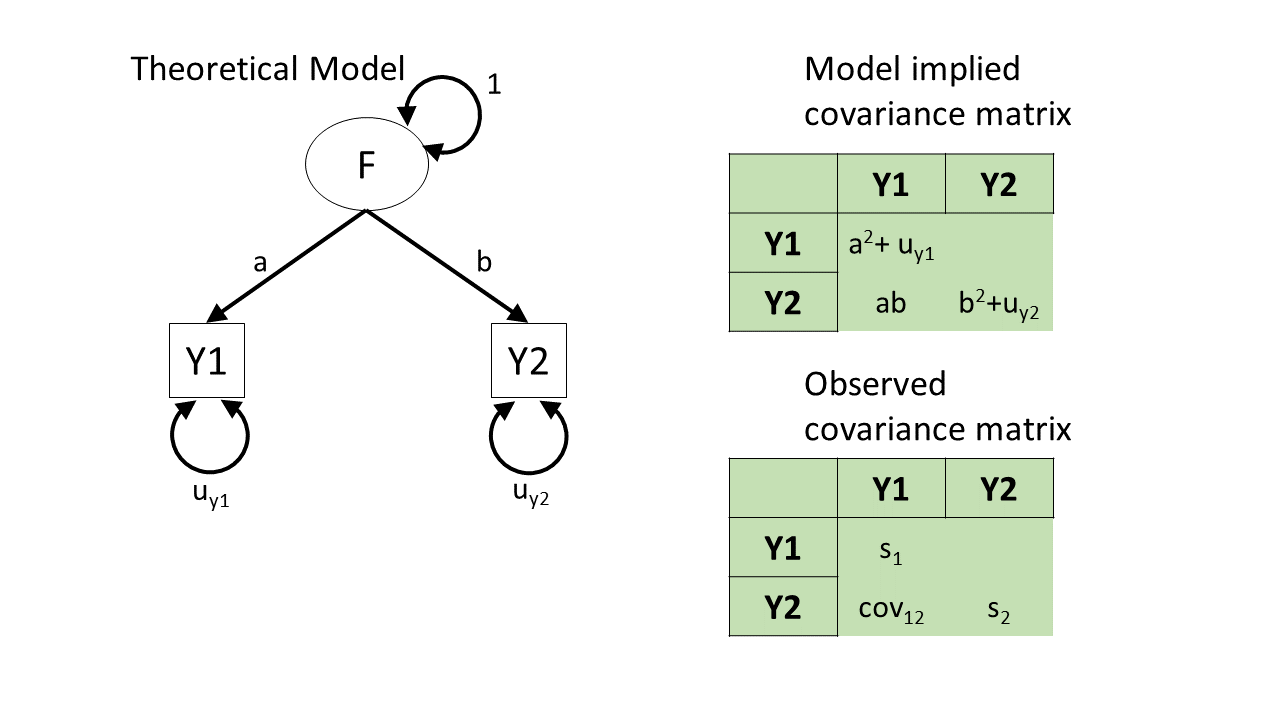
identifiability (2)
identifiability (3)
identifiability (4)
Conceptually:
- Back in linear regression world - with just two datapoints there is only one line we can draw.
- we start with 2 datapoints, and we estimate 2 things (intercept and slope).
- we start with 2 datapoints, and we estimate 2 things (intercept and slope).
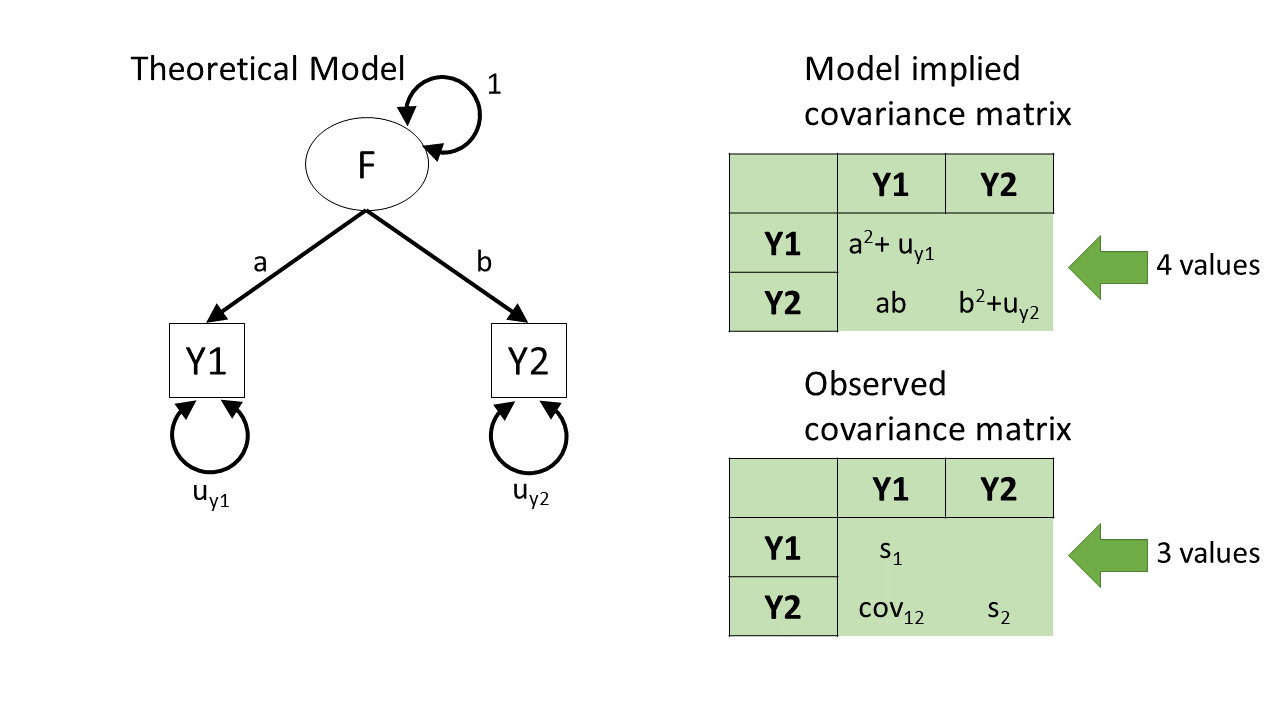
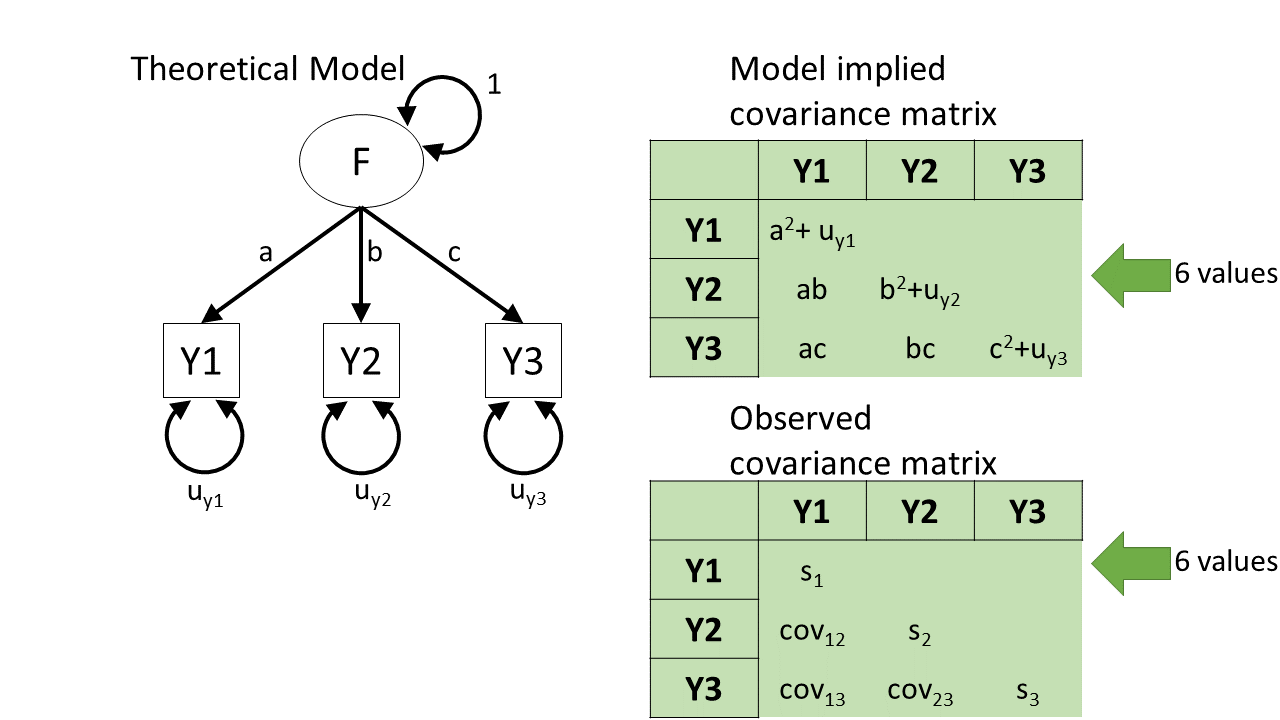
- In CFA world, the same applies for a factor with 3 ‘indicators’ (items)
- we start with 6 values, and we estimate 6 things
To measure ‘model fit’ we need to observe more things than we estimate
degrees of freedom
how many “knowns”?
how many values in our covariance matrix?
for \(k\) variables this is \(\frac{k(k+1)}{2}\)
how many “unknowns”?
- how many parameters are we estimating with our model?
degrees of freedom = knowns - unknowns
example: QRI
how many “knowns”?
s2 d4 c3 c4 d1 c2 s1 s4 d2 c1 s3 d3
s2 1.24 0.32 -0.26 -0.24 0.22 -0.21 0.46 0.39 0.39 -0.46 0.44 0.31
d4 0.32 1.20 -0.19 -0.10 0.39 -0.20 0.20 0.29 0.47 -0.40 0.24 0.41
c3 -0.26 -0.19 1.63 0.41 -0.24 0.43 -0.31 -0.32 -0.34 0.68 -0.24 -0.29
c4 -0.24 -0.10 0.41 1.39 -0.15 0.78 -0.24 -0.24 -0.16 0.62 -0.29 -0.14
d1 0.22 0.39 -0.24 -0.15 1.22 -0.22 0.19 0.16 0.51 -0.42 0.24 0.38
c2 -0.21 -0.20 0.43 0.78 -0.22 1.35 -0.18 -0.18 -0.17 0.62 -0.26 -0.20
s1 0.46 0.20 -0.31 -0.24 0.19 -0.18 1.13 0.36 0.28 -0.38 0.37 0.20
s4 0.39 0.29 -0.32 -0.24 0.16 -0.18 0.36 1.53 0.29 -0.45 0.45 0.24
d2 0.39 0.47 -0.34 -0.16 0.51 -0.17 0.28 0.29 1.48 -0.37 0.32 0.46
c1 -0.46 -0.40 0.68 0.62 -0.42 0.62 -0.38 -0.45 -0.37 2.00 -0.30 -0.32
s3 0.44 0.24 -0.24 -0.29 0.24 -0.26 0.37 0.45 0.32 -0.30 1.61 0.23
d3 0.31 0.41 -0.29 -0.14 0.38 -0.20 0.20 0.24 0.46 -0.32 0.23 1.16how many “unknowns”?
example: QRI
how many “knowns”?
78 variances and covariances
- 12 observed variables
- (12 x 13) / 2 = 78
how many “unknowns”?
27 estimated parameters
- 12 factor loadings
- 12 residual variances
- 3 factor correlations
3 factor variances(fixed to 1)
lavaan 0.6-19 ended normally after 37 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Number of observations 374
Model Test User Model:
Test statistic 81.100
Degrees of freedom 51
P-value (Chi-square) 0.005
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
support =~
s1 1.000
s2 1.177 0.155 7.588 0.000
s3 1.070 0.158 6.759 0.000
s4 1.013 0.153 6.633 0.000
conflict =~
c1 1.000
c2 0.942 0.104 9.025 0.000
c3 0.714 0.100 7.150 0.000
c4 0.940 0.105 8.972 0.000
depth =~
d1 1.000
d2 1.247 0.162 7.702 0.000
d3 1.007 0.137 7.374 0.000
d4 1.027 0.139 7.383 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
support ~~
conflict -0.274 0.052 -5.293 0.000
depth 0.227 0.042 5.450 0.000
conflict ~~
depth -0.226 0.048 -4.678 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.s1 0.763 0.070 10.860 0.000
.s2 0.738 0.077 9.626 0.000
.s3 1.188 0.102 11.625 0.000
.s4 1.151 0.098 11.781 0.000
.c1 1.259 0.116 10.893 0.000
.c2 0.692 0.076 9.128 0.000
.c3 1.251 0.102 12.276 0.000
.c4 0.735 0.078 9.409 0.000
.d1 0.839 0.075 11.146 0.000
.d2 0.885 0.089 9.923 0.000
.d3 0.771 0.071 10.880 0.000
.d4 0.797 0.073 10.861 0.000
support 0.361 0.074 4.883 0.000
conflict 0.740 0.133 5.551 0.000
depth 0.381 0.078 4.880 0.000model fit
Pretty much all based on:
\[
\begin{align}
\text{observed covariance matrix}\,\,\, vs \,\,\, \text{model implied covariance matrix}\\
\end{align}
\]
typically also incorporate degrees of freedom (these represent model complexity/parsimony)
fit indices
there are loooooooaddds of different metrics…
“absolute fit”
“how far from perfect fit?”
smaller is better
| fit index | common threshold |
|---|---|
| RMSEA | <0.05 |
| SRMR | <0.05/<0.08 |
“incremental fit”
“how much better than a null model1?”
bigger is better
| fit index | common threshold |
|---|---|
| TLI | >0.95 |
| CFI | >0.95 |
In R:
fitmeasures(mymod.est)[c("rmsea","srmr","cfi","tli")]
rmsea srmr cfi tli
0.0397 0.0467 0.9619 0.9508 The steps of CFA1
- measures, assumptions, data
- specification ✓
- identification ✓
- estimation ✓
- fit ✓
- possible respecification ⚠
- interpretation
model respecification
modification indices
“how much better would my model fit if we included parameter x?”
but..
- adding in parameters will always improve model fit
- and we lose degrees of freedom
- ⬆model complexity, ⬇ model simplicity
- these should be theoretically justified
modindices()
lhs,op,rhs= the parametermi= change in fitepc,sepc.lv,sepc.all,sepc.nox= expected value of parameter (under various forms of standardisation)
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
101 c2 ~~ c4 50.316 0.561 0.561 0.787 0.787
51 depth =~ c1 15.882 -0.612 -0.378 -0.267 -0.267
31 support =~ c1 14.774 -0.695 -0.417 -0.295 -0.295
54 depth =~ c4 12.504 0.457 0.282 0.239 0.239
32 support =~ c2 9.875 0.478 0.287 0.247 0.247
94 c1 ~~ c3 8.577 0.237 0.237 0.189 0.189
93 c1 ~~ c2 8.101 -0.241 -0.241 -0.258 -0.258
95 c1 ~~ c4 7.628 -0.234 -0.234 -0.243 -0.243
53 depth =~ c3 6.143 -0.351 -0.216 -0.170 -0.170
106 c3 ~~ c4 6.027 -0.170 -0.170 -0.177 -0.177
33 support =~ c3 5.216 -0.378 -0.227 -0.178 -0.178
100 c2 ~~ c3 3.797 -0.134 -0.134 -0.144 -0.144
34 support =~ c4 3.637 0.293 0.176 0.149 0.149
96 c1 ~~ d1 3.523 -0.116 -0.116 -0.113 -0.113
99 c1 ~~ d4 3.320 -0.111 -0.111 -0.111 -0.111
114 c4 ~~ d4 3.179 0.087 0.087 0.114 0.114
52 depth =~ c2 2.985 0.221 0.136 0.117 0.117
68 s2 ~~ c1 2.819 -0.103 -0.103 -0.107 -0.107
108 c3 ~~ d2 2.611 -0.102 -0.102 -0.097 -0.097
85 s4 ~~ c1 2.474 -0.112 -0.112 -0.093 -0.093
103 c2 ~~ d2 2.117 0.076 0.076 0.097 0.097
59 s1 ~~ c2 2.114 0.069 0.069 0.095 0.095
60 s1 ~~ c3 1.940 -0.079 -0.079 -0.081 -0.081
86 s4 ~~ c2 1.895 0.078 0.078 0.087 0.087
77 s3 ~~ c1 1.835 0.099 0.099 0.081 0.081
109 c3 ~~ d3 1.748 -0.076 -0.076 -0.077 -0.077
67 s2 ~~ s4 1.658 -0.089 -0.089 -0.096 -0.096
69 s2 ~~ c2 1.603 0.062 0.062 0.086 0.086
89 s4 ~~ d1 1.592 -0.073 -0.073 -0.074 -0.074
55 s1 ~~ s2 1.525 0.078 0.078 0.103 0.103
35 support =~ d1 1.494 -0.212 -0.127 -0.115 -0.115
72 s2 ~~ d1 1.414 -0.060 -0.060 -0.076 -0.076
47 depth =~ s1 1.403 -0.198 -0.122 -0.115 -0.115
48 depth =~ s2 1.326 0.212 0.131 0.117 0.117
87 s4 ~~ c3 1.326 -0.078 -0.078 -0.065 -0.065
76 s3 ~~ s4 1.244 0.083 0.083 0.071 0.071
92 s4 ~~ d4 1.145 0.061 0.061 0.064 0.064
115 d1 ~~ d2 0.991 0.067 0.067 0.078 0.078
80 s3 ~~ c4 0.971 -0.058 -0.058 -0.062 -0.062
111 c4 ~~ d1 0.853 0.046 0.046 0.059 0.059
73 s2 ~~ d2 0.779 0.048 0.048 0.059 0.059
75 s2 ~~ d4 0.743 0.043 0.043 0.056 0.056
110 c3 ~~ d4 0.682 0.048 0.048 0.048 0.048
65 s1 ~~ d4 0.678 -0.039 -0.039 -0.051 -0.051
44 conflict =~ d2 0.667 0.080 0.069 0.057 0.057
58 s1 ~~ c1 0.660 -0.049 -0.049 -0.050 -0.050
71 s2 ~~ c4 0.616 0.039 0.039 0.053 0.053
113 c4 ~~ d3 0.574 0.036 0.036 0.048 0.048
43 conflict =~ d1 0.558 -0.065 -0.056 -0.051 -0.051
74 s2 ~~ d3 0.541 0.036 0.036 0.047 0.047
40 conflict =~ s2 0.521 0.078 0.067 0.060 0.060
112 c4 ~~ d2 0.493 0.037 0.037 0.046 0.046
64 s1 ~~ d3 0.371 -0.029 -0.029 -0.037 -0.037
78 s3 ~~ c2 0.370 -0.035 -0.035 -0.039 -0.039
118 d2 ~~ d3 0.360 -0.040 -0.040 -0.048 -0.048
119 d2 ~~ d4 0.340 -0.039 -0.039 -0.047 -0.047
102 c2 ~~ d1 0.304 -0.027 -0.027 -0.035 -0.035
36 support =~ d2 0.304 0.109 0.065 0.054 0.054
42 conflict =~ s4 0.285 -0.060 -0.052 -0.042 -0.042
66 s2 ~~ s3 0.263 -0.037 -0.037 -0.039 -0.039
120 d3 ~~ d4 0.259 0.029 0.029 0.037 0.037
56 s1 ~~ s3 0.190 -0.028 -0.028 -0.030 -0.030
84 s3 ~~ d4 0.175 -0.024 -0.024 -0.025 -0.025
38 support =~ d4 0.173 0.072 0.043 0.039 0.039
105 c2 ~~ d4 0.166 -0.020 -0.020 -0.026 -0.026
83 s3 ~~ d3 0.158 -0.023 -0.023 -0.024 -0.024
79 s3 ~~ c3 0.152 0.027 0.027 0.022 0.022
81 s3 ~~ d1 0.147 0.023 0.023 0.023 0.023
45 conflict =~ d3 0.104 -0.028 -0.024 -0.022 -0.022
70 s2 ~~ c3 0.085 0.017 0.017 0.018 0.018
104 c2 ~~ d3 0.074 -0.013 -0.013 -0.018 -0.018
82 s3 ~~ d2 0.042 0.013 0.013 0.013 0.013
91 s4 ~~ d3 0.040 0.011 0.011 0.012 0.012
61 s1 ~~ c4 0.039 -0.010 -0.010 -0.013 -0.013
37 support =~ d3 0.034 0.031 0.019 0.017 0.017
117 d1 ~~ d4 0.033 -0.011 -0.011 -0.013 -0.013
62 s1 ~~ d1 0.031 -0.009 -0.009 -0.011 -0.011
41 conflict =~ s3 0.030 -0.020 -0.017 -0.014 -0.014
46 conflict =~ d4 0.027 0.014 0.012 0.011 0.011
39 conflict =~ s1 0.023 -0.015 -0.013 -0.012 -0.012
49 depth =~ s3 0.021 -0.028 -0.017 -0.014 -0.014
88 s4 ~~ c4 0.019 0.008 0.008 0.009 0.009
63 s1 ~~ d2 0.017 0.007 0.007 0.008 0.008
116 d1 ~~ d3 0.014 -0.007 -0.007 -0.008 -0.008
107 c3 ~~ d1 0.011 -0.006 -0.006 -0.006 -0.006
50 depth =~ s4 0.009 0.018 0.011 0.009 0.009
98 c1 ~~ d3 0.005 0.004 0.004 0.004 0.004
97 c1 ~~ d2 0.004 -0.004 -0.004 -0.004 -0.004
57 s1 ~~ s4 0.003 -0.003 -0.003 -0.004 -0.004
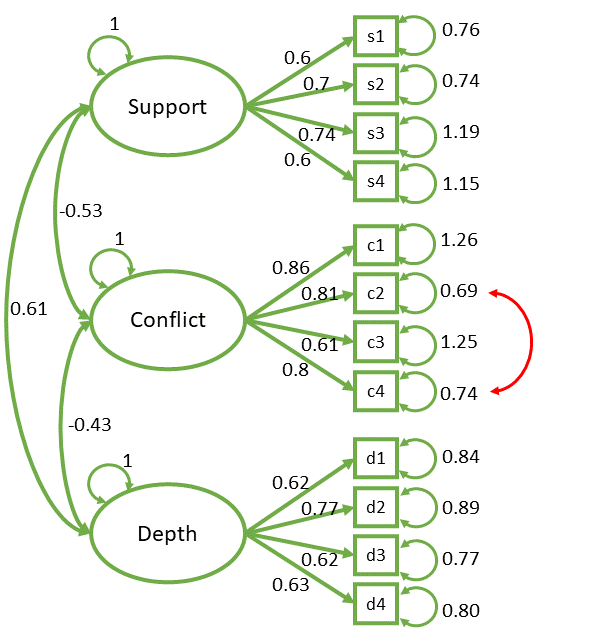
90 s4 ~~ d2 0.002 -0.003 -0.003 -0.003 -0.003modification indices
| var | wording |
|---|---|
| s1 | To what extent could you turn to this person for advice about problems? |
| s2 | To what extent could you count on this person for help with a problem? |
| s3 | To what extent can you really count on this person to distract you from your worries when you feel under stress? |
| s4 | To what extent can you count on this person to listen to you when you are very angry at someone else? |
| c1 | How often do you have to work hard to avoid conflict with this person? |
| c2 | How much do you argue with this person? |
| c3 | How much would you like this person to change? |
| c4 | How often does this person make you feel angry? |
| d1 | How positive a role does this person play in your life? |
| d2 | How significant is this relationship in your life? |
| d3 | How close will your relationship be with this person in 10 years? |
| d4 | How much would you miss this person if the two of you could not see or talk with each other for a month? |
modification indices
Less contentious uses:
- residual covariances for items within a factor
- essentially asserts that the two observed variables share some of their specific variance
More contentious uses:
adding cross-loadings (could argue that an item loading on two factors is not a clean indicator, and so should be removed)
residual covariances for items on different factors - harder to defend
changing paths between the latent variables - very definitely changing your theory!
⚠ model modification is exploratory! ⚠
re-specifying a model is no longer confirmatory
it is exploratory again!
gaahhhh
interpretation
CFA interpretation
there are so many parts to these models that often the “interpretation” such as it is, will boil down to:
- does it fit well? (and did you have to specify additional paths?)
- are the standardised factor loadings big enough? (e.g., \(>|.3|\))
And then the bit we might be more interested in, things like:
- does F1 correlate with F2?
that seemed like a lot of work
All of this, just to test if a theoretical model of a measurement tool is replicated in your sample?
CFA is a gateway…
beyond this point
stuff beyond here definitely won’t be in the exam or in the quiz.

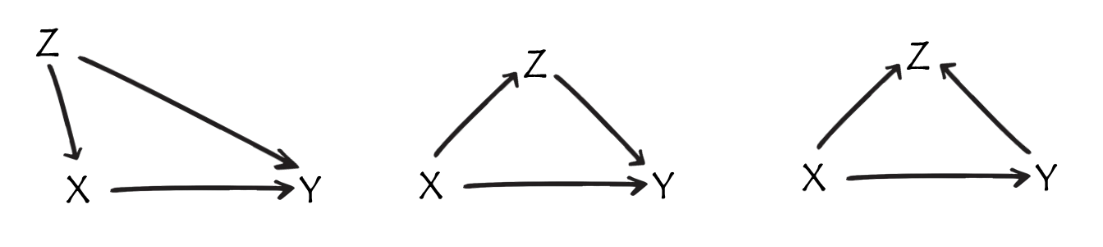
graphical models
there’s a formal logic to diagrams (“do-calculus”).
mainly for back-of-envelope thinking
essentially a way of helping to figure out how to get at an unbiased estimate of the thing we are interested in.
helps with thinking about any part of a study that is observed not manipulated/randomly allocated
I surreptitiously introduced you to this way of thinking in back in Week 1!
Structural Equation Models (SEM)
(essentially just diagrams where the paths are linear associations)
there’s a formal algebra to the linear paths
this “covariance algebra” tells us what the model implied covariances are
- we can also do it by tracing along paths in the diagram!
Uses:
- Testing theories beyond just those about measurement. Essentially, draw lines between variables and ask “how well does this reproduce the cov matrix?”.
- Estimating paths between constructs while explicitly modelling measurement error
error error everywhere

SEM
There’s error everywhere!
Models can have structural parts and measurement parts. It all gets estimated at once!
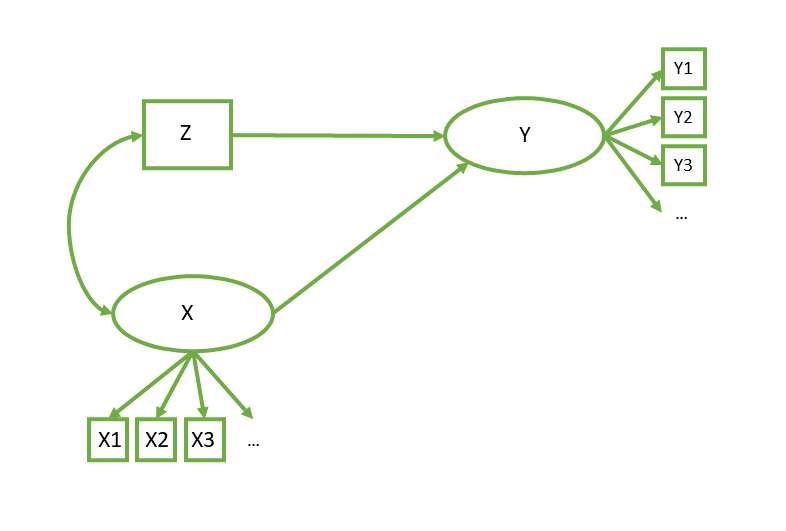
# measurement model
Y =~ y1 + y2 + y3 + ...
X =~ x1 + x2 + x3 + ...
# regressions
Y ~ X + Z
# covariances
X ~~ Zcommon uses of SEM
“Nomological Net”
Do things correlate with other things we expect them to correlate with?
Good for assessing if our measure is measuring the thing we want it to measure!
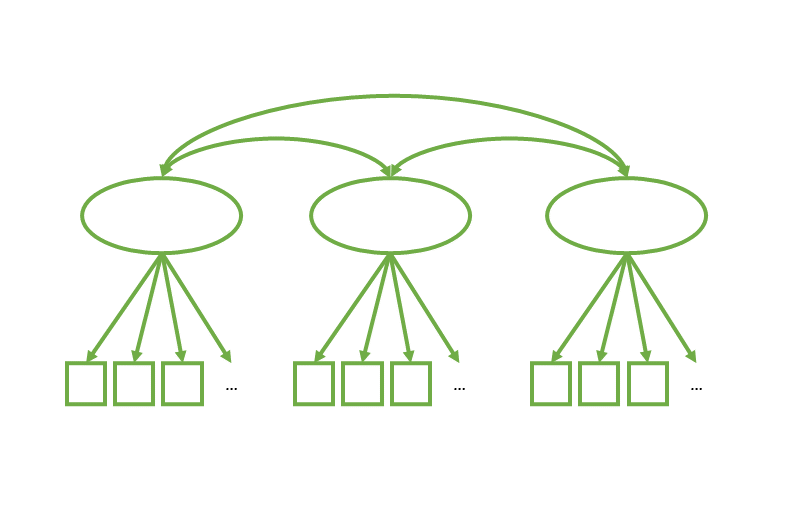
# measurement model
F1 =~ y1 + y2 + y3 + ...
F2 =~ x1 + x2 + x3 + ...
F3 =~ w1 + w2 + w3 + ...
# latent variable covariances
F1 ~~ F2
F1 ~~ F3
F2 ~~ F3common uses of SEM
Measurement Invariance
Do factor loadings differ between groups/timepoints/contexts?
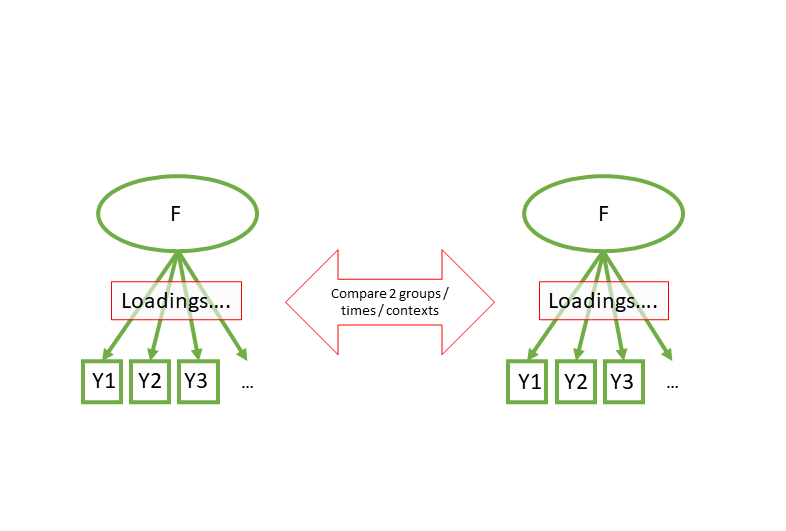
F1 =~ y1 + y2 + y3 + ...m1 <- cfa(model, data, group = "mygroups")
m2 <- cfa(model, data, group = "mygroups",
group.equal = "loadings")
semTools::compareFit(m1,m2)common uses of SEM
Mediation
How much of X -> Y is because of X -> M and M -> Y?
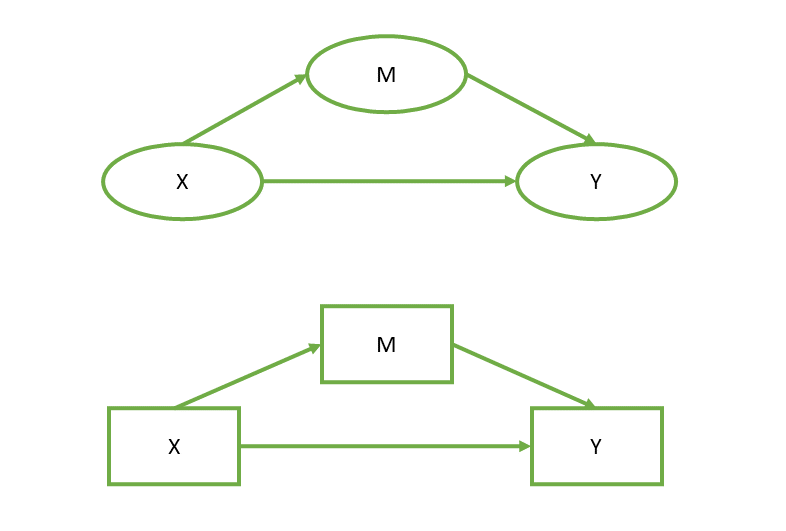
Y ~ a*M + c*X
M ~ b*X
indirect := a*b
direct := csem(model, data)⚠ mediation is almost always incredibly problematic. Many people dismiss it altogether as essentially useless because confounding is everywhere.
cross-sectional observational mediation = “three correlations in a trenchcoat”1
common uses of SEM
Latent Growth Curves
The same as lmer(Y ~ TimePoint + (1 + TimePoint | Person))
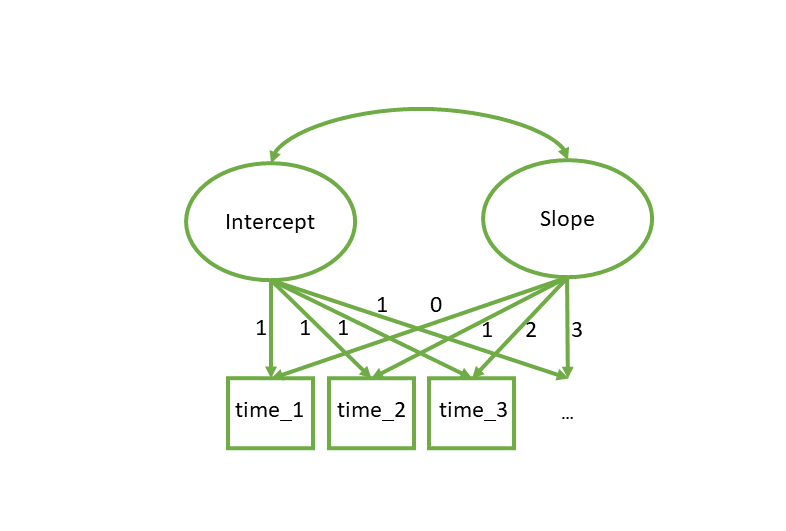
int =~ 1*Time1 + 1*Time2 + 1*Time3 + ...
slope =~ 0*Time1 + 1*Time2 + 2*Time3 + ...
int ~~ slopegrowth(model, data)
This week
Take a look at the readings!!!
Attend the lab!!!
Come to office hours!!