Regression Refresh
Data Analysis for Psychology in R 3
Psychology, PPLS
University of Edinburgh
Announcements
Please check the Learn page for the Course Introduction video!
Please make sure you install (or update) R and Rstudio (see instructions on Learn)
Course Overview
|
multilevel modelling working with group structured data |
regression refresher |
| the multilevel model | |
| more complex groupings | |
| centering, assumptions, and diagnostics | |
| recap | |
|
factor analysis working with multi-item measures |
measurement and dimensionality |
| exploring underlying constructs (EFA) | |
| testing theoretical models (CFA) | |
| reliability and validity | |
| recap & exam prep |
?
This week
- The (generalised) linear model
- how to think about it (multiple predictors, interactions, link functions)
- how to draw inferences (from coefficients and model comparisons)
- assumptions we make
- introduction to group-structured data
- what it looks like
- what we can do with our current tools
Regression Models
Models
deterministic
given the same input, deterministic functions return exactly the same output
area of sphere = \(4\pi r^2\)
height of fall = \(1/2 g t^2\)
statistical
\[ \color{red}{\textrm{outcome}} \color{black}{=} \color{blue}{(\textrm{model})} + \color{black}{\textrm{error}} \]
handspan = height + randomness
cognitive test score = age + premorbid IQ + … + randomness
The Linear Model
\[ \begin{align} \color{red}{\textrm{outcome}} & = \color{blue}{(\textrm{model})} + \textrm{error} \\ \qquad \\ \qquad \\ \color{red}{y_i} & = \color{blue}{b_0 \cdot{} 1 + b_1 \cdot{} x_i} + \varepsilon_i \\ \qquad \\ & \text{where } \varepsilon_i \sim N(0, \sigma) \text{ independently} \\ \end{align} \]
The Linear Model (2)
Our proposed model of the world:
\(\color{red}{y_i} = \color{blue}{b_0 \cdot{} 1 + b_1 \cdot{} x_i} + \varepsilon_i\)
The Linear Model (3)
Our model \(\hat{\textrm{f}}\textrm{itted}\) to some data:
\(\hat{y}_i = \color{blue}{\hat b_0 \cdot{} 1 + \hat b_1 \cdot{} x_i}\)
For the \(i^{th}\) observation:
- \(\color{red}{y_i}\) is the value we observe for \(x_i\)
- \(\hat{y}_i\) is the value the model predicts for \(x_i\)
- \(\color{red}{y_i} = \hat{y}_i + \hat\varepsilon_i\)
The Linear Model (4) an example
Our model \(\hat{\textrm{f}}\textrm{itted}\) to some data:
\(\color{red}{y_i} = \color{blue}{5 \cdot{} 1 + 2 \cdot{} x_i} + \hat\varepsilon_i\)
For the observation where \(x = 1.2\) and \(y = 9.9\):
- \(\color{red}{9.9}\) is the value we observe when \(x=1.2\)
- \((\color{blue}{5 \cdot{}} 1 + \color{blue}{2 \cdot{}} 1.2) = 7.4\) is the value the model predicts when \(x=1.2\)
- \(\color{red}{9.9} = 7.4 + 2.5\)
Categorical Predictors
| y | x |
|---|---|
| 7.99 | Category1 |
| 4.73 | Category0 |
| 3.66 | Category0 |
| 3.41 | Category0 |
| 5.75 | Category1 |
| 5.66 | Category0 |
| ... | ... |
The linear model as variance explained
Sums of Squares
Rather than focussing on slope coefficients, we can also think of our model in terms of sums of squares (SS).
\(SS_{total} = \sum^{n}_{i=1}(y_i - \bar y)^2\)
\(SS_{model} = \sum^{n}_{i=1}(\hat y_i - \bar y)^2\)
\(SS_{residual} = \sum^{n}_{i=1}(y_i - \hat y_i)^2\)
Why?
Linear models “explain”1 variance in an outcome.
Models can accommodate lots of predictors.
With multiple predictors, those predictors are likely to correlate.
Multiple regression is the optimal prediction of the outcome from several predictors, taking into account their redundancy with one another
- how does [predictor of interest] explain variance in [outcome] beyond the variance explained by other variables
Uses of multiple regression
For prediction: multiple predictors may lead to improved prediction.
For theory testing: often our theories suggest that multiple variables together contribute to variation in an outcome
For covariate control: we might want to assess the effect of a specific predictor, controlling for the influence of others.
Multiple Regression
More than one predictor?
\(\color{red}{y} = \color{blue}{b_0 \cdot{} 1 + b_1 \cdot{} x_1 + \, ... \, + b_k \cdot x_k} + \varepsilon\)
Multiple Regression (2)
Call:
lm(formula = y ~ x1 + x2, data = mydata)
Residuals:
Min 1Q Median 3Q Max
-28.85 -6.27 -0.19 6.97 26.05
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.372 1.124 18.12 <2e-16 ***
x1 1.884 1.295 1.46 0.1488
x2 2.042 0.624 3.28 0.0015 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 11.2 on 97 degrees of freedom
Multiple R-squared: 0.135, Adjusted R-squared: 0.118
F-statistic: 7.6 on 2 and 97 DF, p-value: 0.00086| term | est | interpretation |
|---|---|---|
| (Intercept) | 20.37 | estimated y when all predictors are zero/reference level |
| x1 | 1.88 | estimated change in y when x1 increases by 1, and all other predictors are held constant |
| x2 | 2.04 | estimated change in y when x2 increases by 1, and all other predictors are held constant |
![]() Third variables
Third variables
![]() Third variables (2)
Third variables (2)
- X and Y are ‘orthogonal’ (perfectly uncorrelated)
![]() Third variables (3)
Third variables (3)
- X and Y are correlated.
- a = portion of Y’s variance shared with X
- e = portion of Y’s variance unrelated to X
![]() Third variables (4)
Third variables (4)
- X and Y are correlated.
- a = portion of Y’s variance shared with X
- e = portion of Y’s variance unrelated to X
- Z is also related to Y (c)
- Z is orthogonal to X (no overlap)
- relation between X and Y is unaffected (a)
- unexplained variance in Y (e) is reduced, so a:e ratio is greater.
Design is so important! If possible, we could design it so that X and Z are orthogonal (in the long run) by e.g., randomisation.
![]() Third variables (5)
Third variables (5)
- X and Y are correlated.
- Z is also related to Y (c + b)
- Z is related to X (b + d)
Association between X and Y is changed if we adjust for Z (a is smaller than previous slide), because there is a bit (b) that could be attributed to Z instead.
- multiple regression coefficients for X and Z are like areas a and c (scaled to be in terms of ‘per unit change in the predictor’)
- total variance explained by both X and Z is a+b+c
I have control issues..
..and so should you
what do we mean by “control”?
- often quite a vague/nebulous idea
relationship between x and y …
- controlling for z
- accounting for z
- conditional upon z
- holding constant z
- adjusting for z
I have control issues.. (2)
..and so should you
linear regression models provide “linear adjustment” of Z
sort of like stratification across groups, but Z can now be continuous
assumes effect of X on Y is constant across Z
- (but doesn’t have to, as we’ll see shortly)
I have control issues.. (3)
..and so should you
In order to estimate “the effect” of X on Y, deciding on what to control for MUST rely on a theoretical model of causes - i.e. a theory about the underlying data generating process
simple lm(y~x)
what do i do with Z?
Z is… a confounder
Z is… a mediator
Z is… a collider
example
example - observational study
example - randomised trial
example - post-treatment variables
example 2 - colliders
example 2 - colliders
- to play around with this, see https://colliderbias.herokuapp.com/
general heuristics (NOT rules)
control for a confounder
don’t control for a mediator
don’t control for a collider
draw your theoretical model before you collect your data, so that you know what variables you (ideally) need.
Multiple Regression
Call:
lm(formula = BP ~ age + drug, data = mydata)
Residuals:
Min 1Q Median 3Q Max
-14.616 -3.325 0.824 3.709 11.714
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.5566 1.5383 40.7 < 2e-16 ***
age 0.9154 0.0334 27.4 < 2e-16 ***
drugYes -6.7654 1.1661 -5.8 8.2e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.95 on 97 degrees of freedom
Multiple R-squared: 0.898, Adjusted R-squared: 0.896
F-statistic: 427 on 2 and 97 DF, p-value: <2e-16| term | est | interpretation |
|---|---|---|
| (Intercept) | 62.56 | estimated BP when all predictors are zero (age 0, drug = no) |
| age | 0.92 | estimated change in BP when age increases by 1, and drug is held constant |
| drugYes | -6.77 | estimated change in BP between drug = no and drug = yes, holding age constant |
Interactions
what if the relationship of interest depends on the level of some other variable?
adding in a product term (x1 \(\times\) x2) to our model, we can model this..
\[ \color{red}{y} = \color{blue}{\underbrace{b_0 \cdot{} 1}_{\text{intercept}} + \underbrace{b_1 \cdot{} x_1}_{\text{slope of x1 when x2 is 0}} + \underbrace{b_2 \cdot x_2}_{\text{slope of x2 when x1 is 0}} + \underbrace{b_3 \cdot x_1 \cdot x_2}_{\text{interaction term}}} + \varepsilon \]
Interactions (2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.3521 1.0097 35.01 < 2e-16 ***
x1 0.1719 0.0476 3.61 0.00038 ***
x2Level2 -4.3901 0.6740 -6.51 6e-10 ***Interactions (3)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.009 2.008 -2.00 0.052 .
x1 4.345 0.329 13.22 < 2e-16 ***
x2 3.189 0.402 7.93 3.2e-10 ***Interactions (4)
Interactions (5)
Notation
\(\begin{align} \color{red}{y} \;\;\;\; & = \;\;\;\;\; \color{blue}{b_0 \cdot{} 1 + b_1 \cdot{} x_1 + ... + b_k \cdot x_k} & + & \;\;\;\varepsilon \\ \qquad \\ \color{red}{\begin{bmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ \vdots \\ y_n \end{bmatrix}} & = \color{blue}{\begin{bmatrix} 1 & x_{11} & x_{21} & \dots & x_{k1} \\ 1 & x_{12} & x_{22} & & x_{k2} \\ 1 & x_{13} & x_{23} & & x_{k3} \\ 1 & x_{14} & x_{24} & & x_{k4} \\ 1 & x_{15} & x_{25} & & x_{k5} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{1n} & x_{2n} & \dots & x_{kn} \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ \vdots \\ b_k \end{bmatrix}} & + & \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \varepsilon_4 \\ \varepsilon_5 \\ \vdots \\ \varepsilon_n \end{bmatrix} \\ \\\color{red}{\boldsymbol y} \;\;\;\;\; & = \qquad \qquad \;\;\; \mathbf{\color{blue}{X \qquad \qquad \qquad \;\;\;\: \boldsymbol \beta}} & + & \;\;\; \boldsymbol \varepsilon \\ \end{align}\)
Link functions
\(\begin{align} \color{red}{y} = \mathbf{\color{blue}{X \boldsymbol{\beta}} + \boldsymbol{\varepsilon}} & \qquad & (-\infty, \infty) \\ \qquad \\ \qquad \\ \color{red}{ln \left( \frac{p}{1-p} \right) } = \mathbf{\color{blue}{X \boldsymbol{\beta}} + \boldsymbol{\varepsilon}} & \qquad & [0,1] \\ \qquad \\ \qquad \\ \color{red}{ln (y) } = \mathbf{\color{blue}{X \boldsymbol{\beta}} + \boldsymbol{\varepsilon}} & \qquad & (0, \infty) \\ \end{align}\)
Generalised Linear Models in R
- Linear regression
- Logistic regression
- Poisson regression
Inference
What is inference?
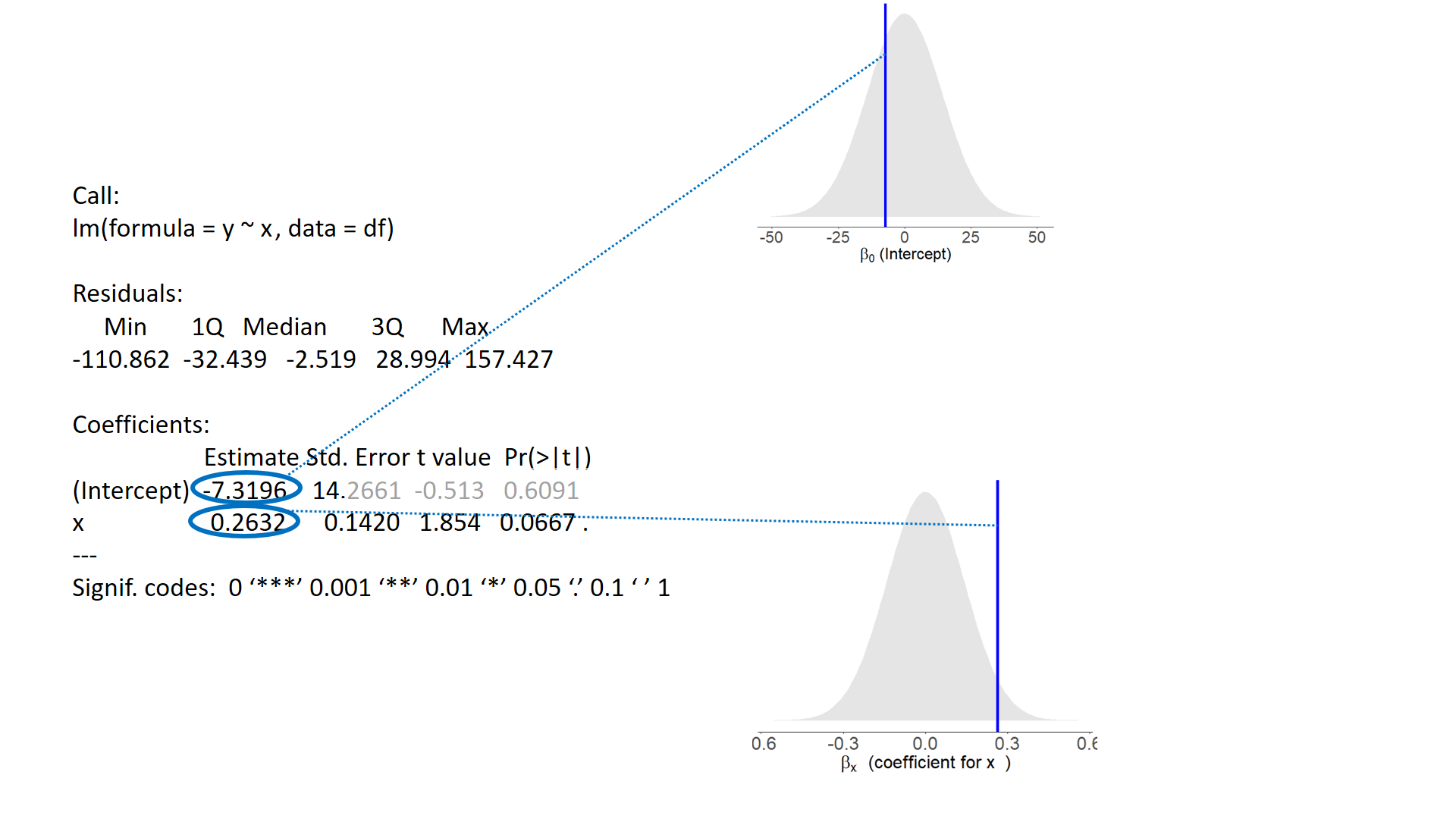
Null Hypothesis Testing
Null Hypothesis Testing (2)
test of individual parameters
test of individual parameters (2)
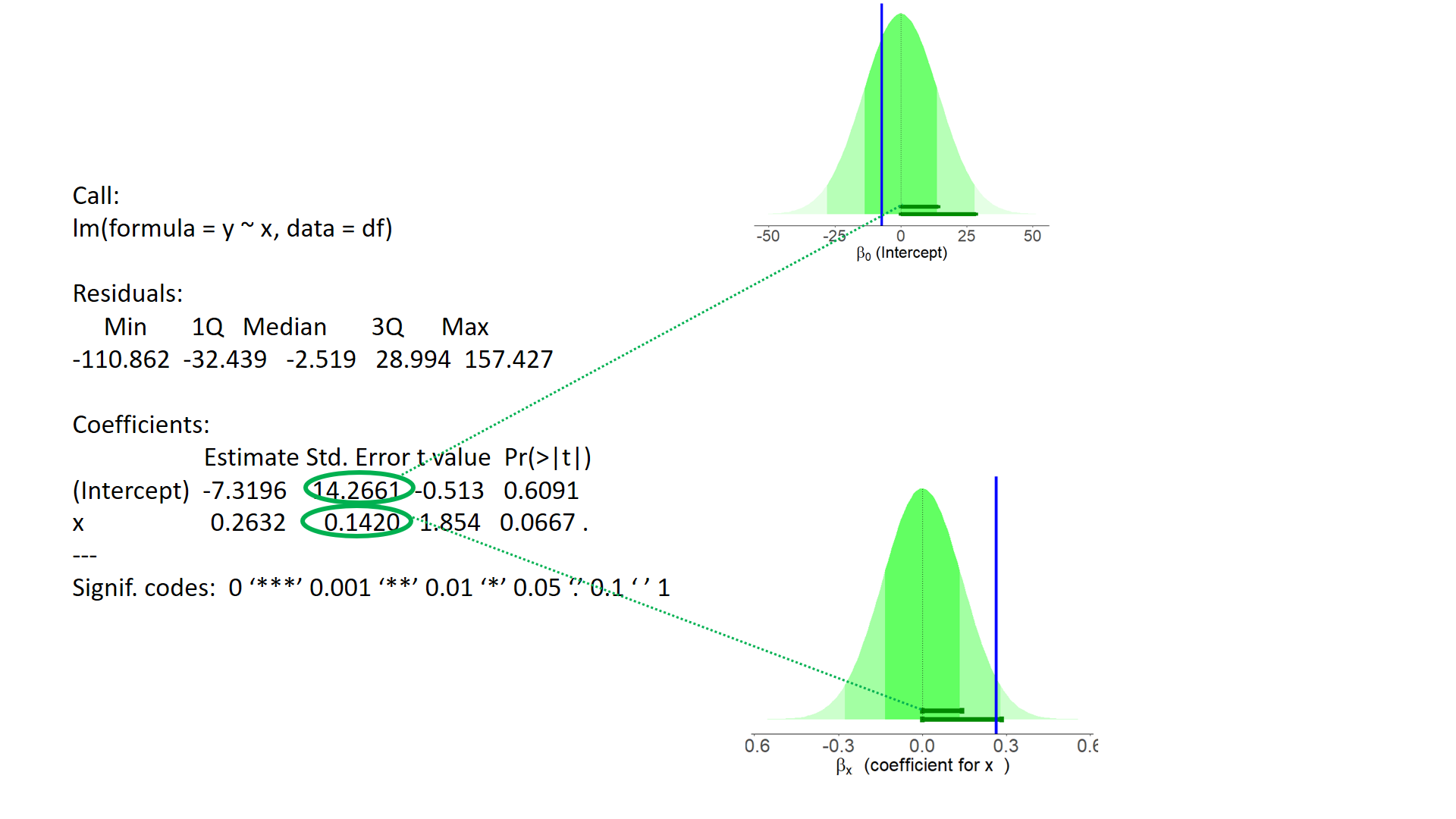
test of individual parameters (3)
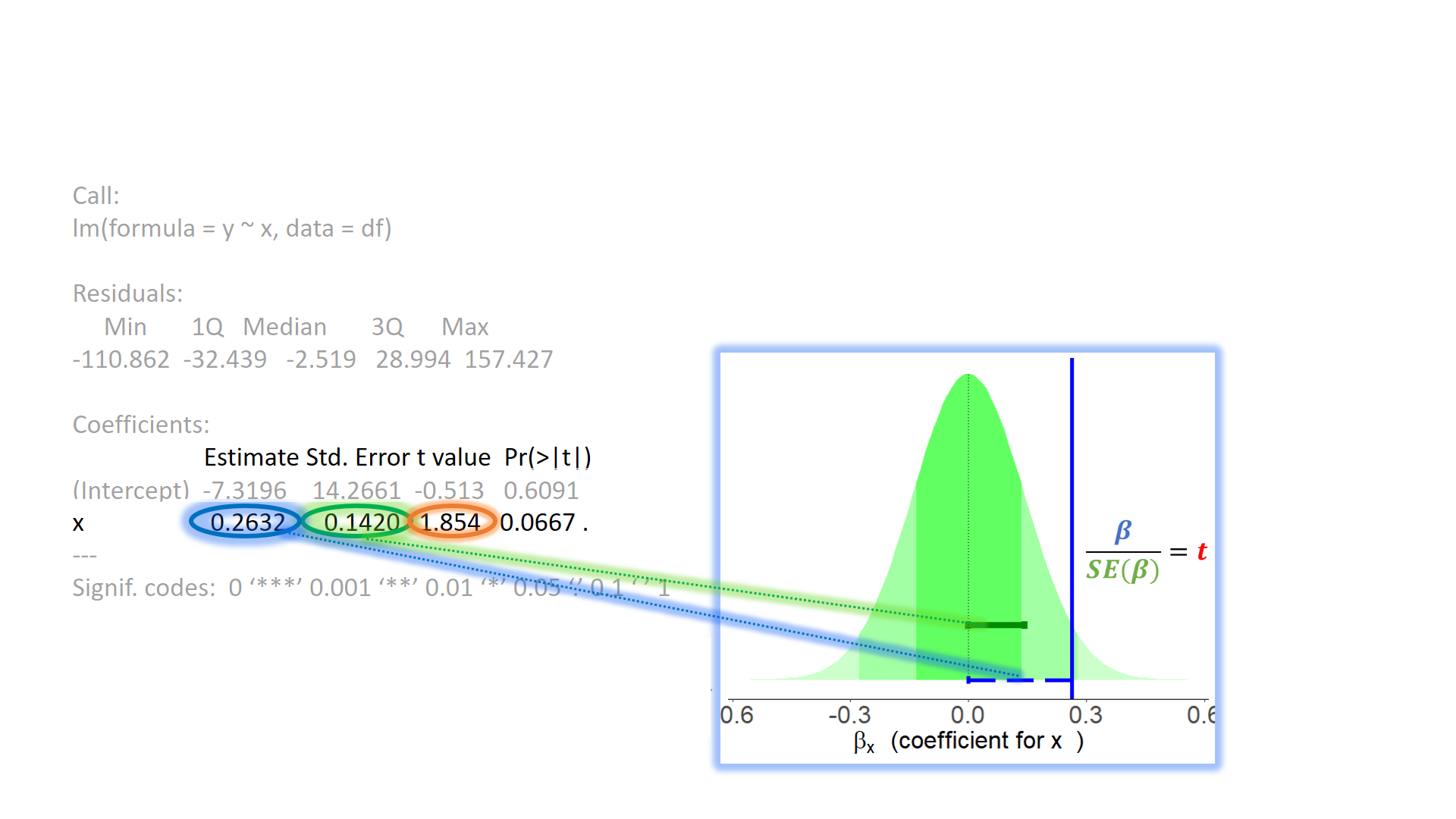
test of individual parameters (4)
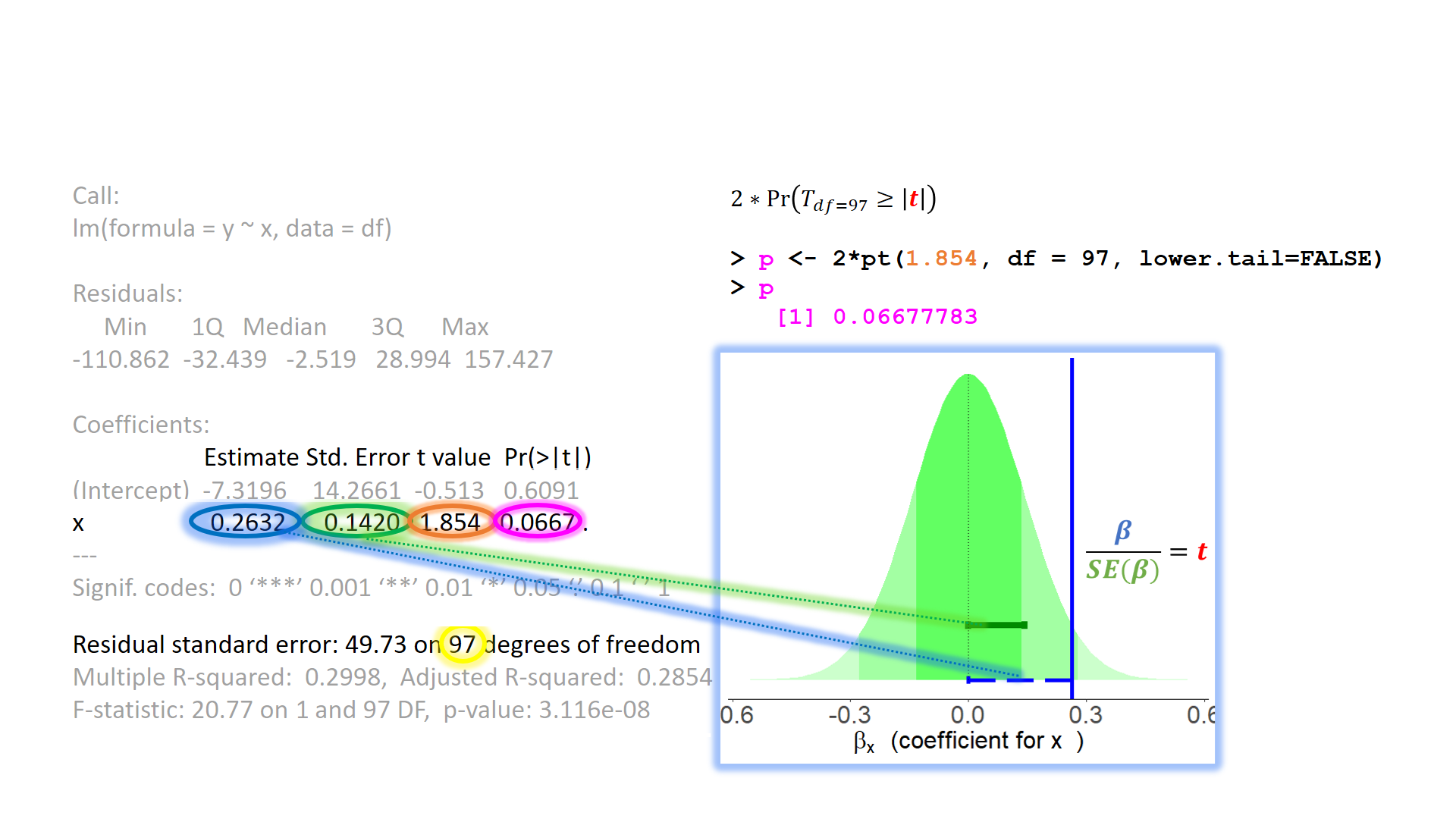
Sums of Squares (2)
- \(SS_{total} = \sum^{n}_{i=1}(y_i - \bar y)^2\)
- a+b+c+e
- \(SS_{model} = \sum^{n}_{i=1}(\hat y_i - \bar y)^2\)
- a+b+c
- \(SS_{residual} = \sum^{n}_{i=1}(y_i - \hat y_i)^2\)
- e
\(R^2\)
\(R^2 = \frac{SS_{Model}}{SS_{Total}} = 1 - \frac{SS_{Residual}}{SS_{Total}}\)
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) ... ... ... ...
z ... ... ... ...
x ... ... ... ...
...
...
Multiple R-squared: 0.134, Adjusted R-squared: 0.116
...tests of multiple parameters
Model comparisons:
tests of multiple parameters (2)
isolate the improvement in model fit due to inclusion of additional parameters
tests of multiple parameters (3)
Test everything in the model all at once by comparing it to a ‘null model’ with no predictors:
tests of multiple parameters (4)
- Recall that a categorical predictor with \(k\) levels involves fitting \(k-1\) coefficients
- We can test “are there differences in group means?” by testing the reduction in residual sums of squares resulting from the inclusion of all \(k-1\) coefficients at once
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.851 0.660 21.00 < 2e-16 ***
speciesdog -3.210 0.933 -3.44 0.00086 ***
specieshorse -3.316 0.933 -3.55 0.00059 ***
speciesparrot -2.903 0.933 -3.11 0.00245 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.3 on 96 degrees of freedom
Multiple R-squared: 0.152, Adjusted R-squared: 0.126
F-statistic: 5.75 on 3 and 96 DF, p-value: 0.00117![]() traditional ANOVA/ANCOVA
traditional ANOVA/ANCOVA
This is kind of where traditional “analysis of (co)variance” sits.
There are different ‘types’ of ANOVA..
- Type 1 (“sequential”): tests the addition of each variable entered in to the model, in order
![]() traditional ANOVA/ANCOVA (2)
traditional ANOVA/ANCOVA (2)
This is kind of where traditional “analysis of (co)variance” sits.
There are different ‘types’ of ANOVA..
- Type 3: tests the addition of each variable as if it were the last one entered in to the model:
Anova Table (Type III tests)
Response: y
Sum Sq Df F value Pr(>F)
(Intercept) 12041 1 3242.2 < 2e-16 ***
z2 301 1 80.9 2.1e-14 ***
z 352 1 94.8 5.4e-16 ***
x 105 1 28.2 7.0e-07 ***
Residuals 357 96
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Assumptions
models have assumptions
Our model:
\(\color{red}{y} = \color{blue}{\mathbf{X \boldsymbol \beta}} + \varepsilon \qquad \text{where } \boldsymbol \varepsilon \sim N(0, \sigma) \text{ independently}\)
Our ability to generalise from the model we fit on sample data to the wider population requires making some assumptions.
- assumptions about the nature of the model (linear)
- assumptions about the nature of the errors (normal)
The broader idea
All our work here is in aim of making models of the world (models of how we think the data are generated).
In an ideal world, our model accounts for all the systematic relationships. The leftovers (our residuals) are just random noise.
If our model is mis-specified then our residuals may reflect this.
We check by examining how much “like randomness” the residuals appear to be
We will never know whether our residuals contain only randomness - we can never observe everything!

assumptions
What does randomness look like?
“zero mean and constant variance iid”
mean of the residuals = zero across the predicted values of the model.
spread of residuals is normally distributed and constant across the predicted values of the model.
assumptions (2)
What does randomness look like?
“zero mean and constant variance iid”
mean of the residuals = zero across the predicted values of the model.
spread of residuals is normally distributed and constant across the predicted values of the model.
assumptions (3)
What does randomness look like?
“zero mean and constant variance iid”
mean of the residuals = zero across the predicted values of the model.
spread of residuals is normally distributed and constant across the predicted values of the model.
assumptions (4)
What does randomness look like?
“zero mean and constant variance iid”
mean of the residuals = zero across the predicted values of the model.
spread of residuals is normally distributed and constant across the predicted values of the model.
when things look weird…
first thing to do: think!
- model mis-specification?
- transformation?
- bootstrap or corrected SEs?
iid?
“independent and identically distributed”
you can’t necessarily see violations of independence in diagnostic plots - we need to think about how the data were generated.
transformations/bootstraps/ etc don’t help us if we have violated our assumption of independence…
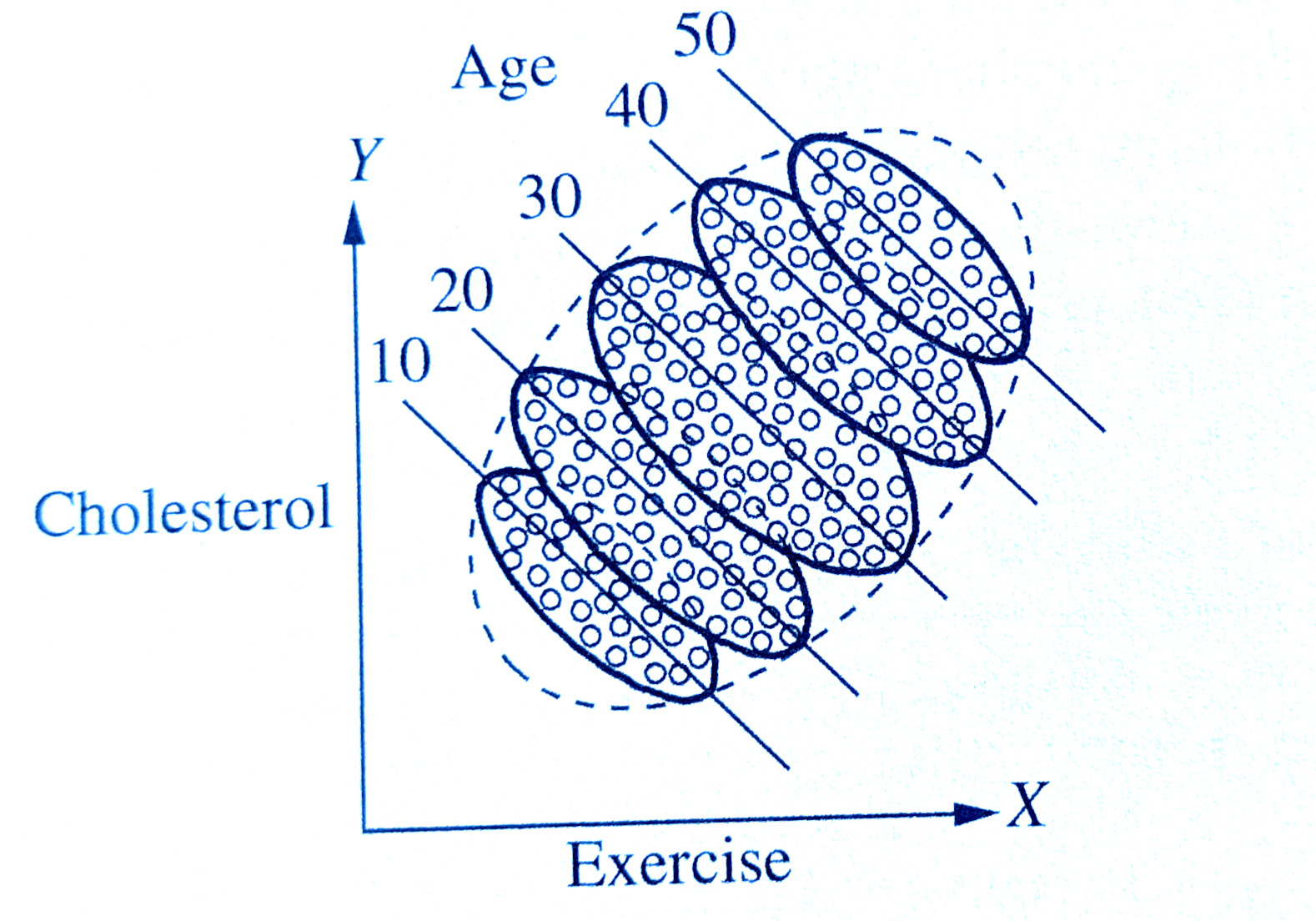
Group Structured Data
Examples of grouped (‘clustered’) data
children within schools
patients within clinics
observations within individuals
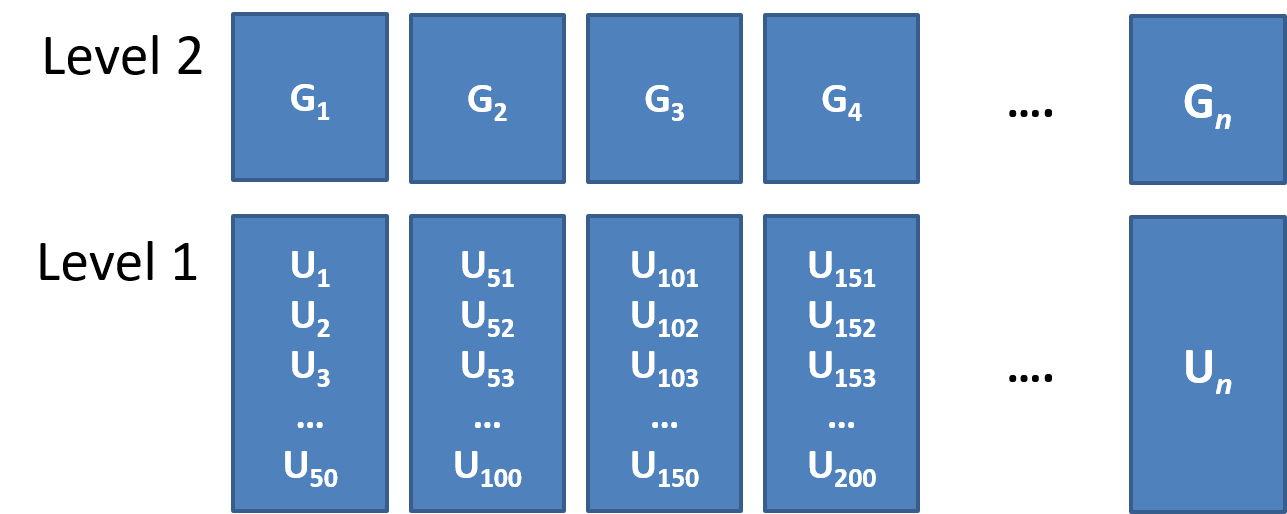
Clusters of clusters
children within classrooms within schools within districts etc…
patients within doctors within hospitals…
time-periods within trials within individuals
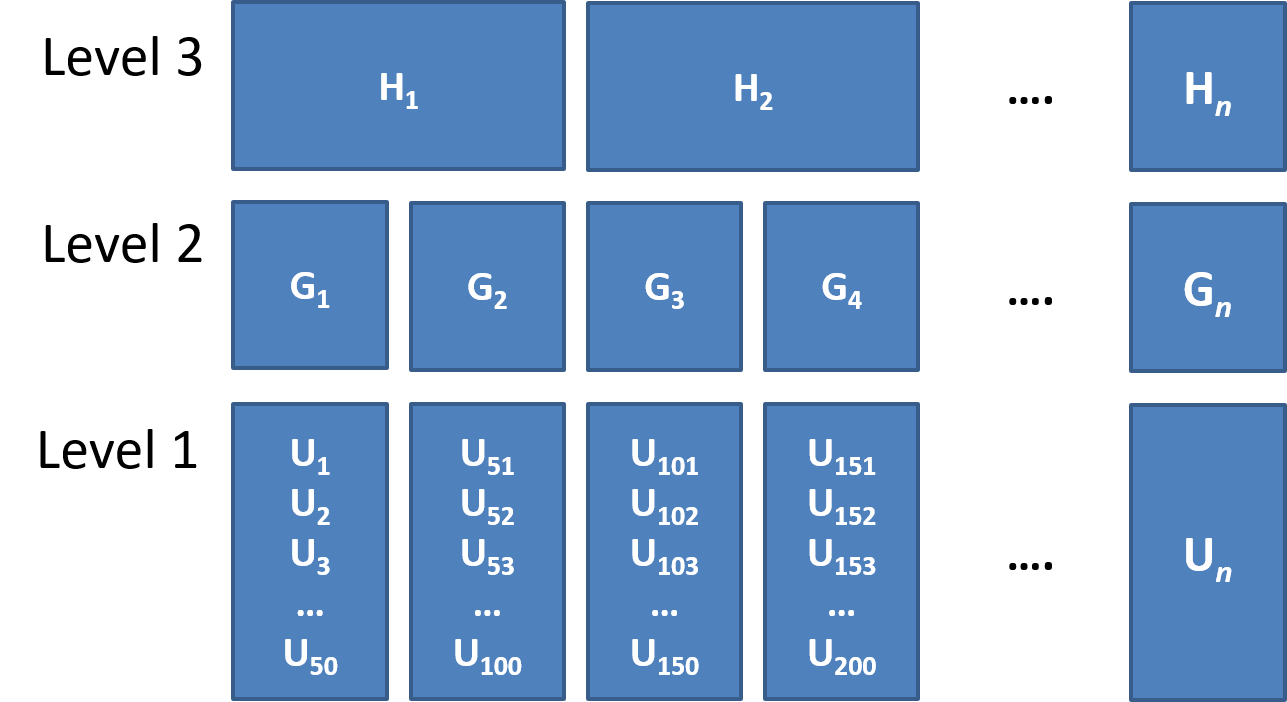
Common study designs

Clustered observations
Measurements on observational units within a given cluster are often more similar to each other than to those in other clusters.
- For example, our measure of academic performance for children in a given class will tend to be more similar to one another (because of class specific things such as the teacher) than to children in other classes.
The impact of clustering
why?
Clustering is something systematic that our model should (arguably) take into account.
- \(\varepsilon \sim N(0, \sigma) \textbf{ independently}\)
how?
Standard errors will often be smaller than they should be, meaning that:
- confidence intervals will often be too narrow
- \(t\)-statistics will often be too large
- \(p\)-values will often be misleadingly small
Quantifying clustering
Clustering can be expressed in terms of the expected correlation among the measurements within the same cluster - known as the intra-class correlation coefficient (ICC).
There are various formulations of ICC, but the basic principle = ratio of variance between groups to total variance.
\(\rho = \frac{\sigma^2_{b}}{\sigma^2_{b} + \sigma^2_e} \\ \qquad \\\textrm{Where:} \\ \sigma^2_{b} = \textrm{variance between clusters} \\ \sigma^2_e = \textrm{variance within clusters (residual variance)} \\\)
Working with clustered data
Wide Data/Long Data
Wide Data
observations are spread across columns
# A tibble: 5 × 5
ID age trial_1 trial_2 trial_3
<chr> <chr> <chr> <chr> <chr>
1 001 62 10 12.5 18
2 002 66 7.5 7 5
3 003 22 12 14.5 11
4 004 34 10.5 17 14
5 ... ... ... ... ... Long Data
each observation of the outcome is a separate row
# A tibble: 13 × 4
ID age trial score
<chr> <chr> <chr> <chr>
1 001 44 trial_1 10
2 001 44 trial_2 12.5
3 001 44 trial_3 18
4 002 38 trial_1 7.5
5 002 38 trial_2 7
6 002 38 trial_3 5
7 003 74 trial_1 12
8 003 74 trial_2 14.5
9 003 74 trial_3 11
10 004 58 trial_1 10.5
11 004 58 trial_2 17
12 004 58 trial_3 14
13 ... ... ... ... Long Data = plots by group
Long Data = computations by-group
Modelling clustered data with lm()
Example data
Are older people more satisfied with life? 112 people from 12 different dwellings (cities/towns) in Scotland. Information on their ages and some measure of life satisfaction.
Ignore it
Ignore it
(Complete pooling)
lm(y ~ 1 + x, data = df)Information from all clusters is pooled together to estimate over x
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.018 4.889 6.14 1.3e-08 ***
age 0.499 0.118 4.22 5.1e-05 ***But residuals are not independent.
Fixed Effects Models
(No pooling)
lm(y ~ cluster + x, data = df)Completely partition out cluster differences in average \(y\).
Treat every cluster as an independent entity.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.3330 4.1493 3.70 0.00036 ***
dwellingDumfries 8.0741 3.8483 2.10 0.03844 *
dwellingDundee 15.9882 3.8236 4.18 6.3e-05 ***
dwellingDunfermline 26.2600 3.8910 6.75 1.0e-09 ***
dwellingEdinburgh 12.6929 3.8195 3.32 0.00125 **
dwellingFort William 1.3577 3.8999 0.35 0.72849
dwellingGlasgow 18.2906 3.8213 4.79 5.9e-06 ***
dwellingInverness 5.0718 3.8542 1.32 0.19124
... ...
... ...age 0.6047 0.0888 6.81 7.6e-10 ***
---Fixed Effects Models
(No pooling)
lm(y ~ cluster * x, data = df)Completely partition out cluster differences in \(y \sim x\).
Treat every cluster as an independent entity.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.345 8.867 -0.49 0.62532
dwellingDumfries 13.480 14.370 0.94 0.35078
dwellingDundee 59.479 17.650 3.37 0.00112 **
dwellingDunfermline 42.938 17.206 2.50 0.01444 *
... ...age 1.159 0.239 4.84 0.0000054 ***
dwellingDumfries:age -0.206 0.360 -0.57 0.56813
dwellingDundee:age -1.181 0.463 -2.55 0.01243 *
dwellingDunfermline:age -0.486 0.408 -1.19 0.23638
... ...Fixed Effects Models
(No pooling)
lm(y ~ cluster * x, data = df)Completely partition out cluster differences in \(y \sim x\).
Treat every cluster as an independent entity.
Prevents us from studying cluster level effects.
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.345 8.867 -0.49 0.62532
dwellingDumfries 13.480 14.370 0.94 0.35078
dwellingDundee 59.479 17.650 3.37 0.00112 **
dwellingDunfermline 42.938 17.206 2.50 0.01444 *
... ...
... ...dwellingPaisley 28.665 16.732 1.71 0.09020 .
dwellingPerth 27.473 12.901 2.13 0.03600 *
dwellingStirling 42.272 13.379 3.16 0.00217 **
age 1.159 0.239 4.84 0.0000054 ***
size>100k NA NA NA NA
dwellingDumfries:age -0.206 0.360 -0.57 0.56813
dwellingDundee:age -1.181 0.463 -2.55 0.01243 *
... ... size
dwelling <100k >100k
Aberdeen 0 10
Dumfries 10 0
Dundee 0 10
Dunfermline 10 0
Edinburgh 0 10
Fort William 10 0
Glasgow 0 10
Inverness 10 0
Kirkcaldy 2 0
Paisley 10 0
Perth 10 0
Stirling 10 0Summary
we can fit a linear regression model which takes the form \(\color{red}{y} = \color{blue}{\mathbf{X} \boldsymbol{\beta}} + \boldsymbol{\varepsilon}\)
in R, we fit this with
lm(y ~ x1 + .... xk, data = mydata).we can extend this to different link functions to model outcome variables which follow different distributions.
when drawing inferences from a fitted model to the broader population, we rely on certain assumptions.
- one of these is that the errors are independent.
This week
Tasks
 Complete readings
Complete readings
Attend your lab and work together on the exercises
Complete the weekly quiz
Support
Piazza forum!
 Office hours (see Learn page for details)
Office hours (see Learn page for details)