Exploratory Factor Analysis 1

Data Analysis for Psychology in R 3

Josiah King & John Martindale

Psychology, PPLS

University of Edinburgh

QR!!!

Course Overview

multilevel modelling working with group structured data	regression refresher
	introducing multilevel models
	more complex groupings
	centering, assumptions, and diagnostics
	recap
factor analysis working with multi-item measures	what is a psychometric test?
	using composite scores to simplify data (PCA)
	uncovering underlying constructs (EFA)
	more EFA
	recap

This week

• Introduction to EFA
• EFA vs PCA
• Estimation & Number of factors
• Factor rotation
• EFA output o # EFA vs PCA

Real friends don’t let friends do PCA. (W. Revelle, 25 October 2020)

Questions to ask before you start

PCA

• Why are your variables correlated?
  • Agnostic/don’t care
• What are your goals?
  • Just reduce the number of variables

EFA

• Why are your variables correlated?
  • Believe there are underlying “causes” of these correlations
• What are your goals?
  • Reduce your variables and learn about/model their underlying (latent) causes

Latent variables

• Theorized common cause (e.g., cognitive ability) of responses to a set of variables

  • Explain correlations between measured variables
  • Held to be real
  • No direct test of this theory

Latent variables?

• Anxiety
• Depression
• Trust
• Motivation
• Identity ?
• Socioeconomic Status ??
• Exposure to distressing events ???

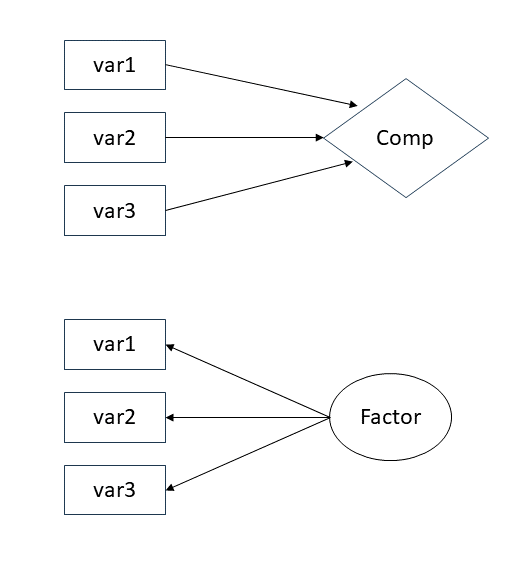
PCA versus EFA: How are they different?

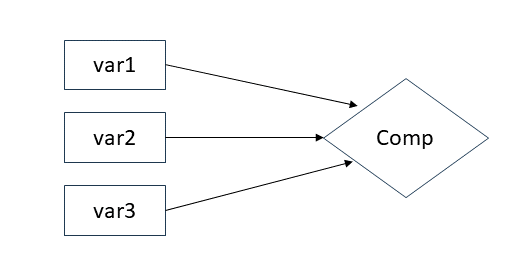
PCA

• The observed measures are independent variables
• The component is like a dependent variable (it’s really just a composite!)
• Components sequentially capture as much variance in the measures as possible
• Components are determinate

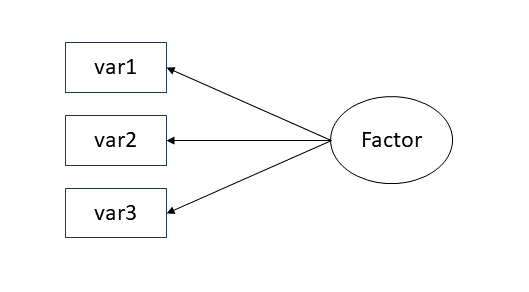
EFA

• The observed measures are dependent variables
• The factor is the independent variable
• Models the relationships between variables \((r_{y_{1},y_{2}},r_{y_{1},y_{3}}, r_{y_{2},y_{3}})\)
• Factors are indeterminate

Modeling the relationships

• We have some observed variables that are correlated

• EFA tries to explain these patterns of correlations

• Aim is that the correlations between items after removing the effect of the Factor are zero

\[ \begin{align} \rho(y_{1},y_{2} | Factor)=0 \\ \rho(y_{1},y_{3} | Factor)=0 \\ \rho(y_{2},y_{3} | Factor)=0 \\ \end{align} \]

variable	wording
item1	I worry that people will think I'm awkward or strange in social situations.
item2	I often fear that others will criticize me after a social event.
item3	I'm afraid that I will embarrass myself in front of others.

Modeling the relationships

• In order to model these correlations, EFA looks to distinguish between common and unique variance.

\[ \begin{equation} var(\text{total}) = var(\text{common}) + var(\text{specific}) + var(\text{error}) \end{equation} \]

common variance	variance shared across items	true and shared
specific variance	variance specific to an item that is not shared with any other items	true and unique
error variance	variance due to measurement error	not ‘true’, unique

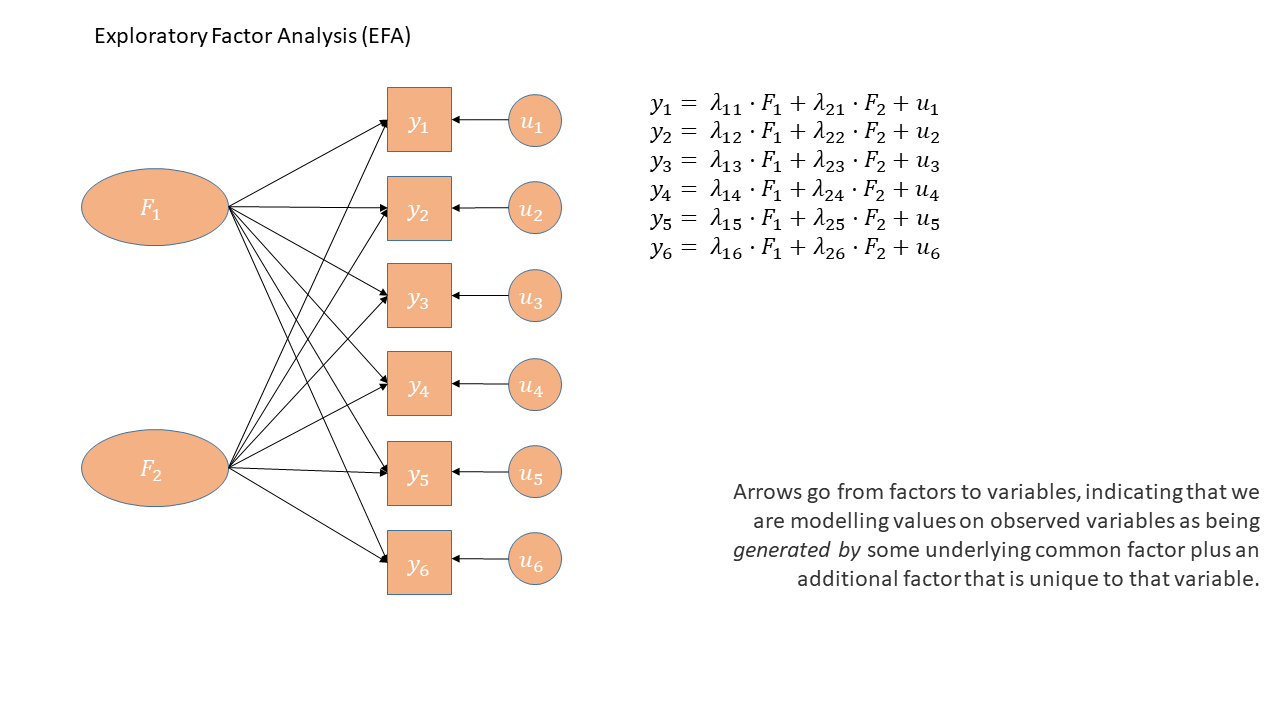
Optional: general factor model equation

\[\mathbf{\Sigma}=\mathbf{\Lambda}\mathbf{\Phi}\mathbf{\Lambda'}+\mathbf{\Psi}\]

• \(\mathbf{\Sigma}\): A \(p \times p\) observed covariance matrix (from data)

• \(\mathbf{\Lambda}\): A \(p \times m\) matrix of factor loading’s (relates the \(m\) factors to the \(p\) items)

• \(\mathbf{\Phi}\): An \(m \times m\) matrix of correlations between factors (“goes away” with orthogonal factors)

• \(\mathbf{\Psi}\): A diagonal matrix with \(p\) elements indicating unique (error) variance for each item

Optional: general factor model equation

\[ \begin{align} \text{Outcome} &= \quad\quad\quad\text{Model} &+ \text{Error} \quad\quad\quad\quad\quad \\ \quad \\ \mathbf{\Sigma} &= \quad\quad\quad\mathbf{\Lambda}\mathbf{\Lambda'} &+ \mathbf{\Psi} \quad\quad\quad\quad\quad\quad \\ \quad \\ \begin{bmatrix} 1 & 0.61 & 0.64 \\ 0.61 & 1 & 0.59 \\ 0.64 & 0.59 & 1 \end{bmatrix} &= \begin{bmatrix} 0.817 \\ 0.750 \\ 0.788 \\ \end{bmatrix} \begin{bmatrix} 0.817 & .750 & .788 \\ \end{bmatrix} &+ \begin{bmatrix} 0.33 & 0 & 0 \\ 0 & 0.44 & 0 \\ 0 & 0 & 0.38 \end{bmatrix} \\ \quad \\ \begin{bmatrix} 1 & 0.61 & 0.64 \\ 0.61 & 1 & 0.59 \\ 0.64 & 0.59 & 1 \end{bmatrix} &= \begin{bmatrix} 0.67 & 0.61 & 0.64 \\ 0.61 & 0.56 & 0.59 \\ 0.64 & 0.59 & 0.62 \end{bmatrix} &+ \begin{bmatrix} 0.33 & 0 & 0 \\ 0 & 0.44 & 0 \\ 0 & 0 & 0.38 \end{bmatrix} \\ \end{align} \]

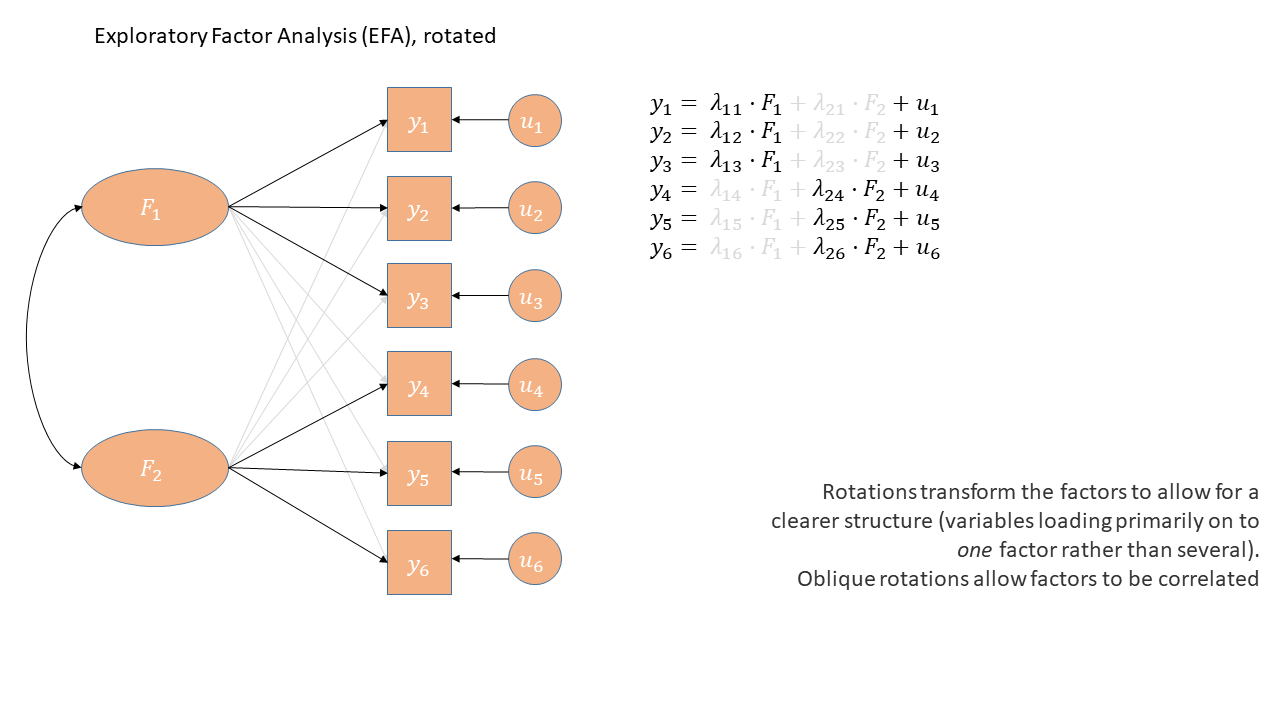
As a diagram

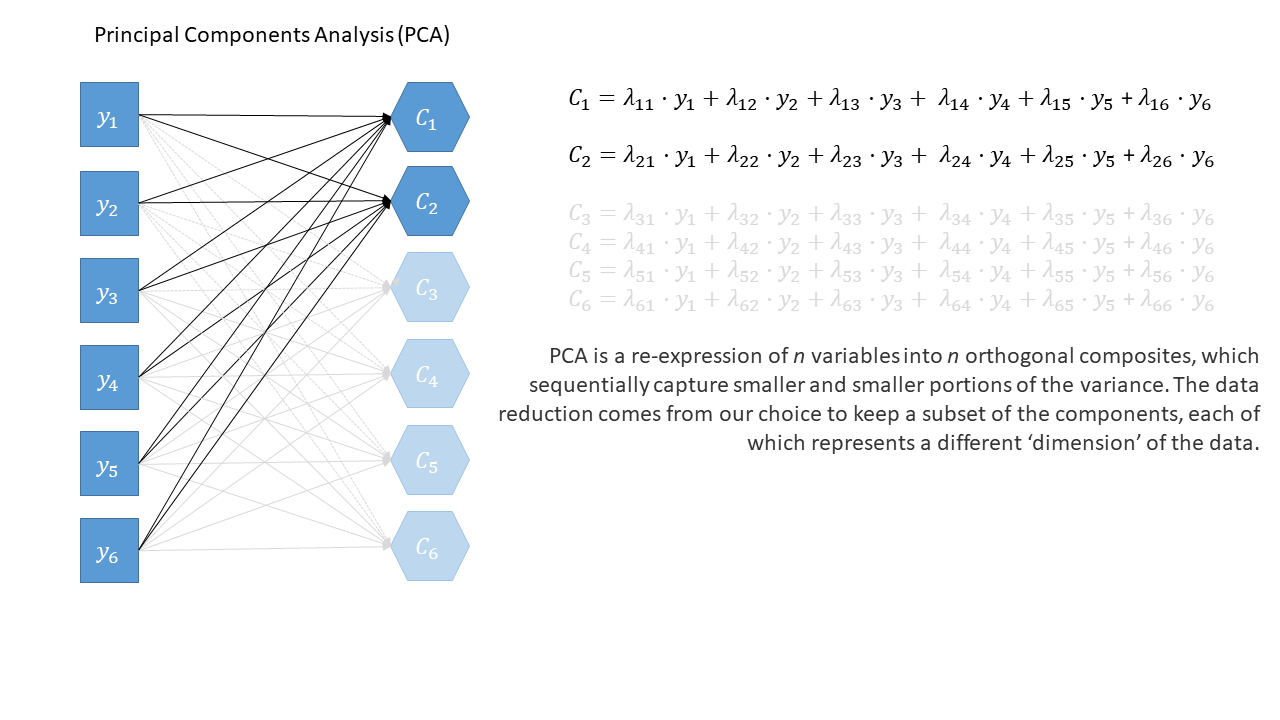
As a diagram (PCA)

As a diagram (PCA)

We make assumptions when we use models

• As EFA is a model, just like linear models and other statistical tools, using it requires us to make some assumptions:

  1. The residuals/error terms should be uncorrelated (it’s a diagonal matrix, remember!)
  2. The residuals/errors should not correlate with factor
  3. Relationships between items and factors should be linear, although there are models that can account for nonlinear relationships

What does an EFA look like?

Some data

variable	wording
item1	I worry that people will think I'm awkward or strange in social situations.
item2	I often fear that others will criticize me after a social event.
item3	I'm afraid that I will embarrass myself in front of others.
item4	I feel self-conscious in social situations, worrying about how others perceive me.
item5	I often avoid social situations because I’m afraid I will say something wrong or be judged.
item6	I avoid social gatherings because I fear feeling uncomfortable.
item7	I try to stay away from events where I don’t know many people.
item8	I often cancel plans because I feel anxious about being around others.
item9	I prefer to spend time alone rather than in social situations.

cor(eg_data) |>
  pheatmap::pheatmap()

What does an EFA look like?

variable	wording
item1	I worry that people will think I'm awkward or strange in social situations.
item2	I often fear that others will criticize me after a social event.
item3	I'm afraid that I will embarrass myself in front of others.
item4	I feel self-conscious in social situations, worrying about how others perceive me.
item5	I often avoid social situations because I’m afraid I will say something wrong or be judged.
item6	I avoid social gatherings because I fear feeling uncomfortable.
item7	I try to stay away from events where I don’t know many people.
item8	I often cancel plans because I feel anxious about being around others.
item9	I prefer to spend time alone rather than in social situations.

library(psych)
myfa <- fa(eg_data, nfactors = 2, 
           fm = "ml", rotate = "oblimin")
myfa

Factor Analysis using method =  ml
Call: fa(r = eg_data, nfactors = 2, rotate = "oblimin", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
         ML1   ML2   h2   u2 com
item_1  0.02 -0.59 0.35 0.65 1.0
item_2  0.00  0.69 0.48 0.52 1.0
item_3  0.00  0.78 0.61 0.39 1.0
item_4 -0.11  0.61 0.37 0.63 1.1
item_5  0.46  0.41 0.40 0.60 2.0
item_6 -0.68 -0.01 0.47 0.53 1.0
item_7  0.81 -0.02 0.65 0.35 1.0
item_8  0.74  0.03 0.55 0.45 1.0
item_9  0.74 -0.11 0.56 0.44 1.0

                       ML1  ML2
SS loadings           2.45 2.00
Proportion Var        0.27 0.22
Cumulative Var        0.27 0.49
Proportion Explained  0.55 0.45
Cumulative Proportion 0.55 1.00

 With factor correlations of 
     ML1  ML2
ML1 1.00 0.06
ML2 0.06 1.00

Mean item complexity =  1.1
Test of the hypothesis that 2 factors are sufficient.

df null model =  36  with the objective function =  2.88 with Chi Square =  1138
df of  the model are 19  and the objective function was  0.05 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.03 

The harmonic n.obs is  400 with the empirical chi square  10.2  with prob <  0.95 
The total n.obs was  400  with Likelihood Chi Square =  20.5  with prob <  0.37 

Tucker Lewis Index of factoring reliability =  0.997
RMSEA index =  0.014  and the 90 % confidence intervals are  0 0.047
BIC =  -93.3
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   ML1  ML2
Correlation of (regression) scores with factors   0.92 0.89
Multiple R square of scores with factors          0.85 0.80
Minimum correlation of possible factor scores     0.70 0.59

What does an EFA look like?

• Factor loading’s, like PCA loading’s, show the relationship of each measured variable to each factor.

  • They range between -1.00 and 1.00
  • Larger absolute values = stronger relationship between measured variable and factor

• We interpret our factor models by the pattern and size of these loading’s.

  • Primary loading’s: refer to the factor on which a measured variable has it’s highest loading
  • Cross-loading’s: refer to all other factor loading’s for a given measured variable

• Square of the factor loading’s tells us how much item variance is explained ( h2 ), and how much isn’t ( u2)

• Factor correlations : When estimated, tell us how closely factors relate (see rotation)

• SS Loading and proportion of variance information is interpreted as we discussed for PCA.

library(psych)
myfa <- fa(eg_data, nfactors = 2, 
           fm = "ml", rotate = "oblimin")
myfa

Factor Analysis using method =  ml
Call: fa(r = eg_data, nfactors = 2, rotate = "oblimin", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
         ML1   ML2   h2   u2 com
item_1  0.02 -0.59 0.35 0.65 1.0
item_2  0.00  0.69 0.48 0.52 1.0
item_3  0.00  0.78 0.61 0.39 1.0
item_4 -0.11  0.61 0.37 0.63 1.1
item_5  0.46  0.41 0.40 0.60 2.0
item_6 -0.68 -0.01 0.47 0.53 1.0
item_7  0.81 -0.02 0.65 0.35 1.0
item_8  0.74  0.03 0.55 0.45 1.0
item_9  0.74 -0.11 0.56 0.44 1.0

                       ML1  ML2
SS loadings           2.45 2.00
Proportion Var        0.27 0.22
Cumulative Var        0.27 0.49
Proportion Explained  0.55 0.45
Cumulative Proportion 0.55 1.00

 With factor correlations of 
     ML1  ML2
ML1 1.00 0.06
ML2 0.06 1.00

Mean item complexity =  1.1
Test of the hypothesis that 2 factors are sufficient.

df null model =  36  with the objective function =  2.88 with Chi Square =  1138
df of  the model are 19  and the objective function was  0.05 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.03 

The harmonic n.obs is  400 with the empirical chi square  10.2  with prob <  0.95 
The total n.obs was  400  with Likelihood Chi Square =  20.5  with prob <  0.37 

Tucker Lewis Index of factoring reliability =  0.997
RMSEA index =  0.014  and the 90 % confidence intervals are  0 0.047
BIC =  -93.3
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   ML1  ML2
Correlation of (regression) scores with factors   0.92 0.89
Multiple R square of scores with factors          0.85 0.80
Minimum correlation of possible factor scores     0.70 0.59

Doing EFA - Overview

So how do we move from data and correlations to a factor analysis?

1. Check the appropriateness of the data and decide of the appropriate estimator.
2. Assess range of number of factors to consider.
3. Decide conceptually whether to apply rotation and how to do so.
4. Decide on the criteria to assess and modify a solution.
5. Fit the factor model(s) for each number of factors
6. Evaluate the solution(s) (apply 4)
   • if developing a measurement scale, consider whether to drop items and start over
7. Select a final solution and interpret the model, labeling the factors.
8. Report your results.

Suitability of data, Estimation, Number of factors

1. Check the appropriateness of the data and decide of the appropriate estimator.
2. Assess range of number of factors to consider.
3. …
4. …

Data suitability

In short “is the data correlated?”.

• check correlation matrix (ideally roughly > .20)
• we can take this a step further and calculate the squared multiple correlations (SMC)
  • regress each item on all other items (e.g., \(R^2\) for item1 ~ all other items)
  • tells us how much shared variation there is between an item and all other items
• there are also some statistical tests (e.g. Bartlett’s test) and metrics (KMO adequacy)

Estimation

• For PCA, we discussed the use of the eigen-decomposition
  • this isn’t estimation, this is just a calculation
• For EFA, we have a model (with error), so we need to estimate the model parameters (the factor loadings)

Estimation Methods

• Maximum Likelihood Estimation (ml)
• Principal Axis Factoring (paf)
• Minimum Residuals (minres)

Maximum likelihood estimation

Find values for the parameters that maximize the likelihood of obtaining the observed covariance matrix

Pros:

• quick and easy, very generalisable estimation method
• we can get various “fit” statistics (useful for model comparisons)

Cons:

• Assumes a normal distribution
• Sometimes fails to converge
• Sometimes produces solutions with impossible values
  • Factor loadings \(> 1\) (Heywood cases)
  • Factor correlations \(> 1\)

Non-continuous data

• Sometimes (often) even when we assume a construct is continuous, we measure it with a discrete scale.

• E.g., Likert!

• Simulation studies tend to suggest \(\geq 5\) response categories can be treated as continuous

  • provided that they have all been used!!

Non-continuous data

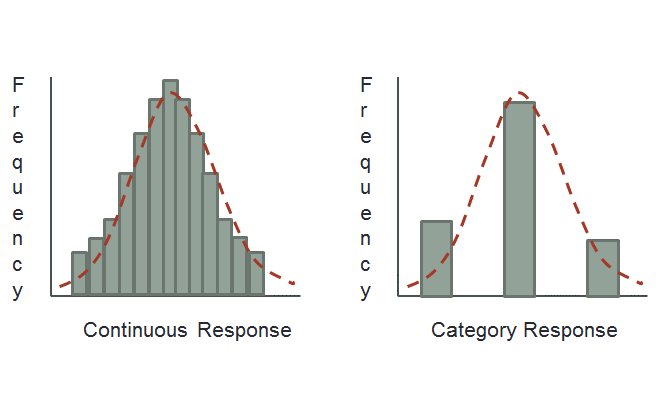
Polychoric Correlations

• Estimates of the correlation between two theorized normally distributed continuous variables, based on their observed ordinal manifestations.

Choosing an estimator

• The straightforward option, as with many statistical models, is ML.

• If ML solutions fail to converge, principal axis is a simple approach which typically yields reliable results.

• If concerns over the distribution of variables, use PAF on the polychoric correlations.

How many factors?

• Variance explained
• Scree plots
• MAP
• Parallel Analysis

But… if there’s no strong steer, then we want a range.

• Treat MAP as a minimum
• PA as a maximum
• Explore all solutions in this range and select the one that yields the best numerically and theoretically.

Factor rotation & Simple Structures

1. …
2. …
3. Decide conceptually whether to apply rotation and how to do so.
4. Decide on the criteria to assess and modify a solution.
5. …

What is rotation?

Factor solutions can sometimes be complex to interpret.

• the pattern of the factor loading’s is not clear.
• The difference between the primary and cross-loading’s is small

Types of rotation

# no rotation
fa(eg_data, nfactors = 2, rotate = "none", fm="ml")
# orthogonal rotations
fa(eg_data, nfactors = 2, rotate = "varimax", fm="ml")
fa(eg_data, nfactors = 2, rotate = "quartimax", fm="ml")
# oblique rotations
fa(eg_data, nfactors = 2, rotate = "oblimin", fm="ml")
fa(eg_data, nfactors = 2, rotate = "promax", fm="ml")

Orthogonal

Oblique

Why rotate?

• Factor rotation is an approach to clarifying the relationships between items and factors.

  • Rotation aims to maximize the relationship of a measured item with a factor.
  • That is, make the primary loading big and cross-loading’s small.

Rotational Indeterminacy

• Rotational indeterminacy means that there are an infinite number of pairs of factor loading’s and factor score matrices which will fit the data equally well, and are thus indistinguishable by any numeric criteria

• There is no unique solution to the factor problem

• We can not numerically tell rotated solutions apart, so theoretical coherence of the solution plays a big role!

Simple structure

Adapted from Sass and Schmitt (2011):

1. Each variable (row) should have at least one zero loading

2. Each factor (column) should have same number of zero’s as there are factors

3. Every pair of factors (columns) should have several variables which load on one factor, but not the other

4. Whenever more than four factors are extracted, each pair of factors (columns) should have a large proportion of variables which do not load on either factor

5. Every pair of factors should have few variables which load on both factors

How do I choose which rotation?

• Clear recommendation: always to choose oblique.

• Why?

  • It is very unlikely factors have correlations of 0
  • If they are close to zero, this is allowed within oblique rotation
  • The whole approach is exploratory, and the constraint is unnecessary.

• However, there is a catch…

Interpretation and oblique rotation

• When we have an obliquely rotated solution, we need to draw a distinction between the pattern and structure matrix.

Pattern Matrix

matrix of regression weights (loading’s) from factors to variables
\(item1 = \lambda_1 Factor1 + \lambda_2 Factor2 + u_{item1}\)

myfa$loadings

Loadings:
       ML1    ML2   
item_1        -0.592
item_2         0.693
item_3         0.782
item_4 -0.105  0.606
item_5  0.458  0.414
item_6 -0.683       
item_7  0.807       
item_8  0.742       
item_9  0.744 -0.107

                 ML1   ML2
SS loadings    2.444 1.993
Proportion Var 0.272 0.221
Cumulative Var 0.272 0.493

Structure Matrix

matrix of correlations between factors and variables.
\(cor(item1, Factor1)\)

myfa$Structure

Loadings:
       ML1    ML2   
item_1        -0.591
item_2         0.693
item_3         0.782
item_4         0.600
item_5  0.482  0.439
item_6 -0.684       
item_7  0.806       
item_8  0.744       
item_9  0.738       

                 ML1   ML2
SS loadings    2.455 2.006
Proportion Var 0.273 0.223
Cumulative Var 0.273 0.496

• For orthogonal rotation, structure matrix == pattern matrix

• When we use oblique rotation, the structure matrix is the pattern matrix multiplied by the factor correlations.

• In most situations, it doesn’t impact what we do, but it’s important to be aware of.
  

The EFA output

3. …
4. …
5. Fit the factor model(s) for each number of factors
6. Evaluate the solution(s) (apply 4)
   • if developing a measurement scale, consider whether to drop items and start over
7. …

Interpretation

6. …
7. Select a final solution and interpret the model, labeling the factors.
8. …

print(myfa$loadings, cutoff=.3, sort = TRUE)

Loadings:
       ML1    ML2   
item_6 -0.683       
item_7  0.807       
item_8  0.742       
item_9  0.744       
item_1        -0.592
item_2         0.693
item_3         0.782
item_4         0.606
item_5  0.458  0.414

                 ML1   ML2
SS loadings    2.444 1.993
Proportion Var 0.272 0.221
Cumulative Var 0.272 0.493

variable	wording
item1	I worry that people will think I'm awkward or strange in social situations.
item2	I often fear that others will criticize me after a social event.
item3	I'm afraid that I will embarrass myself in front of others.
item4	I feel self-conscious in social situations, worrying about how others perceive me.
item5	I often avoid social situations because I’m afraid I will say something wrong or be judged.
item6	I avoid social gatherings because I fear feeling uncomfortable.
item7	I try to stay away from events where I don’t know many people.
item8	I often cancel plans because I feel anxious about being around others.
item9	I prefer to spend time alone rather than in social situations.