Random Effect Structures & Model Building

Data Analysis for Psychology in R 3

Josiah King

Psychology, PPLS

University of Edinburgh

Course Overview

multilevel modelling working with group structured data	regression refresher
	introducing multilevel models
	more complex grouping structures
	centering, assumptions, and diagnostics
	recap
factor analysis working with multi-item measures	what is a psychometric test?
	using composite scores to simplify data (PCA)
	uncovering underlying constructs (EFA)
	more EFA
	recap

This week

• More complicated grouping structures
  
• Model Building - how to simplify random effect structures for models that don’t converge

Random Effect Structures

Grouping structures so far…

• children within schools

• people within areas

• trials within participants

• timepoint within participants

• nurses within hospitals

• and probably some others…

Look at your data! Read the study design!

observations within clusters

when data is in long format:

• rows of data grouped by values of group identifier g

   g        x        y
   1        9      4.8
   1        5      3.9
   1        2      5.6
   2        7      4.7
   2        0      3.5
   2        3      6.4
   3        9      2.6
   3        7      6.9
   3        1      5.1
   4        3        5
   4        5      5.5
   4        9      5.8
   5        1      7.9
   5        0      4.9
   5       10      5.1
   6        7      3.3
   6        4      4.5
   6        1      3.7
 ...      ...      ...

Adding more levels!

observations within clusters within higher clusters

when data is in long format:

• rows of data grouped by values of group identifier g2, which are in turn grouped by values of higher-level group identifier g1

   g1       g2       x        y
   1        1        9      4.8
   1        1        5      3.9
   1        1        2      5.6
   1        2        7      4.7
   1        2        0      3.5
   1        2        3      6.4
   1        3        9      2.6
   1        3        7      6.9
   1        3        1      5.1
   2        4        3        5
   2        4        5      5.5
   2        4        9      5.8
   2        5        1      7.9
   2        5        0      4.9
   2        5       10      5.1
   2        6        7      3.3
   2        6        4      4.5
   2        6        1      3.7
 ...      ...      ...      ...

Adding more levels!

observations within clusters and within some other clusters

when data is in long format:

• rows of data grouped by values of group identifier g, but are also grouped by values of a group identifier gg

   gg       g        x        y
   1        1        9      4.8
   2        1        5      3.9
   3        1        2      5.6
   1        2        7      4.7
   2        2        0      3.5
   3        2        3      6.4
   1        3        9      2.6
   2        3        7      6.9
   3        3        1      5.1
   1        4        3        5
   2        4        5      5.5
   3        4        9      5.8
   1        5        1      7.9
   2        5        0      4.9
   3        5       10      5.1
   1        6        7      3.3
   2        6        4      4.5
   3        6        1      3.7
 ...      ...      ...      ...

Nested Structures

The things in a cluster belong only to that cluster.

Nested Structures

The things in a cluster belong only to that cluster.

(1 | school) + (1 | class:school)

• the order doesn’t matter, so this is also fine: (1 | school) + (1 | school:class)
• we can use (1 | school/class) as shorthand, but it is often preferable to separate them out (allowing different random effects for schools vs for children)

Nested Structures - labels!

The things in a cluster belong only to that cluster.

(1 | school) + (1 | class:school)

• If labels are unique, class:school is the same as class, meaning that the two below are equivalent:
  • (1 | school) + (1 | class:school)
  • (1 | school) + (1 | class)

Example 1

One study site recruits 20 participants.
Each participant has 10 datapoints.

d3 <- read_csv("https://uoepsy.github.io/data/lmm_mindfuldecline.csv")

 sitename    ppt   condition visit age  ACE   imp
    Sncbk  PPT_1     control     1  60 84.5 unimp
    Sncbk  PPT_1     control     2  62 85.6   imp
    Sncbk  PPT_1     control     3  64 84.5   imp
    Sncbk  PPT_1     control     4  66 83.1   imp
      ...    ...         ...   ... ...  ...   ...
    Sncbk PPT_11 mindfulness     1  60 85.6   imp
    Sncbk PPT_11 mindfulness     2  62 84.5 unimp
    Sncbk PPT_11 mindfulness     3  64 85.7   imp
    Sncbk PPT_11 mindfulness     4  66 84.8 unimp

Nested Example

14 study sites each recruit c20 participants.
Each participant has 10 datapoints.

d3full <- read_csv("https://uoepsy.github.io/data/lmm_mindfuldeclineFULL.csv")

 sitename   ppt   condition visit age  ACE imp
    Savdz PPT_1     control     1  60 84.8 imp
    Savdz PPT_1     control     2  62   85 imp
    Savdz PPT_1     control     3  64 83.9 imp
    Savdz PPT_1     control     4  66   83 imp
    Savdz PPT_1     control     5  68 82.2 imp
    Savdz PPT_1     control     6  70 81.9 imp
      ...   ...         ...   ... ...  ... ...
      ...   ...         ...   ... ...  ... ...
    Slonb PPT_8     control     9  76 82.1 imp
    Slonb PPT_8     control    10  78 81.6 imp
    Slonb PPT_9 mindfulness     1  60   85 imp
    Slonb PPT_9 mindfulness     2  62 85.1 imp
      ...   ...         ...   ... ...  ... ...

Crossed Structures

Not nested? ==> “crossed”

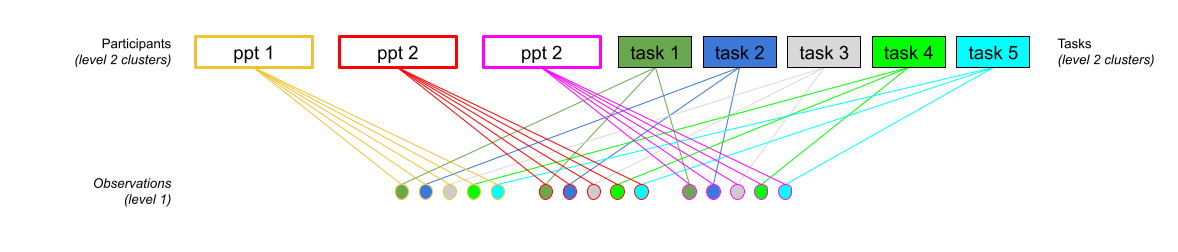
(1 | subject) + (1 | task)

Crossed Example

Participants take part in an experiment where they each complete 10 tasks. Odd numbered participants are in Group 1, Even numbered participants in Group 2. Participants 1-10 see tasks 1-5 in Condition A and tasks 6-10 in B, Participants 11-20 see tasks 1-5 in B and 6-10 in A.

d3cross <- read_csv("https://uoepsy.github.io/data/lmm_egcross.csv")

    ppt    task condition group score
 ppt_01 task_01         A     1   8.8
 ppt_01 task_02         A     1   8.8
    ...     ...       ...   ...   ...
 ppt_01 task_06         B     1   7.2
 ppt_01 task_07         B     1    12
    ...     ...       ...   ...   ...
    ...     ...       ...   ...   ...
 ppt_02 task_01         A     2  18.1
 ppt_02 task_02         A     2  17.7
    ...     ...       ...   ...   ...
 ppt_02 task_06         B     2  15.4
 ppt_02 task_07         B     2  21.6
    ...     ...       ...   ...   ...
    ...     ...       ...   ...   ...
 ppt_11 task_01         B     1  10.6
 ppt_11 task_02         B     1  13.9
    ...     ...       ...   ...   ...
 ppt_11 task_06         A     1   9.3
 ppt_11 task_07         A     1    11
    ...     ...       ...   ...   ...

“Random Effects”

\[ \text{... + }\underbrace{\text{(random intercept + random slopes | grouping structure)}}_{\text{random effects}} \]

People use different phrasings…

• when referring to random slopes:
  • “random effects of x for/by g”
    
  • “by-g random effects of/for x”
    
• when referring to random intercept:
  • “random effect for g”
  • “by-g random intercepts”

common definition: “allow ___ to vary by g”

Random Effects Revisited (2)

Should variable g be fixed or random?

	Repetition: If the experiment were repeated:	Desired inference: The conclusions refer to:
Fixed \(y\,\sim\,~\,...\, +\, g\)	Same groups would be used	The groups used
Random \(y\,\sim\,...\,+\,(\,... |\,g)\)	Different groups would be used	A population from which the groups used are just a (random) sample

If we only have a very small number of groups, estimating variance components may be unstable, and partialling out group-differences as fixed effects may be preferable.

Random Effects Revisited (3)

I have y ~ 1 + x + (1 | g) should I include by-g random slope of x?

if x is a variable for which values differ between groups, then we can’t model the y~x slope varying between groups.

if x is a variable for which values differ within groups, then the y~x slope might vary from one group to another.

• including (1 + x| g) gives better estimate of the uncertainty in the fixed effect of x.
  • important to include especially if x is the thing we’re interested in!

“Ultimately, the random effect structure one uses in an analysis encodes the assumptions that one makes about how sampling units [e.g. participants] vary, and the structure of dependency that this variation creates in one’s data.”

Example 1

• multiple observations from each participant
  (1 | ppt)

• for a single ppt, the slope of ACE ~ visit exists in our study design. This could (quite likely) be different for different ppts!
  (visit | ppt)

• for a single ppt, the slope of ACE ~ condition is not observed in our study design (each ppt is either one condition or the other).
  (condition | ppt) makes no sense

lmer(ACE ~ 1 + visit * condition + ???  

lmer(ACE ~ 1 + visit + condition + 
       (1 + visit | ppt), data)

Nested example

• multiple observations from each participant:
  (1 | sitename)

• multiple participants nested within study sites:
  (1 | sitename) + (1 | ppt:sitename)

• for a single ppt, the slope of ACE ~ visit exists in our study design:
  (visit | ppt)

• for a single study site, the slope of ACE ~ visit exists in our study design:
  (visit | sitename)

• for a single ppt, the slope of ACE ~ condition does not exist in our study design:
  (condition | ppt)

• for a single study site, the slope of ACE ~ condition exists in our study design:
  (condition | sitename)

lmer(ACE ~ 1 + visit * condition + ???  

lmer(ACE ~ 1 + visit * condition + 
      (1 + visit * condition | sitename ) + 
      (1 + visit | ppt:sitename), data)

Crossed Example

Participants take part in an experiment where they each complete 10 tasks. Odd numbered participants are in Group 1, Even numbered participants in Group 2. Participants 1-10 see tasks 1-5 in Condition A and tasks 6-10 in B, Participants 11-20 see tasks 1-5 in B and 6-10 in A.

• multiple observations from each participants:
  (1 | ppt)

• participants are observed in each condition - the effect of condition could be different for participant 1 vs participant 2
  (condition | ppt)

• participants are observed in either group 1 or group 2. The effect of group is not defined for a single participant:
  (group | ppt)

lmer(score ~ condition * group + ???  

Crossed Example

Participants take part in an experiment where they each complete 10 tasks. Odd numbered participants are in Group 1, Even numbered participants in Group 2. Participants 1-10 see tasks 1-5 in Condition A and tasks 6-10 in B, Participants 11-20 see tasks 1-5 in B and 6-10 in A.

• multiple observations from each participants:
  (1 | ppt)

• participants are observed in each condition - the effect of condition could be different for participant 1 vs participant 2
  (condition | ppt)

• participants are observed in either group 1 or group 2. The effect of group is not defined for a single participant:
  (group | ppt)

• multiple observations of each task (not nested within ppts):
  (1 | task)

• tasks are completed by people in each group - the effect of group could be different for task 1 vs task 2:
  (group | task)

• tasks in each condition are completed by both groups. How group effects interact with condition effects could be different for task 1 vs 2:
  (group * condition | task)

lmer(score ~ condition * group + ???  

lmer(score ~ condition * group +
      (1 + condition | ppt ) + 
      (1 + condition * group | task), data = dfcross)

The poke in the eye

• Sometimes a model is too complex to be supported by the data

• Balancing act between simplifying our model while preserving attribution of variance to various sources

Convergence Warnings:

warning(s): Model failed to converge with max|grad| = 0.041777 (tol = 0.002, component 1) (and others)

Singular Fits:

message(s): boundary (singular) fit: see help('isSingular')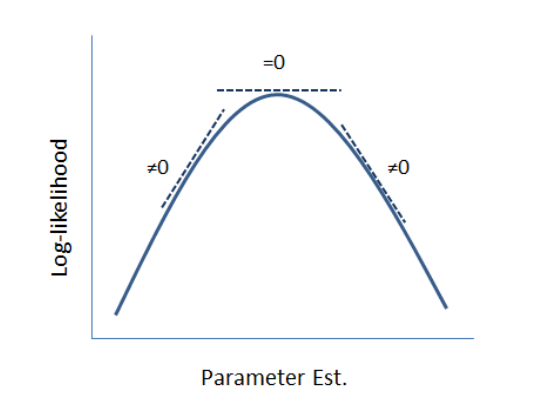

Model Building

underfitting and overfitting

Accurately representing the world

Aim: random effect structure that fully reflects our understanding of how things can vary, given the study design.

(trickier with observational data in which you could argue that everything will vary)

Practical issues with fitting models

in our sample, some things will not vary enough to fit x|g

• predictors on different scales
  • e.g. millimeters|g vs kilometers|g
    • can be fixed with scaling
      
• not enough groups in g
  • fit +g instead of (1|g)
• not enough variance in y~x between groups
  • model estimation can hit boundaries
    • variance \(\nleqq 0\)
    • correlation \(\ngeqq 1\) and \(\nleqq -1\))

Maximal Structures

“maximal model” = the most complex random effect structure supported by the design

• everything that can be modelled as a random effect is included

• requires sufficient variance at all levels (for both intercepts and slopes where relevant). Which is often not the case.

14 Study sites, each with c18 ppts, each with approx 10 observations

d3full <- read_csv("https://uoepsy.github.io/data/lmm_mindfuldeclineFULL.csv")

maxmodelfull <- lmer(ACE ~ visit * condition + 
                   (1 + visit * condition | sitename) +
                   (1 + visit | sitename:ppt), 
                 data = d3full)

boundary (singular) fit: see help('isSingular')

isSingular(maxmodelfull)

[1] TRUE

Deciding on the optimal random effect structure

Keep it maximal

1. Start with maximal model
   
2. Remove random effects with least variance until model converges (see Barr et al., 2013)

Selection based

Use a criterion for model selection (e.g. LRT, AIC, BIC) to choose a random effect structure that is supported by the data (see Matsuchek et al., 2017)

• risk of overfitting

• lots of different ways (e.g., backwards/forwards, criteria for determining order of incl/exclusion, \(\alpha\) adjustments, etc)

No right answer

Barr, D. J., Levy, R., Scheepers, C., & Tily, H. J. (2013). Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of memory and language, 68(3), 255-278.
Matuschek, H., Kliegl, R., Vasishth, S., Baayen, H., & Bates, D. (2017). Balancing Type I error and power in linear mixed models. Journal of memory and language, 94, 305-315.

how to simplify

# to extract random effects
VarCorr(maxmodelfull)

 Groups       Name                       Std.Dev. Corr             
 sitename:ppt (Intercept)                0.460                     
              visit                      0.269    -0.58            
 sitename     (Intercept)                0.000                     
              visit                      0.128      NaN            
              conditionmindfulness       0.122      NaN -1.00      
              visit:conditionmindfulness 0.101      NaN  0.02 -0.02
 Residual                                0.455                     

One thing at a time!

Look for:

• Variances/standard deviations of 0 (or very small, e.g. 3.56e-05)
• Correlations of -1 or 1

how to simplify (2)

# to extract random effects
VarCorr(maxmodelfull)

 Groups       Name                       Std.Dev. Corr             
 sitename:ppt (Intercept)                0.460                     
              visit                      0.269    -0.58            
 sitename     (Intercept)                0.000                     
              visit                      0.128      NaN            
              conditionmindfulness       0.122      NaN -1.00      
              visit:conditionmindfulness 0.101      NaN  0.02 -0.02
 Residual                                0.455                     

model_simp1 <- lmer(ACE ~ visit * condition + 
                   (1 + visit + condition | sitename) +
                   (1 + visit | sitename:ppt), 
                 data = d3full)
VarCorr(model_simp1)

 Groups       Name                 Std.Dev. Corr       
 sitename:ppt (Intercept)          0.445               
              visit                0.274    -0.57      
 sitename     (Intercept)          0.155               
              visit                0.135    -0.10      
              conditionmindfulness 0.152    -0.68 -0.57
 Residual                          0.455               

One thing at a time!

• Consider removing most complex random effects first.

(1 + x1 * x2 | g)
  ↓
(1 + x1 + x2 | g)

• Categorical predictors with >2 levels are “more complex” (they require more parameters than a single slope for a continuous predictor).

how to simplify (3)

# to extract random effects
VarCorr(model_simp1)

 Groups       Name                 Std.Dev. Corr       
 sitename:ppt (Intercept)          0.445               
              visit                0.274    -0.57      
 sitename     (Intercept)          0.155               
              visit                0.135    -0.10      
              conditionmindfulness 0.152    -0.68 -0.57
 Residual                          0.455               

One thing at a time!

• If multiple levels of nesting, you’ll have fewer groups as you go up the levels (fewer groups to be able to fit things to).
  
• depending on what the groups are, you might expect less variability in effects at certain levels
  • e.g. I might expect people to vary a lot in their cognitive trajectories, but study-sites to vary less

how to simplify (4)

removing correlations between random effects

mod <- lmer(y ~ 1 + x * b + 
              (1 + x | group), data = cordat)
VarCorr(mod)

 Groups   Name        Std.Dev. Corr
 group    (Intercept) 0.199        
          x           0.342    1.00
 Residual             0.216        

plot(ranef(mod)$g)

modzc <- lmer(y ~ 1 + x * b + 
              (1 + x || group), data = cordat)
VarCorr(modzc)

 Groups   Name        Std.Dev.
 group    (Intercept) 0.186   
 group.1  x           0.352   
 Residual             0.221   

plot(ranef(modzc)$g)

in certain designs, you might consider there to be no theoretical justification for there to be a correlation between random effects.
however, you have to be careful and this should only be done if your predictor is on a ratio scale - so if it has a meaningful zero. this is for the slghtly complicated reason that the zero correlation model is sensitive to shifts in the predictor. so our estimates from a model with a zero correlation parameter will change slightly as we shift our predictor.

how to simplify (5)

modl <- lmer(bp ~ dosage + length_stay + 
      (1 + dosage + length_stay  | hospital) + 
      (1 + dosage + length_stay  | patient:hospital),
    data = mydata) 
VarCorr(modl)

 Groups           Name        Std.Dev. Corr       
 patient:hospital (Intercept) 1.7047              
                  dosage      0.9504    0.35      
                  length_stay 0.0404   -0.67  0.47
 hospital         (Intercept) 0.3067              
                  dosage      0.1884    1.00      
                  length_stay 0.2370   -1.00 -1.00
 Residual                     2.5737              

One thing at a time!

• You will be faced with subjective choices
  • which simplification can you most easily accept?
• Important: be transparent about decisions made, explain reasoning if necessary.

Summary

• random effect structures can get complicated quite quickly

• there may multiple ways in things can be clustered.

  • clusters can themselves be clustered (nesting).
  • we can have different ways of clustering the same things (crossed)

• the maximal random effect structure is the most complex structure we can fit to the data.

  • it often leads to problems with model convergence

• building lmers is a balancing act between accounting for different sources of variation and attempting to fitting a model that can be supported by our data.

This week

Tasks

Complete readings

Attend your lab and work together on the exercises

Complete the weekly quiz

Support

Piazza forum!

Office hours (see Learn page for details)