Bootstrapping and
confidence intervals


Data Analysis for Psychology in R 2

Elizabeth Pankratz (elizabeth.pankratz@ed.ac.uk)


Department of Psychology
University of Edinburgh
2025–2026

Course Overview


Introduction to Linear Models Intro to Linear Regression
Interpreting Linear Models
Testing Individual Predictors
Model Testing & Comparison
Linear Model Analysis
Analysing Experimental Studies Categorical Predictors & Dummy Coding
Effects Coding & Coding Specific Contrasts
Assumptions & Diagnostics
Bootstrapping
Categorical Predictor Analysis
Interactions Interactions I
Interactions II
Interactions III
Analysing Experiments
Interaction Analysis
Advanced Topics Power Analysis
Binary Logistic Regression I
Binary Logistic Regression II
Logistic Regression Analysis
Exam Prep and Course Q&A

This week’s learning objectives


What is bootstrapping?

How does bootstrapping work?

When would we bootstrap a linear model’s estimates?

What does “confidence” in “95% confidence interval” actually mean?

What’s a bootstrap?


What do bootstraps have to do with stats?

Unclear.


We’ll revisit this question later once we’ve seen the method in action.

Background

What problem does bootstrapping solve?


The core challenge in statistics:

We want to know something about a population, but we can’t possibly study the whole population.

We can only draw a sample from it.


We ask a question of the sample (e.g., what’s the mean?). And we get a single answer (e.g., 10).

How do we know if this answer is representative of the population overall?


Ideally, we would take many samples from the population, get their means, and compare them all.

But we are constrained to this one sample.


One strategy: Use mathematical tools like the formula you learned for the standard error.

But those tools only give valid information if the assumptions behind them are met (e.g., that errors are normally distributed).

Otherwise, they give bad estimates of the actual variability in the population.

Another strategy: Treat the sample we’ve drawn as if it is a population, and draw many new samples from it.

This strategy doesn’t rely on mathematical assumptions.

This method is called bootstrapping.

Other problems that bootstrapping can solve


  1. When samples are very small, uncertainty around parameters like the mean will be high. Bootstrapping can help us get more precise estimates of the parameters, though it assumes that our original sample will accurately represent the population (a shaky assumption when the samples are small!).


  1. Context: Linear models can test whether a coefficient’s value is different from zero because we have a measure of difference (the t value) and we know how this statistic is distributed when the H0 is true. So: If we don’t know the sampling distribution of the measure we’re using when the H0 is true, then we can use bootstrapping to estimate the null distribution of whatever measure we’re using.

Bootstrapping: Resampling from a sample

Why is bootstrapping an OK thing to do?


Our main sample contains the best possible information we can get about a population. (Basically anything that we guessed would be worse.)

If our main sample was drawn at random, it will probably look quite a bit like the population.

So, drawing bootstrap samples from our main sample and summarising them will probably create a sampling distribution that looks a lot like the one we would get if we could sample repeatedly from the whole population.

Generate bootstrapped samples by sampling with replacement

Imagine our main sample contains five shapes:

If we could only sample each data point once:

Each sample is just a shuffled version of the original.

If we could sample each data point repeatedly:

Each sample is distinct!

To create diverse samples, we need to be able to sample each data point repeatedly.

This is called “sampling with replacement”.

Bootstrapping demo

Activity: Bootstrapping our own samples


Population: All numbers from 1 to 100.

Main sample (size 10):

6     8     17     32     70     76     79     81     85     93


Bootstrapped samples (size 10): Over to you!

https://edin.ac/4nTcnMP

What just happened?

Estimating variability using the sampling distribution


  • For each bootstrapped sample, we compute a summary statistic.
  • We represent all those summary statistics together using a sampling distribution.
  • A sampling distribution is useful because with it, we can estimate a parameter’s variability (i.e., standard error, confidence intervals).


The standard error of the parameter = the standard deviation of the sampling distribution.

The 95% CI of the parameter = the range from the 2.5th percentile to the 97.5th percentile of the sampling distribution.

  • 2.5th percentile = 2.5% of values in the distribution are below this value
  • 97.5th percentile = 97.5% of values in the distribution are below this value

Any summary statistic can be bootstrapped


There’s nothing special about the mean.

We can use bootstrapping for any measure that summarises data points.


Most usefully for us: We can bootstrap the parameters of a linear model.

Bootstrapping linear model parameters

Which model assumptions are not met?




  Linearity?


  Independent errors?


  Normally-distributed errors?


  Equal variance of errors?

Check: Linearity


Use geom_smooth() to plot a straight line (method = 'lm') and a curvy line (method = 'loess'). The curvy line should match the straight line.

Not perfect, but relatively good.

Check: Normally-distributed errors


With a Q-Q plot, compare the actual standardised residuals from the model (y axis) to the ones we’d expect, if errors were perfectly normally distributed (x axis).

Big divergences toward the extremes: there are more large residuals in our data than a normal distribution would have.

Check: Equal variance of errors


With a plot of residuals vs. fitted values, check whether the residuals (y axis) are similar across all of the fitted/predicted values (x axis).

There’s a definite cone-shape here (ideally we’d want a random-looking cloud), so residuals do not have equal variance.

The verdict: uh oh


Bootstrapping can’t make a maybe-linear effect more linear.


But it can help us sidestep the problems that arise from non-normal residuals and unequal variance of residuals.

When residuals are not normal and when they have unequal variance, then the standard error that a linear model gives us is a bad estimate of the actual variability.


So instead: we estimate the variability using bootstrapping.

Bootstrapping, step by step

A note




You will never need to do bootstrapping step by step, the way I’m illustrating it here.

I am showing you the steps to help you understand what’s happening behind the scenes when you run the simple code you’ll see later.

Bootstrapping, step by step

  1. From the main sample, take a new sample with replacement. You always sample the same number of data points as there were in the main sample. One sample bootstrapped.

  2. Fit the linear model to the bootstrapped sample. Save the intercept and slope estimates.

  3. Do 1 and 2 again and again. We’ll get a sampling distribution of intercept estimates and a sampling distribution of slope estimates.

(1)

(2)


Call:
lm(formula = y ~ x, data = boot_samples[[1]])

Coefficients:
(Intercept)            x  
      2.462       -0.661

(3)

Bootstrapping, step by step (Sample 2)

  1. From the main sample, take a new sample with replacement. You always sample the same number of data points as there were in the main sample. One sample bootstrapped.

  2. Fit the linear model to the bootstrapped sample. Save the intercept and slope estimates.

  3. Do 1 and 2 again and again. We’ll get a sampling distribution of intercept estimates and a sampling distribution of slope estimates.

(1)

(2)


Call:
lm(formula = y ~ x, data = boot_samples[[2]])

Coefficients:
(Intercept)            x  
      2.160       -0.663

(3)

Bootstrapping, step by step (Sample 3)

  1. From the main sample, take a new sample with replacement. You always sample the same number of data points as there were in the main sample. One sample bootstrapped.

  2. Fit the linear model to the bootstrapped sample. Save the intercept and slope estimates.

  3. Do 1 and 2 again and again. We’ll get a sampling distribution of intercept estimates and a sampling distribution of slope estimates.

(1)

(2)


Call:
lm(formula = y ~ x, data = boot_samples[[3]])

Coefficients:
(Intercept)            x  
      2.211       -0.684

(3)

Sampling distribution of the intercept




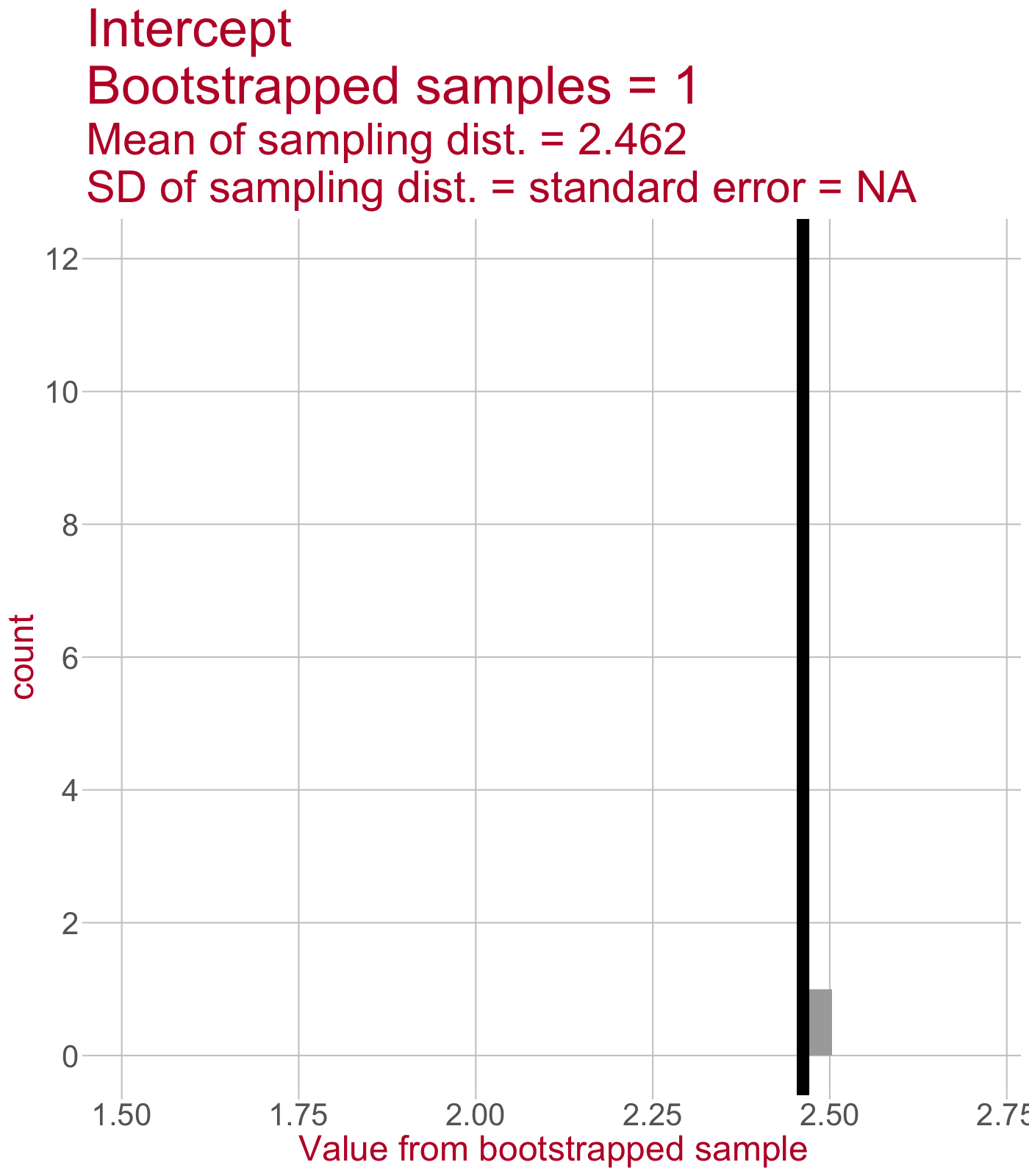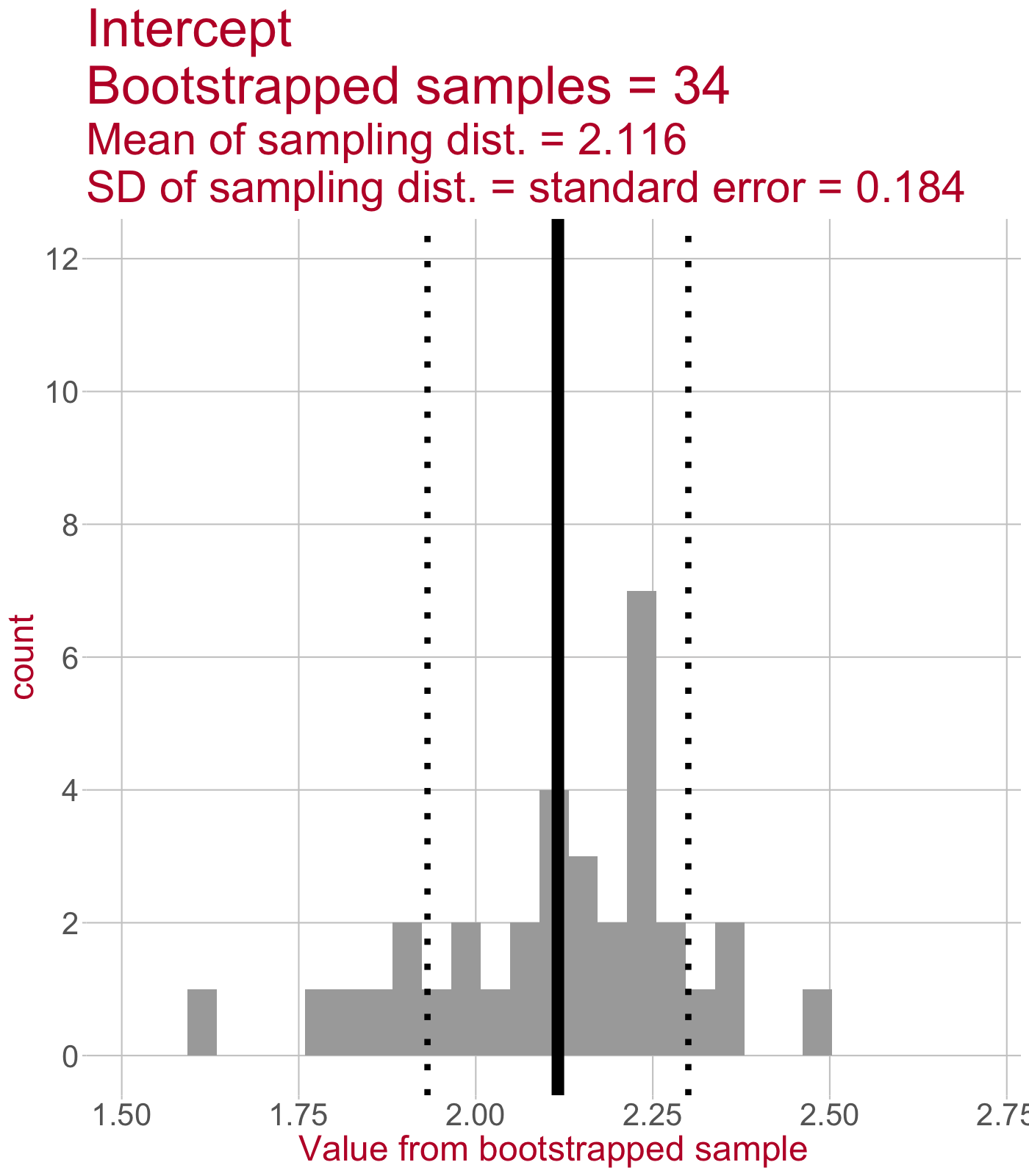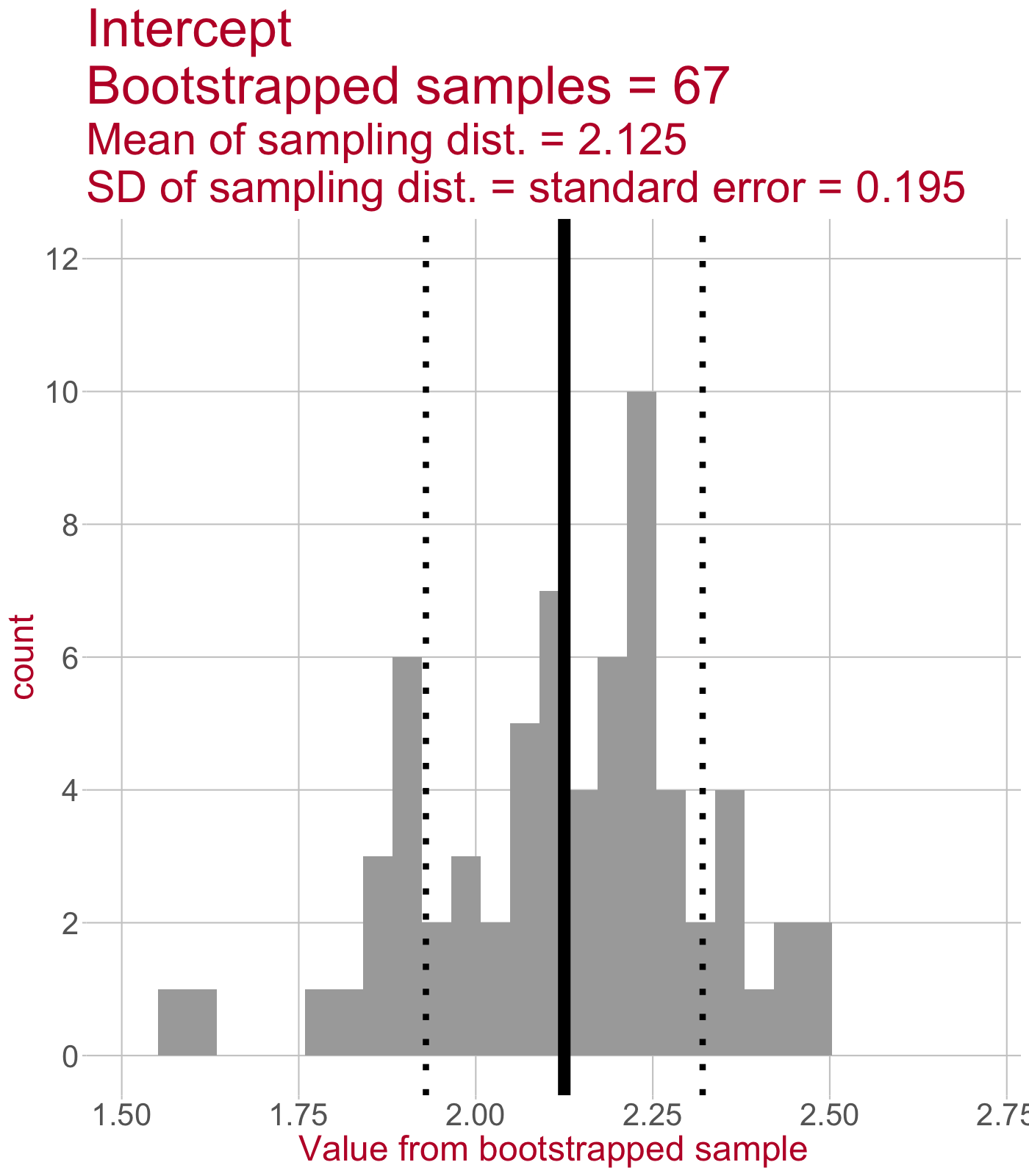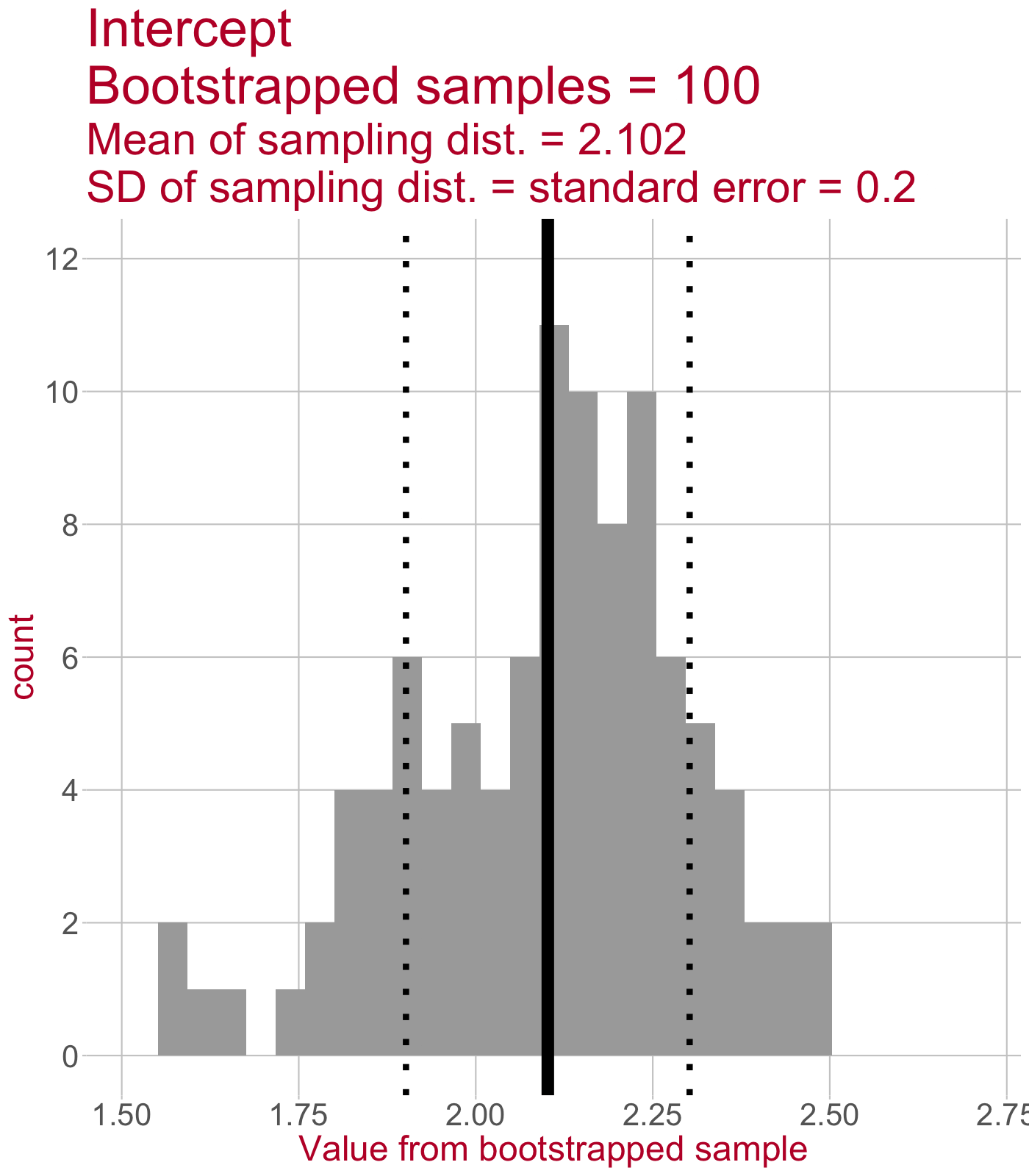
\(\leftarrow\) This sampling distribution consists of every Intercept value estimated by a linear model that was fit to a bootstrapped sample of data.


As we draw more bootstrapped samples, the mean Intercept (solid line) will come to match the original sample’s Intercept.


The standard deviation of the sampling distribution (dotted lines) = the standard error of the Intercept.

Sampling distribution of the slope




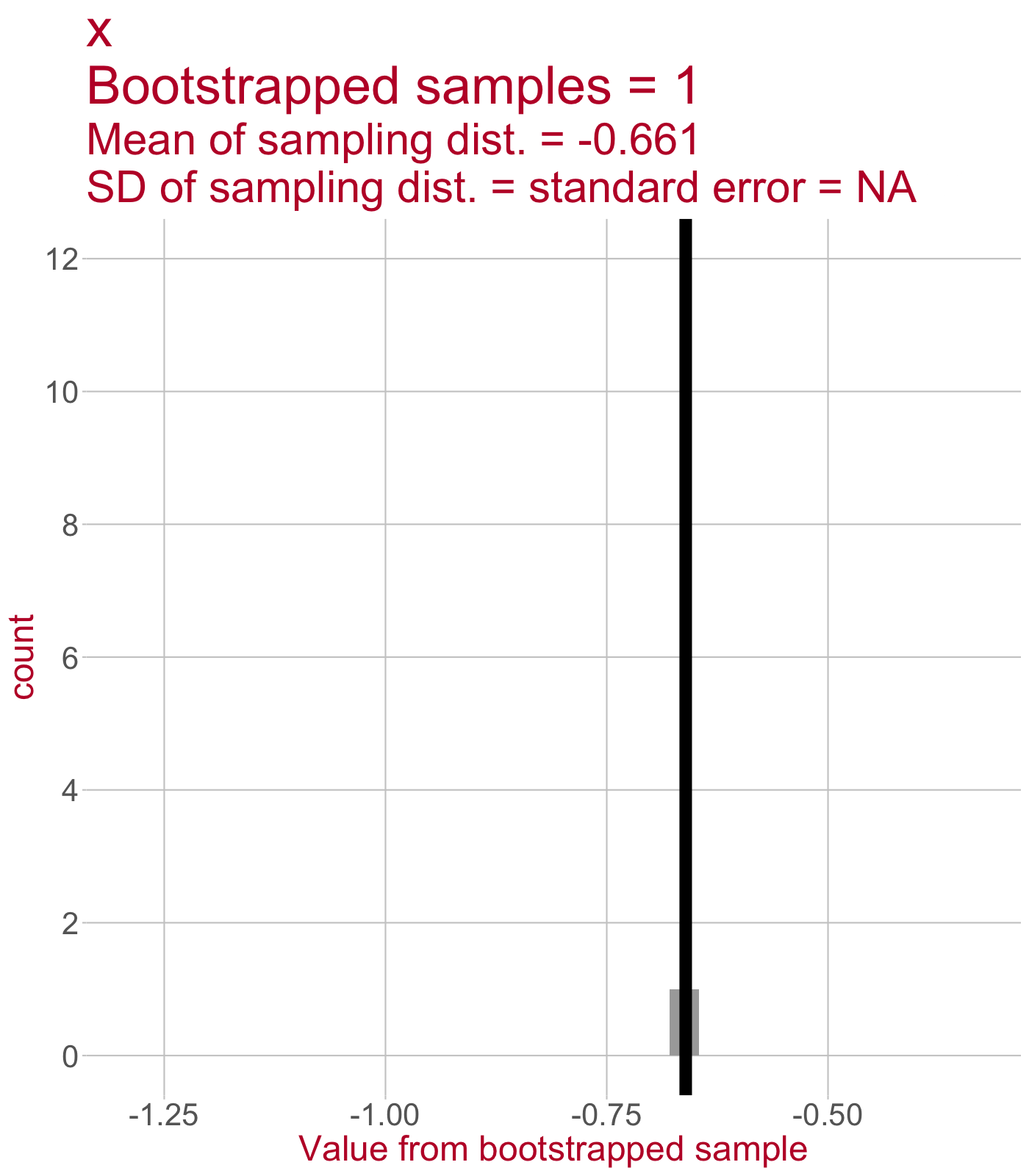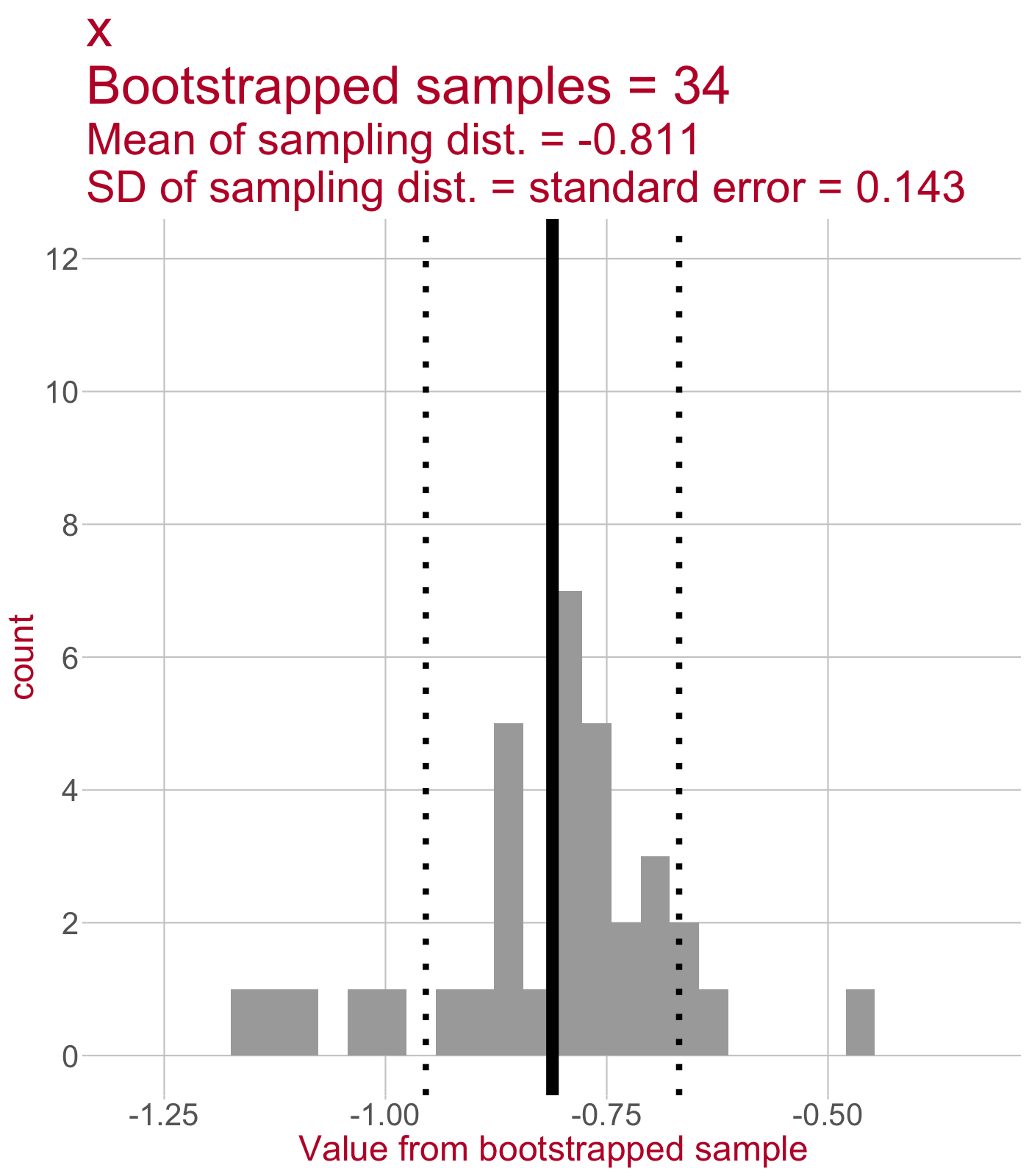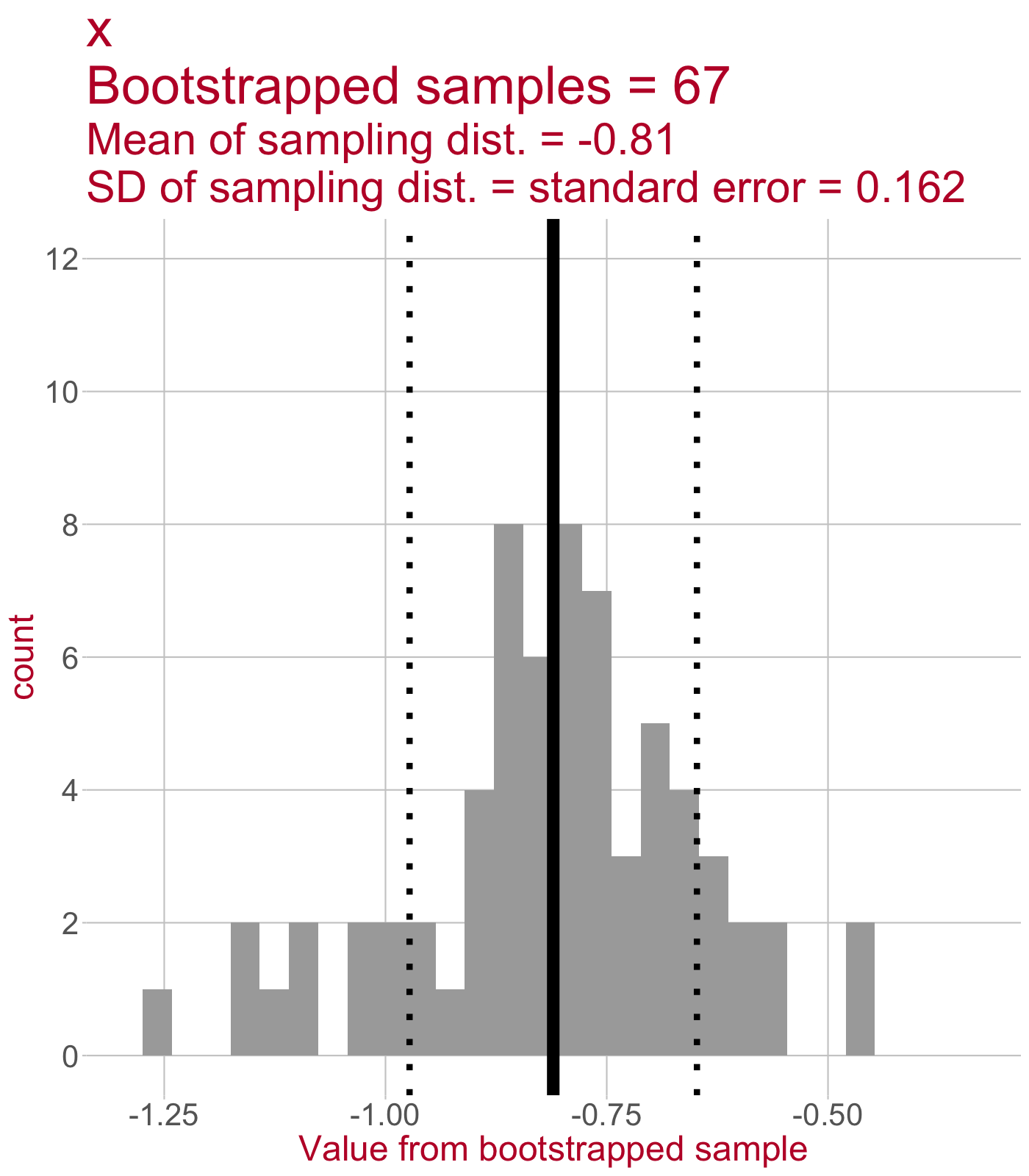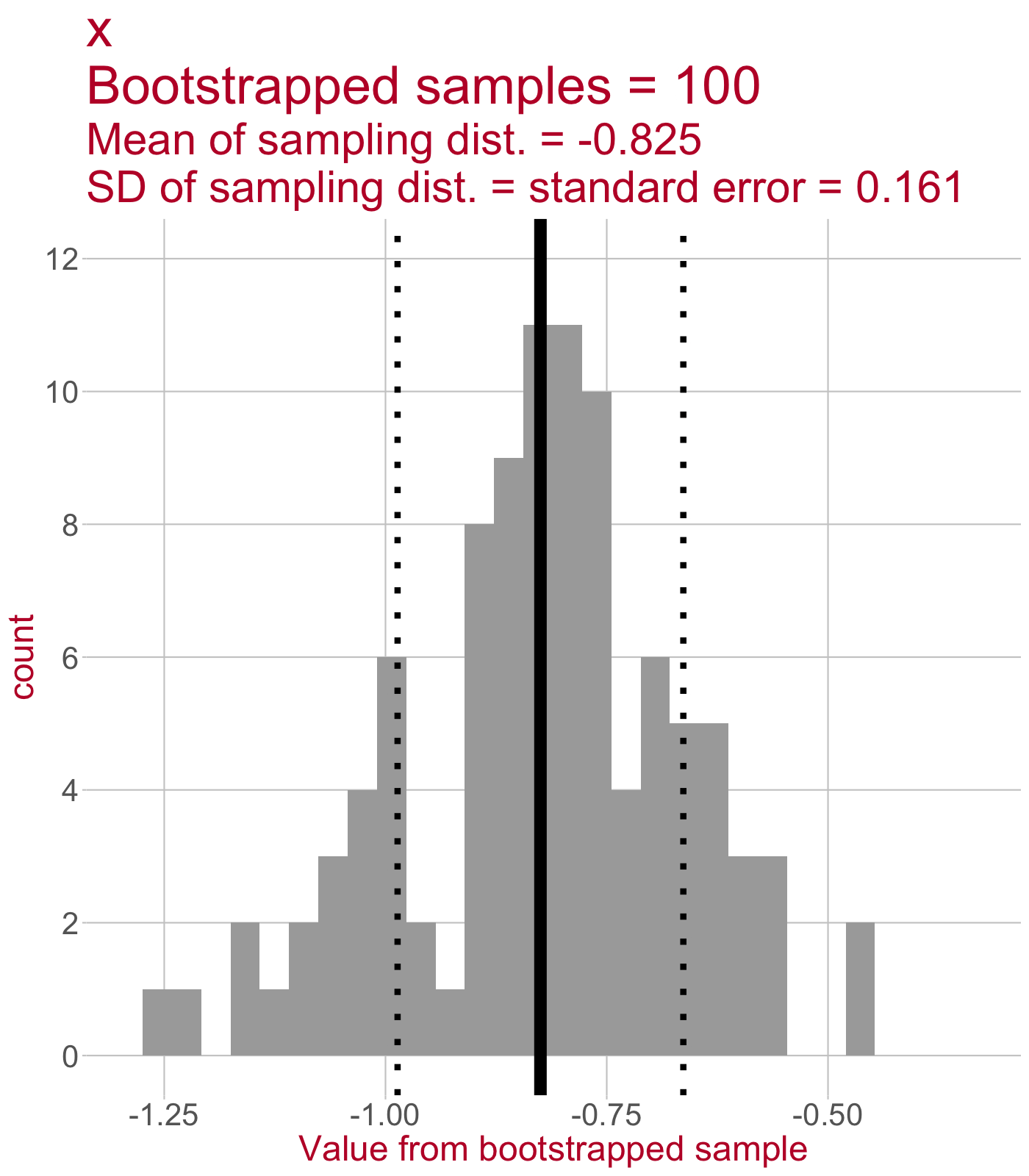
\(\leftarrow\) This sampling distribution consists of every slope value estimated by a linear model that was fit to a bootstrapped sample of data.


As we draw more bootstrapped samples, the mean slope (solid line) will come to match the original sample’s slope.


The standard deviation of the sampling distribution (dotted lines) = the standard error of the slope.


Bootstrapping is a different way of estimating a parameter’s standard error.

Bootstrapping a linear model in R

Bootstrapping a linear model in R


Fit a standard linear model to the main sample.

mod <- lm(y ~ x, data = orig_data)


Use Boot() from the package car to draw R = 1000 bootstrapped samples.

By default, the bootstrapped samples will contain the same number of data points as the original sample.

mod_boot <- car::Boot(mod, R = 1000)


Now summary() will give us a standard error for each parameter (but we know this is just the standard deviation of each parameter’s sampling distribution).

summary(mod_boot)

Number of bootstrap replications R = 1000 
            original bootBias bootSE bootMed
(Intercept)    2.115 0.006860  0.183   2.124
x             -0.813 0.000135  0.160  -0.811

Manual bootstrapping closely matches Boot()


Number of bootstrap replications R = 1000 
            original bootBias bootSE bootMed
(Intercept)    2.115 0.006860  0.183   2.124
x             -0.813 0.000135  0.160  -0.811


Getting our 95% confidence intervals


confint(mod_boot, type = 'perc')
Bootstrap percent confidence intervals

            2.5 % 97.5 %
(Intercept)  1.74  2.477
x           -1.14 -0.526


Hypothesis tests:

Because these 95% confidence intervals don’t include 0,

  • we can reject the H0 that the Intercept = 0 at \(\alpha\) = 0.05.
  • we can reject the H0 that the slope = 0 at \(\alpha\) = 0.05.

Reporting results of a bootstrapped linear model


Report parameter estimates the same way as usual, but make sure to include something like


Because the assumptions of normality of errors and equal variance of errors were not met, all the standard errors and 95% CIs we report here were estimated from 1000 bootstrapped samples, using the Boot() function from the car package (Fox & Weisberg, 2019).


The citation:

^ These are the people who developed the car (Companion to Applied Regression) package.

So, what do bootstraps have to do with stats?

What do bootstraps have to do with stats?


Bradley Efron is the inventor of bootstrapping, and he introduced it in his 1979 paper by saying it’s a method

(Reader, the reasons did not become obvious.)


The internet’s best guess: it has to do with the saying “pull yourself up by your bootstraps”.

  • Previously, this saying meant “a pointless/useless act”.
  • These days, people use it to mean that
    • you’re independent,
    • you’re a self-starter,
    • you’re standing on your own two feet.
  • We think that “bootstrapping” is used in that sense: you can get estimates of uncertainty from just a single sample, so in a way, your sample is “pulling itself up by its bootstraps”.

Confidence interval refresher

Interpreting confidence intervals


It’s common to imagine that a 95% CI means that there’s a 95% probability that our true value is in the interval.

But this isn’t what they really mean! :(

So what do confidence intervals mean?


Confidence intervals rely on the idea of “hypothetical repeated sampling”.

  • hypothetical: we’re imagining something that isn’t really happening
  • repeated: we’re imagining that we’re doing something over and over again
  • sampling: we’re imagining that we’re drawing samples from the same population over and over again


Side note: Hypothetical repeated sampling is different from bootstrapping because

  • hypothetical repeated sampling imagines repeatedly drawing samples from the population
  • bootstrapping really repeatedly draws samples from our original sample

We can simulate hypothetical repeated sampling by defining our own “reality”


Let’s look at the association between hours of sleep and the number of riddles solved in an hour.

In the real true population (which we have defined, in order to illustrate how confidence intervals work),
the true association looks like this:

Repeatedly draw samples from that true population and fit a linear model to each

Some 95% CIs of the slope don’t contain the true population value of 4

How many CIs contain the true value?


If we’re using a 95% CI, then we know that under hypothetical repeated sampling:

  • 95 out of every 100 CIs will contain the true population value.
  • 5 of every 100 CIs will not.

How many CIs contain the true value?


If we’re using a 60% CI, then we know that under hypothetical repeated sampling:

  • 60 out of every 100 CIs will contain the true population value.
  • 40 of every 100 CIs will not.

So what is “confidence”?


“Confidence” refers to the process that generates the intervals.

  • A 95% confidence interval is generated using a process that, in the long run, makes 95 intervals that contain the true population value for every 5 intervals that do not.

  • In general: a \(n\)% confidence interval is generated using a process that, in the long run, makes \(n\) intervals that contain the true population value for every 100 \(-~n\) that do not.


This is why it’s not true to say “there’s a 95% probability that the true value is in the 95% CI”.

  • We have no idea whether any given confidence interval contains the true population value.
  • Either it does contain the true value (then the probability = 100%) or it does not (probability = 0%).
  • For a given confidence interval, we have no way of knowing how likely each of those two outcomes is.

Building an analysis workflow


Revisiting this week’s learning objectives


What is bootstrapping?

  • An alternative way of estimating the variability of a coefficient estimate (i.e., the standard error and confidence interval).
  • Unlike regular linear models, bootstrapping doesn’t require that errors be normally distributed or equal across the range of the predictor.

How does bootstrapping work?

  • It is based on repeatedly resampling from a given sample and then computing summary statistics on those samples.
  • By combining those summary values, we get a sampling distribution: our best guess about how that statistic is distributed in the population.

Revisiting this week’s learning objectives


When would we bootstrap a linear model’s estimates?

  • When a linear model’s residuals don’t fulfil the model’s assumptions about normality of errors and equal variance of errors.
  • Those assumptions are what makes the formulae for estimating standard error and confidence intervals work.
  • When those assumptions aren’t met, then we need a different way of estimating standard error and CIs: bootstrapping.

What does “confidence” in “95% confidence interval” actually mean?

  • “Confidence” is a property of the process that generates confidence intervals.
  • A 95% confidence interval is generated by a process that produces 95 intervals that contain the true value for every 5 that do not.
  • 95% confidence interval \(\neq\) 95% probability that the interval contains the true value!!
    • Either the 95% CI contains the true value or it doesn’t. We have no idea how probable each of those scenarios is.

This week


Tasks


Attend your lab and work together on the exercises

Support


Help each other on the Piazza forum


Complete the weekly quiz

Attend office hours (see Learn page for details)

Appendix

95% CIs from the sampling distribution’s quantiles

confint(mod_boot, type = 'perc')
Bootstrap percent confidence intervals

            2.5 % 97.5 %
(Intercept)  1.74  2.477
x           -1.14 -0.526

The CIs from Boot() are close to the 2.5th and 97.5th quantiles of our manually created sampling distribution:

quantile(
  boot_coefs_df_1k$Intercept,
  probs = c(0.025, 0.975)
)
 2.5% 97.5% 
 1.73  2.47 
quantile(
  boot_coefs_df_1k$x,
  probs = c(0.025, 0.975)
)
  2.5%  97.5% 
-1.151 -0.532