Linear Model: Fundamentals


Data Analysis for Psychology in R 2

Emma Waterston


Department of Psychology
University of Edinburgh
2025–2026

Course Overview

Introduction to Linear Models Intro to Linear Regression
Interpreting Linear Models
Testing Individual Predictors
Model Testing & Comparison
Linear Model Analysis
Analysing Experimental Studies Categorical Predictors & Dummy Coding
Effects Coding & Coding Specific Contrasts
Assumptions & Diagnostics
Bootstrapping
Categorical Predictor Analysis
Interactions Interactions I
Interactions II
Interactions III
Analysing Experiments
Interaction Analysis
Advanced Topics Power Analysis
Binary Logistic Regression I
Binary Logistic Regression II
Logistic Regression Analysis
Exam Prep and Course Q&A

This Week’s Learning Objectives

  1. Be able to interpret the coefficients from a simple linear model

  2. Understand how and why we standardise coefficients and how this impacts interpretation

  3. Understand how these interpretations change when we add more predictors

Part 1: Recap & Coefficient Interpretation

Linear Model

  • Last week we introduced the linear model:

\[y_i = \beta_0 + \beta_1 x_{i} + \epsilon_i\]

  • Where:
    • \(y_i\) is our measured outcome variable
    • \(x_i\) is our measured predictor variable
    • \(\beta_0\) is the model intercept
    • \(\beta_1\) is the model slope
    • \(\epsilon_i\) is the residual error (difference between the model predicted and the observed value of \(y\))
  • We spoke about calculating by hand, and also the key concept of residuals

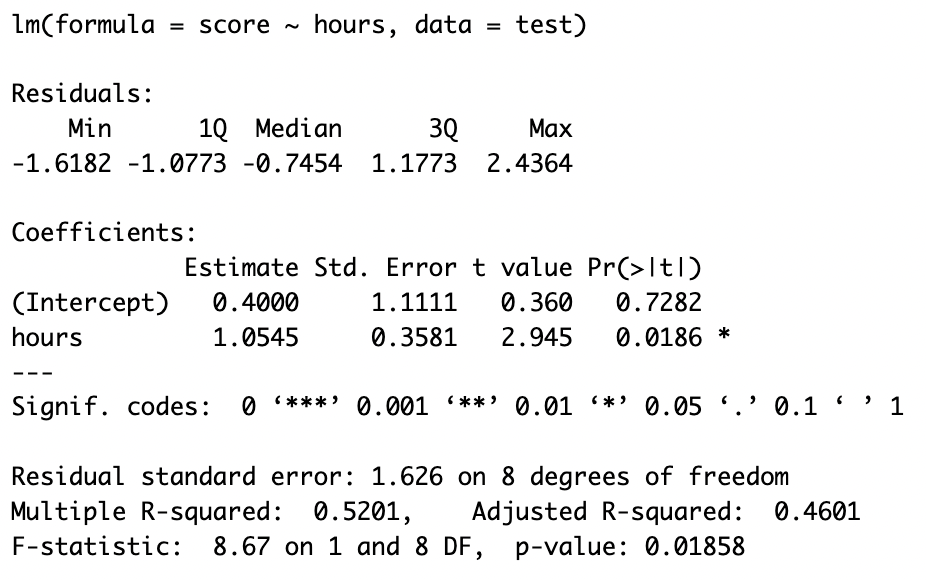
lm in R

  • You also saw the basic structure of the lm() function:
lm(DV ~ IV, data = datasetName)


  • And we ran our first model:
lm(score ~ hours, data = test)

Call:
lm(formula = score ~ hours, data = test)

Coefficients:
(Intercept)        hours  
       0.40         1.05


  • This week, we are going to focus on the interpretation of our model, and how we extend it to include more predictors

lm in R

summary(lm(score ~ hours, data = test))

Call:
lm(formula = score ~ hours, data = test)

Residuals:
   Min     1Q Median     3Q    Max 
-1.618 -1.077 -0.746  1.177  2.436 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)    0.400      1.111    0.36    0.728  
hours          1.055      0.358    2.94    0.019 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.63 on 8 degrees of freedom
Multiple R-squared:  0.52,  Adjusted R-squared:  0.46 
F-statistic: 8.67 on 1 and 8 DF,  p-value: 0.0186

Interpretation

  • Intercept is the expected value of Y when X is 0

    • X = 0 is a student who does not study
    • As the intercept is 0.4000, we conclude that a student who does not study would be expected to score 0.40 on the test


  • Slope is the number of units by which Y increases, on average, for a unit increase in X

    • Unit of Y = 1 point on the test
    • Unit of X = 1 hour of study
    • As the slope for hours is 1.0545, we conclude that for every hour of study, test score increases on average by 1.055 points

Note of Caution on Intercepts

  • In our example, 0 has a meaning

    • It is a student who has studied for 0 hours

  • But it is not always the case that 0 is meaningful

  • Suppose our predictor variable was not hours of study, but age


Imagine the model has age as a predictor variable instead of the number of hours studied. How would we interpret an intercept of 0.4?

  • This is a general lesson about interpreting statistical tests:
    • The interpretation is always in the context of the constructs and how we have measured them

Practice with Scales of Measurement (1)

Imagine a model looking at the association between an employee’s salary and their duration of employment

  • \(x\) = unit is 1 year
  • \(y\) = unit is £1000
  • \(\beta_1\) = 0.4
  • How do we interpret:
    • \(\beta_0\)?
    • \(\beta_1\)?

For reference/hint:

  • \(\beta_0\) = Intercept is the expected value of Y when X is 0

  • \(\beta_1\) = Slope is the number of units by which Y increases, on average, for a unit increase in X

Practice with Scales of Measurement (2)

Imagine a model looking at the association between the length of cats’ tails and their weight

  • \(x\) = unit is 1kg
  • \(y\) = unit is 1cm
  • \(\beta_1\) = -3.2
  • How do we interpret:
    • \(\beta_0\)?
    • \(\beta_1\)?

For reference/hint:

  • \(\beta_0\) = Intercept is the expected value of Y when X is 0

  • \(\beta_1\) = Slope is the number of units by which Y increases, on average, for a unit increase in X

Practice with Scales of Measurement (3)

Imagine a model looking at the association between healthy eating habits and personality

  • \(x\) = unit is 1 increment on a Likert scale ranging from 1 to 5 measuring conscientiousness
  • \(y\) = unit is 1 increment on a healthy eating scale
  • \(\beta_1\) = 0.25
  • How do we interpret:
    • \(\beta_0\)?
    • \(\beta_1\)?

For reference/hint:

  • \(\beta_0\) = Intercept is the expected value of Y when X is 0

  • \(\beta_1\) = Slope is the number of units by which Y increases, on average, for a unit increase in X

Part 2: Standardisation

Unstandardised vs Standardised Coefficients

  • So far we have calculated unstandardised \(\hat \beta_1\)
    • This means we use the units of the variables we measured
    • We interpreted the slope as the change in \(y\) units for a unit change in \(x\) , where the unit is determined by how we have measured our variables
  • However, sometimes these units are not helpful for interpretation
    • We can then perform standardisation to aid interpretation

Standardised Units

Why might standard units be useful?

  • If the scales of our variables are arbitrary
    • Example: A sum score of questionnaire items answered on a Likert scale.
    • A unit here would equal moving from e.g. a 2 to 3 on one item
    • This is not especially meaningful (and actually has A LOT of associated assumptions)
  • If we want to compare the effects of variables on different scales
    • If we want to say something like “the effect of \(x_1\) is stronger than the effect of \(x_2\)”, we need a common scale

Option 1: Standardising the Coefficients

  • After calculating a \(\hat \beta_1\), it can be standardised by:

\[\hat{\beta_1^*} = \hat \beta_1 \frac{s_x}{s_y}\]

  • where:
    • \(\hat{\beta_1^*}\) = standardised beta coefficient
    • \(\hat \beta_1\) = unstandardised beta coefficient
    • \(s_x\) = standard deviation of \(x\)
    • \(s_y\) = standard deviation of \(y\)

Implementing in R

  • Step 1: Obtain coefficients from the model
m1 <- lm(score~hours, data = test)
summary(m1)$coefficients
            Estimate Std. Error t value Pr(>|t|)
(Intercept)     0.40      1.111    0.36   0.7282
hours           1.05      0.358    2.94   0.0186


  • Step 2: Take the slope coefficient and standardise it
round(1.054545 * (sd(test$hours)/sd(test$score)),3)
[1] 0.721

Option 2: Standardising the Variables

  • Another option is to transform continuous predictor and outcome variables to \(z\)-scores (mean=0, SD=1) prior to fitting the model

  • If both \(x\) and \(y\) are standardised, our model coefficients (betas) are standardised too

  • \(z\)-score for \(x\):

\[z_{x_i} = \frac{x_i - \bar{x}}{s_x}\]

  • and the \(z\)-score for \(y\):

\[z_{y_i} = \frac{y_i - \bar{y}}{s_y}\]

  • That is, we divide the individual deviations from the mean by the standard deviation

Implementing in R

  • Step 1: Convert predictor and outcome variables to z-scores (here using the scale function)
test <- test |>
  mutate(
    z_score = scale(score, center = T, scale = T),
    z_hours = scale(hours, center = T, scale = T) 
  )


  • center = T
    • indicates \(x\) should be mean centered

\[z_{x_i} = \frac{\color{#BF1932}{x_i - \bar{x}}}{s_x}\]

  • scale = T
    • indicates \(x\) should be divided by \(s_x\)

\[z_{x_i} = \frac{x_i - \bar{x}}{\color{#BF1932}{s_x}}\]


  • Step 2: Run model on z-scored variables
performance_z <- lm(z_score ~ z_hours, data = test) 
round(summary(performance_z)$coefficients,3)
            Estimate Std. Error t value Pr(>|t|)
(Intercept)    0.000      0.232    0.00    1.000
z_hours        0.721      0.245    2.94    0.019

Option 2: Standardising the Variables (Alternative)

  • Another option is to not transform the variables and save to your dataset, but instead scale the variables directly in the model.

  • The defaults for center and scale are both TRUE.

performance_z2 <- lm(scale(score) ~ scale(hours), data = test)
round(summary(performance_z2)$coefficients,3)
             Estimate Std. Error t value Pr(>|t|)
(Intercept)     0.000      0.232    0.00    1.000
scale(hours)    0.721      0.245    2.94    0.019

Interpreting Standardised Regression Coefficients

Unstandardised

Standardised

  • \(R^2\) , \(F\) and \(t\)-test and their corresponding \(p\)-values remain the same for the standardised coefficients as for unstandardised coefficients

  • \(\beta_0\) (intercept) = zero when all variables are standardised:

\[\beta_0 = \bar{y}-\hat \beta_1\bar{x}\]

\[\bar{y} - \hat \beta_1 \bar{x} = 0 - \hat \beta_1 0 = 0\]

Interpreting Standardised Regression Coefficients

  • The interpretation of the slope coefficient(s) becomes the increase in \(y\) in standard deviation units for every standard deviation increase in \(x\)

  • So, in our example:

For every standard deviation increase in hours of study, test score increases by 0.72 standard deviations

Which Should we use?

  • Unstandardised regression coefficients are often more useful when the variables are on meaningful scales
    • E.g. X additional hours of exercise per week adds Y years of healthy life
  • Sometimes it’s useful to obtain standardised regression coefficients
    • When the scales of variables are arbitrary
    • When there is a desire to compare the effects of variables measured on different scales
  • Cautions
    • Just because you can put regression coefficients on a common metric doesn’t mean they can be meaningfully compared
    • The SD is a poor measure of spread for skewed distributions, therefore, be cautious of their use with skewed variables

Relationship to Correlation ( \(r\) )

  • If a linear model has a single, continuous predictor, then the standardised slope ( \(\hat \beta_1^*\) ) = correlation coefficient ( \(r\) )


  • For example:
round(lm(z_score ~ z_hours, data = test)$coefficients, 2)
(Intercept)     z_hours 
       0.00        0.72 


round(cor(test$hours, test$score),2)
[1] 0.72

Relationship to Correlation ( \(r\) )

  • They are equivalent:
    • \(r\) is a standardised measure of linear association
    • \(\hat \beta_1^*\) is a standardised measure of the linear slope
  • Similar idea for linear models with multiple predictors
    • Slopes are now equivalent to the part correlation coefficient

Part 3: Multiple Regression

Multiple Predictors

  • The aim of a linear model is to explain variance in an outcome

  • In simple linear models, we have a single predictor, but the model can accommodate (in principle) any number of predictors

  • If we have multiple predictors for an outcome, those predictors may be correlated with each other

  • A linear model with multiple predictors finds the optimal prediction of the outcome from several predictors, taking into account their redundancy with one another

Uses of Multiple Regression

  • For prediction: multiple predictors may lead to improved prediction

  • For theory testing: often our theories suggest that multiple variables together contribute to variation in an outcome

  • For covariate control: we might want to assess the effect of a specific predictor, controlling for the influence of others

    • E.g., effects of personality on health after removing the effects of age and gender

Extending the Regression Model

  • Our model for a single predictor:

\[y_i = \beta_0 + \beta_1 \cdot x_{1i} + \epsilon_i\]

  • is extended to include additional \(x\)’s:

\[y_i = \beta_0 + \beta_1 \cdot x_{1i} + \beta_2 \cdot x_{2i} + \beta_3 \cdot x_{3i} + \epsilon_i\]

  • For each \(x\), we have an additional \(\beta\)
    • \(\beta_1\) is the coefficient for the 1st predictor
    • \(\beta_2\) for the second etc.

Interpreting Coefficients in Multiple Regression

\[y_i = \beta_0 + \beta_1 \cdot x_{1i} + \beta_2 \cdot x_{2i} + ... + \beta_j \cdot x_{ji} + \epsilon_i\]

  • Given that we have additional variables, our interpretation of the regression coefficients changes a little

  • \(\beta_0\) = the predicted value for \(y\) when all \(x\) are 0

  • Each \(\beta_j\) is now a partial regression coefficient

    • It captures the change in \(y\) for a one unit change in \(x\) when all other x’s are held constant

What Does Holding Constant Mean?

  • Refers to finding the effect of the predictor when the values of the other predictors are fixed

  • It may also be expressed as the effect of controlling for, or partialling out, or residualising for the other \(x\)’s

  • With multiple predictors lm isolates the effects and estimates the unique contributions of predictors

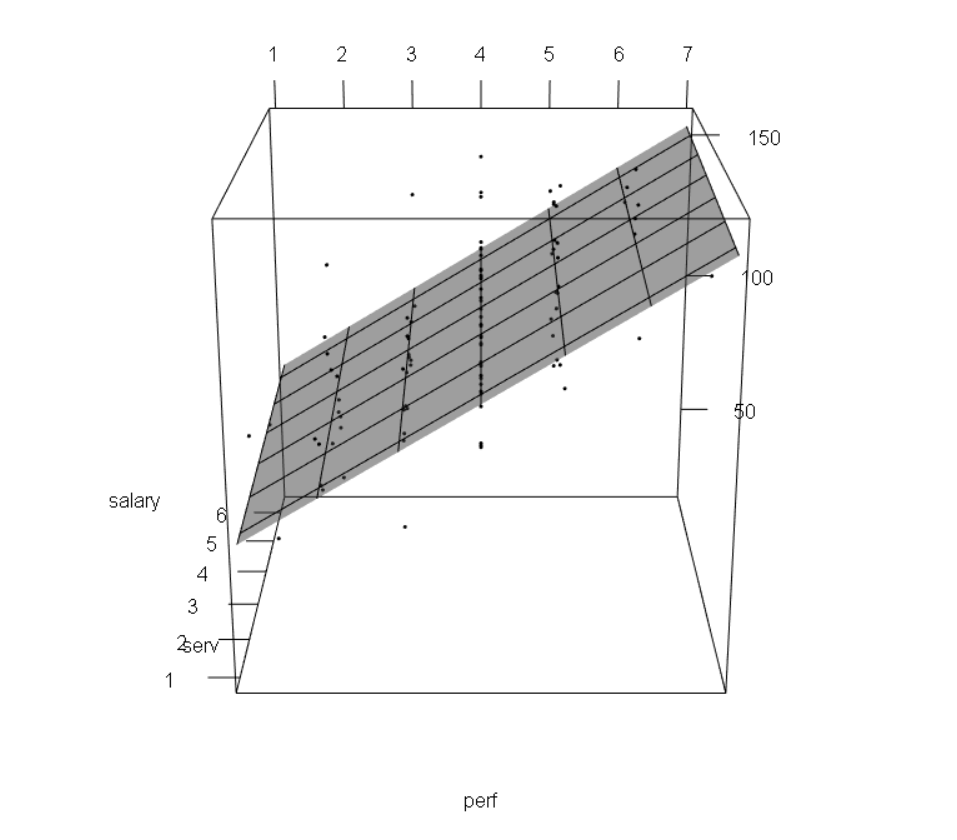
Visualising Models

A linear model with one continuous predictor

A linear model with two continuous predictors

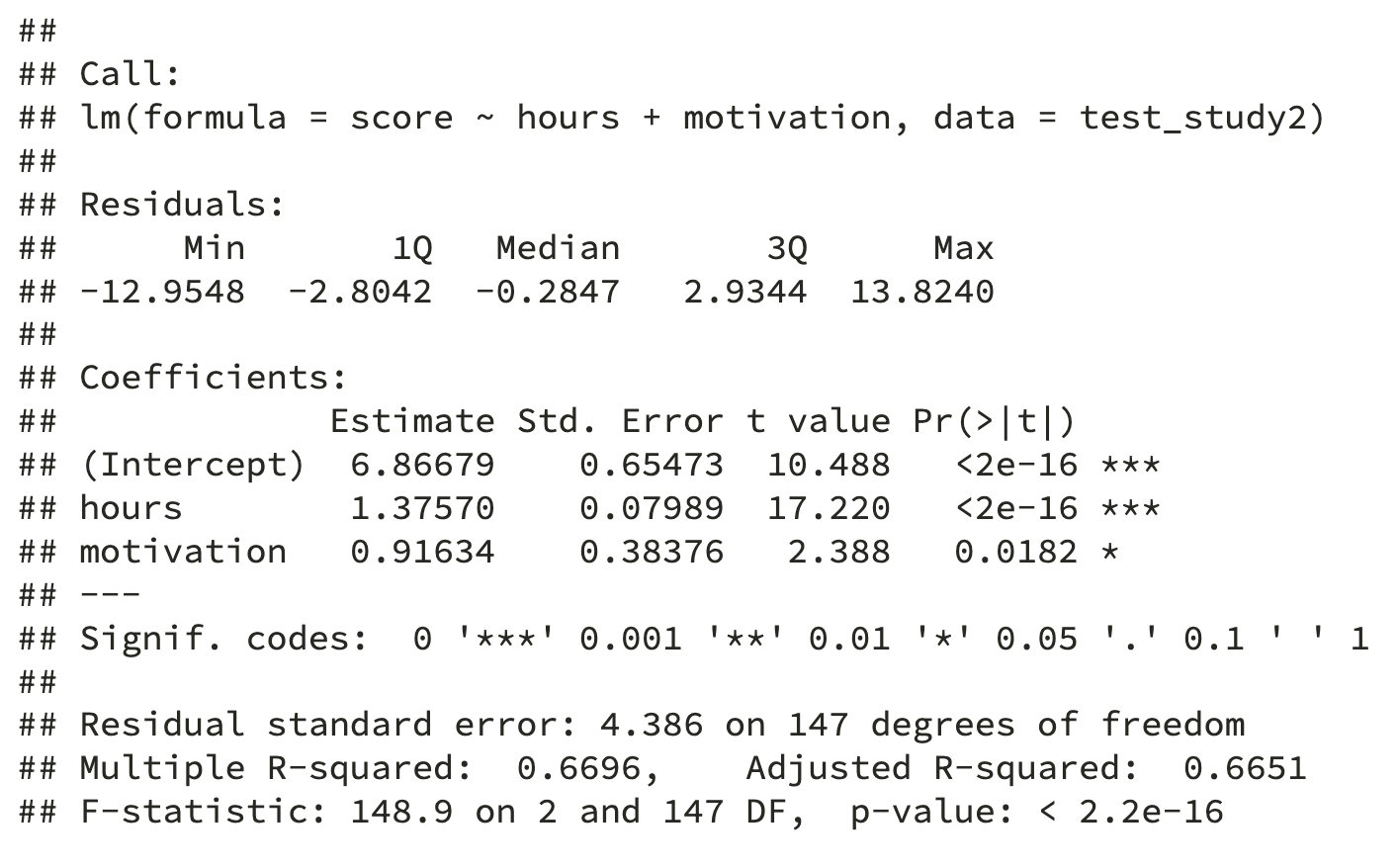
Example: lm with 2 Predictors

  • Imagine we extend our study of test scores

  • We sample 150 students taking a multiple choice Biology exam (max score 40)

  • We give all students a survey at the start of the year measuring their school motivation

    • We standardise this variable so the mean is 0, negative numbers are low motivation, and positive numbers high motivation

  • We then measure the hours they spent studying for the test, and record their scores on the test

Data

head(test_study2)
     ID score hours motivation
1 ID101     7     2      -1.42
2 ID102    23    12      -0.41
3 ID103    17     4       0.49
4 ID104     6     2       0.24
5 ID105    12     2       0.09
6 ID106    24    12       1.05

lm code

  • Multiple predictors are separated by + in the model specification
performance <- lm(score ~ hours + motivation,
          data = test_study2)

Walk-Through of Multiple Regression

  • Let’s run our model and illustrate the application of the linear model equation

\[\text{Score}_i = \color{blue}{\beta_0} + \color{blue}{\beta_1} \cdot \color{orange}{\text{Hours}_{i}} + \color{blue}{\beta_2} \cdot \color{orange}{\text{Motivation}_{i}} + \color{blue}{\epsilon_i}\]

  • values of the linear model (coefficients)

  • values we provide (inputs)

Walk-Through of Multiple Regression

  • Let’s run our model and illustrate the application of the linear model equation

\[\text{Score}_i = \color{blue}{\beta_0} + \color{blue}{\beta_1} \cdot \color{orange}{\text{Hours}_{i}} + \color{blue}{\beta_2} \cdot \color{orange}{\text{Motivation}_{i}} + \epsilon_i\]

round(residuals(performance)[1],2)
    1 
-1.32


  • \(\color{blue}{\beta_0} = 6.87\)
  • \(\color{blue}{\beta_1} = 1.38\)
  • \(\color{blue}{\beta_2} = 0.92\)
  • \(\color{blue}{\epsilon} = -1.32\)
  • Applied to individual ID 101:
test_study2[1,]
     ID score hours motivation
1 ID101     7     2      -1.42


  • \(\color{orange}{y} = 7\)
  • \(\color{orange}{x_1} = 2\)
  • \(\color{orange}{x_2} = -1.42\)

\[7 = 6.87 + (1.38 \times 2) + (0.92 \times -1.42) + (-1.32)\]

Multiple Regression Coefficients

res <- summary(performance)
round(res$coefficients,2)
            Estimate Std. Error t value Pr(>|t|)
(Intercept)     6.87       0.65   10.49     0.00
hours           1.38       0.08   17.22     0.00
motivation      0.92       0.38    2.39     0.02


What is the interpretation of the…

  • intercept coefficient?
  • A student who did not study, and who has average school motivation would be expected to score 6.87 on the test
  • slope for hours?
  • Controlling for students’ level of motivation, for every additional hour studied, there is a 1.38 points increase in test score
  • slope for motivation?
  • Controlling for hours of study, for every SD unit increase in motivation, there is a 0.92 points increase in test score

Summary

  • We run linear models using lm() in R
  • The intercept is the value of \(Y\) when \(X\) = 0
  • The slope is the unit change in \(Y\) for each unit change in \(X\)
  • In certain cases, we may standardise our variables; this will affect their interpretation
  • We can easily add more predictors to our model
  • When we do, our interpretations of the coefficients are when all other predictors are held constant

This Week


Tasks

Attend your lab and work together on the exercises


Complete the weekly quiz

Support

Help each other on the Piazza forum


Attend office hours (see Learn page for details)