Chi-square Tests

class: center, middle, inverse, title-slide

# <b>Chi-square Tests </b>
## Data Analysis for Psychology in R 1<br><br>
### dapR1 Team
### Department of Psychology<br>The University of Edinburgh
### AY 2020-2021

---

# Weeks Learning Objectives
1. Understand how to perform a `$\chi^2$` goodness-of-fit and interpret the results.

2. Understand how to perform a `$\chi^2$` test of independence and interpret the results.

3. Conduct and interpret the assumption checks for `$\chi^2$` tests.

---
# Topics for today

- Recording 1: 
  - Types of `$\chi^2$` test
  - Worked example of `$\chi^2$` goodness-of-fit
  - Relative, observed and expected frequencies

- Recording 2: 
  - Worked example of `$\chi^2$` goodness-of-fit
  - Inferential testing, and write up.

- Recording 3: 
  - Worked example of `$\chi^2$` test of independence.

- Recording 4: 
  - Residuals, assumptions and effect size measures.

- Bonus slides: For those who are interested, the full calculations for recording 2 are given in slides.

---
# Purpose
- `$\chi^2$` goodness of fit test
  - The primary purpose is to test whether the collected data (observed frequencies) are consistent with a hypothesized/known distribution (expected frequencies).

- `$\chi^2$` test of independence:
  - We have 2 categorical variables, drawn from a single population.
  - We want to know if the variables are independent or not.
  - If the category membership is dependent, then knowing what category someone is in on variable 1, helps us predict what category they would be in for variable 2.

---
# Data Requirements
- `$\chi^2$` goodness of fit test
  - Single categorical variable
  
- `$\chi^2$` test of independence:
  - Two categorical variables.
 
---
# Example: Goodness of fit
- Suppose we are interested in the distribution of students across three final year psychology options (Social, Differential, Developmental).

- We have data from 2014-15, and we want to know if the distribution is the same in 2015-16.

---
# Data

```r
head(class)
```

```
## # A tibble: 6 x 2
##   ID    course       
##   <chr> <fct>        
## 1 ID1   Differential 
## 2 ID2   Social       
## 3 ID3   Social       
## 4 ID4   Social       
## 5 ID5   Social       
## 6 ID6   Developmental
```

- `ID` = Unique ID variable
- `course` = factor with 3 levels (Social, Differential, Developmental)

---
# Observed frequencies

```r
tab1 <- class %>%
  group_by(course) %>%
  tally()
```

```r
tab1
```

```
## # A tibble: 3 x 2
##   course            n
##   <fct>         <int>
## 1 Differential     28
## 2 Social           62
## 3 Developmental    60
```

---
# Relative frequencies
- In 2014-15, the department had the following proportions:
  - Social = 0.50, or 50%
  - Differential = 0.30, or 30%
  - Developmental = 0.20, or 20%

---
# Relative frequencies

```r
tab1 <- tab1 %>%
  transmute(
    course = course,
    relative = c(0.30, 0.50, 0.20),
    observed = n
  )
```

```r
tab1
```

```
## # A tibble: 3 x 3
##   course        relative observed
##   <fct>            <dbl>    <int>
## 1 Differential       0.3       28
## 2 Social             0.5       62
## 3 Developmental      0.2       60
```

---
# Expected frequencies
- Given this, and a total number of students (n=150) for the current year, we can calculate the expected frequencies for each area.
  - `$Expected = Relative*N$`

---
# Put it together

```r
tab1 <- tab1 %>%
  mutate(
    expected = relative*sum(observed)
  )
```

```r
tab1
```

```
## # A tibble: 3 x 4
##   course        relative observed expected
##   <fct>            <dbl>    <int>    <dbl>
## 1 Differential       0.3       28       45
## 2 Social             0.5       62       75
## 3 Developmental      0.2       60       30
```

---
class: center, middle
# Time for a break

---
class: center, middle
# Welcome Back!

**Now we have discussed how to calculate the core values from our data, let's think about our hypotheses, test statistic, and inferential testing.**

---
# Hypotheses
$$
`\begin{matrix}
H_0 = P(0.20, 0.50, 0.30) \\
H_1 \neq P(0.20, 0.50, 0.30)
\end{matrix}`
$$

- `$H_0$` says that the data follow a specific and known pattern or probabilities (frequencies)
- `$H_1$` says they don't

---
# Test statistic

$$
\chi^2 = \sum_{i=1}^{k} \frac{(E_i - O_i)^2}{E_i}
$$

- `$E_i$` = expected frequencies
- `$O_i$` = observed frequencies
- `$\sum_{i=1}^{k}$` = do the calculation starting from cell 1 through to cell `$k$` (k=number groups) and add them up.

---
# Null Distribution
- Sampling distribution for `$\chi^2$` test is a `$\chi^2$` distribution.

- `$\chi^2$` distribution describes the distribution of the sum of `$k$` squared independent standard normal variables.
  - Huh?
  
$$
\chi^2 = \sum_{i=1}^{k} \frac{(E_i - O_i)^2}{E_i}
$$

---
# Null Distribution
- Parameter of the `$\chi^2$` distribution is degrees of freedom (df) 
  - Just like `$t$`-test.
  
- df are determined by the number of categories ( `$k$` )

- Goodness of fit test has `$k-1$` degrees of freedom.
  - Why?

---
# Null Distribution

.pull-left[
![](dapR1_lec19_Chisquare_files/figure-html/unnamed-chunk-9-1.png)

]

.pull-right[

- The plot shows `$\chi^2$` distributions for 2 (black), 3 (red), and 5 (blue) df's

- Note that as the df increase, the area under the curve for smaller values increases.

- What does that mean?
  - It means as we add up more things, we would expect the random fluctuations from 0 to to also increase.
  - In any given sample, even if the null is true in the population, sampling variability would mean we have some non-zero values.
  - So we need to account for this.

]

---
# Calculation

```r
tab1 <- tab1 %>%
  mutate(
    step1 = expected - observed,
    step2 = step1^2,
    step3 = step2/expected
  )
tab1
```

```
## # A tibble: 3 x 7
##   course        relative observed expected step1 step2 step3
##   <fct>            <dbl>    <int>    <dbl> <dbl> <dbl> <dbl>
## 1 Differential       0.3       28       45    17   289  6.42
## 2 Social             0.5       62       75    13   169  2.25
## 3 Developmental      0.2       60       30   -30   900 30
```

- Step1 = `$E_i - O_i$`
- Step2 = `$(E_i - O_i)^2$`
- Step3 = `$\frac{(E_i - O_i)^2}{E_i}$`

---
# Calculation
- Last step is to sum the values for step 3 to get the `$\chi^2$`

```r
x2 <- sum(tab1$step3)
x2
```

```
## [1] 38.67556
```

---
# Is my test significant?
- `$\chi^2$` = 38.68

- Degrees of freedom = 3-1 = 2

- `$\alpha$` = 0.05

---
# Is my test significant?

![](dapR1_lec19_Chisquare_files/figure-html/unnamed-chunk-12-1.png)

---
# Is my test significant?

```r
tibble(
  CritValue = round(qchisq(0.95, 2),2),
  Exactp = round(1-pchisq(x2, 2),5)
)
```

```
## # A tibble: 1 x 2
##   CritValue Exactp
##       <dbl>  <dbl>
## 1      5.99      0
```

---
# In R

```r
gof_res <- chisq.test(tab1$observed, p = c(0.3, 0.5, 0.2))
gof_res
```

```
## 
## 	Chi-squared test for given probabilities
## 
## data:  tab1$observed
## X-squared = 38.676, df = 2, p-value = 3.997e-09
```

---
# Write up

A `$\chi^2$` goodness of fit test was conducted in order to investigate whether the distribution of students across Social, Developmental and Differential classes was equivalent in 2014- 15 and 2015-16. The goodness of fit test was significant ( `$\chi^2$`(2) = 38.68, `$p$`<.05) and thus the null hypothesis was rejected. The distribution of student's across courses differs between the two academic years.

---
class: center, middle
# Time for a break

---
class: center, middle
# Welcome Back!

**We will now follow the same steps for a test of independence.**

---
# Example: Independence
- I have conducted an experiment with three conditions (n=120, 40 per group)

- I want to check whether my participants are equally distributed based on some demographic variables.
  - Let's focus on whether English is participants first language

- Recall from an experimental design perspective, I want such things to be randomized across my groups.
  - So I would expect an even distribution.

---
# Data

```r
head(exp)
```

```
## # A tibble: 6 x 3
##   ID    condition lang 
##   <chr> <chr>     <chr>
## 1 ID1   control   Yes  
## 2 ID2   control   No   
## 3 ID3   control   No   
## 4 ID4   control   Yes  
## 5 ID5   control   No   
## 6 ID6   control   No
```

- `ID` = Unique ID variable
- `condition` = experimental conditions (control, group1, group2)
- `lang` = binary Yes/No for English as first language

---
# Tabular format

- It can be very useful to display data for two categorical variables as a contingency table.

```r
tabs <- addmargins(table(exp$condition, exp$lang))
tabs
```

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

---
# Visualizing Data: Mosaic Plot

.pull-left[

```r
#install.packages("ggmosaic")
#library(ggmosaic)

ggplot(data = exp) +
  geom_mosaic(aes(x = product(condition, lang), fill = condition)) +
  labs(x = "\n First Language", y = "")
```

]

.pull-right[
![](dapR1_lec19_Chisquare_files/figure-html/unnamed-chunk-19-1.png)

]

---
# Hypotheses

.pull-left[
$$
`\begin{matrix}
H_0: P_{11} = P_{12}, P_{21} = P_{22}, P_{31} = P_{32} \\
H_1: P_{11} \neq P_{12} | P_{21} \neq P_{22} | P_{31} \neq P_{32}
\end{matrix}`
$$

- `$H_0$` says the proportion of each cell in each row are equal.

- `$H_1$` says at least one of these pairs are not equal.

]

.pull.right[

<table class="table" style="width: auto !important; margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;">  </th>
   <th style="text-align:left;"> No </th>
   <th style="text-align:left;"> Yes </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> Control </td>
   <td style="text-align:left;"> P11 </td>
   <td style="text-align:left;"> P12 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Group1 </td>
   <td style="text-align:left;"> P21 </td>
   <td style="text-align:left;"> P22 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Group2 </td>
   <td style="text-align:left;"> P31 </td>
   <td style="text-align:left;"> P32 </td>
  </tr>
</tbody>
</table>

]

---
# Intuition about the null

.pull-left[

![](dapR1_lec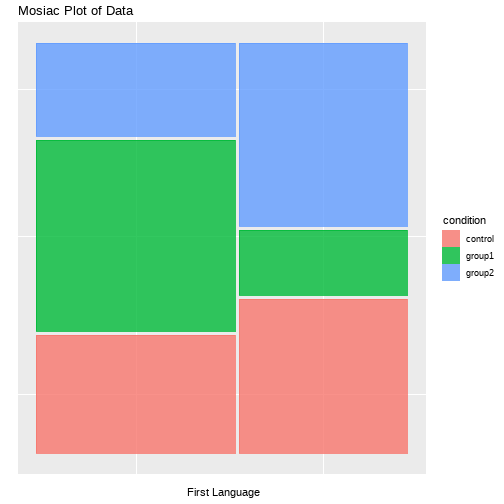19_Chisquare_files/figure-html/unnamed-chunk-21-1.png)

]

.pull-left[

![](dapR1_lec19_Chisquare_files/figure-html/unnamed-chunk-22-1.png)

]

---
# Test statistic
- The test statistic looks much the same as the statistic for the GoF test.

`$$\chi^2 = \sum_{i=1}^{r}\sum_{i=1}^{c} \frac{(\hat{E_{ij}} - O_{ij})^2}{\hat{E_{ij}}}$$`

- What is different?
  - `$\sum_{i=1}^{r}\sum_{i=1}^{c}$` simply means sum the quantities for all cells in all rows (r) and columns (c)
  - But why `$\hat{E_{ij}}$`? Why the hat?

---
# Expected frequencies
- Remember in the GoF test we knew the expected frequencies because we had known proportions and known sample size.
  - Here we do not have that.
  
- So we have to estimate the expected frequencies from the data. 
  - Hence we use `$\hat{E}$` to show this is an estimate.
  
`$$\hat{E_{ij}} = \frac{R_iC_j}{N}$$`

- Where
  - `$R_i$` = the row marginal for a cell `$i$`
  - `$C_i$` = the column marginal for a cell `$j$`
  - `$N$` = total sample size

- Here we will show the calculation for one cell (for the cell by cell calculations see the additional material).

---
# Calculation: Controls-No

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\hat{E_{11}} = \frac{R_1C_1}{N} = \frac{40*65}{120} = \frac{2600}{120} = 21.67 \\$$`

`$$\frac{(\hat{E_{11}} - O_{11})^2}{\hat{E_{11}}} = \frac{(21.67 - 19)^2}{21.67} = \frac{7.1289}{21.67} = 0.33$$`

---
# Null Distribution
- Again, we evaluate the `$\chi^2$` test of independence statistic against the `$\chi^2$`-distribution.

- Here:

$$
df = (r-1)(c-1)
$$

- Note, `$r$` and `$c$` are just the number of levels for each categorical variable.

- In our example `$(r-1)(c-1)=(3-1)(2-1)=2*1=2$`
  - Thus using the same `$\alpha$`=0.05, we would have the same critical value = 5.99

---
# In R

```r
con <- table(exp$condition, exp$lang)
ind_res <- chisq.test(con)
ind_res
```

```
## 
## 	Pearson's Chi-squared test
## 
## data:  con
## X-squared = 13.964, df = 2, p-value = 0.0009286
```

---
# Write up
A `$\chi^2$` test of independence was performed to examine whether the distribution of English first language speakers was consistent across experimental conditions (n=120). The relation between these variables was significant ($\chi^2$(2) = 13.96, p <.05). Therefore, we reject the null hypothesis.

---
class: center, middle
# Time for a break

**For your mid-lecture exercise, please look over the full calculations of the test statistic for this example in the additional slides.**

---
class: center, middle
# Welcome Back!

**Our last recording for this week will look at cell residuals, assumptions, corrections and effect size.**

---
# Output
- Here I want to make brief comment about analysis objects.

- The object `ind_res` contains the output of our analysis.
  - This has lots of elements to it.

- We can view and work with these by using the $ sign

```r
names(ind_res)
```

```
## [1] "statistic" "parameter" "p.value"   "method"    "data.name" "observed" 
## [7] "expected"  "residuals" "stdres"
```

---
# Residuals
- For example, lets look at the residuals.

- The Pearson residuals tell us which cells in the contingency table had the greatest differences.

```r
ind_res$residuals
```

```
##          
##                   No        Yes
##   control -0.5728919  0.6227992
##   group1   2.0051216 -2.1797970
##   group2  -1.4322297  1.5569979
```

---
# Assumptions
- Sufficiently large N to approximate a normal sampling distribution
  - We saw last semester this actually begins to happen pretty fast.

- Expected and observed cell frequencies are sufficiently large.
  - If either drop below 5, then there is not really enough data.

- Each observation appears in only 1 cell.
  - Data are independent.
  - If data are dependent, we can use a McNemar test.

---
# Yate's correction
- Our `$\chi^2$` test only approximates a `$\chi^2$` sampling distribution.

- When we have a 2x2 table with df=1, it turns out this approximation is not very good.
  - So for 2x2 tables we apply Yate’s continuity correction.
  - This subtracts 0.5 from each cell deviation.
  - It is the default in R when we have a 2x2 table.

---
# Effect size
- Three possibilities:
  - Phi coefficient (for 2x2 tables)
  - Odds ratios
  - Cramer's V
  
- We will discuss odds ratios more in year 2, so let's look at Phi and Cramer's V.

---
# Effect size
- The equations for both measures are shown below:

`$$Phi = \sqrt{\frac{\chi^2}{N}}$$`

`$$CramerV = \sqrt{\frac{\chi^2}{N*min(r-1,c-1)}}$$`

- Cramer's V generalizes Phi to larger contingency tables.

---
# Cramer's V
- There is no base R calculation for Cramer's V.

- It is included in the `lsr` package for the Navarro book.

- Else we can construct it ourselves.

---
# Cramer's V

```r
CV = sqrt(ind_res$statistic /
    (length(exp$ID) * 
       (min(length(unique(exp$condition)),
            length(unique(exp$lang))
            ) - 1)))
CV
```

```
## X-squared 
## 0.3411211
```

---
# Summary of today
- We have looked at tests for categorical data:
  1. Against a known distribution
  2. As a test of independence.
  
- We have considered the calculations, inferential tests, and interpretations.

---
class: center, middle
# Additional Materials

---
# Full calculations

```r
ind_res
```

```
## 
## 	Pearson's Chi-squared test
## 
## data:  con
## X-squared = 13.964, df = 2, p-value = 0.0009286
```

- Let's do all the steps to calculate `$\chi^2$` and the exact `$p$`-value.

---
# Full calculations
- Let's start with the expected values

$$
\hat{E_{ij}} = \frac{R_iC_j}{N}
$$

---
# Full calculations

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

$$
\hat{E_{11}} = \frac{R_1C_1}{N} = \frac{40*65}{120} = \frac{2600}{120} = 21.67 \\
$$

- As we have the same number of participants in each condition, this is also the expected value for `$\hat{E_{21}}$` and `$\hat{E_{31}}$`

---
# Full calculations

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

$$
\hat{E_{12}} = \frac{R_1C_2}{N} = \frac{40*55}{120} = \frac{2200}{120} = 18.33 \\
$$

- As we have the same number of participants in each condition, this is also the expected value for `$\hat{E_{22}}$` and `$\hat{E_{23}}$`

---
# Full calculations
- We can check these against the information in the output to the R analysis

```r
ind_res$expected
```

```
##          
##                 No      Yes
##   control 21.66667 18.33333
##   group1  21.66667 18.33333
##   group2  21.66667 18.33333
```

---
# Full calculations
- Now, the `$\chi^2$`

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\frac{(\hat{E_{11}} - O_{11})^2}{\hat{E_{11}}} = \frac{(21.67 - 19)^2}{21.67} = \frac{7.1289}{21.67} = 0.33$$`

---
# Full calculations
- Now, the `$\chi^2$`

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\frac{(\hat{E_{21}} - O_{21})^2}{\hat{E_{21}}} = \frac{(21.67 - 31)^2}{21.67} = \frac{87.05}{21.67} = 4.02$$`

---
# Full calculations
- Now, the `$\chi^2$`

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\frac{(\hat{E_{31}} - O_{31})^2}{\hat{E_{31}}} = \frac{(21.67 - 15)^2}{21.67} = \frac{44.49}{21.67} = 2.05$$`

---
# Full calculations
- Now, the `$\chi^2$`

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\frac{(\hat{E_{12}} - O_{12})^2}{\hat{E_{12}}} = \frac{(18.33 - 21)^2}{18.33} = \frac{7.1289}{18.33} = 0.39$$`

---
# Full calculations
- Now, the `$\chi^2$`

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\frac{(\hat{E_{22}} - O_{22})^2}{\hat{E_{22}}} = \frac{(18.33 - 9)^2}{18.33} = \frac{87.05}{18.33} = 4.75$$`

---
# Full calculations
- Now, the `$\chi^2$`

```
##          
##            No Yes Sum
##   control  19  21  40
##   group1   31   9  40
##   group2   15  25  40
##   Sum      65  55 120
```

`$$\frac{(\hat{E_{32}} - O_{32})^2}{\hat{E_{32}}} = \frac{(18.33 - 25)^2}{18.33} = \frac{44.49}{18.33} = 2.43$$`

---
# Full calculations
- Last step is to add them up:

`$$\chi^2 = \sum_{i=1}^{r}\sum_{i=1}^{c} \frac{(\hat{E_{ij}} - O_{ij})^2}{\hat{E_{ij}}}$$`

```r
x2i <- 0.33 + 4.02 + 2.05 + 0.39 + 4.75 + 2.43
x2i
```

```
## [1] 13.97
```

---
# Full calculations
- And check against the R results (tiny bit of rounding error)

```r
ind_res
```

```
## 
## 	Pearson's Chi-squared test
## 
## data:  con
## X-squared = 13.964, df = 2, p-value = 0.0009286
```

---
# Full calculations
- And the p-value

```r
1 - pchisq(13.964, 2)
```

```
## [1] 0.0009284445
```

---
# Full calculations
- The Pearson's residuals are calculated as:

`$$Residual_{ij} = \frac{(E_{ij} - O_{ij})}{\sqrt{E_{ij}}}$$`

---
# Full calculations
- So let's do one residual and then look at the output of our analysis:

`$$Residual_{11} = \frac{(E_{11} - O_{11})}{\sqrt{E_{11}}} = \frac{(21.67 - 19)}{\sqrt{21.67}} = \frac{2.67}{4.655105} = 0.57$$`

```r
ind_res$residuals
```

```
##          
##                   No        Yes
##   control -0.5728919  0.6227992
##   group1   2.0051216 -2.1797970
##   group2  -1.4322297  1.5569979
```

---
# Full calculations
- Hold on....why is our calculation positive, and the R results negative?

- This is just an interpretation point.
  - In our calculation, we have used `$E_{ij} - O_{ij}$`
  - If instead we calculate `$O_{ij} - E_{ij}$`, then we would get the same absolute value but negative.
  - Why not try it.