class: center, middle, inverse, title-slide # <b>Lecture 10: Samples, Statistics & Sampling Distributions </b> ## Data Analysis for Psychology in R 1<br><br> ### TOM BOOTH & ALEX DOUMAS ### Department of Psychology<br>The University of Edinburgh ### AY 2020-2021 --- # Week's Learning Objectives 1. Understand the difference between a population parameter and a sample statistic. 2. Understand the concept and construction of sampling distributions. 3. Understand the effect of sample size on the sampling distribution. 4. Understand how to quantify the variability of a sample statistic and sampling distribution (standard error). --- # Topics for today - Understand the concept principles sampling from populations. - Be familiar with the specific statistical terminology for sampling. - Understand the concept of a sampling distribution. --- ## Concepts to carry forward - Data can be of different types. - Dependent on type (continuous vs. categorical), we can visualise and describe the distribution of data differently. - When thinking about events ("things happening") we can assign probabilities to the event. - We can define a probability distribution that describes the probability of all possible events. --- ## In Psych Stats - In psychology, we design a study, to calculate a value that carries some meaning. - Reaction time of one group vs another. - Given it has meaning based on the study design, we want to know something about the number: - Is it unusual or not? - This is the task for the next 4-5 weeks. --- ## Today - We will talk about populations, samples, and sampling. - Basic concepts of sampling may seem simple and intuitive. - These concepts will be very useful when we start talking about statistical inference. - Statistical inference = how we make decisions about data. --- ## A question - Suppose I wanted to know the proportion of UG students at the University of Edinburgh were born in Scotland? - In stats talk, all UG at the UoE are our **population**. - The proportion of students born in Scotland is the **population parameter** (the thing we are interested in). - What is the best way to find this out exactly? - What else might we do? --- ## What is a sample? - A sample is a portion of the population that you check. - Use the sample as an estimate of the real population --- ## Parameters and point-estimates - Key idea: - There is population parameter (proportion of Scottish born students at UoE) we are interested in. This is a *true* value of the world. - We can draw a sample, and calculate this proportion (statistic) in the sample. - In a single sample, this **point-estimate** is our best guess at the population parameter. - We might use something like our class as a sample to estimate the true value in the University. --- ## 2017/18 actual proportion <table class="table table-striped" style="width: auto !important; margin-left: auto; margin-right: auto;"> <thead> <tr> <th style="text-align:left;"> Scottish </th> <th style="text-align:right;"> n </th> <th style="text-align:right;"> Freq </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> No </td> <td style="text-align:right;"> 13926 </td> <td style="text-align:right;"> 0.54 </td> </tr> <tr> <td style="text-align:left;"> Yes </td> <td style="text-align:right;"> 12025 </td> <td style="text-align:right;"> 0.46 </td> </tr> </tbody> </table> - Let's assume this is the true value now (it was in 17/18). - As we've just said, we can draw samples from the population and use it to estimate the population value. - A **sampling distribution** is a probability distribution of some statistic obtained from sampling the population. - If we draw a bunch of samples from the population, each is an estimate of the real population value. - Let's simulate drawing a bunch of samples of students from the University and see what proportion of each sample is born in Scotland. - We'll draw 10 samples of 10 students from the population. - We then create a histogram showing how frequently our samples showed particular proportions of students born in Scotland... --- ## Visualizing sampling distributions <!-- --> --- ## Visualizing sampling distributions <!-- --> --- ## Visualizing sampling distributions <!-- --> --- ## Sampling distributions (2) - We have just created three sampling distributions. - Each of these look different. - Each sampling distribution is characterising the **sampling variability** in our **estimate** of the **parameter** of interest (proportion of Scottish students at UoE). - What do we notice? - Do samples with values close to the population value tend to be more or less likely? --- ## More samples - So far we have taken 10 samples. - What if we took more? --- ## More samples <!-- --> --- ## More samples <!-- --> --- ## More samples <!-- --> - What do you notice about the plots on the last three slides? --- ## Frequency = probability - At this point lets pause and remember some things from probability. - When we spoke about probability, we spoke about the relation to frequency. - If something did not happen very often, it has a lower probability. - Now think about our sampling distributions of the proportion of Scottish students. --- ## Frequency gives us probability .pull-left[ <!-- --> ] .pull-right[ <!-- --> ] --- ## Bigger samples <!-- --> - So above is a frequency distribution for `\(n\)`=10. - Let's see what happens when we make `\(n\)` bigger. --- ## Bigger samples <!-- --> --- ## Bigger samples <!-- --> - What do you notice about the last three slides? --- ## Properties of sampling distributions - Remember: frequency distributions are characterising the variability in sample estimates. - Variability can be thought of as the spread in data/plots. - So as we increase `\(n\)` we are getting less variable samples (harder to get an unrepresentative sample as your `\(n\)` increases). --- ## Properties of sampling distributions - Let's put this phenomenon in the language of probability: as `\(n\)` increases, the probability of observing an estimate in a sample that is a long way from the population parameter (here 0.46) decreases (becomes less probable). - So when we have large samples, our estimates from those samples are likely to be closer to the population value. - That's good! --- ## Standard error - We can formally calculate the "narrowness" of a sampling distribution. - This is essentially calculating the standard deviation (as we have done before) of the sampling distribution. - Or at least approximating it! - In the context of sampling distributions, this is called the **standard error** --- ## Mean & SE of sampling distribution - Mean of the sampling distribution is close to the population parameter. - Even with a small number of samples. - As the number of samples increases: - The mean of the sampling distribution approaches the population mean. - The sampling distribution approaches a normal distribution. - Point-estimates pile up around the population value. - As the n per sample increases, the SE of the sampling distribution decreases (becomes narrower). - With large n, all our point-estimates are closer to the population parameter. --- ## Central Limit Theorem - What we have seen throughout this lecture is a demonstration of an important concept in statistics - namely, **central limit theorem**. - The central limit theorem (roughly) states that when estimates of sample means are based on increasingly large samples ($n$), the sampling distribution of means becomes more normal (symmetric), and narrower (quantified by the standard error). --- ## Central limit theorem - We have briefly noted CLT before. To refresh; - The Central Limit Theorem states that the sampling distribution of the sample means from any underlying distribution with a defined mean and variance, approaches a normal distribution as the sample size gets larger. - The resultant sampling distribution has: - `\(\bar{x} = \mu\)` - `\(\sigma_{\bar{x}}^{2} = \frac{\sigma^2}{N}\)` - `\(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{N}}\)` --- ## Uniform distribution - Continuous probability distribution. - There is an equal probability for all values within a given range. - Parameters: - `\(a(min)\)` and `\(b(max)\)` $$ Mean = \frac{1}{2}(a+b) $$ - And $$ Variance = \frac{1}{12}(b-a)^2 $$ --- ## Uniform distribution <!-- --> --- ## Uniform distribution .pull-left[ <img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-15-1.png" width="60%" /><img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-15-2.png" width="60%" /> ] .pull-right[ <img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-16-1.png" width="60%" /><img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-16-2.png" width="60%" /> ] --- ## Chi-square distribution - Continuous probability distribution - Non-symmetric - Parameters = degrees of freedom $$ Mean = df $$ - and $$ Variance = 2*df $$ --- ## Chi-square distribution <!-- --> --- ## Chi-square distribution .pull-left[ <img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-19-1.png" width="60%" /><img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-19-2.png" width="60%" /> ] .pull-right[ <img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-20-1.png" width="60%" /><img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-20-2.png" width="60%" /> ] --- ## t-distribution - Continuous probability distribution. - Symmetric and uni-modal (similar to the normal distribution). - "Heavier tails" = greater chance of observing a value further from the mean - Parameters: - `\(\nu = n-1\)` $$ Mean = 0, \nu>1 $$ - and $$ Variance = \frac{\nu}{\nu - 2}, \nu > 2 $$ --- ## t-distribution 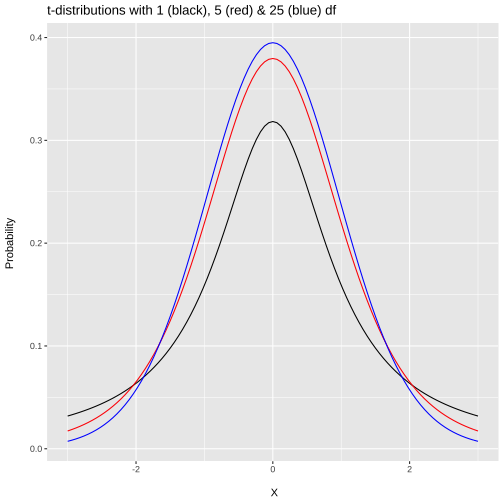<!-- --> --- ## t-distribution .pull-left[ <img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-23-1.png" width="60%" /><img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-23-2.png" width="60%" /> ] .pull-right[ <img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-24-1.png" width="60%" /><img src="dapR1_lec10_Samples-SamplingDist_files/figure-html/unnamed-chunk-24-2.png" width="60%" /> ] --- ## Sampling distributions - `\(\chi^2\)` distribution, *t*-distribution and binomial distribution are all commonly used for statistical inference. - What the CLT demonstrations above show, is that we can often use the normal distribution as an approximation of the sampling distribution. --- ## Standard error - One of the big points we have emphasized is sampling variability is characterized by the SD of the sampling distribution. - But how do we obtain this from a single sample? - We have already seen the answer thanks to CLT. - In the limit, the sampling distribution has: - `\(\bar{x} = \mu\)` - `\(\sigma_{\bar{x}}^{2} = \frac{\sigma^2}{N}\)` - `\(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{N}}\)` = standard error --- ## Key terminology - **Census**: process of asking every member of a population. - **Sampling**: process of selecting subsets of populations. - **Population**: the complete set of units of interest. - **Sample**: A subset of the population --- ## Key terminology - **Parameter**: value of of interest in the population. - **Point estimate**: our "best guess" at the parameter of interest from a sample. - **Sampling distribution**: the distribution of estimates of the population parameter. - **Standard error**: quantification of the variation in estimates. --- ## Features of samples - Is our sample... - Biased? - Representative? - Random? --- ## Good samples - If a sample of `\(n\)` is drawn at random, it will be unbiased and representative of `\(N\)` - Our point estimates from such samples will be good guesses at the population parameter. - Without the need for census. --- # Summary of today - Samples are used to estimate the population. - Samples provide point estimates of population parameters. - Properties of samples and sampling distributions. - Properties of good samples. --- # Next tasks + Look back over any material from term. + This week: + Complete your lab + Come to office hours + Come to Q&A session + Weekly quiz - on week 10 (lect 9) content + Open Tuesday 09:00 + Closes Monday 17:00